 定積分
定積分
 定積分
定積分
福田の数学〜早稲田大学2022年人間科学部第6問〜楕円を軸以外の直線で回転させた立体の体積

単元:
#数Ⅱ#大学入試過去問(数学)#平面上の曲線#微分法と積分法#接線と増減表・最大値・最小値#微分とその応用#積分とその応用#2次曲線#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{6}}$直線$x+y=1$に接する楕円$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a \gt 0,\ b \gt 0)$がある。
このとき、$b^2=\boxed{\ \ ア\ \ }\ a^2+\boxed{\ \ イ\ \ }$である。
この楕円を直線$y=b$のまわりに1回転してできる立体の体積は、
$a=\frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$のとき、
最大値$\frac{\boxed{\ \ オ\ \ }\sqrt{\boxed{\ \ カ\ \ }}}{\boxed{\ \ キ\ \ }}\pi^2$をとる。
2022早稲田大学人間科学部過去問
この動画を見る
${\large\boxed{6}}$直線$x+y=1$に接する楕円$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a \gt 0,\ b \gt 0)$がある。
このとき、$b^2=\boxed{\ \ ア\ \ }\ a^2+\boxed{\ \ イ\ \ }$である。
この楕円を直線$y=b$のまわりに1回転してできる立体の体積は、
$a=\frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$のとき、
最大値$\frac{\boxed{\ \ オ\ \ }\sqrt{\boxed{\ \ カ\ \ }}}{\boxed{\ \ キ\ \ }}\pi^2$をとる。
2022早稲田大学人間科学部過去問
AkiyaMathさんと学ぶ積分計算 Level 2 【難】#定積分
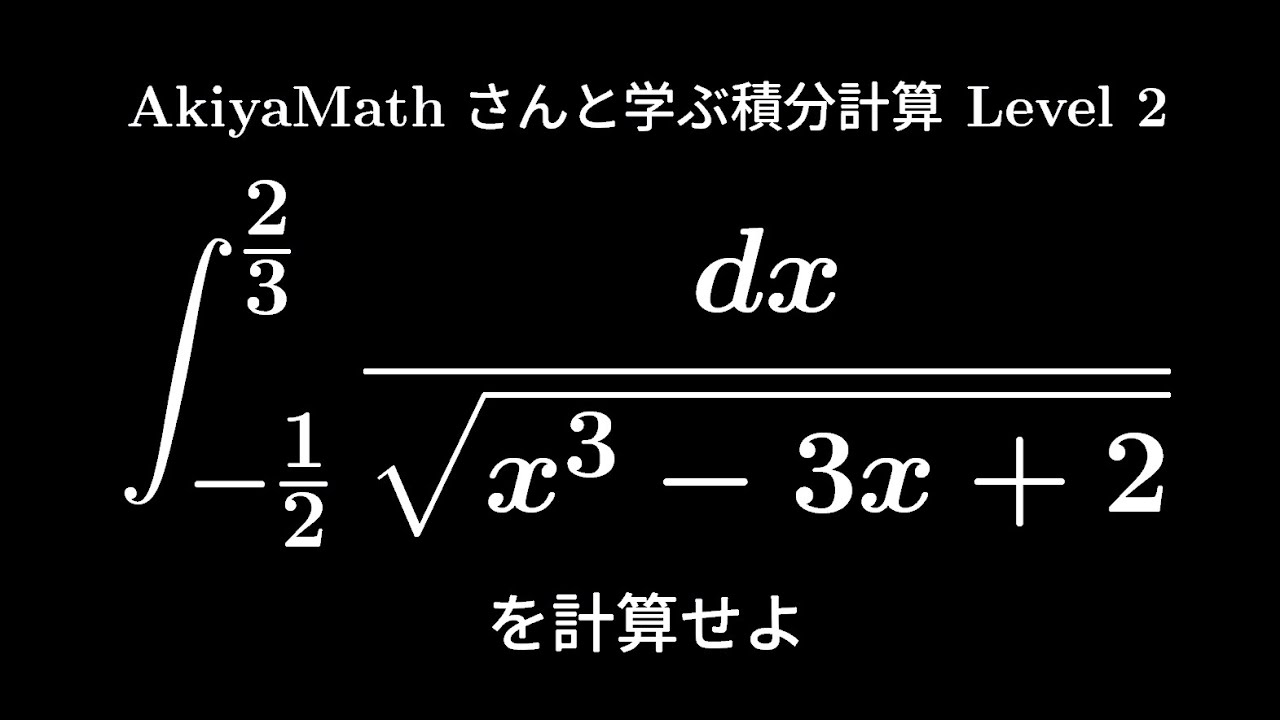
単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{1}{2}}^{\frac{2}{3}}\displaystyle \frac{dx}{\sqrt{ x^3-3x+2 }}$を求めよ。
この動画を見る
$\displaystyle \int_{-\frac{1}{2}}^{\frac{2}{3}}\displaystyle \frac{dx}{\sqrt{ x^3-3x+2 }}$を求めよ。
AkiyaMathさんと学ぶ積分計算 Level 1 #定積分

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{1}{2}}^{\frac{3}{2}}\displaystyle \frac{dx}{x^3-3x+2}$を計算せよ
この動画を見る
$\displaystyle \int_{-\frac{1}{2}}^{\frac{3}{2}}\displaystyle \frac{dx}{x^3-3x+2}$を計算せよ
大学入試問題#254 神戸大学2012 #定積分
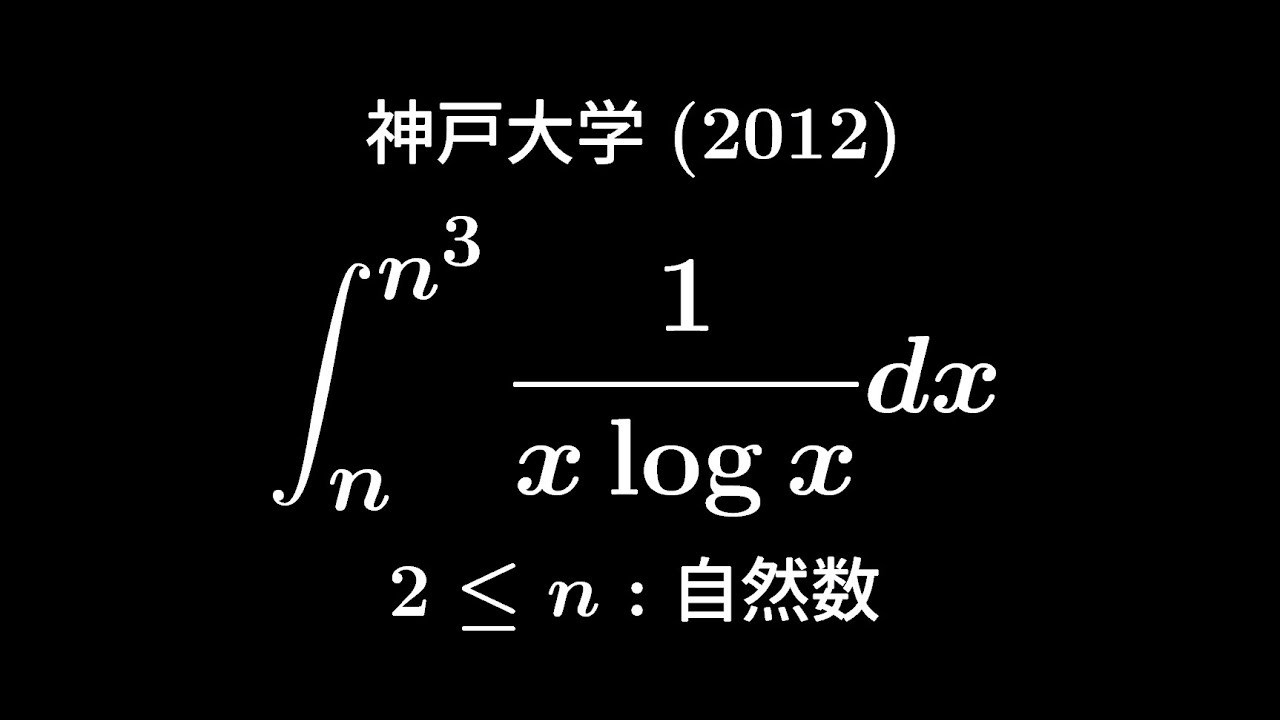
単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#積分とその応用#定積分#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$2 \leqq n$自然数
$\displaystyle \int_{n}^{n^3}\displaystyle \frac{dx}{x\ log\ x}$を計算せよ。
出典:2012年神戸大学 入試問題
この動画を見る
$2 \leqq n$自然数
$\displaystyle \int_{n}^{n^3}\displaystyle \frac{dx}{x\ log\ x}$を計算せよ。
出典:2012年神戸大学 入試問題
大学入試問題#253 青山学院大学(2011) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2\pi}x(\sin\ x+\cos\ 2x)dx$を計算せよ。
出典:2011年青山学院大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{2\pi}x(\sin\ x+\cos\ 2x)dx$を計算せよ。
出典:2011年青山学院大学 入試問題
大学入試問題#252 茨城大学(2012) #定積分

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#指数関数と対数関数#対数関数#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{log2}e^{|x|}e^xdx$を計算せよ。
出典:2012年茨城大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{log2}e^{|x|}e^xdx$を計算せよ。
出典:2012年茨城大学 入試問題
大学入試問題#250 福井大学(2012) #定積分
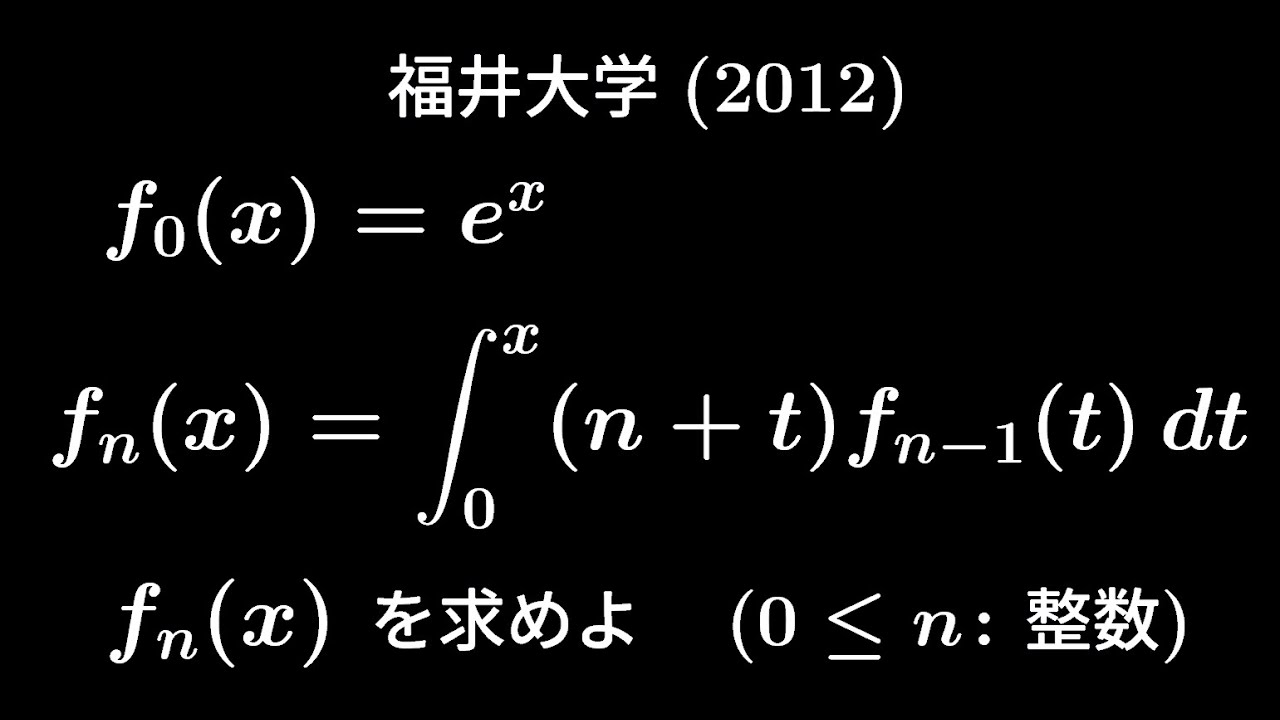
単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#数列#漸化式#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#福井大学#数B#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$n$を0以上の整数とする。
次の2つの条件をみたす関数$f_n(x)$を求めよ。
(ⅰ)$f_0(x)=e^x$
(ⅱ)$f_n(x)=\displaystyle \int_{0}^{x}(n+t)f_{n-1}(t)dt$
出典:2012年福井大学 入試問題
この動画を見る
$n$を0以上の整数とする。
次の2つの条件をみたす関数$f_n(x)$を求めよ。
(ⅰ)$f_0(x)=e^x$
(ⅱ)$f_n(x)=\displaystyle \int_{0}^{x}(n+t)f_{n-1}(t)dt$
出典:2012年福井大学 入試問題
大学入試問題#249 早稲田大学(2014) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#積分とその応用#定積分#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a,b$を正の定数
$\displaystyle \int_{0}^{2\pi}|a\ \sin\ x+b\ \cos\ x|dx$を求めよ。
出典:2014年早稲田大学 入試問題
この動画を見る
$a,b$を正の定数
$\displaystyle \int_{0}^{2\pi}|a\ \sin\ x+b\ \cos\ x|dx$を求めよ。
出典:2014年早稲田大学 入試問題
大学入試問題#244 南山大学(2014) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#南山大学
指導講師:
ますただ
問題文全文(内容文):
$a$:正の定数
$\displaystyle \int_{-a}^{a}\displaystyle \frac{|x|e^x}{(1+e^x)^2}dx$を計算せよ
出典:2014年南山大学 入試問題
この動画を見る
$a$:正の定数
$\displaystyle \int_{-a}^{a}\displaystyle \frac{|x|e^x}{(1+e^x)^2}dx$を計算せよ
出典:2014年南山大学 入試問題
大学入試問題#242 神戸大学(2015) 改 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{6}}\displaystyle \frac{2x\ \sin\ x}{\cos^2x}$dxを計算せよ。
出典:2015年神戸大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{6}}\displaystyle \frac{2x\ \sin\ x}{\cos^2x}$dxを計算せよ。
出典:2015年神戸大学 入試問題
大学入試問題#239 弘前大学(2012) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{3}(x-\displaystyle \frac{1}{x})(log\ x)^2dx$を計算せよ。
出典:2012年
この動画を見る
$\displaystyle \int_{1}^{3}(x-\displaystyle \frac{1}{x})(log\ x)^2dx$を計算せよ。
出典:2012年
【誘導有:概要欄】大学入試問題#238 首都大学東京(2012) #定積分
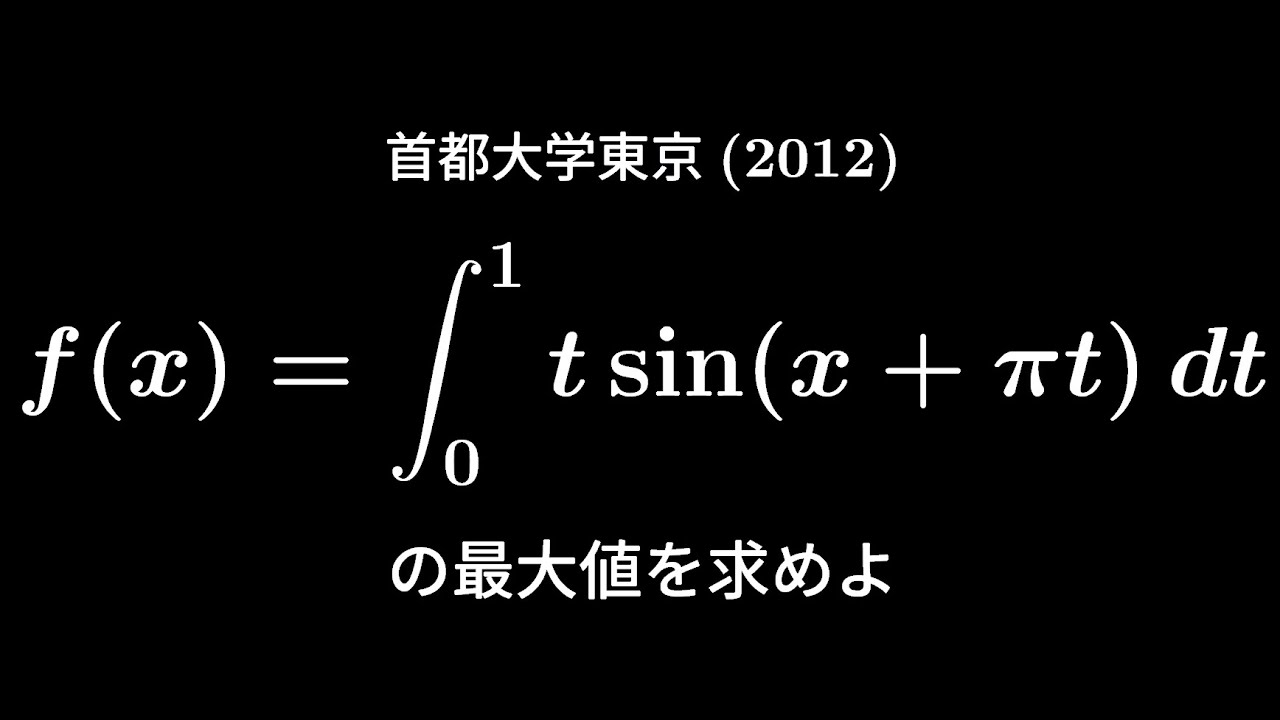
単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
(1)
実数$x$に対して定積分$f(x)=\displaystyle \int_{0}^{1}t\ \sin(x+\pi t)dt$を求めよ。
(2)
関数$f(x)$の最大値を求めよ。
出典:2012年首都大学東京 入試問題
この動画を見る
(1)
実数$x$に対して定積分$f(x)=\displaystyle \int_{0}^{1}t\ \sin(x+\pi t)dt$を求めよ。
(2)
関数$f(x)$の最大値を求めよ。
出典:2012年首都大学東京 入試問題
大学入試問題#234 東京理科大学 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{3}{4}\pi}\sqrt{ 1-\cos\ 4x }\ dx$
出典:2012年東京理科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{3}{4}\pi}\sqrt{ 1-\cos\ 4x }\ dx$
出典:2012年東京理科大学 入試問題
#53 数検1級1次 過去問 #微分方程式

単元:
#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{dx}{dt}=2x+4y ・・・① \\
\displaystyle \frac{dy}{dt}=x-y ・・・②
\end{array}
\right.
\end{eqnarray}$
$x(0)=3,\ y(0=-1)$を満たす解を求めよ。
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{dx}{dt}=2x+4y ・・・① \\
\displaystyle \frac{dy}{dt}=x-y ・・・②
\end{array}
\right.
\end{eqnarray}$
$x(0)=3,\ y(0=-1)$を満たす解を求めよ。
#52 数検1級1次試験 過去問 #微分方程式

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$x\displaystyle \frac{dy}{dx}+y=(log\ x)^2$
$y(1)=1$をみたす解を$y=y(x)$で表せ
この動画を見る
$x\displaystyle \frac{dy}{dx}+y=(log\ x)^2$
$y(1)=1$をみたす解を$y=y(x)$で表せ
大学入試問題#230 首都大学東京(2020) #定積分

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\displaystyle \frac{1}{(x^2+1)^3}dx$
出典:2020年首都大学東京 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{1}{(x^2+1)^3}dx$
出典:2020年首都大学東京 入試問題
大学入試問題#225 埼玉大学 #定積分
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}}\displaystyle \frac{\cos\theta\sin\theta}{\cos^4\theta+\sin^4\theta}d\theta$
$t=\tan^2\theta$で変数変換
出典:埼玉大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}}\displaystyle \frac{\cos\theta\sin\theta}{\cos^4\theta+\sin^4\theta}d\theta$
$t=\tan^2\theta$で変数変換
出典:埼玉大学 入試問題
大学入試問題#223 宮崎大学(2015) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\displaystyle \frac{x^3+3x^2}{x^2+3x+2}\ dx$
出典:2015年宮崎大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{x^3+3x^2}{x^2+3x+2}\ dx$
出典:2015年宮崎大学 入試問題
大学入試問題#221 横浜国立大学(2015) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\sqrt{ \frac{\pi}{2} }}x^3\cos(x^2)dx$を計算せよ
出典:2015年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\sqrt{ \frac{\pi}{2} }}x^3\cos(x^2)dx$を計算せよ
出典:2015年横浜国立大学 入試問題
大学入試問題#220 東海大学医学部【再投稿】 #定積分 #King property

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東海大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\pi}x(\cos^2x)(\sin\ x)dx$
出典:東海大学医学部 入試問題
この動画を見る
$\displaystyle \int_{0}^{\pi}x(\cos^2x)(\sin\ x)dx$
出典:東海大学医学部 入試問題
大学入試問題#219 京都大学? (2016) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a_n=\displaystyle \int_{\sqrt{ 3 }}^{2\sqrt{ 2 }}\displaystyle \frac{x^{2n-1}}{\sqrt{ x^2+1 }}\ dx$
$a_1,\ a_2$を求めよ。
出典:2016年京都大学 入試問題
この動画を見る
$a_n=\displaystyle \int_{\sqrt{ 3 }}^{2\sqrt{ 2 }}\displaystyle \frac{x^{2n-1}}{\sqrt{ x^2+1 }}\ dx$
$a_1,\ a_2$を求めよ。
出典:2016年京都大学 入試問題
福田の数学〜九州大学2022年文系第4問〜定義に従って定積分の性質を証明する

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#微分法と積分法#恒等式・等式・不等式の証明#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#九州大学
指導講師:
福田次郎
問題文全文(内容文):
定積分について述べた次の文章を読んで、後の問いに答えよ。
$f(x)$を整式とする。$F'(x)=f(x)$となる$F(x)$を1つ選び、
$f(x)$のaからbまでの定積分を
$#\int_a^bf(x)dx=F(b)-F(a)\ldots①$
で定義する。定積分の値はF(x)の選び方によらずに定まる。
定積分は次の性質(A),(B),(C)をもつ。
(A)$\int_a^b\left\{kf(x)+lg(x)\right\}dx=k\int_a^bf(x)dx+l\int_a^bg(x)dx$
(B)$a \leqq c \leqq b$のとき、$\int_a^cf(x)dx+\int_c^bf(x)dx=\int_a^bf(x)dx$
(C)区間$a \leqq x \leqq b$において$g(x) \geqq h(x)$ならば、$\int_a^bg(x)dx \geqq \int_a^bh(x)dx$
ただし、f(x),g(x),h(x)は整式、k,lは定数である。
以下、$f(x)$が区間$0 \leqq x \leqq 1$上で増加関数になる場合を考える。
$n$を自然数とする。定積分の性質$\boxed{\ \ ア\ \ }$を用い、定数関数に対する定積分の計算を行うと、
$\frac{1}{n}f(\frac{i-1}{n}) \leqq \int_{\frac{i-1}{n}}^{\frac{i}{n}}f(x)dx \leqq \frac{1}{n}f(\frac{i}{n}) (i = 1,2,\ldots,n) \ldots②$
が成り立つことがわかる。$S_n=\frac{1}{n}\sum_{i=1}^nf(\frac{i-1}{n})$とおくと、
不等式②と定積分の性質$\boxed{\ \ イ\ \ }$より次の不等式が成り立つ。
$0 \leqq \int_0^1f(x)dx-S_n \leqq \frac{f(1)-f(0)}{n} \ldots③$
よって、$n$を限りなく大きくすると$S_n$は$\int_0^1f(x)dx$に限りなく近づく。
(1)関数F(x),G(x)が微分可能であるとき、$\left\{F(x)+G(x)\right\}'=F'(x)+G'(x)$が
成り立つことと定積分の定義①を用いて、性質(A)で$k=l=1$とした場合の等式
$\int_a^b\left\{f(x)+g(x)\right\}dx=\int_a^bf(x)dx+\int_a^bg(x)dx$ を示せ。
(2)定積分の定義①と関数の増減と導関数の関係を用いて、次を示せ。
$a \lt b$のとき、区間$a \leqq x \leqq b$において$g(x) \gt 0$ならば、$\int_a^bg(x)dx \gt 0$
(3)(A),(B),(C)のうち、空欄$\boxed{\ \ ア\ \ }$に入る記号として最もふさわしいものを
1つ選び答えよ。また、文章中の下線部の内容を詳しく説明することで、
不等式②を示せ。
(4)(A),(B),(C)のうち、空欄$\boxed{\ \ イ\ \ }$に入る記号として最もふさわしいものを
1つ選び答えよ。また、不等式③を示せ。
2022九州大学文系過去問
この動画を見る
定積分について述べた次の文章を読んで、後の問いに答えよ。
$f(x)$を整式とする。$F'(x)=f(x)$となる$F(x)$を1つ選び、
$f(x)$のaからbまでの定積分を
$#\int_a^bf(x)dx=F(b)-F(a)\ldots①$
で定義する。定積分の値はF(x)の選び方によらずに定まる。
定積分は次の性質(A),(B),(C)をもつ。
(A)$\int_a^b\left\{kf(x)+lg(x)\right\}dx=k\int_a^bf(x)dx+l\int_a^bg(x)dx$
(B)$a \leqq c \leqq b$のとき、$\int_a^cf(x)dx+\int_c^bf(x)dx=\int_a^bf(x)dx$
(C)区間$a \leqq x \leqq b$において$g(x) \geqq h(x)$ならば、$\int_a^bg(x)dx \geqq \int_a^bh(x)dx$
ただし、f(x),g(x),h(x)は整式、k,lは定数である。
以下、$f(x)$が区間$0 \leqq x \leqq 1$上で増加関数になる場合を考える。
$n$を自然数とする。定積分の性質$\boxed{\ \ ア\ \ }$を用い、定数関数に対する定積分の計算を行うと、
$\frac{1}{n}f(\frac{i-1}{n}) \leqq \int_{\frac{i-1}{n}}^{\frac{i}{n}}f(x)dx \leqq \frac{1}{n}f(\frac{i}{n}) (i = 1,2,\ldots,n) \ldots②$
が成り立つことがわかる。$S_n=\frac{1}{n}\sum_{i=1}^nf(\frac{i-1}{n})$とおくと、
不等式②と定積分の性質$\boxed{\ \ イ\ \ }$より次の不等式が成り立つ。
$0 \leqq \int_0^1f(x)dx-S_n \leqq \frac{f(1)-f(0)}{n} \ldots③$
よって、$n$を限りなく大きくすると$S_n$は$\int_0^1f(x)dx$に限りなく近づく。
(1)関数F(x),G(x)が微分可能であるとき、$\left\{F(x)+G(x)\right\}'=F'(x)+G'(x)$が
成り立つことと定積分の定義①を用いて、性質(A)で$k=l=1$とした場合の等式
$\int_a^b\left\{f(x)+g(x)\right\}dx=\int_a^bf(x)dx+\int_a^bg(x)dx$ を示せ。
(2)定積分の定義①と関数の増減と導関数の関係を用いて、次を示せ。
$a \lt b$のとき、区間$a \leqq x \leqq b$において$g(x) \gt 0$ならば、$\int_a^bg(x)dx \gt 0$
(3)(A),(B),(C)のうち、空欄$\boxed{\ \ ア\ \ }$に入る記号として最もふさわしいものを
1つ選び答えよ。また、文章中の下線部の内容を詳しく説明することで、
不等式②を示せ。
(4)(A),(B),(C)のうち、空欄$\boxed{\ \ イ\ \ }$に入る記号として最もふさわしいものを
1つ選び答えよ。また、不等式③を示せ。
2022九州大学文系過去問
大学入試問題#218 東京都市大学(2019) 定積分と極限

単元:
#関数と極限#積分とその応用#数列の極限#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$n$:自然数
$a_n=\displaystyle \int_{1}^{\sqrt{ 2 }}x(2-x^2)^ndx$とおく
$\displaystyle \lim_{ n \to \infty }n\ a_n$を求めよ。
出典:2019年東京都市大学 入試問題
この動画を見る
$n$:自然数
$a_n=\displaystyle \int_{1}^{\sqrt{ 2 }}x(2-x^2)^ndx$とおく
$\displaystyle \lim_{ n \to \infty }n\ a_n$を求めよ。
出典:2019年東京都市大学 入試問題
大学入試問題#217 東京理科大学 改(2019) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e}\displaystyle \frac{(log\ x)^3}{x}(1-log\ x)^4dx$
出典:2019年東京理科大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{e}\displaystyle \frac{(log\ x)^3}{x}(1-log\ x)^4dx$
出典:2019年東京理科大学 入試問題
大学入試問題#216 宮崎大学(2017) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{3}}^{\frac{\pi}{2}}\cos^2(3x+\displaystyle \frac{\pi}{6})dx$を計算せよ。
出典:2017年宮崎大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{3}}^{\frac{\pi}{2}}\cos^2(3x+\displaystyle \frac{\pi}{6})dx$を計算せよ。
出典:2017年宮崎大学 入試問題
大学入試問題#215 宮崎大学(2011) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{2}^{3}\displaystyle \frac{x^2}{x(x+1)}$を計算せよ。
出典:2011年宮崎大学 入試問題
この動画を見る
$\displaystyle \int_{2}^{3}\displaystyle \frac{x^2}{x(x+1)}$を計算せよ。
出典:2011年宮崎大学 入試問題
大学入試問題#214 徳島大学(2014) 定積分 ウォリス積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#徳島大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}}\sin^4x\ \cos^2x\ dx$を計算せよ。
出典:2014年徳島大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}}\sin^4x\ \cos^2x\ dx$を計算せよ。
出典:2014年徳島大学 入試問題
大学入試問題#213 広島市立大学(2015) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}e^{-\sqrt{ 1-x }}dx$を計算せよ。
出典:2015年広島市立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}e^{-\sqrt{ 1-x }}dx$を計算せよ。
出典:2015年広島市立大学 入試問題
大学入試問題#212 滋賀県立大学(2017) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#滋賀県立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\sqrt{ 3 }}{2}}\sqrt{ 1-\sqrt{ 1-x^2 } }\ dx$を計算せよ
出典:2017年滋賀県立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\sqrt{ 3 }}{2}}\sqrt{ 1-\sqrt{ 1-x^2 } }\ dx$を計算せよ
出典:2017年滋賀県立大学 入試問題
大学入試問題#211 宮崎大学(2018) 定積分
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}}\sqrt{ 1+\sin\ x }\ dx$を計算せよ
出典:2018年宮崎大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}}\sqrt{ 1+\sin\ x }\ dx$を計算せよ
出典:2018年宮崎大学 入試問題
