 積分とその応用
積分とその応用
 積分とその応用
積分とその応用
【高校数学】毎日積分39日目【難易度:★★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\int_1^2\frac{logx}{1+x^2}dx $
これを解け.
この動画を見る
$\int_1^2\frac{logx}{1+x^2}dx $
これを解け.
【高校数学】毎日積分38日目【難易度:★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\int_{logπ}^{log2π}e^xsine^xdx$
これを解け.
この動画を見る
$\int_{logπ}^{log2π}e^xsine^xdx$
これを解け.
【高校数学】毎日積分37日目【難易度:★★★☆☆】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\int_0^2\frac{2x+1}{\sqrt{x^2+4}}dx$
この動画を見る
$\int_0^2\frac{2x+1}{\sqrt{x^2+4}}dx$
【高校数学】毎日積分36日目【バウムクーヘン積分って実際どれくらい便利なの!?】【毎日17時投稿】

【高校数学】毎日積分35日目【バウムクーヘン積分】【毎日17時投稿】

【高校数学】毎日積分34日目【区分求積法】【毎日17時投稿】

【高校数学】毎日積分33日目【難易度:★★★★★】【毎日17時投稿】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の等式が$1\leqq x\leqq 2$で成り立つような関数f(x)と定数A,Bを求めよ.
$\int_{\frac{1}{x}}^{\frac{2}{x}}|logy|f(xy)dy=3x(logx-1)+A+\frac{B}{x}$
ただし,f(x)は$1\leqq x\leqq 2$に対して定義される連続関数とする.(東京工業大学 2019)
この動画を見る
次の等式が$1\leqq x\leqq 2$で成り立つような関数f(x)と定数A,Bを求めよ.
$\int_{\frac{1}{x}}^{\frac{2}{x}}|logy|f(xy)dy=3x(logx-1)+A+\frac{B}{x}$
ただし,f(x)は$1\leqq x\leqq 2$に対して定義される連続関数とする.(東京工業大学 2019)
【高校数学】毎日積分30日目【難易度:★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\int_0^1\sqrt{1+2\sqrt{x}}dx$
これを解け.
この動画を見る
$\int_0^1\sqrt{1+2\sqrt{x}}dx$
これを解け.
【高校数学】毎日積分29日目【難易度:★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\int_1^4\frac{dx}{\sqrt{3-\sqrt{x}}}$
これを解け.
この動画を見る
$\int_1^4\frac{dx}{\sqrt{3-\sqrt{x}}}$
これを解け.
【高校数学】毎日積分28日目【難易度:★★★】【毎日17時投稿】

【高校数学】毎日積分27日目【難易度:★★】【毎日17時投稿】

【高校数学】毎日積分26日目【難易度:★★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\int_0^{\frac{log3}{2}}\frac{e^x+1}{e^{2x}+1}dx$
これを解け.
この動画を見る
$\int_0^{\frac{log3}{2}}\frac{e^x+1}{e^{2x}+1}dx$
これを解け.
【高校数学】毎日積分25日目【難易度:★★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\int_0^{\frac{π}{2}}x|sin^2x-\frac{1}{2}|dx$
これを解け.
この動画を見る
$\int_0^{\frac{π}{2}}x|sin^2x-\frac{1}{2}|dx$
これを解け.
【高校数学】毎日積分24日目【難易度:★★】【毎日17時投稿】

【高校数学】毎日積分23日目【難易度:★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\int_0^{\frac{π}{4}}sinθcos2θdθ$
これを解け.
この動画を見る
$\int_0^{\frac{π}{4}}sinθcos2θdθ$
これを解け.
【高校数学】毎日積分22日目【難易度:★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\int_0^{\frac{π}{4}}sin^2θcos2θdθ$
これを解け.
この動画を見る
$\int_0^{\frac{π}{4}}sin^2θcos2θdθ$
これを解け.
【高校数学】毎日積分21日目【難易度:★★★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\int_0^{\frac{π}{4}}\frac{dx}{sin^2x+3cos^2x}$
これを解け.
この動画を見る
$\int_0^{\frac{π}{4}}\frac{dx}{sin^2x+3cos^2x}$
これを解け.
【高校数学】毎日積分20日目【難易度:★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\int_0^\frac{π}{4}\frac{dx}{1+sinx}$
これを解け.
この動画を見る
$\int_0^\frac{π}{4}\frac{dx}{1+sinx}$
これを解け.
【高校数学】毎日積分19日目【難易度:★★★★】【毎日17時投稿】

【高校数学】毎日積分18日目【難易度:★★★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\int_0^{\frac{π}{4}}\frac{dx}{cos^3x}$
これを解け.
この動画を見る
$\int_0^{\frac{π}{4}}\frac{dx}{cos^3x}$
これを解け.
【高校数学】毎日積分17日目【難易度:★★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\int_0^{\frac{π}{2}}xsin^3xdx$
これを解け.
この動画を見る
$\int_0^{\frac{π}{2}}xsin^3xdx$
これを解け.
福田の数学〜空間図形の通過範囲の面積と体積〜杏林大学2023年医学部第3問後編〜空間図形の通過範囲の面積と体積

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#杏林大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$xy$平面上の単位円$C$の$x\geqq 0$に動点$P$が$A$から$B$へ移動するとき、
$P,Q$を通り頂点$T$の放物線$L$と線分$PQ$で囲まれた図形の
通過範囲の体積を求めよ。
ただし$TM=PQ$とする。
この動画を見る
$xy$平面上の単位円$C$の$x\geqq 0$に動点$P$が$A$から$B$へ移動するとき、
$P,Q$を通り頂点$T$の放物線$L$と線分$PQ$で囲まれた図形の
通過範囲の体積を求めよ。
ただし$TM=PQ$とする。
【高校数学】毎日積分16日目【難易度:★★★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\int_\frac{π}{3}^{\frac{2}{3}π}\frac{dθ}{sinθ}$
これを解け.
この動画を見る
$\int_\frac{π}{3}^{\frac{2}{3}π}\frac{dθ}{sinθ}$
これを解け.
福田の数学〜空間図形の通過範囲の面積と体積〜杏林大学2023年医学部第3問後編〜空間図形の通過範囲の面積と体積

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#杏林大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
座標空間において原点 O を中心とする半径 1 の円 C がxy平面上にあり、x> 0の領域において点 A ( 0 ,- 1 , 0 )から点 B ( 0 , 1,0 )まで移動する C 上の動点を P とする。
(1) 下記の 2 条件を満たす直角二等辺三角形 PQR を考える。
・点 Q は C 上にあり、直線 PQ はx軸に平行である。
・点 R の z 座標は正であり、直線 PR はz軸に平行である。
点 P が点 A から点 B まで移動するとき、三角形 PQR の周および内部が通過してできる立体Vについて、以下の間いに答えよ。
(a) 点 P が点 A から点 B まで移動するとき、線分 PR が通過してできる曲面の展開図は、横軸に弧 AP の長さ、縦軸に線分 PR の長さをとったグラフを考えればよく、アで表される概形となり、その面積はイである。
線分 PQ の中点を M とし、点 M から直線 QR に引いた垂線と線分 QR との交点を H とする。点 H は線分 QR を 1 :ウに内分する点である。点 P の位置に依らず、線分の長さについて$エ×(MH)^2+(OM)^2=1$が成り立つ。点Pが点 A から点 B まで移動するとき、線分 MH が通過する領域の概形はオであり、面積は$\displaystyle \frac{\sqrt{ カ }}{キ}\pi$である。
※ア、オの解答群は動画内参照
(b) 点 P が点 A から点 B まで移動するとき、線分 QR が通過してできる曲面上において、 2 点 A , B を結ぶ最も短い曲線はクが描く曲線である。
クの解答群①点 Q ②点 R ③設間( a )で考えた点 H ④線分 QR とyz平面との交点 ⑤線分 QR を 1 :$\sqrt{ 2 }$に内分する点 ⑥線分 QR を$\sqrt{ 2 }$: 1 に内分する点 ⑦三角形 PQR の重心から線分 QR に引いた垂線と線分 QR との交点
(c) 点 P が点 A から点 B まで移動するとき、線分 PQ を直径とするxz平面に平行な円が通過してできる球の体積は$\displaystyle \frac{ケ}{コ}$である。また△ PQR の面積は、線分 PQを直径とする円の面積の$\displaystyle \frac{サ}{\pi}$倍である。よって、立体Vの体積は$\displaystyle \frac{シ}{ス}$である。
( 2 )$z \geqq 0$ の領域において、yz平面上の点 T を頂点とし、 2 点 P , Q を通る放物線Lを考える。ただし、 Q , T は下記の 2 条件を満たす点とする。
・点 Q は C 上にあり、直線 PQ はx軸に平行である。
・三角形 PQT はxz平面に平行であり、点 T の z 座標は線分 PQ の長さに等しい。点 P が(1,0,0)であるとき、放物線Lを表す式はy=0,$z=セソx^2+タ$(ただし$-1 \leqq x \leqq 1$)であり、この放物線と線分 PQ で囲まれる図形の面積は$\displaystyle \frac{チ}{ツ}$である。
点 P が点 A から点 B まで移動するとき、放物線 L と線分 PQ で囲まれる図形が通過してできる立体の体積は$\displaystyle \frac{テト}{ナ}$である。
点 P が点 A から点 B まで移動するとき、線分 PQ を直径とするxz平面に平行な円が通過してできる球の体積は$\displaystyle \frac{ケ}{コ}\pi$である。また△ PQR の面積は、線分 PQ を直径とする円の面積の$\displaystyle \frac{サ}{\pi}$倍である。よって、立体体積はV の体積は$\displaystyle \frac{シ}{ス}$である。
2023杏林大学過去問
この動画を見る
座標空間において原点 O を中心とする半径 1 の円 C がxy平面上にあり、x> 0の領域において点 A ( 0 ,- 1 , 0 )から点 B ( 0 , 1,0 )まで移動する C 上の動点を P とする。
(1) 下記の 2 条件を満たす直角二等辺三角形 PQR を考える。
・点 Q は C 上にあり、直線 PQ はx軸に平行である。
・点 R の z 座標は正であり、直線 PR はz軸に平行である。
点 P が点 A から点 B まで移動するとき、三角形 PQR の周および内部が通過してできる立体Vについて、以下の間いに答えよ。
(a) 点 P が点 A から点 B まで移動するとき、線分 PR が通過してできる曲面の展開図は、横軸に弧 AP の長さ、縦軸に線分 PR の長さをとったグラフを考えればよく、アで表される概形となり、その面積はイである。
線分 PQ の中点を M とし、点 M から直線 QR に引いた垂線と線分 QR との交点を H とする。点 H は線分 QR を 1 :ウに内分する点である。点 P の位置に依らず、線分の長さについて$エ×(MH)^2+(OM)^2=1$が成り立つ。点Pが点 A から点 B まで移動するとき、線分 MH が通過する領域の概形はオであり、面積は$\displaystyle \frac{\sqrt{ カ }}{キ}\pi$である。
※ア、オの解答群は動画内参照
(b) 点 P が点 A から点 B まで移動するとき、線分 QR が通過してできる曲面上において、 2 点 A , B を結ぶ最も短い曲線はクが描く曲線である。
クの解答群①点 Q ②点 R ③設間( a )で考えた点 H ④線分 QR とyz平面との交点 ⑤線分 QR を 1 :$\sqrt{ 2 }$に内分する点 ⑥線分 QR を$\sqrt{ 2 }$: 1 に内分する点 ⑦三角形 PQR の重心から線分 QR に引いた垂線と線分 QR との交点
(c) 点 P が点 A から点 B まで移動するとき、線分 PQ を直径とするxz平面に平行な円が通過してできる球の体積は$\displaystyle \frac{ケ}{コ}$である。また△ PQR の面積は、線分 PQを直径とする円の面積の$\displaystyle \frac{サ}{\pi}$倍である。よって、立体Vの体積は$\displaystyle \frac{シ}{ス}$である。
( 2 )$z \geqq 0$ の領域において、yz平面上の点 T を頂点とし、 2 点 P , Q を通る放物線Lを考える。ただし、 Q , T は下記の 2 条件を満たす点とする。
・点 Q は C 上にあり、直線 PQ はx軸に平行である。
・三角形 PQT はxz平面に平行であり、点 T の z 座標は線分 PQ の長さに等しい。点 P が(1,0,0)であるとき、放物線Lを表す式はy=0,$z=セソx^2+タ$(ただし$-1 \leqq x \leqq 1$)であり、この放物線と線分 PQ で囲まれる図形の面積は$\displaystyle \frac{チ}{ツ}$である。
点 P が点 A から点 B まで移動するとき、放物線 L と線分 PQ で囲まれる図形が通過してできる立体の体積は$\displaystyle \frac{テト}{ナ}$である。
点 P が点 A から点 B まで移動するとき、線分 PQ を直径とするxz平面に平行な円が通過してできる球の体積は$\displaystyle \frac{ケ}{コ}\pi$である。また△ PQR の面積は、線分 PQ を直径とする円の面積の$\displaystyle \frac{サ}{\pi}$倍である。よって、立体体積はV の体積は$\displaystyle \frac{シ}{ス}$である。
2023杏林大学過去問
【高校数学】毎日積分15日目【難易度:★★★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\int_0^\frac{π}{3}\frac{dx}{sinx+\sqrt{3}cosx}$
これを解け.
この動画を見る
$\int_0^\frac{π}{3}\frac{dx}{sinx+\sqrt{3}cosx}$
これを解け.
福田の数学〜空間図形の通過範囲の面積と体積〜杏林大学2023年医学部第3問前編〜空間図形の通過範囲の面積と体積
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#杏林大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
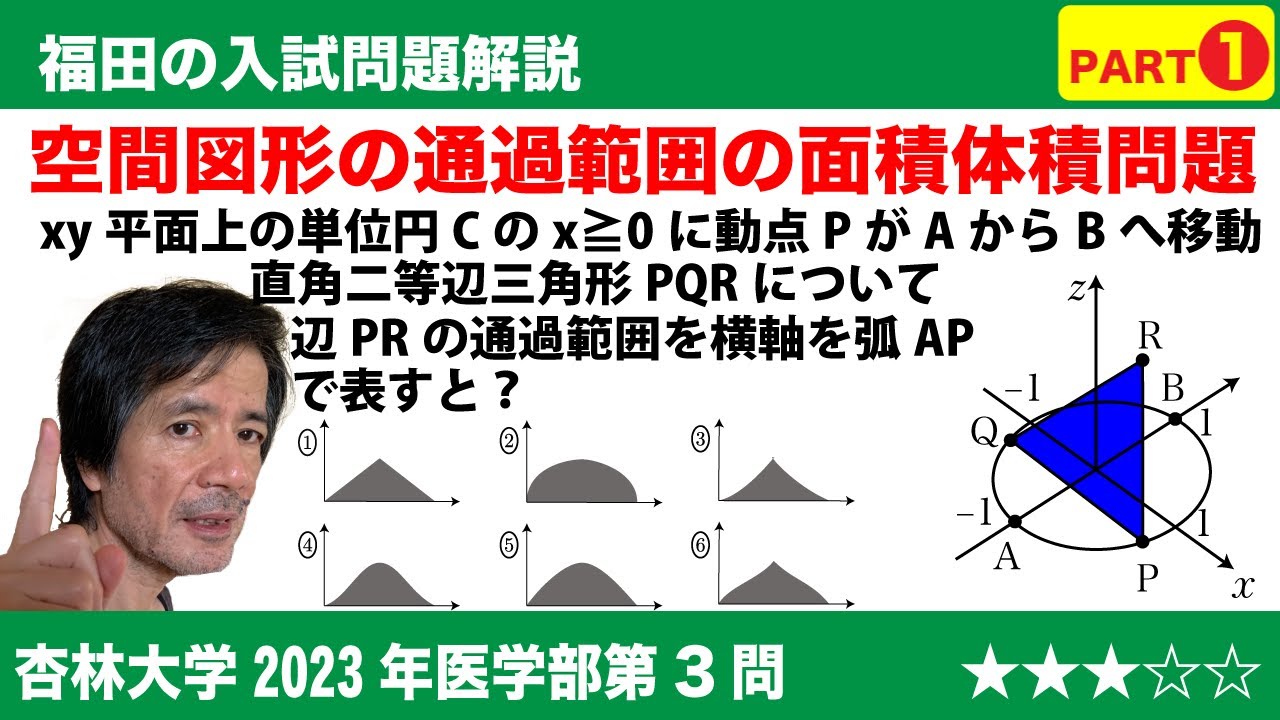
座標空間において原点 O を中心とする半径 1 の円 C がxy平面上にあり、ェ$\gt 0$の領域において点 A ( 0 , -1 , 0 )から点 B ( 0 , 1 , 0 )まで移動する C 上の動点を P とする。
( 1 )下記の 2 条件を満たす直角二等辺三角形 PQR を考える。
・点 Q は C 上にあり、直線 PQ はx軸に平行である。
・点 R のz座標は正であり、直線 PR はz軸に平行である。
点 P が点 A から点 B まで移動するとき、三角形 PQR の周および内部が通過してできる立体について、以下の間いに答えよ。
(a) 点 P が点 A から点 B まで移動するとき、線分 PR が通過してできる曲面の展開図は、横軸に弧 AP の長さ、縦軸に線分 PR の長さをとったグラフを考えればよく、$\fbox{ア}$で表される概形となり、その面積は$\fbox{イ}$である。
線分 PQ の中点を M とし、点 M から直線 QR に引いた垂線と線分 QR との交点を H とする。点 H は線分 QR を 1:$\fbox{ウ}$に内分する点である。点 Pの位置に依らず、線分の長さについて$\fbox{エ}×(MH)^2+(OM)^2=1$が成り立つ。点Pが点 A から点 B まで移動するとき、線分 MHが通過する領域の概形は$\fbox{オ}$であり、面積は$\frac {\sqrt {{\fbox{カ}}}}{\fbox{キ}}\pi$である。
(b) 点 P が点 A から点 B まで移動するとき、線分 QR が通過してできる曲面上において、 2 点 A , B を結ぶ最も短い曲線は$/fbox{ク}$が描く曲線である。
$\fbox{ク}$の解答群
①点Q
②点R
③設問(a)で考えた点H
④線分QRとyz平面との交点
⑤線分QRを1:$\sqrt{2}$に内分する点
⑥線分QRを$\sqrt{2}$:1に内分する点
⑦三角形PQRの重心からッ線分QRに引いた垂線と線分QRとの交点
(c) 点 P が点 A から点 B まで移動するとき、線分 PQ を直径とするxz平面に平行な円が通過してできる球の体積は$\frac{\fbox{ケ}}{\fbox{コ}}\pi$である。また$\angle PQR$の面積は、線分 PQを直径とする円の面積の$\frac{\fbox{サ}}{\pi}$倍である。よって、立体$V$の体積は$\frac{\fbox{シ}}{\fbox{ス}}$である。
( 2 ) $z \geqq 0$の領域において、yz平面上の点 T を頂点とし、 2 点 P , Q を通る放物線$L$を考える。ただし、 Q, T は下記の 2 条件を満たす点とする。
・点 Q は C 上にあり、直線 PQ はx軸に平行である。
・三角形 PQT はxz平面に平行であり、点 T の z 座標は線分 PQ の長さに等しい。
点 P が( 1 , 0 , 0 )であるとき、放物線$L$を表す式は
$y=0,z=\fbox{セソ}x^2+\fbox{タ}$(ただし、-1 \leq x \leq 1)であり、この放物線と線分PQで囲まれる図形の面積は$\frac{\fbox{チ}}{\fbox{ツ}}$である。
点 P が点 A から点 B まで移動するとき、放物線$L$と線分 PQ で囲まれる図形が通過してできる立体の体積は$\frac{\fbox{テト}}{\fbox{ナ}}$である。
2023杏林大学過去問
この動画を見る
座標空間において原点 O を中心とする半径 1 の円 C がxy平面上にあり、ェ$\gt 0$の領域において点 A ( 0 , -1 , 0 )から点 B ( 0 , 1 , 0 )まで移動する C 上の動点を P とする。
( 1 )下記の 2 条件を満たす直角二等辺三角形 PQR を考える。
・点 Q は C 上にあり、直線 PQ はx軸に平行である。
・点 R のz座標は正であり、直線 PR はz軸に平行である。
点 P が点 A から点 B まで移動するとき、三角形 PQR の周および内部が通過してできる立体について、以下の間いに答えよ。
(a) 点 P が点 A から点 B まで移動するとき、線分 PR が通過してできる曲面の展開図は、横軸に弧 AP の長さ、縦軸に線分 PR の長さをとったグラフを考えればよく、$\fbox{ア}$で表される概形となり、その面積は$\fbox{イ}$である。
線分 PQ の中点を M とし、点 M から直線 QR に引いた垂線と線分 QR との交点を H とする。点 H は線分 QR を 1:$\fbox{ウ}$に内分する点である。点 Pの位置に依らず、線分の長さについて$\fbox{エ}×(MH)^2+(OM)^2=1$が成り立つ。点Pが点 A から点 B まで移動するとき、線分 MHが通過する領域の概形は$\fbox{オ}$であり、面積は$\frac {\sqrt {{\fbox{カ}}}}{\fbox{キ}}\pi$である。
(b) 点 P が点 A から点 B まで移動するとき、線分 QR が通過してできる曲面上において、 2 点 A , B を結ぶ最も短い曲線は$/fbox{ク}$が描く曲線である。
$\fbox{ク}$の解答群
①点Q
②点R
③設問(a)で考えた点H
④線分QRとyz平面との交点
⑤線分QRを1:$\sqrt{2}$に内分する点
⑥線分QRを$\sqrt{2}$:1に内分する点
⑦三角形PQRの重心からッ線分QRに引いた垂線と線分QRとの交点
(c) 点 P が点 A から点 B まで移動するとき、線分 PQ を直径とするxz平面に平行な円が通過してできる球の体積は$\frac{\fbox{ケ}}{\fbox{コ}}\pi$である。また$\angle PQR$の面積は、線分 PQを直径とする円の面積の$\frac{\fbox{サ}}{\pi}$倍である。よって、立体$V$の体積は$\frac{\fbox{シ}}{\fbox{ス}}$である。
( 2 ) $z \geqq 0$の領域において、yz平面上の点 T を頂点とし、 2 点 P , Q を通る放物線$L$を考える。ただし、 Q, T は下記の 2 条件を満たす点とする。
・点 Q は C 上にあり、直線 PQ はx軸に平行である。
・三角形 PQT はxz平面に平行であり、点 T の z 座標は線分 PQ の長さに等しい。
点 P が( 1 , 0 , 0 )であるとき、放物線$L$を表す式は
$y=0,z=\fbox{セソ}x^2+\fbox{タ}$(ただし、-1 \leq x \leq 1)であり、この放物線と線分PQで囲まれる図形の面積は$\frac{\fbox{チ}}{\fbox{ツ}}$である。
点 P が点 A から点 B まで移動するとき、放物線$L$と線分 PQ で囲まれる図形が通過してできる立体の体積は$\frac{\fbox{テト}}{\fbox{ナ}}$である。
2023杏林大学過去問
【高校数学】毎日積分14日目【難易度:★★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\int_0^\frac{π}{2}e^{-3x}sinxdx$
これを解け.
この動画を見る
$\int_0^\frac{π}{2}e^{-3x}sinxdx$
これを解け.
【高校数学】毎日積分13日目【難易度:★★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\int_0^1log\frac{x+2}{x+1}dx$
これを解け.
この動画を見る
$\int_0^1log\frac{x+2}{x+1}dx$
これを解け.
【高校数学】毎日積分12日目【難易度:★】【毎日17時投稿】

【高校数学】毎日積分11日目【難易度:★★★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\int_0^{\frac{π}{2}}\frac{sinθ}{sinθ+cosθ}dθ$
これを解け.
この動画を見る
$\int_0^{\frac{π}{2}}\frac{sinθ}{sinθ+cosθ}dθ$
これを解け.
