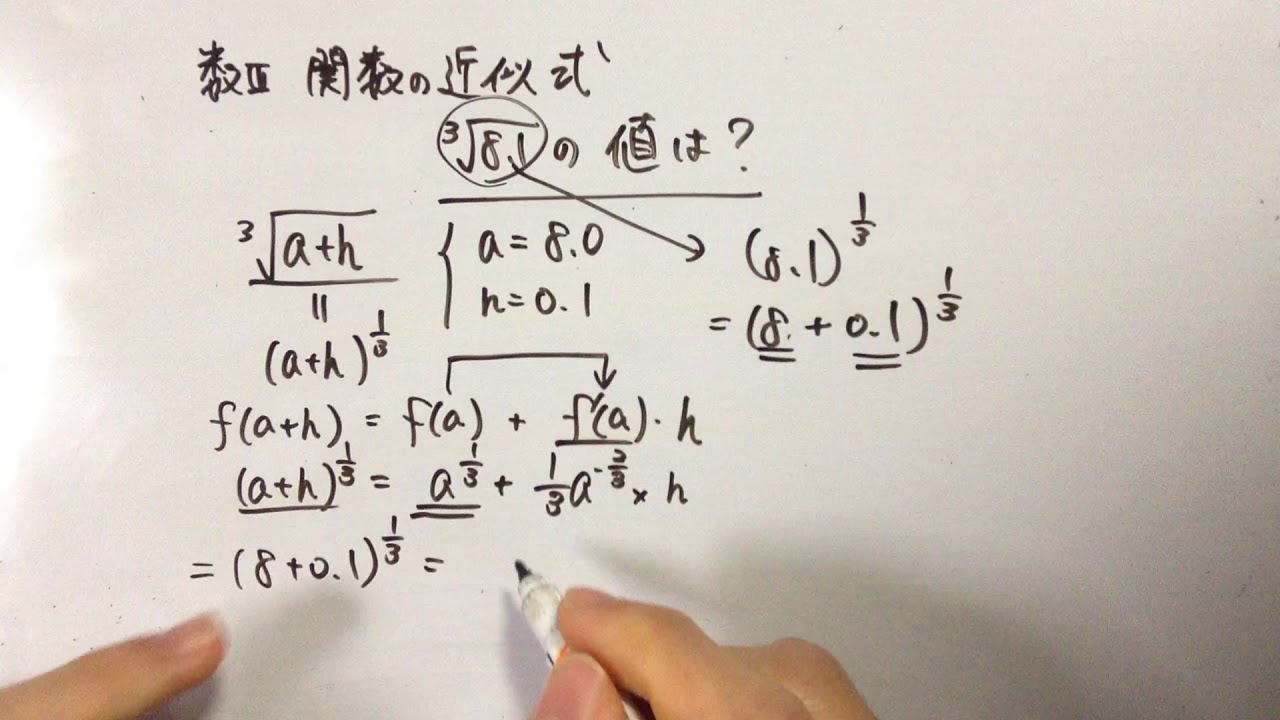数Ⅲ
数Ⅲ
 数Ⅲ
数Ⅲ
16東京都教員採用試験(数学:1-7 極限値)
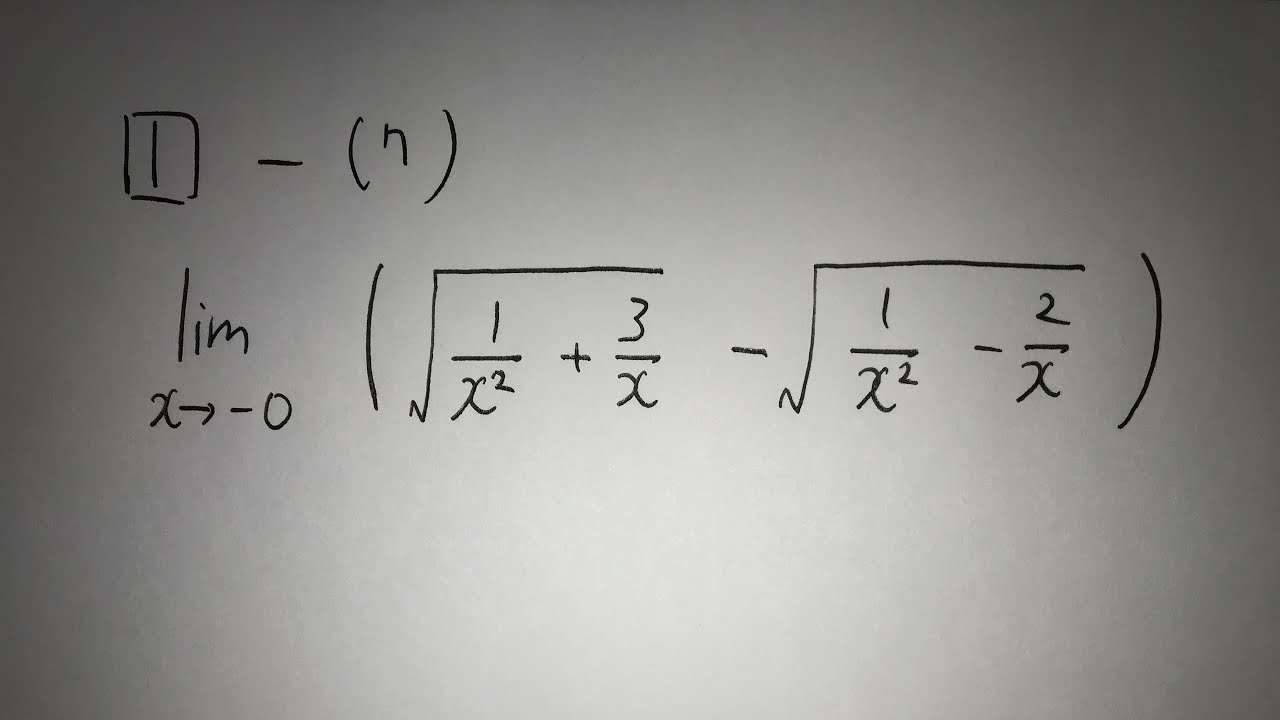
単元:
#関数と極限#関数の極限#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(7)
$\displaystyle \lim_{ n \to -0 } (\sqrt{\frac{1}{x^2}+\frac{3}{x}} - \sqrt{\frac{1}{x^2}-\frac{2}{x}})$
この動画を見る
1⃣-(7)
$\displaystyle \lim_{ n \to -0 } (\sqrt{\frac{1}{x^2}+\frac{3}{x}} - \sqrt{\frac{1}{x^2}-\frac{2}{x}})$
17東京都教員採用試験(数学:1-7番 シグマと極限値)
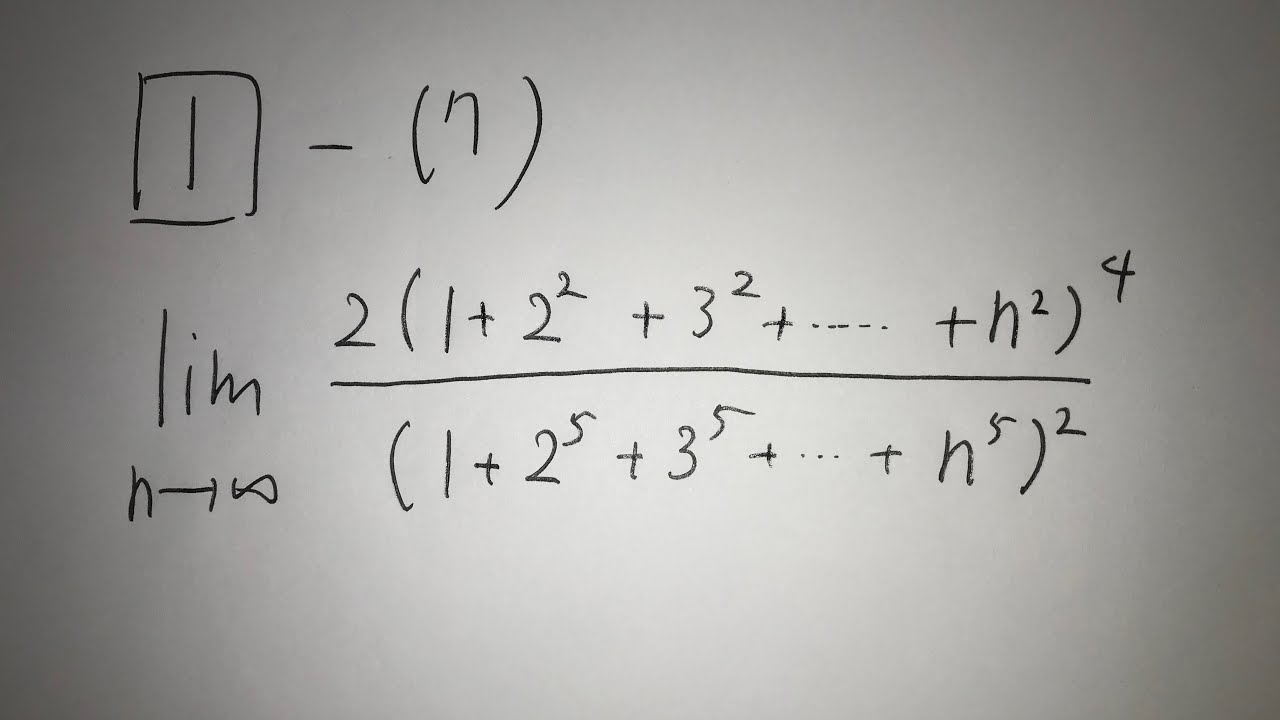
単元:
#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#数列の極限#その他#数学(高校生)#数B#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(7)
$\displaystyle \lim_{ n \to \infty } \frac{2(1+2^2+3^2+\cdots+n^2)^4}{(1+2^5+3^5+\cdots+n^5)^2}$
この動画を見る
1⃣-(7)
$\displaystyle \lim_{ n \to \infty } \frac{2(1+2^2+3^2+\cdots+n^2)^4}{(1+2^5+3^5+\cdots+n^5)^2}$
【数Ⅲ-157】定積分の部分積分法③

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
数Ⅲ(定積分の部分積分法①)
Q次の定積分の値を求めよ
①$\int_1^{e} (\log x)^2dx$
➁$\int_0^{\frac{\pi}{2}}x^2 \cos^2 x \ dx$
この動画を見る
数Ⅲ(定積分の部分積分法①)
Q次の定積分の値を求めよ
①$\int_1^{e} (\log x)^2dx$
➁$\int_0^{\frac{\pi}{2}}x^2 \cos^2 x \ dx$
【数Ⅲ-155】定積分の部分積分法①

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
数Ⅲ(定積分の部分積分法①)
Q次の定積分の値を求めよ。
①$\int_0^{\pi}x \sin x\ dx$
➁$\int_0^{1}xe^{-2x}\ dx$
③$\int_1^e\log x\ dx$
この動画を見る
数Ⅲ(定積分の部分積分法①)
Q次の定積分の値を求めよ。
①$\int_0^{\pi}x \sin x\ dx$
➁$\int_0^{1}xe^{-2x}\ dx$
③$\int_1^e\log x\ dx$
【数Ⅲ-154】定積分の置換積分法③

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
数Ⅲ(定積分の置換積分法③)
Q次の定積分を求めよ。
①$\int_{-\frac{\pi}{3}}^\frac{\pi}{3}x^2\sin x \ dx$
➁$\int_{-1}^1\frac{1-x}{1+x^2} \ dx$
③$\int_{-\frac{\pi}{2}}^\frac{\pi}{2}\cos^3 x \ dx$
この動画を見る
数Ⅲ(定積分の置換積分法③)
Q次の定積分を求めよ。
①$\int_{-\frac{\pi}{3}}^\frac{\pi}{3}x^2\sin x \ dx$
➁$\int_{-1}^1\frac{1-x}{1+x^2} \ dx$
③$\int_{-\frac{\pi}{2}}^\frac{\pi}{2}\cos^3 x \ dx$
【数Ⅲ-153】定積分の置換積分法②(偶関数と奇関数)

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
数Ⅲ(定積分の置換積分法➁・偶数関数と奇関数)
Q次の定積分を求めよ。
①$\int_{-2}^2\sqrt{4-x^2} \ dx$
➁$\int_{-\pi}^\pi\sin x\ dx$
③$\int_{-1}^1 (x^4-5x^3+4x-2)\ dx$
この動画を見る
数Ⅲ(定積分の置換積分法➁・偶数関数と奇関数)
Q次の定積分を求めよ。
①$\int_{-2}^2\sqrt{4-x^2} \ dx$
➁$\int_{-\pi}^\pi\sin x\ dx$
③$\int_{-1}^1 (x^4-5x^3+4x-2)\ dx$
【数Ⅲ】極限:福島県立医大! 極限値lim[n→∞]l[n]_θ[n]を求めよ。

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
Oを原点とする座標平面上に2点A(2,0),B(0,1)がある。自然数nに対し、線分ABを1:nに内分する点を$P_n$とし,$∠AOP_n=θ_n$とする。ただし、$0<θ_n<\dfrac{\pi}{2}$である。線分$AP_n$の長さを$l_n$として、極限値$\displaystyle \lim_{n\to \infty}\dfrac{l_n}{\theta_n}$を求めよ。
この動画を見る
Oを原点とする座標平面上に2点A(2,0),B(0,1)がある。自然数nに対し、線分ABを1:nに内分する点を$P_n$とし,$∠AOP_n=θ_n$とする。ただし、$0<θ_n<\dfrac{\pi}{2}$である。線分$AP_n$の長さを$l_n$として、極限値$\displaystyle \lim_{n\to \infty}\dfrac{l_n}{\theta_n}$を求めよ。
【数Ⅲ】極限:岐阜大の類題! 複素数z[n]をz[1]=1,z[n+1]=i/2(z[n]+1)(n=1,2,3,···)により定める。z[n]の実部x[n],虚部y[n]を求めよ。
単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
複素数$z_1$を$z_1=1$,$z_{n+1}=\dfrac{1}{2}(z_n+1)(n=1,2,3,···)$により定める。$z_n$の実部$x_n$,虚部$y_n$を求めよ。
この動画を見る
複素数$z_1$を$z_1=1$,$z_{n+1}=\dfrac{1}{2}(z_n+1)(n=1,2,3,···)$により定める。$z_n$の実部$x_n$,虚部$y_n$を求めよ。
東工大 末尾の0の個数問題

単元:
#関数と極限#数列の極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$は自然数である.
$f(n)$を$n!$の末尾に並ぶ$0$の個数とする.
(例)$f(10)=2,f(100)=24$
$\displaystyle \lim_{n\to\infty}\dfrac{f(10^n)}{10^n}$を求めよ.
1991東工大過去問
この動画を見る
$n$は自然数である.
$f(n)$を$n!$の末尾に並ぶ$0$の個数とする.
(例)$f(10)=2,f(100)=24$
$\displaystyle \lim_{n\to\infty}\dfrac{f(10^n)}{10^n}$を求めよ.
1991東工大過去問
【数Ⅲ】微分法: 微分係数の利用! f'(a)が存在するとき、次の極限をf(a),f'(a)で表せ。(1)lim(h→0){f(a+4h)-f(a+2h)}/h

単元:
#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$f'(a)$が存在するとき、次の極限を$f(a),f'(a)$で表せ。
(1)$\displaystyle \lim_{h\to 0}\dfrac{f(a+4h)-f(a+2h)}{h}$
この動画を見る
$f'(a)$が存在するとき、次の極限を$f(a),f'(a)$で表せ。
(1)$\displaystyle \lim_{h\to 0}\dfrac{f(a+4h)-f(a+2h)}{h}$
20年5月数学検定1級1次試験(微分)
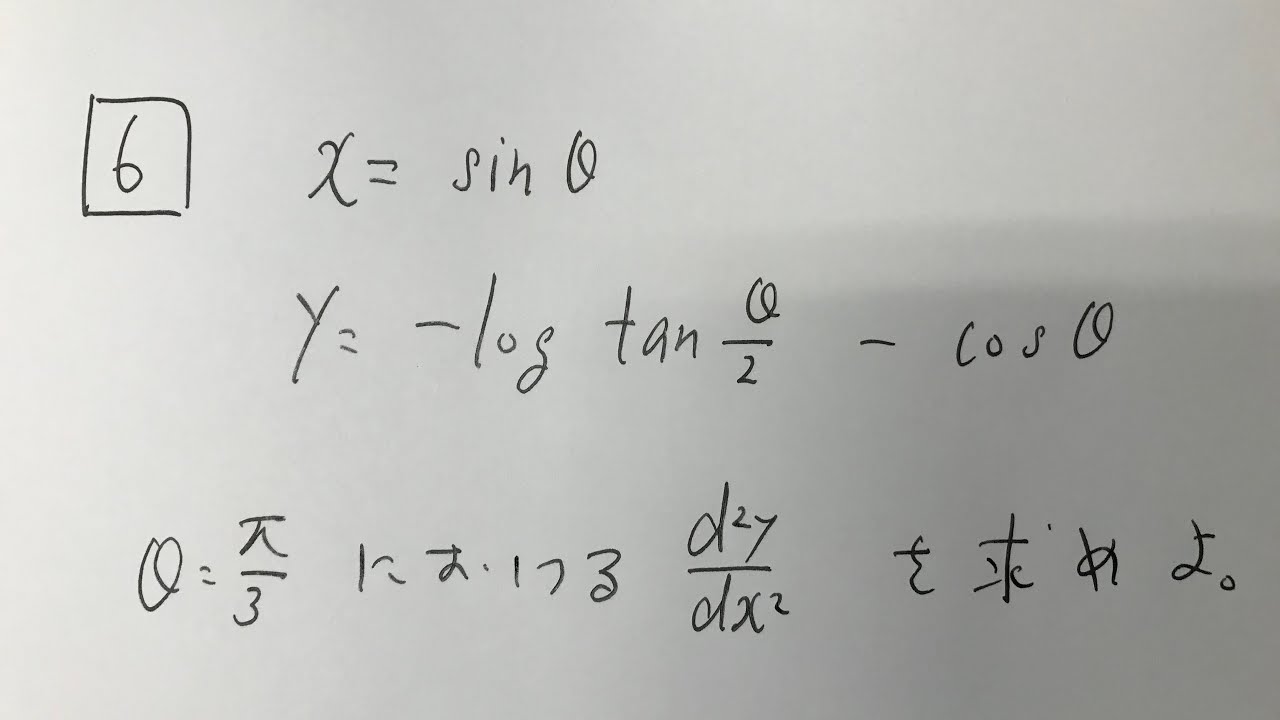
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#三角関数#三角関数とグラフ#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
6⃣
x=sinθ
$y=-log tan \frac{θ}{2}-cosθ$
$θ=\frac{\pi}{3}$における$\frac{dy}{dx^2}$を求めよ。
この動画を見る
6⃣
x=sinθ
$y=-log tan \frac{θ}{2}-cosθ$
$θ=\frac{\pi}{3}$における$\frac{dy}{dx^2}$を求めよ。
【数学Ⅲ】平均値の定理・接線法線問題 すぐ理解できて一生忘れない攻略法!

単元:
#微分とその応用#接線と法線・平均値の定理#数学(高校生)#数Ⅲ
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【数学Ⅲ】平均値の定理・接線法線問題解説動画です
-----------------
$y=\displaystyle \frac{3x}{x+2}$
(1)曲線状の点A(1,1)を通る接線の方程式は?
(2)(0,-1)から$y-log x$に引いた接線の方程式は?
(3)$y=3\sqrt{ x^2 }$の(1,1)上の法線の方程式は?
(4)$f(x)=2x^2-x$において$[0,1]$について、平均値の定理の式を満たすCの値は?
この動画を見る
【数学Ⅲ】平均値の定理・接線法線問題解説動画です
-----------------
$y=\displaystyle \frac{3x}{x+2}$
(1)曲線状の点A(1,1)を通る接線の方程式は?
(2)(0,-1)から$y-log x$に引いた接線の方程式は?
(3)$y=3\sqrt{ x^2 }$の(1,1)上の法線の方程式は?
(4)$f(x)=2x^2-x$において$[0,1]$について、平均値の定理の式を満たすCの値は?
20年5月数検準1級1次試験(極限)
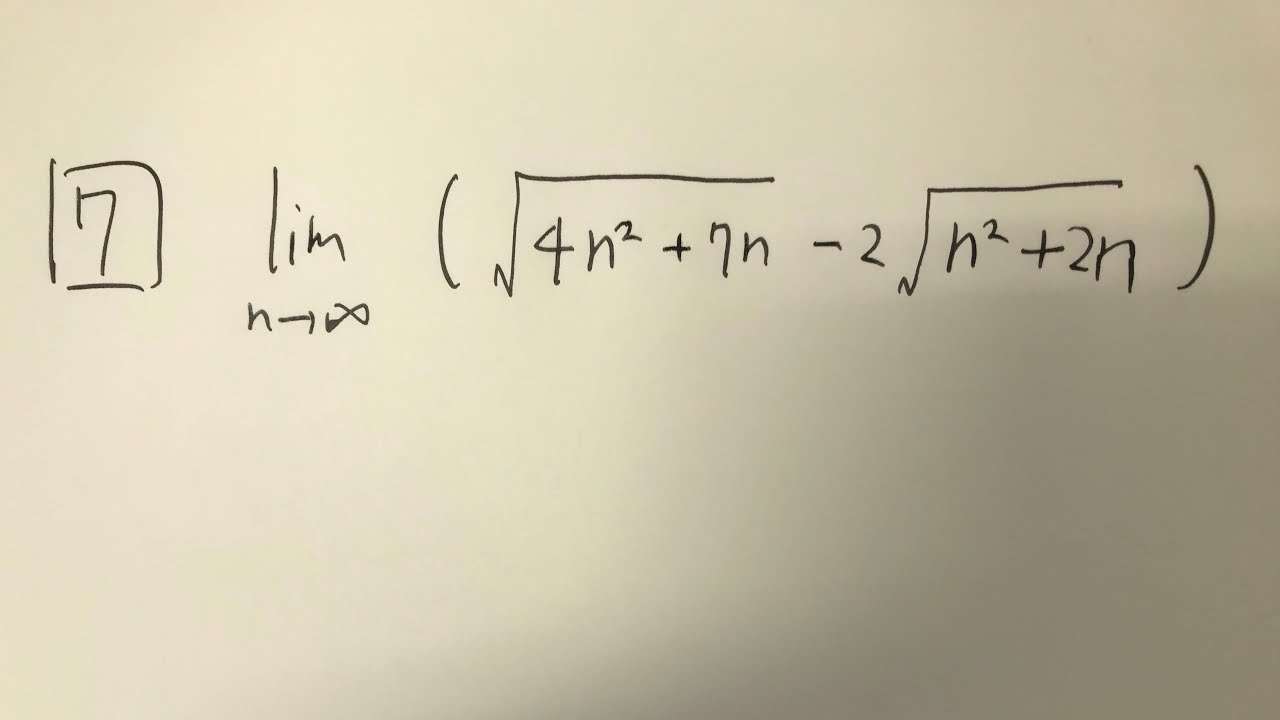
単元:
#数学検定・数学甲子園・数学オリンピック等#関数と極限#数列の極限#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
7⃣$\displaystyle \lim_{ n \to \infty } (\sqrt{4n^2+7n} - 2\sqrt{n^2+2n})$
この動画を見る
7⃣$\displaystyle \lim_{ n \to \infty } (\sqrt{4n^2+7n} - 2\sqrt{n^2+2n})$
20年5月数学検定準1級1次試験(積分)
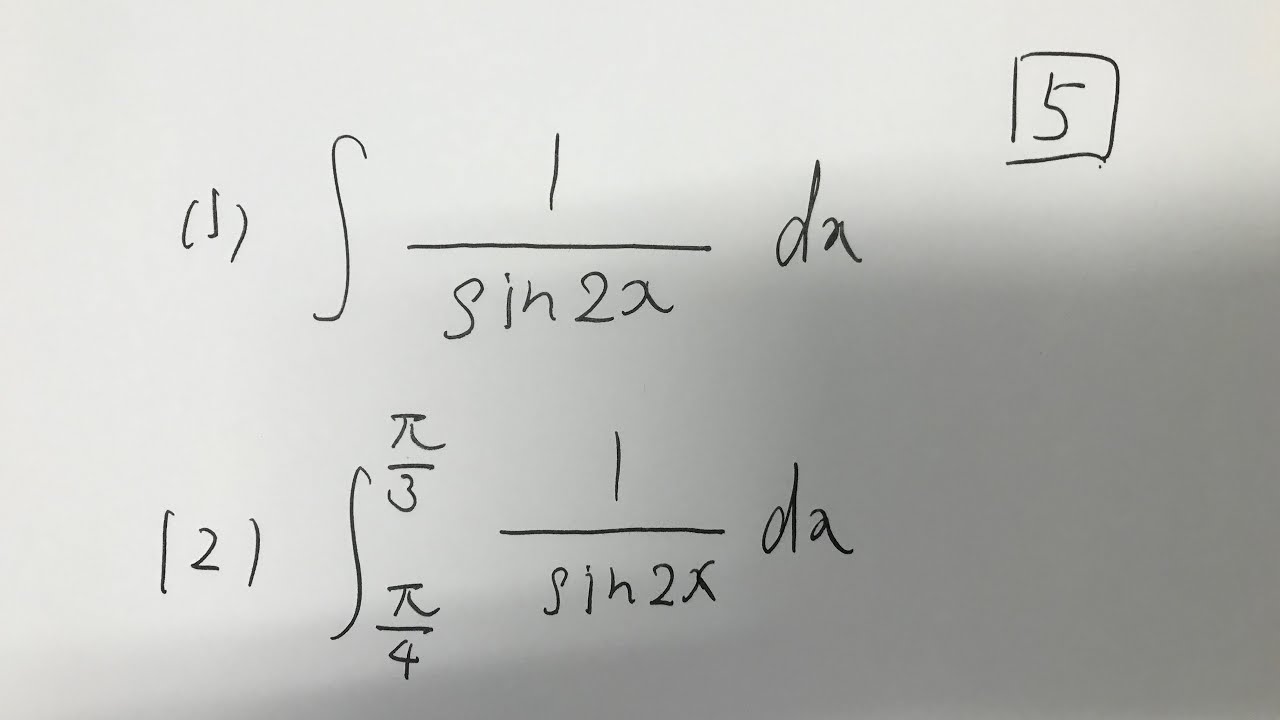
単元:
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#不定積分#定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
5⃣
(1)$\int \frac{dx}{sin2x}$
(2)$\int_{\frac{\pi}{4}}^{\frac{\pi}{3}} \frac{dx}{sin2x}$
この動画を見る
5⃣
(1)$\int \frac{dx}{sin2x}$
(2)$\int_{\frac{\pi}{4}}^{\frac{\pi}{3}} \frac{dx}{sin2x}$
三角関数の基本 合成公式 図書館情報大

単元:
#数Ⅱ#三角関数#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\sqrt3\sin 2x+2\sin^2x-1$,$0\leqq x\lt \pi$における最大値,最小値を求めよ.
1985図書館情報大過去問
この動画を見る
$\sqrt3\sin 2x+2\sin^2x-1$,$0\leqq x\lt \pi$における最大値,最小値を求めよ.
1985図書館情報大過去問
京都府採用試験数学【2016】

単元:
#数Ⅰ#数A#数Ⅱ#数と式#場合の数と確率#平面上のベクトル#複素数平面#図形と計量#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#集合と命題(集合・命題と条件・背理法)#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#整数の性質#場合の数#確率#約数・倍数・整数の割り算と余り・合同式#三角関数#指数関数と対数関数#三角関数とグラフ#指数関数#対数関数#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#微分とその応用#積分とその応用#複素数平面#微分法#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#面積・体積・長さ・速度#数学(高校生)#数C#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
1. x+y+z=10の正の整数解の個数を求めよ。
2. 3つのサイコロを投げる。
出る目の最大値と最小値の差が2になる確率を求めよ。
3. 複素数$(\frac{-1+\sqrt{3}i}{2})^{2015} + (\frac{-1-\sqrt{3}i}{2})^{2015}$
4. $log_{2}3$は無理数を示せ
5. $△OAB = \frac{|a_1b_2-a_2b_1|}{2}$を示せ
*図は動画内参照
6. f(x)=e^x sinx
(1) $0 \leqq x \leqq \pi$ y=f(x)の極大値を求めよ。
(2)x軸とy=f(x) ($0 \leqq x \leqq \pi$)で囲まれた面積を求めよ。
7. $\frac{1}{2015} , \frac{2}{2015} , \cdots , \frac{2015}{2015}$のうち既約分数の個数を求めよ。
8. $n \in \mathbb{ N }$
$2(\sqrt{n+1} - 1) < 1 + \frac{1}{\sqrt 2} + \frac{1}{\sqrt 3} + \cdots + \frac{1}{\sqrt n}$
この動画を見る
1. x+y+z=10の正の整数解の個数を求めよ。
2. 3つのサイコロを投げる。
出る目の最大値と最小値の差が2になる確率を求めよ。
3. 複素数$(\frac{-1+\sqrt{3}i}{2})^{2015} + (\frac{-1-\sqrt{3}i}{2})^{2015}$
4. $log_{2}3$は無理数を示せ
5. $△OAB = \frac{|a_1b_2-a_2b_1|}{2}$を示せ
*図は動画内参照
6. f(x)=e^x sinx
(1) $0 \leqq x \leqq \pi$ y=f(x)の極大値を求めよ。
(2)x軸とy=f(x) ($0 \leqq x \leqq \pi$)で囲まれた面積を求めよ。
7. $\frac{1}{2015} , \frac{2}{2015} , \cdots , \frac{2015}{2015}$のうち既約分数の個数を求めよ。
8. $n \in \mathbb{ N }$
$2(\sqrt{n+1} - 1) < 1 + \frac{1}{\sqrt 2} + \frac{1}{\sqrt 3} + \cdots + \frac{1}{\sqrt n}$
【高校数学】部分分数分解の分母に二乗があるパターン

単元:
#恒等式・等式・不等式の証明#数列とその和(等差・等比・階差・Σ)#積分とその応用#不定積分#数学(高校生)
指導講師:
受験メモ山本
問題文全文(内容文):
部分分数分解の分母に二乗がある場合の解説動画です
この動画を見る
部分分数分解の分母に二乗がある場合の解説動画です
上智大 関数の最大最小

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
問題文全文(内容文):
$f(x)=\displaystyle \frac{x^2+ax+b}{x^2-x+1}$の最大値が$3$、最小値が$\displaystyle \frac{1}{3}$
$(a,b)$の値を求めよ
出典:2005年上智大学 過去問
この動画を見る
$f(x)=\displaystyle \frac{x^2+ax+b}{x^2-x+1}$の最大値が$3$、最小値が$\displaystyle \frac{1}{3}$
$(a,b)$の値を求めよ
出典:2005年上智大学 過去問
佐賀大 三次関数

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$y=x^3-x$上を点$P$が原点から点$A(a,a^3-a)$まで動く
$(a \gt 0)\triangle OAP$の最大値を求めよ
出典:2005年佐賀大学 過去問
この動画を見る
$y=x^3-x$上を点$P$が原点から点$A(a,a^3-a)$まで動く
$(a \gt 0)\triangle OAP$の最大値を求めよ
出典:2005年佐賀大学 過去問
東北大 積分

単元:
#数Ⅱ#微分法と積分法#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=x^3-6ax^2+bx+1$
$x=a(a \gt 0)$で極大値
$f(x)$と直線$y=f(a)$で囲まれた面積が$a^2$
$a$の値を求めよ
出典:1996年東北大学 過去問
この動画を見る
$f(x)=x^3-6ax^2+bx+1$
$x=a(a \gt 0)$で極大値
$f(x)$と直線$y=f(a)$で囲まれた面積が$a^2$
$a$の値を求めよ
出典:1996年東北大学 過去問
慶応義塾大 指数方程式

単元:
#数Ⅱ#指数関数と対数関数#微分法と積分法#指数関数#微分とその応用#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$8^x-6・4^x+5・2^x=k$が異なる3つの実数解をもつ$k$の範囲を求めよ
出典:慶應義塾大学 過去問
この動画を見る
$8^x-6・4^x+5・2^x=k$が異なる3つの実数解をもつ$k$の範囲を求めよ
出典:慶應義塾大学 過去問
東北大 積分

単元:
#微分とその応用#積分とその応用#色々な関数の導関数#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$y=-x^3-2x^2+a$と$y=x^3-16x$は$x$座標が負の点で共有点をもち、その点で共通接線をもつ。
$a$の値と囲まれた面積を求めよ
出典:1996年東北大学 過去問
この動画を見る
$y=-x^3-2x^2+a$と$y=x^3-16x$は$x$座標が負の点で共有点をもち、その点で共通接線をもつ。
$a$の値と囲まれた面積を求めよ
出典:1996年東北大学 過去問
慶応義塾大 4次方程式

単元:
#関数と極限#微分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#関数の極限#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$3x^4-4x^3-12x^2-k=0$が相異なる4つの実数解をもつ$k$の範囲
そのときの4つの解のうち最大のものを$\alpha$とする。
$\alpha$の範囲を求めよ
出典:1989年慶應義塾大学 過去問
この動画を見る
$3x^4-4x^3-12x^2-k=0$が相異なる4つの実数解をもつ$k$の範囲
そのときの4つの解のうち最大のものを$\alpha$とする。
$\alpha$の範囲を求めよ
出典:1989年慶應義塾大学 過去問
甲南大 関数の最小値

単元:
#大学入試過去問(数学)#微分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#甲南大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=(x^2-x+a)^2-x^2+x$の最小値を求めよ
出典:甲南大学 過去問
この動画を見る
$f(x)=(x^2-x+a)^2-x^2+x$の最小値を求めよ
出典:甲南大学 過去問
光文社新書「中学の知識でオイラー公式がわかる」Vol11 sinの微分

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
sinの微分解説動画です
$\displaystyle \lim_{ h \to o } \displaystyle \frac{\sin h}{h} =1$
この動画を見る
sinの微分解説動画です
$\displaystyle \lim_{ h \to o } \displaystyle \frac{\sin h}{h} =1$
光文社新書「中学の知識でオイラーの公式がわかる」Vol.7積の微分の公式証明

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#微分とその応用#積分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
積の微分の公式証明解説動画です
この動画を見る
積の微分の公式証明解説動画です
光文社新書「中学の知識でオイラーの公式がわかる」Vol.6 自由落下運動と微分

対数の近似値の求め方

この問題解けますか。

単元:
#積分とその応用#定積分#数Ⅲ
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
$f(x)=\int_0^2{3x^2-xf(t)}dt$を満たす$f(x)$を求めよ
この動画を見る
$f(x)=\int_0^2{3x^2-xf(t)}dt$を満たす$f(x)$を求めよ
【数学III】関数の近似式を10分でマスターする