 ベクトルと平面図形、ベクトル方程式
ベクトルと平面図形、ベクトル方程式
 ベクトルと平面図形、ベクトル方程式
ベクトルと平面図形、ベクトル方程式
福田の数学〜青山学院大学2025理工学部第5問〜鋭角三角形の条件と垂心の位置ベクトル

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#数学(高校生)#数C#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{5}$
$\triangle OAB$は鋭角三角形であり、
$\vert \overrightarrow{OA}\vert=4,\vert \overrightarrow{OB}\vert=3$
を満たしている。
$\overrightarrow{OA}\cdot \overrightarrow{OB}=k$とおくとき、以下の問いに答えよ。
(1)$k$のとり得る値の範囲を求めよ。
上で与えた$\triangle OAB$の頂点$A,B$から
それぞれの対辺に下ろした$2$本の垂線の交点
を$H$とし、辺$AB$を$2:1$に内分する点を$C$とする。
(2)$\overrightarrow{OH}$を$\overrightarrow{OA},\overrightarrow{OB}$および$k$を用いて表せ。
(3)$3$点$O,H,C$が同一直線上にあるとき、
$k$の値と$\dfrac{OH}{OC}$を求めよ。
$2025$年青山学院大学理工学部過去問題
この動画を見る
$\boxed{5}$
$\triangle OAB$は鋭角三角形であり、
$\vert \overrightarrow{OA}\vert=4,\vert \overrightarrow{OB}\vert=3$
を満たしている。
$\overrightarrow{OA}\cdot \overrightarrow{OB}=k$とおくとき、以下の問いに答えよ。
(1)$k$のとり得る値の範囲を求めよ。
上で与えた$\triangle OAB$の頂点$A,B$から
それぞれの対辺に下ろした$2$本の垂線の交点
を$H$とし、辺$AB$を$2:1$に内分する点を$C$とする。
(2)$\overrightarrow{OH}$を$\overrightarrow{OA},\overrightarrow{OB}$および$k$を用いて表せ。
(3)$3$点$O,H,C$が同一直線上にあるとき、
$k$の値と$\dfrac{OH}{OC}$を求めよ。
$2025$年青山学院大学理工学部過去問題
福田の数学〜早稲田大学2025人間科学部第3問〜外心と内心の位置ベクトル
単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
(1)$\triangle ABC$において$AB=6,AC=4,$
$\cos A=\dfrac{1}{4}$とする。
$\triangle ABC$の外心を$H$とし、直線$AH$が
$\triangle ABC$の外接円と交わる点のうち、
点$A$とは異なる点を$P$とする。
このとき、$\overrightarrow{AP}=\dfrac{\boxed{ス}}{\boxed{セ}}\overrightarrow{AB}+\dfrac{\boxed{ソ}}{\boxed{タ}}\overrightarrow{AC}$である。
(2)$\triangle ABC$において$AB=5,AC=6,$
$\cos A=\dfrac{1}{5}$とする。
$\triangle ABC$の内心を$K$とし、
直線$AK$が$\triangle ABC$の内接円と
交わる点のうち、点$A$に近いほうの点を
$Q$とする。
このとき、$\overrightarrow{AQ}=\dfrac{\boxed{チ}-\sqrt{\boxed{ツ}}}{\boxed{テ}}\overrightarrow{AK}$である。
$2025$年早稲田大学人間科学部過去問題
この動画を見る
$\boxed{3}$
(1)$\triangle ABC$において$AB=6,AC=4,$
$\cos A=\dfrac{1}{4}$とする。
$\triangle ABC$の外心を$H$とし、直線$AH$が
$\triangle ABC$の外接円と交わる点のうち、
点$A$とは異なる点を$P$とする。
このとき、$\overrightarrow{AP}=\dfrac{\boxed{ス}}{\boxed{セ}}\overrightarrow{AB}+\dfrac{\boxed{ソ}}{\boxed{タ}}\overrightarrow{AC}$である。
(2)$\triangle ABC$において$AB=5,AC=6,$
$\cos A=\dfrac{1}{5}$とする。
$\triangle ABC$の内心を$K$とし、
直線$AK$が$\triangle ABC$の内接円と
交わる点のうち、点$A$に近いほうの点を
$Q$とする。
このとき、$\overrightarrow{AQ}=\dfrac{\boxed{チ}-\sqrt{\boxed{ツ}}}{\boxed{テ}}\overrightarrow{AK}$である。
$2025$年早稲田大学人間科学部過去問題
福田の数学〜九州大学2025文系第2問〜円周上の2点との距離の2乗の和の最大値

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#三角関数#三角関数とグラフ#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
半径$1$の円周$C$上の$2$点$A,B$は
$AB=\sqrt3$をみたすとする。
点$P$が円周$C$上を動くとき、
$AP^2+BP^2$の最大値を求めよ。
$2025$年九州大学文系過去問題
この動画を見る
$\boxed{2}$
半径$1$の円周$C$上の$2$点$A,B$は
$AB=\sqrt3$をみたすとする。
点$P$が円周$C$上を動くとき、
$AP^2+BP^2$の最大値を求めよ。
$2025$年九州大学文系過去問題
福田の数学〜九州大学2025理系第1問〜平面に垂直なベクトルの絶対値の最小

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
座標空間内の$3$点$A(1,1,-5),B(-1,-1,7),C(1,-1,3)$を
通る平面を$\alpha$とする。
点$P(a,b,t)$を通り$\alpha$に垂直な直線と
$xy$平面との交点を$Q$とする。
(1)点$Q$の座標を求めよ。
(2)$t$がすべての実数値をとって変化するときの
$OQ$の最小値が$1$以下となるような
$a,b$の条件を求めよ。
ただし、$O$は原点である。
$2025$年九州大学理系過去問題
この動画を見る
$\boxed{1}$
座標空間内の$3$点$A(1,1,-5),B(-1,-1,7),C(1,-1,3)$を
通る平面を$\alpha$とする。
点$P(a,b,t)$を通り$\alpha$に垂直な直線と
$xy$平面との交点を$Q$とする。
(1)点$Q$の座標を求めよ。
(2)$t$がすべての実数値をとって変化するときの
$OQ$の最小値が$1$以下となるような
$a,b$の条件を求めよ。
ただし、$O$は原点である。
$2025$年九州大学理系過去問題
福田の数学〜大阪大学2025理系第3問〜空間図形と最大最小の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#微分法と積分法#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
座標空間に$3$点$O(0,0,0),A(0,1,1),B(x,y,0)$がある。
$\angle OAP=30°$かつ$y\geqq 0$を満たすように
点$P$が動くとき、
$(x+1)(y+1)$の最大値と最小値を求めよ。
$2025$年大阪大学理系過去問題
この動画を見る
$\boxed{3}$
座標空間に$3$点$O(0,0,0),A(0,1,1),B(x,y,0)$がある。
$\angle OAP=30°$かつ$y\geqq 0$を満たすように
点$P$が動くとき、
$(x+1)(y+1)$の最大値と最小値を求めよ。
$2025$年大阪大学理系過去問題
福田の数学〜大阪大学2025理系第1問〜平面図形とベクトルの証明

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
平面上の三角形$OAB$を考える。
$\angle AOB$は鋭角、$OA=3,OB=t$とする。
また、点$A$から直線$OB$に下ろした垂線と
直線$OB$の交点を$C$とし、$OC=1$とする。
線分$AB$を$2:1$に内分する点を$P$、点$A$から
直線$OP$に下ろした垂線と直線$OB$との交点を
$R$とする。
(1)内積$\overrightarrow{OA}・\overrightarrow{OB}$を$t$を用いて表せ。
(2)線分$OR$の長さを$t$を用いて表せ。
(3)線分$OB$の中点を$M$とする。
点$R$が線分$MB$上にあるとき、
$t$のとりうる値の範囲を求めよ。
$2025$年大阪大学理系過去問題
この動画を見る
$\boxed{1}$
平面上の三角形$OAB$を考える。
$\angle AOB$は鋭角、$OA=3,OB=t$とする。
また、点$A$から直線$OB$に下ろした垂線と
直線$OB$の交点を$C$とし、$OC=1$とする。
線分$AB$を$2:1$に内分する点を$P$、点$A$から
直線$OP$に下ろした垂線と直線$OB$との交点を
$R$とする。
(1)内積$\overrightarrow{OA}・\overrightarrow{OB}$を$t$を用いて表せ。
(2)線分$OR$の長さを$t$を用いて表せ。
(3)線分$OB$の中点を$M$とする。
点$R$が線分$MB$上にあるとき、
$t$のとりうる値の範囲を求めよ。
$2025$年大阪大学理系過去問題
福田の数学〜立教大学2025理学部第1問(2)〜内積と絶対値の計算問題

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(2)$2$つの平面ベクトル$\overrightarrow{a},\overrightarrow{b}$は、
$\vert \overrightarrow{a}+\overrightarrow{b} \vert=4,\vert \overrightarrow{a}-\overrightarrow{b} \vert =2$を満たすとする。
このとき、内積$\overrightarrow{a}・\overrightarrow{b}$の値は$\boxed{イ}$である。
また、$\vert 2\overrightarrow{a}-3\overrightarrow{b} \vert^2+\vert 3 \overrightarrow{a}-2\overrightarrow{b} \vert^2$の値は$\boxed{ウ}$である。
$2025$年立教大学理学部過去問題
この動画を見る
$\boxed{1}$
(2)$2$つの平面ベクトル$\overrightarrow{a},\overrightarrow{b}$は、
$\vert \overrightarrow{a}+\overrightarrow{b} \vert=4,\vert \overrightarrow{a}-\overrightarrow{b} \vert =2$を満たすとする。
このとき、内積$\overrightarrow{a}・\overrightarrow{b}$の値は$\boxed{イ}$である。
また、$\vert 2\overrightarrow{a}-3\overrightarrow{b} \vert^2+\vert 3 \overrightarrow{a}-2\overrightarrow{b} \vert^2$の値は$\boxed{ウ}$である。
$2025$年立教大学理学部過去問題
福田の数学〜立教大学2025経済学部第1問(6)〜2つのベクトルの両方に垂直なベクトル

単元:
#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(6)空間のベクトル$\vec{ p}=(x,y,z)$は
$\vec{b}=(0,3,2)$の両方に垂直であり、
$\vec{\vert p \vert}=7$かつ$z \gt 0$を
満たしている。
このとき、$\vec{p}=(\boxed{ク},\boxed{ケ},\boxed{コ})$である。
$2025$年立教大学経済学部過去問題
この動画を見る
$\boxed{1}$
(6)空間のベクトル$\vec{ p}=(x,y,z)$は
$\vec{b}=(0,3,2)$の両方に垂直であり、
$\vec{\vert p \vert}=7$かつ$z \gt 0$を
満たしている。
このとき、$\vec{p}=(\boxed{ク},\boxed{ケ},\boxed{コ})$である。
$2025$年立教大学経済学部過去問題
福田の数学〜慶應義塾大学2025経済学部第5問〜空間における平面と平面の交線

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{5}$
座標平面の原点$O$を中心とする半径$1$の
球面を$C$、点$M(4,0,0)$を中心とする
半径$2$の球面上を$D$とする。
(1)$p,q$を実数とする。
$xy$平面上の直線$y=px+q$は、
球面$C$と$xy$平面が交わってできる円と
点$A_1$で接し、球面$D$と$xy$平面が交わって
できる円と点$A_2$で接し、かつ
$0 \lt p 1$を満たすとする。$p$と$q$の値を求めよ。
(2)$r,s$を実数とする。
$zx$平面上の直線$z=rx+s$は、球面$C$と
$zx$平面が交わってできる円と点$B_1$で接し、
球面$D$と$zx$平面が交わってできる円と点$B_2$で
接し、かつ、$r \lt -1$を満たすとする。
$r$と$s$の値を求めよ。
以下、点$E$は$\overrightarrow{ A_1 E }=(0,0,1)$を満たすとし、
$3$点$A_1,A_2,E$を通る平面を$\alpha$とする。
また、点$F$は$\overrightarrow{ B_1 E }=(0,1,0)$を満たすとし、
$3$点$B_1,B_2,F$を通る平面を$\beta$とする。
$\alpha$と$\beta$が交わってできる直線を
$\ell$とし、$\ell$と$xy$平面の交点を
$G,\ell$と$zx$平面の交点を$H$とする。
(3)$G$の座標を求めよ。
(4)$\ell$上の点$T$を、実数$t$を用いて
$\overrightarrow{OT}=\overrightarrow{OG}+t\overrightarrow{OH}$と表す。
$\triangle OMT$の面積が最小となる$t$の値の求めよ。
$2025$年慶應義塾大学経済学部過去問題
この動画を見る
$\boxed{5}$
座標平面の原点$O$を中心とする半径$1$の
球面を$C$、点$M(4,0,0)$を中心とする
半径$2$の球面上を$D$とする。
(1)$p,q$を実数とする。
$xy$平面上の直線$y=px+q$は、
球面$C$と$xy$平面が交わってできる円と
点$A_1$で接し、球面$D$と$xy$平面が交わって
できる円と点$A_2$で接し、かつ
$0 \lt p 1$を満たすとする。$p$と$q$の値を求めよ。
(2)$r,s$を実数とする。
$zx$平面上の直線$z=rx+s$は、球面$C$と
$zx$平面が交わってできる円と点$B_1$で接し、
球面$D$と$zx$平面が交わってできる円と点$B_2$で
接し、かつ、$r \lt -1$を満たすとする。
$r$と$s$の値を求めよ。
以下、点$E$は$\overrightarrow{ A_1 E }=(0,0,1)$を満たすとし、
$3$点$A_1,A_2,E$を通る平面を$\alpha$とする。
また、点$F$は$\overrightarrow{ B_1 E }=(0,1,0)$を満たすとし、
$3$点$B_1,B_2,F$を通る平面を$\beta$とする。
$\alpha$と$\beta$が交わってできる直線を
$\ell$とし、$\ell$と$xy$平面の交点を
$G,\ell$と$zx$平面の交点を$H$とする。
(3)$G$の座標を求めよ。
(4)$\ell$上の点$T$を、実数$t$を用いて
$\overrightarrow{OT}=\overrightarrow{OG}+t\overrightarrow{OH}$と表す。
$\triangle OMT$の面積が最小となる$t$の値の求めよ。
$2025$年慶應義塾大学経済学部過去問題
【数C】【平面上のベクトル】ベクトル方程式7 ※問題文は概要欄

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
平面上の異なる2つの定点O, Aと任意の点Pに対し,
$\overrightarrow{OA}=\vec{a}$, $\overrightarrow{OP}=\vec{p}$とする。
次のベクトル方程式はどのような図形を表すか。
(1) $|\vec{p}+2\vec{a}|=|\vec{p}-2\vec{a}|$
(2) $2\vec{a}\cdot\vec{p}=|\vec{a}||\vec{p}|$
この動画を見る
平面上の異なる2つの定点O, Aと任意の点Pに対し,
$\overrightarrow{OA}=\vec{a}$, $\overrightarrow{OP}=\vec{p}$とする。
次のベクトル方程式はどのような図形を表すか。
(1) $|\vec{p}+2\vec{a}|=|\vec{p}-2\vec{a}|$
(2) $2\vec{a}\cdot\vec{p}=|\vec{a}||\vec{p}|$
【数C】【平面上のベクトル】ベクトル方程式6 ※問題文は概要欄

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
平面上の$\triangle$ABCに対して,
条件$|\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}|=3$
を満たす動点Pはどのような図形を描くか。
この動画を見る
平面上の$\triangle$ABCに対して,
条件$|\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}|=3$
を満たす動点Pはどのような図形を描くか。
【数C】【平面上のベクトル】ベクトル方程式5 ※問題文は概要欄

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\triangle$ABCの頂点A, B, Cの位置ベクトルを, それぞれ$\vec{a}$, $\vec{b}$, $\vec{c}$とする。
直線上の点をP($\vec{p}$)として, 次の直線のベクトル方程式を求めよ。
(1) Aから直線BCへの垂線$\qquad$
(2) Aと辺BCの中点を通る直線
この動画を見る
$\triangle$ABCの頂点A, B, Cの位置ベクトルを, それぞれ$\vec{a}$, $\vec{b}$, $\vec{c}$とする。
直線上の点をP($\vec{p}$)として, 次の直線のベクトル方程式を求めよ。
(1) Aから直線BCへの垂線$\qquad$
(2) Aと辺BCの中点を通る直線
【数C】【平面上のベクトル】ベクトル方程式4 ※問題文は概要欄

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
A(-6, 2), B(3, -5)とする。線分ABの垂直二等分線の方程式を、ベクトルを利用して求めよ。
この動画を見る
A(-6, 2), B(3, -5)とする。線分ABの垂直二等分線の方程式を、ベクトルを利用して求めよ。
【数C】【平面上のベクトル】ベクトル方程式3 ※問題文は概要欄

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
ベクトル$\left(-1,\sqrt{3}\right)$に垂直で,
原点Oからの距離が4である直線の方程式を求めよ。
この動画を見る
ベクトル$\left(-1,\sqrt{3}\right)$に垂直で,
原点Oからの距離が4である直線の方程式を求めよ。
【数C】【平面上のベクトル】ベクトル方程式2 ※問題文は概要欄

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
O(0,0), A(2,0), B(1,2)に対して、
点Pが次の条件を満たしながら動くとき、
点Pの存在範囲を図示せよ。
(1) $\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$, $0≦s≦1$, $1≦t≦3$
(2) $\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$, $1≦s+t≦3$
(3) $\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$, $0≦2s+3t≦6$, $s≧0$, $t≧0$
この動画を見る
O(0,0), A(2,0), B(1,2)に対して、
点Pが次の条件を満たしながら動くとき、
点Pの存在範囲を図示せよ。
(1) $\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$, $0≦s≦1$, $1≦t≦3$
(2) $\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$, $1≦s+t≦3$
(3) $\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$, $0≦2s+3t≦6$, $s≧0$, $t≧0$
福田の数学〜東京科学大学(旧・東京工業大学)2025理系第2問〜ねじれの位置にある直線上の2点ずつでできる四面体の体積の最大最小

単元:
#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
空間の点$(0,0,1)$を通り
$(1,-1,0)$を方向ベクトルとする
直線を$\ell$とし、点$(1,0,3)$を通り$(0,1,-2)$を
方向ベクトルとする直線を$m$とする。
(1)$P$を$\ell$上の点とし、$Q$を$m$上の点とする。
また直線$PQ$は直線$\ell$と直線$m$に垂線であるとする。
このとき$P$と$Q$の座標、
および線分$PQ$の長さを求めよ。
(2)$\ell$上に$2$点
$A=(t,-t,1),$
$B(2+t+\sin t,-2-t-\sin t,1)$
があり、$m$上に$2$点
$C=(1,t,3,-2t),$
$D=(1,2+t<\cos t,-1-2t-2\cos t)$
があるとする。ただし、$y$は実数とする。
四面体$ABCD$の体積を$V(t)$とする。
$V(0)$を求めよ。
(3)$t$が$t\geqq 0$を動くとき、
$V(t)$の最大値と最小値を求めよ。
$2025$年東京科学大学(旧・東京工業大学)
理系過去問題
この動画を見る
$\boxed{2}$
空間の点$(0,0,1)$を通り
$(1,-1,0)$を方向ベクトルとする
直線を$\ell$とし、点$(1,0,3)$を通り$(0,1,-2)$を
方向ベクトルとする直線を$m$とする。
(1)$P$を$\ell$上の点とし、$Q$を$m$上の点とする。
また直線$PQ$は直線$\ell$と直線$m$に垂線であるとする。
このとき$P$と$Q$の座標、
および線分$PQ$の長さを求めよ。
(2)$\ell$上に$2$点
$A=(t,-t,1),$
$B(2+t+\sin t,-2-t-\sin t,1)$
があり、$m$上に$2$点
$C=(1,t,3,-2t),$
$D=(1,2+t<\cos t,-1-2t-2\cos t)$
があるとする。ただし、$y$は実数とする。
四面体$ABCD$の体積を$V(t)$とする。
$V(0)$を求めよ。
(3)$t$が$t\geqq 0$を動くとき、
$V(t)$の最大値と最小値を求めよ。
$2025$年東京科学大学(旧・東京工業大学)
理系過去問題
福田の数学〜一橋大学2025文系第4問〜ベクトル方程式と領域と角を2等分するベクトル

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#図形と方程式#軌跡と領域#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
原点を$O$とする座標空間内の
$2$点$A(0,3,-5),B(5,-2,10)$に対して
$\overrightarrow{OP}=s\left \{ (1-t)\overrightarrow{OA}+t\overrightarrow{OB} \right \},x\geqq 0,\dfrac{1}{5} \leqq t \leqq \dfrac{3}{5}$
で定まる点$P$が存在する範囲を$D$とする。
$D$に含まれる半径$10\sqrt2$の円のうち、
その中心と原点との距離が最小となるものを
$C$とする。
円$C$の中心の座標を求めよ。
$2025$年一橋大学文系過去問題
この動画を見る
$\boxed{4}$
原点を$O$とする座標空間内の
$2$点$A(0,3,-5),B(5,-2,10)$に対して
$\overrightarrow{OP}=s\left \{ (1-t)\overrightarrow{OA}+t\overrightarrow{OB} \right \},x\geqq 0,\dfrac{1}{5} \leqq t \leqq \dfrac{3}{5}$
で定まる点$P$が存在する範囲を$D$とする。
$D$に含まれる半径$10\sqrt2$の円のうち、
その中心と原点との距離が最小となるものを
$C$とする。
円$C$の中心の座標を求めよ。
$2025$年一橋大学文系過去問題
福田の数学〜慶應義塾大学看護医療学部2025第2問(2)〜円のベクトル方程式

単元:
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
(2)平面上の異なる$2$点$A(\overrightarrow{a}),B(\overrightarrow{b})$に対して、
ベクトル方程式
$2 \vert \overrightarrow{p}-\overrightarrow{a}=\vert \overrightarrow{p}-\overrightarrow{b}\vert$
を満たす点$P(\overrightarrow{p})$全体の集合は円となる。
この円の中心の位置ベクトルは$\boxed{サ}$で半径は
$\boxed{シ}$となる。
ただし、$\boxed{シ}$では根号を用いない表記とすること。
$2025$年慶應義塾大学看護医療学部過去問題
この動画を見る
$\boxed{2}$
(2)平面上の異なる$2$点$A(\overrightarrow{a}),B(\overrightarrow{b})$に対して、
ベクトル方程式
$2 \vert \overrightarrow{p}-\overrightarrow{a}=\vert \overrightarrow{p}-\overrightarrow{b}\vert$
を満たす点$P(\overrightarrow{p})$全体の集合は円となる。
この円の中心の位置ベクトルは$\boxed{サ}$で半径は
$\boxed{シ}$となる。
ただし、$\boxed{シ}$では根号を用いない表記とすること。
$2025$年慶應義塾大学看護医療学部過去問題
福田の数学〜東北大学2025文系第3問〜四面体を拡張した四角錐の位置ベクトル

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
四面体$OABC$において、
$\overrightarrow{OA}=\overrightarrow{a},\overrightarrow{OB}=\overrightarrow{b},\overrightarrow{OC}=\overrightarrow{c}$とする。
点$D$は
$\overrightarrow{AD}=3\overrightarrow{AB}+2\overrightarrow{AC}$を満たすとする。
このとき、以下の問いに答えよ。
(1)四面体$OABC$の体積を$V$とするとき、
四角錐$OABDC$の体積を$V$を用いて表せ。
(2)$\overrightarrow{OD}$を$\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$で表せ。
(3)線分$AD$と線分$BC$の交点を$P$とするとき、
$\overrightarrow{OP}$を$\overrightarrow{b},\overrightarrow{c}$を用いて表せ。
(4)四面体$OABC$が$1$辺の長さ$1$の正四面体であるとき、
線分$OD$の長さを求めよ。
$2025$年東北大学文系過去問題
この動画を見る
$\boxed{3}$
四面体$OABC$において、
$\overrightarrow{OA}=\overrightarrow{a},\overrightarrow{OB}=\overrightarrow{b},\overrightarrow{OC}=\overrightarrow{c}$とする。
点$D$は
$\overrightarrow{AD}=3\overrightarrow{AB}+2\overrightarrow{AC}$を満たすとする。
このとき、以下の問いに答えよ。
(1)四面体$OABC$の体積を$V$とするとき、
四角錐$OABDC$の体積を$V$を用いて表せ。
(2)$\overrightarrow{OD}$を$\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$で表せ。
(3)線分$AD$と線分$BC$の交点を$P$とするとき、
$\overrightarrow{OP}$を$\overrightarrow{b},\overrightarrow{c}$を用いて表せ。
(4)四面体$OABC$が$1$辺の長さ$1$の正四面体であるとき、
線分$OD$の長さを求めよ。
$2025$年東北大学文系過去問題
福田の数学〜京都大学2025文系第5問〜平面が定点を通ることの証明

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#平面上のベクトル#恒等式・等式・不等式の証明#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{5}$
座標空間の$4$点$O,A,B,C$同一平面上にないとする。
$s,t,u$は$0$でない実数とする。
直線$OA$上の点$L$、直線$OB$の点$M$、直線$OC$上の点$N$を
$\overrightarrow{ OL }=s\overrightarrow{ OA},\quad \overrightarrow{ OM }=t\overrightarrow{ OB},\quad \overrightarrow{ ON }=u\overrightarrow{ OC }$
が成り立つようにとる。
$s,t,u$が$\dfrac{1}{s}+\dfrac{2}{t}+\dfrac{3}{u}=4$を満たす範囲で
あらゆる値をとるとき、
$3$点$L,M,N$の定める平面$LMN$は、
$s,t,u$の値に無関係な一定の点を通ることを示せ。
$2025$年京都大学文系過去問題
この動画を見る
$\boxed{5}$
座標空間の$4$点$O,A,B,C$同一平面上にないとする。
$s,t,u$は$0$でない実数とする。
直線$OA$上の点$L$、直線$OB$の点$M$、直線$OC$上の点$N$を
$\overrightarrow{ OL }=s\overrightarrow{ OA},\quad \overrightarrow{ OM }=t\overrightarrow{ OB},\quad \overrightarrow{ ON }=u\overrightarrow{ OC }$
が成り立つようにとる。
$s,t,u$が$\dfrac{1}{s}+\dfrac{2}{t}+\dfrac{3}{u}=4$を満たす範囲で
あらゆる値をとるとき、
$3$点$L,M,N$の定める平面$LMN$は、
$s,t,u$の値に無関係な一定の点を通ることを示せ。
$2025$年京都大学文系過去問題
【数C】【平面上のベクトル】ベクトル方程式1 ※問題文は概要欄

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題1
$\triangle ABC$の重心を$G$、辺$BC$の中点を$M$とし、$\overrightarrow{GA}=\vec{a}, \overrightarrow{GB}=\vec{b}$とする。
(1) $\overrightarrow{AM}$、$\overrightarrow{GC}$を$\vec{a}, \vec{b}$を用いて表せ。
(2)点$M$を通り、辺$CA$に平行な直線上の点を$P$とし、$\overrightarrow{GP}=\vec{p}$とする。この直線のベクトル方程式を、$\vec{a}, \vec{b}, \vec{p}$を用いて求めよ。
問題2
2直線 $l:(x,y)=(0,3)+s(1,2), m:(x,y)=(6,1)+t(-2,3)$について、次の問いに答えよ。ただし、$s,t$は媒介変数とする。
(1)$l$と$m$の交点の座標を求めよ。
(2)点$P(4,1)$から$l$に垂線$PQ$を下ろす。このとき、点$Q$の座標を求めよ。
問題3
$\triangle OAB$に対して、点$P$が次の条件を満たしながら動くとき、点$P$の存在範囲を図示せよ。
(1) $\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}, s+t=4, s\geqq0, t\geqq0$
(2) $\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}, 0\leqq s+t\leqq4, s\geqq0, t\geqq0$
この動画を見る
問題1
$\triangle ABC$の重心を$G$、辺$BC$の中点を$M$とし、$\overrightarrow{GA}=\vec{a}, \overrightarrow{GB}=\vec{b}$とする。
(1) $\overrightarrow{AM}$、$\overrightarrow{GC}$を$\vec{a}, \vec{b}$を用いて表せ。
(2)点$M$を通り、辺$CA$に平行な直線上の点を$P$とし、$\overrightarrow{GP}=\vec{p}$とする。この直線のベクトル方程式を、$\vec{a}, \vec{b}, \vec{p}$を用いて求めよ。
問題2
2直線 $l:(x,y)=(0,3)+s(1,2), m:(x,y)=(6,1)+t(-2,3)$について、次の問いに答えよ。ただし、$s,t$は媒介変数とする。
(1)$l$と$m$の交点の座標を求めよ。
(2)点$P(4,1)$から$l$に垂線$PQ$を下ろす。このとき、点$Q$の座標を求めよ。
問題3
$\triangle OAB$に対して、点$P$が次の条件を満たしながら動くとき、点$P$の存在範囲を図示せよ。
(1) $\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}, s+t=4, s\geqq0, t\geqq0$
(2) $\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}, 0\leqq s+t\leqq4, s\geqq0, t\geqq0$
【数C】【平面上のベクトル】ベクトルと図形3 ※問題文は概要欄

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題1
$\triangle \rm{ABC}$において、$\rm{AB}=3,AC=2, \angle A=60^{ \circ }$,外心を$\rm{O}$とする。$\overrightarrow{{\textrm{AB}}}=\vec{b},\overrightarrow{{\textrm{AC}}}=\vec{c}$とするとき、$\overrightarrow{{\textrm{AO}}}$を$\vec{b},\vec{c}$を用いて表せ。
問題2
平行四辺形$\rm{ABCD}$において、次の等式が成り立つことを証明せよ。
$\rm{2(AB^2+BC^2)=AC^2+BD^2}$
問題3
$\triangle \rm{ABC}$の辺$\rm{BC}$を1:2に内分する点を$\rm{D}$とする。このとき、等式$\rm{2AB^2+AC^2=3(AD^2+2BD^2)}$が成り立つことを証明せよ。
この動画を見る
問題1
$\triangle \rm{ABC}$において、$\rm{AB}=3,AC=2, \angle A=60^{ \circ }$,外心を$\rm{O}$とする。$\overrightarrow{{\textrm{AB}}}=\vec{b},\overrightarrow{{\textrm{AC}}}=\vec{c}$とするとき、$\overrightarrow{{\textrm{AO}}}$を$\vec{b},\vec{c}$を用いて表せ。
問題2
平行四辺形$\rm{ABCD}$において、次の等式が成り立つことを証明せよ。
$\rm{2(AB^2+BC^2)=AC^2+BD^2}$
問題3
$\triangle \rm{ABC}$の辺$\rm{BC}$を1:2に内分する点を$\rm{D}$とする。このとき、等式$\rm{2AB^2+AC^2=3(AD^2+2BD^2)}$が成り立つことを証明せよ。
【数C】【平面上のベクトル】位置ベクトル ※問題文は概要欄

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題1
$\triangle \rm{ABC}$の重心を$\rm{G}$とするとき、この平面上の任意の点$\rm{P}$に対して、等式$\rm{\overrightarrow{AP}+\overrightarrow{BP}-2\overrightarrow{CP}=3\overrightarrow{GC}}$が成り立つことを証明せよ。
問題2
$\triangle \rm{ABC}$と点$\rm{P}$に対して、次の等式が成り立つとき、点$\rm{P}$の位置をいえ。
(1) $\rm{\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}=\overrightarrow{AB}}$
(2)$\rm{\overrightarrow{AP}+\overrightarrow{BP}+\overrightarrow{CP}=\vec{0}} $
(3)$\rm{\overrightarrow{PA}+\overrightarrow{PC}=\overrightarrow{AC}}$
問題3
$\triangle \rm{ABC}$と点$\rm{P}$に対して、等式 $\rm{5\overrightarrow{AP}+4\overrightarrow{BP}+3\overrightarrow{CP}=\vec{0}}$が成り立っている。
(1)点$\rm{P}$の位置をいえ。
(2)$\triangle \rm{PBC}:\triangle \rm{PCA}:\triangle \rm{PAB}$を求めよ。
この動画を見る
問題1
$\triangle \rm{ABC}$の重心を$\rm{G}$とするとき、この平面上の任意の点$\rm{P}$に対して、等式$\rm{\overrightarrow{AP}+\overrightarrow{BP}-2\overrightarrow{CP}=3\overrightarrow{GC}}$が成り立つことを証明せよ。
問題2
$\triangle \rm{ABC}$と点$\rm{P}$に対して、次の等式が成り立つとき、点$\rm{P}$の位置をいえ。
(1) $\rm{\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}=\overrightarrow{AB}}$
(2)$\rm{\overrightarrow{AP}+\overrightarrow{BP}+\overrightarrow{CP}=\vec{0}} $
(3)$\rm{\overrightarrow{PA}+\overrightarrow{PC}=\overrightarrow{AC}}$
問題3
$\triangle \rm{ABC}$と点$\rm{P}$に対して、等式 $\rm{5\overrightarrow{AP}+4\overrightarrow{BP}+3\overrightarrow{CP}=\vec{0}}$が成り立っている。
(1)点$\rm{P}$の位置をいえ。
(2)$\triangle \rm{PBC}:\triangle \rm{PCA}:\triangle \rm{PAB}$を求めよ。
【数C】【平面上のベクトル】ベクトルと図形2 ※問題文は概要欄

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題1
$\triangle \rm OAB$において、辺$\rm OB$の中点を$\rm M$辺$\rm AB$を$1:2$に内分する点を$\rm C$、辺$\rm OA$を$2:3$に内分する点を$\rm D$、線分$\rm CM$と線分$\rm BD$の交点を$\rm P$とする。また、$\overrightarrow {\rm OA}=\vec{a},\overrightarrow{\rm OB}=\vec{b}$とする。
(1)$\overrightarrow{\rm OP}$を$\vec{a},\vec{b}$を用いて表せ。
(2)直線$\rm OP$と辺$\rm AB$の交点を$\rm Q$とするとき、$\rm AQ:QB$を求めよ。
問題2
$\rm OA=3, OC=2$である長方形$\rm OABC$がある。辺$\rm OA$を$1:2$に内分する点を$\rm D$、辺$\rm AB$を$3:1$に内分する点を$\rm E$とするとき、$\rm CD\perp OE$であることを証明せよ。
問題3
鋭角三角形$\rm ABC$の外心を$\rm O$、辺$\rm BC$の中点を$\rm M$とする。頂点$\rm A$から辺$\rm BC$に垂線$\rm AN$を下ろし、線分$\rm AN$上に点$\rm H$を$\rm AH=2OM$となるようにとると、$\rm H$は$\triangle \rm ABC$の垂心であることを証明せよ。
問題4
$\rm OA=6,OB=4,\angle AOB=60°$である$\triangle \rm OAB$において、頂点$\rm A$から辺$\rm OB$に垂線$\rm AC$,頂点$\rm B$から辺$\rm OA$に垂線$\rm BD$を下ろす。線分$\rm AC$と線分$\rm BD$の交点を$\rm H$とするとき、$\overrightarrow{\rm OH}$を$\rm \overrightarrow{OA},\overrightarrow{OB}$を用いて表せ。
この動画を見る
問題1
$\triangle \rm OAB$において、辺$\rm OB$の中点を$\rm M$辺$\rm AB$を$1:2$に内分する点を$\rm C$、辺$\rm OA$を$2:3$に内分する点を$\rm D$、線分$\rm CM$と線分$\rm BD$の交点を$\rm P$とする。また、$\overrightarrow {\rm OA}=\vec{a},\overrightarrow{\rm OB}=\vec{b}$とする。
(1)$\overrightarrow{\rm OP}$を$\vec{a},\vec{b}$を用いて表せ。
(2)直線$\rm OP$と辺$\rm AB$の交点を$\rm Q$とするとき、$\rm AQ:QB$を求めよ。
問題2
$\rm OA=3, OC=2$である長方形$\rm OABC$がある。辺$\rm OA$を$1:2$に内分する点を$\rm D$、辺$\rm AB$を$3:1$に内分する点を$\rm E$とするとき、$\rm CD\perp OE$であることを証明せよ。
問題3
鋭角三角形$\rm ABC$の外心を$\rm O$、辺$\rm BC$の中点を$\rm M$とする。頂点$\rm A$から辺$\rm BC$に垂線$\rm AN$を下ろし、線分$\rm AN$上に点$\rm H$を$\rm AH=2OM$となるようにとると、$\rm H$は$\triangle \rm ABC$の垂心であることを証明せよ。
問題4
$\rm OA=6,OB=4,\angle AOB=60°$である$\triangle \rm OAB$において、頂点$\rm A$から辺$\rm OB$に垂線$\rm AC$,頂点$\rm B$から辺$\rm OA$に垂線$\rm BD$を下ろす。線分$\rm AC$と線分$\rm BD$の交点を$\rm H$とするとき、$\overrightarrow{\rm OH}$を$\rm \overrightarrow{OA},\overrightarrow{OB}$を用いて表せ。
【数C】【平面上のベクトル】ベクトルと図形1 ※問題文は概要欄
単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題1
$△ABC$の辺$AB$,$BC$,$CA$を2:1に内分する点を、それぞれ$A_1$,$B1_1$,$C_1$とする。更に、$△A_1B_1C_1$の辺$A_1B_1$,$B_1C_1$を2:1に内分する点を、それぞれ$A_2$,$B_2$とする。このとき、$A_2B_2//AB$であることを示せ。
問題2
△ABCにおいて、辺BCを2:1に外分する点をP,辺ABを1:2に内分する点をQ、辺CAの中点をRとする。
(1)3点P,Q,Rは一直線上にあることを証明せよ。
(2)QR:QPを求めよ。
問題3
平行四辺形ABCDにおいて、辺ABを3:2に内分する点をP、対角線BDを2:5に内分する点をQとする。
(1)3点P,Q,Cは一直線上にあることを証明せよ。
(2)PQ:QCを求めよ。
問題4
△ABCにおいて、辺ABを1:2に内分する点をD、辺ACを3:1に内分する点をEとし、線分CD、BEの交点をPとする。$\overrightarrow{ AB }=\overrightarrow{ b }$,$\overrightarrow{ AC }=\overrightarrow{ c }$とするとき、$\overrightarrow{ AP }$を$\overrightarrow{b}$,$\overrightarrow{c}$を用いて表せ。
この動画を見る
問題1
$△ABC$の辺$AB$,$BC$,$CA$を2:1に内分する点を、それぞれ$A_1$,$B1_1$,$C_1$とする。更に、$△A_1B_1C_1$の辺$A_1B_1$,$B_1C_1$を2:1に内分する点を、それぞれ$A_2$,$B_2$とする。このとき、$A_2B_2//AB$であることを示せ。
問題2
△ABCにおいて、辺BCを2:1に外分する点をP,辺ABを1:2に内分する点をQ、辺CAの中点をRとする。
(1)3点P,Q,Rは一直線上にあることを証明せよ。
(2)QR:QPを求めよ。
問題3
平行四辺形ABCDにおいて、辺ABを3:2に内分する点をP、対角線BDを2:5に内分する点をQとする。
(1)3点P,Q,Cは一直線上にあることを証明せよ。
(2)PQ:QCを求めよ。
問題4
△ABCにおいて、辺ABを1:2に内分する点をD、辺ACを3:1に内分する点をEとし、線分CD、BEの交点をPとする。$\overrightarrow{ AB }=\overrightarrow{ b }$,$\overrightarrow{ AC }=\overrightarrow{ c }$とするとき、$\overrightarrow{ AP }$を$\overrightarrow{b}$,$\overrightarrow{c}$を用いて表せ。
落とせないベクトル!京大でもびびる必要なし!【京都大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数C
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
三角形ABCと点Pに対して、次の二つの条件は同値であることを証明せよ。
(i) 点Pは三角形ABCの内部(周は除く)にある
(ii)正の数a,b,cがあって、aPA+bPB+cPC=0が成り立つ。
この動画を見る
三角形ABCと点Pに対して、次の二つの条件は同値であることを証明せよ。
(i) 点Pは三角形ABCの内部(周は除く)にある
(ii)正の数a,b,cがあって、aPA+bPB+cPC=0が成り立つ。
福田の数学〜早稲田大学2024社会科学部第2問〜三角形の内心と垂心の位置ベクトル

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$
\begin{eqnarray}
\fcolorbox{black}{ white }{$2$}OA = 6, \,OB = 5,\,AB=7である\triangle OABにおいて、\vec{a} \ = \ \vec{OA} , \ \vec{b} \ = \ \vec{OB}とおく。
\end{eqnarray}
$
$
\begin{eqnarray}
(1)\triangle OABの内心を1、辺ABと直線OIの交点をCとする。\vec{OC}を\vec{a}, \ \vec{b}で表せ。
\end{eqnarray}
$
$
\begin{eqnarray}
(1) \vec{OI}を \vec{a}, \ \vec{b}で表せ。
\end{eqnarray}
$
この動画を見る
$
\begin{eqnarray}
\fcolorbox{black}{ white }{$2$}OA = 6, \,OB = 5,\,AB=7である\triangle OABにおいて、\vec{a} \ = \ \vec{OA} , \ \vec{b} \ = \ \vec{OB}とおく。
\end{eqnarray}
$
$
\begin{eqnarray}
(1)\triangle OABの内心を1、辺ABと直線OIの交点をCとする。\vec{OC}を\vec{a}, \ \vec{b}で表せ。
\end{eqnarray}
$
$
\begin{eqnarray}
(1) \vec{OI}を \vec{a}, \ \vec{b}で表せ。
\end{eqnarray}
$
福田の数学〜上智大学2024理工学部第3問〜円の内部を反射しながら進む点の通過範囲

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$O$ を中心とする半径1の円周上の点 $P_1$ から図のように (図は動画内参照) 点 $Q$ を発射すると円の中を $P_2, \, P_3, \, \ldots $ と反射しながら止まることなく動き続けるとする。$\vec{OP_i}=\vec{p_i}$ とおく。$\vec{p_3}, \, \vec{p_4}$ を $\vec{p_1}, \, \vec{p_2}$ で表せ。$\vec{p_i}=\vec{p_1}$ となる最小の $i\ge2$ を求めよ。点 $Q$ が再び点 $P_1$ に到達するまでに、線分 $OQ$ がちょうど2回通過する領域の面積は?
この動画を見る
$O$ を中心とする半径1の円周上の点 $P_1$ から図のように (図は動画内参照) 点 $Q$ を発射すると円の中を $P_2, \, P_3, \, \ldots $ と反射しながら止まることなく動き続けるとする。$\vec{OP_i}=\vec{p_i}$ とおく。$\vec{p_3}, \, \vec{p_4}$ を $\vec{p_1}, \, \vec{p_2}$ で表せ。$\vec{p_i}=\vec{p_1}$ となる最小の $i\ge2$ を求めよ。点 $Q$ が再び点 $P_1$ に到達するまでに、線分 $OQ$ がちょうど2回通過する領域の面積は?
福田の数学〜中央大学2024経済学部第1問(5)〜ベクトルの基本的な演算

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\bigtriangleup \mathrm{ABC}$ と点 $\mathrm{P}$ があり、$2\vec{\mathrm{AP}}+3\vec{\mathrm{BP}}+5\vec{\mathrm{CP}}=\vec{0}$ を満たしている。このとき、$\vec{\mathrm{AB}}=\vec{b}, \, \vec{\mathrm{AC}}=\vec{c}$ として、$\vec{\mathrm{AP}}$ を $\vec{b}$ と $\vec{c}$ で表せ。
この動画を見る
$\bigtriangleup \mathrm{ABC}$ と点 $\mathrm{P}$ があり、$2\vec{\mathrm{AP}}+3\vec{\mathrm{BP}}+5\vec{\mathrm{CP}}=\vec{0}$ を満たしている。このとき、$\vec{\mathrm{AB}}=\vec{b}, \, \vec{\mathrm{AC}}=\vec{c}$ として、$\vec{\mathrm{AP}}$ を $\vec{b}$ と $\vec{c}$ で表せ。
福田の数学〜筑波大学2024理系第1問〜交点の位置ベクトルと面積面積
単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
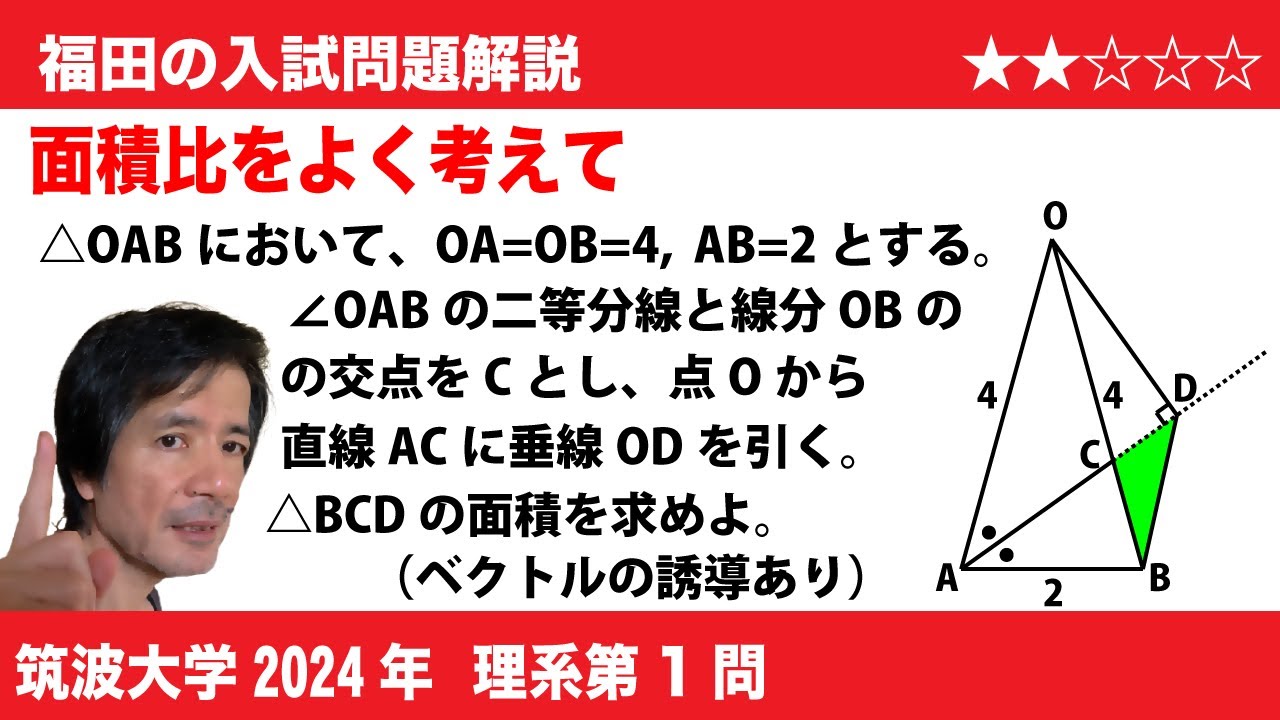
$\triangle \mathrm{OAB}$ において、$\mathrm{OA}=\mathrm{OB}=2$ とする。$\angle \mathrm{OAB}$ の二等分線と線分 $\mathrm{OB}$ の交点を $\mathrm{C}$ とし、点 $\mathrm{O}$ から直線 $\mathrm{AC}$ に垂線 $\mathrm{OD}$ を引く。$\vec{\mathrm{OA}}=\vec{a}, \, \vec{\mathrm{OB}}=\vec{b}$ とおく。以下の問いに答えよ。
$(1)$ $\vec{\mathrm{AC}}$ を $\vec{a}$ と $\vec{b}$ を用いて表せ。
$(2)$ $\vec{\mathrm{OD}}$ を $\vec{a}$ と $\vec{b}$ を用いて表せ。
この動画を見る
$\triangle \mathrm{OAB}$ において、$\mathrm{OA}=\mathrm{OB}=2$ とする。$\angle \mathrm{OAB}$ の二等分線と線分 $\mathrm{OB}$ の交点を $\mathrm{C}$ とし、点 $\mathrm{O}$ から直線 $\mathrm{AC}$ に垂線 $\mathrm{OD}$ を引く。$\vec{\mathrm{OA}}=\vec{a}, \, \vec{\mathrm{OB}}=\vec{b}$ とおく。以下の問いに答えよ。
$(1)$ $\vec{\mathrm{AC}}$ を $\vec{a}$ と $\vec{b}$ を用いて表せ。
$(2)$ $\vec{\mathrm{OD}}$ を $\vec{a}$ と $\vec{b}$ を用いて表せ。
