 ベクトルと平面図形、ベクトル方程式
ベクトルと平面図形、ベクトル方程式
 ベクトルと平面図形、ベクトル方程式
ベクトルと平面図形、ベクトル方程式
福田の一夜漬け数学〜平面ベクトル(1)〜受験編・文理共通
単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
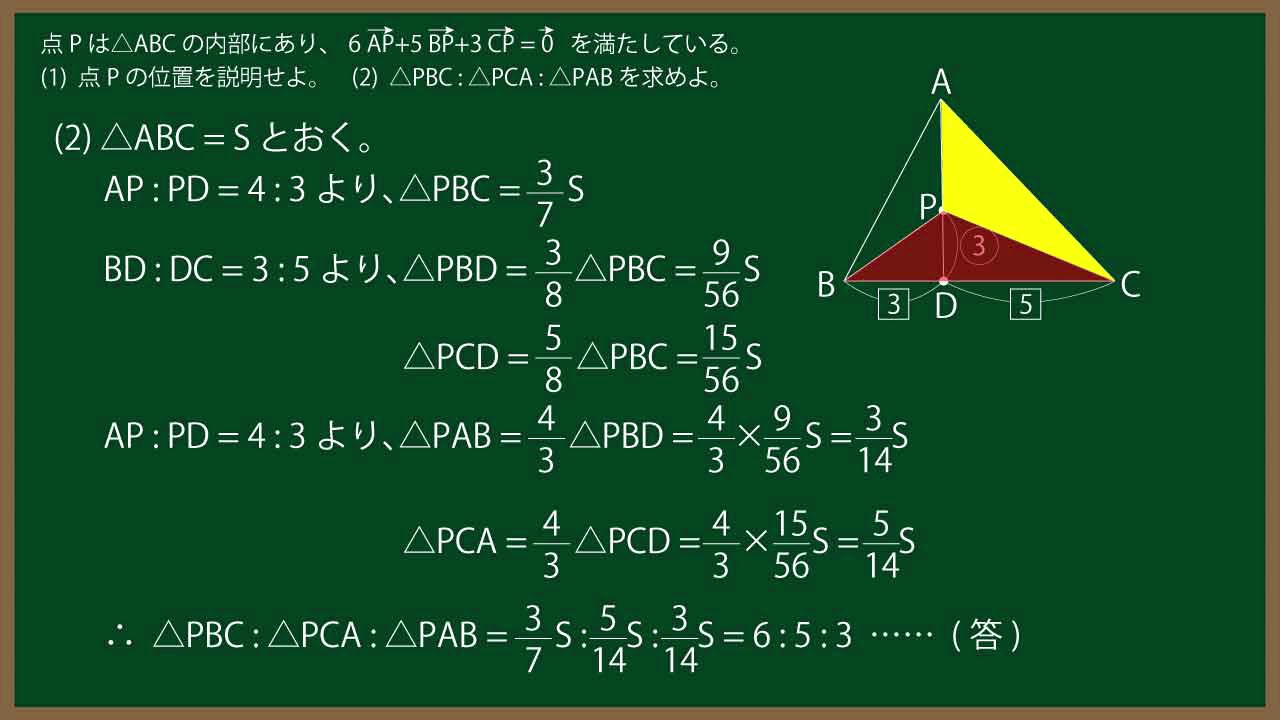
$k$を正の実数とする。点Pは$\triangle ABC$の内部にあり、
$k\ \overrightarrow{ AP }+5\ \overrightarrow{ BP }+3\ \overrightarrow{ CP }=\overrightarrow{ 0 }\\$
を満たしている。また、辺$BC$を$3:5$に内分する点を$D$とする。
(1)$\overrightarrow{ AP }$を、$\overrightarrow{ AB },\overrightarrow{ AC },k$を用いて表せ。
(2)3点$A,P,D$は一直線上にあることを示せ。
(3)$\triangle ABP$の面積が$\triangle CDP$の面積の$\frac{6}{5}$倍に等しいとき
$k$の値を求めよ。
【もとになる問題】
点$P$は$\triangle ABC$の内部にあり、
$6\ \overrightarrow{ AP }+5\ \overrightarrow{ BP }+3\ \overrightarrow{ CP }=\overrightarrow{ 0 }$
を満たしている。
(1)点$P$の位置を説明せよ。
(2)$\triangle PBC:\triangle PCA:\triangle PAB$を求めよ。
この動画を見る
$k$を正の実数とする。点Pは$\triangle ABC$の内部にあり、
$k\ \overrightarrow{ AP }+5\ \overrightarrow{ BP }+3\ \overrightarrow{ CP }=\overrightarrow{ 0 }\\$
を満たしている。また、辺$BC$を$3:5$に内分する点を$D$とする。
(1)$\overrightarrow{ AP }$を、$\overrightarrow{ AB },\overrightarrow{ AC },k$を用いて表せ。
(2)3点$A,P,D$は一直線上にあることを示せ。
(3)$\triangle ABP$の面積が$\triangle CDP$の面積の$\frac{6}{5}$倍に等しいとき
$k$の値を求めよ。
【もとになる問題】
点$P$は$\triangle ABC$の内部にあり、
$6\ \overrightarrow{ AP }+5\ \overrightarrow{ BP }+3\ \overrightarrow{ CP }=\overrightarrow{ 0 }$
を満たしている。
(1)点$P$の位置を説明せよ。
(2)$\triangle PBC:\triangle PCA:\triangle PAB$を求めよ。
【高校数学】数Ⅲ-49 極座標と極方程式⑥

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の図形の極方程式を求めよ。ただし、$O$は極とする。
①極座標が$\left(4,\dfrac{3}{4}\pi\right)$である点$A$を通り、
直線$OA$に垂直な直線
②中心が極$O$、半径が1の円に$\left(2,\dfrac{\pi}{6}\right)$から引いた接線
この動画を見る
次の図形の極方程式を求めよ。ただし、$O$は極とする。
①極座標が$\left(4,\dfrac{3}{4}\pi\right)$である点$A$を通り、
直線$OA$に垂直な直線
②中心が極$O$、半径が1の円に$\left(2,\dfrac{\pi}{6}\right)$から引いた接線
【高校数学】数Ⅲ-48 極座標と極方程式⑤

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の直交座標を用いて表された曲線を、極方程式で表せ。
①$\sqrt3x-y-4=0$
②$x^2-y^2=-4$
③$x^2+y^2=-2x$
この動画を見る
次の直交座標を用いて表された曲線を、極方程式で表せ。
①$\sqrt3x-y-4=0$
②$x^2-y^2=-4$
③$x^2+y^2=-2x$
【高校数学】数Ⅲ-47 極座標と極方程式④

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$O$を極とする次の極方程式を直交座標で表される方程式に直せ。
①$r=\dfrac{1}{2\cos\theta-\sin\theta}$
②$r=\dfrac{2}{1-\sqrt2\cos\theta}$
③$r=\dfrac{2}{1-\cos\theta}$
この動画を見る
$O$を極とする次の極方程式を直交座標で表される方程式に直せ。
①$r=\dfrac{1}{2\cos\theta-\sin\theta}$
②$r=\dfrac{2}{1-\sqrt2\cos\theta}$
③$r=\dfrac{2}{1-\cos\theta}$
【高校数学】数Ⅲ-46 極座標と極方程式③

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$O$を極とする極座標において、
2点$A\left(2,\dfrac{\pi}{6}\right),B\left(4,\dfrac{5}{6}\pi\right)$がある。
①線分$AB$の長さを求めよ。
②$\triangle OAB$の面積を求めよ。
この動画を見る
$O$を極とする極座標において、
2点$A\left(2,\dfrac{\pi}{6}\right),B\left(4,\dfrac{5}{6}\pi\right)$がある。
①線分$AB$の長さを求めよ。
②$\triangle OAB$の面積を求めよ。
【高校数学】数Ⅲ-45 極座標と極方程式②

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の極座標の点$A,B$の直交座標を求めよ。
①$A\left(3,\dfrac{\pi}{6}\right)$
②$B\left(2,-\dfrac{5}{6}\pi\right)$
次の直交座標の点$C,D$の極座標$(r,\theta)$を求めよ。
ただし、$0\leqq \theta \leqq 2\pi$とする。
③$C(0,-2)$
④$D(\sqrt3,-3)$
この動画を見る
次の極座標の点$A,B$の直交座標を求めよ。
①$A\left(3,\dfrac{\pi}{6}\right)$
②$B\left(2,-\dfrac{5}{6}\pi\right)$
次の直交座標の点$C,D$の極座標$(r,\theta)$を求めよ。
ただし、$0\leqq \theta \leqq 2\pi$とする。
③$C(0,-2)$
④$D(\sqrt3,-3)$
【高校数学】数Ⅲ-44 極座標と極方程式①

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右図において$(r、0)$を点$P$の極座標といい、
点$O$を①、半直線$OX$を②、角$\theta$を③という。
極座標に対して、$x、y$座標の組$(x,y)$を④座標といい、
x= ⑤、y=⑥、$r = \sqrt{x ^ 2 + y ^ 2}$が成り立つ。
平面上の曲線が、極座標$(r,\theta)$を用いた式$r=f(\theta)$または
$F(r,\theta)=0$で表されるとき、この方程式を曲線の極方程式という。
中心が極$O$、半径が$a$の円→⑦
中心が$(a,0)$、半径が$a$の円→⑧
極$O$を通り、始線となす角が$\beta$の直線→⑨
図は動画内参照
この動画を見る
右図において$(r、0)$を点$P$の極座標といい、
点$O$を①、半直線$OX$を②、角$\theta$を③という。
極座標に対して、$x、y$座標の組$(x,y)$を④座標といい、
x= ⑤、y=⑥、$r = \sqrt{x ^ 2 + y ^ 2}$が成り立つ。
平面上の曲線が、極座標$(r,\theta)$を用いた式$r=f(\theta)$または
$F(r,\theta)=0$で表されるとき、この方程式を曲線の極方程式という。
中心が極$O$、半径が$a$の円→⑦
中心が$(a,0)$、半径が$a$の円→⑧
極$O$を通り、始線となす角が$\beta$の直線→⑨
図は動画内参照
【高校数学】 数B-55 空間における平面・直線の方程式③

単元:
#数Ⅱ#平面上のベクトル#図形と方程式#点と直線#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①直線$\ell:x=-1+t,y=3+t,z=1+2t$上に点$P$がある.
線分$OP$が最小となる点$P$の座標を求めよう.
②2点$A(3,1,4),B(1,2,-1)$を通る直線上に点のうちで,
原点に最も近い点の座標を求めよう.
この動画を見る
①直線$\ell:x=-1+t,y=3+t,z=1+2t$上に点$P$がある.
線分$OP$が最小となる点$P$の座標を求めよう.
②2点$A(3,1,4),B(1,2,-1)$を通る直線上に点のうちで,
原点に最も近い点の座標を求めよう.
【高校数学】 数B-54 空間における平面・直線の方程式②

単元:
#数Ⅱ#平面上のベクトル#図形と方程式#点と直線#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次のような直線の方程式を媒介変数$t$を用いて表そう.
①点$(3,2,1)$を通り,$\overrightarrow{a}=(0,2,1)$に平行な直線
②2点$(5,8,-7),(6,-9,3)$を通る直線
③点$(2,-1,3)$を通り,ベクトル$(5,2,-2)$に平行な直線と,
平面$3x-2y=-4$との交点の座標を求めよう.
この動画を見る
次のような直線の方程式を媒介変数$t$を用いて表そう.
①点$(3,2,1)$を通り,$\overrightarrow{a}=(0,2,1)$に平行な直線
②2点$(5,8,-7),(6,-9,3)$を通る直線
③点$(2,-1,3)$を通り,ベクトル$(5,2,-2)$に平行な直線と,
平面$3x-2y=-4$との交点の座標を求めよう.
【高校数学】 数B-53 空間における平面・直線の方程式①

単元:
#数Ⅱ#平面上のベクトル#図形と方程式#点と直線#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$(x+5)^2+(y-1)^2+(z-2)^2=13$が$xy$平面と交わってできる
図形の方程式を求めよう.
②中心が$(1,a,2)$,半径が6の球面が$zx$平面と交わってできる円の半径が
$3\sqrt3$であるとき,$a$の値を求めよう.
③方程式$x^2+y^2+z^2-2x+4y+6z=2$はどのような図形を
表しているか答えよう.
この動画を見る
①$(x+5)^2+(y-1)^2+(z-2)^2=13$が$xy$平面と交わってできる
図形の方程式を求めよう.
②中心が$(1,a,2)$,半径が6の球面が$zx$平面と交わってできる円の半径が
$3\sqrt3$であるとき,$a$の値を求めよう.
③方程式$x^2+y^2+z^2-2x+4y+6z=2$はどのような図形を
表しているか答えよう.
【高校数学】 数B-52 座標空間における図形③

単元:
#平面上のベクトル#複素数平面#ベクトルと平面図形、ベクトル方程式#図形への応用#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$(x+5)^2+(y-1)^2+(z-2)^2=13$が$xy$平面と交わってできる
図形の方程式を求めよう.
②中心が$(1,a,2)$,半径が6の球面が$zx$平面と交わってできる
円の半径が$3\sqrt3$であるとき,$a$の値を求めよ.
③方程式$x^2+y^2+z^2-2x+4y+6z=2$はどのような図形を
表しているか答えよう.
この動画を見る
①$(x+5)^2+(y-1)^2+(z-2)^2=13$が$xy$平面と交わってできる
図形の方程式を求めよう.
②中心が$(1,a,2)$,半径が6の球面が$zx$平面と交わってできる
円の半径が$3\sqrt3$であるとき,$a$の値を求めよ.
③方程式$x^2+y^2+z^2-2x+4y+6z=2$はどのような図形を
表しているか答えよう.
【高校数学】 数B-51 座標空間における図形②

単元:
#平面上のベクトル#複素数平面#ベクトルと平面図形、ベクトル方程式#図形への応用#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
問題1
点$A(5,-4,7)$を通る,次のような平面の方程式を求めよう.
①$x$軸に垂直
②$z$軸に垂直
③$xy$平面に平行
問題2
次の球面の方程式を求めよう.
④中心が$(3,-1,2)$,半径が5の球面
⑤中心が$(1,3,-1)$で,点$(5,-1,1)$を通る球面
この動画を見る
問題1
点$A(5,-4,7)$を通る,次のような平面の方程式を求めよう.
①$x$軸に垂直
②$z$軸に垂直
③$xy$平面に平行
問題2
次の球面の方程式を求めよう.
④中心が$(3,-1,2)$,半径が5の球面
⑤中心が$(1,3,-1)$で,点$(5,-1,1)$を通る球面
【高校数学】 数B-50 座標空間における図形①

単元:
#平面上のベクトル#複素数平面#ベクトルと平面図形、ベクトル方程式#図形への応用#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
3点$A(8,-7,5),B(-2,3,-5),C(3,-2,-3)$に体して,
次の各点の座標を求めよう.
①線分$AB$を$3:2$に内分する点
②線分$AC$を$2:3$に外分する点
③線分$AB$の中点
④$\triangle ABC$の重心
この動画を見る
3点$A(8,-7,5),B(-2,3,-5),C(3,-2,-3)$に体して,
次の各点の座標を求めよう.
①線分$AB$を$3:2$に内分する点
②線分$AC$を$2:3$に外分する点
③線分$AB$の中点
④$\triangle ABC$の重心
【高校数学】 数B-49 位置ベクトルと図形⑤

単元:
#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
四面体$OABC$と点$P$について,
$7\overrightarrow{OP}+2\overrightarrow{AP}+4\overrightarrow{BP}+5\overrightarrow{CP}=\overrightarrow{O}$が成り立つ.
①点$P$はどのような位置にあるか答えよう.
②四面体$OABC,PABC$の体積をそれぞれ$V_1,V_2$とするとき,
$V_1:V_2$を求めよう.
この動画を見る
四面体$OABC$と点$P$について,
$7\overrightarrow{OP}+2\overrightarrow{AP}+4\overrightarrow{BP}+5\overrightarrow{CP}=\overrightarrow{O}$が成り立つ.
①点$P$はどのような位置にあるか答えよう.
②四面体$OABC,PABC$の体積をそれぞれ$V_1,V_2$とするとき,
$V_1:V_2$を求めよう.
【高校数学】 数B-48 位置ベクトルと図形④

単元:
#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①四面体$OABC$において,辺$AB$を$1:2$に内分する点を$P$,
線分$PC$を$2;3$に内分する点を$Q$とする.
また,辺$OA$の中点を$D$,辺$OB$を$2:1$に内分する点を$E$,
辺$OC$を$1:2$に内分する点を$F$とする.
平面$DEF$と線分$OQ$の交点を$R$とするとき,$OR:OQ$を求めよう.
この動画を見る
①四面体$OABC$において,辺$AB$を$1:2$に内分する点を$P$,
線分$PC$を$2;3$に内分する点を$Q$とする.
また,辺$OA$の中点を$D$,辺$OB$を$2:1$に内分する点を$E$,
辺$OC$を$1:2$に内分する点を$F$とする.
平面$DEF$と線分$OQ$の交点を$R$とするとき,$OR:OQ$を求めよう.
【高校数学】 数B-47 位置ベクトルと図形③

単元:
#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①3点$A(4,3,a),B(2,-1,5),C(5,b,-13)$が一直線上にあるように
$a,b$の値を定めよう.
②4点$A(5,2,5),B(3,1,2),C(-2,-1,-6),D(a,2,3)$が同じ平面上にあるように
定数$a$の値を定めよう.
この動画を見る
①3点$A(4,3,a),B(2,-1,5),C(5,b,-13)$が一直線上にあるように
$a,b$の値を定めよう.
②4点$A(5,2,5),B(3,1,2),C(-2,-1,-6),D(a,2,3)$が同じ平面上にあるように
定数$a$の値を定めよう.
【高校数学】 数B-46 位置ベクトルと図形②

単元:
#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①四面体$OABC$がある.
線分$AB$を$1:2$に内分する点を$D$,線分$BC$の中点を$E$とする.
線分$AE$と線分$CD$の交点を$P$とするとき,
$\overrightarrow{OP}$を$\overrightarrow{OA}=\large{\overrightarrow{a}},\overrightarrow{OB}=\large{\overrightarrow{b}},\overrightarrow{OC}=\large{\overrightarrow{c}}$を用いて表そう.
この動画を見る
①四面体$OABC$がある.
線分$AB$を$1:2$に内分する点を$D$,線分$BC$の中点を$E$とする.
線分$AE$と線分$CD$の交点を$P$とするとき,
$\overrightarrow{OP}$を$\overrightarrow{OA}=\large{\overrightarrow{a}},\overrightarrow{OB}=\large{\overrightarrow{b}},\overrightarrow{OC}=\large{\overrightarrow{c}}$を用いて表そう.
【高校数学】 数B-45 位置ベクトルと図形①

単元:
#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$A(\overrightarrow{a}),B(\overrightarrow{b}),C(\overrightarrow{c}),D(\overrightarrow{d})$を頂点とする四面体の辺$BC$を$3:1$に内分する点を
$P,DP$を$4:3$に外分する点を$Q$,線分$AQ$の中点を$R$とする.
点$P$,点$Q$,点$R$の位置ベクトルを,$\overrightarrow{a},\overrightarrow{b},\overrightarrow{c},\overrightarrow{d}$で表そう.
②四面体$OABC$がある.線分$AB$を$2:3$に内分する点を$P$,
線分$OP$を$10:1$に外分する点を$Q$,線分$CQ$を$3:1$に内分する点を$R$とする.
$\triangle ARB$の重心を$G$とするとき,
$\overrightarrow{OG}$を$\overrightarrow{OA}=\large{\overrightarrow{a}}=\overrightarrow{OB}=\large{\overrightarrow{b}},\overrightarrow{OC},\large{\overrightarrow{c}}$で表そう.
この動画を見る
①$A(\overrightarrow{a}),B(\overrightarrow{b}),C(\overrightarrow{c}),D(\overrightarrow{d})$を頂点とする四面体の辺$BC$を$3:1$に内分する点を
$P,DP$を$4:3$に外分する点を$Q$,線分$AQ$の中点を$R$とする.
点$P$,点$Q$,点$R$の位置ベクトルを,$\overrightarrow{a},\overrightarrow{b},\overrightarrow{c},\overrightarrow{d}$で表そう.
②四面体$OABC$がある.線分$AB$を$2:3$に内分する点を$P$,
線分$OP$を$10:1$に外分する点を$Q$,線分$CQ$を$3:1$に内分する点を$R$とする.
$\triangle ARB$の重心を$G$とするとき,
$\overrightarrow{OG}$を$\overrightarrow{OA}=\large{\overrightarrow{a}}=\overrightarrow{OB}=\large{\overrightarrow{b}},\overrightarrow{OC},\large{\overrightarrow{c}}$で表そう.
【高校数学】 数B-40 点の座標とベクトルの成分

単元:
#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
問題1
$A(1,2,-1),B(0,3,2),C(5,-1,4)$のとき,
次のベクトルを成分で表し,その大きさを求めよう.
①$\overrightarrow{ AB }$
②$\overrightarrow{ BC }$
③4点$A(1,2,4),B(2,-3,2),C(4,-1,5),D$を頂点とする
平行四辺形$ABCD$がある.頂点$D$の座標を求めよう.
この動画を見る
問題1
$A(1,2,-1),B(0,3,2),C(5,-1,4)$のとき,
次のベクトルを成分で表し,その大きさを求めよう.
①$\overrightarrow{ AB }$
②$\overrightarrow{ BC }$
③4点$A(1,2,4),B(2,-3,2),C(4,-1,5),D$を頂点とする
平行四辺形$ABCD$がある.頂点$D$の座標を求めよう.
【高校数学】 数B-34 平面上の点の存在位置③

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎O(0.0)、A(2.1)、B(1.2)、$\overrightarrow{ OP }=s\overrightarrow{ OA }+t\overrightarrow{ OB } $とする。実数S、tが次の条件を満たし ながら変化するとき、点Pの存在範囲を図示しよう。
①$\displaystyle \frac{1}{2}s+t \leqq 2,s \geqq 0,t \geqq 0$
②$ 1\leqq s \leqq 2 ,0 \leqq t \leqq 1$
この動画を見る
◎O(0.0)、A(2.1)、B(1.2)、$\overrightarrow{ OP }=s\overrightarrow{ OA }+t\overrightarrow{ OB } $とする。実数S、tが次の条件を満たし ながら変化するとき、点Pの存在範囲を図示しよう。
①$\displaystyle \frac{1}{2}s+t \leqq 2,s \geqq 0,t \geqq 0$
②$ 1\leqq s \leqq 2 ,0 \leqq t \leqq 1$
【高校数学】 数B-33 平面上の点の存在位置②

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎△OABに対し、$\overrightarrow{ OP }=s\overrightarrow{ OA }+t\overrightarrow{ OB } $とする。実数S,tが次の条件を満たしながら動くとき、 点Pの存在範囲を図示しよう。
①$s+t \leqq \displaystyle \frac{1}{2},s \geqq 0,t \geqq 0$
②$3s+2t \leqq 3,S \geqq 0,t \geqq 0$
この動画を見る
◎△OABに対し、$\overrightarrow{ OP }=s\overrightarrow{ OA }+t\overrightarrow{ OB } $とする。実数S,tが次の条件を満たしながら動くとき、 点Pの存在範囲を図示しよう。
①$s+t \leqq \displaystyle \frac{1}{2},s \geqq 0,t \geqq 0$
②$3s+2t \leqq 3,S \geqq 0,t \geqq 0$
【高校数学】 数B-33 平面上の点の存在位置②

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$\overrightarrow{ OP }=s\overrightarrow{ OA }+t\overrightarrow{ OB } $において
$s+t=1,s \geqq 0,t \geqq 0\Leftrightarrow$①____________
$s+t \leqq1,s \geqq 0,t \geqq 0 \Leftrightarrow$②____________
$0\leqq s \leqq 1, 0 \leqq ,t \leqq 1 \Leftrightarrow$③____________
④△OABに対し$\overrightarrow{ OP }=s\overrightarrow{ OA }+t\overrightarrow{ OB }$とする。
実数s,tが、$s+t=3,s \geqq0、t \geqq 0$を満たしながら動くとき、点Pの存在範囲を図示しよう。
この動画を見る
$\overrightarrow{ OP }=s\overrightarrow{ OA }+t\overrightarrow{ OB } $において
$s+t=1,s \geqq 0,t \geqq 0\Leftrightarrow$①____________
$s+t \leqq1,s \geqq 0,t \geqq 0 \Leftrightarrow$②____________
$0\leqq s \leqq 1, 0 \leqq ,t \leqq 1 \Leftrightarrow$③____________
④△OABに対し$\overrightarrow{ OP }=s\overrightarrow{ OA }+t\overrightarrow{ OB }$とする。
実数s,tが、$s+t=3,s \geqq0、t \geqq 0$を満たしながら動くとき、点Pの存在範囲を図示しよう。
【高校数学】 数B-31 ベクトル方程式⑥

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①A(-1,5)、B(3,3)とする。線分ABの垂直二等分線の方程式を求めよう。
②2通線$x-2y-5=0,3x-y+4=0$のなす角aを求めよう。ただし、$0° \leqq x \leqq 90°$とする。
この動画を見る
①A(-1,5)、B(3,3)とする。線分ABの垂直二等分線の方程式を求めよう。
②2通線$x-2y-5=0,3x-y+4=0$のなす角aを求めよう。ただし、$0° \leqq x \leqq 90°$とする。
【高校数学】 数B-30 ベクトル方程式⑤

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①点A(1,-3)を通り、$\vec{ d }$=(2,6)に平行な直線と垂直な直線の方程式を求めよう。
② 直線$2x-3y-5=0$は$\vec{ d }$=(a,2)に平行、$\vec{ n }$=(2.b)に垂直で、 直線$5x+Cy+2=0$に垂直に交わる。定数a,b,Cの値を求めよう。
この動画を見る
①点A(1,-3)を通り、$\vec{ d }$=(2,6)に平行な直線と垂直な直線の方程式を求めよう。
② 直線$2x-3y-5=0$は$\vec{ d }$=(a,2)に平行、$\vec{ n }$=(2.b)に垂直で、 直線$5x+Cy+2=0$に垂直に交わる。定数a,b,Cの値を求めよう。
【高校数学】 数B-29 ベクトル方程式④

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
定点$C(\vec{ c })$を中心とする半径rの円は①_________ と表され、 これを円のベクトル方程式という。ちなみに、2点$A(\vec{ a })$、$B(\vec{ b })$を直径の 両端とする円のベクトル方程式は② である。
次の円の方程式をベクトル方程式を利用して求めよう。
③点C(2,3)が中心で、点A(1.1)を通る円
④2点A(1,6)、B(3,0)を直径の両端とする円
この動画を見る
定点$C(\vec{ c })$を中心とする半径rの円は①_________ と表され、 これを円のベクトル方程式という。ちなみに、2点$A(\vec{ a })$、$B(\vec{ b })$を直径の 両端とする円のベクトル方程式は② である。
次の円の方程式をベクトル方程式を利用して求めよう。
③点C(2,3)が中心で、点A(1.1)を通る円
④2点A(1,6)、B(3,0)を直径の両端とする円
【高校数学】 数B-28 ベクトル方程式③

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
定点$A(\vec{ a })$を通り、$\overrightarrow{ n }(≠\vec{ 0 })$に垂直な直線のベクトル方程式は①__________で、$\vec{ n }$を直線の法線ベクトルという。
また、$ax+by+c=0$において、$\overrightarrow{ n }=(a,b)$はその法線ベクトルである。
◎次の点Aを通り、$\overrightarrow{ n }$が法線ベクトルである直線の方程式を求めよう。
②$A(2,-1),\vec{ n }=(3,4)$
③$A(-1,3),\vec{ n }(5,-1)$
この動画を見る
定点$A(\vec{ a })$を通り、$\overrightarrow{ n }(≠\vec{ 0 })$に垂直な直線のベクトル方程式は①__________で、$\vec{ n }$を直線の法線ベクトルという。
また、$ax+by+c=0$において、$\overrightarrow{ n }=(a,b)$はその法線ベクトルである。
◎次の点Aを通り、$\overrightarrow{ n }$が法線ベクトルである直線の方程式を求めよう。
②$A(2,-1),\vec{ n }=(3,4)$
③$A(-1,3),\vec{ n }(5,-1)$
【高校数学】 数B-26 ベクトル方程式①

【高校数学】 数B-25 ベクトルと図形③

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①△ABCにおいて、辺ABを3:2に内分する点をD、辺ACを2:1に内分する点をEとし、 線分BE、CDの交点をFとする。$\overrightarrow{ AB }=\vec{ b },\overrightarrow{ AC }=\vec{ c }$とするとき、$\overrightarrow{ AF }$を$\vec{ b },\vec{ c }$を用いて表そう。
この動画を見る
①△ABCにおいて、辺ABを3:2に内分する点をD、辺ACを2:1に内分する点をEとし、 線分BE、CDの交点をFとする。$\overrightarrow{ AB }=\vec{ b },\overrightarrow{ AC }=\vec{ c }$とするとき、$\overrightarrow{ AF }$を$\vec{ b },\vec{ c }$を用いて表そう。
【高校数学】 数B-24 ベクトルと図形②

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$\vec{ a }≠\vec{ 0 },\vec{ b }≠\vec{ 0 },\vec{ a }≠\vec{ b }$のとき
$S\vec{ a }+t\vec{ b }=S'\vec{ a }+t'\vec{ b } \Leftrightarrow S=S',t=t'$
◎$\vec{ a }≠\vec{ 0 },\vec{ b }≠\vec{ 0 },\vec{ a }≠\vec{ b }$とする。次の等式を満たす実数S,tの値を求めよう。
①$5\vec{ a }+S\vec{ b }=t\vec{ a }-2\vec{ b }$
②$(3S-5)\vec{ a }+t\vec{ b }=\vec{ 0 }$
③$\vec{ c }=2\vec{ a }+3\vec{ b },\vec{ d }=\vec{ a }+2\vec{ b }$のとき、$5\vec{ a }+4\vec{ b }=S\vec{ c }+t\vec{ d }$
この動画を見る
$\vec{ a }≠\vec{ 0 },\vec{ b }≠\vec{ 0 },\vec{ a }≠\vec{ b }$のとき
$S\vec{ a }+t\vec{ b }=S'\vec{ a }+t'\vec{ b } \Leftrightarrow S=S',t=t'$
◎$\vec{ a }≠\vec{ 0 },\vec{ b }≠\vec{ 0 },\vec{ a }≠\vec{ b }$とする。次の等式を満たす実数S,tの値を求めよう。
①$5\vec{ a }+S\vec{ b }=t\vec{ a }-2\vec{ b }$
②$(3S-5)\vec{ a }+t\vec{ b }=\vec{ 0 }$
③$\vec{ c }=2\vec{ a }+3\vec{ b },\vec{ d }=\vec{ a }+2\vec{ b }$のとき、$5\vec{ a }+4\vec{ b }=S\vec{ c }+t\vec{ d }$
【高校数学】 数B-23 ベクトルと図形①

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
3点A,B,Cが一直線上にある $\Leftrightarrow$ ①______となる実数kがある。
② △ABCにおいて、辺ABを3:1に内分する点をP、辺ACを1:2に内分する点をQ、 線分BQを1:2に内分する点をRとする。3点、P、R、Cが一直線上にあることを証明しよう。
この動画を見る
3点A,B,Cが一直線上にある $\Leftrightarrow$ ①______となる実数kがある。
② △ABCにおいて、辺ABを3:1に内分する点をP、辺ACを1:2に内分する点をQ、 線分BQを1:2に内分する点をRとする。3点、P、R、Cが一直線上にあることを証明しよう。
