 平面上のベクトル
平面上のベクトル
 平面上のベクトル
平面上のベクトル
【数学】中高一貫校用問題集:平面上のベクトル:ベクトル方程式:ベクトル方程式の復習②

単元:
#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
【問題】
$△ABC$(それぞれの位置ベクトルを$a、b、c$とする)について、以下の問いに答えよ。
(2)頂点$A$と辺$BC$の中点を通る直線のベクトル方程式
※(1)は①の動画で解説しています。
この動画を見る
【問題】
$△ABC$(それぞれの位置ベクトルを$a、b、c$とする)について、以下の問いに答えよ。
(2)頂点$A$と辺$BC$の中点を通る直線のベクトル方程式
※(1)は①の動画で解説しています。
【数C】中高一貫校問題集4 464:平面上のベクトル:ベクトル方程式:ベクトル方程式の復習②

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
教材:
#TK数学#TK数学問題集4#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
△ABC(それぞれの位置ベクトルをa、b、cとする)について、以下の問いに答えよ。
(2)頂点Aと辺BCの中点を通る直線のベクトル方程式を求めよ
この動画を見る
△ABC(それぞれの位置ベクトルをa、b、cとする)について、以下の問いに答えよ。
(2)頂点Aと辺BCの中点を通る直線のベクトル方程式を求めよ
【数学】中高一貫校用問題集:平面上のベクトル:ベクトル方程式:ベクトル方程式の復習①

単元:
#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
$△ABC$(それぞれの位置ベクトルを$a、b、c$とする)。
この時、次の問いに答えよ。
(1)点$A$から辺$BC$に下した垂線のベクトル方程式を求めよ。
※(2)は②の動画で説明
この動画を見る
$△ABC$(それぞれの位置ベクトルを$a、b、c$とする)。
この時、次の問いに答えよ。
(1)点$A$から辺$BC$に下した垂線のベクトル方程式を求めよ。
※(2)は②の動画で説明
【数C】中高一貫校問題集4 464:平面上のベクトル:ベクトル方程式:ベクトル方程式の復習①

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
教材:
#TK数学#TK数学問題集4#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
△ABC(それぞれの位置ベクトルをa、b、cとする)。
この時、次の問いに答えよ。
(1)点Aから辺BCに下した垂線のベクトル方程式を求めよ。
この動画を見る
△ABC(それぞれの位置ベクトルをa、b、cとする)。
この時、次の問いに答えよ。
(1)点Aから辺BCに下した垂線のベクトル方程式を求めよ。
福田の数学〜九州大学2023年理系第3問〜ベクトルと論証PART3

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#平面上のベクトル#集合と命題(集合・命題と条件・背理法)#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 点Oを原点とする座標平面上の$\overrightarrow{0}$でない2つのベクトル
$\overrightarrow{m}$=($a$, $c$), $\overrightarrow{n}$=($b$, $d$)
に対して、D=ad-bc とおく。座標平面上のベクトル$\overrightarrow{q}$に対して、次の条件を考える。
条件Ⅰ $r\overrightarrow{m}$+$s\overrightarrow{n}$=$\overrightarrow{q}$を満たす実数r, sが存在する。
条件Ⅱ $r\overrightarrow{m}$+$s\overrightarrow{n}$=$\overrightarrow{q}$を満たす整数r, sが存在する。
以下の問いに答えよ。
(1)条件Ⅰがすべての$\overrightarrow{q}$に対して成り立つとする。D $\ne$ 0であることを示せ。
以下、D $\ne$ 0であるとする。
(2)座標平面上のベクトル$\overrightarrow{v}$, $\overrightarrow{w}$で
$\overrightarrow{m}・\overrightarrow{v}$=$\overrightarrow{n}・\overrightarrow{w}$=1, $\overrightarrow{m}・\overrightarrow{w}$=$\overrightarrow{n}・\overrightarrow{v}$=0
を満たすものを求めよ。
(3)さらにa, b, c, dが整数であるとし、x成分とy成分がともに整数であるすべてのベクトル$\overrightarrow{q}$に対して条件Ⅱが成り立つとする。Dのとりうる値をすべて求めよ。
2023九州大学理系過去問
この動画を見る
$\Large\boxed{3}$ 点Oを原点とする座標平面上の$\overrightarrow{0}$でない2つのベクトル
$\overrightarrow{m}$=($a$, $c$), $\overrightarrow{n}$=($b$, $d$)
に対して、D=ad-bc とおく。座標平面上のベクトル$\overrightarrow{q}$に対して、次の条件を考える。
条件Ⅰ $r\overrightarrow{m}$+$s\overrightarrow{n}$=$\overrightarrow{q}$を満たす実数r, sが存在する。
条件Ⅱ $r\overrightarrow{m}$+$s\overrightarrow{n}$=$\overrightarrow{q}$を満たす整数r, sが存在する。
以下の問いに答えよ。
(1)条件Ⅰがすべての$\overrightarrow{q}$に対して成り立つとする。D $\ne$ 0であることを示せ。
以下、D $\ne$ 0であるとする。
(2)座標平面上のベクトル$\overrightarrow{v}$, $\overrightarrow{w}$で
$\overrightarrow{m}・\overrightarrow{v}$=$\overrightarrow{n}・\overrightarrow{w}$=1, $\overrightarrow{m}・\overrightarrow{w}$=$\overrightarrow{n}・\overrightarrow{v}$=0
を満たすものを求めよ。
(3)さらにa, b, c, dが整数であるとし、x成分とy成分がともに整数であるすべてのベクトル$\overrightarrow{q}$に対して条件Ⅱが成り立つとする。Dのとりうる値をすべて求めよ。
2023九州大学理系過去問
福田の数学〜九州大学2023年理系第3問〜ベクトルと論証PART2

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#平面上のベクトル#集合と命題(集合・命題と条件・背理法)#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 点Oを原点とする座標平面上の$\overrightarrow{0}$でない2つのベクトル
$\overrightarrow{m}$=($a$, $c$), $\overrightarrow{n}$=($b$, $d$)
に対して、D=ad-bc とおく。座標平面上のベクトル$\overrightarrow{q}$に対して、次の条件を考える。
条件Ⅰ $r\overrightarrow{m}$+$s\overrightarrow{n}$=$\overrightarrow{q}$を満たす実数r, sが存在する。
条件Ⅱ $r\overrightarrow{m}$+$s\overrightarrow{n}$=$\overrightarrow{q}$を満たす整数r, sが存在する。
以下の問いに答えよ。
(1)条件Ⅰがすべての$\overrightarrow{q}$に対して成り立つとする。D $\ne$ 0であることを示せ。
以下、D $\ne$ 0であるとする。
(2)座標平面上のベクトル$\overrightarrow{v}$, $\overrightarrow{w}$で
$\overrightarrow{m}・\overrightarrow{v}$=$\overrightarrow{n}・\overrightarrow{w}$=1, $\overrightarrow{m}・\overrightarrow{w}$=$\overrightarrow{n}・\overrightarrow{v}$=0
を満たすものを求めよ。
(3)さらにa, b, c, dが整数であるとし、x成分とy成分がともに整数であるすべてのベクトル$\overrightarrow{q}$に対して条件Ⅱが成り立つとする。Dのとりうる値をすべて求めよ。
2023九州大学理系過去問
この動画を見る
$\Large\boxed{3}$ 点Oを原点とする座標平面上の$\overrightarrow{0}$でない2つのベクトル
$\overrightarrow{m}$=($a$, $c$), $\overrightarrow{n}$=($b$, $d$)
に対して、D=ad-bc とおく。座標平面上のベクトル$\overrightarrow{q}$に対して、次の条件を考える。
条件Ⅰ $r\overrightarrow{m}$+$s\overrightarrow{n}$=$\overrightarrow{q}$を満たす実数r, sが存在する。
条件Ⅱ $r\overrightarrow{m}$+$s\overrightarrow{n}$=$\overrightarrow{q}$を満たす整数r, sが存在する。
以下の問いに答えよ。
(1)条件Ⅰがすべての$\overrightarrow{q}$に対して成り立つとする。D $\ne$ 0であることを示せ。
以下、D $\ne$ 0であるとする。
(2)座標平面上のベクトル$\overrightarrow{v}$, $\overrightarrow{w}$で
$\overrightarrow{m}・\overrightarrow{v}$=$\overrightarrow{n}・\overrightarrow{w}$=1, $\overrightarrow{m}・\overrightarrow{w}$=$\overrightarrow{n}・\overrightarrow{v}$=0
を満たすものを求めよ。
(3)さらにa, b, c, dが整数であるとし、x成分とy成分がともに整数であるすべてのベクトル$\overrightarrow{q}$に対して条件Ⅱが成り立つとする。Dのとりうる値をすべて求めよ。
2023九州大学理系過去問
福田の数学〜九州大学2023年理系第3問〜ベクトルと論証PART1

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#平面上のベクトル#集合と命題(集合・命題と条件・背理法)#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 点Oを原点とする座標平面上の$\overrightarrow{0}$でない2つのベクトル
$\overrightarrow{m}$=($a$, $c$), $\overrightarrow{n}$=($b$, $d$)
に対して、D=ad-bc とおく。座標平面上のベクトル$\overrightarrow{q}$に対して、次の条件を考える。
条件Ⅰ $r\overrightarrow{m}$+$s\overrightarrow{n}$=$\overrightarrow{q}$を満たす実数r, sが存在する。
条件Ⅱ $r\overrightarrow{m}$+$s\overrightarrow{n}$=$\overrightarrow{q}$を満たす整数r, sが存在する。
以下の問いに答えよ。
(1)条件Ⅰがすべての$\overrightarrow{q}$に対して成り立つとする。D $\ne$ 0であることを示せ。
以下、D $\ne$ 0であるとする。
(2)座標平面上のベクトル$\overrightarrow{v}$, $\overrightarrow{w}$で
$\overrightarrow{m}・\overrightarrow{v}$=$\overrightarrow{n}・\overrightarrow{w}$=1, $\overrightarrow{m}・\overrightarrow{w}$=$\overrightarrow{n}・\overrightarrow{v}$=0
を満たすものを求めよ。
(3)さらにa, b, c, dが整数であるとし、x成分とy成分がともに整数であるすべてのベクトル$\overrightarrow{q}$に対して条件Ⅱが成り立つとする。Dのとりうる値をすべて求めよ。
2023九州大学理系過去問
この動画を見る
$\Large\boxed{3}$ 点Oを原点とする座標平面上の$\overrightarrow{0}$でない2つのベクトル
$\overrightarrow{m}$=($a$, $c$), $\overrightarrow{n}$=($b$, $d$)
に対して、D=ad-bc とおく。座標平面上のベクトル$\overrightarrow{q}$に対して、次の条件を考える。
条件Ⅰ $r\overrightarrow{m}$+$s\overrightarrow{n}$=$\overrightarrow{q}$を満たす実数r, sが存在する。
条件Ⅱ $r\overrightarrow{m}$+$s\overrightarrow{n}$=$\overrightarrow{q}$を満たす整数r, sが存在する。
以下の問いに答えよ。
(1)条件Ⅰがすべての$\overrightarrow{q}$に対して成り立つとする。D $\ne$ 0であることを示せ。
以下、D $\ne$ 0であるとする。
(2)座標平面上のベクトル$\overrightarrow{v}$, $\overrightarrow{w}$で
$\overrightarrow{m}・\overrightarrow{v}$=$\overrightarrow{n}・\overrightarrow{w}$=1, $\overrightarrow{m}・\overrightarrow{w}$=$\overrightarrow{n}・\overrightarrow{v}$=0
を満たすものを求めよ。
(3)さらにa, b, c, dが整数であるとし、x成分とy成分がともに整数であるすべてのベクトル$\overrightarrow{q}$に対して条件Ⅱが成り立つとする。Dのとりうる値をすべて求めよ。
2023九州大学理系過去問
福田の数学〜一橋大学2023年文系第3問〜ベクトルと四面体の体積の最大

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 原点をOとする座標空間内に3点A(-3, 2, 0), B(1, 5, 0), C(4, 5, 1)がある。
Pは|$\overrightarrow{PA}$+3$\overrightarrow{PB}$+2$\overrightarrow{PC}$|≦36 を満たす点である。
4点O, A, B, Pが同一平面上にないとき、四面体OABPの体積の最大値を求めよ。
2023一橋大学文系過去問
この動画を見る
$\Large\boxed{3}$ 原点をOとする座標空間内に3点A(-3, 2, 0), B(1, 5, 0), C(4, 5, 1)がある。
Pは|$\overrightarrow{PA}$+3$\overrightarrow{PB}$+2$\overrightarrow{PC}$|≦36 を満たす点である。
4点O, A, B, Pが同一平面上にないとき、四面体OABPの体積の最大値を求めよ。
2023一橋大学文系過去問
【高校数学】ベクトルの減法~逆ベクトル・零ベクトル~【数学C】

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
ベクトルの減法計算方法の確認動画です
逆ベクトル・零ベクトルとは??
この動画を見る
ベクトルの減法計算方法の確認動画です
逆ベクトル・零ベクトルとは??
福田の数学〜東北大学2023年理系第5問〜空間ベクトルと内積
単元:
#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
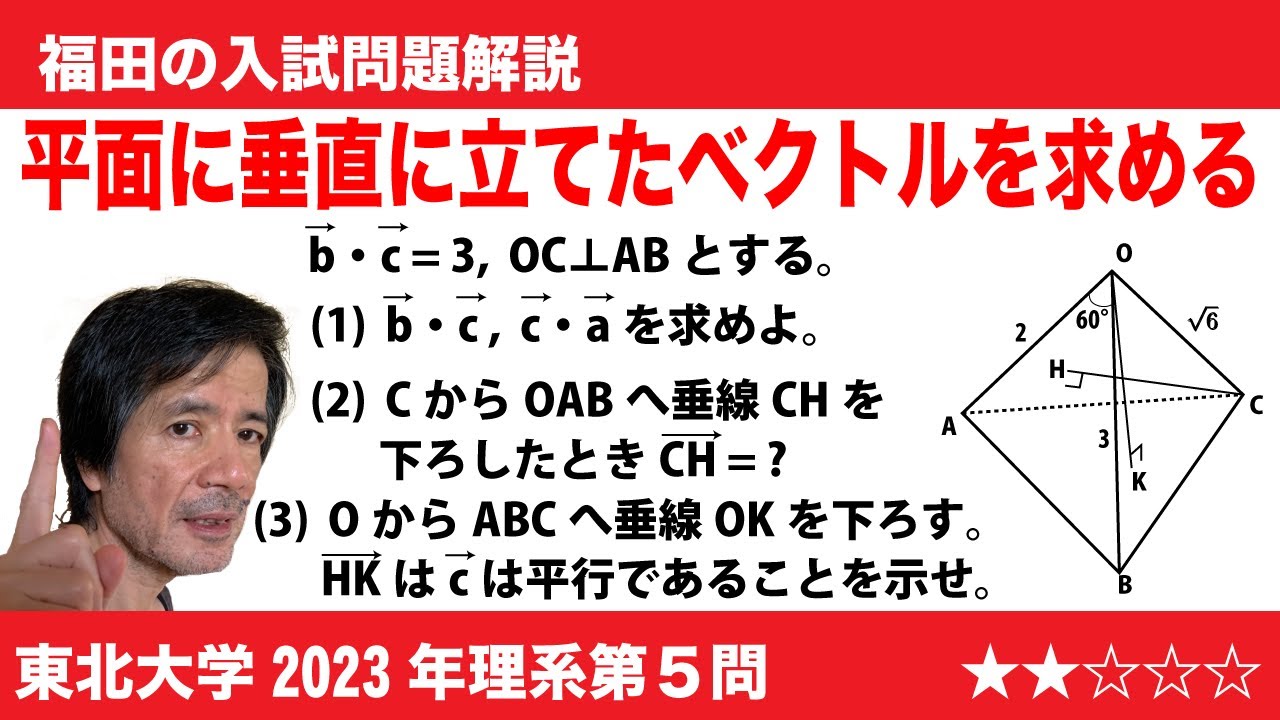
$\Large\boxed{5}$ 四面体OABCにおいて、$\overrightarrow{a}$=$\overrightarrow{OA}$, $\overrightarrow{b}$=$\overrightarrow{OB}$, $\overrightarrow{c}$=$\overrightarrow{OC}$とおき、次が成り立つとする。
$\angle$AOB=60°, |$\overrightarrow{a}$|=2, |$\overrightarrow{b}$|=3, |$\overrightarrow{c}$|=$\sqrt 6$, $\overrightarrow{b}$・$\overrightarrow{c}$=3
ただし、$\overrightarrow{b}$・$\overrightarrow{c}$は、2つのベクトル$\overrightarrow{b}$と$\overrightarrow{c}$の内積を表す。さらに、線分OCと線分ABは垂直であるとする。点Cから3点O, A, Bを含む平面に下ろした垂線をCHとし、点Oから3点A, B, Cを含む平面に下ろした垂線をOKとする。
(1)$\overrightarrow{a}$・$\overrightarrow{b}$と$\overrightarrow{c}$・$\overrightarrow{a}$を求めよ。
(2)ベクトル$\overrightarrow{OH}$を$\overrightarrow{a}$と$\overrightarrow{b}$を用いて表せ。
(3)ベクトル$\overrightarrow{c}$とベクトル$\overrightarrow{HK}$は平行であることを示せ。
2023東北大学理系過去問
この動画を見る
$\Large\boxed{5}$ 四面体OABCにおいて、$\overrightarrow{a}$=$\overrightarrow{OA}$, $\overrightarrow{b}$=$\overrightarrow{OB}$, $\overrightarrow{c}$=$\overrightarrow{OC}$とおき、次が成り立つとする。
$\angle$AOB=60°, |$\overrightarrow{a}$|=2, |$\overrightarrow{b}$|=3, |$\overrightarrow{c}$|=$\sqrt 6$, $\overrightarrow{b}$・$\overrightarrow{c}$=3
ただし、$\overrightarrow{b}$・$\overrightarrow{c}$は、2つのベクトル$\overrightarrow{b}$と$\overrightarrow{c}$の内積を表す。さらに、線分OCと線分ABは垂直であるとする。点Cから3点O, A, Bを含む平面に下ろした垂線をCHとし、点Oから3点A, B, Cを含む平面に下ろした垂線をOKとする。
(1)$\overrightarrow{a}$・$\overrightarrow{b}$と$\overrightarrow{c}$・$\overrightarrow{a}$を求めよ。
(2)ベクトル$\overrightarrow{OH}$を$\overrightarrow{a}$と$\overrightarrow{b}$を用いて表せ。
(3)ベクトル$\overrightarrow{c}$とベクトル$\overrightarrow{HK}$は平行であることを示せ。
2023東北大学理系過去問
福田の数学〜慶應義塾大学2023年看護医療学部第1問(1)〜交点の位置ベクトル
単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
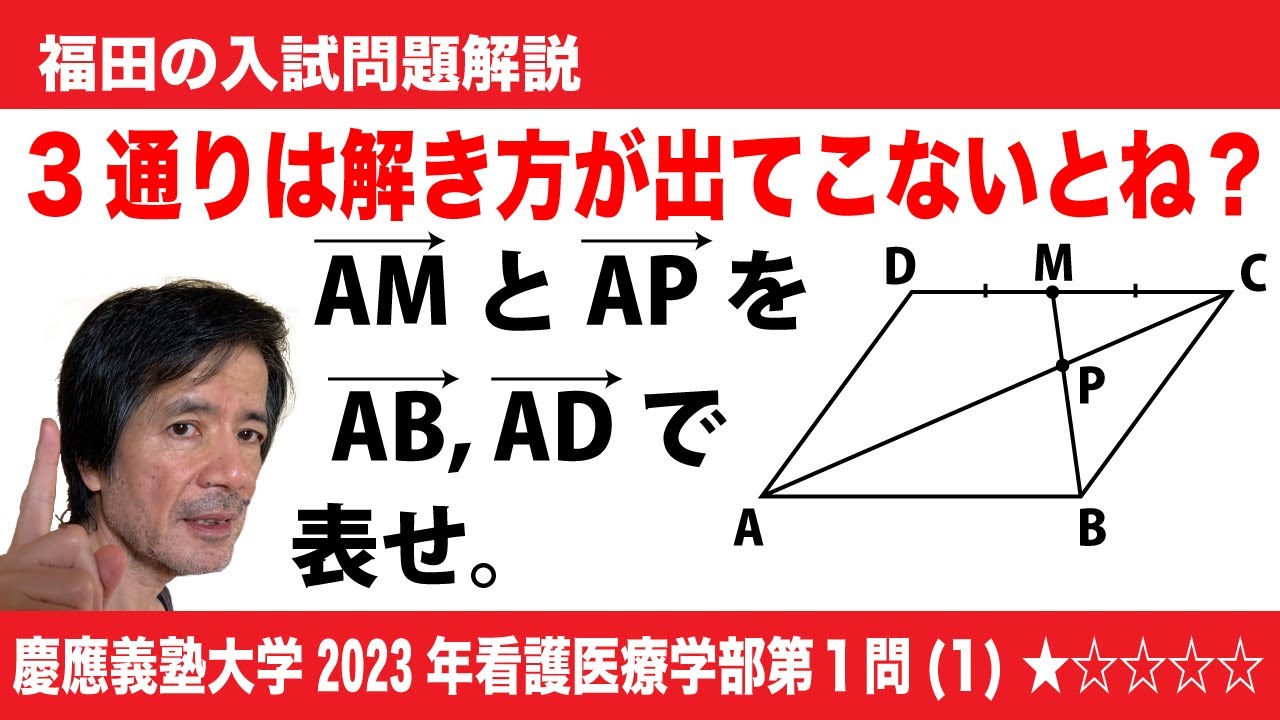
$\Large\boxed{1}$ (1)平行四辺形ABCDにおいて、辺CDの中点をMとし、直線ACと直線BMの交点をPとする。このとき、$\overrightarrow{AM}$, $\overrightarrow{AP}$をそれぞれ$\overrightarrow{AB}$, $\overrightarrow{AD}$を用いて表すと
$\overrightarrow{AM}$=$\boxed{\ \ ア\ \ }$, $\overrightarrow{AP}$=$\boxed{\ \ イ\ \ }$
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{1}$ (1)平行四辺形ABCDにおいて、辺CDの中点をMとし、直線ACと直線BMの交点をPとする。このとき、$\overrightarrow{AM}$, $\overrightarrow{AP}$をそれぞれ$\overrightarrow{AB}$, $\overrightarrow{AD}$を用いて表すと
$\overrightarrow{AM}$=$\boxed{\ \ ア\ \ }$, $\overrightarrow{AP}$=$\boxed{\ \ イ\ \ }$
2023慶應義塾大学看護医療学部過去問
【高校数学】平面上のベクトルの基礎~加法・ベクトルの足し算~【数学C】

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
平面上のベクトルの基礎
加法・ベクトルの足し算を確認します!
この動画を見る
平面上のベクトルの基礎
加法・ベクトルの足し算を確認します!
福田の数学〜慶應義塾大学2023年医学部第1問(1)〜図形の証明

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#式と証明#平面上のベクトル#図形と計量#三角比への応用(正弦・余弦・面積)#図形と方程式#恒等式・等式・不等式の証明#点と直線#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)三角形ABCにおいて辺BCを4:3に内分する点をDとするとき、等式
$\boxed{\ \ あ\ \ }$$AB^2$+$\boxed{\ \ い\ \ }$$AC^2$=$AD^2$+$\boxed{\ \ う\ \ }$$BD^2$
が成り立つ。
203慶應義塾大学医学部過去問
この動画を見る
$\Large\boxed{1}$ (1)三角形ABCにおいて辺BCを4:3に内分する点をDとするとき、等式
$\boxed{\ \ あ\ \ }$$AB^2$+$\boxed{\ \ い\ \ }$$AC^2$=$AD^2$+$\boxed{\ \ う\ \ }$$BD^2$
が成り立つ。
203慶應義塾大学医学部過去問
福田の数学〜慶應義塾大学2023年薬学部第1問(4)〜球面上の3点が作る三角形

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#図形と計量#三角比(三角比・拡張・相互関係・単位円)#図形と方程式#円と方程式#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (4)座標空間に球面S:$(x-3)^2$+$(y+2)^2$+$(z-1)^2$=36 がある。球面Sが平面y=2 と交わってできる円をCとおく。
(i)円Cの中心の座標は$\boxed{\ \ ク\ \ }$であり、半径は$\boxed{\ \ ケ\ \ }$である。
(ii)円Cと平面x=3の交点をA,Bとし、AとB以外の球面S上の任意の点をPとする。三角形PABにおいて、辺PBを4:3に内分する点をD、線分ADを5:3に内分する点をMとし、直線PMと辺ABとの交点をEとする。このとき、AEの長さは$\boxed{\ \ コ\ \ }$である。ただし、Bのz座標はAのz座標よりも大きいとする。
2023慶應義塾大学薬学部過去問
この動画を見る
$\Large\boxed{1}$ (4)座標空間に球面S:$(x-3)^2$+$(y+2)^2$+$(z-1)^2$=36 がある。球面Sが平面y=2 と交わってできる円をCとおく。
(i)円Cの中心の座標は$\boxed{\ \ ク\ \ }$であり、半径は$\boxed{\ \ ケ\ \ }$である。
(ii)円Cと平面x=3の交点をA,Bとし、AとB以外の球面S上の任意の点をPとする。三角形PABにおいて、辺PBを4:3に内分する点をD、線分ADを5:3に内分する点をMとし、直線PMと辺ABとの交点をEとする。このとき、AEの長さは$\boxed{\ \ コ\ \ }$である。ただし、Bのz座標はAのz座標よりも大きいとする。
2023慶應義塾大学薬学部過去問
福田の数学〜北海道大学2023年文系第2問〜角の2等分線の位置ベクトル

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 三角形OABは辺の長さがOA=3, OB=5, AB=7であるとする。また、$\angle$AOBの2等分線と直線ABとの交点をPとし、頂点Bにおける外角の2等分線と直線OPとの交点をQとする。
(1)$\overrightarrow{ OP }$を$\overrightarrow{ OA }$, $\overrightarrow{ OB }$を用いて表せ。また、|$\overrightarrow{ OP }$|の値を求めよ。
(2)$\overrightarrow{ OQ }$を$\overrightarrow{ OA }$, $\overrightarrow{ OB }$を用いて表せ。また、|$\overrightarrow{ OQ }$|の値を求めよ。
2023北海道大学文系過去問
この動画を見る
$\Large\boxed{2}$ 三角形OABは辺の長さがOA=3, OB=5, AB=7であるとする。また、$\angle$AOBの2等分線と直線ABとの交点をPとし、頂点Bにおける外角の2等分線と直線OPとの交点をQとする。
(1)$\overrightarrow{ OP }$を$\overrightarrow{ OA }$, $\overrightarrow{ OB }$を用いて表せ。また、|$\overrightarrow{ OP }$|の値を求めよ。
(2)$\overrightarrow{ OQ }$を$\overrightarrow{ OA }$, $\overrightarrow{ OB }$を用いて表せ。また、|$\overrightarrow{ OQ }$|の値を求めよ。
2023北海道大学文系過去問
福田の数学〜大阪大学2023年理系第2問〜ベクトルと領域

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#図形と方程式#軌跡と領域#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 平面上の3点O,A,Bが
|2$\overrightarrow{OA}$+$\overrightarrow{OB}$|=|$\overrightarrow{OA}$+2$\overrightarrow{OB}$|=1 かつ (2$\overrightarrow{OA}$+$\overrightarrow{OB}$)・($\overrightarrow{OA}$+$\overrightarrow{OB}$)=$\displaystyle\frac{1}{3}$
を満たすとする。
(1)(2$\overrightarrow{OA}$+$\overrightarrow{OB}$)・($\overrightarrow{OA}$+2$\overrightarrow{OB}$)を求めよ。
(2)平面上の点Pが
|$\overrightarrow{OP}$ー($\overrightarrow{OA}$+$\overrightarrow{OB}$)|≦$\frac{1}{3}$ かつ $\overrightarrow{OP}$・(2$\overrightarrow{OA}$+$\overrightarrow{OB}$)≦$\frac{1}{3}$
を満たすように動くとき、|$\overrightarrow{OP}$|の最大値と最小値を求めよ。
2023大阪大学理系過去問
この動画を見る
$\Large\boxed{2}$ 平面上の3点O,A,Bが
|2$\overrightarrow{OA}$+$\overrightarrow{OB}$|=|$\overrightarrow{OA}$+2$\overrightarrow{OB}$|=1 かつ (2$\overrightarrow{OA}$+$\overrightarrow{OB}$)・($\overrightarrow{OA}$+$\overrightarrow{OB}$)=$\displaystyle\frac{1}{3}$
を満たすとする。
(1)(2$\overrightarrow{OA}$+$\overrightarrow{OB}$)・($\overrightarrow{OA}$+2$\overrightarrow{OB}$)を求めよ。
(2)平面上の点Pが
|$\overrightarrow{OP}$ー($\overrightarrow{OA}$+$\overrightarrow{OB}$)|≦$\frac{1}{3}$ かつ $\overrightarrow{OP}$・(2$\overrightarrow{OA}$+$\overrightarrow{OB}$)≦$\frac{1}{3}$
を満たすように動くとき、|$\overrightarrow{OP}$|の最大値と最小値を求めよ。
2023大阪大学理系過去問
福田の数学〜東京大学2023年理系第4問〜球面と三角形が共有点をもつ条件

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#平面上のベクトル#空間ベクトル#集合と命題(集合・命題と条件・背理法)#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 座標空間内の4点O(0,0,0), A(2,0,0), B(1,1,1), C(1,2,3)を考える。
(1)$\overrightarrow{OP}\bot\overrightarrow{OA}$, $\overrightarrow{OP}\bot\overrightarrow{OB}$, $\overrightarrow{OP}\bot\overrightarrow{OC}$=1 を満たす点Pの座標を求めよ。
(2)点Pから直線ABに垂線を下ろし、その垂線と直線ABの交点をHとする。
$\overrightarrow{OH}$を$\overrightarrow{OA}$と$\overrightarrow{OB}$を用いて表せ。
(3)点Qを$\overrightarrow{OQ}$=$\frac{3}{4}\overrightarrow{OA}$+$\overrightarrow{OP}$により定め、Qを中心とする半径rの球面Sを考える。Sが三角形OHBと共有点を持つようなrの範囲を求めよ。ただし、三角形OHBは3点O, H, Bを含む平面内にあり、周とその内部からなるものとする。
2023東京大学理系過去問
この動画を見る
$\Large\boxed{4}$ 座標空間内の4点O(0,0,0), A(2,0,0), B(1,1,1), C(1,2,3)を考える。
(1)$\overrightarrow{OP}\bot\overrightarrow{OA}$, $\overrightarrow{OP}\bot\overrightarrow{OB}$, $\overrightarrow{OP}\bot\overrightarrow{OC}$=1 を満たす点Pの座標を求めよ。
(2)点Pから直線ABに垂線を下ろし、その垂線と直線ABの交点をHとする。
$\overrightarrow{OH}$を$\overrightarrow{OA}$と$\overrightarrow{OB}$を用いて表せ。
(3)点Qを$\overrightarrow{OQ}$=$\frac{3}{4}\overrightarrow{OA}$+$\overrightarrow{OP}$により定め、Qを中心とする半径rの球面Sを考える。Sが三角形OHBと共有点を持つようなrの範囲を求めよ。ただし、三角形OHBは3点O, H, Bを含む平面内にあり、周とその内部からなるものとする。
2023東京大学理系過去問
福田の数学〜東京工業大学2023年理系第5問(PART2)〜4直線に接する球面の決定

単元:
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ xyz空間の4点A(1,0,0), B(1,1,1), C(-1,1,-1), D(-1,0,0)を考える。
(1)2直線AB,BCから等距離にある点全体のなす図形を求めよ。
(2)4直線AB, BC, CD, DAに共に接する球面の中心と半径の組を全て求めよ。
2023東京工業大学理系過去問
この動画を見る
$\Large\boxed{5}$ xyz空間の4点A(1,0,0), B(1,1,1), C(-1,1,-1), D(-1,0,0)を考える。
(1)2直線AB,BCから等距離にある点全体のなす図形を求めよ。
(2)4直線AB, BC, CD, DAに共に接する球面の中心と半径の組を全て求めよ。
2023東京工業大学理系過去問
福田の数学〜東京工業大学2023年理系第5問(PART1)〜4直線に接する球面の決定

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#図形と方程式#点と直線#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ xyz空間の4点A(1,0,0), B(1,1,1), C(-1,1,-1), D(-1,0,0)を考える。
(1)2直線AB,BCから等距離にある点全体のなす図形を求めよ。
(2)4直線AB, BC, CD, DAに共に接する球面の中心と半径の組を全て求めよ。
2023東京工業大学理系過去問
この動画を見る
$\Large\boxed{5}$ xyz空間の4点A(1,0,0), B(1,1,1), C(-1,1,-1), D(-1,0,0)を考える。
(1)2直線AB,BCから等距離にある点全体のなす図形を求めよ。
(2)4直線AB, BC, CD, DAに共に接する球面の中心と半径の組を全て求めよ。
2023東京工業大学理系過去問
福田の1.5倍速演習〜合格する重要問題092〜神戸大学2018年度理系第5問〜回転体の体積

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 座標空間において、Oを原点とし、A(2,0,0), B(0,2,0), C(1,1,0)とする。$\triangle$OABを直線OCの周りに1回転してできる回転体をLとする。
(1)直線OC上にない点P(x,y,z)から直線OCにおろした垂線をPHとする。
$\overrightarrow{OH}$と$\overrightarrow{HP}$をx,y,zの式で表せ。
(2)点P(x,y,z)がLの点であるための条件は
$z^2≦2xy$ かつ $0≦x+y≦2$
であることを示せ。
(3)$1≦a≦2$とする。Lを平面x=aで切った切り口の面積S(a)を求めよ。
(4)立体${(x,y,z)|(x,y,z)\in L, 1≦x≦2}$の体積を求めよ。
2018神戸大学理系過去問
この動画を見る
$\Large\boxed{5}$ 座標空間において、Oを原点とし、A(2,0,0), B(0,2,0), C(1,1,0)とする。$\triangle$OABを直線OCの周りに1回転してできる回転体をLとする。
(1)直線OC上にない点P(x,y,z)から直線OCにおろした垂線をPHとする。
$\overrightarrow{OH}$と$\overrightarrow{HP}$をx,y,zの式で表せ。
(2)点P(x,y,z)がLの点であるための条件は
$z^2≦2xy$ かつ $0≦x+y≦2$
であることを示せ。
(3)$1≦a≦2$とする。Lを平面x=aで切った切り口の面積S(a)を求めよ。
(4)立体${(x,y,z)|(x,y,z)\in L, 1≦x≦2}$の体積を求めよ。
2018神戸大学理系過去問
【数検2級】高校数学:数学検定2級2次:問題4

単元:
#数学検定・数学甲子園・数学オリンピック等#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学検定#数学検定2級#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
AB=5,BC=6,CA=4である△ABCの内接円の中心をIとします。また、直線AIと辺BCの交点をDとします。
このとき、$\overrightarrow{ AB }=\vec{ b }$ ,$\overrightarrow{ AC }=\vec{ c }$として、次の問いに答えなさい。
(1) $\overrightarrow{ AD }$を$\vec{ b }$ ,$\vec{ c }$を用いて表しなさい。
(2) $\overrightarrow{ AI }$を$\vec{ b }$ ,$\vec{ c }$を用いて表しなさい。
この動画を見る
AB=5,BC=6,CA=4である△ABCの内接円の中心をIとします。また、直線AIと辺BCの交点をDとします。
このとき、$\overrightarrow{ AB }=\vec{ b }$ ,$\overrightarrow{ AC }=\vec{ c }$として、次の問いに答えなさい。
(1) $\overrightarrow{ AD }$を$\vec{ b }$ ,$\vec{ c }$を用いて表しなさい。
(2) $\overrightarrow{ AI }$を$\vec{ b }$ ,$\vec{ c }$を用いて表しなさい。
福田の1.5倍速演習〜合格する重要問題077〜東京大学2018年度理系第3問〜ベクトル方程式の表す点の存在範囲と面積

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#微分法と積分法#ベクトルと平面図形、ベクトル方程式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#面積、体積#東京大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
第3問
放物線y=$x^2$のうち-1≦x≦1を満たす部分をCとする。
座標平面上の原点Oと点A(1,0)を考える。k>0を実数とする。点PがC上を動き、点Qが線分OA上を動くとき
$\overrightarrow{OR}$=$\frac{1}{k}\overrightarrow{OP}$+$k\overrightarrow{OQ}$
を満たす点Rが動く領域の面積をS(k)とする。
S(k)および$\displaystyle\lim_{k \to +0}S(k)$, $\displaystyle\lim_{k \to \infty}S(k)$を求めよ。
2018東京大学理系過去問
この動画を見る
第3問
放物線y=$x^2$のうち-1≦x≦1を満たす部分をCとする。
座標平面上の原点Oと点A(1,0)を考える。k>0を実数とする。点PがC上を動き、点Qが線分OA上を動くとき
$\overrightarrow{OR}$=$\frac{1}{k}\overrightarrow{OP}$+$k\overrightarrow{OQ}$
を満たす点Rが動く領域の面積をS(k)とする。
S(k)および$\displaystyle\lim_{k \to +0}S(k)$, $\displaystyle\lim_{k \to \infty}S(k)$を求めよ。
2018東京大学理系過去問
福田の1.5倍速演習〜合格する重要問題071〜東京医科歯科大学2017年度医学部第2問〜空間における球面と軌跡の問題

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#図形と方程式#円と方程式#軌跡と領域#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#数学(高校生)#数C#東京医科歯科大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{2}}$ xyz空間において、点O(0, 0, 0)と点A(0, 0, 1)を結ぶ線分OAを直径にもつ球面を$\sigma$とする。このとき以下の各問に答えよ。
(1) 球面$\sigma$の方程式を求めよ。
(2) xy平面上にあってOと異なる点Pに対して、線分APと球面$\sigma$との交点をQとするとき、$\overrightarrow{ OQ } \bot \overrightarrow{ AP }$を示せ。
(3) 点S(p, q, r)を$\overrightarrow{OS}・\overrightarrow{ AS }=-|\overrightarrow{ OS }|^2$を満たす、xy平面上にない定点とする。$\sigma$上の点Qが$\overrightarrow{ OS } \bot \overrightarrow{ SQ }$を満たしながら動くとき、直線AQとxy平面上の交点Pはどのような図形を描くか。p, q, rを用いて答えよ。
2017東京医科歯科大学医学部過去問
この動画を見る
$\Large{\boxed{2}}$ xyz空間において、点O(0, 0, 0)と点A(0, 0, 1)を結ぶ線分OAを直径にもつ球面を$\sigma$とする。このとき以下の各問に答えよ。
(1) 球面$\sigma$の方程式を求めよ。
(2) xy平面上にあってOと異なる点Pに対して、線分APと球面$\sigma$との交点をQとするとき、$\overrightarrow{ OQ } \bot \overrightarrow{ AP }$を示せ。
(3) 点S(p, q, r)を$\overrightarrow{OS}・\overrightarrow{ AS }=-|\overrightarrow{ OS }|^2$を満たす、xy平面上にない定点とする。$\sigma$上の点Qが$\overrightarrow{ OS } \bot \overrightarrow{ SQ }$を満たしながら動くとき、直線AQとxy平面上の交点Pはどのような図形を描くか。p, q, rを用いて答えよ。
2017東京医科歯科大学医学部過去問
福田の1.5倍速演習〜合格する重要問題041〜上智大学2019年度TEAP文系第3問〜長方形の紙を折り返す問題

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#平面上のベクトル#図形と方程式#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$AB=2,BC=3$の長方形ABCDの形の紙がある。DE=aとなる辺DC上の
点Eを考える。AがEと重なるように紙を折るとき、折り目となる線と辺AD,
辺BCとの交点をそれぞれP,Qとする。
(1)aを用いて表すと、$AP=\frac{\boxed{二}}{\boxed{ヌ}}a^2+\frac{\boxed{ネ}}{\boxed{ノ}}$である.
(2)aを用いて表すと、$BQ=\frac{\boxed{ハ}}{\boxed{ヒ}}a^2+
\frac{\boxed{フ}}{\boxed{ヘ}}a+\frac{\boxed{ホ}}{\boxed{マ}}$である。
(3)aを用いて表すと、$PQ=\frac{\boxed{ミ}}{\boxed{ム}}\sqrt{a^2+\boxed{メ}}$である。
(4)四角形ABQPの面積はaを用いて表すと、$\frac{\boxed{モ}}{\boxed{ヤ}}a^2+\frac{\boxed{ユ}}{\boxed{ヨ}}a+\boxed{ラ}$
であり、その最小値は$\frac{\boxed{リ}}{\boxed{ル}}$である。
2019上智大過去問
この動画を見る
$AB=2,BC=3$の長方形ABCDの形の紙がある。DE=aとなる辺DC上の
点Eを考える。AがEと重なるように紙を折るとき、折り目となる線と辺AD,
辺BCとの交点をそれぞれP,Qとする。
(1)aを用いて表すと、$AP=\frac{\boxed{二}}{\boxed{ヌ}}a^2+\frac{\boxed{ネ}}{\boxed{ノ}}$である.
(2)aを用いて表すと、$BQ=\frac{\boxed{ハ}}{\boxed{ヒ}}a^2+
\frac{\boxed{フ}}{\boxed{ヘ}}a+\frac{\boxed{ホ}}{\boxed{マ}}$である。
(3)aを用いて表すと、$PQ=\frac{\boxed{ミ}}{\boxed{ム}}\sqrt{a^2+\boxed{メ}}$である。
(4)四角形ABQPの面積はaを用いて表すと、$\frac{\boxed{モ}}{\boxed{ヤ}}a^2+\frac{\boxed{ユ}}{\boxed{ヨ}}a+\boxed{ラ}$
であり、その最小値は$\frac{\boxed{リ}}{\boxed{ル}}$である。
2019上智大過去問
福田の1.5倍速演習〜合格する重要問題034〜東京大学2017年度文系第2問〜点の存在範囲

単元:
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
1辺の長さが1の正六角形ABCDEFが与えられている。点Pが辺AB上を、
点Qが辺CD上をそれぞれ独立に動くとき、線分PQを2:1に内分する点Rが
通りうる範囲の面積を求めよ。
2017東京大学文系過去問
この動画を見る
1辺の長さが1の正六角形ABCDEFが与えられている。点Pが辺AB上を、
点Qが辺CD上をそれぞれ独立に動くとき、線分PQを2:1に内分する点Rが
通りうる範囲の面積を求めよ。
2017東京大学文系過去問
【数C】ベクトルの基本⑰2直線のなす鋭角を求める

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
教材:
#チャート式#青チャートⅡ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
2直線√3x+3y-1=0, -x+√3y-2=0のなす鋭角αを求めよ
この動画を見る
2直線√3x+3y-1=0, -x+√3y-2=0のなす鋭角αを求めよ
【数B】ベクトル:ベクトルの基本⑰2直線のなす鋭角を求める

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
2直線$\sqrt3 x+3y-1=0, -x+\sqrt3 y-2=0$のなす鋭角$\alpha$を求めよ
この動画を見る
2直線$\sqrt3 x+3y-1=0, -x+\sqrt3 y-2=0$のなす鋭角$\alpha$を求めよ
福田の1.5倍速演習〜合格する重要問題030〜東京大学2016年度文系第1問〜鋭角三角形となる条件

単元:
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#平面上のベクトル#図形と方程式#円と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
座標平面上の3点$P(x,y), Q(-x,-y), R(1,0)$が鋭角三角形をなすための$(x,y)$
についての条件を求めよ。また、その条件を満たす点P(x,y)の範囲を図示せよ。
2016東京大学文系過去問
この動画を見る
座標平面上の3点$P(x,y), Q(-x,-y), R(1,0)$が鋭角三角形をなすための$(x,y)$
についての条件を求めよ。また、その条件を満たす点P(x,y)の範囲を図示せよ。
2016東京大学文系過去問
【数B】ベクトル:ベクトルの基本⑯点の存在範囲を考える

【数C】ベクトルの基本⑯点の存在範囲を考える

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
教材:
#チャート式#青チャートⅡ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
点の存在範囲を考える問題
この動画を見る
点の存在範囲を考える問題
