 複素数平面
複素数平面
 複素数平面
複素数平面
【数C】【複素数平面】 極形式から三角比の値を求める ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#複素数平面
指導講師:
理数個別チャンネル
問題文全文(内容文):
$1+i$、$\sqrt{3}+i$を極形式で表すことにより、$cos \displaystyle \frac{5π}{12}$と$sin \displaystyle \frac{5π}{12}$の値を求めよ。
この動画を見る
$1+i$、$\sqrt{3}+i$を極形式で表すことにより、$cos \displaystyle \frac{5π}{12}$と$sin \displaystyle \frac{5π}{12}$の値を求めよ。
【数C】【複素数平面】 極形式で表す ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#複素数平面
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の複素数を 極形式で表せ。ただし、偏角θは0≦θ<2πとする。
(1)$\displaystyle \frac{4+3i}{1+7i}$
(2)$\sqrt{3}+\displaystyle \frac{1-i}{1+i}$
(3)$ー4(\cos \displaystyle \frac{π}{6} + i\sin \displaystyle \frac{π}{6})$
(4)$cos\displaystyle \frac{2π}{3}ーisin \displaystyle \frac{2π}{3}$
(5)$2(sin \displaystyle \frac{π}{3} + i cos \displaystyle \frac{π}{3})$
この動画を見る
次の複素数を 極形式で表せ。ただし、偏角θは0≦θ<2πとする。
(1)$\displaystyle \frac{4+3i}{1+7i}$
(2)$\sqrt{3}+\displaystyle \frac{1-i}{1+i}$
(3)$ー4(\cos \displaystyle \frac{π}{6} + i\sin \displaystyle \frac{π}{6})$
(4)$cos\displaystyle \frac{2π}{3}ーisin \displaystyle \frac{2π}{3}$
(5)$2(sin \displaystyle \frac{π}{3} + i cos \displaystyle \frac{π}{3})$
【数C】【複素数平面】複素数の大きさ・対称式の利用 ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\alpha,\beta$は複素数とする。$|\alpha|=|\beta|=1,\alpha+\beta+1=0$のとき、$\alpha^2+\beta^2$の値を求めよ。
この動画を見る
$\alpha,\beta$は複素数とする。$|\alpha|=|\beta|=1,\alpha+\beta+1=0$のとき、$\alpha^2+\beta^2$の値を求めよ。
【数C】【複素数平面】複素数の大きさと式変形 ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
$|z|=3$かつ$|z-2|=4$を満たす複素数$z$について、次の値を求めよ。
(1)$z\bar{z}$ (2) $z+\bar{z}$
この動画を見る
$|z|=3$かつ$|z-2|=4$を満たす複素数$z$について、次の値を求めよ。
(1)$z\bar{z}$ (2) $z+\bar{z}$
【数C】【複素数平面】複素数の大きさ ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#複素数平面
指導講師:
理数個別チャンネル
問題文全文(内容文):
$z=2-i$のとき、$|z+\displaystyle \frac{1}{z}|^2$の値を求めよ。
この動画を見る
$z=2-i$のとき、$|z+\displaystyle \frac{1}{z}|^2$の値を求めよ。
【数C】【複素数平面】実数であることの証明 ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#複素数平面
指導講師:
理数個別チャンネル
問題文全文(内容文):
α、βを複素数とし、α≠0とするとき、次のことを証明せよ。
αβが実数 ⇔ β=kαとなる実数kがある
この動画を見る
α、βを複素数とし、α≠0とするとき、次のことを証明せよ。
αβが実数 ⇔ β=kαとなる実数kがある
【数C】【複素数平面】基本公式と式変形 ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#複素数平面
指導講師:
理数個別チャンネル
問題文全文(内容文):
複素数$z$が$3z+\bar{z}=2-2i$を満たすとき、以下の問いに答えよ。
(1)$3\bar{z}+z$を求めよ。
(2)$z$を求めよ。
この動画を見る
複素数$z$が$3z+\bar{z}=2-2i$を満たすとき、以下の問いに答えよ。
(1)$3\bar{z}+z$を求めよ。
(2)$z$を求めよ。
福田のおもしろ数学342〜複素数に関する三角不等式と等号成立条件

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
複素数$z_1,z_2$に対して、$|z_1+z_2|\leqq |z_1|+|z_2|が成り立つことを証明してください。$
この動画を見る
複素数$z_1,z_2$に対して、$|z_1+z_2|\leqq |z_1|+|z_2|が成り立つことを証明してください。$
福田のおもしろ数学304〜複素数の実部の最大値

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
複素数 $z$ が $|z|=4$ を満たすとき $\displaystyle (75+117i) z + \frac{96 + 144i}{z}$ の実部の最大値を求めよ。
この動画を見る
複素数 $z$ が $|z|=4$ を満たすとき $\displaystyle (75+117i) z + \frac{96 + 144i}{z}$ の実部の最大値を求めよ。
福田の数学〜早稲田大学2024教育学部第2問〜複素数の集合に関する論証

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$3$つの複素数 $z_1, z_2, z_3$に関する条件$P$を次のように定める。
P: 「$z_1, z_2, z_3$はどれも0ではなく、互いに異なり、かつ$ \{{z_1}^n | n は整数\} = \{{z_2}^n | nは整数\} = \{{z_3}^n |n は整数\}$
である。」
次の問いに答えよ。
(1) $3$つの複素数 $z_1,z_2,z_3$が条件$P$を満たしているとする。このとき$ |z_1| = 1$ であることを示せ。また集合$ \{{z_1}^n | n は整数\}$の要素の個数は有限であることを示せ。
(2) 条件$P$を満たす3つの複素数 $z_1,z_2,z_3$のうち、集合$ \{{z_1}^n | n は整数\}$の要素の個数が最小となるものを考える。このとき集合$ \{{z_1}^n | n は整数\}$を求めよ。
この動画を見る
$3$つの複素数 $z_1, z_2, z_3$に関する条件$P$を次のように定める。
P: 「$z_1, z_2, z_3$はどれも0ではなく、互いに異なり、かつ$ \{{z_1}^n | n は整数\} = \{{z_2}^n | nは整数\} = \{{z_3}^n |n は整数\}$
である。」
次の問いに答えよ。
(1) $3$つの複素数 $z_1,z_2,z_3$が条件$P$を満たしているとする。このとき$ |z_1| = 1$ であることを示せ。また集合$ \{{z_1}^n | n は整数\}$の要素の個数は有限であることを示せ。
(2) 条件$P$を満たす3つの複素数 $z_1,z_2,z_3$のうち、集合$ \{{z_1}^n | n は整数\}$の要素の個数が最小となるものを考える。このとき集合$ \{{z_1}^n | n は整数\}$を求めよ。
福田の数学〜東京理科大学2024創域理工学部第1問(1)〜複素数と三角形の外接円

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}(1)a$を正の実数とする。$x$についての方程式
$(x^2+ax+2)(x^2-ax-1)=0・・・①$
が異なる2つの実数解と異なる2つの虚数解をもつのは
$\boxed{ア} \lt a \lt \boxed{イ}\sqrt{\boxed{ウ}}・・・②$
のときである。
以下では、$a$は不等式$②$を満たす最大の整数とし、$i$は虚数単位とする。このとき、複素数平面上において、方程式$①$の異なる2つの虚数解と$3+i$を頂点とする三角形の面積は$\boxed{エ}$であり、この三角形の外接円を複素数zの方程式で表すと
$|x-\boxed{オ}|=\sqrt{\boxed{カ}}$
である。
この動画を見る
$\boxed{1}(1)a$を正の実数とする。$x$についての方程式
$(x^2+ax+2)(x^2-ax-1)=0・・・①$
が異なる2つの実数解と異なる2つの虚数解をもつのは
$\boxed{ア} \lt a \lt \boxed{イ}\sqrt{\boxed{ウ}}・・・②$
のときである。
以下では、$a$は不等式$②$を満たす最大の整数とし、$i$は虚数単位とする。このとき、複素数平面上において、方程式$①$の異なる2つの虚数解と$3+i$を頂点とする三角形の面積は$\boxed{エ}$であり、この三角形の外接円を複素数zの方程式で表すと
$|x-\boxed{オ}|=\sqrt{\boxed{カ}}$
である。
福田の数学〜上智大学2024理工学部第1問(1)〜複素数の絶対値と三角関数の計算

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
複素数 $z=(-3+2 \cos\theta )+(4+2 \sin \theta)i$ の絶対値は、$\theta = \theta_1$ のとき最小値 $\fbox{ア}$ をとる。このとき、 $\sin{\theta_1} = \frac{\fbox{イ}}{\fbox{ウ}}$ である。
この動画を見る
複素数 $z=(-3+2 \cos\theta )+(4+2 \sin \theta)i$ の絶対値は、$\theta = \theta_1$ のとき最小値 $\fbox{ア}$ をとる。このとき、 $\sin{\theta_1} = \frac{\fbox{イ}}{\fbox{ウ}}$ である。
福田の数学〜上智大学2024TEAP利用型理系第1問(2)〜複素数の極形式とド・モアブルの定理

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$
\begin{eqnarray}
\fcolorbox{#000}{ #fff }{1}(2)\
複素数(\sqrt{2}+\sqrt{6}i)^{2024}を極形式で表したときの絶対値をr、偏角をθとする。ただし、0\leqqθ<2π\
このとき、\dfrac{log_2r}{2024}=\fcolorbox{#000}{ #fff }{$あ \ \ \ $}、θ=\fcolorbox{#000}{ #fff }{$い \ \ \ $}πである。
\end{eqnarray}
$
この動画を見る
$
\begin{eqnarray}
\fcolorbox{#000}{ #fff }{1}(2)\
複素数(\sqrt{2}+\sqrt{6}i)^{2024}を極形式で表したときの絶対値をr、偏角をθとする。ただし、0\leqqθ<2π\
このとき、\dfrac{log_2r}{2024}=\fcolorbox{#000}{ #fff }{$あ \ \ \ $}、θ=\fcolorbox{#000}{ #fff }{$い \ \ \ $}πである。
\end{eqnarray}
$
福田のおもしろ数学263〜複素数平面上の3点が正三角形をなす必要十分条件

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
複素数平面上の$3$点$α,β,γ$が正三角形になるための必要十分条件は$α^2+β^2+γ^2=αβ+βγ+γα$であることを証明して下さい。
この動画を見る
複素数平面上の$3$点$α,β,γ$が正三角形になるための必要十分条件は$α^2+β^2+γ^2=αβ+βγ+γα$であることを証明して下さい。
福田のおもしろ数学256〜高次方程式と極形式

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
方程式
\begin{equation*}
z^6+z^4+z^3+z^2+1=0
\end{equation*}
の解を極形式の形で表せ。
この動画を見る
方程式
\begin{equation*}
z^6+z^4+z^3+z^2+1=0
\end{equation*}
の解を極形式の形で表せ。
福田の数学〜明治大学2024全学部統一III第2問〜複素数平面上の点の移動と確率

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$i$は虚数単位とし、$\omega =\frac{-1+\sqrt{3}i}{2}$とする。
投げたときに表と裏の出る確率がそれぞれ$\frac{1}{2}$の硬貨を用意する$ z_{0} = 0$ とおき、この硬貨を4回投げて、複素数$z_1, z_2, z_3, z_4$を次の規則により定める。
$n = 1, 2, 3, 4$ に対して、$n$回目に投げたとき、表が出たならば$z_n = \omega z_{n-1}$とし、 裏が出れば$ z_n = z_{n−1}+1$とする。例えば、4回投げた結果、順に「裏、表、裏、 表」と出た場合、$z_{1} = z_{0} + 1 = 1, z_2 = \omega z_1 = \omega, z_{3} = z_{2} + 1 = \omega + 1, z_{4} = \omega z_{3} = \omega ^ 2 + \omega$ となる。
上の規則により$z_1, z_2, z_3, z_4$を定めたとき、$P$を$ z_{4} = 0 $となる確率、$Q$を$ z_{4} = 1$ となる確率、$R$を $z_{4} = \omega + 1$ となる確率とすると$2^4P=\fbox{ア}、2Q=\fbox{イ}, 2R=\fbox{ウ}$である。また、$S$を$|z_4|=1$となる確率、$T$を$|z_4|=2$となる確率とすると$2^4S=\fbox{エ}, 2^4T=\fbox{オ}$である。
この動画を見る
$i$は虚数単位とし、$\omega =\frac{-1+\sqrt{3}i}{2}$とする。
投げたときに表と裏の出る確率がそれぞれ$\frac{1}{2}$の硬貨を用意する$ z_{0} = 0$ とおき、この硬貨を4回投げて、複素数$z_1, z_2, z_3, z_4$を次の規則により定める。
$n = 1, 2, 3, 4$ に対して、$n$回目に投げたとき、表が出たならば$z_n = \omega z_{n-1}$とし、 裏が出れば$ z_n = z_{n−1}+1$とする。例えば、4回投げた結果、順に「裏、表、裏、 表」と出た場合、$z_{1} = z_{0} + 1 = 1, z_2 = \omega z_1 = \omega, z_{3} = z_{2} + 1 = \omega + 1, z_{4} = \omega z_{3} = \omega ^ 2 + \omega$ となる。
上の規則により$z_1, z_2, z_3, z_4$を定めたとき、$P$を$ z_{4} = 0 $となる確率、$Q$を$ z_{4} = 1$ となる確率、$R$を $z_{4} = \omega + 1$ となる確率とすると$2^4P=\fbox{ア}、2Q=\fbox{イ}, 2R=\fbox{ウ}$である。また、$S$を$|z_4|=1$となる確率、$T$を$|z_4|=2$となる確率とすると$2^4S=\fbox{エ}, 2^4T=\fbox{オ}$である。
福田の数学〜明治大学2024全学部統一IⅡAB第3問〜変わった規則の数列と点列と面積

単元:
#大学入試過去問(数学)#平面上のベクトル#複素数平面#数列#平面上のベクトルと内積#漸化式#複素数平面#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数B#数C
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle
\fcolorbox{#000}{ #fff }{3}
整数からなる数列\{a_n\} \ (n=1,2,3,...)を次の規則1、2により定める。
$
$\displaystyle
(規則1)a_1=0 , \ a_2=1である。
$
$
\displaystyle(規則2)k=1,2,3,...について、初項から第2^{k+1}項までに値のそれぞれに1を加え、\\ それらすべてを逆の順序にしたものが第2^k+1項から第2^{k+1}項までの値と定める。
$
$\displaystyle
(1)以上の規則により得られる数列\{ a_n \}において、a_{10}=\fcolorbox{#000}{ #fff }{$ア \ \ \ $}であり、a_{16}=\fcolorbox{#000}{ #fff }{$イ \ \ \ $}である。 \\
また第2^k項(k=5,6,7,...)の値は\fcolorbox{#000}{ #fff }{$ウ \ \ \ $}である。
$
$\displaystyle
(2)a_{518}を求めたい。上記の規則2によれば、1 \leqq i \leqq 2^kを満たすiに対して、 \\
a_iに1を加えた数と第
\fcolorbox{#000}{ #fff }{$エ \ \ \ $}
項が、等しいと定めている。 \\
実際に、2^b < 518 \leqq 2^{b+1}を満たすような整数bは
\fcolorbox{#000}{ #fff }{$オ \ \ \ $}
であることに注意すれば、a_{518}=
\fcolorbox{#000}{ #fff }{$カ \ \ \ $}
である。
$
$\displaystyle
(3)点O_k(k=1,2,3,...)を次のように定める。\\
数列 \{ a_n \}の初項から第2^k項に着目し、a_nを4で割った余りにしたがって、ベクトル\vec{e_n}を
$
$
\vec{e_n}=
\left\{
\begin{array}{l}
(1,0) \quad a_nが4の倍数のとき \\
(0,1) \quad a_nを4で割った余りが1のとき \\
(-1,0) \quad a_nが4で割った余りが2のとき \\
(0,-1) \quad a_nを4で割った余りが3のとき
\end{array}
\right.
$
$
\displaystyle
によって定め、\\
点P_1の位置ベクトルを\overrightarrow{OP_1}=\vec{e_1}+\vec{e_2}とし、\\
点P_k(k=2,3,4,...)の位置ベクトルを\\
\overrightarrow{OP_k}=\vec{e_1}+\vec{e_2}+\vec{e_3}+...+\vec{e_{2^k}}とする。\\
たとえば、 \\
\overrightarrow{OP_w}=(1,0)+(0,1)+(-1,0)+(0,1)=(0,2)である。\\
\{a_n\}を定める規則に注目すると、 \\
\overrightarrow{OP_{k+1}} は \overrightarrow{OP_k} の\fcolorbox{#000}{ #fff }{$キ \ \ \ $}倍であり、\\
\angle P_kOP_{k+1}=\fcolorbox{#000}{ #fff }{$ク \ \ \ $}である。\\
このことから\\
\overrightarrow{OP_{99}}=(\fcolorbox{#000}{ #fff }{$ケ \ \ \ $},\fcolorbox{#000}{ #fff }{$コ \ \ \ $})である。
$
この動画を見る
$\displaystyle
\fcolorbox{#000}{ #fff }{3}
整数からなる数列\{a_n\} \ (n=1,2,3,...)を次の規則1、2により定める。
$
$\displaystyle
(規則1)a_1=0 , \ a_2=1である。
$
$
\displaystyle(規則2)k=1,2,3,...について、初項から第2^{k+1}項までに値のそれぞれに1を加え、\\ それらすべてを逆の順序にしたものが第2^k+1項から第2^{k+1}項までの値と定める。
$
$\displaystyle
(1)以上の規則により得られる数列\{ a_n \}において、a_{10}=\fcolorbox{#000}{ #fff }{$ア \ \ \ $}であり、a_{16}=\fcolorbox{#000}{ #fff }{$イ \ \ \ $}である。 \\
また第2^k項(k=5,6,7,...)の値は\fcolorbox{#000}{ #fff }{$ウ \ \ \ $}である。
$
$\displaystyle
(2)a_{518}を求めたい。上記の規則2によれば、1 \leqq i \leqq 2^kを満たすiに対して、 \\
a_iに1を加えた数と第
\fcolorbox{#000}{ #fff }{$エ \ \ \ $}
項が、等しいと定めている。 \\
実際に、2^b < 518 \leqq 2^{b+1}を満たすような整数bは
\fcolorbox{#000}{ #fff }{$オ \ \ \ $}
であることに注意すれば、a_{518}=
\fcolorbox{#000}{ #fff }{$カ \ \ \ $}
である。
$
$\displaystyle
(3)点O_k(k=1,2,3,...)を次のように定める。\\
数列 \{ a_n \}の初項から第2^k項に着目し、a_nを4で割った余りにしたがって、ベクトル\vec{e_n}を
$
$
\vec{e_n}=
\left\{
\begin{array}{l}
(1,0) \quad a_nが4の倍数のとき \\
(0,1) \quad a_nを4で割った余りが1のとき \\
(-1,0) \quad a_nが4で割った余りが2のとき \\
(0,-1) \quad a_nを4で割った余りが3のとき
\end{array}
\right.
$
$
\displaystyle
によって定め、\\
点P_1の位置ベクトルを\overrightarrow{OP_1}=\vec{e_1}+\vec{e_2}とし、\\
点P_k(k=2,3,4,...)の位置ベクトルを\\
\overrightarrow{OP_k}=\vec{e_1}+\vec{e_2}+\vec{e_3}+...+\vec{e_{2^k}}とする。\\
たとえば、 \\
\overrightarrow{OP_w}=(1,0)+(0,1)+(-1,0)+(0,1)=(0,2)である。\\
\{a_n\}を定める規則に注目すると、 \\
\overrightarrow{OP_{k+1}} は \overrightarrow{OP_k} の\fcolorbox{#000}{ #fff }{$キ \ \ \ $}倍であり、\\
\angle P_kOP_{k+1}=\fcolorbox{#000}{ #fff }{$ク \ \ \ $}である。\\
このことから\\
\overrightarrow{OP_{99}}=(\fcolorbox{#000}{ #fff }{$ケ \ \ \ $},\fcolorbox{#000}{ #fff }{$コ \ \ \ $})である。
$
福田の数学〜筑波大学2024理系第6問〜純虚数となる条件と複素数平面上の点

単元:
#数Ⅱ#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
定数$\alpha$は実数でない複素数とする。以下の問いに答えよ。
(1) $\dfrac{\alpha - | \alpha|}{\alpha + | \alpha|} $は純虚数であることを示せ。
(2) 純虚数$\beta$で$\dfrac{\beta - | \alpha|}{\alpha + | \alpha|}$が純虚数となるものがただ1つ存在することを示せ。
(3) 複素数$z$を$\dfrac{z - | \alpha|}{\alpha + | \alpha|}$が純虚数となるように動かすとき、$|z|$が最小となる$z$を$\alpha$を用いて示せ。
この動画を見る
定数$\alpha$は実数でない複素数とする。以下の問いに答えよ。
(1) $\dfrac{\alpha - | \alpha|}{\alpha + | \alpha|} $は純虚数であることを示せ。
(2) 純虚数$\beta$で$\dfrac{\beta - | \alpha|}{\alpha + | \alpha|}$が純虚数となるものがただ1つ存在することを示せ。
(3) 複素数$z$を$\dfrac{z - | \alpha|}{\alpha + | \alpha|}$が純虚数となるように動かすとき、$|z|$が最小となる$z$を$\alpha$を用いて示せ。
福田のおもしろ数学214〜与えられた方程式の表すグラフが放物線であることの証明

単元:
#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\sqrt{x}+\sqrt{y}=1$のグラフは放物線の一部であることを示してください。
この動画を見る
$\sqrt{x}+\sqrt{y}=1$のグラフは放物線の一部であることを示してください。
福田の数学〜千葉大学2024年理系第4問(2)〜複素数平面乗の正三角形の頂点を求める

単元:
#大学入試過去問(数学)#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
複素数平面上の3点$\mathrm{P}(z), \mathrm{Q}(-1),\mathrm{R}(\sqrt3-1-i)$が正三角形をなすとき、複素数$z$を求めよ。
この動画を見る
複素数平面上の3点$\mathrm{P}(z), \mathrm{Q}(-1),\mathrm{R}(\sqrt3-1-i)$が正三角形をなすとき、複素数$z$を求めよ。
福田のおもしろ数学200〜3次方程式の解の公式、カルダノの公式

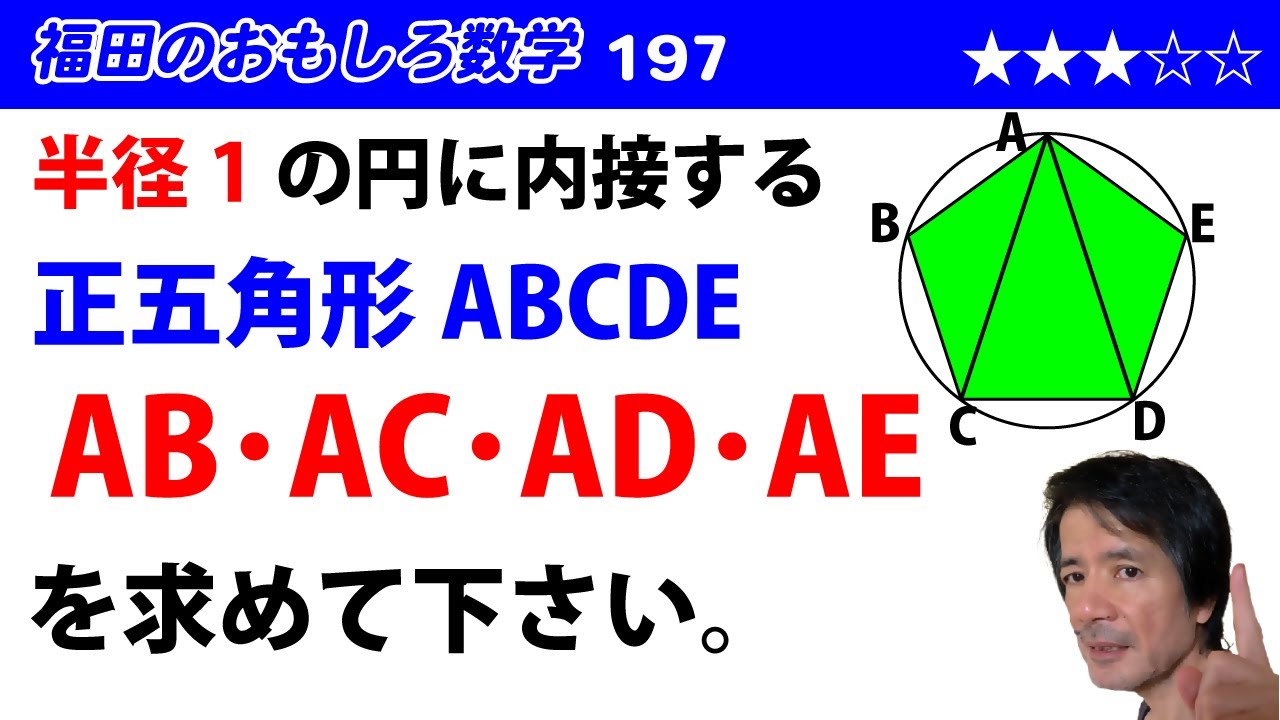
福田のおもしろ数学197〜正五角形の辺、対角線の積の値
単元:
#数Ⅰ#複素数平面#図形と計量#三角比への応用(正弦・余弦・面積)#図形への応用#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
半径$1$の円に内接する正五角形$\mathrm{ABCDE}$について$\mathrm{AB}\cdot\mathrm{AC}\cdot\mathrm{AD}\cdot\mathrm{AE}$を求めよ。
この動画を見る
半径$1$の円に内接する正五角形$\mathrm{ABCDE}$について$\mathrm{AB}\cdot\mathrm{AC}\cdot\mathrm{AD}\cdot\mathrm{AE}$を求めよ。
福田の数学〜名古屋大学2024年理系第2問〜3次方程式の共通解と複素数平面

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ $c$を1より大きい実数とする。また、$i$を虚数単位として、$\alpha$=$\displaystyle\frac{1-i}{\sqrt 2}$ とおく。
複素数$z$に対して、
$P(z)$=$z^3$-$3z^2$+$(c+2)z$-$c$, $Q(z)$=$-\alpha^7z^3$+$3\alpha^6z^2$+$(c+2)\alpha z$-$c$
と定める。
(1)方程式$P(z)$=0を満たす複素数$z$をすべて求め、それらを複素数平面上に図示せよ。
(2)方程式$Q(z)$=0を満たす複素数$z$のうち実部が最大のものを求めよ。
(3)複素数$z$についての2つの方程式$P(z)$=0, $Q(z)$=0が共通解$\beta$を持つとする。そのときの$c$の値と$\beta$を求めよ。
この動画を見る
$\Large\boxed{2}$ $c$を1より大きい実数とする。また、$i$を虚数単位として、$\alpha$=$\displaystyle\frac{1-i}{\sqrt 2}$ とおく。
複素数$z$に対して、
$P(z)$=$z^3$-$3z^2$+$(c+2)z$-$c$, $Q(z)$=$-\alpha^7z^3$+$3\alpha^6z^2$+$(c+2)\alpha z$-$c$
と定める。
(1)方程式$P(z)$=0を満たす複素数$z$をすべて求め、それらを複素数平面上に図示せよ。
(2)方程式$Q(z)$=0を満たす複素数$z$のうち実部が最大のものを求めよ。
(3)複素数$z$についての2つの方程式$P(z)$=0, $Q(z)$=0が共通解$\beta$を持つとする。そのときの$c$の値と$\beta$を求めよ。
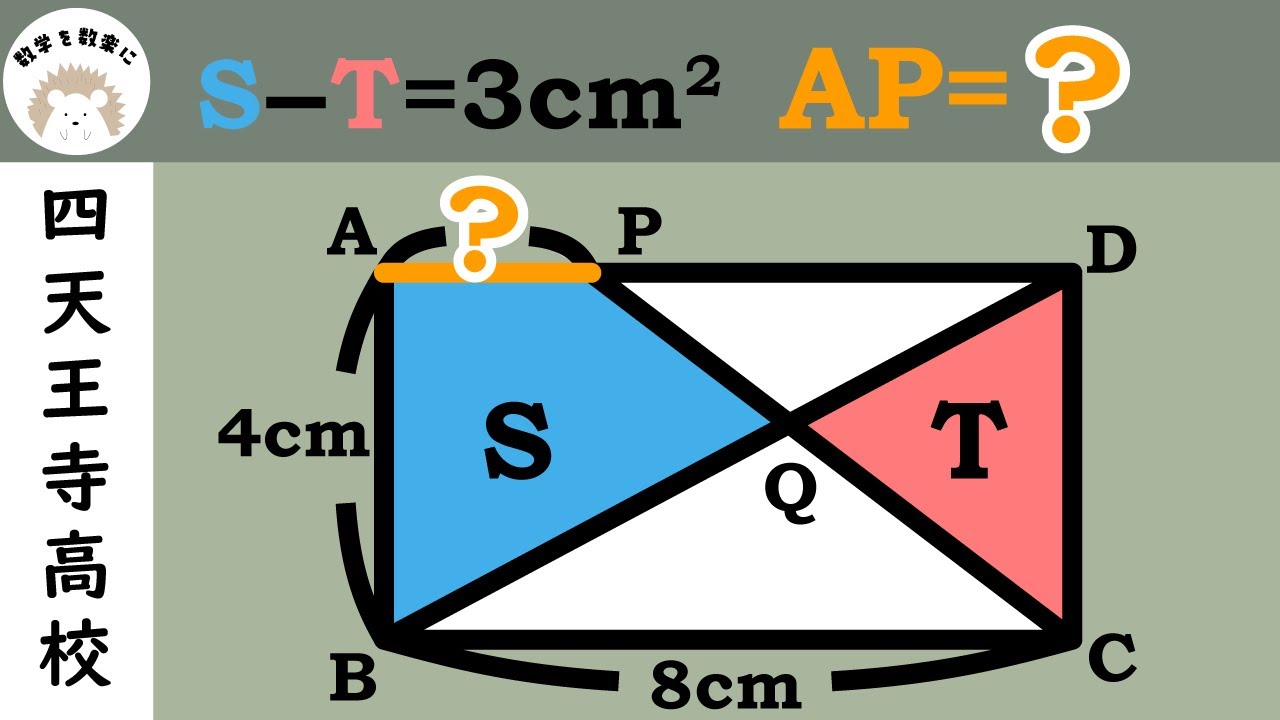
頭の体操に 四天王寺
単元:
#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
数学を数楽に
問題文全文(内容文):
$S-T=3\,\rm{cm}^2$
$AP=?$
*図は動画内参照
四天王寺高等学校
この動画を見る
$S-T=3\,\rm{cm}^2$
$AP=?$
*図は動画内参照
四天王寺高等学校
東京女子医大 二次方程式

福田の数学〜東京工業大学2024年理系第5問〜2次方程式の解が1のn乗根である条件

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 整数の組($a$,$b$)に対して2次式$f(x)$=$x^2$+$ax$+$b$ を考える。方程式$f(x)$=0 の複素数の範囲のすべての解$\alpha$に対して$\alpha^n$=1 となる正の整数$n$が存在するような組($a$,$b$)をすべて求めよ。
この動画を見る
$\Large\boxed{5}$ 整数の組($a$,$b$)に対して2次式$f(x)$=$x^2$+$ax$+$b$ を考える。方程式$f(x)$=0 の複素数の範囲のすべての解$\alpha$に対して$\alpha^n$=1 となる正の整数$n$が存在するような組($a$,$b$)をすべて求めよ。
札幌医科大 2024 複素数の方程式

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
x>0,y≠0
z=x+yi
$z^3=\overline{z}^2$のときxを求めよ
2024札幌医科大過去問
この動画を見る
x>0,y≠0
z=x+yi
$z^3=\overline{z}^2$のときxを求めよ
2024札幌医科大過去問
【数ⅢC】複素数平面の基本⑦内分点、外分点、重心を考える

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
$A(-3+2i),B(4-8i)$のとき線分ABの中点、3:1に内分、外分する点を表す複素数を求めよ
$\alpha=0,\beta=2+3i,γ=1+6i$の3点で表される三角形の重心を表す複素数を求めよ
この動画を見る
$A(-3+2i),B(4-8i)$のとき線分ABの中点、3:1に内分、外分する点を表す複素数を求めよ
$\alpha=0,\beta=2+3i,γ=1+6i$の3点で表される三角形の重心を表す複素数を求めよ
福田の数学〜東京大学2018年理系第5問〜複素数平面上の点の軌跡

単元:
#大学入試過去問(数学)#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
複素数平面上の原点を中心とする半径 1 の円を C とする。
点 P(z) は C 上にあり、点 A(I) とは異なるとする。
点 P における円 C の接線に関して、点 A と対称な点を Q(u) とする。
$\omega=\displaystyle \frac{1}{1-u}$とおき$\omega$と共役な複素数を$\overline{ \omega }$で表す。
(1)uと$\displaystyle \frac{\overline{ \omega }}{\omega}$をzについての整数として表し、絶対値の値$\displaystyle \frac{\vert \omega+\overline{ \omega }-1 \vert}{\vert \omega \vert}$を求めよ。
(2)Cのうち実部が$\frac{1}{2}$以下の複素数平面で表される部分をCとする。点P(z)がC’上を動くときの点R($\omega$)の軌跡を求めよ。
$\omega=x+yi$(x,yは実数)とおく。
2018東大理系過去問
この動画を見る
複素数平面上の原点を中心とする半径 1 の円を C とする。
点 P(z) は C 上にあり、点 A(I) とは異なるとする。
点 P における円 C の接線に関して、点 A と対称な点を Q(u) とする。
$\omega=\displaystyle \frac{1}{1-u}$とおき$\omega$と共役な複素数を$\overline{ \omega }$で表す。
(1)uと$\displaystyle \frac{\overline{ \omega }}{\omega}$をzについての整数として表し、絶対値の値$\displaystyle \frac{\vert \omega+\overline{ \omega }-1 \vert}{\vert \omega \vert}$を求めよ。
(2)Cのうち実部が$\frac{1}{2}$以下の複素数平面で表される部分をCとする。点P(z)がC’上を動くときの点R($\omega$)の軌跡を求めよ。
$\omega=x+yi$(x,yは実数)とおく。
2018東大理系過去問
輪ゴムは切ってないよ!取っ手も壊してない!トポロジー(位相幾何学)

