 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
福田の数学〜名古屋大学2025理系第4問〜コインを裏返す操作の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
コイン$①,\cdots,⑥$が下図のようにマス目の中に
置かれている。
これらのコインから無作為にひとつを選び、
選んだコインはそのままにし、
そのコインのあるマス目と
辺を共有して隣接するマス目のコインを裏返す
操作を考える。
例えば、①を選べば、②,④を裏返し、
②を選べば、①,③,⑤を繰り返す。
最初はすべてのコインが
表向きに置かれていたとする。
正の整数$n$に対し、
$n$回目の操作終了時点ですべてのコインが
裏向きである確率$p_n$とするとき、
以下の問いに答えよ。
(1)$p_2$を求めよ。
(2)コイン$①,\cdots,⑥$をグループ$A,B$に
分けることによって、
$n$回目の操作終了時点ですべてのコインが
裏向きであるための必要十分条件を
次の形に表すことができる。
図は動画内参照
$2025$年名古屋大学理系過去問題
この動画を見る
$\boxed{4}$
コイン$①,\cdots,⑥$が下図のようにマス目の中に
置かれている。
これらのコインから無作為にひとつを選び、
選んだコインはそのままにし、
そのコインのあるマス目と
辺を共有して隣接するマス目のコインを裏返す
操作を考える。
例えば、①を選べば、②,④を裏返し、
②を選べば、①,③,⑤を繰り返す。
最初はすべてのコインが
表向きに置かれていたとする。
正の整数$n$に対し、
$n$回目の操作終了時点ですべてのコインが
裏向きである確率$p_n$とするとき、
以下の問いに答えよ。
(1)$p_2$を求めよ。
(2)コイン$①,\cdots,⑥$をグループ$A,B$に
分けることによって、
$n$回目の操作終了時点ですべてのコインが
裏向きであるための必要十分条件を
次の形に表すことができる。
図は動画内参照
$2025$年名古屋大学理系過去問題
河合塾講師のストで荻野先生が炎上 #shorts

単元:
#大学入試過去問(数学)#情報Ⅰ(高校生)#全統模試(河合塾)#英語(高校生)#大学入試過去問(英語)#全統模試(河合塾)#数学(高校生)#模試解説・過去問解説#【河合塾】全統共通テスト模試
指導講師:
Morite2 English Channel
問題文全文(内容文):
緊急速報!河合塾講師のストライキ問題が飛び火!なぜかあの予備校講師が**炎上**する事態に!
人気YouTubeチャンネル「Morite2 English Channel」が、先日投稿した**塾講師のストライキ動画**に寄せられたコメントが波紋を呼んでいる。なんと、予備校の**荻野(おぎの)先生**が「炎上」しているというのだ!
炎上のきっかけは、荻野先生がSNS(X)で「**生徒に迷惑をかけたらダメ**」と投稿したこと。生徒にとっては授業をしないことは迷惑がかかる、という予備校講師目線、生徒目線からの当然の意見だった。授業が中断されれば進度が遅れる可能性もあるからだ。
ところがこれに対し、「**ストライキは迷惑をかけなきゃ意味がない**」といったコメントが殺到!労働者として生きる社会人から見れば、消費者側に迷惑がかかるのが「スト」なのだ、という意見がぶつけられた形だ。
荻野先生からすると、「あんたたちの目線で予備校や教育業界を語るな」ということだろう。これは、予備校講師目線と、労働者(社会人)目線という、**目線が全く違う**ために、折り合いがつくわけがない状況だという。
この動画では、交渉や条件という意味を持つ重要な単語「**terms**」について、「**come to terms**(折り合いがつく)」という形で出題されやすいと解説し、受験生への学習アドバイスも添えられている。
このストライキ論争、あなたはどちらの意見に共感する?予備校業界を揺るがす議論から目が離せない!
この動画を見る
緊急速報!河合塾講師のストライキ問題が飛び火!なぜかあの予備校講師が**炎上**する事態に!
人気YouTubeチャンネル「Morite2 English Channel」が、先日投稿した**塾講師のストライキ動画**に寄せられたコメントが波紋を呼んでいる。なんと、予備校の**荻野(おぎの)先生**が「炎上」しているというのだ!
炎上のきっかけは、荻野先生がSNS(X)で「**生徒に迷惑をかけたらダメ**」と投稿したこと。生徒にとっては授業をしないことは迷惑がかかる、という予備校講師目線、生徒目線からの当然の意見だった。授業が中断されれば進度が遅れる可能性もあるからだ。
ところがこれに対し、「**ストライキは迷惑をかけなきゃ意味がない**」といったコメントが殺到!労働者として生きる社会人から見れば、消費者側に迷惑がかかるのが「スト」なのだ、という意見がぶつけられた形だ。
荻野先生からすると、「あんたたちの目線で予備校や教育業界を語るな」ということだろう。これは、予備校講師目線と、労働者(社会人)目線という、**目線が全く違う**ために、折り合いがつくわけがない状況だという。
この動画では、交渉や条件という意味を持つ重要な単語「**terms**」について、「**come to terms**(折り合いがつく)」という形で出題されやすいと解説し、受験生への学習アドバイスも添えられている。
このストライキ論争、あなたはどちらの意見に共感する?予備校業界を揺るがす議論から目が離せない!
【数Ⅲ】【積分とその応用】定積分の種々の問題3 ※問題文は概要欄

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数$\displaystyle F(x)=\int_x^{2x^2}(x+t)\sin t~dt$
を$x$について微分せよ。
この動画を見る
関数$\displaystyle F(x)=\int_x^{2x^2}(x+t)\sin t~dt$
を$x$について微分せよ。
【数Ⅲ】【積分とその応用】定積分の種々の問題2 ※問題文は概要欄

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数を$x$について微分せよ。
(1) $\displaystyle y=\int_x^{2x}\cos^2t~dt$
(2) $\displaystyle y=\int_x^{x^2}e^t\sin t~dt$
この動画を見る
次の関数を$x$について微分せよ。
(1) $\displaystyle y=\int_x^{2x}\cos^2t~dt$
(2) $\displaystyle y=\int_x^{x^2}e^t\sin t~dt$
【数Ⅲ】【積分とその応用】定積分の種々の問題1 ※問題文は概要欄

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数を$x$について微分せよ。
(1) $\displaystyle F(x)=\int_0^x(x+t)e^t~dt$
(2) $\displaystyle F(x)=\int_1^x(t-x)\log t~dt$
この動画を見る
次の関数を$x$について微分せよ。
(1) $\displaystyle F(x)=\int_0^x(x+t)e^t~dt$
(2) $\displaystyle F(x)=\int_1^x(t-x)\log t~dt$
福田のおもしろ数学500〜循環形式の連立方程式を解こう

単元:
#連立方程式#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x-1)(y^2+6)=y(x^2+1) \\
(y-1)(x^2+6)=x(y^2+1)
\end{array}
\right.
\end{eqnarray}$
を満たす実数$x,y$をすべて求めて下さい。
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x-1)(y^2+6)=y(x^2+1) \\
(y-1)(x^2+6)=x(y^2+1)
\end{array}
\right.
\end{eqnarray}$
を満たす実数$x,y$をすべて求めて下さい。
福田の数学〜名古屋大学2025理系第3問〜球の通過範囲の体積

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
以下の問いに答えよ。
(1)実数$r,\alpha$は$0\lt r \leqq 1,0\leqq \alpha \lt \pi$をみたすとする。
$xy$平面内で、点$(1,0)$を中心にもつ半径$r$の
円周およびその内部を$C$とする。
$C$を原点$(0,0)$を中心に反時計回りに角度$\alpha$だけ
回転させるとき、$C$が通過する領域の面積を求めよ。
(2)実数$R,\alpha$は$0\lt R \leqq 1,0\leqq \alpha \lt \pi$をみたすとする。
$xyz$空間内で、点$(1,0,0)$を中心にもつ半径$R$の
球面およびその内部を$B$とする。
$B$を$z$軸のまわりに角度$\alpha$だけ回転させるとき、
$B$が通過する領域の体積を求めよ。
ただし、回転の向きは回転後の$B$の中心が
$(\cos \alpha,\sin \alpha,0)$になるように選ぶものとする。
$2025$年名古屋大学理系過去問題
この動画を見る
$\boxed{3}$
以下の問いに答えよ。
(1)実数$r,\alpha$は$0\lt r \leqq 1,0\leqq \alpha \lt \pi$をみたすとする。
$xy$平面内で、点$(1,0)$を中心にもつ半径$r$の
円周およびその内部を$C$とする。
$C$を原点$(0,0)$を中心に反時計回りに角度$\alpha$だけ
回転させるとき、$C$が通過する領域の面積を求めよ。
(2)実数$R,\alpha$は$0\lt R \leqq 1,0\leqq \alpha \lt \pi$をみたすとする。
$xyz$空間内で、点$(1,0,0)$を中心にもつ半径$R$の
球面およびその内部を$B$とする。
$B$を$z$軸のまわりに角度$\alpha$だけ回転させるとき、
$B$が通過する領域の体積を求めよ。
ただし、回転の向きは回転後の$B$の中心が
$(\cos \alpha,\sin \alpha,0)$になるように選ぶものとする。
$2025$年名古屋大学理系過去問題
【数C】【複素数平面】複素数と図形12 ※問題文は概要欄
単元:
#複素数平面#図形への応用#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#複素数平面
指導講師:
理数個別チャンネル
問題文全文(内容文):
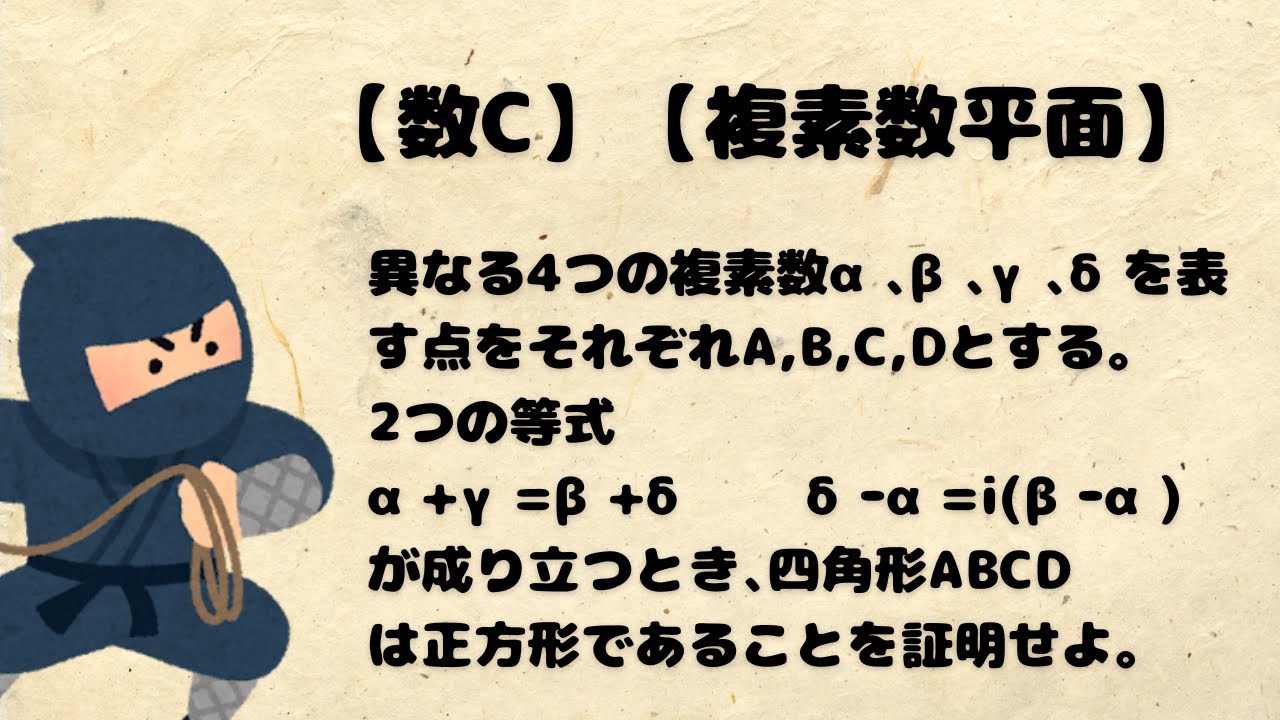
異なる4つの複素数α、β、γ、δを表す点を
それぞれA,B,C,Dとする。2つの等式
α+γ=β+δ δーα=i(βーα)
が成り立つとき、四角形ABCD
は正方形であることを証明せよ。
この動画を見る
異なる4つの複素数α、β、γ、δを表す点を
それぞれA,B,C,Dとする。2つの等式
α+γ=β+δ δーα=i(βーα)
が成り立つとき、四角形ABCD
は正方形であることを証明せよ。
【数C】【複素数平面】複素数と図形11 ※問題文は概要欄
単元:
#複素数平面#図形への応用#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#複素数平面
指導講師:
理数個別チャンネル
問題文全文(内容文):
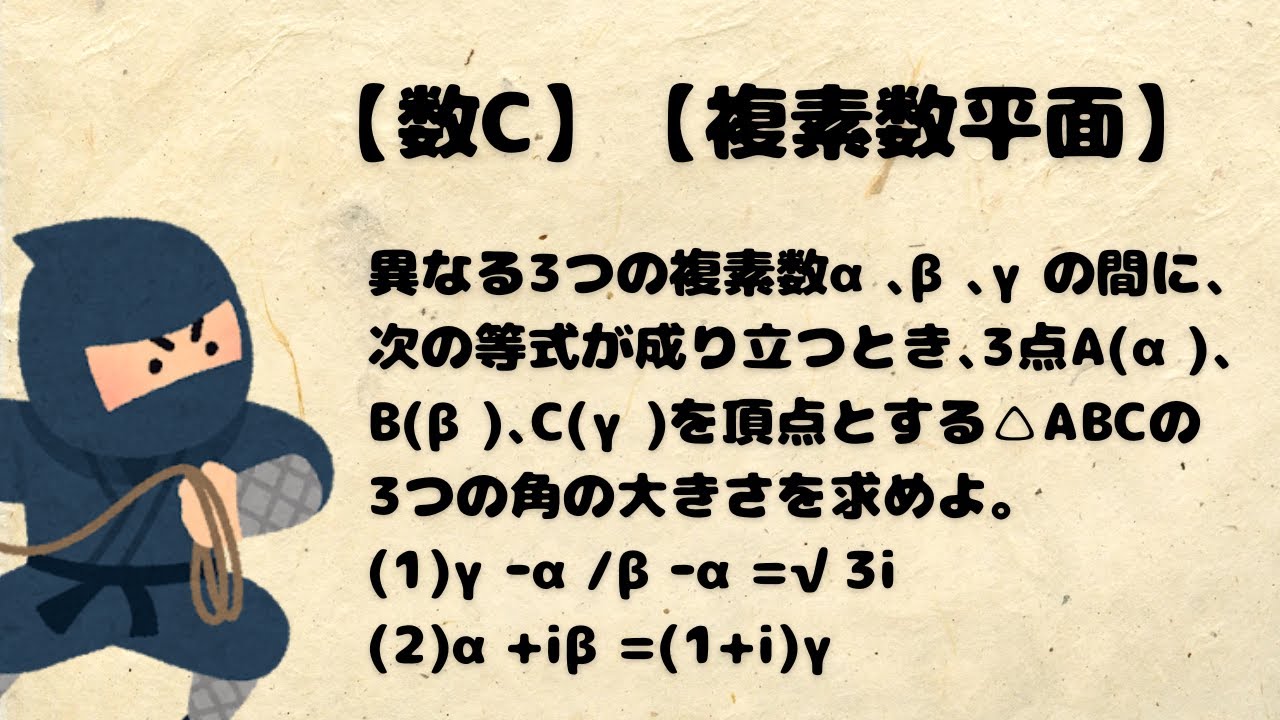
異なる3つの複素数α、β、γの間に、次の等式が成り立つとき、3点A(α)、B(β)、C(γ)を頂点とする△ABCの3つの角の大きさを求めよ。
(1)$\displaystyle \frac{γーα}{βーα}=\sqrt{3}i $
(2)$α+iβ=(1+i)γ$
この動画を見る
異なる3つの複素数α、β、γの間に、次の等式が成り立つとき、3点A(α)、B(β)、C(γ)を頂点とする△ABCの3つの角の大きさを求めよ。
(1)$\displaystyle \frac{γーα}{βーα}=\sqrt{3}i $
(2)$α+iβ=(1+i)γ$
【数C】【複素数平面】複素数と図形10 ※問題文は概要欄
単元:
#複素数平面#図形への応用#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#複素数平面
指導講師:
理数個別チャンネル
問題文全文(内容文):
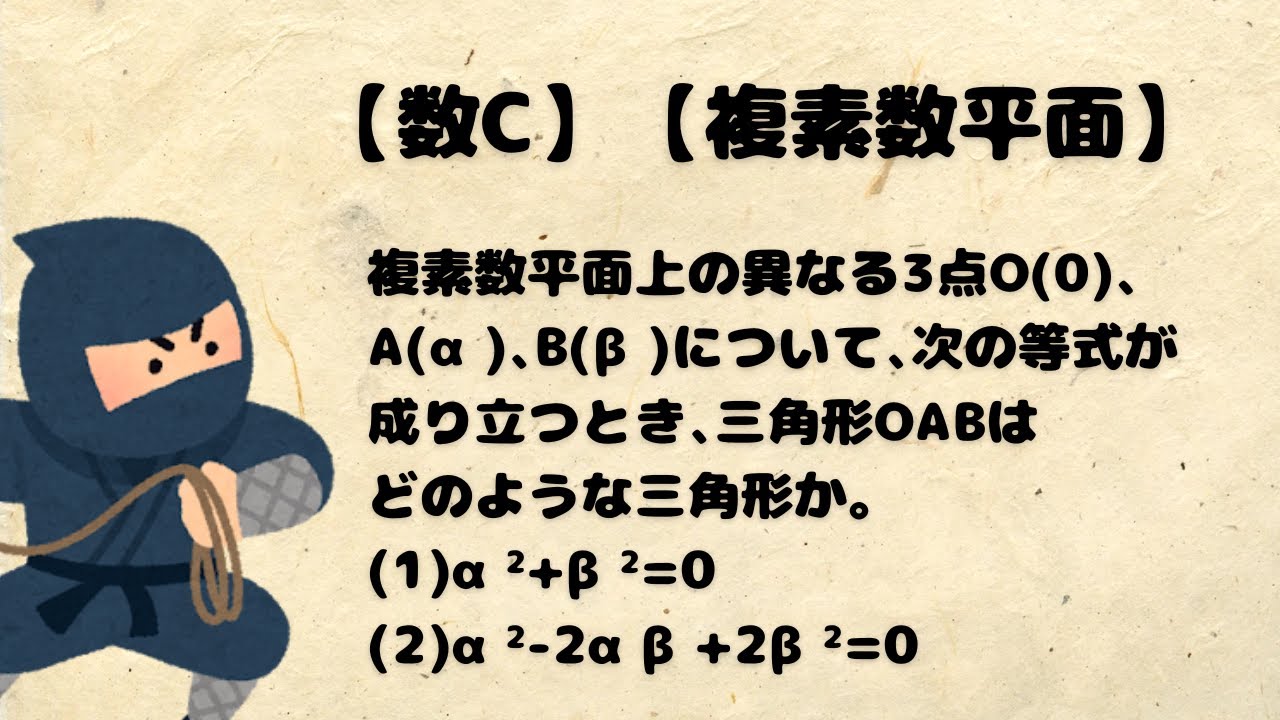
複素数平面上の異なる3点O(0)、A(α)、B(β)について、次の等式が成り立つとき、三角形OABはどのような三角形か。
(1)α²+β²=0
(2)α²-2αβ+2β²=0
この動画を見る
複素数平面上の異なる3点O(0)、A(α)、B(β)について、次の等式が成り立つとき、三角形OABはどのような三角形か。
(1)α²+β²=0
(2)α²-2αβ+2β²=0
【数C】【複素数平面】複素数と図形9 ※問題文は概要欄

単元:
#複素数平面#図形への応用#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#複素数平面
指導講師:
理数個別チャンネル
問題文全文(内容文):
複素数平面上の異なる2点A,Bを表す複素数をそれぞれ
1+i、4+3iとする。線分ABを1辺とする正方形の
他の2つの頂点を表す複素数をそれぞれ求めよ。
この動画を見る
複素数平面上の異なる2点A,Bを表す複素数をそれぞれ
1+i、4+3iとする。線分ABを1辺とする正方形の
他の2つの頂点を表す複素数をそれぞれ求めよ。
河合塾で初のストライキ【元講師が詳細解説】

単元:
#大学入試過去問(数学)#情報Ⅰ(高校生)#全統模試(河合塾)#英語(高校生)#大学入試過去問(英語)#全統模試(河合塾)#数学(高校生)#模試解説・過去問解説#【河合塾】全統共通テスト模試
指導講師:
Morite2 English Channel
問題文全文(内容文):
大手の河合塾で異例の**ストライキ**が発生!元講師がその詳細を解説する激震の内容だ!
予備校・学習塾業界で大手としては**初めて**となる授業中のストライキが実施された! 今回ストライキを決行したのは、河合塾ユニオンの委員長で、物理を担当する竹達さん(講師歴38年目のベテラン)だという。ストライキは授業全てではなく、90分間の授業の**最後の15分間**に限定して行われる予定だ!
ストライキの背景には、ベテラン講師の**コマ単価が10年以上変わっていない**現状がある。竹達委員長は、コマ単価が約1万7,000円という状況が続き、年収は約500万円から600万円程度だと明かしている。時給に換算すると1万円を超えると見ることもできるが、コマがなければ生活できない、安定しない職業であり、会社からの手当も少ないため、これを高いと取るか低いと取るかは人によると述べられている。
ユニオン側が要求しているのは主に3点だ。
1. **賃上げの実現**:1分あたり35円(1コマ90分で3,150円)の賃上げ。これは時給換算で2,100円の賃上げとなり、この業界では「強欲な申し出」とも聞こえるが、講師は授業準備や採点、生徒の質問対応、保護者への連絡などの業務を無給で行っており、長時間拘束されている点を訴えている。
2. **私学共済への加入**:業務委託契約の講師でも私学共済に加入できるようにすること。
3. **無期転換権の承認**:業務委託契約の講師にも5年間で無期転換を認めるよう要求。
ユニオン側は、物価高騰で実質賃金が下がる中、賃上げ要求を河合塾に一蹴されたため、今回のストライキを決行したとしている。
委員長は、「生徒に迷惑をかけたくない」という思いから授業の最後の15分間に限定したストを実施。ストライキは労働者の基本的な権利であり、業界の多くの場所で若者が疲弊している現状を見て、**「塾講師も労働者である」**ことを示すために、あえて最も象徴的な「スト」の権利を発揮し、他の塾講師がストライキを起こす際のハードルを下げる狙いがあるという。
これに対し河合塾側は、「要求項目に対する弊方の見解が理解いただけず残念」としつつも、適法に行われるストライキは受け入れ、**別の講師による補填授業**(90分間まるまる授業)を用意することで対応するとしている。
この慰霊のストライキが、予備校業界の労働環境をどう変えるのか、結果に注目が集まっている!
この動画を見る
大手の河合塾で異例の**ストライキ**が発生!元講師がその詳細を解説する激震の内容だ!
予備校・学習塾業界で大手としては**初めて**となる授業中のストライキが実施された! 今回ストライキを決行したのは、河合塾ユニオンの委員長で、物理を担当する竹達さん(講師歴38年目のベテラン)だという。ストライキは授業全てではなく、90分間の授業の**最後の15分間**に限定して行われる予定だ!
ストライキの背景には、ベテラン講師の**コマ単価が10年以上変わっていない**現状がある。竹達委員長は、コマ単価が約1万7,000円という状況が続き、年収は約500万円から600万円程度だと明かしている。時給に換算すると1万円を超えると見ることもできるが、コマがなければ生活できない、安定しない職業であり、会社からの手当も少ないため、これを高いと取るか低いと取るかは人によると述べられている。
ユニオン側が要求しているのは主に3点だ。
1. **賃上げの実現**:1分あたり35円(1コマ90分で3,150円)の賃上げ。これは時給換算で2,100円の賃上げとなり、この業界では「強欲な申し出」とも聞こえるが、講師は授業準備や採点、生徒の質問対応、保護者への連絡などの業務を無給で行っており、長時間拘束されている点を訴えている。
2. **私学共済への加入**:業務委託契約の講師でも私学共済に加入できるようにすること。
3. **無期転換権の承認**:業務委託契約の講師にも5年間で無期転換を認めるよう要求。
ユニオン側は、物価高騰で実質賃金が下がる中、賃上げ要求を河合塾に一蹴されたため、今回のストライキを決行したとしている。
委員長は、「生徒に迷惑をかけたくない」という思いから授業の最後の15分間に限定したストを実施。ストライキは労働者の基本的な権利であり、業界の多くの場所で若者が疲弊している現状を見て、**「塾講師も労働者である」**ことを示すために、あえて最も象徴的な「スト」の権利を発揮し、他の塾講師がストライキを起こす際のハードルを下げる狙いがあるという。
これに対し河合塾側は、「要求項目に対する弊方の見解が理解いただけず残念」としつつも、適法に行われるストライキは受け入れ、**別の講師による補填授業**(90分間まるまる授業)を用意することで対応するとしている。
この慰霊のストライキが、予備校業界の労働環境をどう変えるのか、結果に注目が集まっている!
【保存版】たすき掛けの因数分解の考え方

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
因数分解しなさい。
$5x^{ 2 }-11x+2$
この動画を見る
因数分解しなさい。
$5x^{ 2 }-11x+2$
福田のおもしろ数学499〜1分チャレンジ!数値計算

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\dfrac{(4\times 7+2)(6\times 9+2)(8\times 11+2)\cdots}{(5\times 8 +2)(7\times 10 +2)(9\times 12 +2)\cdots }$
$\dfrac{\cdots (100\times 103+2)}{\cdots (99\times 102+2)}$
を計算して下さい。
この動画を見る
$\dfrac{(4\times 7+2)(6\times 9+2)(8\times 11+2)\cdots}{(5\times 8 +2)(7\times 10 +2)(9\times 12 +2)\cdots }$
$\dfrac{\cdots (100\times 103+2)}{\cdots (99\times 102+2)}$
を計算して下さい。
福田の数学〜名古屋大学2025理系第2問〜不定方程式の整数解

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
整数$a,b,c$に対し次の条件を考える。
(*)$ a\geqq b \geqq 0$かつ$a^2-b^2=c$
以下の問いに答えよ。
(1)$c=24,25,26$それぞれの場合に
条件(*)をみたす
整数の組$(a,b)$をすべて求めよ。
(2)$p$は$3$以上の素数、$n$は正の整数、
$c=4p^{2n}$とする。
このとき、条件(*)をみたす整数の組$(a,b)$を
すべて求めよ。
$2025$年名古屋大学理系過去問題
この動画を見る
$\boxed{2}$
整数$a,b,c$に対し次の条件を考える。
(*)$ a\geqq b \geqq 0$かつ$a^2-b^2=c$
以下の問いに答えよ。
(1)$c=24,25,26$それぞれの場合に
条件(*)をみたす
整数の組$(a,b)$をすべて求めよ。
(2)$p$は$3$以上の素数、$n$は正の整数、
$c=4p^{2n}$とする。
このとき、条件(*)をみたす整数の組$(a,b)$を
すべて求めよ。
$2025$年名古屋大学理系過去問題
【数C】【平面上のベクトル】ベクトルの内積1 ※問題文は概要欄

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の条件を満たす2つのベクトル$\vec{ a }$ ,$\vec{ b }$のなす角θを求めよ。
(1) $| \vec{ a } |=2$ ,$|\vec{ b }|=1$ ,$|3\vec{ a }+2\vec{ b } |=2\sqrt{7}$
(2) $| \vec{ a } |=4$ ,$|2\vec{ a } -\vec{ b } |=7$ ,$(\vec{ a } +\vec{ b } )·(\vec{ b } -3\vec{ a } )=-43$
この動画を見る
次の条件を満たす2つのベクトル$\vec{ a }$ ,$\vec{ b }$のなす角θを求めよ。
(1) $| \vec{ a } |=2$ ,$|\vec{ b }|=1$ ,$|3\vec{ a }+2\vec{ b } |=2\sqrt{7}$
(2) $| \vec{ a } |=4$ ,$|2\vec{ a } -\vec{ b } |=7$ ,$(\vec{ a } +\vec{ b } )·(\vec{ b } -3\vec{ a } )=-43$
福田のおもしろ数学498〜定積分で定義された関数の極限

単元:
#関数と極限#積分とその応用#関数の極限#定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$0\lt t \leqq 1$に対し、
$f(t)=\dfrac{1}{t} \displaystyle \int_{0}^{\frac{\pi}{2}t} \vert \cos 2x \vert dx$とする。
$\displaystyle \lim_{t\to 0} f(t)$を求めよ。
この動画を見る
$0\lt t \leqq 1$に対し、
$f(t)=\dfrac{1}{t} \displaystyle \int_{0}^{\frac{\pi}{2}t} \vert \cos 2x \vert dx$とする。
$\displaystyle \lim_{t\to 0} f(t)$を求めよ。
福田の数学〜名古屋大学2025理系第1問〜関数の増減と最大

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(1)実数$x$を変数とする関数$f(x)$が導関数$f'(x)$および
第$2$次導関数$f''(x)$をもち、
すべての$x$に対し$f''(x)\gt 0$をみたすとする。
さらに以下の極限値$a,b(a\lt b)$が存在すると仮定する。
$\displaystyle \lim_{x\to -\infty} f'(x)=a,\displaystyle \lim_{x\to\infty}f'(x)=b$
このとき、
$a\lt c \lt b$をみたす任意の実数$c$に対し、
関数$g(x)=cx-f(x)$の値を最大にする
$x=x_0$がただひとつ存在することを示せ。
(2)実数$x$を変数とする関数
$f(x)=\log \left(\dfrac{e^x+e^{-x}}{2}\right)$
はすべての$x$に対し$f''(x)\gt 0$をみたすことを示せ。
また、この$f$に対し小問(1)の極限値$a,b$を求めよ。
(3)小問(2)の関数$f$および極限値$a,b$を考える。
$a \lt c \lt b$をみたす任意の実数$c$に対し
小問(1)の$x_0$および$g(x_0)$を$c$で表せ。
$2025$年名古屋大学理系過去問題
この動画を見る
$\boxed{1}$
(1)実数$x$を変数とする関数$f(x)$が導関数$f'(x)$および
第$2$次導関数$f''(x)$をもち、
すべての$x$に対し$f''(x)\gt 0$をみたすとする。
さらに以下の極限値$a,b(a\lt b)$が存在すると仮定する。
$\displaystyle \lim_{x\to -\infty} f'(x)=a,\displaystyle \lim_{x\to\infty}f'(x)=b$
このとき、
$a\lt c \lt b$をみたす任意の実数$c$に対し、
関数$g(x)=cx-f(x)$の値を最大にする
$x=x_0$がただひとつ存在することを示せ。
(2)実数$x$を変数とする関数
$f(x)=\log \left(\dfrac{e^x+e^{-x}}{2}\right)$
はすべての$x$に対し$f''(x)\gt 0$をみたすことを示せ。
また、この$f$に対し小問(1)の極限値$a,b$を求めよ。
(3)小問(2)の関数$f$および極限値$a,b$を考える。
$a \lt c \lt b$をみたす任意の実数$c$に対し
小問(1)の$x_0$および$g(x_0)$を$c$で表せ。
$2025$年名古屋大学理系過去問題
福田のおもしろ数学497〜gcdとlcmを使った方程式の整数解

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
正の整数$a,b$が次の式を満たしている。
$ab=gcd(a,b)+Icm(a,b)$
このような$(a,b)$の組をすべて求めて下さい。
$gcd(a,b)$は$a,b$の最大公約数、
$Icm(a,b)$は$a,b$の最小公倍数とする。
この動画を見る
正の整数$a,b$が次の式を満たしている。
$ab=gcd(a,b)+Icm(a,b)$
このような$(a,b)$の組をすべて求めて下さい。
$gcd(a,b)$は$a,b$の最大公約数、
$Icm(a,b)$は$a,b$の最小公倍数とする。
福田の数学〜東京科学大学(旧・東京工業大学)2025理系第5問〜分数関数のグラフと解の存在範囲

単元:
#大学入試過去問(数学)#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{5}$
(1)関数
$f(t)=\dfrac{t^2-1}{t^3} (t\neq 0)$
の増減を調べ、グラフの概形をかけ。
(2)実数$x,y,z$が、条件
$\begin{eqnarray}
\left\{
\begin{array}{l}
x \lt y \lt z \\
xyz \neq 0 \\\
x^3y^2-x^3=x^2y^3-y^3 \\\
y^3z^2-y^3=y^2z^3-z^3
\end{array}
\right.
\end{eqnarray}$
を満たしながら動くとき、
$x$が取り得る値の範囲を求めよ。
$2025$年東京科学大学(旧・東京工業大学)
理系過去問題
この動画を見る
$\boxed{5}$
(1)関数
$f(t)=\dfrac{t^2-1}{t^3} (t\neq 0)$
の増減を調べ、グラフの概形をかけ。
(2)実数$x,y,z$が、条件
$\begin{eqnarray}
\left\{
\begin{array}{l}
x \lt y \lt z \\
xyz \neq 0 \\\
x^3y^2-x^3=x^2y^3-y^3 \\\
y^3z^2-y^3=y^2z^3-z^3
\end{array}
\right.
\end{eqnarray}$
を満たしながら動くとき、
$x$が取り得る値の範囲を求めよ。
$2025$年東京科学大学(旧・東京工業大学)
理系過去問題
mathematical formula : Shirotan's cute kawaii math show #数学 #小学生テスト #高校入試 #勉強 #高校受験

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
x²-5x+3=0の解a,b
1/a+1/b=?
この動画を見る
x²-5x+3=0の解a,b
1/a+1/b=?
福田のおもしろ数学496〜少なくとも1つは−1より大きくないことの証明

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
実数$a,b,c,d$が次の式を満たしている。
$a+b+c+d=-2$
$ab+ac+ad+bc+bd+cd=0$
このとき、$a,b,c,d$の少なくとも$1$つは
$-1$より大きくないことを証明して下さい。
この動画を見る
実数$a,b,c,d$が次の式を満たしている。
$a+b+c+d=-2$
$ab+ac+ad+bc+bd+cd=0$
このとき、$a,b,c,d$の少なくとも$1$つは
$-1$より大きくないことを証明して下さい。
福田の数学〜東京科学大学(旧・東京工業大学)2025理系第4問〜フィボナッチ数列と無限級数の和

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
数列$\{a_n\}$を
$a_1=a_2=1,a_{n+2}=a_{n+1}+a_n (n=1,2,3,\cdots)$
により定め、数列$\{b_n\}$を
$\tan b_n=\dfrac{1}{a_n}$
により定める。
ただし、$0\lt b_n \lt \dfrac{\pi}{2}$であるものとする。
(1)$n\geqq 2$に対して、$a_{n+1}a_{n-1}-{a_n}^2$を求めよ。
(2)$m\geqq 1$($m$は整数)に対して、
$a_{2m}・\tan(b_{2m+1}+b_{2m+2})$を求めよ。
(3)無限級数$\displaystyle \sum_{m=0}^{\infty} b_{2m+1}$を求めよ。
$2025$年東京科学大学(旧・東京工業大学)
理系過去問題
この動画を見る
$\boxed{4}$
数列$\{a_n\}$を
$a_1=a_2=1,a_{n+2}=a_{n+1}+a_n (n=1,2,3,\cdots)$
により定め、数列$\{b_n\}$を
$\tan b_n=\dfrac{1}{a_n}$
により定める。
ただし、$0\lt b_n \lt \dfrac{\pi}{2}$であるものとする。
(1)$n\geqq 2$に対して、$a_{n+1}a_{n-1}-{a_n}^2$を求めよ。
(2)$m\geqq 1$($m$は整数)に対して、
$a_{2m}・\tan(b_{2m+1}+b_{2m+2})$を求めよ。
(3)無限級数$\displaystyle \sum_{m=0}^{\infty} b_{2m+1}$を求めよ。
$2025$年東京科学大学(旧・東京工業大学)
理系過去問題
【暗記じゃない…!】数列:興南高等学校~全国入試問題解法
単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
1/1,1/2,2/2,1/3,2/3,3/3,1/4,2/4,3/4,4/4,・・・
の時、左から85番目の分数?
この動画を見る
1/1,1/2,2/2,1/3,2/3,3/3,1/4,2/4,3/4,4/4,・・・
の時、左から85番目の分数?
福田のおもしろ数学495〜次数の高い連立方程式

単元:
#連立方程式#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
a^3+3ab^2+3ac^2-6abc=1 \\
b^3+3ba^2+3bc^2-6abc=1 \\\
c^2+3ca^2+3cb^2-6abc=1
\end{array}
\right.
\end{eqnarray}$
を満たす実数$a,b,c$を求めよ。
この動画を見る
連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
a^3+3ab^2+3ac^2-6abc=1 \\
b^3+3ba^2+3bc^2-6abc=1 \\\
c^2+3ca^2+3cb^2-6abc=1
\end{array}
\right.
\end{eqnarray}$
を満たす実数$a,b,c$を求めよ。
福田の数学〜東京科学大学(旧・東京工業大学)2025理系第3問〜確率漸化式と無限級数の和

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
$0\lt p\lt 1$とする。
表が出る確率が$p$、裏が出る確率が$1-p$である
$1$枚のコインを使って次のゲームを行う。
・ゲームの開始時点で点数は$0$点
・コインを投げ続け、表が出るごとに$1$点加算し、
裏が出たときは点数はそのまま
・$2$回続けて裏が出たらゲームは終了。
$0$以上の整数$n$に対し、ゲームが終わったときに
$n$点となっている確率を$Q_n$とする。
(1)$Q_1,Q_2$を$p$を用いて表せ。
(2)$Q_2$を$n$と$p$を用いて表せ。
(3)$0\lt x\lt 1$を満たす実数$x$に対して次式が
成り立つことを示せ。
$\dfrac{1}{(1-x)^2}=\displaystyle \sum_{k=0}^{\infty}(n+1)x^n$
必要ならば$0\lt x \lt 1$のとき
$\displaystyle \lim_{n\to\infty} nx^n=0$であることを
証明なしで使ってもよい。
(4)無限級数$\displaystyle \sum_{n=0}^{\infty} nQn$を$p$を用いて表せ。
$2025$年東京科学大学(旧・東京工業大学)
理系過去問題
この動画を見る
$\boxed{3}$
$0\lt p\lt 1$とする。
表が出る確率が$p$、裏が出る確率が$1-p$である
$1$枚のコインを使って次のゲームを行う。
・ゲームの開始時点で点数は$0$点
・コインを投げ続け、表が出るごとに$1$点加算し、
裏が出たときは点数はそのまま
・$2$回続けて裏が出たらゲームは終了。
$0$以上の整数$n$に対し、ゲームが終わったときに
$n$点となっている確率を$Q_n$とする。
(1)$Q_1,Q_2$を$p$を用いて表せ。
(2)$Q_2$を$n$と$p$を用いて表せ。
(3)$0\lt x\lt 1$を満たす実数$x$に対して次式が
成り立つことを示せ。
$\dfrac{1}{(1-x)^2}=\displaystyle \sum_{k=0}^{\infty}(n+1)x^n$
必要ならば$0\lt x \lt 1$のとき
$\displaystyle \lim_{n\to\infty} nx^n=0$であることを
証明なしで使ってもよい。
(4)無限級数$\displaystyle \sum_{n=0}^{\infty} nQn$を$p$を用いて表せ。
$2025$年東京科学大学(旧・東京工業大学)
理系過去問題
この因数分解できますか?

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
因数分解しなさい。
$ab(a+b)+bc(b+c)+ca(c+a)+2abc$
この動画を見る
因数分解しなさい。
$ab(a+b)+bc(b+c)+ca(c+a)+2abc$
福田のおもしろ数学494〜3乗根の付いた数の大小比較

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
大小を比較せよ。
$\sqrt[3]{4(2197+2025)}$
VS
$13+\sqrt[3]{2025}$
この動画を見る
大小を比較せよ。
$\sqrt[3]{4(2197+2025)}$
VS
$13+\sqrt[3]{2025}$
福田の数学〜東京科学大学(旧・東京工業大学)2025理系第2問〜ねじれの位置にある直線上の2点ずつでできる四面体の体積の最大最小

単元:
#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
空間の点$(0,0,1)$を通り
$(1,-1,0)$を方向ベクトルとする
直線を$\ell$とし、点$(1,0,3)$を通り$(0,1,-2)$を
方向ベクトルとする直線を$m$とする。
(1)$P$を$\ell$上の点とし、$Q$を$m$上の点とする。
また直線$PQ$は直線$\ell$と直線$m$に垂線であるとする。
このとき$P$と$Q$の座標、
および線分$PQ$の長さを求めよ。
(2)$\ell$上に$2$点
$A=(t,-t,1),$
$B(2+t+\sin t,-2-t-\sin t,1)$
があり、$m$上に$2$点
$C=(1,t,3,-2t),$
$D=(1,2+t<\cos t,-1-2t-2\cos t)$
があるとする。ただし、$y$は実数とする。
四面体$ABCD$の体積を$V(t)$とする。
$V(0)$を求めよ。
(3)$t$が$t\geqq 0$を動くとき、
$V(t)$の最大値と最小値を求めよ。
$2025$年東京科学大学(旧・東京工業大学)
理系過去問題
この動画を見る
$\boxed{2}$
空間の点$(0,0,1)$を通り
$(1,-1,0)$を方向ベクトルとする
直線を$\ell$とし、点$(1,0,3)$を通り$(0,1,-2)$を
方向ベクトルとする直線を$m$とする。
(1)$P$を$\ell$上の点とし、$Q$を$m$上の点とする。
また直線$PQ$は直線$\ell$と直線$m$に垂線であるとする。
このとき$P$と$Q$の座標、
および線分$PQ$の長さを求めよ。
(2)$\ell$上に$2$点
$A=(t,-t,1),$
$B(2+t+\sin t,-2-t-\sin t,1)$
があり、$m$上に$2$点
$C=(1,t,3,-2t),$
$D=(1,2+t<\cos t,-1-2t-2\cos t)$
があるとする。ただし、$y$は実数とする。
四面体$ABCD$の体積を$V(t)$とする。
$V(0)$を求めよ。
(3)$t$が$t\geqq 0$を動くとき、
$V(t)$の最大値と最小値を求めよ。
$2025$年東京科学大学(旧・東京工業大学)
理系過去問題
田のおもしろ数学493〜2つの方程式の解が非負実数である条件

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$2$つの方程式
$3x^2-12x-2a=0$
$x^3+ax^2+bx-8=0$
の解がすべて非負実数であるような
実数の組$(a,b)$をすべて求めよ。
この動画を見る
$2$つの方程式
$3x^2-12x-2a=0$
$x^3+ax^2+bx-8=0$
の解がすべて非負実数であるような
実数の組$(a,b)$をすべて求めよ。
