 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
福田のおもしろ数学416〜条件付きの不等式の証明
単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
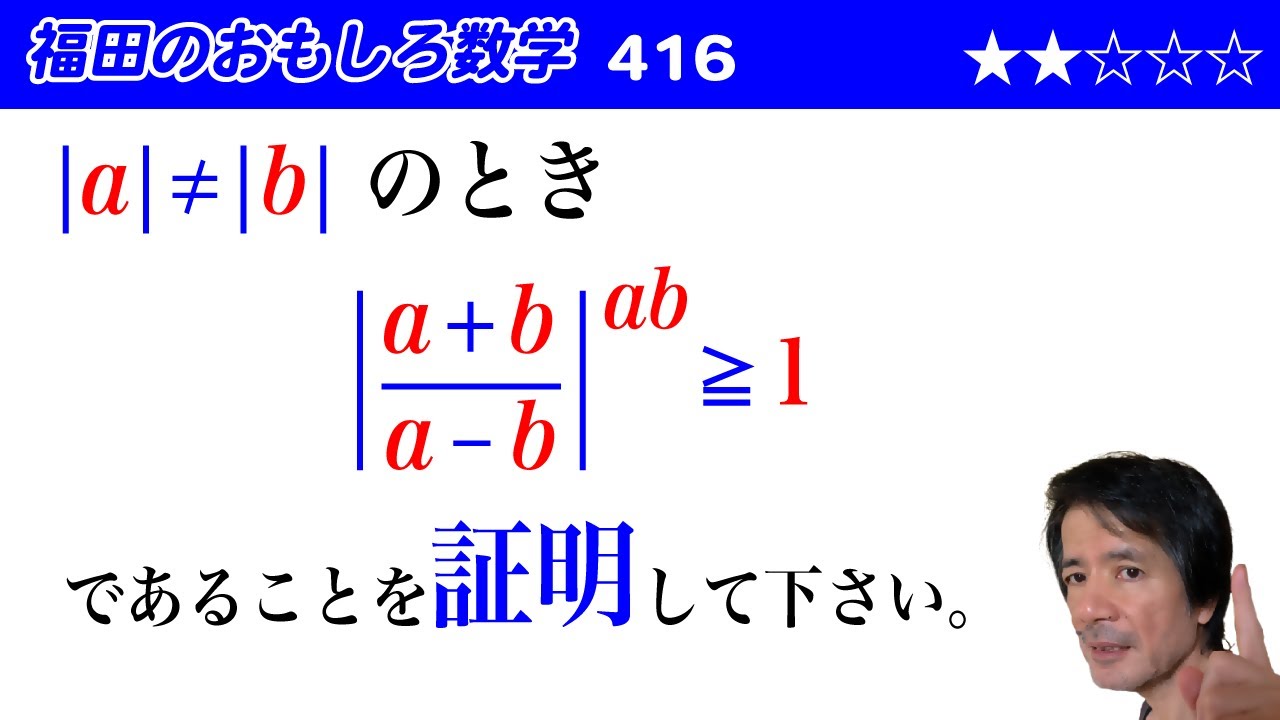
$\vert a \vert \neq \vert b \vert$のとき、
$\left\vert \dfrac{a+b}{a-b}\right \vert^{ab} \geqq 1$
であることを証明して下さい。
この動画を見る
$\vert a \vert \neq \vert b \vert$のとき、
$\left\vert \dfrac{a+b}{a-b}\right \vert^{ab} \geqq 1$
であることを証明して下さい。
【数A】【場合の数と確率】条件付き確率の基本 ※問題文は概要欄

単元:
#数A#場合の数と確率#確率#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#場合の数と確率#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
10本のくじの中に3本の当たりくじが入っている。このくじから1本ずつ順に、引いたくじはもとに戻さずに2本を引いたら、2本の中に当たりくじがあることがわかった。このとき、1本目のくじが当たりくじである確率を求めよ。
この動画を見る
10本のくじの中に3本の当たりくじが入っている。このくじから1本ずつ順に、引いたくじはもとに戻さずに2本を引いたら、2本の中に当たりくじがあることがわかった。このとき、1本目のくじが当たりくじである確率を求めよ。
【数A】【場合の数と確率】トランプを引く順番と確率 ※問題文は概要欄

単元:
#数A#場合の数と確率#確率#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#場合の数と確率#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ジョーカーを1枚だけ含む1組53枚のトランプがある。カードをもとに戻さずに1枚ずつ続けて引いていくとき、10枚目にジョーカーが出る確率を求めよ。
この動画を見る
ジョーカーを1枚だけ含む1組53枚のトランプがある。カードをもとに戻さずに1枚ずつ続けて引いていくとき、10枚目にジョーカーが出る確率を求めよ。
【数A】【場合の数と確率】反復試行の確率、サイコロの確率 ※問題文は概要欄

単元:
#数A#場合の数と確率#確率#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#場合の数と確率#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
1個のさいころを7回投げるとき、1の目が3回、2の目が2回、その他の目が2回出る確率を求めよ。
この動画を見る
1個のさいころを7回投げるとき、1の目が3回、2の目が2回、その他の目が2回出る確率を求めよ。
【数A】【場合の数と確率】反復試行の確率、対戦ゲームの確率 ※問題文は概要欄

単元:
#数A#場合の数と確率#確率#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#場合の数と確率#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
硬貨を何回か投げ、先に表が2回出るとAの勝ちとし、先に裏が4回出るとBの勝ちとするゲームを考える。次の確率を求めよ。
(1)5回目にBが勝つ確率。
(2)A,Bそれぞれの勝つ確率。
この動画を見る
硬貨を何回か投げ、先に表が2回出るとAの勝ちとし、先に裏が4回出るとBの勝ちとするゲームを考える。次の確率を求めよ。
(1)5回目にBが勝つ確率。
(2)A,Bそれぞれの勝つ確率。
福田のおもしろ数学415〜1から16の整数を直線または円形に並べ隣り合う2数の和を平方数とできるか

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数B
指導講師:
福田次郎
問題文全文(内容文):
$1,2,3,\cdots 16$を並びかえて
(1)直線上に配置する。(それぞれの場合に)
(2)円周上に配置する。(それぞれの場合に)
隣り合う$2$つの数の和が
平方数になることは可能か?
この動画を見る
$1,2,3,\cdots 16$を並びかえて
(1)直線上に配置する。(それぞれの場合に)
(2)円周上に配置する。(それぞれの場合に)
隣り合う$2$つの数の和が
平方数になることは可能か?
【数A】【場合の数と確率】重複組合せ4 ※問題文は概要欄

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#場合の数と確率#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
1個のさいころを3回投げて出る目の数を順に$a,b,c$とする。次の場合は何通りあるか。
(1) $a < b < c$
(2) $a \leqq b\leqq c$
この動画を見る
1個のさいころを3回投げて出る目の数を順に$a,b,c$とする。次の場合は何通りあるか。
(1) $a < b < c$
(2) $a \leqq b\leqq c$
【数A】【場合の数と確率】重複組合せ3 ※問題文は概要欄

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#場合の数と確率#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)等式$x+y+z=7$を満たす負でない整数$x,y,z$の組は、全部で何個あるか。
(2)等式$x+y+z=9$を満たす正の整数$x,y,z$の組は、全部で何個あるか。
この動画を見る
(1)等式$x+y+z=7$を満たす負でない整数$x,y,z$の組は、全部で何個あるか。
(2)等式$x+y+z=9$を満たす正の整数$x,y,z$の組は、全部で何個あるか。
【数A】【場合の数と確率】重複組合せ2 ※問題文は概要欄

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#場合の数と確率#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
候補者が3人で、投票者が8人いる無記名投票で、1人1票を投票するときの表の分かれ方の総数を求めよ。ただし、候補者は投票できないとする。
この動画を見る
候補者が3人で、投票者が8人いる無記名投票で、1人1票を投票するときの表の分かれ方の総数を求めよ。ただし、候補者は投票できないとする。
【数A】【場合の数と確率】重複組合せ1 ※問題文は概要欄

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#場合の数と確率#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
5個のリンゴを3人に分配する。1個ももらわない人があってもよいとすると何通りの分け方があるか。また、1人に少なくとも1個は与えるものとするとどうか。
この動画を見る
5個のリンゴを3人に分配する。1個ももらわない人があってもよいとすると何通りの分け方があるか。また、1人に少なくとも1個は与えるものとするとどうか。
【数A】【場合の数と確率】同じ文字を含む並び替え2 ※問題文は概要欄

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#場合の数と確率#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
DEFENSEの7文字から4文字を取り出すとき、次のような組分けおよび順列は、それぞれ何通りあるか。
(1)Eを3個含む場合。
(2)Eを2個だけ含む場合。
(3)4文字とも異なる場合。
(4)すべての場合。
この動画を見る
DEFENSEの7文字から4文字を取り出すとき、次のような組分けおよび順列は、それぞれ何通りあるか。
(1)Eを3個含む場合。
(2)Eを2個だけ含む場合。
(3)4文字とも異なる場合。
(4)すべての場合。
【数A】【場合の数と確率】同じ文字を含む並び替え1 ※問題文は概要欄

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#場合の数と確率#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
YOKOHAMAの8文字を1列に並べる。
(1)OとAが必ず偶数番目にあるものは何通りあるか。
(2)Y,K,H,Mがこの順にあるものは何通りあるか。
この動画を見る
YOKOHAMAの8文字を1列に並べる。
(1)OとAが必ず偶数番目にあるものは何通りあるか。
(2)Y,K,H,Mがこの順にあるものは何通りあるか。
中央大学経済学部の数学で範囲外出題 #shorts

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
Morite2 English Channel
問題文全文(内容文):
まさかの事態発生!中央大学経済学部の数学入試で、**出題範囲外**の疑惑が浮上しました!
今年の入まさかの事態発生!中央大学経済学部の数学入試で、**出題範囲外**の疑惑が浮上しました!
今年の入試では、「整数問題は出題しない」としていたにも関わらず、受験生から「整数問題が出てるじゃないか」という声が複数上がっています。
今回問題視されているのは、「2025の正の約数のうち、素数でないものは何個あるか?」という問題。これは基本中の基本だという意見もあれば、「これは整数問題の範囲だからダメだろう」という意見も出ています。
中央大学経済学部の数学の範囲は、数学I・IIと、数学Aの「図形の性質」「場合の数と確率」と明記されています。この問題が、範囲外とされる整数問題とみなすべきなのか、それとも基礎的な問題として許容されるのか、専門家の間でも意見が分かれている状況です。
この問題、範囲内?それとも範囲外?数学の先生方の意見が待たれます!
この動画を見る
まさかの事態発生!中央大学経済学部の数学入試で、**出題範囲外**の疑惑が浮上しました!
今年の入まさかの事態発生!中央大学経済学部の数学入試で、**出題範囲外**の疑惑が浮上しました!
今年の入試では、「整数問題は出題しない」としていたにも関わらず、受験生から「整数問題が出てるじゃないか」という声が複数上がっています。
今回問題視されているのは、「2025の正の約数のうち、素数でないものは何個あるか?」という問題。これは基本中の基本だという意見もあれば、「これは整数問題の範囲だからダメだろう」という意見も出ています。
中央大学経済学部の数学の範囲は、数学I・IIと、数学Aの「図形の性質」「場合の数と確率」と明記されています。この問題が、範囲外とされる整数問題とみなすべきなのか、それとも基礎的な問題として許容されるのか、専門家の間でも意見が分かれている状況です。
この問題、範囲内?それとも範囲外?数学の先生方の意見が待たれます!
【考え方が大切…!】二次方程式:山口県~全国入試問題解法

単元:
#数A#整数の性質#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
差が$1$である大小$2$つの正の数がある。これらの積が$3$であるとき
$2$つの数のうち大きい方を求めなさい
この動画を見る
差が$1$である大小$2$つの正の数がある。これらの積が$3$であるとき
$2$つの数のうち大きい方を求めなさい
福田のおもしろ数学414〜3辺の長さと内接円の直径で等差数列ができる三角形は直角三角形であることの証明

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
ある三角形の$3$辺の長さとその内接円の直径を
ある順序で並べると等差数列になるという。
この三角形が直角三角形であることを証明せよ。
この動画を見る
ある三角形の$3$辺の長さとその内接円の直径を
ある順序で並べると等差数列になるという。
この三角形が直角三角形であることを証明せよ。
【数Ⅱ】【微分法と積分法】微分の基本6 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$k$は0ではない定数とする。次の等式を満たす2次関数$f(x)$を求めよ。
$f(x)-x^2f'(x)=k^2x^3-kx+5$
この動画を見る
$k$は0ではない定数とする。次の等式を満たす2次関数$f(x)$を求めよ。
$f(x)-x^2f'(x)=k^2x^3-kx+5$
【数Ⅱ】【微分法と積分法】微分の基本5 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数を求めよ。
(1) 等式 $f(x)+(x+2)f'(x)=9x^2+8x-3$ を満たす2次関数$f(x)$
(2) 等式 $g(x)+xg'(x)=4x^3+6x^2+4x+1$ を満たす3次関数$g(x)$
この動画を見る
次の関数を求めよ。
(1) 等式 $f(x)+(x+2)f'(x)=9x^2+8x-3$ を満たす2次関数$f(x)$
(2) 等式 $g(x)+xg'(x)=4x^3+6x^2+4x+1$ を満たす3次関数$g(x)$
【数Ⅱ】【微分法と積分法】微分の基本4 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
1辺の長さ$x$の正四面体がある。
(1)正四面体の表面積を$S$とするとき,$S$を$x$の関数で表せ。
(2)$x$が変化するとき,$S$の$x=5$における微分係数を求めよ。
この動画を見る
1辺の長さ$x$の正四面体がある。
(1)正四面体の表面積を$S$とするとき,$S$を$x$の関数で表せ。
(2)$x$が変化するとき,$S$の$x=5$における微分係数を求めよ。
【数Ⅱ】【微分法と積分法】微分の基本3 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\{(ax+b)^n\}'=na(ax+b)^{n-1}$ ($n$ は正の整数) であることを用いて、次の関数を微分せよ。
$(1)\ y=(2x+1)^3$
$(2)\ y=(x-1)^4$
$(3)\ y=(-2x+1)^5$
この動画を見る
$\{(ax+b)^n\}'=na(ax+b)^{n-1}$ ($n$ は正の整数) であることを用いて、次の関数を微分せよ。
$(1)\ y=(2x+1)^3$
$(2)\ y=(x-1)^4$
$(3)\ y=(-2x+1)^5$
【数Ⅱ】【微分法と積分法】微分の基本2 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$f(x)=x^2-3x$ とする。
関数 $y=f(x)$ のグラフ上の2点 $(1,\,f(1)),\ (a,\,f(a))$ を結ぶ直線の傾きが、$x=b$ $(1< b < a)$ における微分係数 $f'(b)$ に等しい。
$b$ を $a$ で表せ。
この動画を見る
$f(x)=x^2-3x$ とする。
関数 $y=f(x)$ のグラフ上の2点 $(1,\,f(1)),\ (a,\,f(a))$ を結ぶ直線の傾きが、$x=b$ $(1< b < a)$ における微分係数 $f'(b)$ に等しい。
$b$ を $a$ で表せ。
【数Ⅱ】【微分法と積分法】微分の基本1 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数 $f(x)$ について、$x=a$ における微分係数 $f'(x)$ を求めよ。また、$f'(a)$ が、$x$ が $0$ から $2$ まで変化するときの平均変化率に一致するとき、$a$ の値を求めよ。
$(1)\ f(x)=x^2-x$
$(2)\ f(x)=x^3-x^2+1$
この動画を見る
次の関数 $f(x)$ について、$x=a$ における微分係数 $f'(x)$ を求めよ。また、$f'(a)$ が、$x$ が $0$ から $2$ まで変化するときの平均変化率に一致するとき、$a$ の値を求めよ。
$(1)\ f(x)=x^2-x$
$(2)\ f(x)=x^3-x^2+1$
【数Ⅱ】【微分法と積分法】極限の計算 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)$\displaystyle \lim_{ x \to -2 } (x^2+1)(x-1)$
(2)$\displaystyle \lim_{ x \to 1 } (x^3-1)(x-1)$
(3)$\displaystyle \lim_{ x \to 2 } (x^2-x-2)(x^2+x-6)$
(4)$\displaystyle \lim_{ x \to -3 } \frac{1}{x+3}(\frac{12}{x-3}+2)$
この動画を見る
(1)$\displaystyle \lim_{ x \to -2 } (x^2+1)(x-1)$
(2)$\displaystyle \lim_{ x \to 1 } (x^3-1)(x-1)$
(3)$\displaystyle \lim_{ x \to 2 } (x^2-x-2)(x^2+x-6)$
(4)$\displaystyle \lim_{ x \to -3 } \frac{1}{x+3}(\frac{12}{x-3}+2)$
福田のおもしろ数学413〜2024個の分数からk個選んできて積を作って合計しよう

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\dfrac{1}{2},\dfrac{1}{3},\dfrac{1}{4},\dfrac{1}{5},\cdots \dfrac{1}{2025}$の$2024$個の数から
異なる$k$個を選んで作った積の総和を$s(k)$とする。
$s(2)+s(4)+s(6)+\cdots +s(2024)$
の値を求めて下さい。
この動画を見る
$\dfrac{1}{2},\dfrac{1}{3},\dfrac{1}{4},\dfrac{1}{5},\cdots \dfrac{1}{2025}$の$2024$個の数から
異なる$k$個を選んで作った積の総和を$s(k)$とする。
$s(2)+s(4)+s(6)+\cdots +s(2024)$
の値を求めて下さい。
【数Ⅱ】【複素数と方程式】剰余の定理と因数定理1 ※問題文は概要欄

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#複素数と方程式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の有理数の範囲で因数分解せよ。
(1)$4x^3+x+1$
(2)$2x^3-x^2+9$
(3)$3x^3+8x^2-1$
次の式を因数分解せよ。
(1)$x^4+5x^3+5x^2-5x-6$
(2)$x^4+4x^3-x^2-16x-12$
$P(x)=x^3+ax^2+bx^+c$とする。$P(x)$は$x^2-1$で割り切れ、また、$P(x)$を$2$で割ると余りが$3$である。このとき、定数$a,b,c$の値を求めよ。
この動画を見る
次の有理数の範囲で因数分解せよ。
(1)$4x^3+x+1$
(2)$2x^3-x^2+9$
(3)$3x^3+8x^2-1$
次の式を因数分解せよ。
(1)$x^4+5x^3+5x^2-5x-6$
(2)$x^4+4x^3-x^2-16x-12$
$P(x)=x^3+ax^2+bx^+c$とする。$P(x)$は$x^2-1$で割り切れ、また、$P(x)$を$2$で割ると余りが$3$である。このとき、定数$a,b,c$の値を求めよ。
【数Ⅱ】【複素数と方程式】2次方程式の解と判別式7 ※問題文は概要欄

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#複素数と方程式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
2次方程式$(x+1)(x-1)+(x-1)(x-2)+(x-2)(x+1)=0$の2つの解をα、βとするとき、次の式の値を求めよ。
$\frac{1}{(α-2)(β-2)}+\frac{1}{(α-1)(β-1)}+\frac{1}{(α+1)(β+1)}$
解の公式を用いて、次の2次式を因数分解せよ。
(1)$x^2-xy-xz+2y-2$
(2)$2x^2-5xy+2y^2+x+y-1$
次の連立方程式を解け。
(1)$x+y=3$
$x+y+xy=-7$
(2)$x^2+y^2=13$
$xy=6$
この動画を見る
2次方程式$(x+1)(x-1)+(x-1)(x-2)+(x-2)(x+1)=0$の2つの解をα、βとするとき、次の式の値を求めよ。
$\frac{1}{(α-2)(β-2)}+\frac{1}{(α-1)(β-1)}+\frac{1}{(α+1)(β+1)}$
解の公式を用いて、次の2次式を因数分解せよ。
(1)$x^2-xy-xz+2y-2$
(2)$2x^2-5xy+2y^2+x+y-1$
次の連立方程式を解け。
(1)$x+y=3$
$x+y+xy=-7$
(2)$x^2+y^2=13$
$xy=6$
【数Ⅱ】【複素数と方程式】2次方程式の解と判別式6 ※問題文は概要欄

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#複素数と方程式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の式を、(ア)有理数(イ)実数(ウ)複素数 の各範囲で因数分解せよ。
(1)$x^4-3x^2+2$ (2)$6x^4-7x^2-3$ (3)$x^4+4$
2次方程式$x^2-2(m-3)x+4m=0$が次のような異なる2つの解をもつように、定数$m$の値の範囲を定めよ。
(1)2つとも正 (2)2つとも負 (3)異符号
2次方程式$x^2+2mx+2m^2-5=0$が、次のような異なる2つの解をもつように、定数$m$の値の範囲を定めよ。
(1)2つの解がともに1より大きい。
(2)2つの解がともに1より小さい。
(3)1つの解が1より大きく、他の解が1より小さい。
この動画を見る
次の式を、(ア)有理数(イ)実数(ウ)複素数 の各範囲で因数分解せよ。
(1)$x^4-3x^2+2$ (2)$6x^4-7x^2-3$ (3)$x^4+4$
2次方程式$x^2-2(m-3)x+4m=0$が次のような異なる2つの解をもつように、定数$m$の値の範囲を定めよ。
(1)2つとも正 (2)2つとも負 (3)異符号
2次方程式$x^2+2mx+2m^2-5=0$が、次のような異なる2つの解をもつように、定数$m$の値の範囲を定めよ。
(1)2つの解がともに1より大きい。
(2)2つの解がともに1より小さい。
(3)1つの解が1より大きく、他の解が1より小さい。
shape problems : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study

shape problems : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study
福田のおもしろ数学412〜正n角形の内部の点から各辺に下ろした垂線の長さに関する不等式の証明
単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
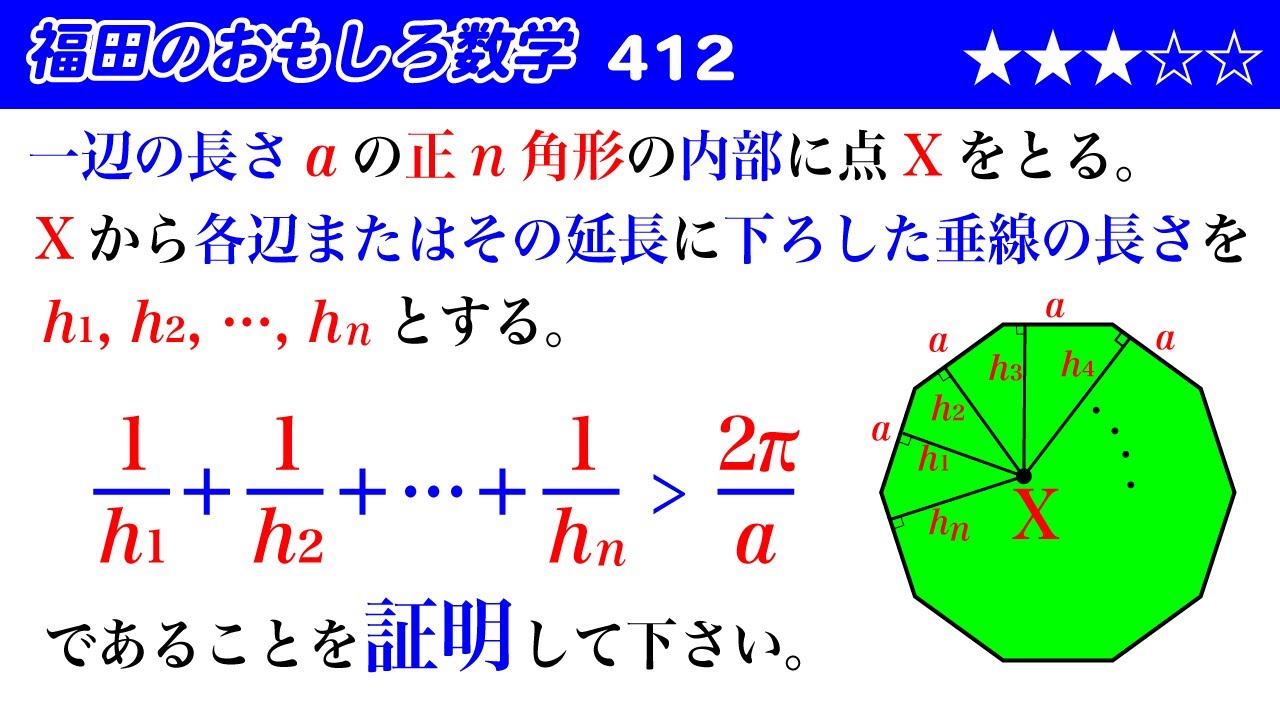
一辺の長さ$a$の正$n$角形の内部に点$X$をとる。
$X$から各辺またはその延長に下ろした垂線の長さを
$h_1,h_2,\cdots h_n$とする。
$\dfrac{1}{h_1}+\dfrac{1}{h_2}+\cdots +\dfrac{1}{h_n} \gt \dfrac{2\pi}{a}$
であることを証明して下さい。
図は動画内参照
この動画を見る
一辺の長さ$a$の正$n$角形の内部に点$X$をとる。
$X$から各辺またはその延長に下ろした垂線の長さを
$h_1,h_2,\cdots h_n$とする。
$\dfrac{1}{h_1}+\dfrac{1}{h_2}+\cdots +\dfrac{1}{h_n} \gt \dfrac{2\pi}{a}$
であることを証明して下さい。
図は動画内参照
【数C】【平面上のベクトル】ベクトルを使った面積、内心 ※問題文は概要欄

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題1
次の3点を頂点とする三角形の面積$S$を求めよ。
(1)$O(0, 0), A(2, -3), B(-1, 2)$
(2)$A(1, 2), B(2+\sqrt{ 3}, 1+\sqrt{ 3}), C(2, 2+\sqrt{ 3 })$
(3)$A(1+\sqrt{ 3 }, 2), B(\sqrt{ 3 }, 5), C(4+\sqrt{ 3 }, 1)$
問題2
$\triangle OAB$において、$\overrightarrow{ OA } = \vec{ a } , \overrightarrow{ OB } = \vec{ b }$とする。$|\vec{ a }|=2, |\vec{ b }|=3, |\vec{ a }+\vec{ b }|=4$のとき、$\triangle OAB$の面積$S$を求めよ。
問題3
$\angle A=60°, AB=8, AC=5$である$\triangle ABC$の内心を$I$とする。$\overrightarrow{ AB } = \vec{ b }, \overrightarrow{ AC } = \vec{ c }$とするとき、$\overrightarrow{ AI }$を$\vec{ b }, \vec{ c }$を用いて表せ。
問題4
三角形ABCの辺BC, CA, ABの中点をそれぞれA(1), B(1), C(1)とし、平面上の任意の点Oに対し、線分OA, OB, OCの中点をそれぞれA(2), B(2), C(2)とする。線分A(1)A(2), B(1)B(2),C(1)C(2)の中点は一致することを証明せよ。
この動画を見る
問題1
次の3点を頂点とする三角形の面積$S$を求めよ。
(1)$O(0, 0), A(2, -3), B(-1, 2)$
(2)$A(1, 2), B(2+\sqrt{ 3}, 1+\sqrt{ 3}), C(2, 2+\sqrt{ 3 })$
(3)$A(1+\sqrt{ 3 }, 2), B(\sqrt{ 3 }, 5), C(4+\sqrt{ 3 }, 1)$
問題2
$\triangle OAB$において、$\overrightarrow{ OA } = \vec{ a } , \overrightarrow{ OB } = \vec{ b }$とする。$|\vec{ a }|=2, |\vec{ b }|=3, |\vec{ a }+\vec{ b }|=4$のとき、$\triangle OAB$の面積$S$を求めよ。
問題3
$\angle A=60°, AB=8, AC=5$である$\triangle ABC$の内心を$I$とする。$\overrightarrow{ AB } = \vec{ b }, \overrightarrow{ AC } = \vec{ c }$とするとき、$\overrightarrow{ AI }$を$\vec{ b }, \vec{ c }$を用いて表せ。
問題4
三角形ABCの辺BC, CA, ABの中点をそれぞれA(1), B(1), C(1)とし、平面上の任意の点Oに対し、線分OA, OB, OCの中点をそれぞれA(2), B(2), C(2)とする。線分A(1)A(2), B(1)B(2),C(1)C(2)の中点は一致することを証明せよ。
