 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
福田のわかった数学〜高校2年生014〜直線の方程式

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 直線の方程式
2直線$\left\{\begin{array}{1}
x + y -2= 0\\
7x - y -2 = 0
\end{array}
\right.\\$
のなす角の二等分線の方程式を求めよ。
この動画を見る
数学$\textrm{II}$ 直線の方程式
2直線$\left\{\begin{array}{1}
x + y -2= 0\\
7x - y -2 = 0
\end{array}
\right.\\$
のなす角の二等分線の方程式を求めよ。
18和歌山県教員採用試験(数学:6番 二項定理)

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{6}$
$(x+5)^{70}$を展開したとき,$x$の何乗の係数が
最大になるか求めよ.
この動画を見る
$\boxed{6}$
$(x+5)^{70}$を展開したとき,$x$の何乗の係数が
最大になるか求めよ.
大分大 漸化式

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
一般項$a_n$を求めよ.
$S_n=(n+3)(\dfrac{1}{3}a_n-2)$
2020大分大過去問
この動画を見る
一般項$a_n$を求めよ.
$S_n=(n+3)(\dfrac{1}{3}a_n-2)$
2020大分大過去問
線形代数:#2線形写像の判定

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
次の写像$\varsigma_i(i=1,2,3,4)$は線形代数であるか調べよ.
(1)
$\varsigma_1:IR^2\to IR$を
$\varsigma_1 \begin{pmatrix}
x \\
y
\end{pmatrix}=2x+3y$と定める.
(2)
$\varsigma_2:IR^2\to IR^2$を
$\varsigma_2 \begin{pmatrix}
x \\
y
\end{pmatrix}=\begin{pmatrix}
x+1 \\
y-1
\end{pmatrix}$と定める.
(3)
$\varsigma_3:IR^2\to IR^2$を
$\varsigma_3 \begin{pmatrix}
x \\
y
\end{pmatrix}=\begin{pmatrix}
\vert x\vert \\
y
\end{pmatrix}$と定める.
(3)
$\varsigma_4:IR^2\to IR^2$を
$\varsigma_4 \begin{pmatrix}
x \\
y
\end{pmatrix}=\begin{pmatrix}
y \\
x
\end{pmatrix}$と定める.
この動画を見る
次の写像$\varsigma_i(i=1,2,3,4)$は線形代数であるか調べよ.
(1)
$\varsigma_1:IR^2\to IR$を
$\varsigma_1 \begin{pmatrix}
x \\
y
\end{pmatrix}=2x+3y$と定める.
(2)
$\varsigma_2:IR^2\to IR^2$を
$\varsigma_2 \begin{pmatrix}
x \\
y
\end{pmatrix}=\begin{pmatrix}
x+1 \\
y-1
\end{pmatrix}$と定める.
(3)
$\varsigma_3:IR^2\to IR^2$を
$\varsigma_3 \begin{pmatrix}
x \\
y
\end{pmatrix}=\begin{pmatrix}
\vert x\vert \\
y
\end{pmatrix}$と定める.
(3)
$\varsigma_4:IR^2\to IR^2$を
$\varsigma_4 \begin{pmatrix}
x \\
y
\end{pmatrix}=\begin{pmatrix}
y \\
x
\end{pmatrix}$と定める.
ルートを外せ! 12

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{25-n}+2\sqrt{n}$が整数となる自然数nをすべて求めよ。
城西大学付属川越高等学校
この動画を見る
$\sqrt{25-n}+2\sqrt{n}$が整数となる自然数nをすべて求めよ。
城西大学付属川越高等学校
【数Ⅰ】図形と計量:三角比の表②

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
・sin120°, sin135°, sin150°の値を求めよ。
・cos120°, cos135°, cos150°の値を求めよ。
・tan120°, tan135°, tan150°の値を求めよ。
この動画を見る
・sin120°, sin135°, sin150°の値を求めよ。
・cos120°, cos135°, cos150°の値を求めよ。
・tan120°, tan135°, tan150°の値を求めよ。
数学「大学入試良問集」【7−4 絶対値と定数分離】を宇宙一わかりやすく

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#大阪府立大学#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$a$を定数とする。
放物線$y=x^2+a$と関数$y=4|x-1|-3$のグラフの共有点の個数を求めよ。
この動画を見る
$a$を定数とする。
放物線$y=x^2+a$と関数$y=4|x-1|-3$のグラフの共有点の個数を求めよ。
線形代数:部分空間の判定 #線形代数 #部分空間 #ベクトル空間

単元:
#平面上のベクトル#空間ベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
次の集合がベクトル空間の部分空間をなすか判定せよ.
(1)$W_1=\left[\begin{pmatrix}
x \\
y \\
z
\end{pmatrix} \in IR^3 | x\neq 2y\right]$
(2)$W_2=\left[\begin{pmatrix}
x \\
y \\
z
\end{pmatrix} \in IR^3 | x+2y+3z=0 \right]$
(3)$W_3=\left[\begin{pmatrix}
x \\
y \\
z
\end{pmatrix} \in IR^3 | x+2y+3z\geqq 0 \right]$
この動画を見る
次の集合がベクトル空間の部分空間をなすか判定せよ.
(1)$W_1=\left[\begin{pmatrix}
x \\
y \\
z
\end{pmatrix} \in IR^3 | x\neq 2y\right]$
(2)$W_2=\left[\begin{pmatrix}
x \\
y \\
z
\end{pmatrix} \in IR^3 | x+2y+3z=0 \right]$
(3)$W_3=\left[\begin{pmatrix}
x \\
y \\
z
\end{pmatrix} \in IR^3 | x+2y+3z\geqq 0 \right]$
福田のわかった数学〜高校1年生014〜絶対不等式(2)

単元:
#数Ⅰ#数と式#2次関数#一次不等式(不等式・絶対値のある方程式・不等式)#2次方程式と2次不等式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 絶対不等式(2)
ある実数$x$に対して
$ax^2 + 4x + a \gt 0$
が成り立つような$a$の値の範囲は?
この動画を見る
数学$\textrm{I}$ 絶対不等式(2)
ある実数$x$に対して
$ax^2 + 4x + a \gt 0$
が成り立つような$a$の値の範囲は?
17滋賀県教員採用試験 3番 極限について

単元:
#関数と極限#数列の極限#関数の極限#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{3}$
$\sqrt{\sqrt{3+{\sqrt{3+{\sqrt3+・・・}}}}}$の値を求めよ.
この動画を見る
$\boxed{3}$
$\sqrt{\sqrt{3+{\sqrt{3+{\sqrt3+・・・}}}}}$の値を求めよ.
【数Ⅰ】図形と計量:三角比の表①30°45°60°から!

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
・sin30°, sin45°, sin60°の値を求めよ。
・cos30°, cos45°, cos60°の値を求めよ。
・tan30°, tan45°, tan60°の値を求めよ。
この動画を見る
・sin30°, sin45°, sin60°の値を求めよ。
・cos30°, cos45°, cos60°の値を求めよ。
・tan30°, tan45°, tan60°の値を求めよ。
3乗根と平方根の方程式

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\sqrt[3]{4-x^2}+\sqrt{x^2-3}=1$
この動画を見る
これを解け.
$\sqrt[3]{4-x^2}+\sqrt{x^2-3}=1$
【理数個別の過去問解説】2021年度東京大学 数学 理科第3問(2)解説

単元:
#大学入試過去問(数学)#微分とその応用#接線と法線・平均値の定理#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
東京大学 2021年理科第3問(2)それぞれの項で分けて丁寧に積分せよ
関数
$f(x)=\dfrac{x}{x²+3}$
に対して、$y=f(x)$のグラフをCとする。点A($1,f(1)$)におけるCの接線を
$l:y=g(x)$
とする。
(1)Cとlの共有点でAと異なるものがただ1つ存在することを示し、その点のx座標を求めよ。
(2)(1)で求めた共有点のx座標をαとする。定積分
$\displaystyle \int_{\alpha}^1{f(x)-g(x)}^2 dx$
を計算せよ。
この動画を見る
東京大学 2021年理科第3問(2)それぞれの項で分けて丁寧に積分せよ
関数
$f(x)=\dfrac{x}{x²+3}$
に対して、$y=f(x)$のグラフをCとする。点A($1,f(1)$)におけるCの接線を
$l:y=g(x)$
とする。
(1)Cとlの共有点でAと異なるものがただ1つ存在することを示し、その点のx座標を求めよ。
(2)(1)で求めた共有点のx座標をαとする。定積分
$\displaystyle \int_{\alpha}^1{f(x)-g(x)}^2 dx$
を計算せよ。
【理数個別の過去問解説】2021年度東京大学 数学 理科第3問(1)解説

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
2021年度東京大学 数学 理科第3問(1)解説
東京大学 2021年理科第3問(2)それぞれの項で分けて丁寧に積分せよ
関数
$f(x)=\dfrac{x}{x²+3}$
に対して、$y=f(x)$のグラフをCとする。点A($1,f(1)$)におけるCの接線を
$l:y=g(x)$
とする。
(1)Cとlの共有点でAと異なるものがただ1つ存在することを示し、その点のx座標を求めよ。
(2)(1)で求めた共有点のx座標をαとする。定積分
$\displaystyle \int_{\alpha}^1{f(x)-g(x)}^2 dx$
を計算せよ。
この動画を見る
2021年度東京大学 数学 理科第3問(1)解説
東京大学 2021年理科第3問(2)それぞれの項で分けて丁寧に積分せよ
関数
$f(x)=\dfrac{x}{x²+3}$
に対して、$y=f(x)$のグラフをCとする。点A($1,f(1)$)におけるCの接線を
$l:y=g(x)$
とする。
(1)Cとlの共有点でAと異なるものがただ1つ存在することを示し、その点のx座標を求めよ。
(2)(1)で求めた共有点のx座標をαとする。定積分
$\displaystyle \int_{\alpha}^1{f(x)-g(x)}^2 dx$
を計算せよ。
数学「大学入試良問集」【7−3 絶対値と解の個数】を宇宙一わかりやすく

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)#法政大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$f(x)=|2x^2-10x+9|$とおく。
(1)$y=f(x)$のグラフをかけ。
(2)$y=f(x)$のグラフと直線$y=ax+1$がちょうど4個の共通点をもつような、実数の定数$a$の値の範囲を求めよ。
この動画を見る
$f(x)=|2x^2-10x+9|$とおく。
(1)$y=f(x)$のグラフをかけ。
(2)$y=f(x)$のグラフと直線$y=ax+1$がちょうど4個の共通点をもつような、実数の定数$a$の値の範囲を求めよ。
数学Ⅲが1時間で分かる動画!極限、微分積分をメインに!複素数平面を添えて【篠原好】

単元:
#数Ⅱ#複素数平面#微分法と積分法#平均変化率・極限・導関数#複素数平面#数学(高校生)#数C
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
極限、微分積分をメインに!複素数平面を添えて
「数学Ⅲが1時間で分かる」動画です。
この動画を見る
極限、微分積分をメインに!複素数平面を添えて
「数学Ⅲが1時間で分かる」動画です。
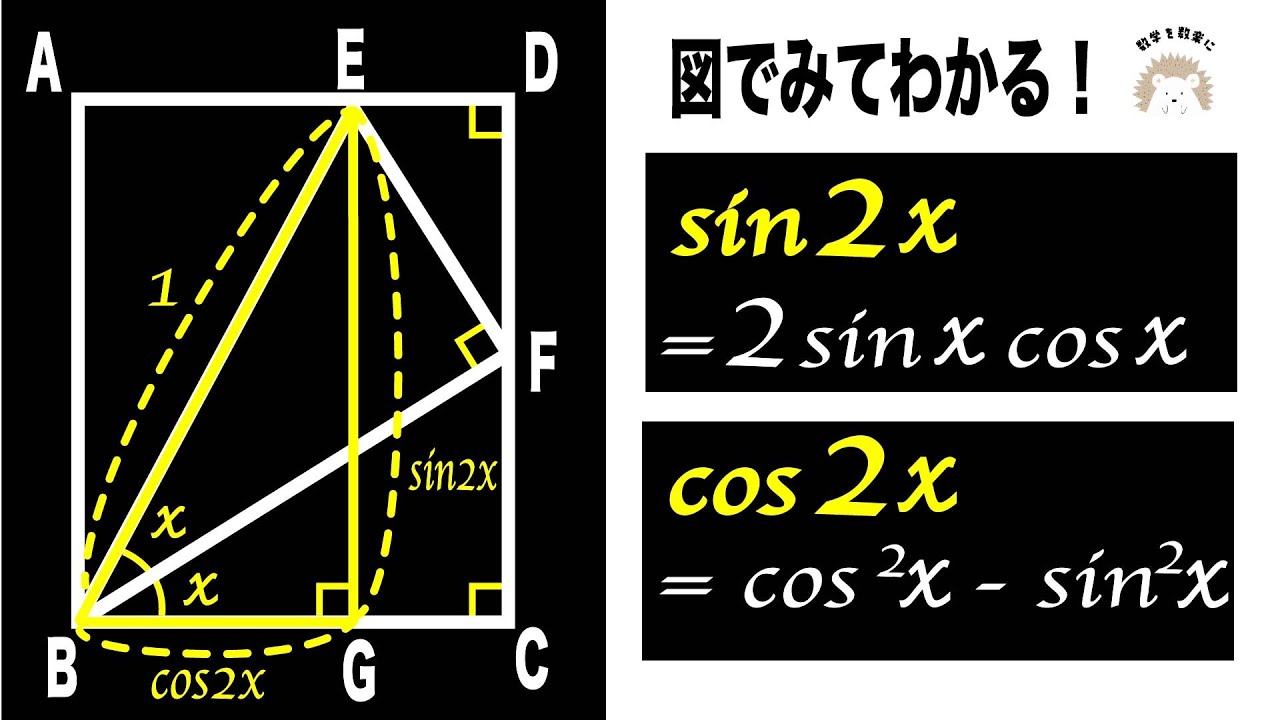
2倍角の公式
単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$sin2x=2sinxcosx$
$cos2x=cos^2x-sin^2x$
*図は動画内参照
この動画を見る
$sin2x=2sinxcosx$
$cos2x=cos^2x-sin^2x$
*図は動画内参照
福田のわかった数学〜高校3年生理系007〜極限(7)

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 極限(7)
$\displaystyle\lim_{n \to \infty}\displaystyle \frac{n^2}{2^n}$を求めよ。
この動画を見る
数学$\textrm{III}$ 極限(7)
$\displaystyle\lim_{n \to \infty}\displaystyle \frac{n^2}{2^n}$を求めよ。
福田のわかった数学〜高校2年生013〜直線の方程式

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 直線の方程式
3直線$\left\{
\begin{array}{1}
a_1x+b_1y=1\\
a_2x+b_2y=1\\
a_3x+b_3y=1
\end{array}
\right.$
が1点で交わるとき、
3点$(a_1,b_1),(a_2,b_2),(a_3,b_3)$は一直線上にあることを示せ。
この動画を見る
数学$\textrm{II}$ 直線の方程式
3直線$\left\{
\begin{array}{1}
a_1x+b_1y=1\\
a_2x+b_2y=1\\
a_3x+b_3y=1
\end{array}
\right.$
が1点で交わるとき、
3点$(a_1,b_1),(a_2,b_2),(a_3,b_3)$は一直線上にあることを示せ。
20滋賀県教員採用試験(数学:2番 整数問題)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{2}$
$x^2-xy-6y^2-2x+11y+5=0$をみたす
整数の組$(x,y)$をすべて求めよ.
この動画を見る
$\boxed{2}$
$x^2-xy-6y^2-2x+11y+5=0$をみたす
整数の組$(x,y)$をすべて求めよ.
指数方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$3^x-5^x=\sqrt{15^x-25^x}$
この動画を見る
実数解を求めよ.
$3^x-5^x=\sqrt{15^x-25^x}$
【理数個別の過去問解説】2021年度東京大学 数学 理科・文科第3問(1)解説

単元:
#大学入試過去問(数学)#微分とその応用#接線と法線・平均値の定理#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
東京大学 2021年理科第3問(1)曲線と接線の接点以外の共有点を求めよ
関数
f(x)=x/(x²+3)
に対して、y=f(x)のグラフをCとする。点A(1,f(1))におけるCの接線を
l:y=g(x)
とする。
(1)Cとlの共有点でAと異なるものがただ1つ存在することを示し、その点のx座標を求めよ。
(2)(1)で求めた共有点のx座標をαとする。定積分
∫{f(x)-g(x)}²dx
を計算せよ。
この動画を見る
東京大学 2021年理科第3問(1)曲線と接線の接点以外の共有点を求めよ
関数
f(x)=x/(x²+3)
に対して、y=f(x)のグラフをCとする。点A(1,f(1))におけるCの接線を
l:y=g(x)
とする。
(1)Cとlの共有点でAと異なるものがただ1つ存在することを示し、その点のx座標を求めよ。
(2)(1)で求めた共有点のx座標をαとする。定積分
∫{f(x)-g(x)}²dx
を計算せよ。
#13数検1級1次過去問 複素関数

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#複素数#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{2}$
$z=a+bi$とする.
$e^z=-i$を解け.ただし,$0\leqq b\lt 2\pi$とする.
この動画を見る
$\boxed{2}$
$z=a+bi$とする.
$e^z=-i$を解け.ただし,$0\leqq b\lt 2\pi$とする.
福田のわかった数学〜高校1年生013〜絶対不等式(1)

単元:
#数Ⅰ#数と式#2次関数#一次不等式(不等式・絶対値のある方程式・不等式)#2次方程式と2次不等式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 絶対不等式(1)
任意の実数$x$に対して
$ax^2+4x+a \gt 0$
が成り立つような$a$の値の範囲は?
この動画を見る
数学$\textrm{I}$ 絶対不等式(1)
任意の実数$x$に対して
$ax^2+4x+a \gt 0$
が成り立つような$a$の値の範囲は?
ケンブリッジ大学の入試問題
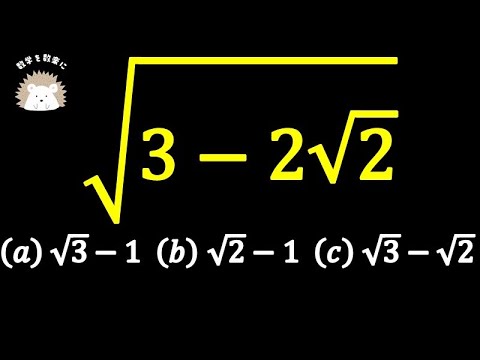
単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{3-2\sqrt 2} =$
a. $\sqrt 3 -1$
b. $\sqrt 2 -1$
c. $\sqrt 3 -\sqrt 2$
University of Cambridge
この動画を見る
$\sqrt{3-2\sqrt 2} =$
a. $\sqrt 3 -1$
b. $\sqrt 2 -1$
c. $\sqrt 3 -\sqrt 2$
University of Cambridge
20滋賀県教員採用試験(数学:1-(3) 因数分解)

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}-(3)$
$3x^3+(y-3)x^2-y$を因数分解せよ.
この動画を見る
$\boxed{1}-(3)$
$3x^3+(y-3)x^2-y$を因数分解せよ.
数学「大学入試良問集」【7−2 二次関数と不等式】を宇宙一わかりやすく

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$a$を実数の定義とする。
区間$1 \leqq x \leqq 4$を定義域とする2つの関数$f(x)=ax,g(x)=x^2-4x+9$を考える。
以下の条件を満たすような$a$の範囲をそれぞれ求めよ。
(1)定義域に属するすべての$x$に対して、$f(x) \geqq g(x)$が成り立つ。
(2)定義域に属する$x$で、$f(x) \geqq g(x)$を満たすものがある。
(3)定義域に属するすべての$x_1$と$x_2$に対して、$f(x_1) \geqq g(x_2)$が成り立つ
(4)定義域に属する$x_1$と$x_2$で、$f(x_1) \geqq g(x_2)$を満たすものがある。
この動画を見る
$a$を実数の定義とする。
区間$1 \leqq x \leqq 4$を定義域とする2つの関数$f(x)=ax,g(x)=x^2-4x+9$を考える。
以下の条件を満たすような$a$の範囲をそれぞれ求めよ。
(1)定義域に属するすべての$x$に対して、$f(x) \geqq g(x)$が成り立つ。
(2)定義域に属する$x$で、$f(x) \geqq g(x)$を満たすものがある。
(3)定義域に属するすべての$x_1$と$x_2$に対して、$f(x_1) \geqq g(x_2)$が成り立つ
(4)定義域に属する$x_1$と$x_2$で、$f(x_1) \geqq g(x_2)$を満たすものがある。
福田のわかった数学〜高校3年生理系006〜極限(6)

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 極限(6)
$\displaystyle\lim_{n \to \infty}\displaystyle \frac{\log(2n^2+1)}{\log(n+2)}$ を求めよ。
この動画を見る
数学$\textrm{III}$ 極限(6)
$\displaystyle\lim_{n \to \infty}\displaystyle \frac{\log(2n^2+1)}{\log(n+2)}$ を求めよ。
福田のわかった数学〜高校2年生012〜高次方程式の作成

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 高次方程式
$\alpha=\sqrt{13}+\sqrt{9+2\sqrt{17}}+$$\sqrt{9-2\sqrt{17}}$
を解にもつ整数係数であり$x^4$の係数1の
4次方程式を作れ。また、残りの解を求めよ。
この動画を見る
数学$\textrm{II}$ 高次方程式
$\alpha=\sqrt{13}+\sqrt{9+2\sqrt{17}}+$$\sqrt{9-2\sqrt{17}}$
を解にもつ整数係数であり$x^4$の係数1の
4次方程式を作れ。また、残りの解を求めよ。
19滋賀県教員採用試験(数学:3番 極限)

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{3}$
$\displaystyle \lim_{x\to 0}\dfrac{1-\cos x}{\sqrt{1+x^2}\sqrt{1-x^2}}$を解け.
この動画を見る
$\boxed{3}$
$\displaystyle \lim_{x\to 0}\dfrac{1-\cos x}{\sqrt{1+x^2}\sqrt{1-x^2}}$を解け.
