 高校入試過去問(数学)
高校入試過去問(数学)
 高校入試過去問(数学)
高校入試過去問(数学)
【見切った…!】図形:福井県~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#福井県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
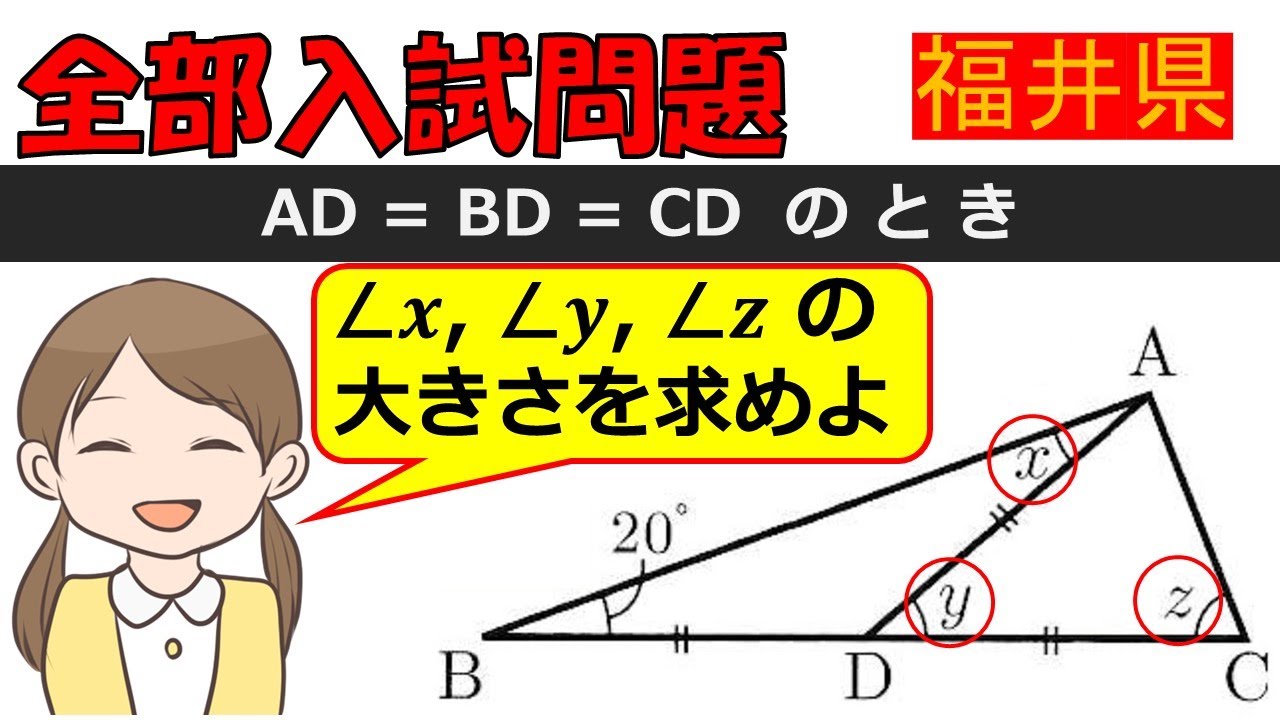
$ AD=BD=CD$のとき,
$ \angle x,\angle y,\angle z$の大きさを求めよ.
福井県公立高等学校過去問
この動画を見る
$ AD=BD=CD$のとき,
$ \angle x,\angle y,\angle z$の大きさを求めよ.
福井県公立高等学校過去問
【よく出る…!】二次関数:精華女子高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#精華女子高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
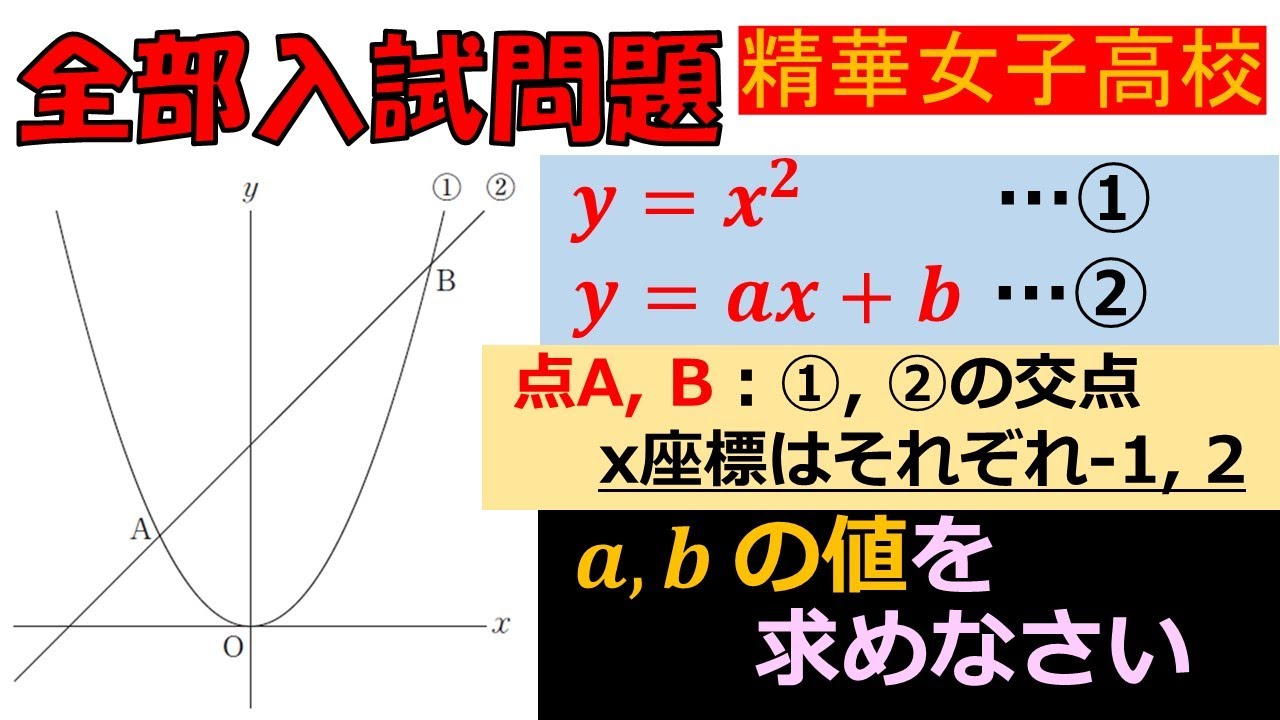
$ y=x^2 ・・・①$
$ y=ax+b・・・②$
点A,B:①,②の交点x座標はそれぞれ-1,2である.
$ a,b $の値を求めなさい.
精華女子高等学校過去問
この動画を見る
$ y=x^2 ・・・①$
$ y=ax+b・・・②$
点A,B:①,②の交点x座標はそれぞれ-1,2である.
$ a,b $の値を求めなさい.
精華女子高等学校過去問
【式をよく見て…!】連立方程式:関西学院高等部~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#関西学院高等部
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{2}{3}(x+y)-\dfrac{1}{5}(x-y)=\dfrac{9}{5} \\
\dfrac{2}{5}(2x+y)-\dfrac{3}{4}(x-y)=\dfrac{5}{4}
\end{array}
\right.
\end{eqnarray}$
連立方程式を解け.
関西学院高等部過去問
この動画を見る
$ \begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{2}{3}(x+y)-\dfrac{1}{5}(x-y)=\dfrac{9}{5} \\
\dfrac{2}{5}(2x+y)-\dfrac{3}{4}(x-y)=\dfrac{5}{4}
\end{array}
\right.
\end{eqnarray}$
連立方程式を解け.
関西学院高等部過去問
【一度解いてみたくなる…!】文字式:函館白百合学園高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#函館白百合学園高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x=\dfrac{3}{4},y=\dfrac{7}{4}$のとき,
$(3x-2y)^2-(3x+2y)^2$の値を求めなさい.
函館白百合学園高等学校過去問
この動画を見る
$ x=\dfrac{3}{4},y=\dfrac{7}{4}$のとき,
$(3x-2y)^2-(3x+2y)^2$の値を求めなさい.
函館白百合学園高等学校過去問
【問題のホンシツをつかめ…!】整数:大阪教育大学附属高等学校池田校舎~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#大阪教育大学附属高等学校池田校舎
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \sqrt n $を電卓を使って少数で表し,小数第一位で四捨五入すると8になった.
このような自然数nはいくつあるか.
大阪教育大学附属高等学校池田校舎過去問
この動画を見る
$ \sqrt n $を電卓を使って少数で表し,小数第一位で四捨五入すると8になった.
このような自然数nはいくつあるか.
大阪教育大学附属高等学校池田校舎過去問
【サンペンの長さと言えば…!】三平方の定理:興南高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#興南高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
3辺の長さがそれぞれ$ x+3,x+2,x-5 $である三角形が直角三角形であるとき・・・
xの値を求めなさい.
興南高等学校過去問
この動画を見る
3辺の長さがそれぞれ$ x+3,x+2,x-5 $である三角形が直角三角形であるとき・・・
xの値を求めなさい.
興南高等学校過去問
【ポイントは2つ…!】立体図形:精華女子高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#精華女子高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
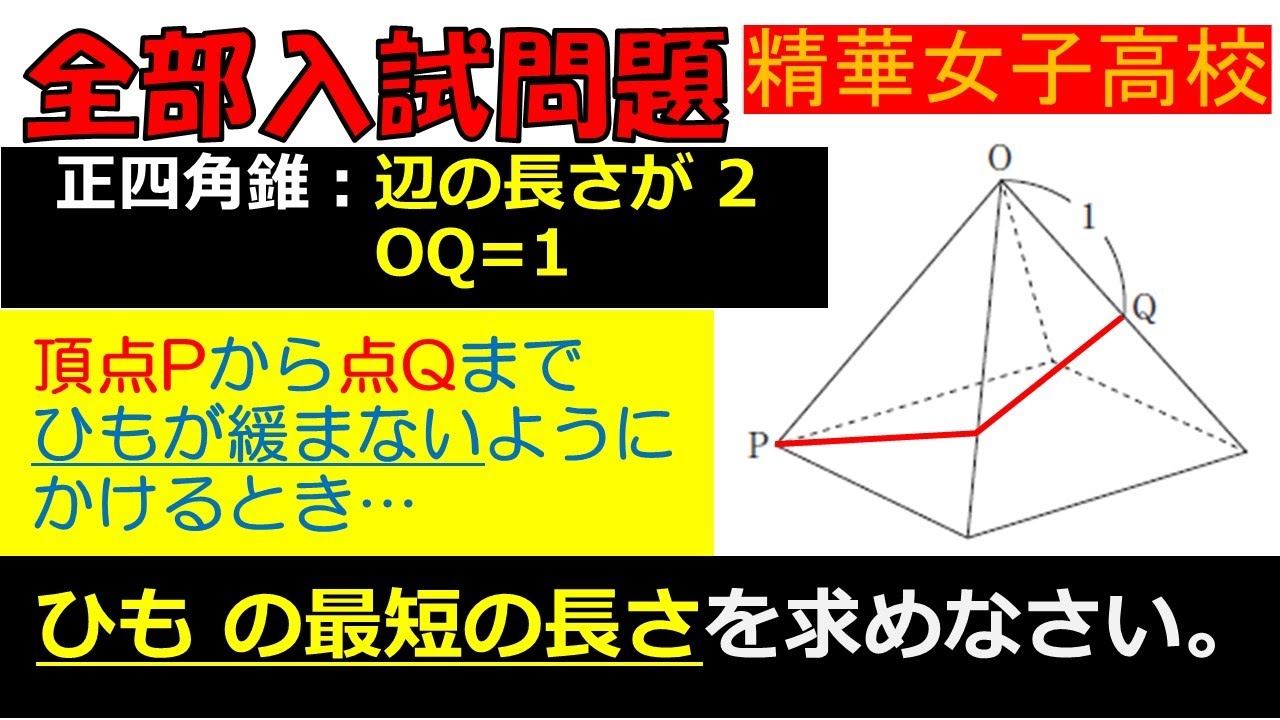
正四角錐のすべての辺の長さが2cmであり,OQ=1cmである.
頂点Pから点Qまでひもが緩まないようにかけるとき・・・
ひもの最短の長さを求めなさい.
精華女子高等学校過去問
この動画を見る
正四角錐のすべての辺の長さが2cmであり,OQ=1cmである.
頂点Pから点Qまでひもが緩まないようにかけるとき・・・
ひもの最短の長さを求めなさい.
精華女子高等学校過去問
【知ってる or 知らない…!】平方根:興南高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#興南高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の計算をしなさい.
$ \left(\dfrac{\sqrt{432}}{\sqrt3} \right)^2+\sqrt{121}\div \left(-\dfrac{1}{\sqrt9}\right)$
興南高等学校過去問
この動画を見る
次の計算をしなさい.
$ \left(\dfrac{\sqrt{432}}{\sqrt3} \right)^2+\sqrt{121}\div \left(-\dfrac{1}{\sqrt9}\right)$
興南高等学校過去問
【分かる人が次に進む…!】二次関数:日本大学第三高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#日本大学第三高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
関数$ y=\dfrac{1}{2}x^2 $について
xの変域が$ a-3 \leqq x \leqq a+3$のとき,yの変域は$ b \leqq y \leqq 8$である.
*但し, $ -3 \lt a \lt 0 $
定数$ a,b $の値を求めなさい.
この動画を見る
関数$ y=\dfrac{1}{2}x^2 $について
xの変域が$ a-3 \leqq x \leqq a+3$のとき,yの変域は$ b \leqq y \leqq 8$である.
*但し, $ -3 \lt a \lt 0 $
定数$ a,b $の値を求めなさい.
【完答できるか…!?】文章題:興南高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#興南高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2つの負の数がある.
この2つの数の差が7で積が144であるとき,小さい方の数を求めなさい.
興南高等学校過去問
この動画を見る
2つの負の数がある.
この2つの数の差が7で積が144であるとき,小さい方の数を求めなさい.
興南高等学校過去問
【使えるものは使え…!】整数:同志社高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#同志社高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
Nは十の位の数字がa,一の位の数字がbである2桁の自然数である.
MはNの十の位の数字と一の位の数字を入れ替えてできる自然数である.
$ N^2-M^2=693 $であるとき,自然数Nを求めよ.
同志社高等学校過去問
この動画を見る
Nは十の位の数字がa,一の位の数字がbである2桁の自然数である.
MはNの十の位の数字と一の位の数字を入れ替えてできる自然数である.
$ N^2-M^2=693 $であるとき,自然数Nを求めよ.
同志社高等学校過去問
【ライバルは多い…!】因数分解:中央大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#中央大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ a^2b^2-2abd-c^2+d^2 $を因数分解しなさい.
中央大附属高校過去問
この動画を見る
$ a^2b^2-2abd-c^2+d^2 $を因数分解しなさい.
中央大附属高校過去問
【初手をどう攻める…!?】整数:大阪教育大学附属高等学校池田校舎~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#大阪教育大学附属高等学校池田校舎
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
1~20までの自然数のうち,
Aは素数であるものの積であり,Bは素数でないものの積である.
AとBの最大公約数を求めなさい.
大教大高校過去問
この動画を見る
1~20までの自然数のうち,
Aは素数であるものの積であり,Bは素数でないものの積である.
AとBの最大公約数を求めなさい.
大教大高校過去問
【ロンリ的思考と計算力…!】整数:早稲田大学系属早稲田実業学校高等部~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#早稲田大学系属早稲田実業学校高等部
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
a,bは連続しない正の整数とする.
$ (a-b)(a^2+b^2)=2023 $を満たすa,bの値を求めよ.
早稲田大学系属早稲田実業学校高等部過去問
この動画を見る
a,bは連続しない正の整数とする.
$ (a-b)(a^2+b^2)=2023 $を満たすa,bの値を求めよ.
早稲田大学系属早稲田実業学校高等部過去問
【道は1つではない…!】比例式:洛南高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#洛南高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \dfrac{9}{2}x-y=3x+\dfrac{5}{3}y$のとき,
x:yを最も簡単な整数の比で表しなさい.
洛南高校過去問
この動画を見る
$ \dfrac{9}{2}x-y=3x+\dfrac{5}{3}y$のとき,
x:yを最も簡単な整数の比で表しなさい.
洛南高校過去問
【シンプルに大切…!】文章題:大阪教育大学附属高等学校池田校舎~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#大阪教育大学附属高等学校池田校舎
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
1辺の長さが2a cmの正方形と,2辺の長さが5 cm,4a cmの長方形がある.
2つの図形の面積の差が24 $cm^2$である.
aの値をすべて求めなさい.
大教大高校過去問
この動画を見る
1辺の長さが2a cmの正方形と,2辺の長さが5 cm,4a cmの長方形がある.
2つの図形の面積の差が24 $cm^2$である.
aの値をすべて求めなさい.
大教大高校過去問
【『強』印 二重…!】確率:日本大学習志野高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#日本大学習志野高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
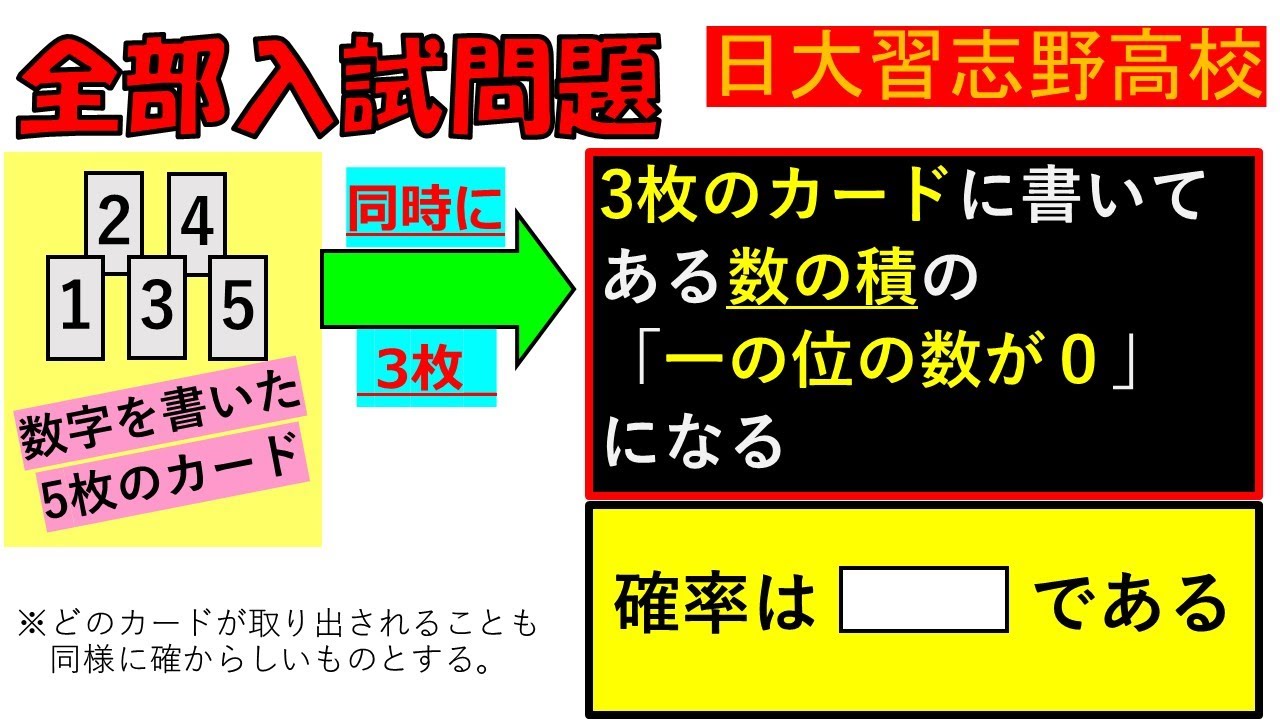
数字を書いた5枚のカードを同時に3枚取り出す.
3枚のカードに書いてある数の積の「一の位の数が0」になる確率は$ \Box $である.
*どのカードが取り出されることも同様に確からしいものとする.
日大習志野高校過去問
この動画を見る
数字を書いた5枚のカードを同時に3枚取り出す.
3枚のカードに書いてある数の積の「一の位の数が0」になる確率は$ \Box $である.
*どのカードが取り出されることも同様に確からしいものとする.
日大習志野高校過去問
【考えてみれば…!】整数:大阪星光学院高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#大阪星光学院高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ f(x):x $を3で割った余り(xは0以上の整数である)
$ f(1)+f(2)+f(3)+・・・+f(2023)=\Box $である.
大阪星光学院高等学校過去問
この動画を見る
$ f(x):x $を3で割った余り(xは0以上の整数である)
$ f(1)+f(2)+f(3)+・・・+f(2023)=\Box $である.
大阪星光学院高等学校過去問
【スッキリするには…!】文字式:江戸川学園取手高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#江戸川学園取手高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ A=x^2+x+1 $
$ B=x^2-x-1 $
$ C=x^3-1 $ のとき,$ 2A-{A-(2B-C)}-(B-C)$を計算しなさい.
江戸川取手高校過去問
この動画を見る
$ A=x^2+x+1 $
$ B=x^2-x-1 $
$ C=x^3-1 $ のとき,$ 2A-{A-(2B-C)}-(B-C)$を計算しなさい.
江戸川取手高校過去問
🍭【峠を越えれば…!】整数:慶応義塾高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ 7^{123}$を$100$で割ると,余りは$ \Box $である.
次の空欄をうめよ.
慶應義塾高校過去問
この動画を見る
$ 7^{123}$を$100$で割ると,余りは$ \Box $である.
次の空欄をうめよ.
慶應義塾高校過去問
【信じて進め…!】連立方程式:関西学院高等部~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#関西学院高等部
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{4}x+0.3y=3 \\
0.7x+\dfrac{2}{7}y=1
\end{array}
\right.
\end{eqnarray}$
次の連立方程式を解け.
関西学院高等学校過去問
この動画を見る
$ \begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{4}x+0.3y=3 \\
0.7x+\dfrac{2}{7}y=1
\end{array}
\right.
\end{eqnarray}$
次の連立方程式を解け.
関西学院高等学校過去問
【条件をよく見て…!】図形:愛知県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#愛知県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
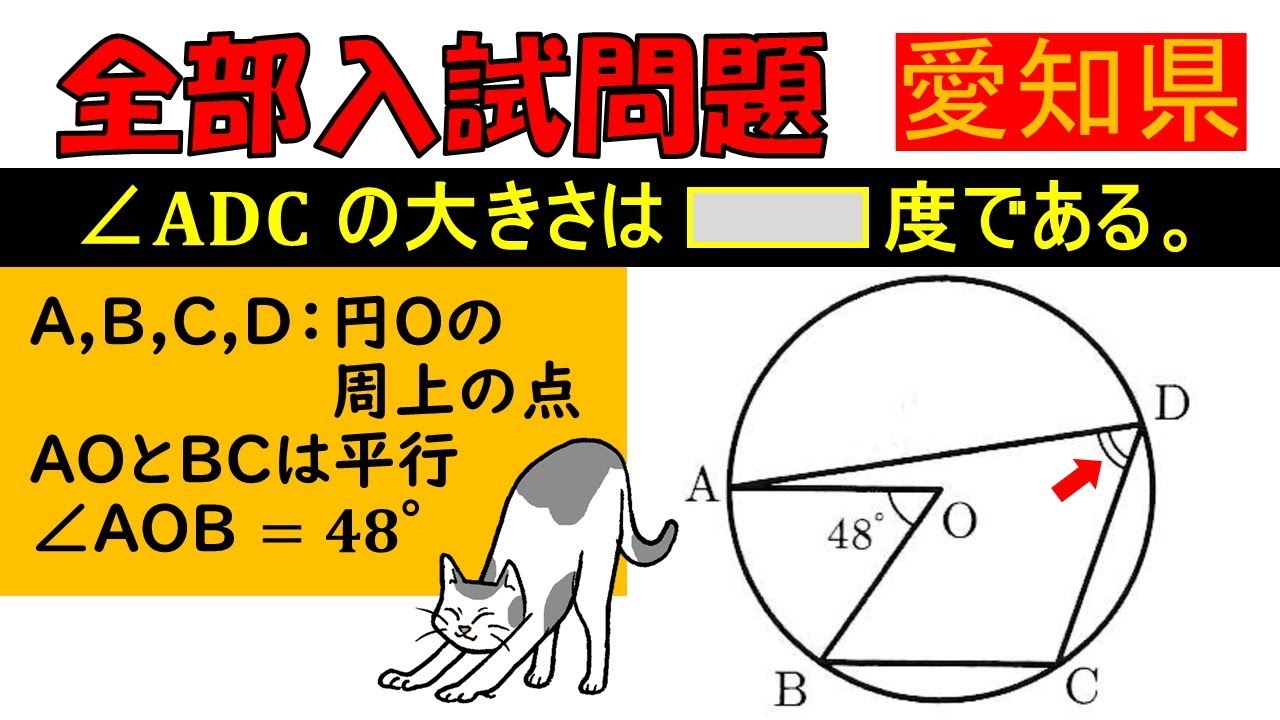
$ A,B,C,D$は円$O$の周上の点である.
$ AO $と$ BC $は平行であり, $ \angle AOB=48°$である.
$ \angle ADC $の大きさは$ \Box $度である.
愛知県入試問題過去問
この動画を見る
$ A,B,C,D$は円$O$の周上の点である.
$ AO $と$ BC $は平行であり, $ \angle AOB=48°$である.
$ \angle ADC $の大きさは$ \Box $度である.
愛知県入試問題過去問
【よく見てやれば…!】平方根:青山学院高等部~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#青山学院高等部
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \left(\dfrac{1}{2\sqrt2}+\sqrt3 \right)\left(\sqrt2-\dfrac{1}{2\sqrt3}\right)$
次の計算をせよ.
青山学院高等部過去問
この動画を見る
$ \left(\dfrac{1}{2\sqrt2}+\sqrt3 \right)\left(\sqrt2-\dfrac{1}{2\sqrt3}\right)$
次の計算をせよ.
青山学院高等部過去問
【ルールに忠実に…!】平方根:東京学芸大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#東京学芸大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \dfrac{\sqrt{(-2)^2}(\sqrt2+\sqrt3)^2}{\sqrt2}+\dfrac{(3-\sqrt6)^2}{\sqrt3}$
を計算しなさい.
東京学芸大附属高校過去問
この動画を見る
$ \dfrac{\sqrt{(-2)^2}(\sqrt2+\sqrt3)^2}{\sqrt2}+\dfrac{(3-\sqrt6)^2}{\sqrt3}$
を計算しなさい.
東京学芸大附属高校過去問
【条件をフル活用…!】図形:兵庫県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)#兵庫県公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
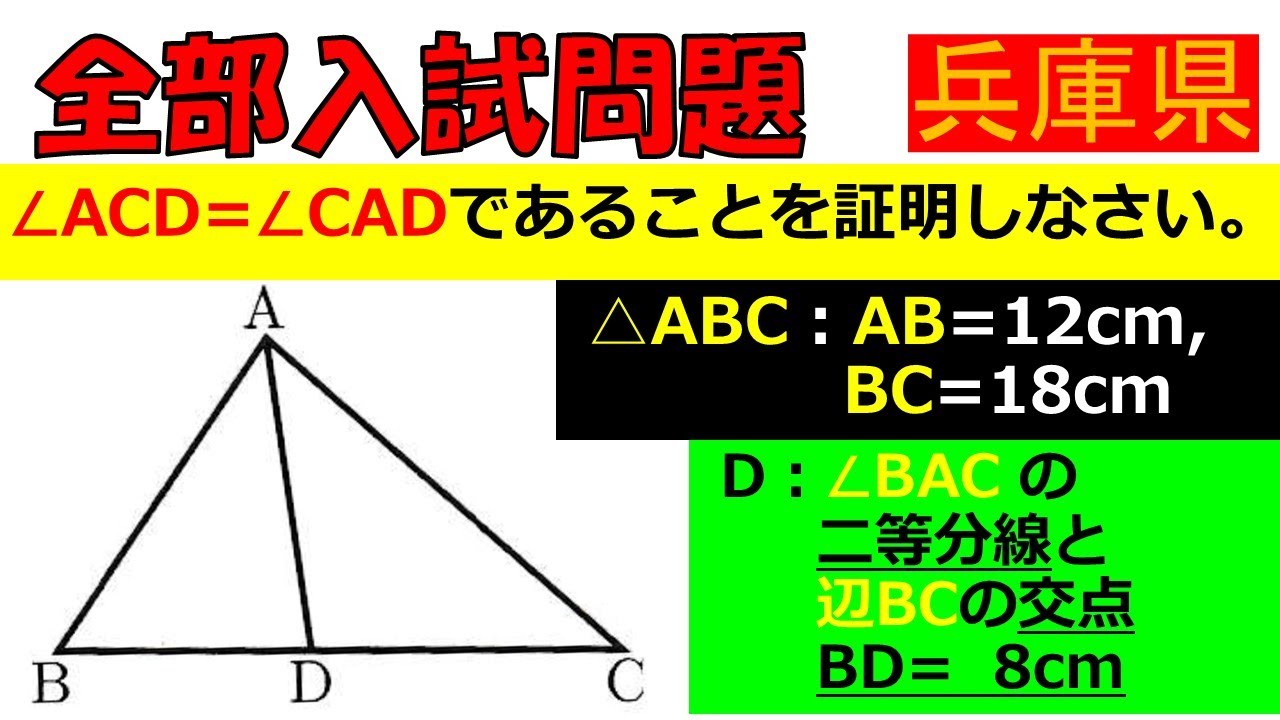
$ \triangle ABC $の$ AB$は12cmであり,$ BC $は18cmである.
$ D $は$ \angle BAC $の二等分線と辺$ BC $の交点である.
$ \angle ACD=\angle CAD $であることを証明しなさい.
兵庫県公立高等学校過去問
この動画を見る
$ \triangle ABC $の$ AB$は12cmであり,$ BC $は18cmである.
$ D $は$ \angle BAC $の二等分線と辺$ BC $の交点である.
$ \angle ACD=\angle CAD $であることを証明しなさい.
兵庫県公立高等学校過去問
【それを決めるのは…!】整数:大阪府公立高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#大阪府公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ n $を自然数とするとき,$ 5-\dfrac{78}{n}$の値が自然数となるような
最も小さい自然数$ n $の値を求めなさい.
大阪府公立高等学校過去問
この動画を見る
$ n $を自然数とするとき,$ 5-\dfrac{78}{n}$の値が自然数となるような
最も小さい自然数$ n $の値を求めなさい.
大阪府公立高等学校過去問
【まず手を付けよう…!】二次方程式:法政大学第二高等学校~全国入試問題解法

単元:
#中3数学#2次方程式#高校入試過去問(数学)#法政大学第二高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2次方程式$ (x+2)^2+x^2=(x+4)^2-12 $を解きなさい.
法政大学第二高等学校過去問
この動画を見る
2次方程式$ (x+2)^2+x^2=(x+4)^2-12 $を解きなさい.
法政大学第二高等学校過去問
【これなら「分かる」…!】整数:大阪府公立高等学校~全国入試問題解法

単元:
#高校入試過去問(数学)#大阪府公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ n $を自然数とする.
$ n \leqq \sqrt x \leqq n+1 $を満たす自然数$ x $の個数が100であるときの
$ n $の値を求めなさい.
大阪府公立高等学校過去問
この動画を見る
$ n $を自然数とする.
$ n \leqq \sqrt x \leqq n+1 $を満たす自然数$ x $の個数が100であるときの
$ n $の値を求めなさい.
大阪府公立高等学校過去問
【学んだことを活かせ…!】連立方程式:明治大学付属中野高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#明治大学付属中野高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x,y $についての連立方程式 $ \begin{eqnarray}
\left\{
\begin{array}{l}
4x+3y=11 \\
x-ky=-\dfrac{1}{2}k
\end{array}
\right.
\end{eqnarray}$ の解が $\begin{eqnarray}
\left\{
\begin{array}{l}
x=p \\
y=q
\end{array}
\right.
\end{eqnarray}$ であり,
$ p+q=3 $が成り立つ.$ k $の値を求めなさい.
明治大学付属中野高等学校過去問
この動画を見る
$ x,y $についての連立方程式 $ \begin{eqnarray}
\left\{
\begin{array}{l}
4x+3y=11 \\
x-ky=-\dfrac{1}{2}k
\end{array}
\right.
\end{eqnarray}$ の解が $\begin{eqnarray}
\left\{
\begin{array}{l}
x=p \\
y=q
\end{array}
\right.
\end{eqnarray}$ であり,
$ p+q=3 $が成り立つ.$ k $の値を求めなさい.
明治大学付属中野高等学校過去問
【な、長い…!】平方根:洛南高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#洛南高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ (1+\sqrt2+\sqrt4+\sqrt8+\sqrt{16}+\sqrt{32})$
$ \times (1-\sqrt2+\sqrt4-\sqrt8+\sqrt{16}-\sqrt{32}$
を計算しなさい.
洛南高等学校過去問
この動画を見る
$ (1+\sqrt2+\sqrt4+\sqrt8+\sqrt{16}+\sqrt{32})$
$ \times (1-\sqrt2+\sqrt4-\sqrt8+\sqrt{16}-\sqrt{32}$
を計算しなさい.
洛南高等学校過去問
