 高校入試過去問(数学)
高校入試過去問(数学)
 高校入試過去問(数学)
高校入試過去問(数学)
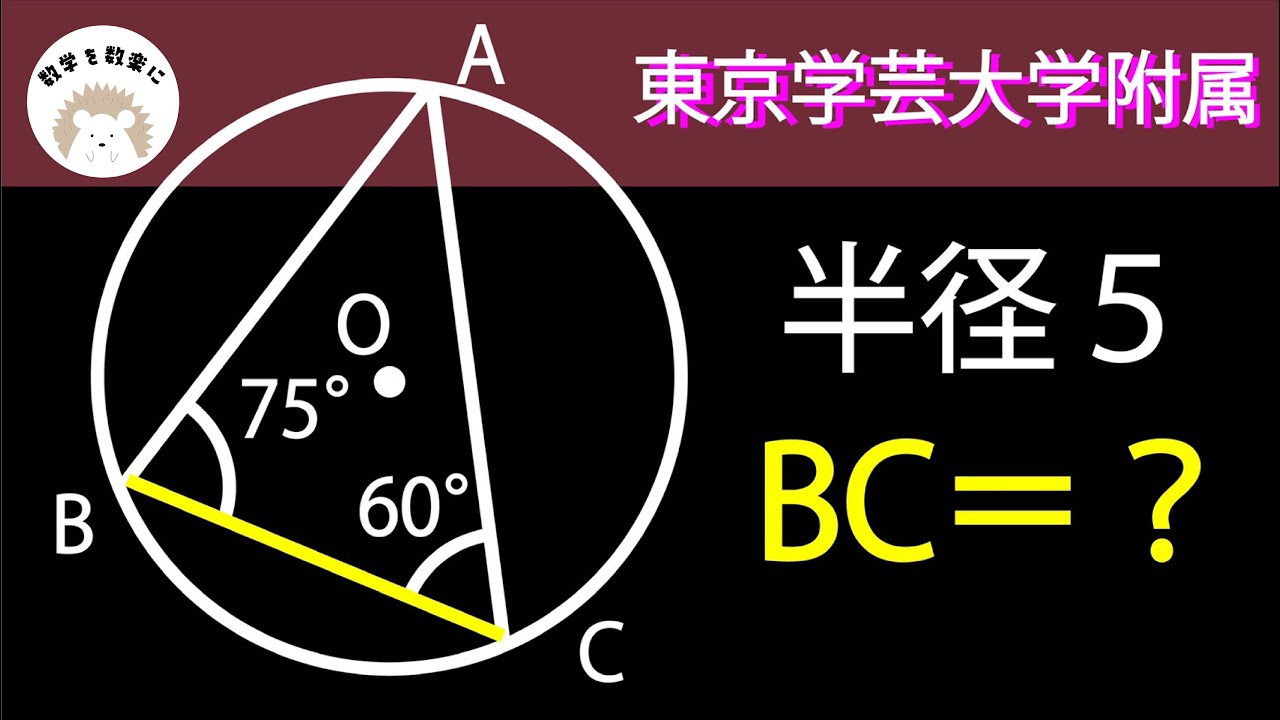
円 東京学芸大学附属
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
半径=5
BC=?
*図は動画内参照
東京学芸大学附属高校
この動画を見る
半径=5
BC=?
*図は動画内参照
東京学芸大学附属高校
【5分で基礎から応用へ!】二次方程式:法政大学高等学校~全国入試問題解法【裏ワザ付き!】

単元:
#数学(中学生)#2次方程式#高校入試過去問(数学)#法政大学高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 法政大学高等学校
$x^2-ax+6=0$
の解の1つが$\sqrt{ 3 }$であるとき、
もう1つの解を求めなさい。
この動画を見る
入試問題 法政大学高等学校
$x^2-ax+6=0$
の解の1つが$\sqrt{ 3 }$であるとき、
もう1つの解を求めなさい。
階乗(❗️)に関する問題 常総学院

単元:
#数学(中学生)#数列#数列とその和(等差・等比・階差・Σ)#高校入試過去問(数学)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{(n+2)!}{n!} = 20$のときn=?
常総学院高等学校(改)
この動画を見る
$\frac{(n+2)!}{n!} = 20$のときn=?
常総学院高等学校(改)
【3分で学ぶ基礎力!】文字式:法政大学高等学校~全国入試問題解法【タイガー】

単元:
#数学(中学生)#文字と式#高校入試過去問(数学)#法政大学高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 法政大学高等学校
次の問いの計算をしなさい。
$\displaystyle \frac{5x-2y}{3}-\displaystyle \frac{2x-3y}{2}-\displaystyle \frac{3x+2y}{5}$
この動画を見る
入試問題 法政大学高等学校
次の問いの計算をしなさい。
$\displaystyle \frac{5x-2y}{3}-\displaystyle \frac{2x-3y}{2}-\displaystyle \frac{3x+2y}{5}$
整数問題 大阪教育大附属天王寺

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
自然数A,B,Cを求めよ。
$
\begin{eqnarray}
\left\{
\begin{array}{l}
A \div B \times C=12 \\
A \div B - C=1 \\
A \div B =10
\end{array}
\right.
\end{eqnarray}
$
大阪教育大学附属高等学校天王寺校舎
この動画を見る
自然数A,B,Cを求めよ。
$
\begin{eqnarray}
\left\{
\begin{array}{l}
A \div B \times C=12 \\
A \div B - C=1 \\
A \div B =10
\end{array}
\right.
\end{eqnarray}
$
大阪教育大学附属高等学校天王寺校舎
二次方程式 大阪教育大附属天王寺

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式を解け
$40000x^2-1500x+9 = 0$
大阪教育大学附属高等学校天王寺校舎
この動画を見る
2次方程式を解け
$40000x^2-1500x+9 = 0$
大阪教育大学附属高等学校天王寺校舎
2次方程式 筆算はしたくない。 日大習志野

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式を解け
$\frac{1}{2}x(x+15) = 19 \times 53$
日本大学習志野高等学校
この動画を見る
2次方程式を解け
$\frac{1}{2}x(x+15) = 19 \times 53$
日本大学習志野高等学校
【5分で得意分野へ!】図形:専修大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#平面図形#高校入試過去問(数学)#専修大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 専修大学附属高等学校
線分$AH$の長さを求めなさい。
$\angle AHB=90°$
三角形$ABC:$
AB=13
BC=14
CA=15
※図は動画内参照
この動画を見る
入試問題 専修大学附属高等学校
線分$AH$の長さを求めなさい。
$\angle AHB=90°$
三角形$ABC:$
AB=13
BC=14
CA=15
※図は動画内参照
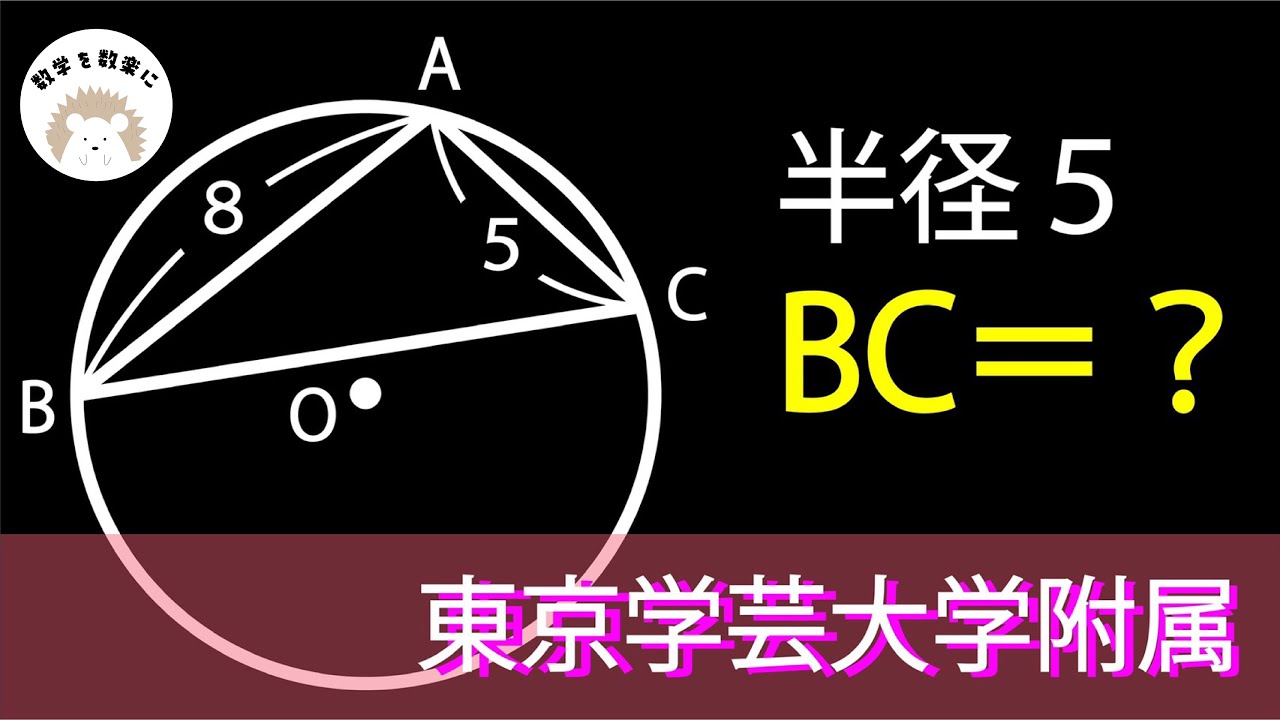
円 学芸大学附属 B
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
円の半径=5
BC=?
*図は動画内参照
東京学芸大学附属高校
この動画を見る
円の半径=5
BC=?
*図は動画内参照
東京学芸大学附属高校
7の倍数になる確率=❓ 日比谷

単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
大小2コのサイコロを投げる
百の位を1
十の位を小さいサイコロの目
一の位を大きいサイコロの目
3ケタの整数が7の倍数となる確率=?
日比谷高等学校
この動画を見る
大小2コのサイコロを投げる
百の位を1
十の位を小さいサイコロの目
一の位を大きいサイコロの目
3ケタの整数が7の倍数となる確率=?
日比谷高等学校
【3分で基礎から発展まで・確実点取りから時短へ!】確率:函館ラ・サール高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)#函館ラ・サール高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
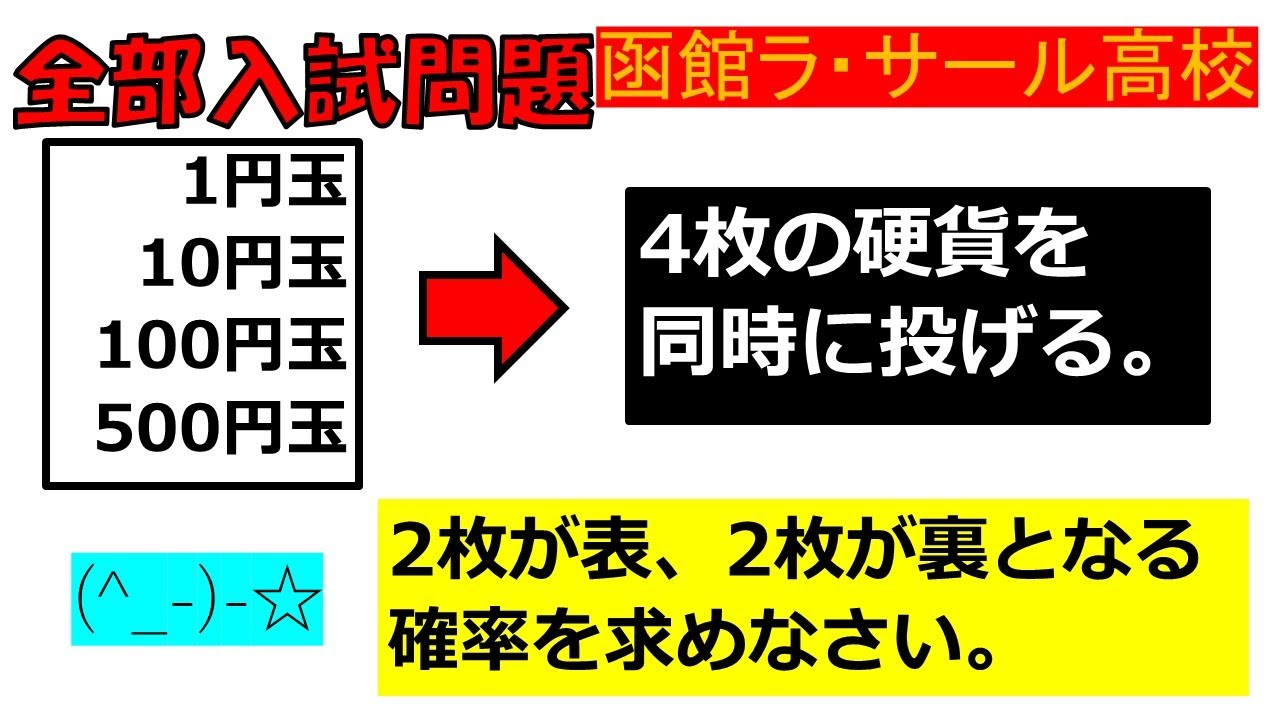
入試問題 函館ラ・サール高等学校
1円玉 10円玉 100円玉 500円玉
↓
4枚の硬貨を同時に投げ、
2枚が表、2枚が裏となる 確率を求めなさい。
この動画を見る
入試問題 函館ラ・サール高等学校
1円玉 10円玉 100円玉 500円玉
↓
4枚の硬貨を同時に投げ、
2枚が表、2枚が裏となる 確率を求めなさい。
【5分で高校入試から大学受験まで!「型」を見抜け!】整数:立教新座高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#立教新座高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 立教新座高等学校
$x$と$y$は自然数とします。
【方程式】
$4x^2-9y^2=31
を満たす x,y の値をそれぞれ求めなさい。
この動画を見る
入試問題 立教新座高等学校
$x$と$y$は自然数とします。
【方程式】
$4x^2-9y^2=31
を満たす x,y の値をそれぞれ求めなさい。
灘高校の式の値 伝えたいこと、たくさん
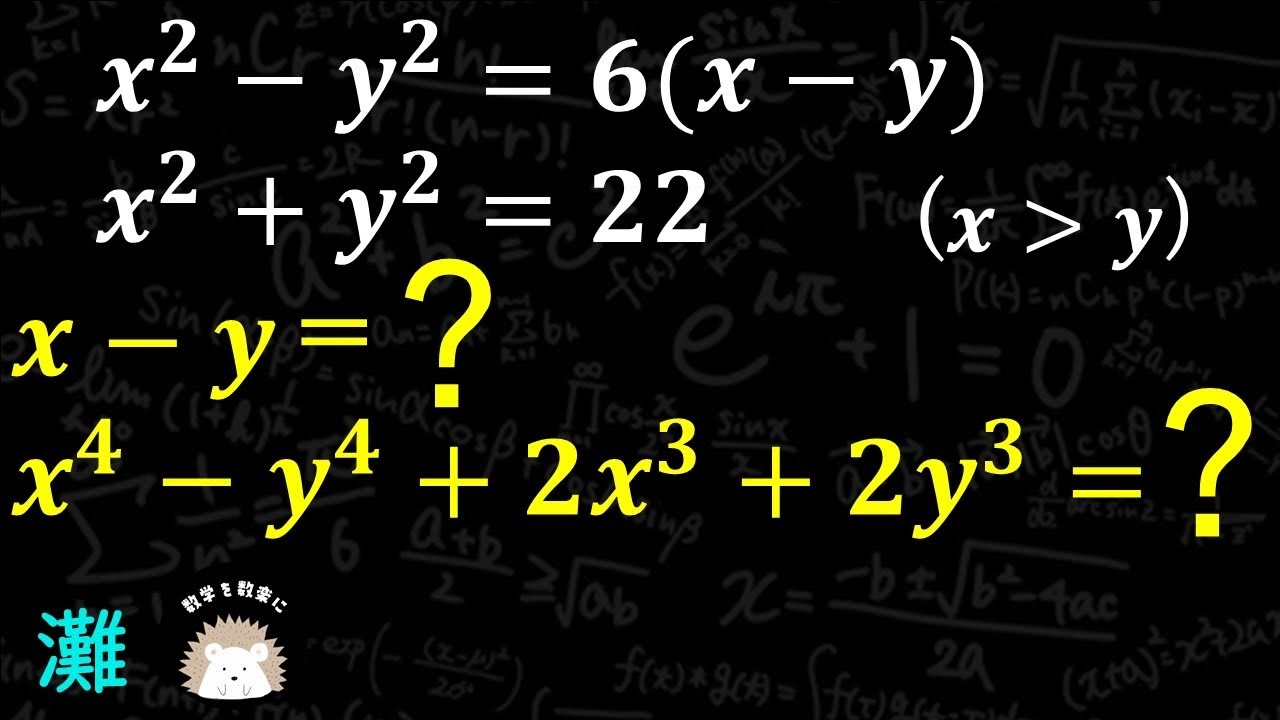
単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2-y^2=6(x-y)$ , $x^2+y^2 = 22$ (x>y)
$x-y=?$
$x^4-y^4+2x^3+2y^3=?$
灘高等学校
この動画を見る
$x^2-y^2=6(x-y)$ , $x^2+y^2 = 22$ (x>y)
$x-y=?$
$x^4-y^4+2x^3+2y^3=?$
灘高等学校
【全てに通じる5分間!】計算:洛南高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#洛南高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 洛南高等学校
次の式を計算せよ。
$\{(-1)^2+(-2)^3-(-3)^4-(-4)^3\} \div (-6)$
1,計算のルールを守る。
2,要領よく処理する。
この動画を見る
入試問題 洛南高等学校
次の式を計算せよ。
$\{(-1)^2+(-2)^3-(-3)^4-(-4)^3\} \div (-6)$
1,計算のルールを守る。
2,要領よく処理する。
垂線の長さの和=❓ B
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
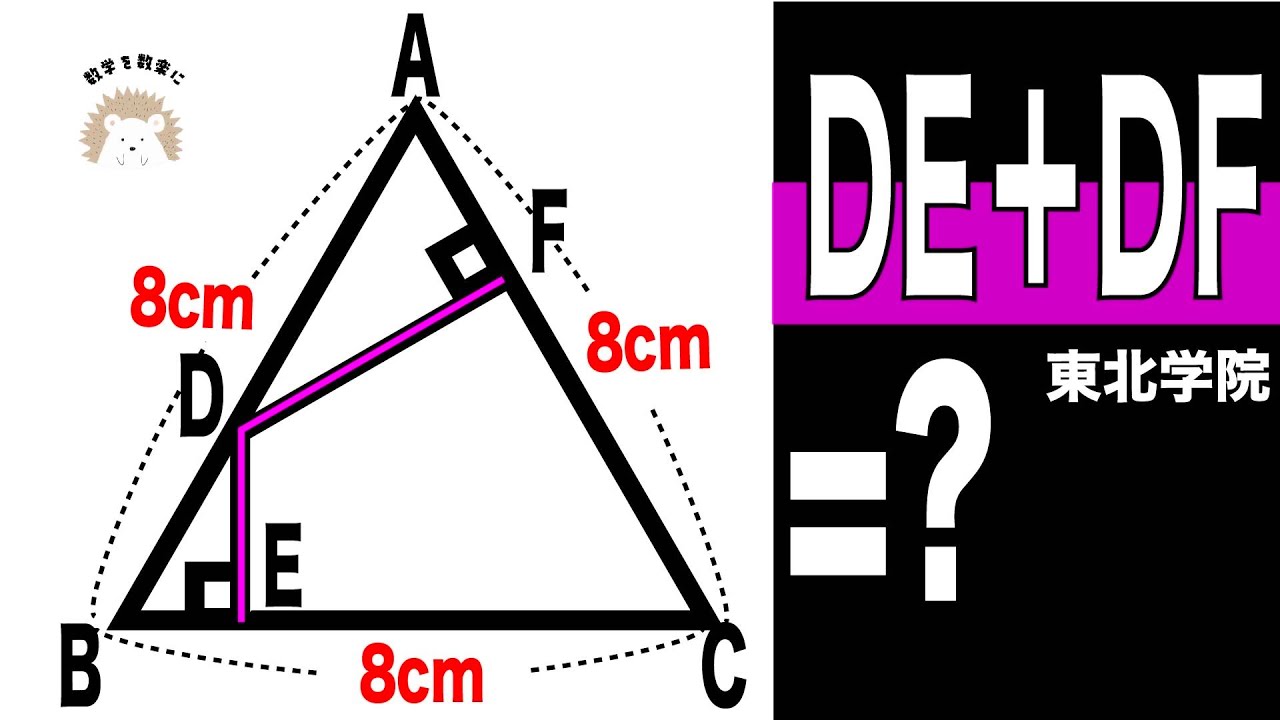
DE+EF=?
*図は動画内参照
東北学院高等学校
この動画を見る
DE+EF=?
*図は動画内参照
東北学院高等学校
ひし形 気づけば一瞬
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
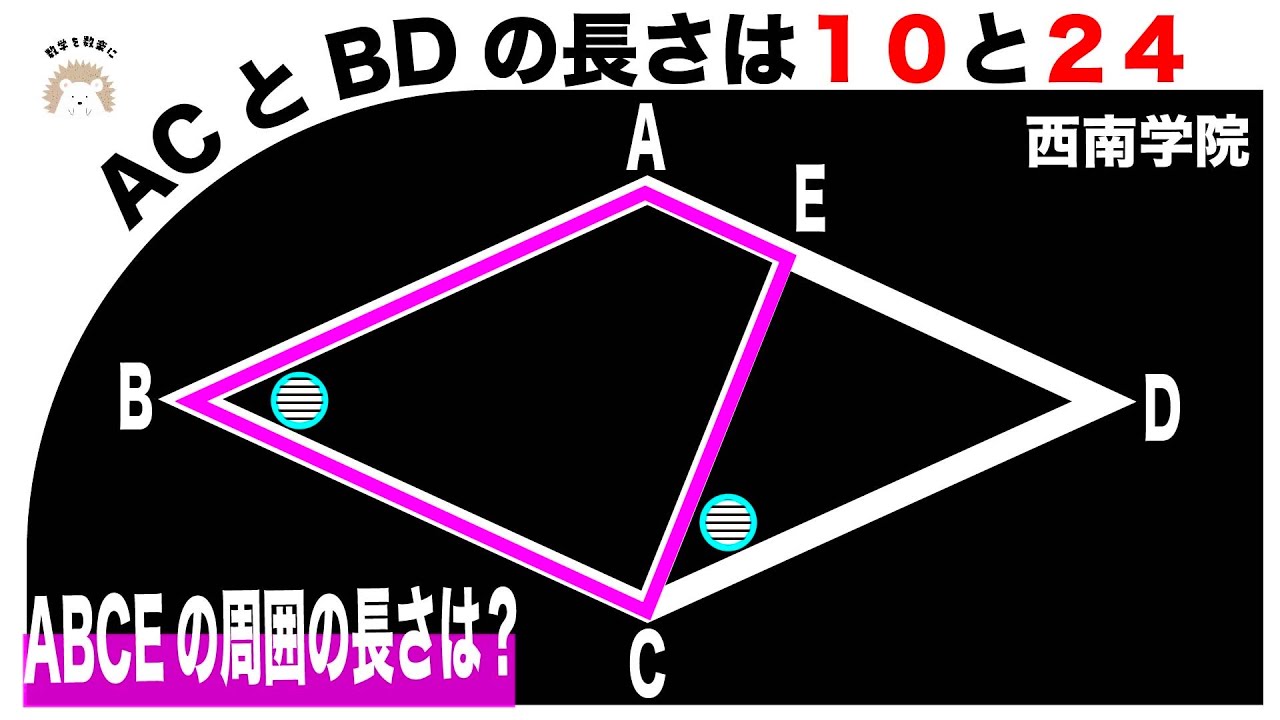
AC=10 , BD=24
四角形ABCEの周囲の長さ=?
*図は動画内参照
西南学院高等学校
この動画を見る
AC=10 , BD=24
四角形ABCEの周囲の長さ=?
*図は動画内参照
西南学院高等学校
平方根の利用 A

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt {1.23} = a$とする。
$\sqrt{123} + \sqrt{0.0123}$をaで表せ。
福岡大学附属大濠高等学校
この動画を見る
$\sqrt {1.23} = a$とする。
$\sqrt{123} + \sqrt{0.0123}$をaで表せ。
福岡大学附属大濠高等学校
【5分で理解!「それ以外」が難しい!】連立方程式:早稲田大学系属早稲田実業学校高等部~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#早稲田大学系属早稲田実業学校高等部
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 早稲田大学系属早稲田実業学校高等部
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x + y)^2+x^2+y^2+(x-y)^2 = 2019 \\
(x + y)(x-y) = 385
\end{array}
\right.
\end{eqnarray}$
$x \gt 0,y \gt 0$のとき、
連立方程式を解け。
この動画を見る
入試問題 早稲田大学系属早稲田実業学校高等部
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x + y)^2+x^2+y^2+(x-y)^2 = 2019 \\
(x + y)(x-y) = 385
\end{array}
\right.
\end{eqnarray}$
$x \gt 0,y \gt 0$のとき、
連立方程式を解け。
式の値 日大習志野

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=\frac{1}{a}+3$ , $y=\frac{1}{a}-3$のとき
$xy^3+x^3y$をaで表せ。
日本大学習志野高等学校
この動画を見る
$x=\frac{1}{a}+3$ , $y=\frac{1}{a}-3$のとき
$xy^3+x^3y$をaで表せ。
日本大学習志野高等学校
正しいか、正しくないか 慶應義塾高校(改)

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
正しいか正しくないか?
(ア)a,b,cについてac=bcならばa=b
(イ)a,bについて$a^2+b^2=2ab$ならばa=b
(ウ)a,bについて$a^2>b^2$ならばa>b
慶應義塾高等学校(改)
この動画を見る
正しいか正しくないか?
(ア)a,b,cについてac=bcならばa=b
(イ)a,bについて$a^2+b^2=2ab$ならばa=b
(ウ)a,bについて$a^2>b^2$ならばa>b
慶應義塾高等学校(改)
【5分で通常の3倍学ぶ!】連立方程式:青森県~全国入試問題解法

単元:
#数学(中学生)#連立方程式#高校入試過去問(数学)#青森県公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 青森県の公立校
次の連立方程式を解きなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
y=4(x+2) \\
6x - y = -10
\end{array}
\right.
\end{eqnarray}$
この動画を見る
入試問題 青森県の公立校
次の連立方程式を解きなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
y=4(x+2) \\
6x - y = -10
\end{array}
\right.
\end{eqnarray}$
【良問で身に付く数学の応用力!】空間図形:茨城県公立高等学校~全国入試問題解法【とんとん♪】
単元:
#数学(中学生)#空間図形#高校入試過去問(数学)#茨城県公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
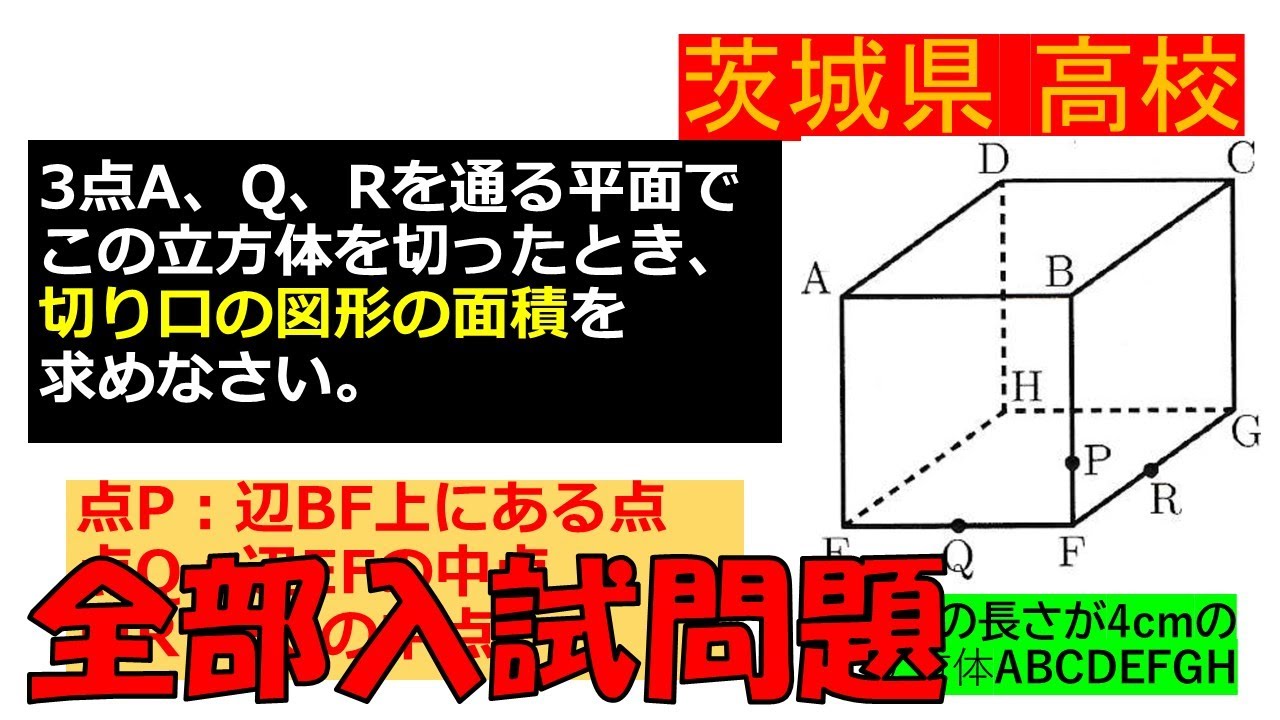
入試問題 茨城県の公立高等学校
3点A、Q、Rを通る平面で この立方体を切ったとき、
切り口の図形の面積を求めなさい。
点P:辺BF上にある点
点Q:辺EFの中点
点R: FGの中点
※図は動画内参照
この動画を見る
入試問題 茨城県の公立高等学校
3点A、Q、Rを通る平面で この立方体を切ったとき、
切り口の図形の面積を求めなさい。
点P:辺BF上にある点
点Q:辺EFの中点
点R: FGの中点
※図は動画内参照
高校入試 図形 慶應湘南藤沢

【3分で身に付く基礎力!】連立方程式:広島大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#連立方程式#高校入試過去問(数学)#広島大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 広島大学附属高等学校
連立方程式を解け
$3x+4y=5x+6y=7$
この動画を見る
入試問題 広島大学附属高等学校
連立方程式を解け
$3x+4y=5x+6y=7$
式の値 昭和学院秀英
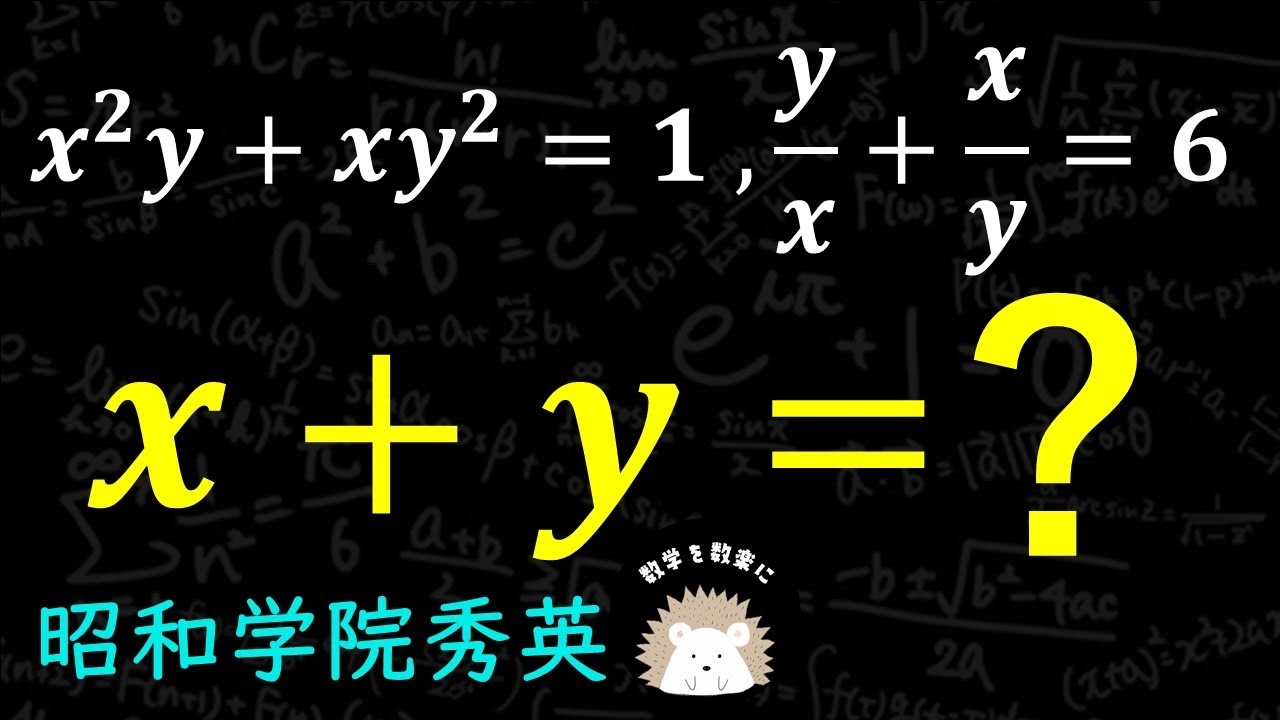
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2y+xy^2=1$ , $\frac{y}{x}+\frac{x}{y} = 6$のとき x+y=?
昭和学院秀英高等学校
この動画を見る
$x^2y+xy^2=1$ , $\frac{y}{x}+\frac{x}{y} = 6$のとき x+y=?
昭和学院秀英高等学校
【順を追って、理解深まる!】一次関数:佐賀県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#佐賀県立高校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
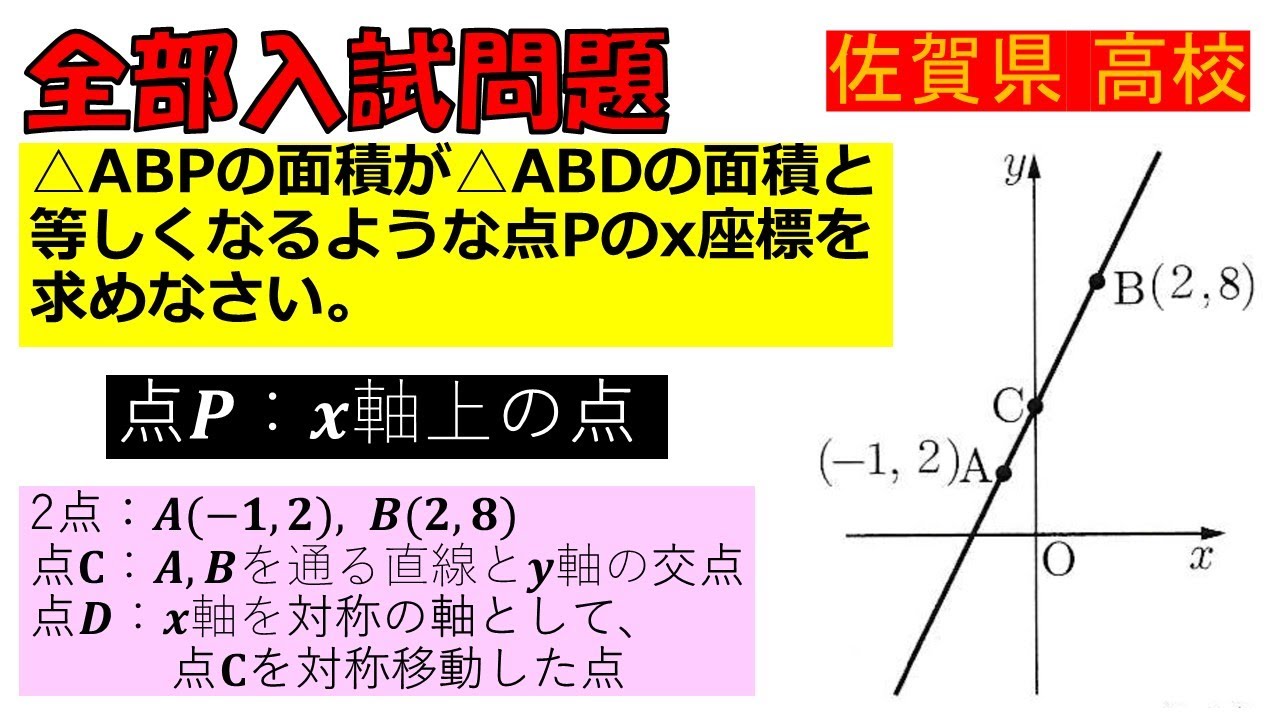
入試問題 佐賀県の公立高等学校
$\triangle ABP$の面積が$\triangle ABD$の面積と
等しくなるような点Pのx座標を 求めなさい。
点P:x軸上の点
2点:A(-1,2), B(2,8)
点C: A, Bを通る直線と軸の交点
点D:x軸を対称の軸として、
点Cを対称移動した点
※図は動画内参照
この動画を見る
入試問題 佐賀県の公立高等学校
$\triangle ABP$の面積が$\triangle ABD$の面積と
等しくなるような点Pのx座標を 求めなさい。
点P:x軸上の点
2点:A(-1,2), B(2,8)
点C: A, Bを通る直線と軸の交点
点D:x軸を対称の軸として、
点Cを対称移動した点
※図は動画内参照
連立方程式 解がない 2通りの解説 滝高校

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
連立方程式が解をもたないときa=?
$
\begin{eqnarray}
\left\{
\begin{array}{l}
3x+2y=4 \cdots①\\
ax+y=3 \cdots②\\
\end{array}
\right.
\end{eqnarray}
$
滝高等学校
この動画を見る
連立方程式が解をもたないときa=?
$
\begin{eqnarray}
\left\{
\begin{array}{l}
3x+2y=4 \cdots①\\
ax+y=3 \cdots②\\
\end{array}
\right.
\end{eqnarray}
$
滝高等学校
【5分で広がる数学の世界!】連立方程式からの比の計算~全国入試問題解法

単元:
#数学(中学生)#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$x:y: z$を求めよ。
$\begin{eqnarray}
\left\{
\begin{array}{l}
x + y +z= 0 \\
2x + 3y +5z= 0
\end{array}
\right.
\end{eqnarray}$
※高校入試では出ませんので、念のため・・・。
この動画を見る
$x:y: z$を求めよ。
$\begin{eqnarray}
\left\{
\begin{array}{l}
x + y +z= 0 \\
2x + 3y +5z= 0
\end{array}
\right.
\end{eqnarray}$
※高校入試では出ませんので、念のため・・・。
気付けば、ほらそこに答えが
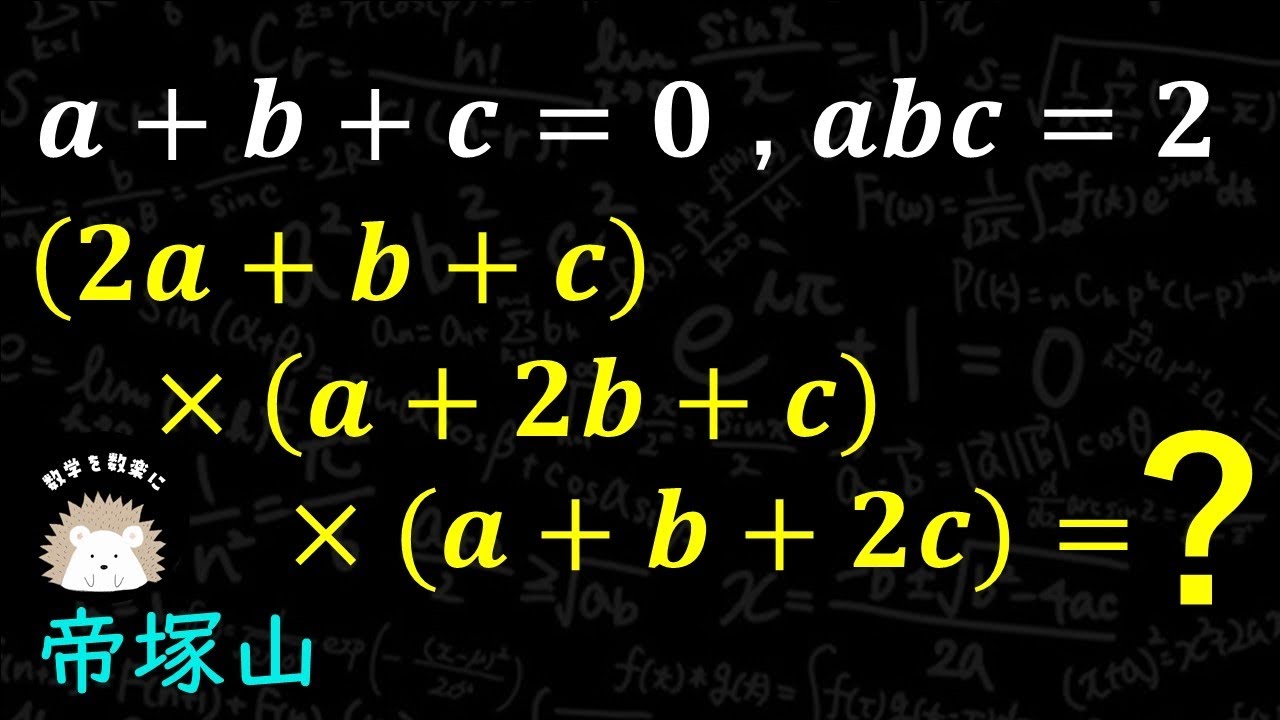
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
a+b+c=0 , abc=2のとき
(2a+b+c)(a+2b+c)(a+b+2c)=
帝塚山高等学校
この動画を見る
a+b+c=0 , abc=2のとき
(2a+b+c)(a+2b+c)(a+b+2c)=
帝塚山高等学校
【3分でいろいろ身に付く!】二次方程式:和洋国府台女子高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#和洋国府台女子高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 和洋国府台女子高等学校
次の2次方程式を解け。
$2x^2 + 6 = (x + 2)^2$
この動画を見る
入試問題 和洋国府台女子高等学校
次の2次方程式を解け。
$2x^2 + 6 = (x + 2)^2$
