 2次方程式
2次方程式
 2次方程式
2次方程式
これ裏技?

単元:
#数学(中学生)#中3数学#2次方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
2次関数上の2点を通る直線の方程式を素早く求める方法についての動画です。
この動画を見る
2次関数上の2点を通る直線の方程式を素早く求める方法についての動画です。
【うまいやり方とは…!】二次方程式:東京都立新宿高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#東京都立新宿高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$x^2+ax+b=0\;$の解が1と2であるとき、
$\displaystyle\frac{\left(a+b\right)\left(2a+b\right)}{\left(a+b+2\right)\left(2a+b+2\right)}\;$の値を求めよ。
この動画を見る
$x^2+ax+b=0\;$の解が1と2であるとき、
$\displaystyle\frac{\left(a+b\right)\left(2a+b\right)}{\left(a+b+2\right)\left(2a+b+2\right)}\;$の値を求めよ。
【分かる人だけ…!】二次方程式:早稲田大学系属早稲田実業学校高等部~全国入試問題解法
単元:
#数学(中学生)#2次方程式#高校入試過去問(数学)#早稲田大学系属早稲田実業学校高等部
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$3x^2-4x-2=0$の2つの解を$a,b$とするとき, $(3a^2-4a+2)(6b^2-8b)$の値を求めよ
この動画を見る
$3x^2-4x-2=0$の2つの解を$a,b$とするとき, $(3a^2-4a+2)(6b^2-8b)$の値を求めよ
【どれも大切…!】二次方程式:慶応義塾高等学校~全国入試問題解法
単元:
#数学(中学生)#2次方程式#高校入試過去問(数学)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$2x^2+10\sqrt{2}x+9=0$の解を求めよ。
この動画を見る
$2x^2+10\sqrt{2}x+9=0$の解を求めよ。
解の公式を忘れてしまったときの対処法

ルートが入っている二次方程式 広尾学園

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#広尾学園高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
方程式を解け
$x^2-\sqrt{2}(1+\sqrt{5})x+2\sqrt{5}=0$
この動画を見る
方程式を解け
$x^2-\sqrt{2}(1+\sqrt{5})x+2\sqrt{5}=0$
二次方程式の応用 三田学園

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
次の2つの2次方程式の共通な解が
$x=-2$だけになるとき、
a,bの値を求めよ
$x^2-(b+2)x-b^2=0$
$x^2+ax+2b=0$
この動画を見る
次の2つの2次方程式の共通な解が
$x=-2$だけになるとき、
a,bの値を求めよ
$x^2-(b+2)x-b^2=0$
$x^2+ax+2b=0$
equation : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#平方根#2次方程式#高校入試過去問(数学)#渋谷教育学園幕張高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\left(x+\sqrt{3}+\sqrt{5}\right)^2-3\sqrt{5}\left(x-2\sqrt{5}+\sqrt{3}\right)-35=0\;$を計算しなさい。
この動画を見る
$\left(x+\sqrt{3}+\sqrt{5}\right)^2-3\sqrt{5}\left(x-2\sqrt{5}+\sqrt{3}\right)-35=0\;$を計算しなさい。
方程式の解が一個 函館ラ・サール

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#函館ラ・サール高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
$xの方程式 \ kx^2-6x+1=0の解の個数が1個となるようなkの値を2個求めよ。$
この動画を見る
$xの方程式 \ kx^2-6x+1=0の解の個数が1個となるようなkの値を2個求めよ。$
二次方程式 法政ニ

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#法政大学第二高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
次の方程式を解け
$7(x^2-10x+25)-3=0$
この動画を見る
次の方程式を解け
$7(x^2-10x+25)-3=0$
二次方程式 あなたはどう解く? 東邦大附属東邦

equation : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study
単元:
#数学(中学生)#2次方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$x^2 -2(a+6)x + a^2 + 8a = 0$の解が$x = -3$のみのとき、$a$の値を求めよ。
この動画を見る
$x^2 -2(a+6)x + a^2 + 8a = 0$の解が$x = -3$のみのとき、$a$の値を求めよ。
ごめんなさい

単元:
#数学(中学生)#中3数学#平方根#2次方程式#高校入試過去問(数学)#江戸川学園取手高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
a^2=2+√3
b^2=2+√3
b>a>0
abの値を求めよ
a-bの値を求めよ
この動画を見る
a^2=2+√3
b^2=2+√3
b>a>0
abの値を求めよ
a-bの値を求めよ
気づいた?
X=2 堀川高校

単元:
#数学(中学生)#中2数学#中3数学#2次方程式#1次関数#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=2$が解の1つであるものをすべて選べ
$2x^2+8x-8=0$
$x^3-3x^2+5x-6=0$
$6 \leqq 3x \leqq x+4$
$1+\displaystyle \frac{1}{x}+\displaystyle \frac{1}{x^2}+\displaystyle \frac{1}{x^3} \lt 2$
この動画を見る
$x=2$が解の1つであるものをすべて選べ
$2x^2+8x-8=0$
$x^3-3x^2+5x-6=0$
$6 \leqq 3x \leqq x+4$
$1+\displaystyle \frac{1}{x}+\displaystyle \frac{1}{x^2}+\displaystyle \frac{1}{x^3} \lt 2$
【数学受験組の実力チェック】三平方の定理と二次方程式の解の公式を証明せよ【東大・早稲田・国立志望】

単元:
#数学(中学生)#中3数学#2次方程式#数Ⅰ#2次関数#三平方の定理#2次方程式と2次不等式#数学(高校生)
指導講師:
Morite2 English Channel
問題文全文(内容文):
数学系YouTuberの鈴木貫太郎先生が「三平方の定理」と「二次方程式の解の公式」を証明します。
考え方を学んで、復習の参考にしましょう!
この動画を見る
数学系YouTuberの鈴木貫太郎先生が「三平方の定理」と「二次方程式の解の公式」を証明します。
考え方を学んで、復習の参考にしましょう!
見た目であなたは騙される
連立方程式だけど2次式 清風南海

単元:
#数学(中学生)#中2数学#中3数学#連立方程式#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
以下の連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
(2x^2+4x)-(y^2-4y)=2 \\
(x^2+2x)+(y^2-4y)=-5
\end{array}
\right.
\end{eqnarray}$
出典:清風南海高等学校
この動画を見る
以下の連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
(2x^2+4x)-(y^2-4y)=2 \\
(x^2+2x)+(y^2-4y)=-5
\end{array}
\right.
\end{eqnarray}$
出典:清風南海高等学校
半円の面積🟰❓ (area of semicircle🟰❓)
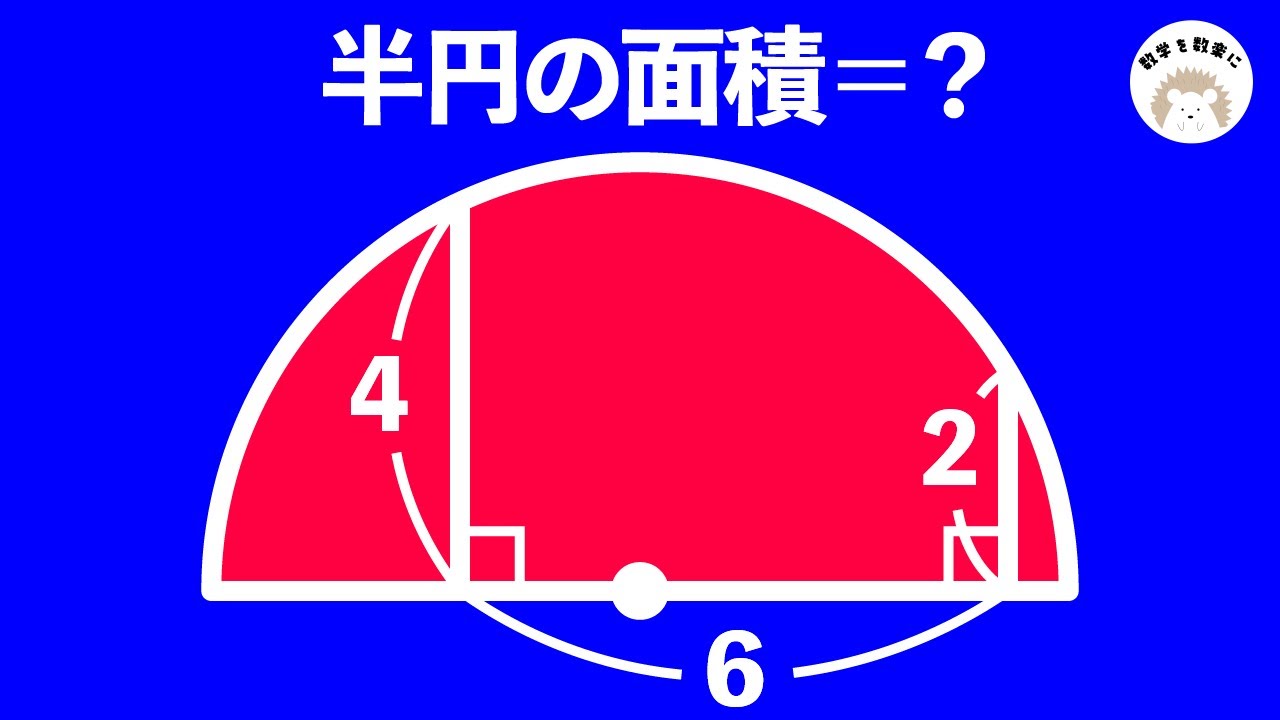
二次方程式 あなたはどっちは派?
【『盾』印 二重…!】解の公式の使い方:二次方程式(その2)~中学からの二次方程式

単元:
#数学(中学生)#中3数学#2次方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x^2+px-(4+2p)=0 $を公式を使って解け.
この動画を見る
$ x^2+px-(4+2p)=0 $を公式を使って解け.
【「勝ち」に必要なら…!】解の公式:二次方程式(その1)~中学からの二次方程式

単元:
#数学(中学生)#中3数学#2次方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x^2+4x-5=0$
解の公式を使って,次の2次方程式を解け.
この動画を見る
$ x^2+4x-5=0$
解の公式を使って,次の2次方程式を解け.
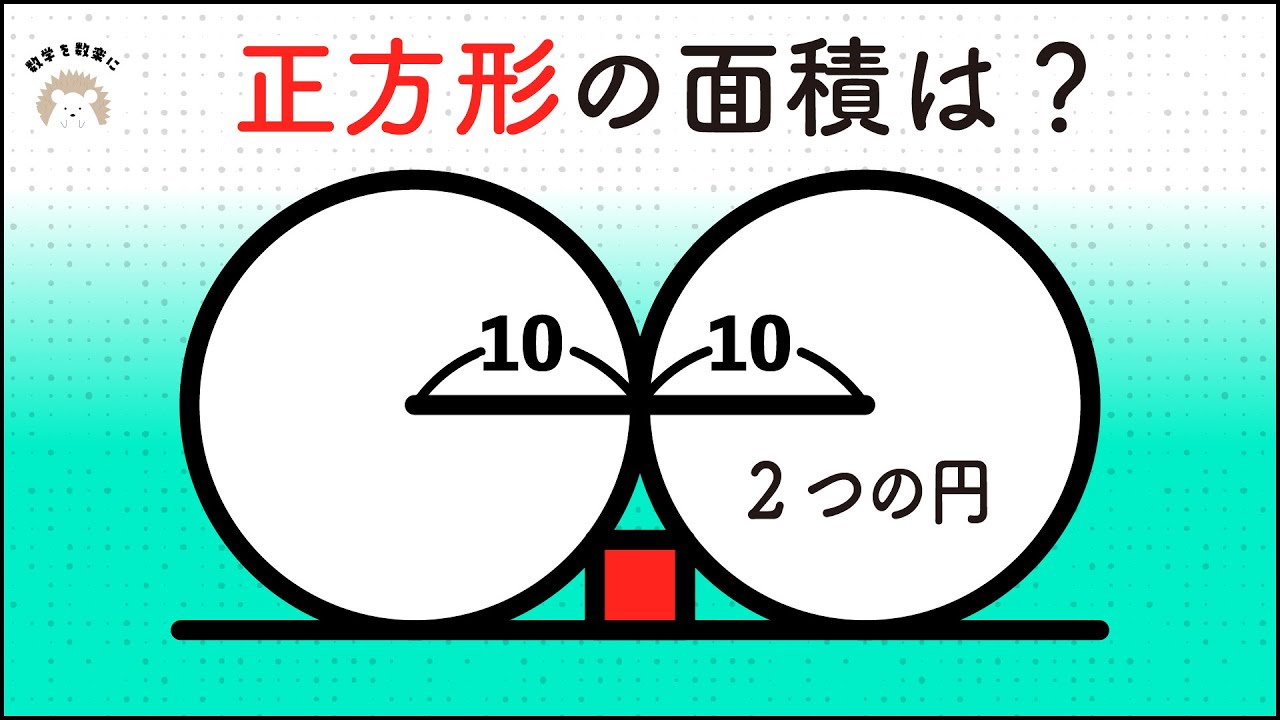
2つの円と正方形
4つの正方形
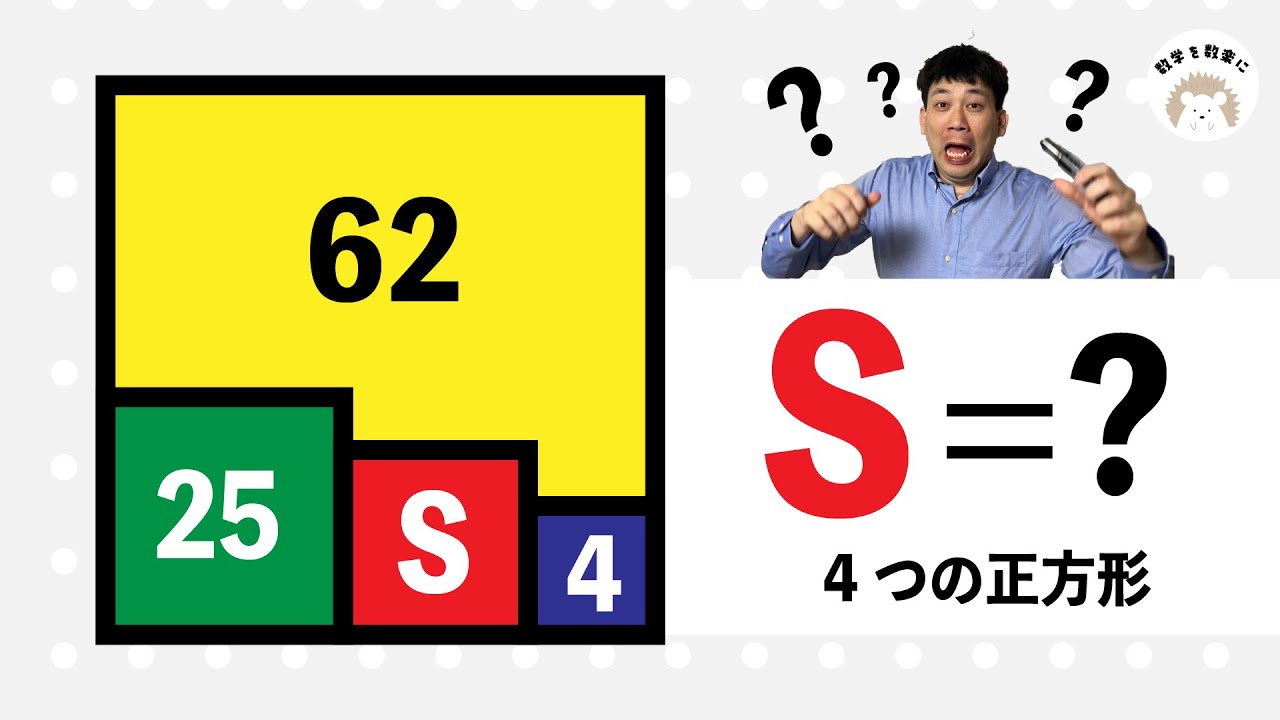
【まず手を付けよう…!】二次方程式:法政大学第二高等学校~全国入試問題解法

単元:
#中3数学#2次方程式#高校入試過去問(数学)#法政大学第二高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2次方程式$ (x+2)^2+x^2=(x+4)^2-12 $を解きなさい.
法政大学第二高等学校過去問
この動画を見る
2次方程式$ (x+2)^2+x^2=(x+4)^2-12 $を解きなさい.
法政大学第二高等学校過去問
【理解すれば一瞬…!】方程式:法政大学国際高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#法政大学国際高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x(x+1)(2x+1)=0 $を満たす$ x $の値をすべて求めよ.
法政大国際高校過去問
この動画を見る
$ x(x+1)(2x+1)=0 $を満たす$ x $の値をすべて求めよ.
法政大国際高校過去問
【ミスしやすい構造とは…!】二次方程式:東京都立八王子東高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#東京都立八王子東高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2次方程式$ 3(3-x)=2(x-2)^2$を解け.
都立八王子東高校過去問
この動画を見る
2次方程式$ 3(3-x)=2(x-2)^2$を解け.
都立八王子東高校過去問
数学とサウンド(二次方程式編)~全国入試問題解法 #shorts #数学 #高校入試 #動体視力 #サウンド

単元:
#数学(中学生)#中3数学#2次方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x^2+ax-8=0 $
$ x=-1 $が1つの解のとき,
ア)$ \color{red}{aの値}$を求めなさい.
イ)$ \color{red}{他の解}$を求めなさい.
岐阜県入試問題過去問
この動画を見る
$ x^2+ax-8=0 $
$ x=-1 $が1つの解のとき,
ア)$ \color{red}{aの値}$を求めなさい.
イ)$ \color{red}{他の解}$を求めなさい.
岐阜県入試問題過去問
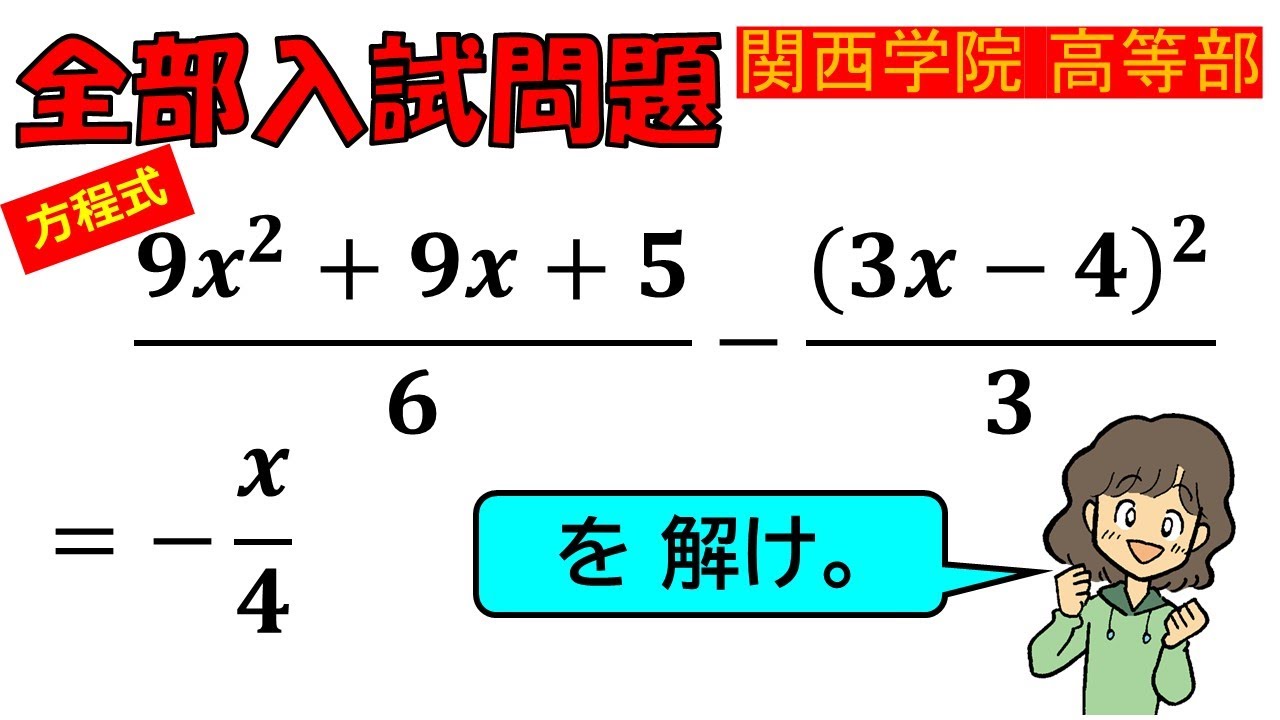
【見た目より難しい…!】二次方程式:関西学院高等部~全国入試問題解法
単元:
#数学(中学生)#中3数学#2次方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
方程式$ \dfrac{9x^2+9x+5}{6}-\dfrac{(3x-4)^2}{3}=-\dfrac{x}{4}$ を解け.
関西学院高等学校過去問
この動画を見る
方程式$ \dfrac{9x^2+9x+5}{6}-\dfrac{(3x-4)^2}{3}=-\dfrac{x}{4}$ を解け.
関西学院高等学校過去問
【知識を活用…!】二次方程式:巣鴨高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#巣鴨高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
同じ正の解をもつ3つの2次方程式
$ x^2+ax+b=0 $
$ 2x^2+3ax+4b=0 $
$ x^2-2x-3=0 $
定数$ a,b $の値を求めなさい.
巣鴨高校過去問
この動画を見る
同じ正の解をもつ3つの2次方程式
$ x^2+ax+b=0 $
$ 2x^2+3ax+4b=0 $
$ x^2-2x-3=0 $
定数$ a,b $の値を求めなさい.
巣鴨高校過去問
