 中3数学
中3数学
 中3数学
中3数学
【数学】中高一貫校用問題集幾何:三平方の定理:平面図形 合同の利用

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図において、四角形の頂点A,B,C,DはBDを直径とする円Oの周上にあり、Eは直線BAとCDの交点で、辺DAは∠BDEを2等分している。DC=3cm、BD=6cmであるとき、辺DAの長さを求めなさい。
この動画を見る
右の図において、四角形の頂点A,B,C,DはBDを直径とする円Oの周上にあり、Eは直線BAとCDの交点で、辺DAは∠BDEを2等分している。DC=3cm、BD=6cmであるとき、辺DAの長さを求めなさい。
よくある円のパターン 〇〇をみつけろ! 灘高校
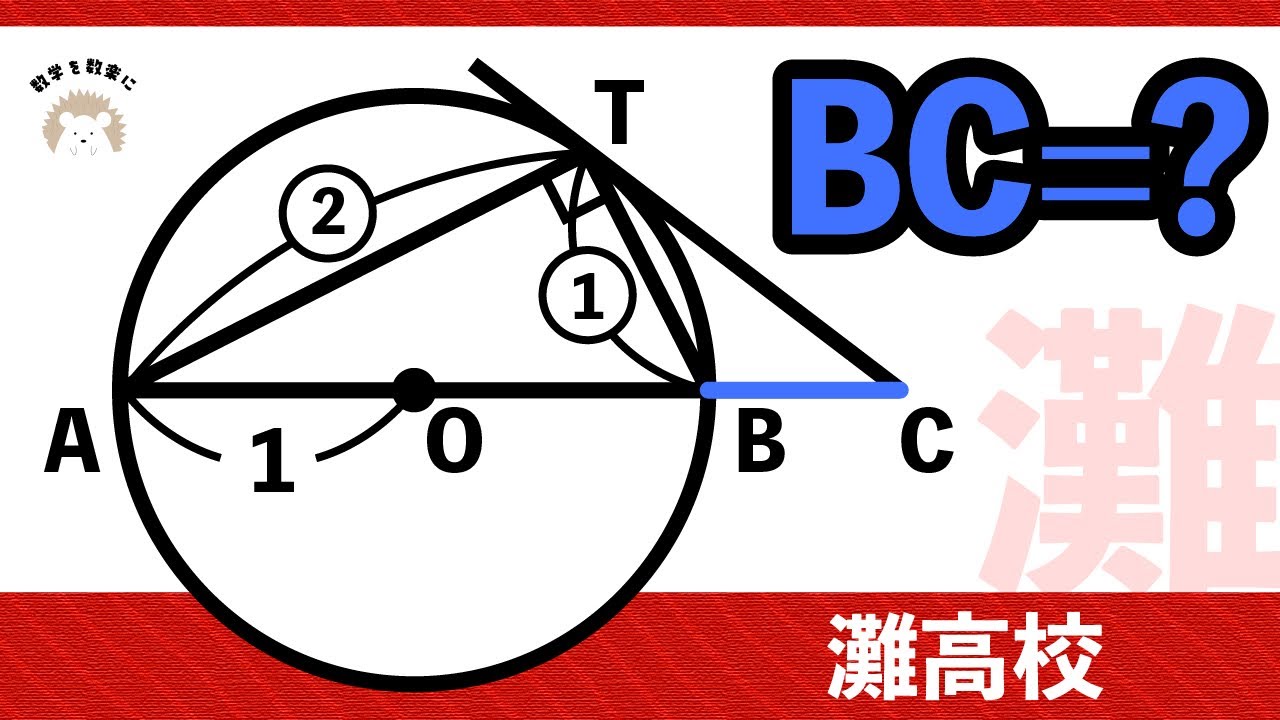
よくある円のパターン 〇〇をみつけろ! 灘高校

4つの正方形
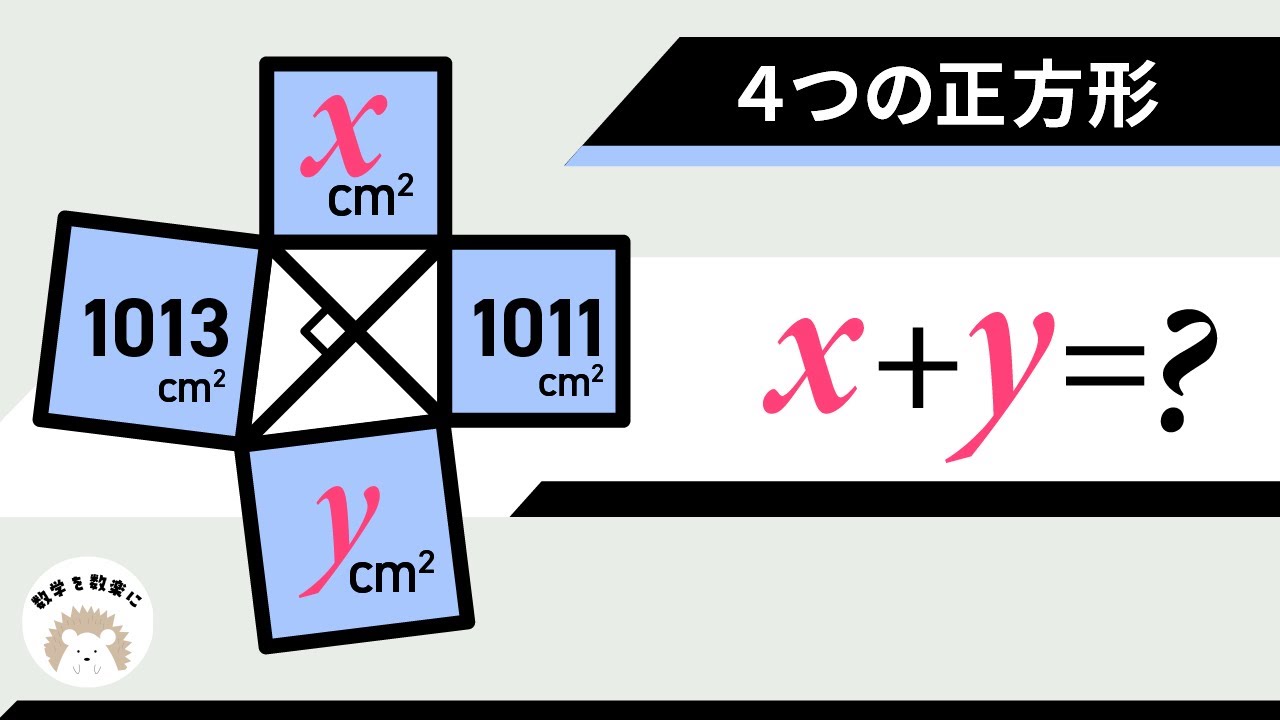
4つの正方形

4つの正方形

気づいた?
気づいた?
正方形の折り返し 大分東明
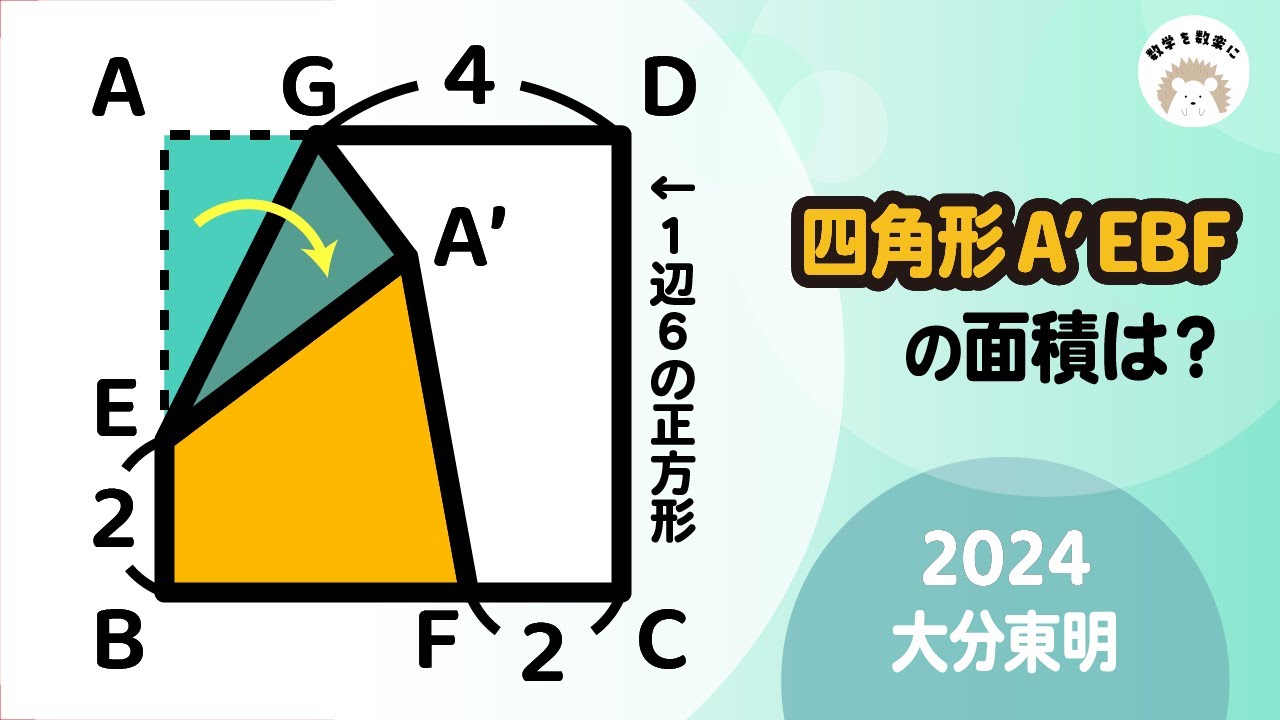
正方形の折り返し 大分東明

【数学】中高一貫校用問題集幾何:三平方の定理:平面図形 折り返した図形2

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図は、1辺の長さが9cmの正方形ABCDを、頂点Aが辺DC上の点Eに重なるように折り返したもので、PQは折り目の線である。
DE=3cmであるとき、次の問いに答えなさい。
(1)線分APの長さを求めなさい。
(2)線分BQの長さを求めなさい。
この動画を見る
右の図は、1辺の長さが9cmの正方形ABCDを、頂点Aが辺DC上の点Eに重なるように折り返したもので、PQは折り目の線である。
DE=3cmであるとき、次の問いに答えなさい。
(1)線分APの長さを求めなさい。
(2)線分BQの長さを求めなさい。
2024 渋谷幕張 因数分解

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#渋谷教育学園幕張高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
以下を因数分解せよ。
$x^3-xy^2+2xy-x^2+y^2-x-2y+1$
出典:2024渋谷教育学園幕張中学校
この動画を見る
以下を因数分解せよ。
$x^3-xy^2+2xy-x^2+y^2-x-2y+1$
出典:2024渋谷教育学園幕張中学校
【数学】中高一貫校用問題集幾何:三平方の定理:平面図形 折り返した図形1

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図のように、円A,B,Cは縦4cm,横6cmの長方形の辺に接し、円AとCおよび円BとCはそれぞれ外接している。円A,Bの半径がともに1cmであるとき、円Cの半径を求めなさい。
この動画を見る
右の図のように、円A,B,Cは縦4cm,横6cmの長方形の辺に接し、円AとCおよび円BとCはそれぞれ外接している。円A,Bの半径がともに1cmであるとき、円Cの半径を求めなさい。
square root : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study

単元:
#数学(中学生)#中3数学#平方根
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
square root : Shirotan's cute kawaii math show
$\displaystyle \frac{(\sqrt{ 14 }-\sqrt{ 6 })(\sqrt{ 7}+\sqrt{ 3 } )}{2}-(\sqrt{ 2 }+1)^2=?$
を計算せよ。
この動画を見る
square root : Shirotan's cute kawaii math show
$\displaystyle \frac{(\sqrt{ 14 }-\sqrt{ 6 })(\sqrt{ 7}+\sqrt{ 3 } )}{2}-(\sqrt{ 2 }+1)^2=?$
を計算せよ。
福田のおもしろ数学181〜連続する4つの自然数の積は平方数にならないことの証明

X=2 堀川高校

単元:
#数学(中学生)#中2数学#中3数学#2次方程式#1次関数#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=2$が解の1つであるものをすべて選べ
$2x^2+8x-8=0$
$x^3-3x^2+5x-6=0$
$6 \leqq 3x \leqq x+4$
$1+\displaystyle \frac{1}{x}+\displaystyle \frac{1}{x^2}+\displaystyle \frac{1}{x^3} \lt 2$
この動画を見る
$x=2$が解の1つであるものをすべて選べ
$2x^2+8x-8=0$
$x^3-3x^2+5x-6=0$
$6 \leqq 3x \leqq x+4$
$1+\displaystyle \frac{1}{x}+\displaystyle \frac{1}{x^2}+\displaystyle \frac{1}{x^3} \lt 2$
中央大杉並 因数分解

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#中央大学杉並高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
以下を因数分解せよ。
$-\displaystyle \frac{1}{2}x^2+2x+48$
出典:中央大学杉並高等学校
この動画を見る
以下を因数分解せよ。
$-\displaystyle \frac{1}{2}x^2+2x+48$
出典:中央大学杉並高等学校
【数学】中高一貫校問題集 幾何:三平方の定理:平面図形 内接円の半径2

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
3辺の長さがAB=7cm,BC=8cm,CA=9cmの△ABCがあり、円Oは△ABCに内接している。
(1)Aから辺BCに引いた垂線の長さを求めなさい。
(2)円Oの半径を求めなさい。
この動画を見る
3辺の長さがAB=7cm,BC=8cm,CA=9cmの△ABCがあり、円Oは△ABCに内接している。
(1)Aから辺BCに引いた垂線の長さを求めなさい。
(2)円Oの半径を求めなさい。
今だから伸びる数学!~全国入試問題解法 #数学 #数検 #歌ってみた #弾き語り #中間テスト #勉強

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
今だから伸びる数学!
定数$a,b$の値を求めよ。
$\displaystyle \frac{1}{6}x^2-ax-18$
を因数分解すると、
$\displaystyle \frac{1}{6}(x-12)(x+ℓ)$となる。
この動画を見る
今だから伸びる数学!
定数$a,b$の値を求めよ。
$\displaystyle \frac{1}{6}x^2-ax-18$
を因数分解すると、
$\displaystyle \frac{1}{6}(x-12)(x+ℓ)$となる。
式の値 西大和学園 2024
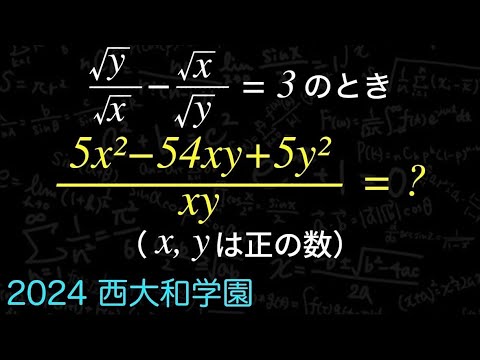
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#西大和学園高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
$\displaystyle \frac{\sqrt{ y }}{\sqrt{ x }}-\displaystyle \frac{\sqrt{ x }}{\sqrt{ y }}=3$のとき
$\displaystyle \frac{5x^2-54xy+5y^2 }{xy}=??$
($x,y$は正の数)
出典:西大和学園中学校・高等学校 2024
この動画を見る
$\displaystyle \frac{\sqrt{ y }}{\sqrt{ x }}-\displaystyle \frac{\sqrt{ x }}{\sqrt{ y }}=3$のとき
$\displaystyle \frac{5x^2-54xy+5y^2 }{xy}=??$
($x,y$は正の数)
出典:西大和学園中学校・高等学校 2024
【数学受験組の実力チェック】三平方の定理と二次方程式の解の公式を証明せよ【東大・早稲田・国立志望】

単元:
#数学(中学生)#中3数学#2次方程式#数Ⅰ#2次関数#三平方の定理#2次方程式と2次不等式#数学(高校生)
指導講師:
Morite2 English Channel
問題文全文(内容文):
数学系YouTuberの鈴木貫太郎先生が「三平方の定理」と「二次方程式の解の公式」を証明します。
考え方を学んで、復習の参考にしましょう!
この動画を見る
数学系YouTuberの鈴木貫太郎先生が「三平方の定理」と「二次方程式の解の公式」を証明します。
考え方を学んで、復習の参考にしましょう!
明るい気分で数学の流れ!~全国入試問題解法 #数学 #数検 #歌ってみた #点数 #弾き語り

単元:
#数学(中学生)#中3数学#平方根
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
明るい気分で数学の流れ!
$\sqrt{ 2023 \times 2021 - 4044 + 2 }=?$
の値を求めよ。
この動画を見る
明るい気分で数学の流れ!
$\sqrt{ 2023 \times 2021 - 4044 + 2 }=?$
の値を求めよ。
福田のおもしろ数学177〜長さ1.5メートルの剣を列車に積み込む方法

単元:
#数学(中学生)#中3数学#三平方の定理
指導講師:
福田次郎
問題文全文(内容文):
あなたは1.5 mの剣を列車に持ち込もうとしましたが車掌に拒否されました。
一辺の最大の寸法が1 mを超すものは持ち込めません。
あなたはどうする?
この動画を見る
あなたは1.5 mの剣を列車に持ち込もうとしましたが車掌に拒否されました。
一辺の最大の寸法が1 mを超すものは持ち込めません。
あなたはどうする?
普通に解いても解けるかもしれないけどさ。。

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
数学を数楽に
問題文全文(内容文):
以下の■を求めよ。(■は整数)
$30^3+40^3+50^3=■^3$
この動画を見る
以下の■を求めよ。(■は整数)
$30^3+40^3+50^3=■^3$
数学を数楽にする計算
【数学】中高一貫校問題集 幾何:三平方の定理:平面図形 内接円の半径

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図において、円Oは∠A=90°の直角三角形ABCに内接している。このとき、内接円Oの半径を求めなさい。
この動画を見る
右の図において、円Oは∠A=90°の直角三角形ABCに内接している。このとき、内接円Oの半径を求めなさい。
2024開成高校最初の1問

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#開成高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
動画内の図を参照し、$Z$の座標を求めなさい。
出典:2024開成高等学校
この動画を見る
動画内の図を参照し、$Z$の座標を求めなさい。
出典:2024開成高等学校
ミスする人が多い因数分解

【数学】中高一貫校問題集2幾何179:三平方の定理:平面図形 外接円の半径

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の△ABCについて、外接円の半径を求めなさい。
この動画を見る
次の△ABCについて、外接円の半径を求めなさい。
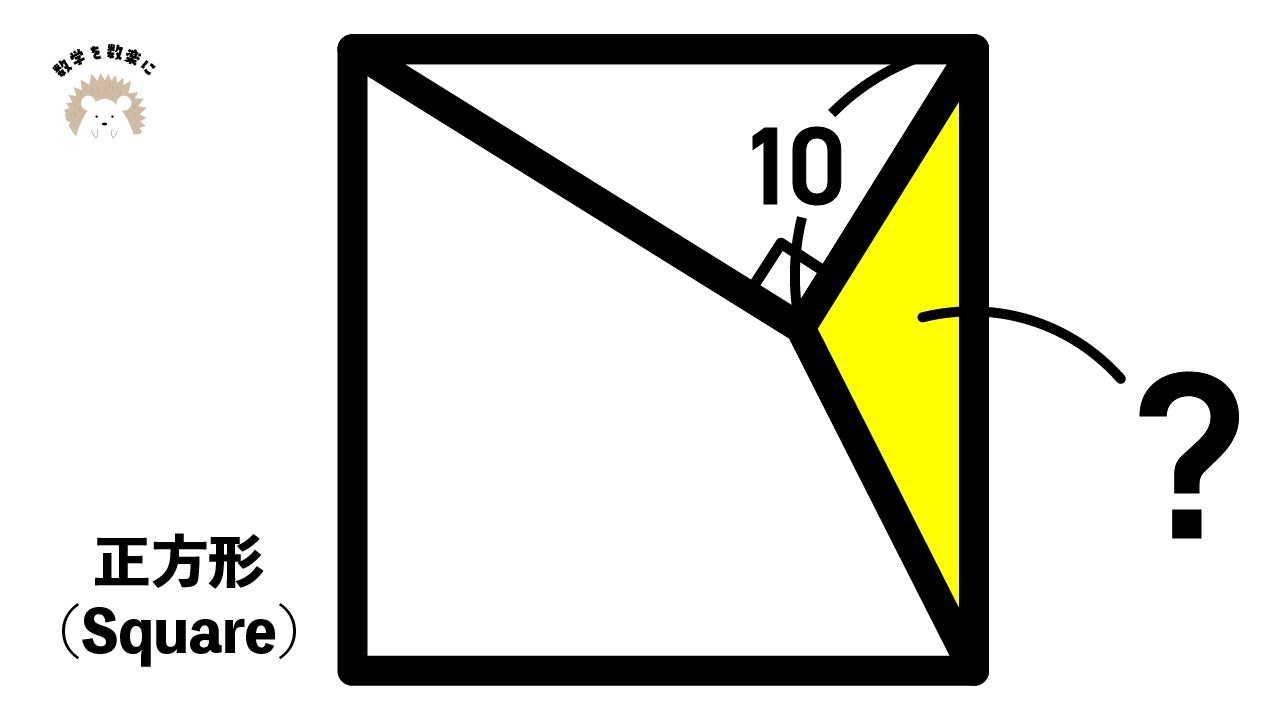
気付けば爽快!!正方形(square)
単元:
#数学(中学生)#中2数学#平行と合同#相似な図形#三角形と四角形
指導講師:
数学を数楽に
問題文全文(内容文):
動画の四角形において、その中にある$\triangle \rm{CDE}$を求めよ。
この動画を見る
動画の四角形において、その中にある$\triangle \rm{CDE}$を求めよ。
