 中3数学
中3数学
 中3数学
中3数学
【2つの解法!2分で?4分30秒で?】二次関数:宮城県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
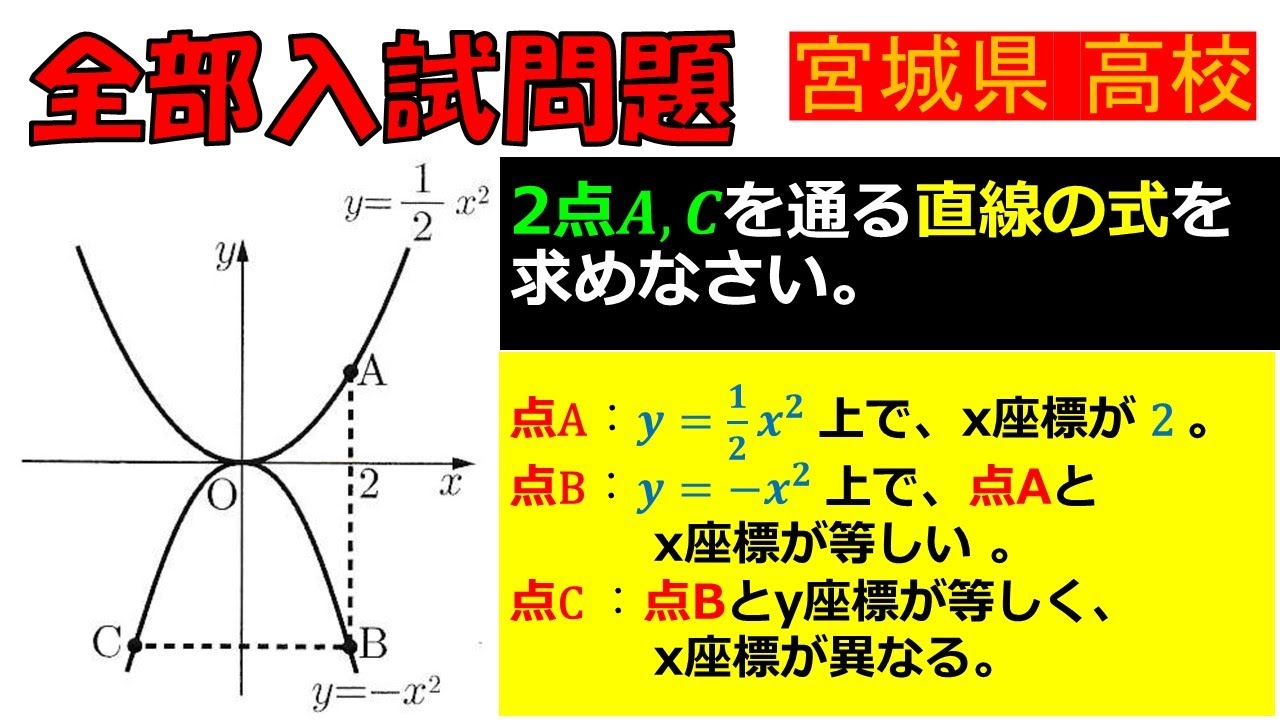
2点$A,C$を通る直線の式を求めなさい.
宮城県高校過去問
この動画を見る
2点$A,C$を通る直線の式を求めなさい.
宮城県高校過去問
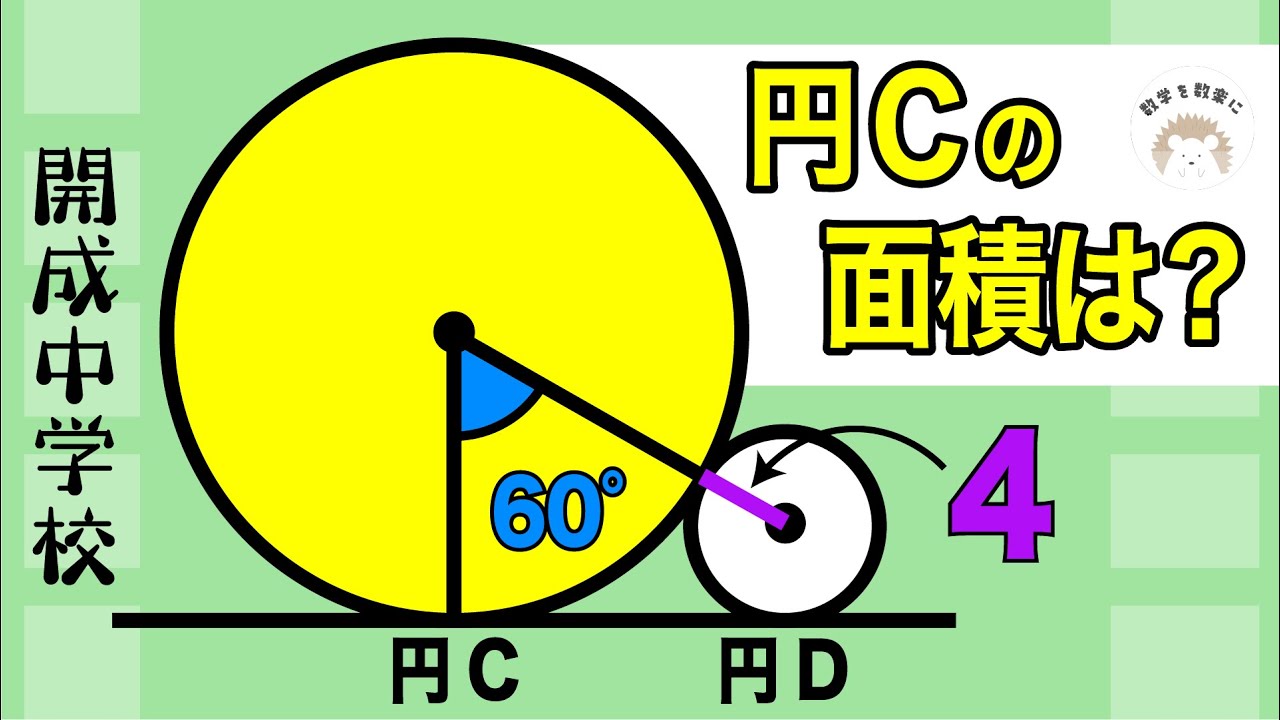
中学入試でも二つの円!!開成中
二次方程式

単元:
#数学(中学生)#中3数学#2次方程式#数Ⅰ#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\dfrac{1}{2}x^2-4×10×82×6562=\dfrac{1}{2}$
この動画を見る
これを解け.
$\dfrac{1}{2}x^2-4×10×82×6562=\dfrac{1}{2}$
【さらに学べば見方も変わる!】二次方程式:成蹊高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
方程式$ 3\left(x-\dfrac{1}{2}\right)^2=3x+\dfrac{7}{4}$を解け.
成蹊高校過去問
この動画を見る
方程式$ 3\left(x-\dfrac{1}{2}\right)^2=3x+\dfrac{7}{4}$を解け.
成蹊高校過去問
眠れない夜に学ぶ数学~全国入試問題解法 #shorts #数学 #sound

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x-\dfrac{\sqrt2-2}{2}$のとき,$x^2+2x+\dfrac{1}{x+1}+1$の値を求めなさい.
立命館高校過去問
この動画を見る
$ x-\dfrac{\sqrt2-2}{2}$のとき,$x^2+2x+\dfrac{1}{x+1}+1$の値を求めなさい.
立命館高校過去問
【よく出題される形式!4問分の解説】平方根:群馬県公立高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
数について述べた次のア~エのうち,正しいものをすべて選びなさい.
ア すべての自然数は,その逆数も自然数となる.
イ 異なる2つの整数について,大きい方から小さい方をひいた差は,いつでも自然数となる.
ウ すべての2次方程式の解は,無理数となる.
エ すべての有理数や無理数は,数直線上に対応する点がある.
群馬県高校過去問
この動画を見る
数について述べた次のア~エのうち,正しいものをすべて選びなさい.
ア すべての自然数は,その逆数も自然数となる.
イ 異なる2つの整数について,大きい方から小さい方をひいた差は,いつでも自然数となる.
ウ すべての2次方程式の解は,無理数となる.
エ すべての有理数や無理数は,数直線上に対応する点がある.
群馬県高校過去問
x=❓
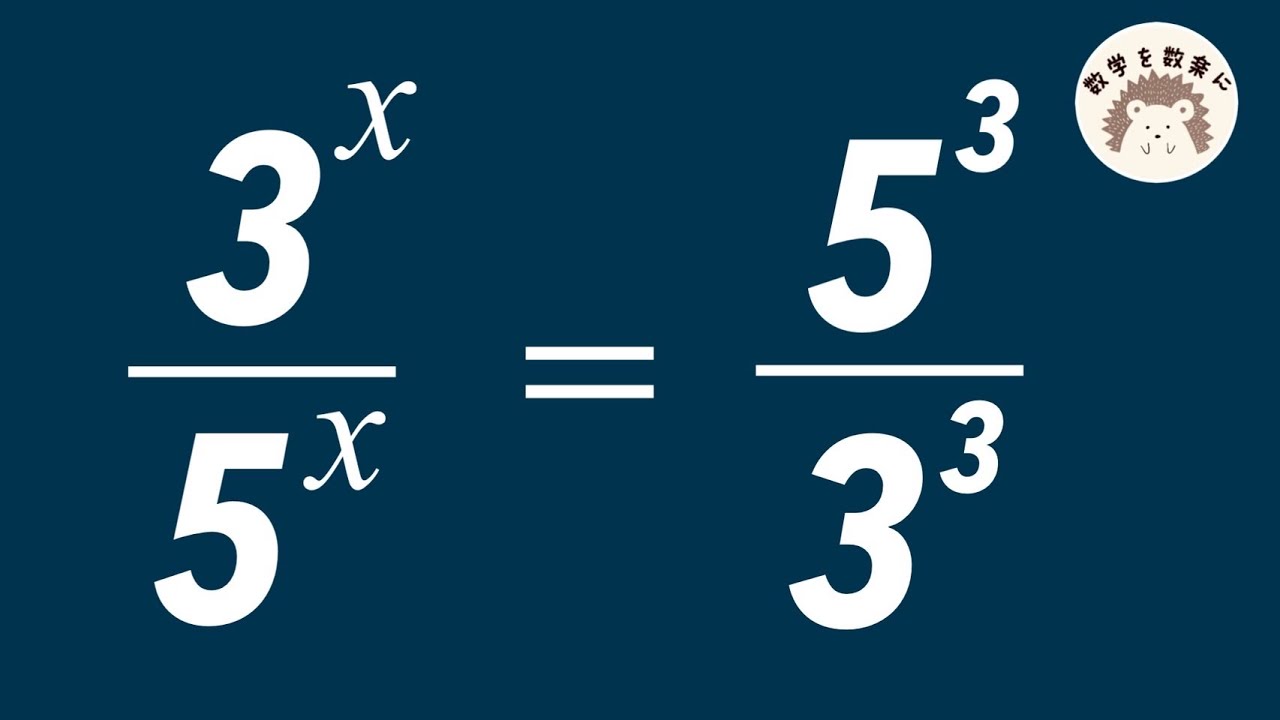
【数学】有理化がなぜ必要なのか?解説してみた!

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
有理化って何のためにしてるか知っていますか??
この動画を見る
有理化って何のためにしてるか知っていますか??
【中学生のひらめき!】因数分解:中央大学杉並高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
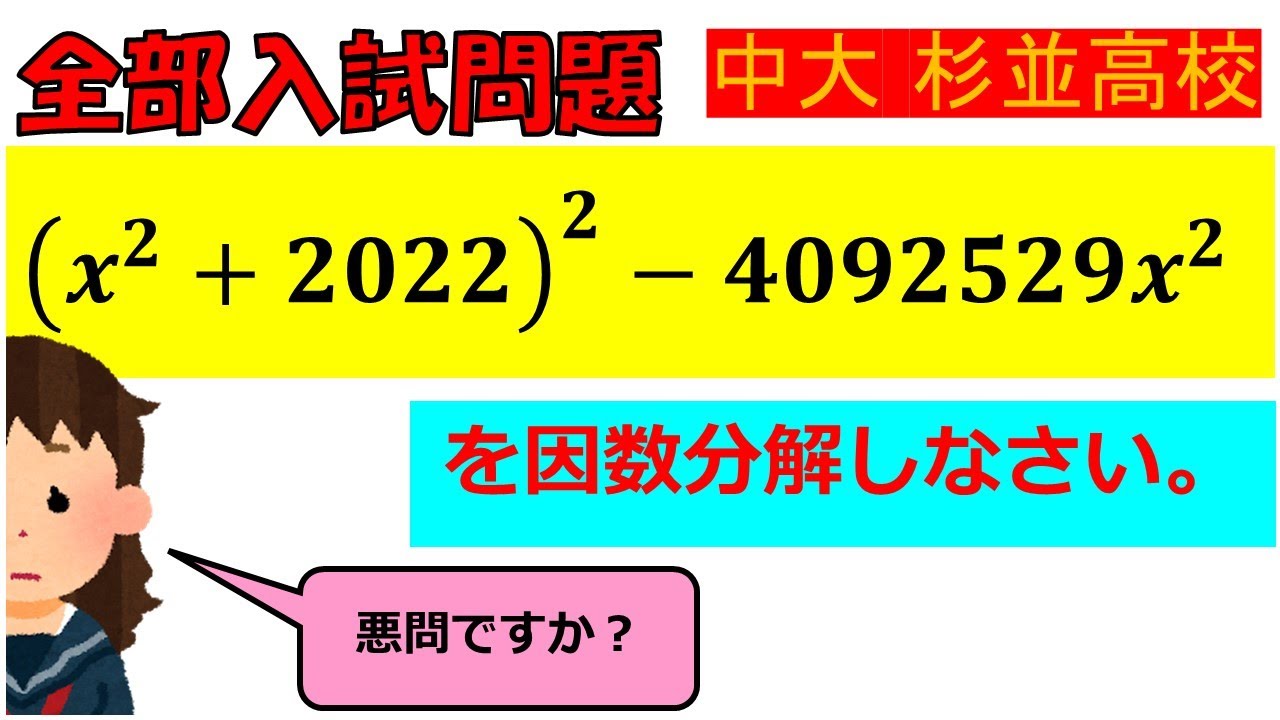
$ (x^2+2022)^2-4092529x^2$を因数分解しなさい.
中大杉並高校過去問
この動画を見る
$ (x^2+2022)^2-4092529x^2$を因数分解しなさい.
中大杉並高校過去問
気付けば一瞬!!式の値
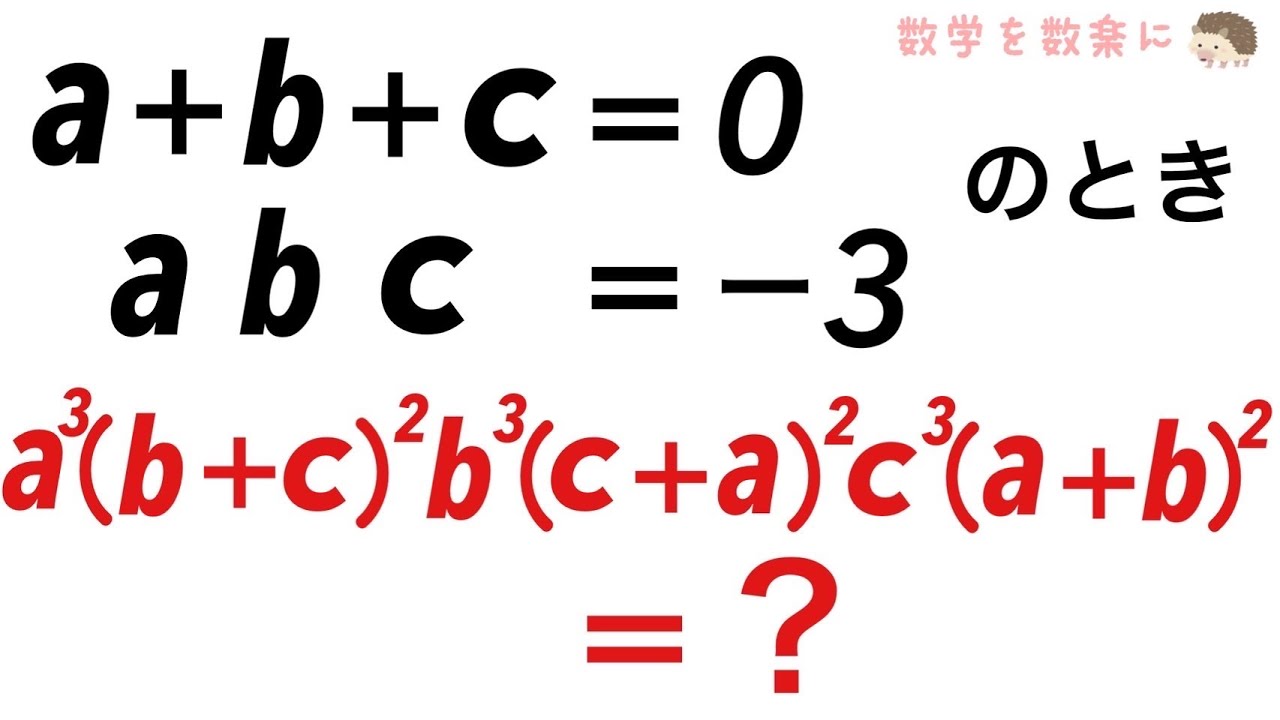
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
数学を数楽に
問題文全文(内容文):
\begin{eqnarray}
\left\{
\begin{array}{l}
a+b+c=0 \\
abc=-3
\end{array}
\right.
\end{eqnarray}
のとき
$a^3(b+c)^2b^3(c+a)^2c^3(a+b)^2=?$
この動画を見る
\begin{eqnarray}
\left\{
\begin{array}{l}
a+b+c=0 \\
abc=-3
\end{array}
\right.
\end{eqnarray}
のとき
$a^3(b+c)^2b^3(c+a)^2c^3(a+b)^2=?$
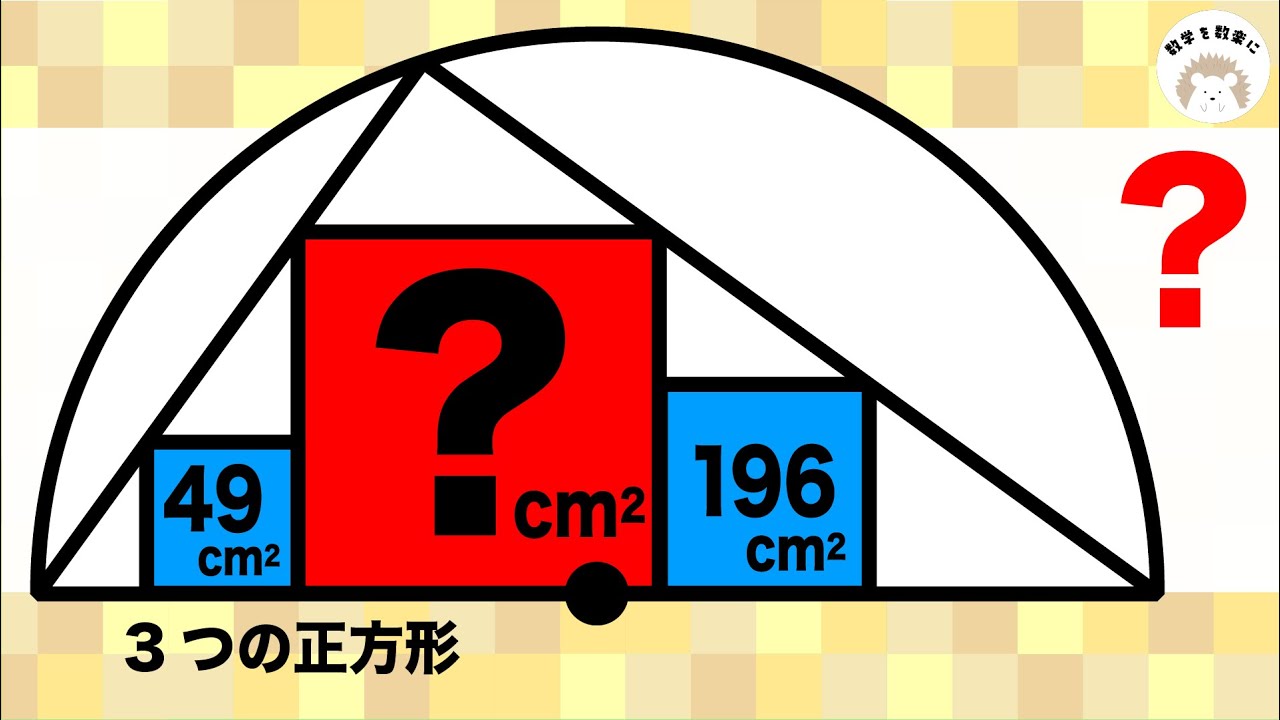
半円と正方形
音楽と数学が共に生きる二次方程式~全国入試問題解法 #shorts #数学 #高校受験

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2次方程式$ ax^2+2x+b=0$の解が$x=2$のただ一つである.
定数$a,b$の値をそれぞれ求めなさい.
立命館高校過去問
この動画を見る
2次方程式$ ax^2+2x+b=0$の解が$x=2$のただ一つである.
定数$a,b$の値をそれぞれ求めなさい.
立命館高校過去問
通分せよ!渋谷教育学園幕張

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
次の?に当てはまる式を求めよ。
$\frac{a+2}{a+1} -\frac{a+3}{a+2} +\frac{a+4}{a+3} - \frac{a+5}{a+4}
= \frac{?}{(a+1)(a+2)(a+3)(a+4)}$
渋谷教育学園幕張高等学校
この動画を見る
次の?に当てはまる式を求めよ。
$\frac{a+2}{a+1} -\frac{a+3}{a+2} +\frac{a+4}{a+3} - \frac{a+5}{a+4}
= \frac{?}{(a+1)(a+2)(a+3)(a+4)}$
渋谷教育学園幕張高等学校
【得意分野にしよう!】図形:福岡大学附属大濠高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#中3数学#円#三角形と四角形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
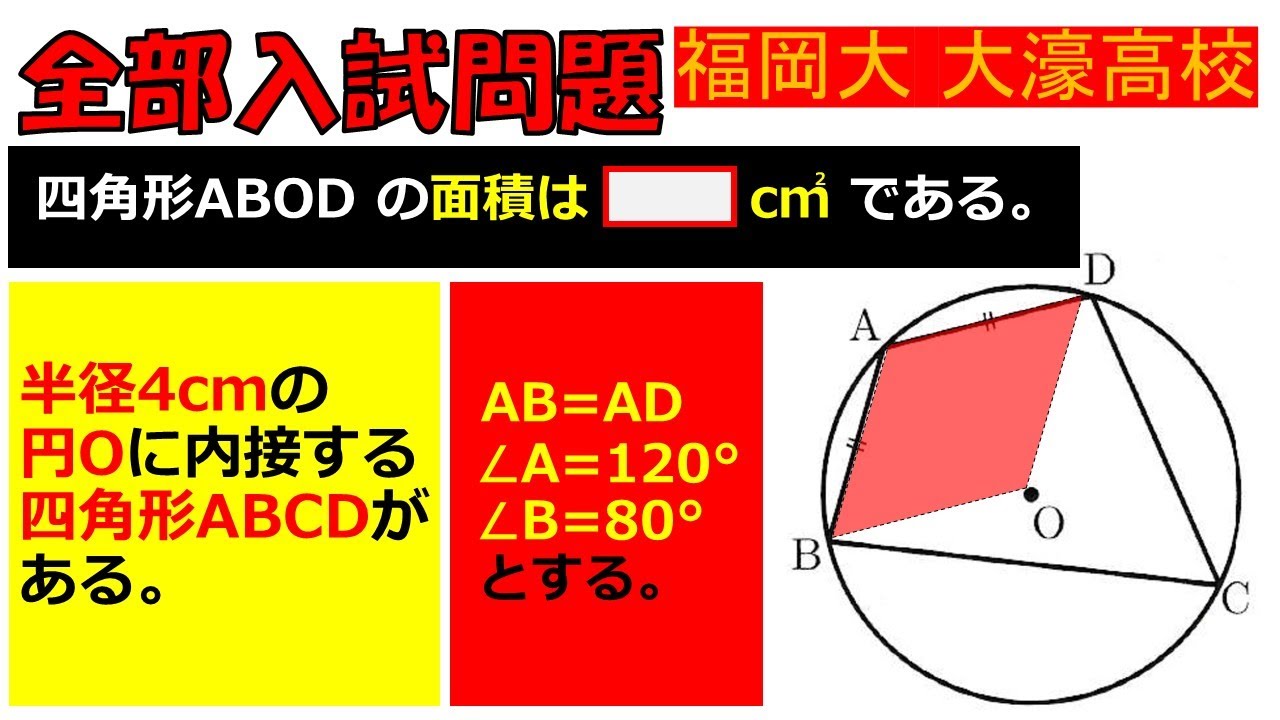
半径4cmの円$O$に内接する四角形$ABCD$がある.
$AB=AD,\angle A=120°,\angle B=80°$とする.
四角形$ABCD$の面積は$\Box cm^2$である.
福岡大学附属大濠高等学校過去問
この動画を見る
半径4cmの円$O$に内接する四角形$ABCD$がある.
$AB=AD,\angle A=120°,\angle B=80°$とする.
四角形$ABCD$の面積は$\Box cm^2$である.
福岡大学附属大濠高等学校過去問
いきなり代入すると地獄

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
数学を数楽に
問題文全文(内容文):
$a=\frac{1}{5}$のとき
$\frac{10}{a} + \frac{10}{a^3} + \frac{10}{a^5}+\frac{10}{a^7}$の値は
$\frac{1}{a^2} + \frac{1}{a^4} + \frac{1}{a^6} + \frac{1}{a^8}$の値の何倍か?
函館ラ・サール高等学校
この動画を見る
$a=\frac{1}{5}$のとき
$\frac{10}{a} + \frac{10}{a^3} + \frac{10}{a^5}+\frac{10}{a^7}$の値は
$\frac{1}{a^2} + \frac{1}{a^4} + \frac{1}{a^6} + \frac{1}{a^8}$の値の何倍か?
函館ラ・サール高等学校
【まず流れを理解しよう!】二次方程式:慶応義塾志木高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x^2-(4t-1)x+4t^2-2t=0$の2解を$\alpha,\beta$とする.
3辺の長さが,$5,\alpha,\beta$である三角形が直角三角形である.
$t$の値を求めよ.
慶応義塾志木高等学校過去問
この動画を見る
$ x^2-(4t-1)x+4t^2-2t=0$の2解を$\alpha,\beta$とする.
3辺の長さが,$5,\alpha,\beta$である三角形が直角三角形である.
$t$の値を求めよ.
慶応義塾志木高等学校過去問
解の公式って他にもありますか?

難しそうでいて簡単にできそうだけどやっぱり難しい数学~全国入試問題解法 #Shorts #数学 #sound #高校受験

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ (x+1)(x+2)(x+3)(x+4)=x^4+10x^3+9$を解け.
この動画を見る
$ (x+1)(x+2)(x+3)(x+4)=x^4+10x^3+9$を解け.
高校入試としては難問です!因数分解 甲陽学院

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$(x^2-1)(y^2-1)-4xy$
甲陽学院高等学校
この動画を見る
因数分解せよ
$(x^2-1)(y^2-1)-4xy$
甲陽学院高等学校
【見慣れないから出題される!】方程式:明治学院高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
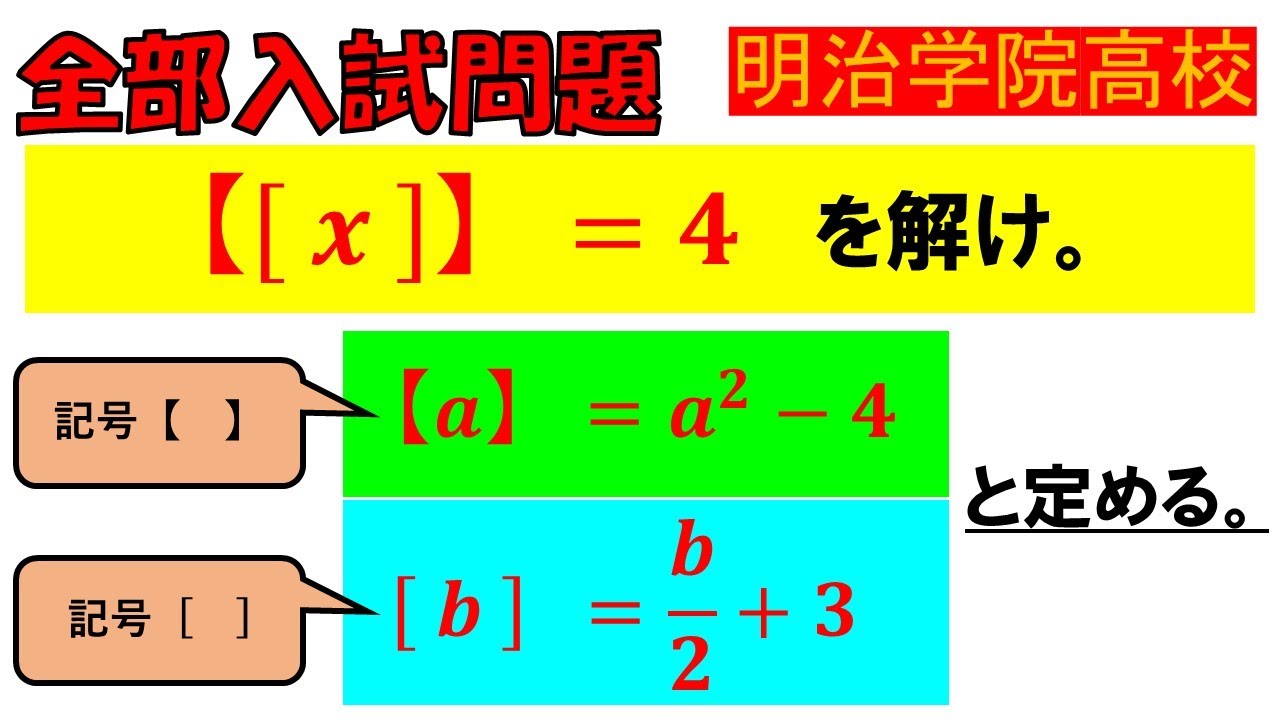
$【[a]】=a^2-4$,$[b]=\dfrac{b}{2}+3$と定める.
$【[x]】=4$を解け.
明治学院高校過去問
この動画を見る
$【[a]】=a^2-4$,$[b]=\dfrac{b}{2}+3$と定める.
$【[x]】=4$を解け.
明治学院高校過去問
【比べてみれば!】因数分解:明治学院高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \dfrac{1}{6}x^2-ax-18$を因数分解すると$\dfrac{1}{6}(x-12)(x+b)$となる.
$a,b$の値を求めよ.
明治学院高校過去問
この動画を見る
$ \dfrac{1}{6}x^2-ax-18$を因数分解すると$\dfrac{1}{6}(x-12)(x+b)$となる.
$a,b$の値を求めよ.
明治学院高校過去問
2つの半円
【中学数学】三角形の相似をどこよりも丁寧に~相似条件~ 5-1【中3数学】

【短時間でマスター!!】2次関数のグラフの書き方を解説!〔現役塾講師解説、数学〕

単元:
#数学(中学生)#中3数学#数Ⅰ#2次関数#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
数学1A
2次関数のグラフの書き方を解説します。
$y=x^2+2x-1$
①$-3≦x≦0$
②$0≦x≦2$の最大・最小
この動画を見る
数学1A
2次関数のグラフの書き方を解説します。
$y=x^2+2x-1$
①$-3≦x≦0$
②$0≦x≦2$の最大・最小
【短時間で各パターン解説!!】2次関数の変域の基礎を現役塾講師が簡単に解説!〔現役塾講師解説、数学〕

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
3rd School
問題文全文(内容文):
中学3年生 数学
二次関数の変域
$y=2x^2$について、$1≦x≦5$のとき$y$の変域は?
$y=x^2$について、$-3≦x≦2$のとき$y$の変域は?
$y=-2x^2$について、$-4≦x≦2$のとき$y$の変域は?
この動画を見る
中学3年生 数学
二次関数の変域
$y=2x^2$について、$1≦x≦5$のとき$y$の変域は?
$y=x^2$について、$-3≦x≦2$のとき$y$の変域は?
$y=-2x^2$について、$-4≦x≦2$のとき$y$の変域は?
【解を代入しても式は1つだけ…!】二次方程式:立命館高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2次方程式$ax^2+2x+b=0$の解が$x=2$のただ1つである.
定数$a,b$の値をそれぞれ求めなさい.
立命館高校過去問
この動画を見る
2次方程式$ax^2+2x+b=0$の解が$x=2$のただ1つである.
定数$a,b$の値をそれぞれ求めなさい.
立命館高校過去問
【中学数学】2次関数の変化の割合~どこよりも丁寧に~ 4-3【中3数学】

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
2次関数の変化の割合
(例題1)$y=2x^2$でxの値が1から5まで増加するときの変化の割合を求めよ。
(例題2)$y=2x^2$でxの値が-1から2まで増加するときの変化の割合を求めよ。
この動画を見る
2次関数の変化の割合
(例題1)$y=2x^2$でxの値が1から5まで増加するときの変化の割合を求めよ。
(例題2)$y=2x^2$でxの値が-1から2まで増加するときの変化の割合を求めよ。
式の値 西大和学園
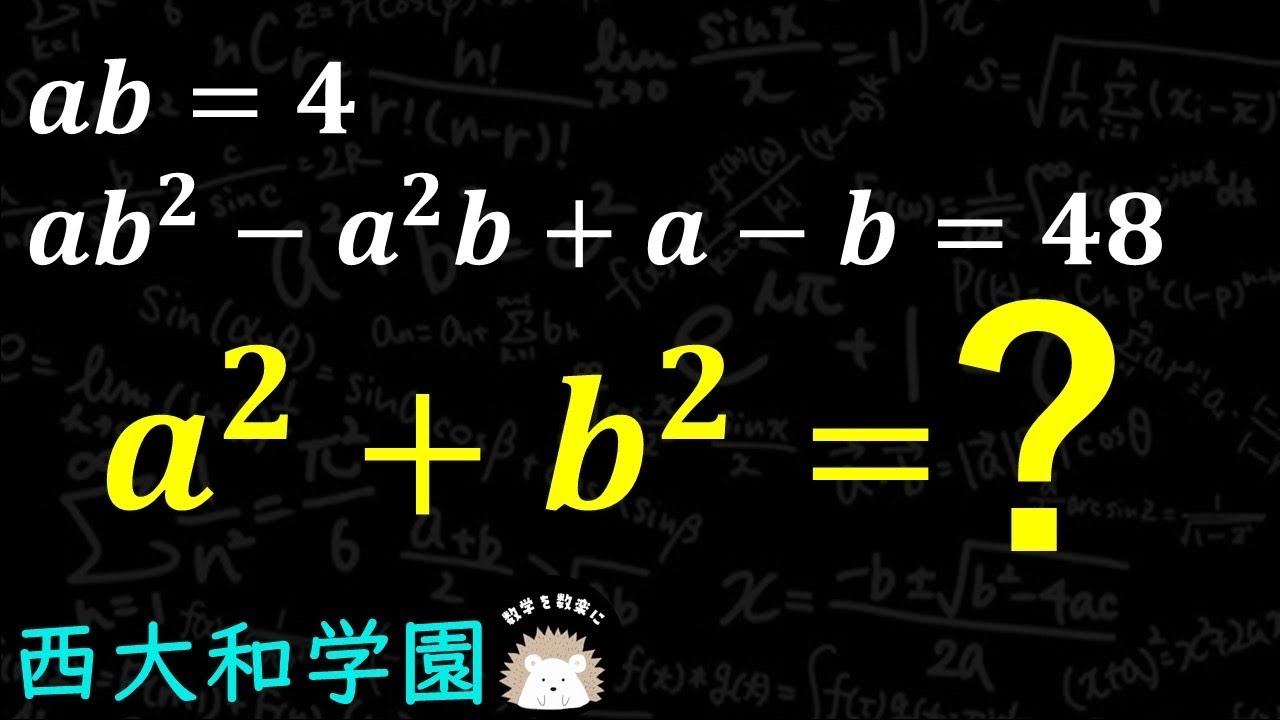
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$ab=4$
$ab^2-a^2b+a-b=48$
$a^2+b^2 = ?$
西大和学園高等学校
この動画を見る
$ab=4$
$ab^2-a^2b+a-b=48$
$a^2+b^2 = ?$
西大和学園高等学校
30秒でまとめた高校入試の必出問題!~全国入試問題解法 #Shorts #sound #mathematics #数学

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
(1)$y-\dfrac{1}{4}x^2$について,$A→B:$変化の割合は?
(2)直線$CD$の式は?
この動画を見る
(1)$y-\dfrac{1}{4}x^2$について,$A→B:$変化の割合は?
(2)直線$CD$の式は?
2通りで解説!!良問 玉川学園

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$(x+3)(x^2-x-6)(x-2)$を展開せよ
玉川学園
この動画を見る
$(x+3)(x^2-x-6)(x-2)$を展開せよ
玉川学園
