 中3数学
中3数学
 中3数学
中3数学
円に内接する四角形(数A 高校入試数学)

単元:
#数学(中学生)#中3数学#数A#図形の性質#円#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係
指導講師:
数学を数楽に
問題文全文(内容文):
円に内接する四角形の性質について説明動画です
この動画を見る
円に内接する四角形の性質について説明動画です
正五角形の対角線の長さ(高校入試数学、大学入試数学)

正三角形と正六角形(高校受験数学)

直角三角形の垂線の長さ(高校受験数学)

【中学受験算数】ピラミッド相似、リボン相似、色々な相似問題はこう解け! ゼロから始める中学受験算数41
単元:
#算数(中学受験)#数学(中学生)#中3数学#相似な図形#平面図形#相似と相似を利用した問題
指導講師:
こばちゃん塾
問題文全文(内容文):
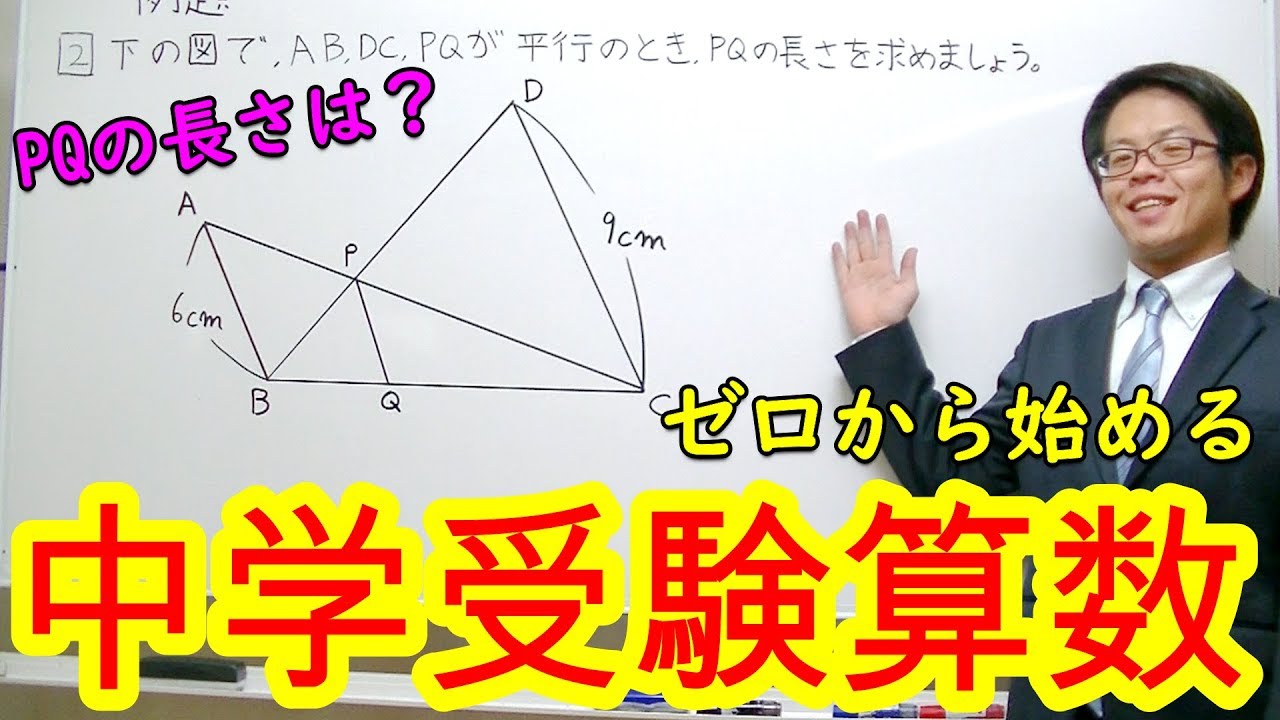
1⃣下の図で、BCとDEが平行のとき、XYの値を求めましょう。
2⃣下の図で、AB、DC、PQが平行のとき、PQの長さを求めましょう。
*図は動画内参照
この動画を見る
1⃣下の図で、BCとDEが平行のとき、XYの値を求めましょう。
2⃣下の図で、AB、DC、PQが平行のとき、PQの長さを求めましょう。
*図は動画内参照
中学数学 作図4 共通外接線

【高校受験対策】数学-関数43

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・関数43
Q.
右の図において、曲線アは関数$y=\frac{1}{2}x^2$のグラフである。
曲線ア上の点で$x$座標が$4$である点を$A$、$y$軸上の点で$y$座標が$10,6$である点をそれぞれ$B,C$とし、線分$OB$の中点を$D$とする。
また、線分$OA$上に点$E$をとる。ただし$O$は原点とする。
①2点$A,D$を通る直線の式を求めなさい。
②$△OAB$の面積を求めなさい。
③四角形$ABCE$の面積が$△OAB$の面積の$\frac{1}{2}$であるとき、 点$E$の座標を求めなさい。
この動画を見る
高校受験対策・関数43
Q.
右の図において、曲線アは関数$y=\frac{1}{2}x^2$のグラフである。
曲線ア上の点で$x$座標が$4$である点を$A$、$y$軸上の点で$y$座標が$10,6$である点をそれぞれ$B,C$とし、線分$OB$の中点を$D$とする。
また、線分$OA$上に点$E$をとる。ただし$O$は原点とする。
①2点$A,D$を通る直線の式を求めなさい。
②$△OAB$の面積を求めなさい。
③四角形$ABCE$の面積が$△OAB$の面積の$\frac{1}{2}$であるとき、 点$E$の座標を求めなさい。
【高校受験対策】数学-死守38

単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#連立方程式#2次方程式#1次関数#確率#2次関数#円
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守38
①$-7+5$を計算しなさい。
➁$\frac{3x-2}{5} \times10$を計算しなさい。
③$5ab^2 \div\frac{a}{3}$を計算しなさい。
④$(x+8)(x-6)$を計算しなさい。
⑤$25$の平方根を求めなさい。
⑥関数$y=\frac{a}{x}$のグラフが点$(6,-2)$を通るとき、$a$の値をを求めなさい。
⑦連立方程式を解きなさい。
$3x+y=-5$
$2x+3y=6$
⑧二次方程式を解きなさい。
$x^2+7x+1=0$
⑨右の図1で$\angle x$大きさを求めなさい。
⑩大小2つのさいころを同時に投げるとき、 2つとも同じ目が出る確率を求めなさい。
⑪右の図2において、点$A,B,C$は円$O$の周上の点である。
$\angle x$の大きさを求めなさい。
⑫左の図3のように、$y=ax^2(a\gt0)$のグラフ上 に2点$A,B$があり、$x$座標はそれぞれ$-6,4$である。
直線$AB$の傾きがであるとき、$a$の値を求めなさい。
この動画を見る
高校受験対策・死守38
①$-7+5$を計算しなさい。
➁$\frac{3x-2}{5} \times10$を計算しなさい。
③$5ab^2 \div\frac{a}{3}$を計算しなさい。
④$(x+8)(x-6)$を計算しなさい。
⑤$25$の平方根を求めなさい。
⑥関数$y=\frac{a}{x}$のグラフが点$(6,-2)$を通るとき、$a$の値をを求めなさい。
⑦連立方程式を解きなさい。
$3x+y=-5$
$2x+3y=6$
⑧二次方程式を解きなさい。
$x^2+7x+1=0$
⑨右の図1で$\angle x$大きさを求めなさい。
⑩大小2つのさいころを同時に投げるとき、 2つとも同じ目が出る確率を求めなさい。
⑪右の図2において、点$A,B,C$は円$O$の周上の点である。
$\angle x$の大きさを求めなさい。
⑫左の図3のように、$y=ax^2(a\gt0)$のグラフ上 に2点$A,B$があり、$x$座標はそれぞれ$-6,4$である。
直線$AB$の傾きがであるとき、$a$の値を求めなさい。
甲陽学院高校 整数問題 高校入試

単元:
#算数(中学受験)#数学(中学生)#中3数学#平方根#過去問解説(学校別)#甲陽学院中学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$S_n=1!+2!+3!+…+n!$
$S_n$が平方数となる$n$を全て求めよ
(1)
$5!$を求めよ
$S_{10}$の1の位
出典:甲陽学院高等学校 入試問題
この動画を見る
$S_n=1!+2!+3!+…+n!$
$S_n$が平方数となる$n$を全て求めよ
(1)
$5!$を求めよ
$S_{10}$の1の位
出典:甲陽学院高等学校 入試問題
中学生向け計算問題 因数分解 暇つぶし

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
鈴木貫太郎
問題文全文(内容文):
因数分解
$\sqrt{ 900・901・902・903+1 }$を計算せよ
$(x+1)(x+2)(x+3)(x+4)-3$
この動画を見る
因数分解
$\sqrt{ 900・901・902・903+1 }$を計算せよ
$(x+1)(x+2)(x+3)(x+4)-3$
大阪教育大 複雑な3乗根の外し方

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#平方根#2次方程式#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#大阪教育大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\sqrt[3]{ \sqrt{ \displaystyle \frac{28}{27} }+1 }-\sqrt[3]{ \sqrt{ \displaystyle \frac{28}{27} }-1 }$の値を求めよ
出典:大阪教育大学
この動画を見る
$\sqrt[3]{ \sqrt{ \displaystyle \frac{28}{27} }+1 }-\sqrt[3]{ \sqrt{ \displaystyle \frac{28}{27} }-1 }$の値を求めよ
出典:大阪教育大学
【中学数学】2次方程式:2次方程式x²+ax+b=0の解が3と8のとき、a,bの値を求めよ。

【中学数学】三平方の定理:相似と三平方の定理を駆使して長さを出します!!

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
図は1辺の長さが9cmの正方形ABCDを、頂点Aが辺DC上の点Eに重なるように折り返したもので、PQは折り目の線である。DE=3cmであるとき、次の問いに答えなさい。
(2)線分BQの長さを求めなさい。
この動画を見る
図は1辺の長さが9cmの正方形ABCDを、頂点Aが辺DC上の点Eに重なるように折り返したもので、PQは折り目の線である。DE=3cmであるとき、次の問いに答えなさい。
(2)線分BQの長さを求めなさい。
立教大 2次方程式の解 Mathematics Japanese university entrance exam

単元:
#2次方程式#数Ⅰ#大学入試過去問(数学)#2次関数#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^2-2(a-1)x+(a-2)^2=0$の2つの解を$\alpha,\beta$
$0 \lt \alpha \lt 1 \lt \beta \lt 2$となる$a$の範囲は?
出典:立教大学 過去問
この動画を見る
$x^2-2(a-1)x+(a-2)^2=0$の2つの解を$\alpha,\beta$
$0 \lt \alpha \lt 1 \lt \beta \lt 2$となる$a$の範囲は?
出典:立教大学 過去問
中学生でもわかる解の公式の証明【中3以上必見】

【高校受験対策】数学-死守36

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守36
①$5+4 \times 6$を計算せよ
②$\frac{9}{5}\div 0.8-\frac{1}{2}$を計算せよ
③$\sqrt{60}\div \sqrt{5}+\sqrt{27}$を計算せよ
④比例式$3:4=(x-6):8$について$x$の値を求めよ。
⑤$3x^2+9x-12$を因数分解せよ。
⑥$n$を50以下の正の整数とするとき、$\sqrt{5n}$の値が整数となるような$n$の値をすべて求めよ。
⑦次の口と△にどんな自然数を入れても、計算の結果がつねに自然数 になるものはどれか。
下のア~エの中からあてはまるものをすべて答えよ。
ア 口+△
イ 口-△
ウ 口×△
エ 口÷△
⑧大小2つのさいころを同時に投げる。
大きいさいころの出た目の数を$x$座標、小さいさいころの出た目の数を$y$座標とする点を$P(x,y)$とするとき、点$P$が1次関数$y=-x+8$のグラフ上の点となる確率を求めよ。
⑨右の図は半径$rcm$の球を切断して できた半球で、切断面の円周の長さは$4\pi cm$であった。
このとき$r$の値を求めよ。
また、この半球の体積は何$cm^3$か。 ただし$\pi$は円周率とする。
この動画を見る
高校受験対策・死守36
①$5+4 \times 6$を計算せよ
②$\frac{9}{5}\div 0.8-\frac{1}{2}$を計算せよ
③$\sqrt{60}\div \sqrt{5}+\sqrt{27}$を計算せよ
④比例式$3:4=(x-6):8$について$x$の値を求めよ。
⑤$3x^2+9x-12$を因数分解せよ。
⑥$n$を50以下の正の整数とするとき、$\sqrt{5n}$の値が整数となるような$n$の値をすべて求めよ。
⑦次の口と△にどんな自然数を入れても、計算の結果がつねに自然数 になるものはどれか。
下のア~エの中からあてはまるものをすべて答えよ。
ア 口+△
イ 口-△
ウ 口×△
エ 口÷△
⑧大小2つのさいころを同時に投げる。
大きいさいころの出た目の数を$x$座標、小さいさいころの出た目の数を$y$座標とする点を$P(x,y)$とするとき、点$P$が1次関数$y=-x+8$のグラフ上の点となる確率を求めよ。
⑨右の図は半径$rcm$の球を切断して できた半球で、切断面の円周の長さは$4\pi cm$であった。
このとき$r$の値を求めよ。
また、この半球の体積は何$cm^3$か。 ただし$\pi$は円周率とする。
【高校受験対策】数学-図形25

単元:
#数学(中学生)#中3数学#三平方の定理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
1辺の長さが$4cm$の正方形$ABCD$がある。同1・間2に答えなさい。
問1
右の図のように、点$P$が$A$を出発し、正方形$ABCD$の周上を、 毎秒$1cm$の速さで$B$、$C$を通って$D$まで移動する。
(1)(2)に 答えなさい。
(1)点$P$が$A$を出発してから6秒後の線分$AP$の長さを求めなさい。
(2) 点$P$が$CD$上にあり、四角形$ABCP$の面積が$10cm^2$となるのは、点$P$が$A$を出発してから何秒後か、求めなさい。
問2
下の図のように、正方形$ABCD$の外側に、正三角形$ABE$と$\angle CBF=90°$の直角三角形$BCF$をつくる。
辺$CF$の中点を$M$とし、$BF=4\sqrt{3}cm$であるとき、(1)・(2)に答えなさい。
(1)$△BDE$の面積を求めなさい
(2)線分$BM$と線分$DF$の交点を$Q$とするとき、$BQ:QM$を求めなさい。
この動画を見る
1辺の長さが$4cm$の正方形$ABCD$がある。同1・間2に答えなさい。
問1
右の図のように、点$P$が$A$を出発し、正方形$ABCD$の周上を、 毎秒$1cm$の速さで$B$、$C$を通って$D$まで移動する。
(1)(2)に 答えなさい。
(1)点$P$が$A$を出発してから6秒後の線分$AP$の長さを求めなさい。
(2) 点$P$が$CD$上にあり、四角形$ABCP$の面積が$10cm^2$となるのは、点$P$が$A$を出発してから何秒後か、求めなさい。
問2
下の図のように、正方形$ABCD$の外側に、正三角形$ABE$と$\angle CBF=90°$の直角三角形$BCF$をつくる。
辺$CF$の中点を$M$とし、$BF=4\sqrt{3}cm$であるとき、(1)・(2)に答えなさい。
(1)$△BDE$の面積を求めなさい
(2)線分$BM$と線分$DF$の交点を$Q$とするとき、$BQ:QM$を求めなさい。
【高校受験対策】数学-関数41

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図のように、関数$y=\frac{1}{2}x^2$のグラフ上に2点$A$・$B$があり、点$A$の$x$座標は$-3$、点$B$は点$A$と$y$軸について対称である。
このとき次の問いに答えなさい。
問1
関数$y=\frac{1}{2}x^2$について、$x$の変域が$-3 \leqq x \leqq 4$のときの$y$の変域を求めなさい。
問2
$y$軸上に点$C$を、四角形$OBCA$がひし形となるようにとる。
このとき次の問いに答えなさい。
(1) 直線$AC$の式を求めなさい。
(2) 線分$AC$上に点$D$をとる。$△ODA$と四角形$OBCA$の面積比が$1:4$となるとき、点$D$の座標を求 めなさい。
この動画を見る
右の図のように、関数$y=\frac{1}{2}x^2$のグラフ上に2点$A$・$B$があり、点$A$の$x$座標は$-3$、点$B$は点$A$と$y$軸について対称である。
このとき次の問いに答えなさい。
問1
関数$y=\frac{1}{2}x^2$について、$x$の変域が$-3 \leqq x \leqq 4$のときの$y$の変域を求めなさい。
問2
$y$軸上に点$C$を、四角形$OBCA$がひし形となるようにとる。
このとき次の問いに答えなさい。
(1) 直線$AC$の式を求めなさい。
(2) 線分$AC$上に点$D$をとる。$△ODA$と四角形$OBCA$の面積比が$1:4$となるとき、点$D$の座標を求 めなさい。
【高校受験対策】数学-関数40

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
下の図のように、関数$y=\frac{1}{3}x^2$のグラフ上に2点$A$、$B$がある。
点Aの$x$座標は$-6$、点$B$の$x$座標は$3$であり、2点$A$、$B$を通る直線と$x$軸との交点を$C$とする。
このとき、次の間1~問6に答えなさい。
問1 点$B$の$y$座標を求めなさい。
問2 関数$y=\frac{1}{3}x^2$について、 $x$の変域が$-6 \leqq x \leqq 3$のときの$y$の変域を求めなさい。
問3 2点$A$、$B$を通る直線の式を求めなさい。
問4 点$C$の座標を求めなさい。
問5 $△OAB$の面積を求めなさい。
問6 $y=\frac{1}{3}x^2$のグラフ上に点$P$にある。$△POC$の面積が$△OAB$の面積と等しくなるような点$P$の$x$座標をすべて求めなさい。
この動画を見る
下の図のように、関数$y=\frac{1}{3}x^2$のグラフ上に2点$A$、$B$がある。
点Aの$x$座標は$-6$、点$B$の$x$座標は$3$であり、2点$A$、$B$を通る直線と$x$軸との交点を$C$とする。
このとき、次の間1~問6に答えなさい。
問1 点$B$の$y$座標を求めなさい。
問2 関数$y=\frac{1}{3}x^2$について、 $x$の変域が$-6 \leqq x \leqq 3$のときの$y$の変域を求めなさい。
問3 2点$A$、$B$を通る直線の式を求めなさい。
問4 点$C$の座標を求めなさい。
問5 $△OAB$の面積を求めなさい。
問6 $y=\frac{1}{3}x^2$のグラフ上に点$P$にある。$△POC$の面積が$△OAB$の面積と等しくなるような点$P$の$x$座標をすべて求めなさい。
【高校受験対策】数学-図形24

単元:
#数学(中学生)#中1数学#中3数学#空間図形#三平方の定理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
問2
右の図の正四面体は、1辺の長さが8cmである。辺$BC$、$CD$の中点をそれぞれ点$P$、Q、 点$Q$から$AP$にひいた垂線と$AP$との交点を$R$とする。次の(1)~(4)に答えなさい。
(1) $AQ$の長さを求めなさい。
(2) $△APQ$の面積を求めなさい。
(3) $QR$の長さを求めなさい。
(4) 三角すい$RBCD$の体積は、正四面体$ABCD$の体積の何倍か、求めなさい
この動画を見る
問2
右の図の正四面体は、1辺の長さが8cmである。辺$BC$、$CD$の中点をそれぞれ点$P$、Q、 点$Q$から$AP$にひいた垂線と$AP$との交点を$R$とする。次の(1)~(4)に答えなさい。
(1) $AQ$の長さを求めなさい。
(2) $△APQ$の面積を求めなさい。
(3) $QR$の長さを求めなさい。
(4) 三角すい$RBCD$の体積は、正四面体$ABCD$の体積の何倍か、求めなさい
【高校受験対策】数学-図形23

単元:
#数学(中学生)#中2数学#中3数学#平行と合同#相似な図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・図形23
右の図において、$△ABC$は$AB=AC$の二等辺三角形であり、 点$D$、$E$はそれぞれ辺$AB$、$AC$の中点である。
また、点$F$は直線DE上の点であり、$EF=DE$である。 このとき次の問1、問2に答えなさい。
問1
$AF=BE$であることを証明しなさい。
問2
線分$BF$と線分$CE$との交点を$G$とする。
$△AEF$において辺AFを底辺とするときの高さを$x$、$△BGE$において辺$BE$を底辺とするときの高さを$y$とするとき、$x:y$を求めなさい。
この動画を見る
高校受験対策・図形23
右の図において、$△ABC$は$AB=AC$の二等辺三角形であり、 点$D$、$E$はそれぞれ辺$AB$、$AC$の中点である。
また、点$F$は直線DE上の点であり、$EF=DE$である。 このとき次の問1、問2に答えなさい。
問1
$AF=BE$であることを証明しなさい。
問2
線分$BF$と線分$CE$との交点を$G$とする。
$△AEF$において辺AFを底辺とするときの高さを$x$、$△BGE$において辺$BE$を底辺とするときの高さを$y$とするとき、$x:y$を求めなさい。
【1/6】中3冬特訓13日目

単元:
#数学(中学生)#中3数学#三平方の定理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図は、1辺の長さが4cmの立方体で、点$P$は辺$FG$の中点、点$Q$は辺$GH$の中点である。また点$R$は直線$HP$と直線$EQ$との交点である。
①$ER:RQ$を求めよ。答えは最も簡単な整数比で表せ。
②線分$EQ$の長さを求めよ。
③$△DEQ$の面積を求めよ。
この動画を見る
右の図は、1辺の長さが4cmの立方体で、点$P$は辺$FG$の中点、点$Q$は辺$GH$の中点である。また点$R$は直線$HP$と直線$EQ$との交点である。
①$ER:RQ$を求めよ。答えは最も簡単な整数比で表せ。
②線分$EQ$の長さを求めよ。
③$△DEQ$の面積を求めよ。
【1/3】中3冬特訓10日目

単元:
#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
Q.
右の図で、点A・Bは関数$y=x^2$のグラフ上の点、点Cは関数$y=\frac{1}{4}x^2$のグラフ上の点である。また、AC・BCはそれぞれ$x$軸、$y$軸に平行である。
次の問いに答えなさい。ただし3点、A・B・Cは$x \gt 0$にあるものとする。
①点Aの座標が$(2,4)$のとき、点Bの座標を求めよ。
②AC=BCのとき、点Aの座標を求めよ。
この動画を見る
Q.
右の図で、点A・Bは関数$y=x^2$のグラフ上の点、点Cは関数$y=\frac{1}{4}x^2$のグラフ上の点である。また、AC・BCはそれぞれ$x$軸、$y$軸に平行である。
次の問いに答えなさい。ただし3点、A・B・Cは$x \gt 0$にあるものとする。
①点Aの座標が$(2,4)$のとき、点Bの座標を求めよ。
②AC=BCのとき、点Aの座標を求めよ。
【1/1】中3冬特訓8日目

単元:
#中3数学
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
Q.
右の図のように、$AB=\sqrt{10}cm$、$BC=3\sqrt{2}cm$、$CA=4cm$の $△ABC$の外接円の中心を$o$とし、直線$AO$と外接円との交点のうち、$A$と異なるものを$D$とする。
また、$A$から辺$BC$へひいた垂線と$BC$との交点を$H$とし、$AD$と$BC$の交点を$E$とする。
①$BH$の長さを求めよ。
②外接円の半径を求めよ。
③$BE:EC$を求めよ。
この動画を見る
Q.
右の図のように、$AB=\sqrt{10}cm$、$BC=3\sqrt{2}cm$、$CA=4cm$の $△ABC$の外接円の中心を$o$とし、直線$AO$と外接円との交点のうち、$A$と異なるものを$D$とする。
また、$A$から辺$BC$へひいた垂線と$BC$との交点を$H$とし、$AD$と$BC$の交点を$E$とする。
①$BH$の長さを求めよ。
②外接円の半径を求めよ。
③$BE:EC$を求めよ。
【割合難問】中3冬特訓(特別編)

単元:
#数学(中学生)#中3数学#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①
ある商品をいくつか仕入れた。
この商品を定価の25%引きで売ったとき、仕入れた個数の 5%が売れ残っても、仕入れ総額の14%以上の利益が出るようにしたい。定価を仕入れ値の何%増し以上にすればよいか答えなさい。
この動画を見る
①
ある商品をいくつか仕入れた。
この商品を定価の25%引きで売ったとき、仕入れた個数の 5%が売れ残っても、仕入れ総額の14%以上の利益が出るようにしたい。定価を仕入れ値の何%増し以上にすればよいか答えなさい。
【12/30】中3冬特訓6日目
単元:
#中3数学
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
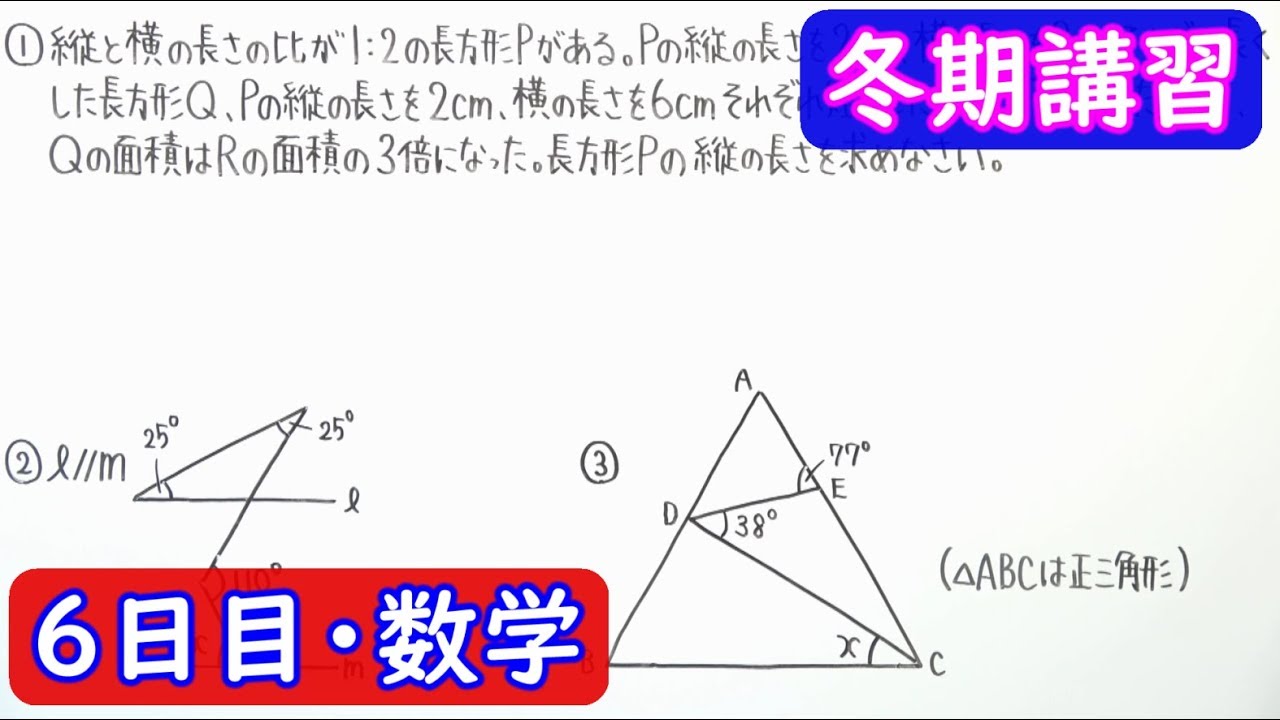
①
縦と横の長さの比が1:2の長方形Pがある。
Pの縦の長さを2cm、横の長さを2cmそれぞれ長くした長方形Q、Pの縦の長さを2cm、横の長さを6cmそれぞれ短くした長方形Rをつくったところ、Qの面積はRの面積の3倍になった。長方形Pの縦の長さを求めなさい。
この動画を見る
①
縦と横の長さの比が1:2の長方形Pがある。
Pの縦の長さを2cm、横の長さを2cmそれぞれ長くした長方形Q、Pの縦の長さを2cm、横の長さを6cmそれぞれ短くした長方形Rをつくったところ、Qの面積はRの面積の3倍になった。長方形Pの縦の長さを求めなさい。
【トンネル】中3冬特訓(特別編)

単元:
#数学(中学生)#中3数学
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①
あるトンネルに、A列車が秒速30mで入り始めた。この10秒後に反対側からB列車が秒速40mで入り始めた。その後、2つの列車はトンネルの中央で出会ったという。
このトンネルの長さを求めなさい。
この動画を見る
①
あるトンネルに、A列車が秒速30mで入り始めた。この10秒後に反対側からB列車が秒速40mで入り始めた。その後、2つの列車はトンネルの中央で出会ったという。
このトンネルの長さを求めなさい。
【12/28】中3冬特訓4日目

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#平方根#2次方程式#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$x^3+x^2-x-1$を因数分解しなさい。
➁関数$y=ax^2$は$x$の変域が$-4 \leqq x \leqq3$のとき、$y$の変域が$0 \leqq y \leqq8$である。
$x$の値が1から5まで増加するとき、この関数の変化の割合を求めよ。
③二次方程式$x^2-ax-5=0$の解の1つが$x=5$のとき、$a$の値ともう一つの解を求めよ。
④$\sqrt{6a}$を小数第一位で四捨五入すると2になるような整数$a$を求めよ。
この動画を見る
①$x^3+x^2-x-1$を因数分解しなさい。
➁関数$y=ax^2$は$x$の変域が$-4 \leqq x \leqq3$のとき、$y$の変域が$0 \leqq y \leqq8$である。
$x$の値が1から5まで増加するとき、この関数の変化の割合を求めよ。
③二次方程式$x^2-ax-5=0$の解の1つが$x=5$のとき、$a$の値ともう一つの解を求めよ。
④$\sqrt{6a}$を小数第一位で四捨五入すると2になるような整数$a$を求めよ。
【12/26】中3冬特訓2日目

単元:
#数学(中学生)#中3数学
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$\sqrt{32}-2\sqrt{3} \times \sqrt{6}$
➁$\sqrt{3}-\sqrt{27} + \sqrt{48}$
③$7\sqrt{2}-\sqrt{18} + \frac{8}{\sqrt{2}}$
④
列車が鉄橋を渡り始めてから渡り終わるまでにかかる時間は、長さ 200mの普通列車では30秒、長さ160mの特急列車では14秒であった。 また、特急列車の速さは普通列車の速さの2倍であった。
この鉄橋の長さは何mか求めなさい。
この動画を見る
①$\sqrt{32}-2\sqrt{3} \times \sqrt{6}$
➁$\sqrt{3}-\sqrt{27} + \sqrt{48}$
③$7\sqrt{2}-\sqrt{18} + \frac{8}{\sqrt{2}}$
④
列車が鉄橋を渡り始めてから渡り終わるまでにかかる時間は、長さ 200mの普通列車では30秒、長さ160mの特急列車では14秒であった。 また、特急列車の速さは普通列車の速さの2倍であった。
この鉄橋の長さは何mか求めなさい。
【何秒で終わる?】ルートの変形特訓

単元:
#数学(中学生)#中3数学#平方根
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
1 $\sqrt{8}=$
2 $\sqrt{9}=$
3 $\sqrt{12}=$
4 $\sqrt{6}=$
5 $\sqrt{20}=$
6 $\sqrt{4}=$
7 $\sqrt{18}=$
8 $\sqrt{32}=$
9 $\sqrt{15}=$
10 $\sqrt{24}=$
11 $\sqrt{100}=$
12 $\sqrt{40}=$
13 $\sqrt{25}=$
14 $\sqrt{45}=$
15 $\sqrt{30}=$
16 $\sqrt{600}=$
17 $\sqrt{16}=$
18 $\sqrt{50}=$
19 $\sqrt{28}=$
20 $\sqrt{72}=$
21 $\sqrt{56}=$
22 $\sqrt{38}=$
23 $\sqrt{75}=$
24 $\sqrt{1000}=$
25 $\sqrt{80}=$
26 $\sqrt{98}=$
27 $\sqrt{33}=$
28 $\sqrt{20000}=$
29 $\sqrt{90000}=$
30 $\sqrt{1200000}=$
この動画を見る
1 $\sqrt{8}=$
2 $\sqrt{9}=$
3 $\sqrt{12}=$
4 $\sqrt{6}=$
5 $\sqrt{20}=$
6 $\sqrt{4}=$
7 $\sqrt{18}=$
8 $\sqrt{32}=$
9 $\sqrt{15}=$
10 $\sqrt{24}=$
11 $\sqrt{100}=$
12 $\sqrt{40}=$
13 $\sqrt{25}=$
14 $\sqrt{45}=$
15 $\sqrt{30}=$
16 $\sqrt{600}=$
17 $\sqrt{16}=$
18 $\sqrt{50}=$
19 $\sqrt{28}=$
20 $\sqrt{72}=$
21 $\sqrt{56}=$
22 $\sqrt{38}=$
23 $\sqrt{75}=$
24 $\sqrt{1000}=$
25 $\sqrt{80}=$
26 $\sqrt{98}=$
27 $\sqrt{33}=$
28 $\sqrt{20000}=$
29 $\sqrt{90000}=$
30 $\sqrt{1200000}=$
