 数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
【高校受験対策】数学-死守45

単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守45
①$-5+2$を計算しなさい。
②$(x+2)^2$を展開しなさい。
③$y$は$x$に反比例し、比例定数は 3である。
$x$と$y$の関係を式に表しなさい。
④正五角形の内角の和は何度か、求めなさい。
⑤二次方程式 $2x^2-x=0$を解きなさい。
⑥となる自然数$a$をすべて求めなさい。
⑦直線$6x-y=1$0と$x$軸との交点をPとする。
直線$ax-2y=15$が点Pを通るとき、$a$の値を求めなさい。
⑧500円、100円、50円、10円の硬質が1枚ずつある。
この4枚の硬貨を同時に投げるとき、表が出た硬貨の合計金額が、600円以上になる確率を求めなさい。
ただしすべての硬貨の表と裏の出かたは同様に確からしいものとする。
⑨右の図は円錐の展開図です。
この展開図を組み立てたとき、側面となるおうぎ形は半径が16cm、中心角が135°である。
底面となる円の半径を求めなさい。
⑩右の表は、生徒100人の通学時間を度数分布表に表したものである。
$a:b=4:3$であるとき、中央値が含まれる階級の相対度数を求めなさい。
この動画を見る
高校受験対策・死守45
①$-5+2$を計算しなさい。
②$(x+2)^2$を展開しなさい。
③$y$は$x$に反比例し、比例定数は 3である。
$x$と$y$の関係を式に表しなさい。
④正五角形の内角の和は何度か、求めなさい。
⑤二次方程式 $2x^2-x=0$を解きなさい。
⑥となる自然数$a$をすべて求めなさい。
⑦直線$6x-y=1$0と$x$軸との交点をPとする。
直線$ax-2y=15$が点Pを通るとき、$a$の値を求めなさい。
⑧500円、100円、50円、10円の硬質が1枚ずつある。
この4枚の硬貨を同時に投げるとき、表が出た硬貨の合計金額が、600円以上になる確率を求めなさい。
ただしすべての硬貨の表と裏の出かたは同様に確からしいものとする。
⑨右の図は円錐の展開図です。
この展開図を組み立てたとき、側面となるおうぎ形は半径が16cm、中心角が135°である。
底面となる円の半径を求めなさい。
⑩右の表は、生徒100人の通学時間を度数分布表に表したものである。
$a:b=4:3$であるとき、中央値が含まれる階級の相対度数を求めなさい。
ゆく年くる年連立方程式 ちょっと外積

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
2019x+2020y=66 \\
1009x+1011y=33
\end{array}
\right.
\end{eqnarray}$
これを解け.
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
2019x+2020y=66 \\
1009x+1011y=33
\end{array}
\right.
\end{eqnarray}$
これを解け.
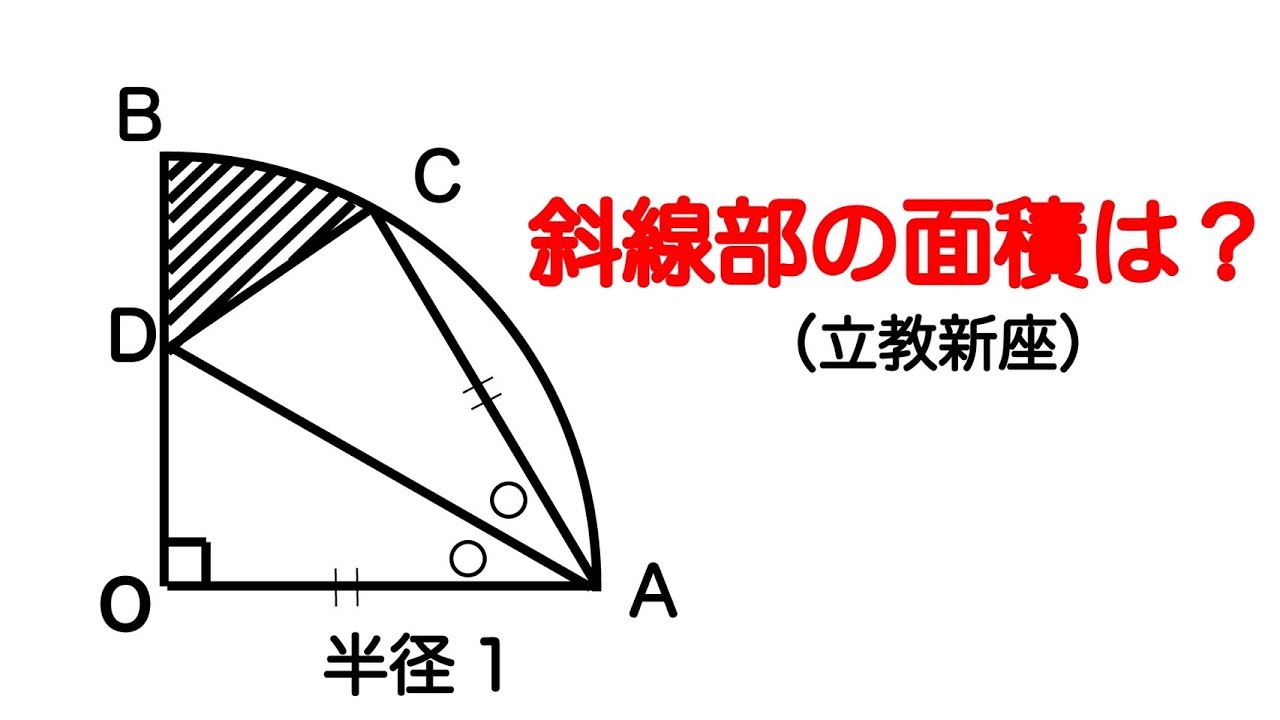
立教新座2016(高校入試)
単元:
#数学(中学生)#中3数学#円#高校入試過去問(数学)#立教新座高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
動画内の図を参照し、斜線部の面積を求めよ。
出典:2016年立教新座高等学校 高校入試問題
この動画を見る
動画内の図を参照し、斜線部の面積を求めよ。
出典:2016年立教新座高等学校 高校入試問題
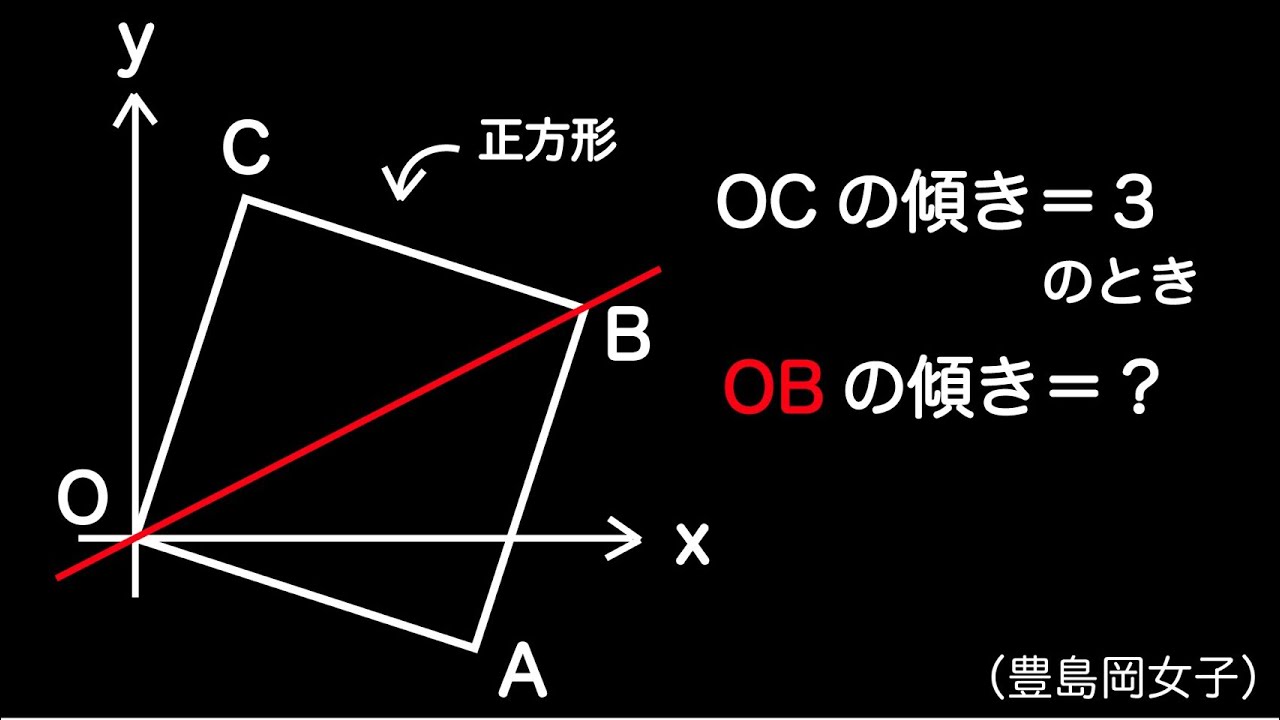
斜めの正方形(豊島岡女子2016)
単元:
#数学(中学生)#中2数学#1次関数#高校入試過去問(数学)#豊島岡女子高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
動画内の図を参照してください。
座標平面上に傾いた正方形があります。
点$\textrm{OB}$の傾きを求めよ。
出典:2016年豊島岡女子学園 中学校・高等学校
この動画を見る
動画内の図を参照してください。
座標平面上に傾いた正方形があります。
点$\textrm{OB}$の傾きを求めよ。
出典:2016年豊島岡女子学園 中学校・高等学校
息抜き ゆく年くる年連立方程式

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
2019x+2020y=4055 \\
2020x+2019y=4023
\end{array}
\right.
\end{eqnarray}$
これを解け.
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
2019x+2020y=4055 \\
2020x+2019y=4023
\end{array}
\right.
\end{eqnarray}$
これを解け.
素因数分解せよ!(2000慶應女子)

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#慶應義塾女子高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
$110\times90+13\times7$を素因数分解せよ。
出典:2000年慶應義塾女子高等学校
この動画を見る
$110\times90+13\times7$を素因数分解せよ。
出典:2000年慶應義塾女子高等学校
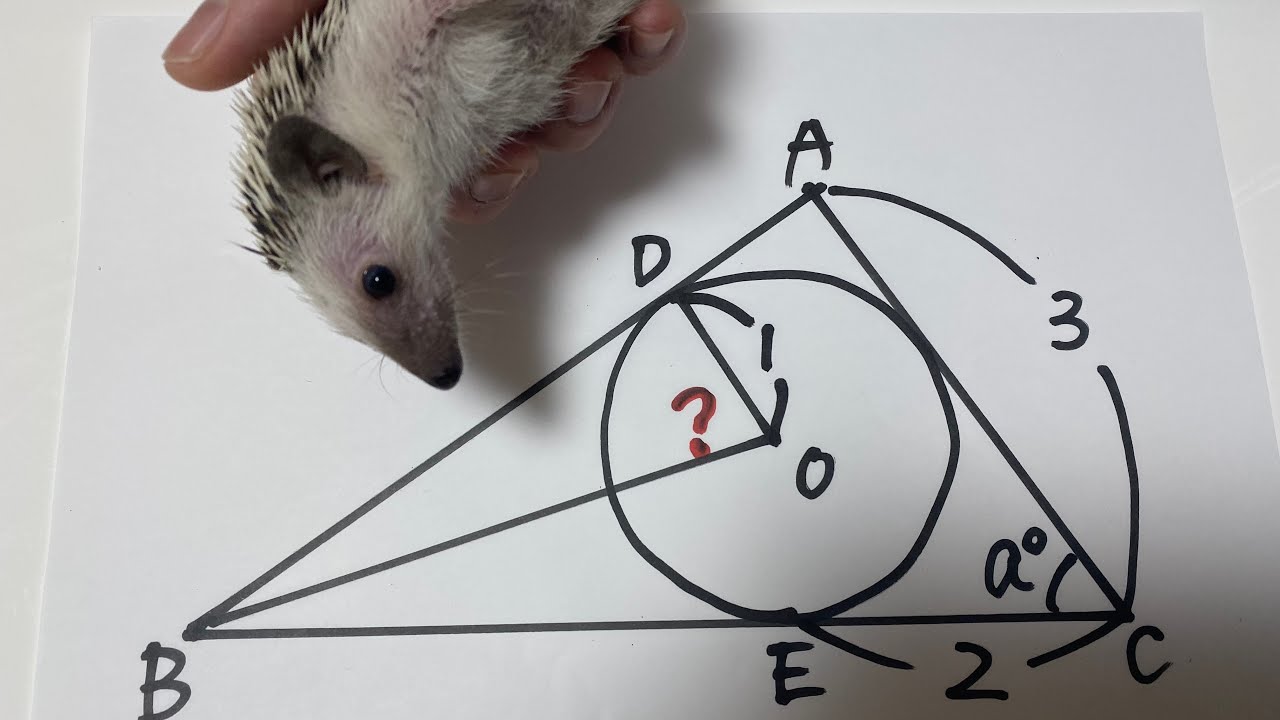
角度を求める(2006国立高校)
単元:
#数学(中学生)#中2数学#中3数学#円#三角形と四角形#高校入試過去問(数学)#東京都立国立高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
動画内の図を参照し、?の角度を求めよ。
出典:2006年国立高校
この動画を見る
動画内の図を参照し、?の角度を求めよ。
出典:2006年国立高校
【中1数学】元大手塾講師が教える!中学数学基礎講座 第15回 式の値

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
こばちゃん塾
問題文全文(内容文):
例題 次の式の値を求めなさい
(1)a=4のとき、2a+3
(2)b=4のとき、10-3b
(3)x=-2のとき、-x
(4)y=-7のとき、-2y+3
(5)x=-3のとき、$\frac{9}{x}$
(6)a=-4のとき、$a^2$
例題 次の式の値を求めなさい
(1)x=3,y=6のとき、4x+3y
(2)x=-2,y=4のとき、-7x+5y
(3)x=-1,y=-9のとき、$x-\frac{4}{3}y$
この動画を見る
例題 次の式の値を求めなさい
(1)a=4のとき、2a+3
(2)b=4のとき、10-3b
(3)x=-2のとき、-x
(4)y=-7のとき、-2y+3
(5)x=-3のとき、$\frac{9}{x}$
(6)a=-4のとき、$a^2$
例題 次の式の値を求めなさい
(1)x=3,y=6のとき、4x+3y
(2)x=-2,y=4のとき、-7x+5y
(3)x=-1,y=-9のとき、$x-\frac{4}{3}y$
平方根の計算!!(2019立命館)
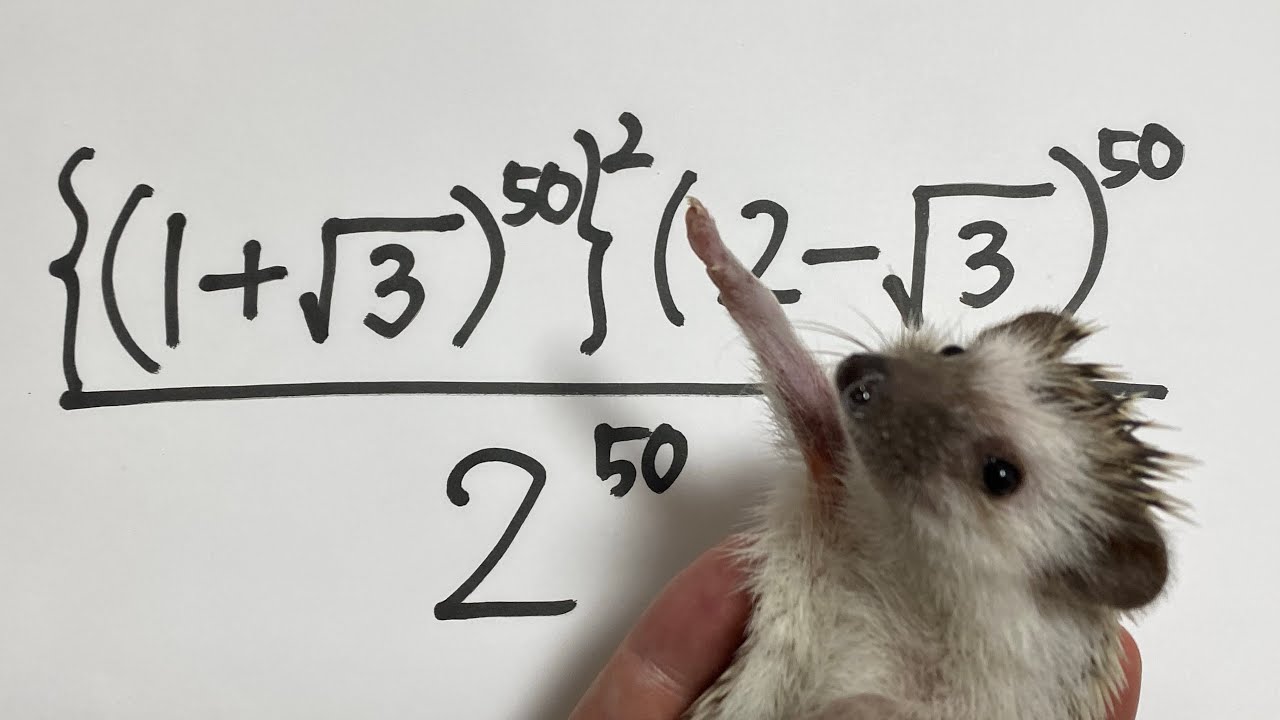
単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#立命館高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
以下を計算せよ
$\displaystyle \frac{\{(1+\sqrt{ 3 })^{50}\}^2(2-\sqrt{ 3 })^{50}}{2^{50}}$
出典:2019年立命館大学
この動画を見る
以下を計算せよ
$\displaystyle \frac{\{(1+\sqrt{ 3 })^{50}\}^2(2-\sqrt{ 3 })^{50}}{2^{50}}$
出典:2019年立命館大学
都立西2010の最初の1問

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#東京都立西高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{ (\displaystyle \frac{13}{23}-\displaystyle \frac{16}{31})^2 }+\sqrt{ (\displaystyle \frac{11}{23}-\displaystyle \frac{16}{31})^2 }$
出典:2010年東京都立西高等学校
この動画を見る
$\sqrt{ (\displaystyle \frac{13}{23}-\displaystyle \frac{16}{31})^2 }+\sqrt{ (\displaystyle \frac{11}{23}-\displaystyle \frac{16}{31})^2 }$
出典:2010年東京都立西高等学校
角度を求める!(都立西2005 2006)

【高校受験対策】数学-死守44

単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守44
①$2-(-5)$を計算せよ。
②$7+3×(-4)$を計算せよ。
③$\sqrt{45}-\frac{25}{\sqrt{5}}$を計算せよ。
④$4(2a-3b)-(a+2b)$を計算せよ。
⑤1次方程式$5x-2=2(4x-7)$を解け。
⑥2次方程式$x(x-1)=3(x+4)$を解け。
⑦次の連立方程式を解け。
$x-2y=7$
$4x+3y=6$
⑧A市におけるある日の最高気温と最低気温の温度差は19℃でした。
この日のA市の最高気温は15℃でした。最低気温は何℃求めなさい。
⑨比例式$x:x-3=\frac{3}{2}$を満たす$x$の値を求めなさい。
➉関数$y=-7x^2$グラフ上に$y$座標が-28である点があります。
この点の$x$座標を求めなさい。
⑪$y$は$x$に反比例し、$x=3$のとき$y=8$である。
$x=-2$のときの$y$の値を求めなさい。
⑫ 右の表はA中学校の1年生と3年生の通学時間を調査し、その結果を度数分布表に整理したものである。
この表をもとに、中央値が大きい方の学年とその学年の中央値がふくまれる階級を答えなさい。
この動画を見る
高校受験対策・死守44
①$2-(-5)$を計算せよ。
②$7+3×(-4)$を計算せよ。
③$\sqrt{45}-\frac{25}{\sqrt{5}}$を計算せよ。
④$4(2a-3b)-(a+2b)$を計算せよ。
⑤1次方程式$5x-2=2(4x-7)$を解け。
⑥2次方程式$x(x-1)=3(x+4)$を解け。
⑦次の連立方程式を解け。
$x-2y=7$
$4x+3y=6$
⑧A市におけるある日の最高気温と最低気温の温度差は19℃でした。
この日のA市の最高気温は15℃でした。最低気温は何℃求めなさい。
⑨比例式$x:x-3=\frac{3}{2}$を満たす$x$の値を求めなさい。
➉関数$y=-7x^2$グラフ上に$y$座標が-28である点があります。
この点の$x$座標を求めなさい。
⑪$y$は$x$に反比例し、$x=3$のとき$y=8$である。
$x=-2$のときの$y$の値を求めなさい。
⑫ 右の表はA中学校の1年生と3年生の通学時間を調査し、その結果を度数分布表に整理したものである。
この表をもとに、中央値が大きい方の学年とその学年の中央値がふくまれる階級を答えなさい。
【中1数学】元大手塾講師が教える!中学数学基礎講座 第14回 文字式の表し方

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
こばちゃん塾
問題文全文(内容文):
例題
(1)b×4×a
(2)m×m×3
(3)(a+b)÷2
例題
(1)1000円を出して、1個x円のボールを2個買ったときのおつり
(2)時速ykmで3時間走ったときの道のり
(3)全校生徒a人の11%の人数
1本a円のばらと1本b円のゆりがあります。
a+3b(円)は何を表していますか。
この動画を見る
例題
(1)b×4×a
(2)m×m×3
(3)(a+b)÷2
例題
(1)1000円を出して、1個x円のボールを2個買ったときのおつり
(2)時速ykmで3時間走ったときの道のり
(3)全校生徒a人の11%の人数
1本a円のばらと1本b円のゆりがあります。
a+3b(円)は何を表していますか。
2019日比谷高校数学の最初の2問!!(高校入試数学)

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#平方根#高校入試過去問(数学)#東京都立日比谷高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
問1
$(3-\displaystyle \frac{1}{\sqrt{ 3 }})^2+\displaystyle \frac{(\sqrt{ 6 }-\sqrt{ 2 })(3+-\sqrt{ 3 })}{\sqrt{ 2 }}$
問2
$(6-x)^2+9(x-6)-90$を因数分解せよ
出典:2019年東京都立日比谷高等学校 高校入試
この動画を見る
問1
$(3-\displaystyle \frac{1}{\sqrt{ 3 }})^2+\displaystyle \frac{(\sqrt{ 6 }-\sqrt{ 2 })(3+-\sqrt{ 3 })}{\sqrt{ 2 }}$
問2
$(6-x)^2+9(x-6)-90$を因数分解せよ
出典:2019年東京都立日比谷高等学校 高校入試
放物線と平行な2直線(高校受験数学)

放物線上の2点を通る直線

【高校受験対策】数学-死守43

単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守43
①$-6+9$の計算をしなさい。
➁$-15 \times \frac{3}{10}$の計算をしなさい。
③$\sqrt{75}-4\sqrt{3}$の計算をしなさい。
④$\frac{x+y}{2}-\frac{2x-y}{3}$の計算をしなさい。
⑤$x^2-x-56$を因数分解しなさい。
⑥10以下の素数をすべて書きなさい。
⑦下の図はある反比例のグラフである。この関係の式を求めなさい。
⑧1本$a$円のえんぴつを6本と1冊$b$円のノートを5冊買うと、代金の合計は1000円以下になる。
このときの数量関係を不等式で表しなさい。
⑨右の図はある立体の投影図である。
この立体の表面積を求めなさい。
⑩4点、A,B,C,Dが同じ円周上にあるものを次のア~エの中からすべて選び、番号を書きなさい。
この動画を見る
高校受験対策・死守43
①$-6+9$の計算をしなさい。
➁$-15 \times \frac{3}{10}$の計算をしなさい。
③$\sqrt{75}-4\sqrt{3}$の計算をしなさい。
④$\frac{x+y}{2}-\frac{2x-y}{3}$の計算をしなさい。
⑤$x^2-x-56$を因数分解しなさい。
⑥10以下の素数をすべて書きなさい。
⑦下の図はある反比例のグラフである。この関係の式を求めなさい。
⑧1本$a$円のえんぴつを6本と1冊$b$円のノートを5冊買うと、代金の合計は1000円以下になる。
このときの数量関係を不等式で表しなさい。
⑨右の図はある立体の投影図である。
この立体の表面積を求めなさい。
⑩4点、A,B,C,Dが同じ円周上にあるものを次のア~エの中からすべて選び、番号を書きなさい。
【高校受験対策】数学-図形29(番号間違えました)

単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・図形28
Q
図1のように、円$o$の円周上に3点、$A,B,C$を$AB=AC$となるようにとり、 $△ABC$をつくる。
点$C$をふくまない$\stackrel{\huge\frown}{AB}$上に、点$D$を$\angle DAB \lt \angle BAC$となるようにとり、点$B$と点$D$を線分で結ぶ。
線分$CD$上に点$E$を$∠EAC=∠DAB$となるようにとる。
①図1において、$\triangle ADE \backsim \triangle ABC$を証明しなさい。
②図2は、図1において$\angle BAC=60°$、点$C$を含まない$\stackrel{\huge\frown}{AD}$と$\stackrel{\huge\frown}{DB}$の長さの比が$3:1$となる場合を表している。
図2において、円$o$の半径が4cmのとき、$△ADC$の面積を求めなさい。
この動画を見る
高校受験対策・図形28
Q
図1のように、円$o$の円周上に3点、$A,B,C$を$AB=AC$となるようにとり、 $△ABC$をつくる。
点$C$をふくまない$\stackrel{\huge\frown}{AB}$上に、点$D$を$\angle DAB \lt \angle BAC$となるようにとり、点$B$と点$D$を線分で結ぶ。
線分$CD$上に点$E$を$∠EAC=∠DAB$となるようにとる。
①図1において、$\triangle ADE \backsim \triangle ABC$を証明しなさい。
②図2は、図1において$\angle BAC=60°$、点$C$を含まない$\stackrel{\huge\frown}{AD}$と$\stackrel{\huge\frown}{DB}$の長さの比が$3:1$となる場合を表している。
図2において、円$o$の半径が4cmのとき、$△ADC$の面積を求めなさい。
円周角を一発で!!(中3数学)

30°、30°、120°の二等辺三角形(高校入試数学)

正四面体の体積を3通りで求めてみた(高校入試数学 数I)

三平方の定理の計算の工夫(2)
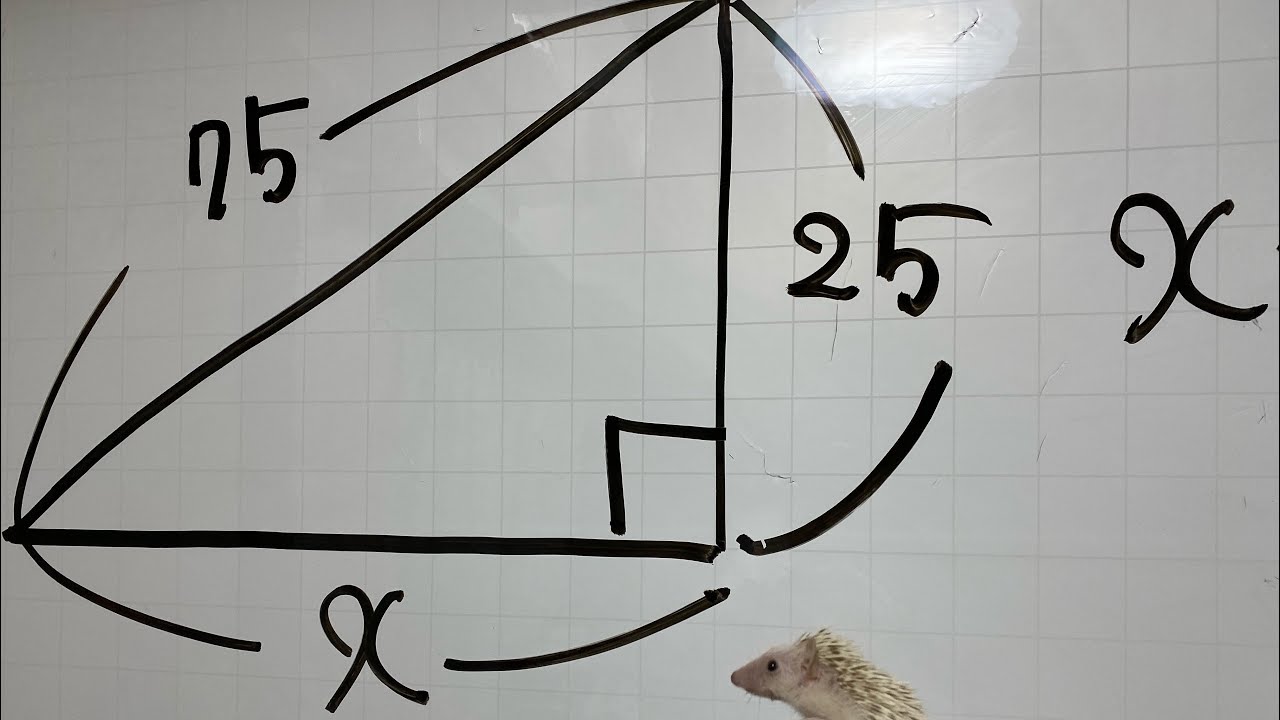
二等辺三角形の内接円の半径を3通りで求めてみた(高校入試数学 数1)

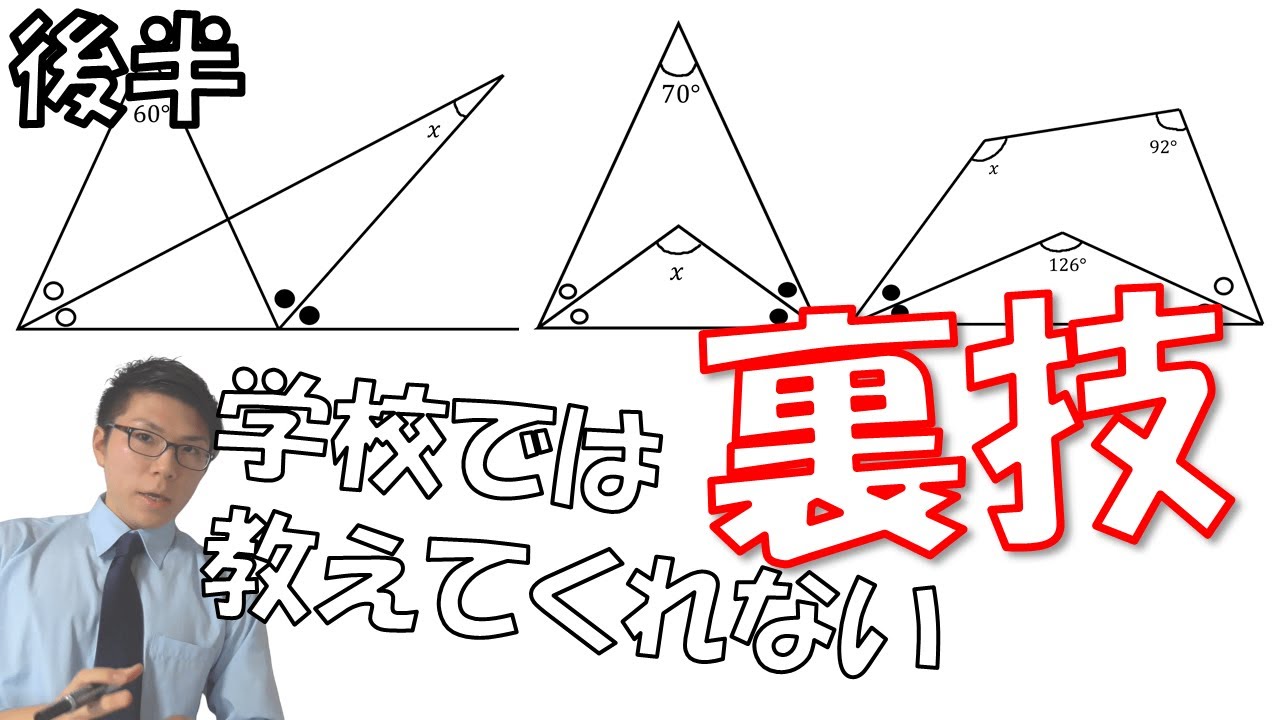
【中学数学】平面図形と角度~〇●の二等分線の裏技教えます~後半 4-6.5【中2数学】
円錐の公式(高校入試数学)

すべての辺の長さが等しい正四角錐(高校入試数学)

【中1数学】元大手塾講師が教える!中学数学基礎講座 第13回 数量を文字で表す!

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
こばちゃん塾
問題文全文(内容文):
・1本50円の鉛筆を1本、2本、3本・・・と買うとき、次の問いに答えましょう。
(1)3本買うときの代金を式で表しましょう。
(2)a本買うときの代金を式で表しましょう。
・1個x(g)のケーキ4個を60gの箱に入れたときの全体の重さ。
・水2L入りのペットボトルがあります。
xLずつ3回飲みました。残りの水は何Lでしょう。
・この長方形の周の長さを文字を使って表しましょう。
*図は動画内参照
この動画を見る
・1本50円の鉛筆を1本、2本、3本・・・と買うとき、次の問いに答えましょう。
(1)3本買うときの代金を式で表しましょう。
(2)a本買うときの代金を式で表しましょう。
・1個x(g)のケーキ4個を60gの箱に入れたときの全体の重さ。
・水2L入りのペットボトルがあります。
xLずつ3回飲みました。残りの水は何Lでしょう。
・この長方形の周の長さを文字を使って表しましょう。
*図は動画内参照
【中1数学】元大手塾講師が教える!正負の数まとめ② 定期テスト対策や復習に最適!

単元:
#数学(中学生)#中1数学#正の数・負の数
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣
(1)(-46)-(-14)×(-3)=
(2){(9-15)÷(-2)+13}+(-5)=
(3)$(-6)^2× \frac{5}{9}-0.5^2×(-16)$
2⃣
(1)最も気温が低かったのは何曜日で何℃
(2)最も気温の高い曜日と低い曜日の差は何℃
(3)この1週間の平均気温は何度?
この動画を見る
1⃣
(1)(-46)-(-14)×(-3)=
(2){(9-15)÷(-2)+13}+(-5)=
(3)$(-6)^2× \frac{5}{9}-0.5^2×(-16)$
2⃣
(1)最も気温が低かったのは何曜日で何℃
(2)最も気温の高い曜日と低い曜日の差は何℃
(3)この1週間の平均気温は何度?
三辺の長さがわかっているときの三角形の面積の求め方(高校入試数学)

三平方の定理の計算の工夫(高校入試数学)

