 数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
整数問題 大阪教育大附属天王寺

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
自然数A,B,Cを求めよ。
$
\begin{eqnarray}
\left\{
\begin{array}{l}
A \div B \times C=12 \\
A \div B - C=1 \\
A \div B =10
\end{array}
\right.
\end{eqnarray}
$
大阪教育大学附属高等学校天王寺校舎
この動画を見る
自然数A,B,Cを求めよ。
$
\begin{eqnarray}
\left\{
\begin{array}{l}
A \div B \times C=12 \\
A \div B - C=1 \\
A \div B =10
\end{array}
\right.
\end{eqnarray}
$
大阪教育大学附属高等学校天王寺校舎
【中学数学】平方根・ルートの整数部分・小数部分を求める問題 2-6【中3数学】

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\sqrt{ 7 }$の整数部分と少数部分を求めよ
この動画を見る
$\sqrt{ 7 }$の整数部分と少数部分を求めよ
二次方程式 大阪教育大附属天王寺

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式を解け
$40000x^2-1500x+9 = 0$
大阪教育大学附属高等学校天王寺校舎
この動画を見る
2次方程式を解け
$40000x^2-1500x+9 = 0$
大阪教育大学附属高等学校天王寺校舎
見えない変域 xの遺言

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
数学を数楽に
問題文全文(内容文):
x,yを実数とし、$2x^2+y^2=4$とする。
$P=x^2+y$をyの式で表すとP=$\boxed{ア}$であり、Pの最小値は$\boxed{イ}$である。
この動画を見る
x,yを実数とし、$2x^2+y^2=4$とする。
$P=x^2+y$をyの式で表すとP=$\boxed{ア}$であり、Pの最小値は$\boxed{イ}$である。
【中学数学】イコールが2つある方程式の解き方~連立方程式の応用~ 2-5.5【中2数学】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
以下の方程式を解け。
$3x-4y+5=2x+y-4=5x-3y+1$
この動画を見る
以下の方程式を解け。
$3x-4y+5=2x+y-4=5x-3y+1$
2次方程式 筆算はしたくない。 日大習志野

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式を解け
$\frac{1}{2}x(x+15) = 19 \times 53$
日本大学習志野高等学校
この動画を見る
2次方程式を解け
$\frac{1}{2}x(x+15) = 19 \times 53$
日本大学習志野高等学校
【5分で得意分野へ!】図形:専修大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#平面図形#高校入試過去問(数学)#専修大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 専修大学附属高等学校
線分$AH$の長さを求めなさい。
$\angle AHB=90°$
三角形$ABC:$
AB=13
BC=14
CA=15
※図は動画内参照
この動画を見る
入試問題 専修大学附属高等学校
線分$AH$の長さを求めなさい。
$\angle AHB=90°$
三角形$ABC:$
AB=13
BC=14
CA=15
※図は動画内参照
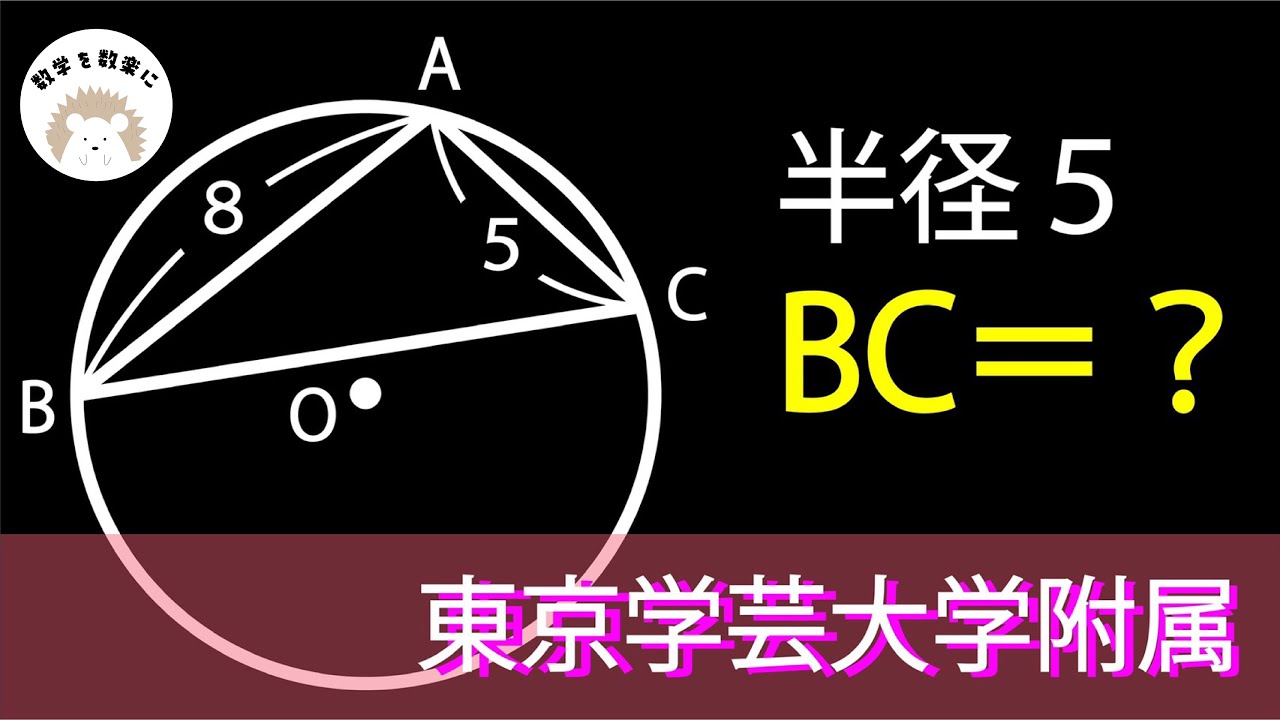
円 学芸大学附属 B
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
円の半径=5
BC=?
*図は動画内参照
東京学芸大学附属高校
この動画を見る
円の半径=5
BC=?
*図は動画内参照
東京学芸大学附属高校
割合の面白い性質~計算が楽になるよ~

7の倍数になる確率=❓ 日比谷

単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
大小2コのサイコロを投げる
百の位を1
十の位を小さいサイコロの目
一の位を大きいサイコロの目
3ケタの整数が7の倍数となる確率=?
日比谷高等学校
この動画を見る
大小2コのサイコロを投げる
百の位を1
十の位を小さいサイコロの目
一の位を大きいサイコロの目
3ケタの整数が7の倍数となる確率=?
日比谷高等学校
相似の典型問題!!
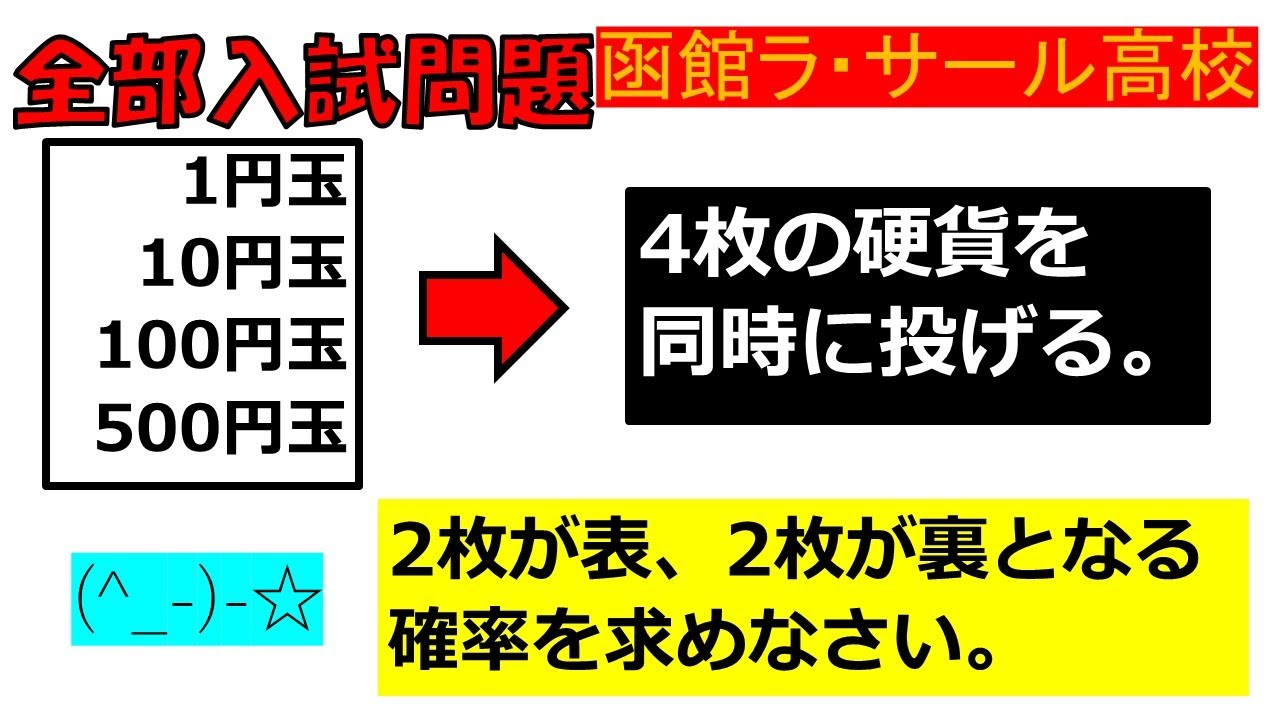
【3分で基礎から発展まで・確実点取りから時短へ!】確率:函館ラ・サール高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)#函館ラ・サール高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 函館ラ・サール高等学校
1円玉 10円玉 100円玉 500円玉
↓
4枚の硬貨を同時に投げ、
2枚が表、2枚が裏となる 確率を求めなさい。
この動画を見る
入試問題 函館ラ・サール高等学校
1円玉 10円玉 100円玉 500円玉
↓
4枚の硬貨を同時に投げ、
2枚が表、2枚が裏となる 確率を求めなさい。
【中学数学】平方根・ルートの問題演習~計算の仕方~ 2-4.5【中3数学】

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
$\sqrt{ 147 }-\sqrt{ 27 }-\sqrt{ 48 }$
2⃣
$\displaystyle \frac{2\sqrt{ 6 }}{3} \div \displaystyle \frac{4\sqrt{ 2 }}{3} \times \displaystyle \frac{7\sqrt{ 5 }}{2}$
この動画を見る
1⃣
$\sqrt{ 147 }-\sqrt{ 27 }-\sqrt{ 48 }$
2⃣
$\displaystyle \frac{2\sqrt{ 6 }}{3} \div \displaystyle \frac{4\sqrt{ 2 }}{3} \times \displaystyle \frac{7\sqrt{ 5 }}{2}$
【5分で高校入試から大学受験まで!「型」を見抜け!】整数:立教新座高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#立教新座高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 立教新座高等学校
$x$と$y$は自然数とします。
【方程式】
$4x^2-9y^2=31
を満たす x,y の値をそれぞれ求めなさい。
この動画を見る
入試問題 立教新座高等学校
$x$と$y$は自然数とします。
【方程式】
$4x^2-9y^2=31
を満たす x,y の値をそれぞれ求めなさい。
灘高校の式の値 伝えたいこと、たくさん
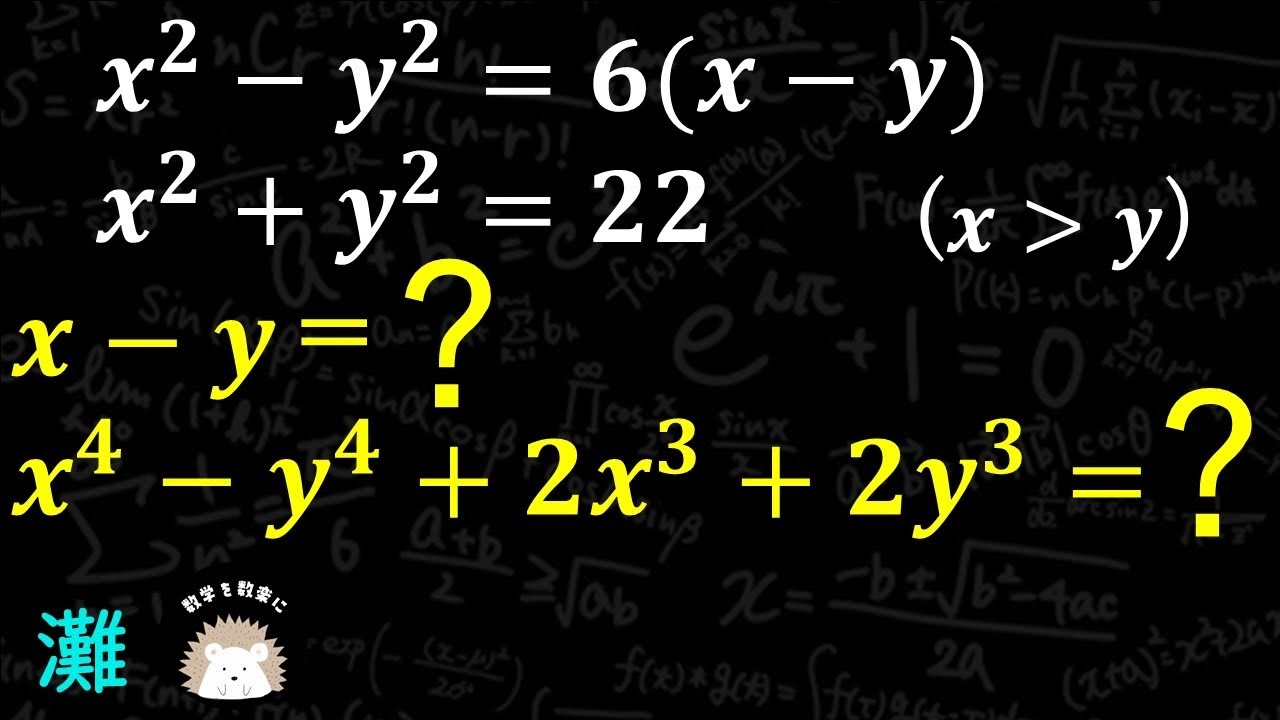
単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2-y^2=6(x-y)$ , $x^2+y^2 = 22$ (x>y)
$x-y=?$
$x^4-y^4+2x^3+2y^3=?$
灘高等学校
この動画を見る
$x^2-y^2=6(x-y)$ , $x^2+y^2 = 22$ (x>y)
$x-y=?$
$x^4-y^4+2x^3+2y^3=?$
灘高等学校
式の値 注意点あり!

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
数学を数楽に
問題文全文(内容文):
$a+b=14$ , $a^2-b^2=56$のときa=? b=?
昭和学院秀英高等学校
この動画を見る
$a+b=14$ , $a^2-b^2=56$のときa=? b=?
昭和学院秀英高等学校
【中学数学】平方根・ルートの足し算をどこよりも分かりやすく 2-4.5【中3数学】

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
$5 \times 2\sqrt{ 3 }$
2⃣
$5\sqrt{ 2 }+7\sqrt{ 2 }$
3⃣
$2\sqrt{ 3 }+5\sqrt{ 2 }+3\sqrt{ 3 }+\sqrt{ 2 }$
この動画を見る
1⃣
$5 \times 2\sqrt{ 3 }$
2⃣
$5\sqrt{ 2 }+7\sqrt{ 2 }$
3⃣
$2\sqrt{ 3 }+5\sqrt{ 2 }+3\sqrt{ 3 }+\sqrt{ 2 }$
【中学数学】連立方程式a,b を求める問題演習 2-5.5【中2数学】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
連立方程式の解が$x=2,y=-1$であるとき、$a,b$の値を求めよ
\begin{eqnarray}
\left\{
\begin{array}{l}
ax+by=3 \\
bx-2ay=18
\end{array}
\right.
\end{eqnarray}
この動画を見る
連立方程式の解が$x=2,y=-1$であるとき、$a,b$の値を求めよ
\begin{eqnarray}
\left\{
\begin{array}{l}
ax+by=3 \\
bx-2ay=18
\end{array}
\right.
\end{eqnarray}
【全てに通じる5分間!】計算:洛南高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#洛南高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 洛南高等学校
次の式を計算せよ。
$\{(-1)^2+(-2)^3-(-3)^4-(-4)^3\} \div (-6)$
1,計算のルールを守る。
2,要領よく処理する。
この動画を見る
入試問題 洛南高等学校
次の式を計算せよ。
$\{(-1)^2+(-2)^3-(-3)^4-(-4)^3\} \div (-6)$
1,計算のルールを守る。
2,要領よく処理する。
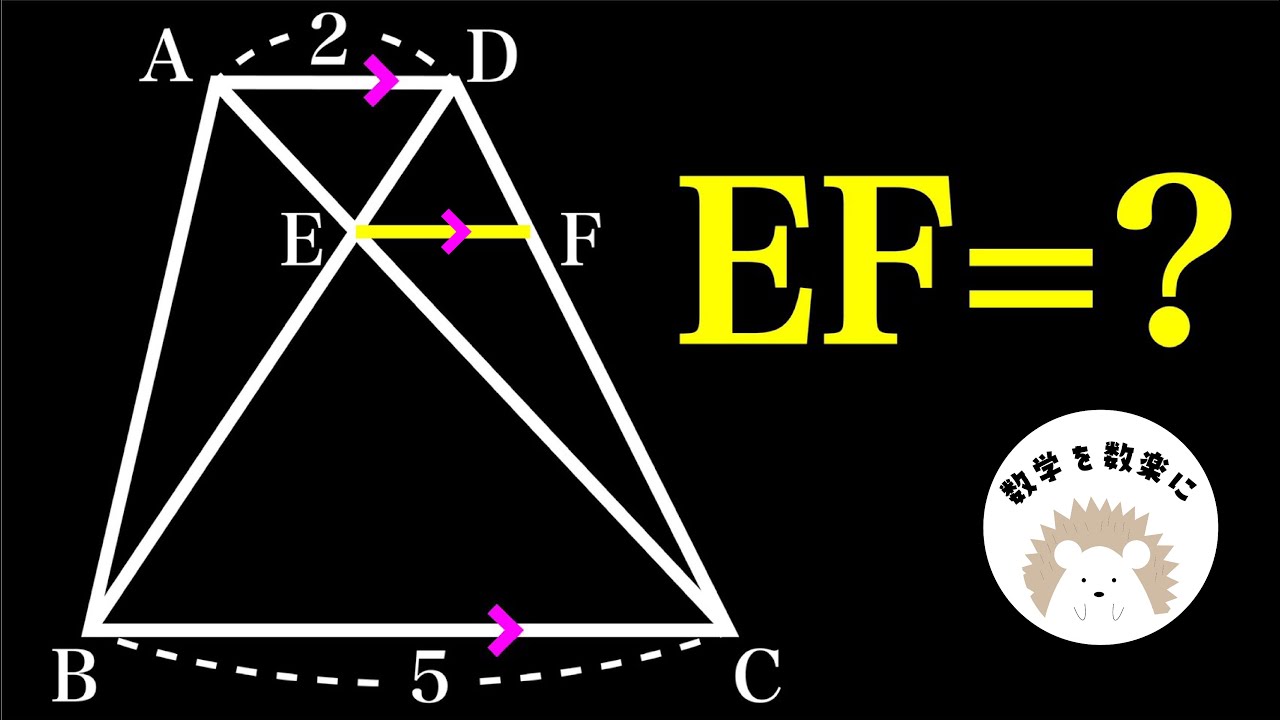
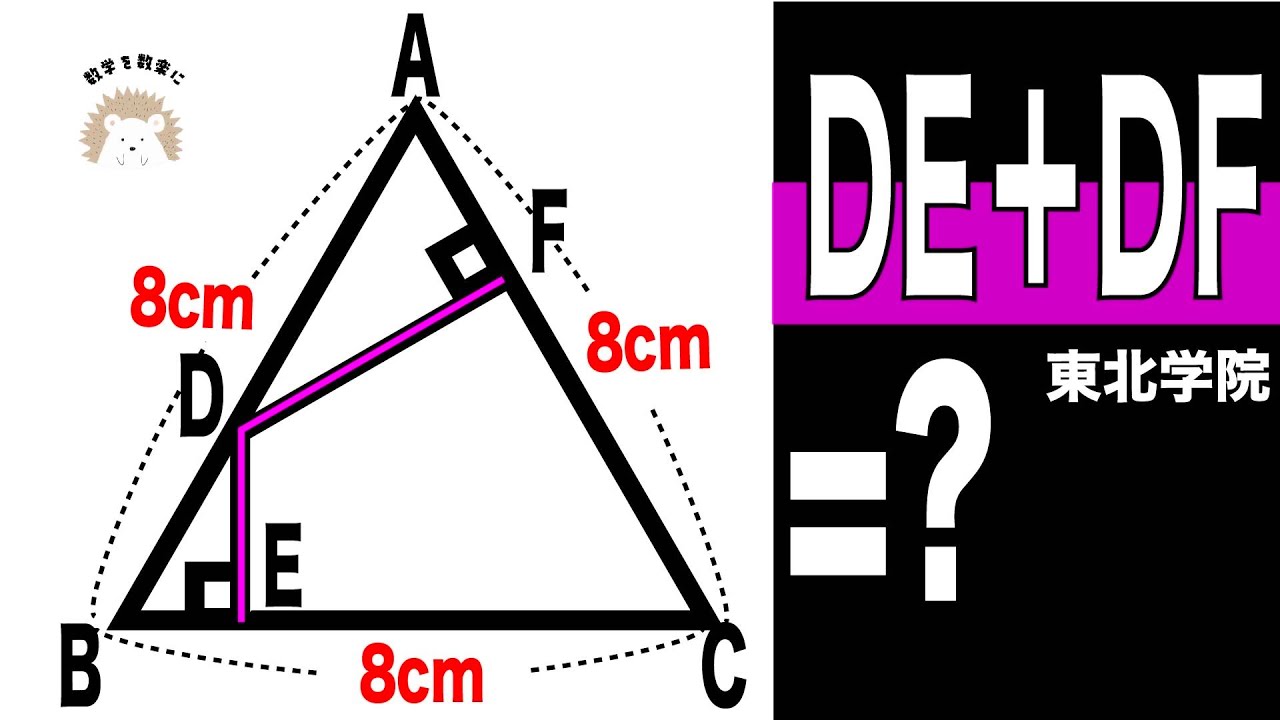
垂線の長さの和=❓ B
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
DE+EF=?
*図は動画内参照
東北学院高等学校
この動画を見る
DE+EF=?
*図は動画内参照
東北学院高等学校
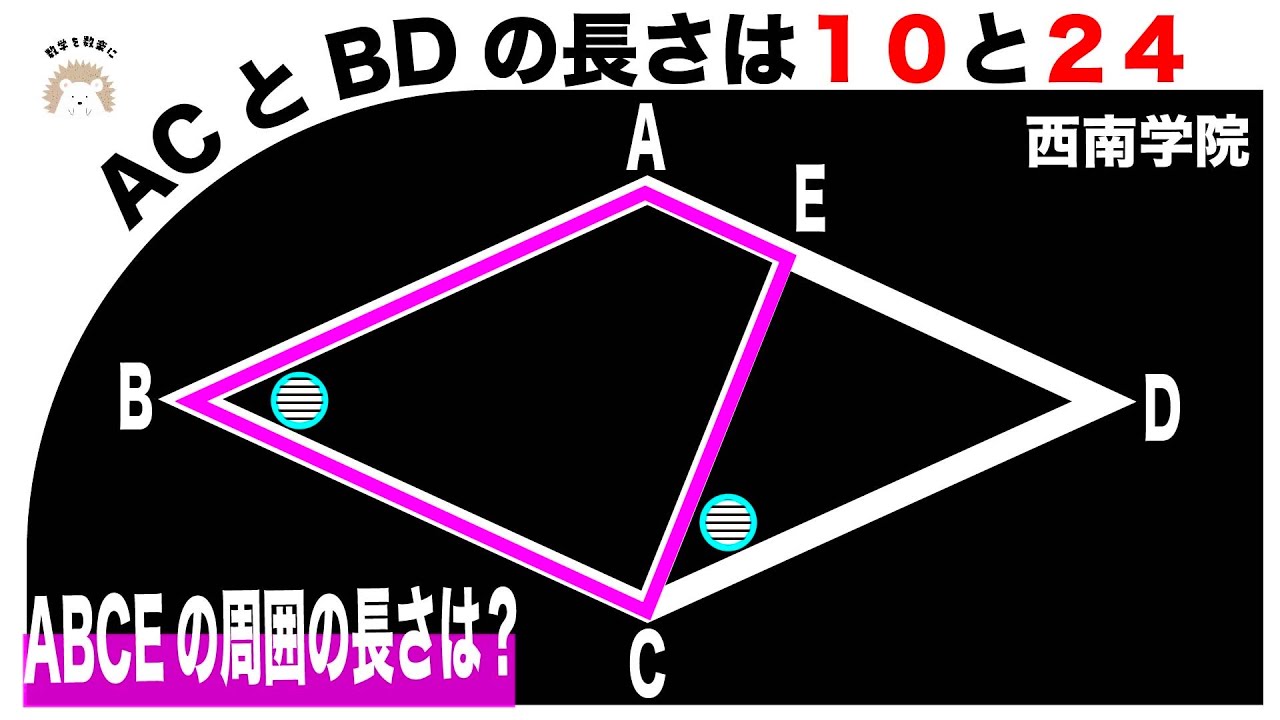
ひし形 気づけば一瞬
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
AC=10 , BD=24
四角形ABCEの周囲の長さ=?
*図は動画内参照
西南学院高等学校
この動画を見る
AC=10 , BD=24
四角形ABCEの周囲の長さ=?
*図は動画内参照
西南学院高等学校
平方根の利用 A

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt {1.23} = a$とする。
$\sqrt{123} + \sqrt{0.0123}$をaで表せ。
福岡大学附属大濠高等学校
この動画を見る
$\sqrt {1.23} = a$とする。
$\sqrt{123} + \sqrt{0.0123}$をaで表せ。
福岡大学附属大濠高等学校
【5分で理解!「それ以外」が難しい!】連立方程式:早稲田大学系属早稲田実業学校高等部~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#早稲田大学系属早稲田実業学校高等部
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 早稲田大学系属早稲田実業学校高等部
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x + y)^2+x^2+y^2+(x-y)^2 = 2019 \\
(x + y)(x-y) = 385
\end{array}
\right.
\end{eqnarray}$
$x \gt 0,y \gt 0$のとき、
連立方程式を解け。
この動画を見る
入試問題 早稲田大学系属早稲田実業学校高等部
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x + y)^2+x^2+y^2+(x-y)^2 = 2019 \\
(x + y)(x-y) = 385
\end{array}
\right.
\end{eqnarray}$
$x \gt 0,y \gt 0$のとき、
連立方程式を解け。
【中学数学】平方根・ルートの大小比較の問題 2-5【中3数学】

単元:
#数学(中学生)#中3数学#平方根
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
次の数を小さい順に並べよ
1⃣
$\sqrt{ 0.2 },2\sqrt{ 2 },\sqrt{ 5 },2$
2⃣
$\sqrt{ 0.7 },0.8,\sqrt{ \displaystyle \frac{1}{2} }$
この動画を見る
次の数を小さい順に並べよ
1⃣
$\sqrt{ 0.2 },2\sqrt{ 2 },\sqrt{ 5 },2$
2⃣
$\sqrt{ 0.7 },0.8,\sqrt{ \displaystyle \frac{1}{2} }$
高校入試 図形 意外と苦戦するかも 図形
式の値 日大習志野

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=\frac{1}{a}+3$ , $y=\frac{1}{a}-3$のとき
$xy^3+x^3y$をaで表せ。
日本大学習志野高等学校
この動画を見る
$x=\frac{1}{a}+3$ , $y=\frac{1}{a}-3$のとき
$xy^3+x^3y$をaで表せ。
日本大学習志野高等学校
円の面積の公式の面白い証明を2種類紹介します

単元:
#算数(中学受験)#数学(中学生)#中1数学#平面図形#図形の移動#平面図形その他#平面図形#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
円の面積の公式の面白い証明 2種類紹介動画です
この動画を見る
円の面積の公式の面白い証明 2種類紹介動画です
正しいか、正しくないか 慶應義塾高校(改)

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
正しいか正しくないか?
(ア)a,b,cについてac=bcならばa=b
(イ)a,bについて$a^2+b^2=2ab$ならばa=b
(ウ)a,bについて$a^2>b^2$ならばa>b
慶應義塾高等学校(改)
この動画を見る
正しいか正しくないか?
(ア)a,b,cについてac=bcならばa=b
(イ)a,bについて$a^2+b^2=2ab$ならばa=b
(ウ)a,bについて$a^2>b^2$ならばa>b
慶應義塾高等学校(改)
【中学数学】式の計算の利用の演習~展開の文章題・土地の大きさ~ 1-8.5【中3数学】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
縦am、横2amの長方形の土地があります。
この土地の縦を5m長くし、横を3m短くすると、面積はもとの土地よりどれだけ大きくなるか。
また、このとき、面積が55m²大きくなるとすると、もとの土地の縦の長さは何mですか。
この動画を見る
縦am、横2amの長方形の土地があります。
この土地の縦を5m長くし、横を3m短くすると、面積はもとの土地よりどれだけ大きくなるか。
また、このとき、面積が55m²大きくなるとすると、もとの土地の縦の長さは何mですか。
【中学数学】平方根・ルートの割り算の演習 2-4.5【中3数学】

単元:
#数学(中学生)#中3数学#平方根
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
$\sqrt{ 15 } \div (- \sqrt{ 3 })$
2⃣
$\sqrt{ \displaystyle \frac{7}{28} } \div \sqrt{ \displaystyle \frac{5}{20} }$
3⃣
$\sqrt{ 2 } \div \sqrt{ 5 }$
この動画を見る
1⃣
$\sqrt{ 15 } \div (- \sqrt{ 3 })$
2⃣
$\sqrt{ \displaystyle \frac{7}{28} } \div \sqrt{ \displaystyle \frac{5}{20} }$
3⃣
$\sqrt{ 2 } \div \sqrt{ 5 }$
