数学検定・数学甲子園・数学オリンピック等
数学検定・数学甲子園・数学オリンピック等
#50数検1級１次 過去問 重積分の積分順序の変更
単元：
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{2}dy\displaystyle \int_{y}^{2}x\sqrt{ x^3+1 }\ dx$を計算せよ。
この動画を見る
$\displaystyle \int_{0}^{2}dy\displaystyle \int_{y}^{2}x\sqrt{ x^3+1 }\ dx$を計算せよ。
数学ゴールデン#2【漫画】で紹介された数オリの問題の解答がなかったから作成してみた。
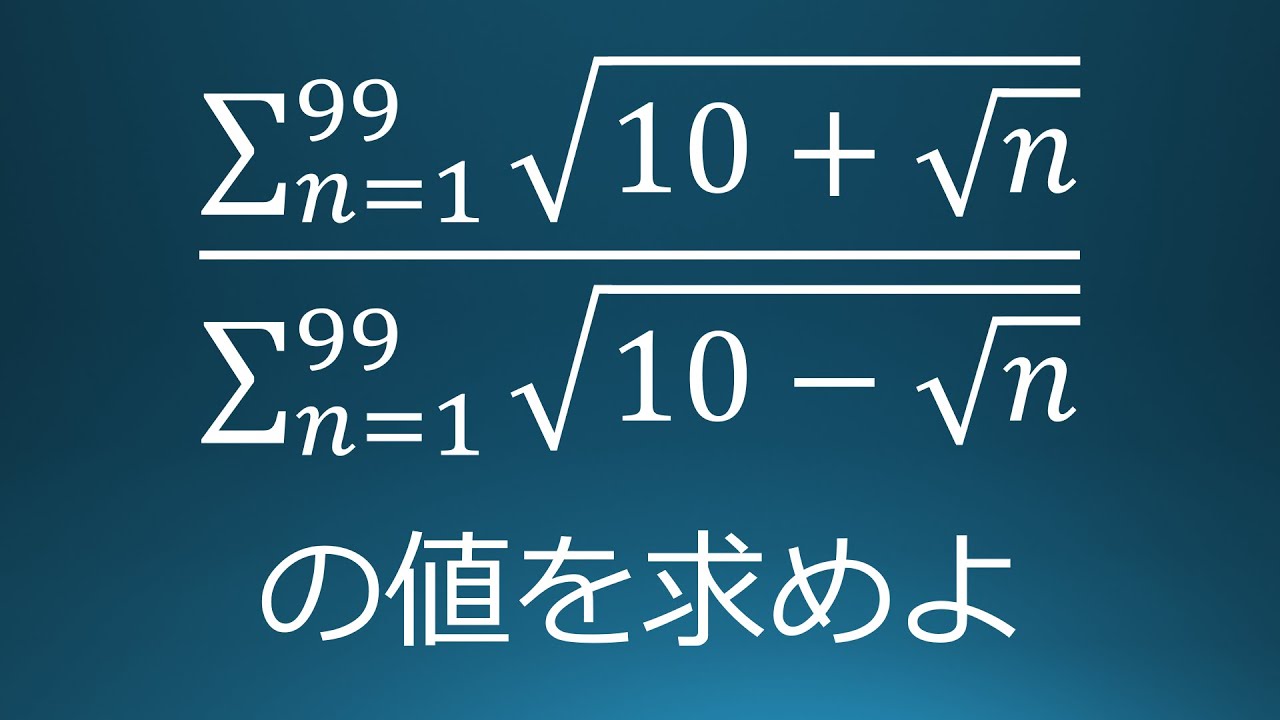
単元：
#数学検定・数学甲子園・数学オリンピック等#数学オリンピック
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \frac{\sqrt{ 10+\sqrt{ 1 } }+\sqrt{ 10+\sqrt{ 2 } }+・・・+\sqrt{ 10+\sqrt{ 99 } }}{\sqrt{ 10-\sqrt{ 1 } }+\sqrt{ 10-\sqrt{ 2 } }+・・・+\sqrt{ 10-\sqrt{ 99 } }}$を計算せよ。
出典：数学ゴールデン 数学オリンピック
この動画を見る
$\displaystyle \frac{\sqrt{ 10+\sqrt{ 1 } }+\sqrt{ 10+\sqrt{ 2 } }+・・・+\sqrt{ 10+\sqrt{ 99 } }}{\sqrt{ 10-\sqrt{ 1 } }+\sqrt{ 10-\sqrt{ 2 } }+・・・+\sqrt{ 10-\sqrt{ 99 } }}$を計算せよ。
出典：数学ゴールデン 数学オリンピック
【数検2級】数学検定2級 問題9～問題12
単元：
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定2級
指導講師：
理数個別チャンネル
問題文全文(内容文)：
問題9.整式$x^4＋3x^2＋3x-2$を$x^2-2x+2$で割ったときの余りを求めなさい。
問題10.xy平面上の2点Ａ(-2,0)，Ｂ(4,-3)を結んでできる線分ABを2:1に内分する点Pの座標を求めなさい。
問題11.次の計算をしなさい。
$\log_{10}\dfrac{1}{36}+2\log_{10}\dfrac{6}{5}-\log_{10}4$
問題12.$0\leqq\theta\leqq 2\pi$のとき、次の方程式を満たす$\theta$の値を求めなさい。
$-2\sin\theta+1＝0$
この動画を見る
問題9.整式$x^4＋3x^2＋3x-2$を$x^2-2x+2$で割ったときの余りを求めなさい。
問題10.xy平面上の2点Ａ(-2,0)，Ｂ(4,-3)を結んでできる線分ABを2:1に内分する点Pの座標を求めなさい。
問題11.次の計算をしなさい。
$\log_{10}\dfrac{1}{36}+2\log_{10}\dfrac{6}{5}-\log_{10}4$
問題12.$0\leqq\theta\leqq 2\pi$のとき、次の方程式を満たす$\theta$の値を求めなさい。
$-2\sin\theta+1＝0$
【数検2級】数学検定2級 問題4～問題8
単元：
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定2級
指導講師：
理数個別チャンネル
問題文全文(内容文)：
問題4. 2次関数$ｙ＝x^2+4x+a$の最小値が1となるように、定数aの値を定めなさい。
問題5. $0°\leqq\theta\leqq 180°$とします。$\tan\theta＝\dfrac{1}{2}$のとき、$\cos\theta$の値を求めなさい。
問題6. 3個のさいころを同時に振るとき、3個とも異なる目が出る確率を求めなさい。ただし、さいころの目は1から6まであり、どの目も出る確率は等しいものとします。
問題7. 2進法で表された数$1011010_{(2)}$を10進法で表しなさい。
問題8. 次の計算をしなさい。$\dfrac{x+1}{x+2} -\dfrac{x+2}{x+3}$
この動画を見る
問題4. 2次関数$ｙ＝x^2+4x+a$の最小値が1となるように、定数aの値を定めなさい。
問題5. $0°\leqq\theta\leqq 180°$とします。$\tan\theta＝\dfrac{1}{2}$のとき、$\cos\theta$の値を求めなさい。
問題6. 3個のさいころを同時に振るとき、3個とも異なる目が出る確率を求めなさい。ただし、さいころの目は1から6まであり、どの目も出る確率は等しいものとします。
問題7. 2進法で表された数$1011010_{(2)}$を10進法で表しなさい。
問題8. 次の計算をしなさい。$\dfrac{x+1}{x+2} -\dfrac{x+2}{x+3}$
【数検2級】数学検定2級 問題1～問題3
単元：
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定2級
指導講師：
理数個別チャンネル
問題文全文(内容文)：
問題１.次の式を展開して計算しなさい。
$(ｘ＋1)^2(ｘ－1)^2$
問題２.次の式を因数分解しなさい。
$8a^2＋22a＋15$
問題３.次の式の分母を有理化しなさい。
$\dfrac{2}{\sqrt7}-1$
この動画を見る
問題１.次の式を展開して計算しなさい。
$(ｘ＋1)^2(ｘ－1)^2$
問題２.次の式を因数分解しなさい。
$8a^2＋22a＋15$
問題３.次の式の分母を有理化しなさい。
$\dfrac{2}{\sqrt7}-1$
数学ゴールデン【漫画】で紹介された数オリの問題の解答がなかったから作成してみた。
単元：
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#数と式#式の計算（整式・展開・因数分解）#数学オリンピック#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$0 \lt x$：実数
$x+\sqrt{ x(x+1) }+\sqrt{ x(x+2) }+\sqrt{ (x+1)(x+2) }=2$を解け。
出典：数学ゴールデン 数学オリンピック
この動画を見る
$0 \lt x$：実数
$x+\sqrt{ x(x+1) }+\sqrt{ x(x+2) }+\sqrt{ (x+1)(x+2) }=2$を解け。
出典：数学ゴールデン 数学オリンピック
#49 数検1級1次 過去問 根号を外す
単元：
#数Ⅰ#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#数と式#２次関数#複素数と方程式#式の計算（整式・展開・因数分解）#2次方程式と2次不等式#2次関数とグラフ#解と判別式・解と係数の関係#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\sqrt[ 3 ]{ -5+2\sqrt{ 13 } }\ $の二重根号をはずせ
この動画を見る
$\sqrt[ 3 ]{ -5+2\sqrt{ 13 } }\ $の二重根号をはずせ
【数学】海賊と金貨
単元：
#数学検定・数学甲子園・数学オリンピック等#その他#その他#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
100枚の金貨を海賊が見つけ、これを配分する。
まず海賊の親分が分け方を提案し、親分を含む全員で投票。
半分以上の海賊がその案に賛成であれば、
金貨はその分け方で分け、
賛成が足りなければ親分を除外し、やり直す。除外されると
以降、金貨が分配されず、また投票もできなくなる。
また、以降同様の分配にも参加できなくなる。
やり直しは、次に偉い海賊が提案し、同じルールで投票。
また否決されれば海賊がその海賊が除外され、
次に偉い海賊が分配の仕方を提案する。
全員が十分に賢く利己的な時、
親分が得られる金貨の最大枚とその分配を答えよ
この動画を見る
100枚の金貨を海賊が見つけ、これを配分する。
まず海賊の親分が分け方を提案し、親分を含む全員で投票。
半分以上の海賊がその案に賛成であれば、
金貨はその分け方で分け、
賛成が足りなければ親分を除外し、やり直す。除外されると
以降、金貨が分配されず、また投票もできなくなる。
また、以降同様の分配にも参加できなくなる。
やり直しは、次に偉い海賊が提案し、同じルールで投票。
また否決されれば海賊がその海賊が除外され、
次に偉い海賊が分配の仕方を提案する。
全員が十分に賢く利己的な時、
親分が得られる金貨の最大枚とその分配を答えよ
#48 数検1級2次 過去問 整数問題
単元：
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$m,n$：正の整数
$3^m=n^2-117^2$を満たす$m,n$の値を求めよ。
この動画を見る
$m,n$：正の整数
$3^m=n^2-117^2$を満たす$m,n$の値を求めよ。
#47 数検1級1次 過去問 二項定理
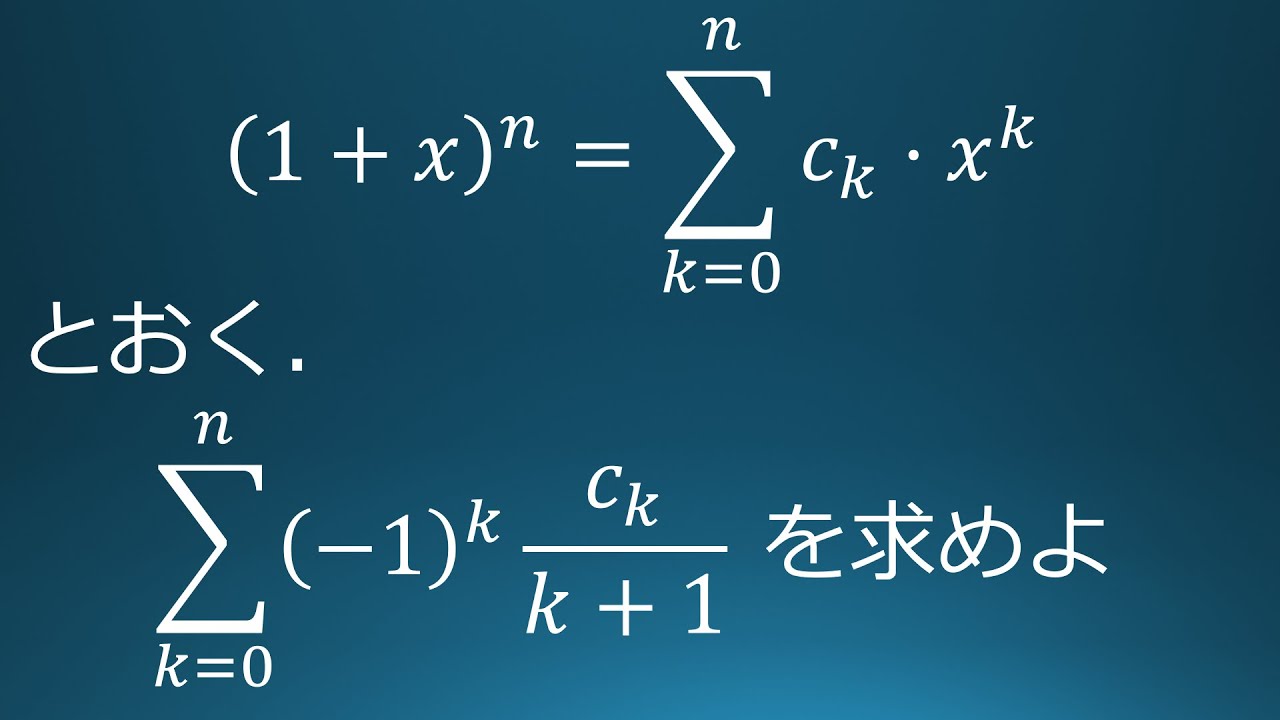
単元：
#数Ⅰ#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#式と証明#微分法と積分法#整式の除法・分数式・二項定理#不定積分・定積分#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$(1+x)^n$を$c_0+c_1x+・・・+c_nx^n$とおく。
$\displaystyle \sum_{k=1}^n(-1)^k\displaystyle \frac{c_k}{k+1}$の値を求めよ。
この動画を見る
$(1+x)^n$を$c_0+c_1x+・・・+c_nx^n$とおく。
$\displaystyle \sum_{k=1}^n(-1)^k\displaystyle \frac{c_k}{k+1}$の値を求めよ。
【数A】確率：期待値の巧みな利用
単元：
#数A#数学検定・数学甲子園・数学オリンピック等#場合の数と確率#確率#その他#その他#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
【高校数学 数学A 場合の数と確率 期待値】
無限に続く階段がある。さいころを振って出た目の数だけ登っては立ち止まるということを繰り返す。このとき十分上の方のとある段に立ち止まる確率を求めよ。
（出典 上級国家公務員試験より）
この動画を見る
【高校数学 数学A 場合の数と確率 期待値】
無限に続く階段がある。さいころを振って出た目の数だけ登っては立ち止まるということを繰り返す。このとき十分上の方のとある段に立ち止まる確率を求めよ。
（出典 上級国家公務員試験より）
#39 数検1級1次 過去問 解と係数の関係 整数問題
単元：
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$m,n:$正の整数
$x^3-mx^2+nx-n=0$のすべての解が正の整数であるような組$(m,n)$を求めよ。
この動画を見る
$m,n:$正の整数
$x^3-mx^2+nx-n=0$のすべての解が正の整数であるような組$(m,n)$を求めよ。
#38 数検1級1次 過去問 解と係数の関係
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#解と判別式・解と係数の関係#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$z^3+2z^2+2z+1=0$の3つの解を$\alpha,\beta,\gamma$とする
$\alpha^{2019}+\beta^{2019}+\gamma^{2019}$の値を求めよ。
この動画を見る
$z^3+2z^2+2z+1=0$の3つの解を$\alpha,\beta,\gamma$とする
$\alpha^{2019}+\beta^{2019}+\gamma^{2019}$の値を求めよ。
#37 数検1級1次 過去問 重積分
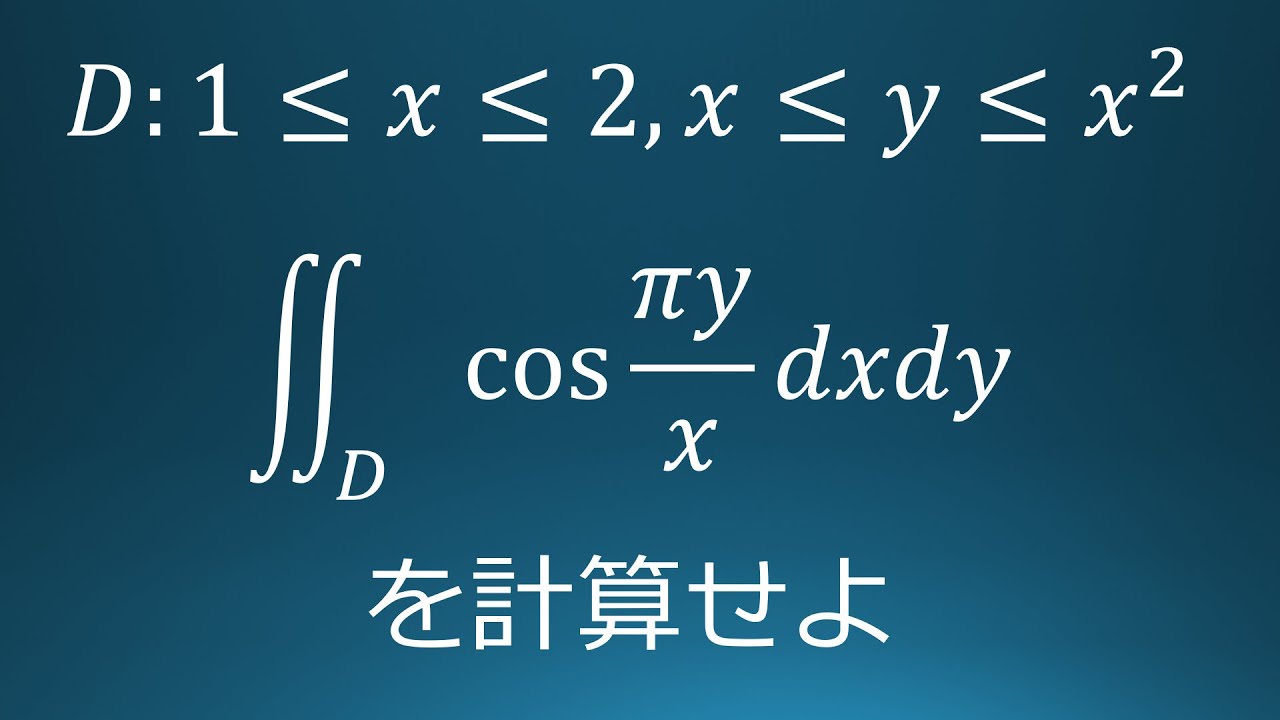
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$D:1 \leqq x \leqq 2,x \leqq y \leqq x^2$
$\displaystyle \int \displaystyle \int \cos\displaystyle \frac{\pi y}{x}\ dxdy$を計算せよ。
この動画を見る
$D:1 \leqq x \leqq 2,x \leqq y \leqq x^2$
$\displaystyle \int \displaystyle \int \cos\displaystyle \frac{\pi y}{x}\ dxdy$を計算せよ。
#36 数検1級1次 過去問 積分
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-1}^{1}\sqrt{ \displaystyle \frac{1+x}{1-x} }\ dx$を計算せよ。
この動画を見る
$\displaystyle \int_{-1}^{1}\sqrt{ \displaystyle \frac{1+x}{1-x} }\ dx$を計算せよ。
#35 数検１級１次 過去問 複素数
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#複素数平面#複素数#複素数平面#数学検定#数学検定1級#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$\sqrt{ 1+\sqrt{ 3 }i }+\sqrt{ 1-\sqrt{ 3 }i }$を簡単にせよ
ただし、外側の平方根の実数部の値は正とする。
この動画を見る
$\sqrt{ 1+\sqrt{ 3 }i }+\sqrt{ 1-\sqrt{ 3 }i }$を簡単にせよ
ただし、外側の平方根の実数部の値は正とする。
#34 数検1級1次 過去問 積分
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\infty}\displaystyle \frac{1}{(x^2+1)^4}\ dx$を計算せよ。
この動画を見る
$\displaystyle \int_{0}^{\infty}\displaystyle \frac{1}{(x^2+1)^4}\ dx$を計算せよ。
#33 数検1級1次 過去問 区分求積法
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty }\displaystyle \sum_{k=1}^n\displaystyle \frac{1}{\sqrt{ 2nk-k^2 }}$の極限値を求めよ。
この動画を見る
$\displaystyle \lim_{ n \to \infty }\displaystyle \sum_{k=1}^n\displaystyle \frac{1}{\sqrt{ 2nk-k^2 }}$の極限値を求めよ。
#32 数検1級1次 過去問 複素数の方程式
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#複素数平面#複素数#複素数平面#数学検定#数学検定1級#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$z:$複素数
方程式$z^2-z+i\bar{ z }=i$を解け。
この動画を見る
$z:$複素数
方程式$z^2-z+i\bar{ z }=i$を解け。
#31 数検1級1次 過去問 整数問題
単元：
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$x^3-y^3=331$を満たす正の整数$x,y$を求めよ。
この動画を見る
$x^3-y^3=331$を満たす正の整数$x,y$を求めよ。
#30 数検1級1次 過去問 複雑な定積分
単元：
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#不定積分#定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
定積分
$\displaystyle \int_{-1}^{1}\displaystyle \frac{x^4+2x^3+4x^2+6x+2}{x^3+2x^2+2x+4}\ dx$を計算せよ。
この動画を見る
定積分
$\displaystyle \int_{-1}^{1}\displaystyle \frac{x^4+2x^3+4x^2+6x+2}{x^3+2x^2+2x+4}\ dx$を計算せよ。
#29 数検1級1次 過去問 解と係数の関係
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#解と判別式・解と係数の関係#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$x^3+2x^2+4x+7=0$の3つの解を$\alpha,\beta,\gamma$とする
$\alpha^4,\beta^4,\gamma^4$の値を求めよ。
この動画を見る
$x^3+2x^2+4x+7=0$の3つの解を$\alpha,\beta,\gamma$とする
$\alpha^4,\beta^4,\gamma^4$の値を求めよ。
#28 数検1級1次 過去問 Arctanの加法定理
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#三角関数#三角関数とグラフ#数学検定#数学検定1級
指導講師：
ますただ
問題文全文(内容文)：
$\tan^{-1}1+\tan^{-1}2+\tan^{-1}3$の値を求めよ。
この動画を見る
$\tan^{-1}1+\tan^{-1}2+\tan^{-1}3$の値を求めよ。
#27 数検1級1次 過去問 整数問題
単元：
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$x,y:$正の整数
$x+y=316$
$x:13$の倍数
$y:11$の倍数
をみたす組$(x,y)$をすべて求めよ。
この動画を見る
$x,y:$正の整数
$x+y=316$
$x:13$の倍数
$y:11$の倍数
をみたす組$(x,y)$をすべて求めよ。
#26 数検1級1次 過去問 複雑な方程式
単元：
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#数と式#数学検定#数学検定1級
指導講師：
ますただ
問題文全文(内容文)：
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y+z=6 \\
x^3+y^3+z^3=36 \\
xyz=6
\end{array}
\right.
\end{eqnarray}$
において、$x \gt y \gt z$を満たす解を求めよ。
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y+z=6 \\
x^3+y^3+z^3=36 \\
xyz=6
\end{array}
\right.
\end{eqnarray}$
において、$x \gt y \gt z$を満たす解を求めよ。
#25 数検1級1次 過去問 複雑な方程式
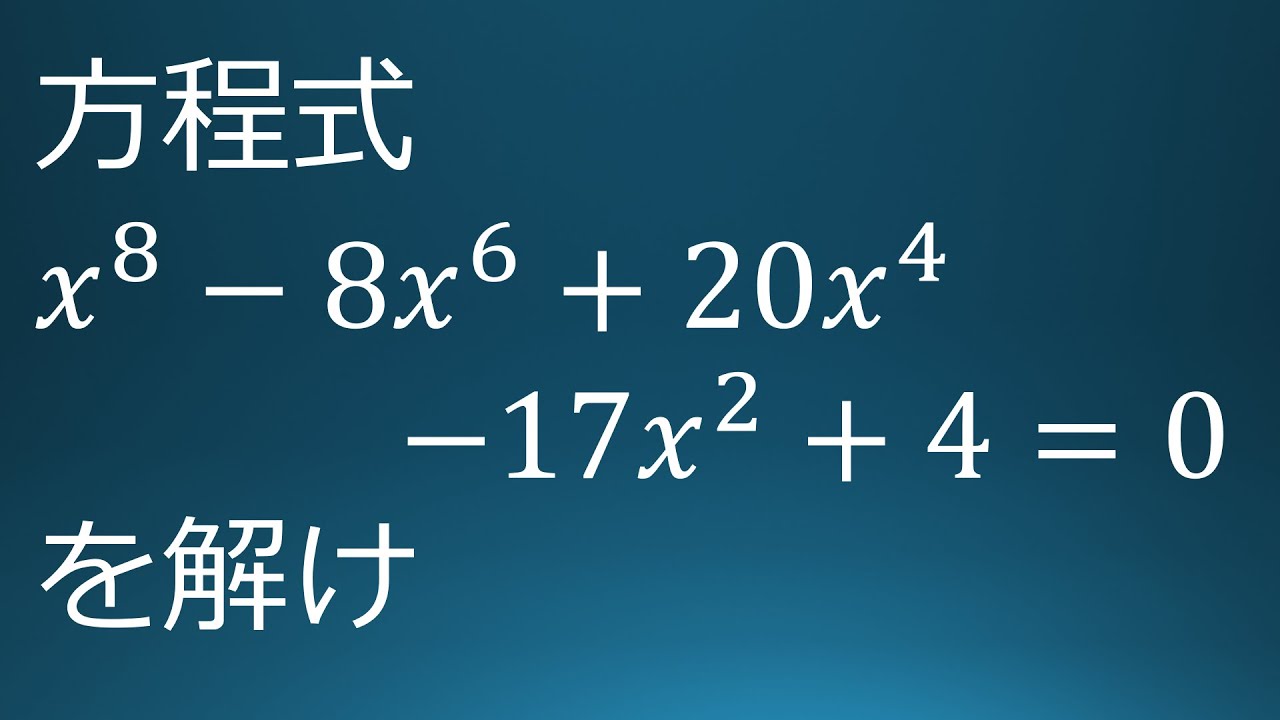
単元：
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#数と式#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
方程式
$x^8-8x^6+20x^4-17x^2+4=0$を解け。
この動画を見る
方程式
$x^8-8x^6+20x^4-17x^2+4=0$を解け。
#23 数検1級1次過去問 行列
単元：
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級
指導講師：
ますただ
問題文全文(内容文)：
$A=(\begin{eqnarray}
1\ 2\ 2 \\
2\ 1\ 2 \\
2\ 2\ 1
\end{eqnarray})$
$A^5$を求めよ。
この動画を見る
$A=(\begin{eqnarray}
1\ 2\ 2 \\
2\ 1\ 2 \\
2\ 2\ 1
\end{eqnarray})$
$A^5$を求めよ。
#22 数検1級1次 過去問 無限級数
単元：
#数学検定・数学甲子園・数学オリンピック等#関数と極限#関数の極限#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \sum_{i=1}^\infty\ \tan^{-1}\displaystyle \frac{1}{k^2+k+1}$を求めよ。
この動画を見る
$\displaystyle \sum_{i=1}^\infty\ \tan^{-1}\displaystyle \frac{1}{k^2+k+1}$を求めよ。
#21 数検1級1次 過去問 無限級数
単元：
#数学検定・数学甲子園・数学オリンピック等#関数と極限#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \sum_{k=1}^\infty\ \displaystyle \frac{k}{1+k^2+k^4}$を求めよ。
この動画を見る
$\displaystyle \sum_{k=1}^\infty\ \displaystyle \frac{k}{1+k^2+k^4}$を求めよ。
【高校化学】構造決定II②「立体異性体」（シス・トランス異性体、鏡像異性体、ジアステレオマー）【有機化学#12】
単元：
#化学#有機化合物の特徴と構造#脂肪族炭化水素#酸素を含む脂肪族化合物#数学検定5級#理科(高校生)
指導講師：
受験メモ山本
問題文全文(内容文)：
立体異性体（シス・トランス異性体、鏡像異性体、ジアステレオマー）の説明動画です
この動画を見る
立体異性体（シス・トランス異性体、鏡像異性体、ジアステレオマー）の説明動画です