 福田次郎
福田次郎
 福田次郎
福田次郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
福田のおもしろ数学107〜京都大学の有名問題〜車両の色塗り

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$n$両編成($n$≧2)に各車両に赤、青、黄の3色のいずれかを塗る。隣り合った車両の少なくとも一方が赤になるような塗り方は何通りあるか。
この動画を見る
$n$両編成($n$≧2)に各車両に赤、青、黄の3色のいずれかを塗る。隣り合った車両の少なくとも一方が赤になるような塗り方は何通りあるか。
福田の数学〜北海道大学2024年理系第3問〜関数方程式の解

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ 次の問いに答えよ。
(1)$\alpha$ を実数とする。次のように定められた数列$\left\{a_n\right\}$ の一般項を求めよ。
$a_1$=$\alpha$, $a_{n+1}$=$\frac{1}{2}a_n$+1 ($n$=1,2,3,...)
(2)関数$f_1(x)$, $f_2(x)$, $f_3(x)$,... を次の関係式で定める。
$f_1(x)$=$3x$
$f_{n+1}(x)$=$(n+2)x^{n+1}$+$\displaystyle\left(\int_0^1f_n(t)dt\right)x$ ($n$=1,2,3,...)
関数$f_n(x)$を$x$と$n$の式で表せ。
この動画を見る
$\Large{\boxed{3}}$ 次の問いに答えよ。
(1)$\alpha$ を実数とする。次のように定められた数列$\left\{a_n\right\}$ の一般項を求めよ。
$a_1$=$\alpha$, $a_{n+1}$=$\frac{1}{2}a_n$+1 ($n$=1,2,3,...)
(2)関数$f_1(x)$, $f_2(x)$, $f_3(x)$,... を次の関係式で定める。
$f_1(x)$=$3x$
$f_{n+1}(x)$=$(n+2)x^{n+1}$+$\displaystyle\left(\int_0^1f_n(t)dt\right)x$ ($n$=1,2,3,...)
関数$f_n(x)$を$x$と$n$の式で表せ。
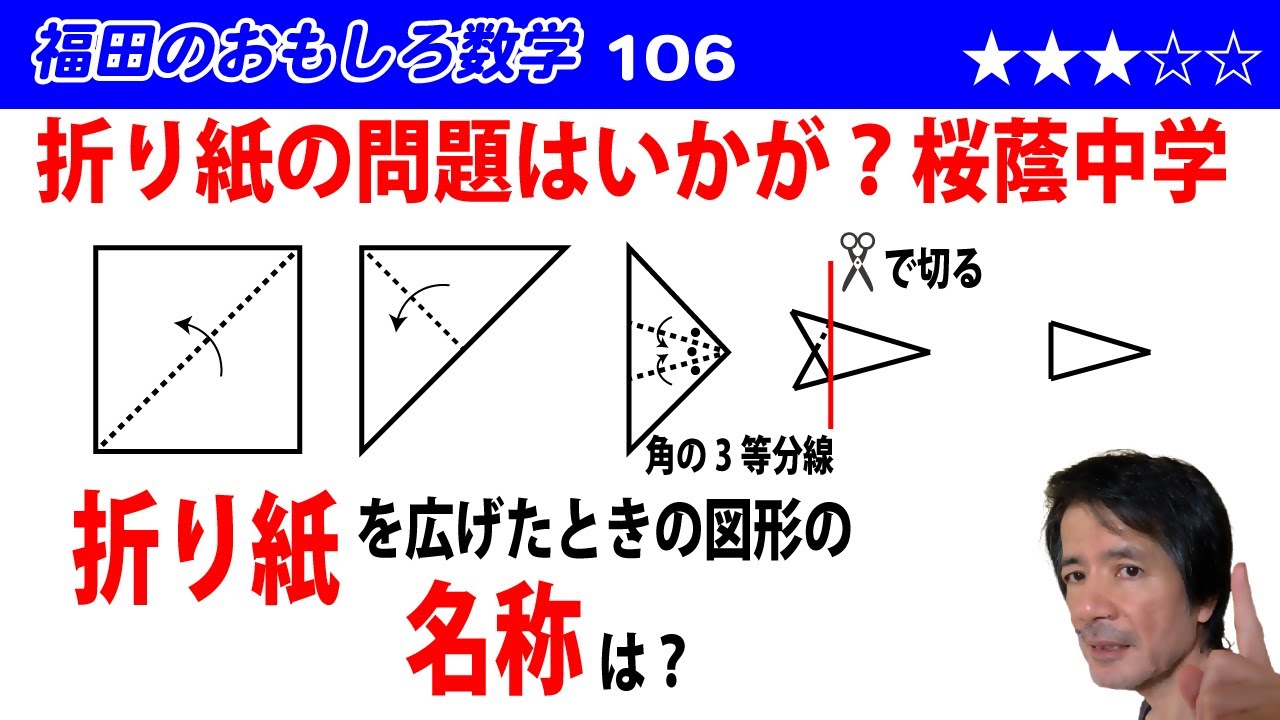
福田のおもしろ数学106〜折り紙の問題〜折ってから一部を切り取り元にもどした図形
福田の数学〜北海道大学2024年理系第2問〜反復試行の確率と条件付き確率

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 各面に1つずつ数が書かれた正八面体のさいころがある。「1」、「2」、「3」が書かれた面がそれぞれ1つずつあり、残りの5つの面には「0」が書かれている。このさいころを水平な面に投げて、出た面に書かれた数を持ち点に加えるという試行を考える。最初の持ち点は0とし、この試行を繰り返す。例えば、3回の試行を行ったとき、出た面に書かれた数が「0」、「2」、「3」であれば、持ち点は5となる。なお、さいころが水平な床面にあるとき、さいころの上部の水平な面を出た面と呼ぶ。また、さいころを投げるとき、各面が出ることは同様に確からしいとする。
(1)この試行を$n$回行ったとき、持ち点が2以下である確率を求めよ。ただし、$n$は2以上の自然数とする。
(2)この試行を4回行って持ち点が10以上であった時に、さらにこの試行を2回行って持ち点が17以上である条件付き確率を求めよ。
この動画を見る
$\Large\boxed{2}$ 各面に1つずつ数が書かれた正八面体のさいころがある。「1」、「2」、「3」が書かれた面がそれぞれ1つずつあり、残りの5つの面には「0」が書かれている。このさいころを水平な面に投げて、出た面に書かれた数を持ち点に加えるという試行を考える。最初の持ち点は0とし、この試行を繰り返す。例えば、3回の試行を行ったとき、出た面に書かれた数が「0」、「2」、「3」であれば、持ち点は5となる。なお、さいころが水平な床面にあるとき、さいころの上部の水平な面を出た面と呼ぶ。また、さいころを投げるとき、各面が出ることは同様に確からしいとする。
(1)この試行を$n$回行ったとき、持ち点が2以下である確率を求めよ。ただし、$n$は2以上の自然数とする。
(2)この試行を4回行って持ち点が10以上であった時に、さらにこの試行を2回行って持ち点が17以上である条件付き確率を求めよ。
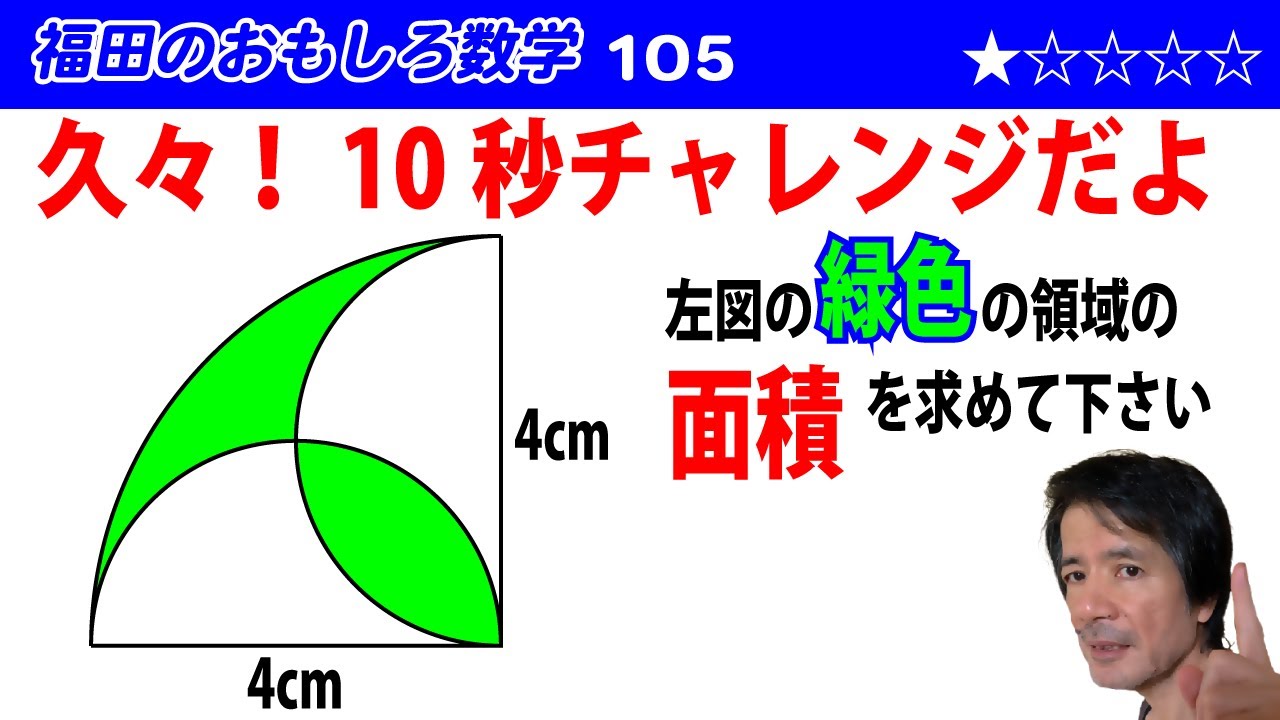
福田のおもしろ数学105〜10秒チャレンジ〜円弧と円弧で囲まれた図形の面積
福田の数学〜北海道大学2024年理系第1問〜点の一致条件と軌跡

単元:
#平面上の曲線#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ $t$を実数とし、$xy$平面上の点P($\cos 2t$, $\cos t$)および点Q($\sin t$, $\sin 2t$)を考える。
(1)点Pと点Qが一致するような$t$の値をすべて求めよ。
(2)$t$が0<$t$<$2\pi$ の範囲で変化するとき、点Pの軌跡を$xy$平面上に図示せよ。
ただし、$x$軸、$y$軸との共有点がある場合は、それらの座標を求め、図中に記せ。
この動画を見る
$\Large\boxed{1}$ $t$を実数とし、$xy$平面上の点P($\cos 2t$, $\cos t$)および点Q($\sin t$, $\sin 2t$)を考える。
(1)点Pと点Qが一致するような$t$の値をすべて求めよ。
(2)$t$が0<$t$<$2\pi$ の範囲で変化するとき、点Pの軌跡を$xy$平面上に図示せよ。
ただし、$x$軸、$y$軸との共有点がある場合は、それらの座標を求め、図中に記せ。
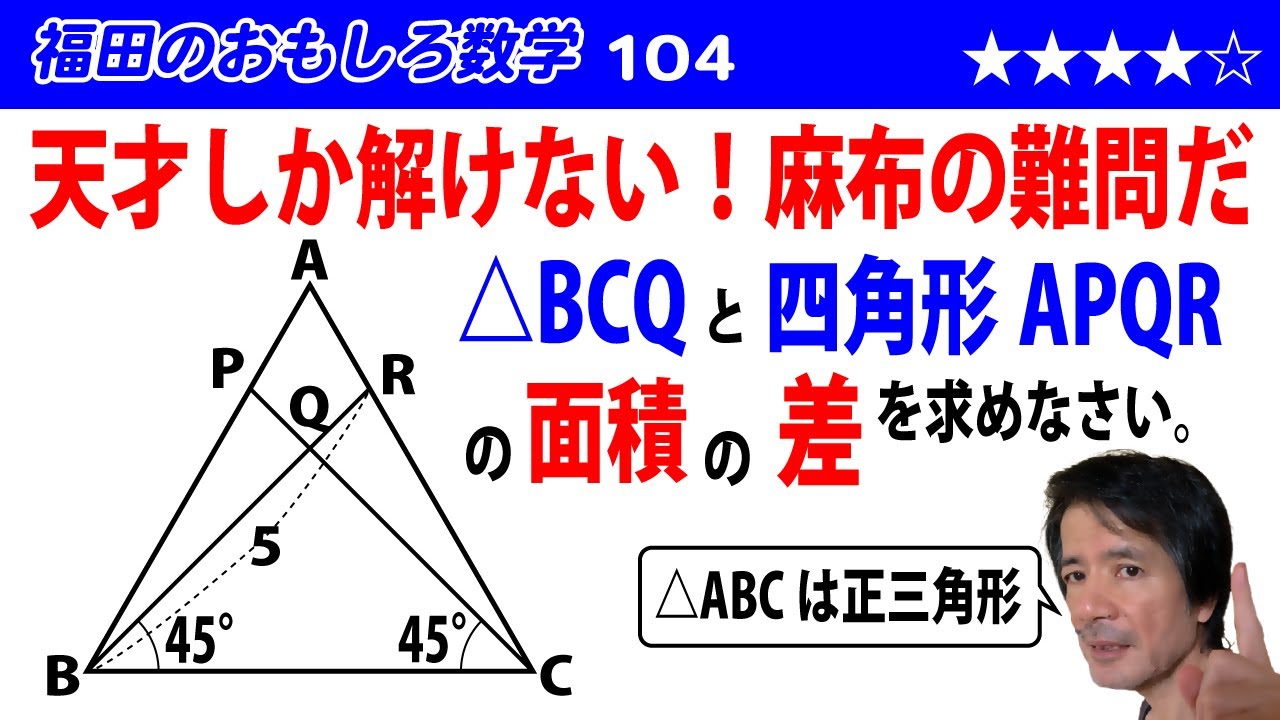
福田のおもしろ数学104〜麻布中学の算数〜三角形と四角形の面積の差
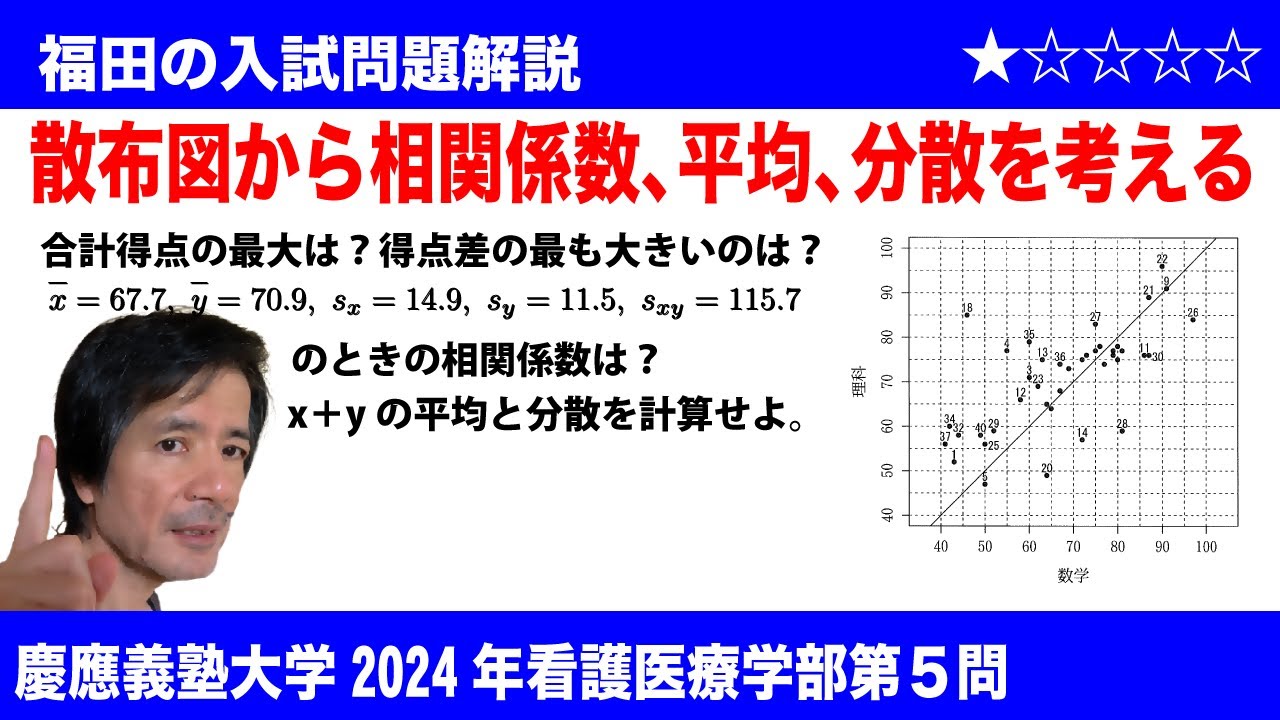
福田の数学〜慶應義塾大学2024年看護医療学部第5問〜散布図と相関係数と分散
単元:
#データの分析#データの分析#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 下図(※動画参照)は、あるクラスの40人の生徒の数学と理科の試験得点の散布図である。
データ点の近くの数値はそのデータ点の生徒の出席番号である。
(1)数学と理科の合計得点が最も高い生徒の出席番号は$\boxed{\ \ ヒ\ \ }$である。また、数学と理科の得点差の絶対値が最も大きい生徒の出席番号は$\boxed{\ \ フ\ \ }$である。
(2)数学と理科それぞれの得点の平均値を$\bar{x}$, $\bar{y}$、標準偏差を$s_x$, $s_y$、数学と理科の得点の共分散を$s_{xy}$と表すと、これらの数値は以下であった。
$\bar{x}$=67.7, $\bar{y}$=70.9, $s_x$=14.9, $s_y$=11.5, $s_{xy}$=115.7
数学の得点と理科の得点の相関係数は$\boxed{\ \ ヘ\ \ }$である。なお、答えは小数第3位を四捨五入し、小数第2位まで求めなさい。
(3)各生徒の数学の得点を$x_1$, $x_2$, ..., $x_{40}$、理科の得点を$y_1$, $y_2$, ..., $y_{40}$で表す。
数学と理科の合計得点$x_1$+$y_1$, $x_2$+$y_2$, ..., $x_{40}$+$y_{40}$の平均値は$\bar{x}$, $\bar{y}$を用いると$\boxed{\ \ ホ\ \ }$と表せる。合計得点の分散は、
$\displaystyle\frac{1}{40}\sum_{i=1}^{40}\left(x_i+y_i-\boxed{\ ホ\ }\right)^2$
であるから、これを式変形すると、合計得点の分散は、$s_x$, $s_y$, $s_{xy}$を用いて$\boxed{\ \ マ\ \ }$と表せる。これらの式に(2)で与えられた数値を入れて計算すると、数学と理科の合計得点の平均値は$\boxed{\ \ ミ\ \ }$、分散は$\boxed{\ \ ム\ \ }$である。なお、答えは小数第2位を四捨五入し、小数第1位まで求めなさい。
この動画を見る
$\Large\boxed{5}$ 下図(※動画参照)は、あるクラスの40人の生徒の数学と理科の試験得点の散布図である。
データ点の近くの数値はそのデータ点の生徒の出席番号である。
(1)数学と理科の合計得点が最も高い生徒の出席番号は$\boxed{\ \ ヒ\ \ }$である。また、数学と理科の得点差の絶対値が最も大きい生徒の出席番号は$\boxed{\ \ フ\ \ }$である。
(2)数学と理科それぞれの得点の平均値を$\bar{x}$, $\bar{y}$、標準偏差を$s_x$, $s_y$、数学と理科の得点の共分散を$s_{xy}$と表すと、これらの数値は以下であった。
$\bar{x}$=67.7, $\bar{y}$=70.9, $s_x$=14.9, $s_y$=11.5, $s_{xy}$=115.7
数学の得点と理科の得点の相関係数は$\boxed{\ \ ヘ\ \ }$である。なお、答えは小数第3位を四捨五入し、小数第2位まで求めなさい。
(3)各生徒の数学の得点を$x_1$, $x_2$, ..., $x_{40}$、理科の得点を$y_1$, $y_2$, ..., $y_{40}$で表す。
数学と理科の合計得点$x_1$+$y_1$, $x_2$+$y_2$, ..., $x_{40}$+$y_{40}$の平均値は$\bar{x}$, $\bar{y}$を用いると$\boxed{\ \ ホ\ \ }$と表せる。合計得点の分散は、
$\displaystyle\frac{1}{40}\sum_{i=1}^{40}\left(x_i+y_i-\boxed{\ ホ\ }\right)^2$
であるから、これを式変形すると、合計得点の分散は、$s_x$, $s_y$, $s_{xy}$を用いて$\boxed{\ \ マ\ \ }$と表せる。これらの式に(2)で与えられた数値を入れて計算すると、数学と理科の合計得点の平均値は$\boxed{\ \ ミ\ \ }$、分散は$\boxed{\ \ ム\ \ }$である。なお、答えは小数第2位を四捨五入し、小数第1位まで求めなさい。
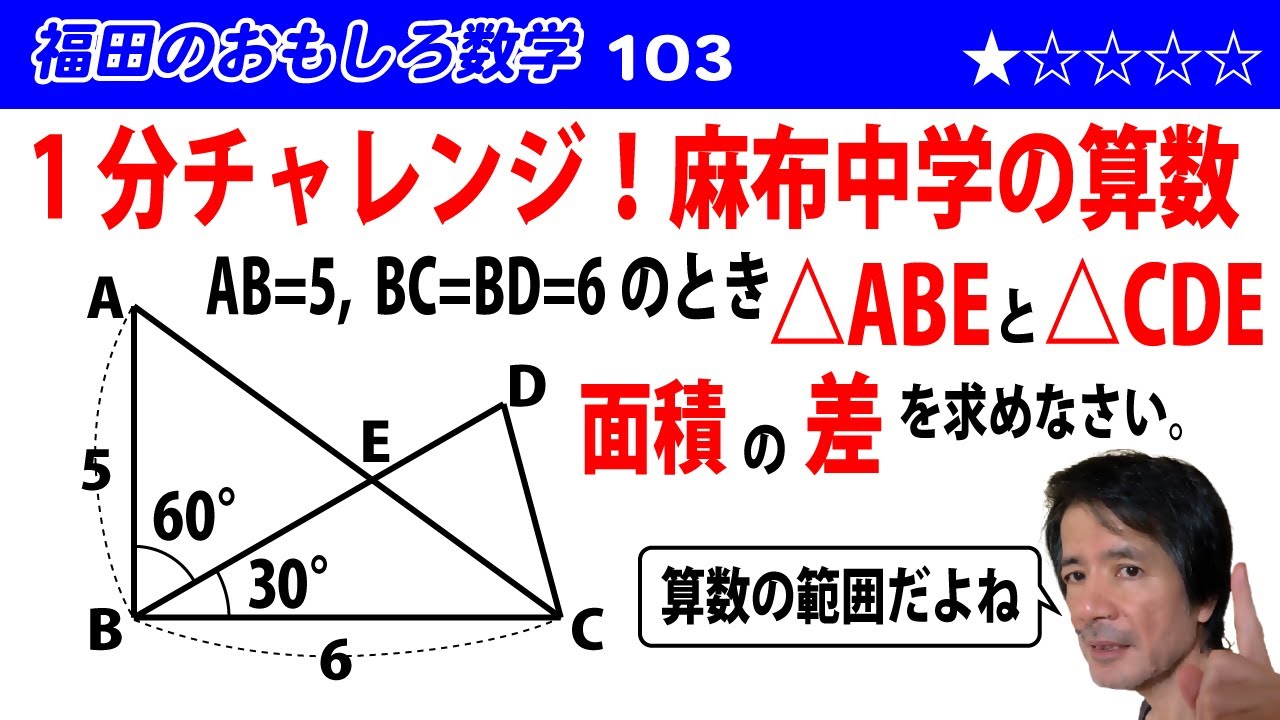
福田のおもしろ数学103〜麻布中学の算数〜二つの三角形の面積の差
単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
福田次郎
問題文全文(内容文):
AB=5, BC=BD=6のとき、$\triangle$ABEと$\triangle$CDEの面積の差を求めよ。(※動画参照)
この動画を見る
AB=5, BC=BD=6のとき、$\triangle$ABEと$\triangle$CDEの面積の差を求めよ。(※動画参照)
福田の数学〜慶應義塾大学2024年看護医療学部第4問〜接線と面積計算

単元:
#微分とその応用#接線と法線・平均値の定理#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 関数$f(x)$を
$f(x)$=$x^2(x-3)$
で定める。以下に答えなさい。
(1)関数$f(x)$は$x$=$\boxed{\ \ ト\ \ }$で極小値$\boxed{\ \ ナ\ \ }$をとる。
(2)曲線$y$=$f(x)$ を$C$とする。点A(0,1)から曲線$C$へは2本の接線が引ける。
そのうち、傾きが正の接線を$l$とし、傾きが負の接線を$m$とするとき、直線$l$の方程式は$y$=$\boxed{\ \ ニ\ \ }$であり、直線$m$の方程式は$y$=$\boxed{\ \ ヌ\ \ }$である。
(3)曲線$C$と直線$l$の接点Pの$x$座標は$\boxed{\ \ ネ\ \ }$である。また、曲線$C$と直線$l$は2つの共有点をもつが、点Pとは異なる共有点Qの$x$座標は$\boxed{\ \ ノ\ \ }$である。さらに、曲線$C$と直線$l$で囲まれた図形の面積は$\boxed{\ \ ハ\ \ }$である。
この動画を見る
$\Large\boxed{4}$ 関数$f(x)$を
$f(x)$=$x^2(x-3)$
で定める。以下に答えなさい。
(1)関数$f(x)$は$x$=$\boxed{\ \ ト\ \ }$で極小値$\boxed{\ \ ナ\ \ }$をとる。
(2)曲線$y$=$f(x)$ を$C$とする。点A(0,1)から曲線$C$へは2本の接線が引ける。
そのうち、傾きが正の接線を$l$とし、傾きが負の接線を$m$とするとき、直線$l$の方程式は$y$=$\boxed{\ \ ニ\ \ }$であり、直線$m$の方程式は$y$=$\boxed{\ \ ヌ\ \ }$である。
(3)曲線$C$と直線$l$の接点Pの$x$座標は$\boxed{\ \ ネ\ \ }$である。また、曲線$C$と直線$l$は2つの共有点をもつが、点Pとは異なる共有点Qの$x$座標は$\boxed{\ \ ノ\ \ }$である。さらに、曲線$C$と直線$l$で囲まれた図形の面積は$\boxed{\ \ ハ\ \ }$である。
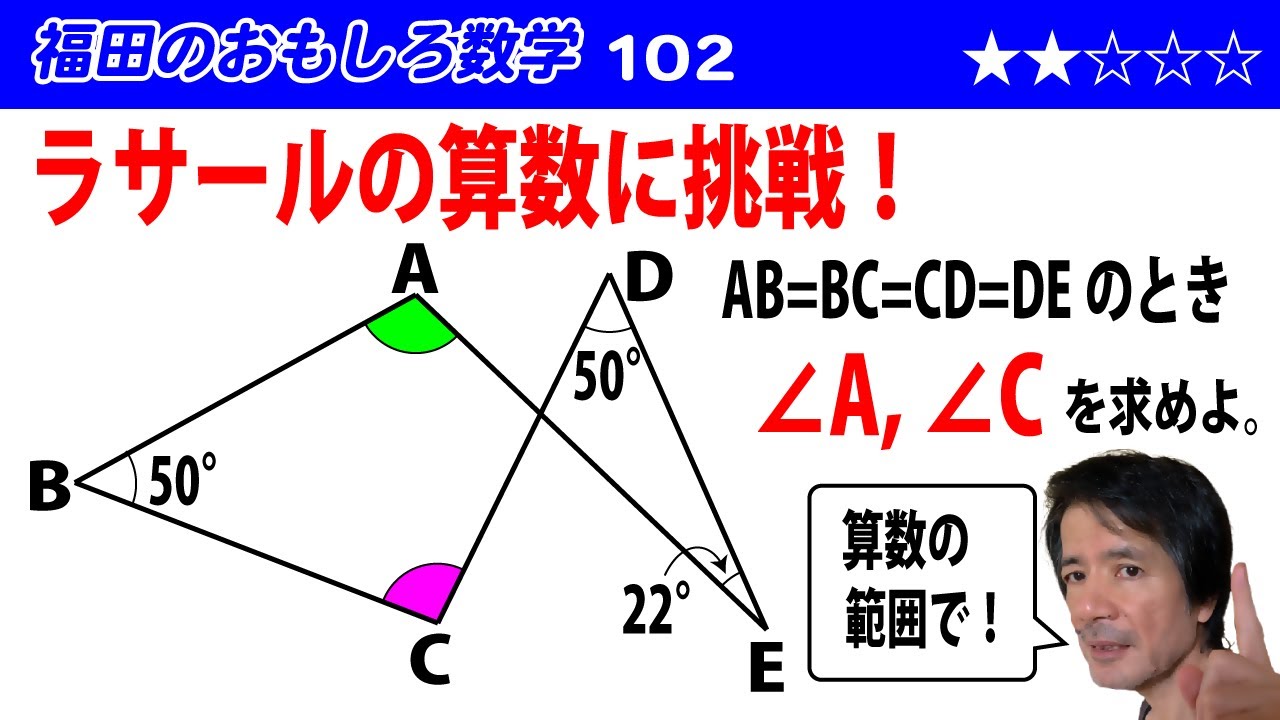
福田のおもしろ数学102〜ラサール中学の算数〜折れ線で結ばれた図形から角を求める
福田の数学〜慶應義塾大学2024年看護医療学部第3問〜群数列

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 数列 $\frac{0}{1}$, $\frac{1}{1}$, $\frac{0}{2}$, $\frac{1}{2}$, $\frac{2}{2}$, $\frac{0}{3}$, $\frac{1}{3}$, $\frac{2}{3}$, $\frac{3}{3}$, $\frac{0}{4}$, $\frac{1}{4}$, $\frac{2}{4}$, $\frac{3}{4}$, $\frac{4}{4}$, $\frac{0}{5}$, ...
の第$n$項を$a_n$とする。
(1)約分することで$a_n$=1 を満たす自然数$n$のうち、$k$番目に小さいものを$N_k$で表す。例えば、$N_1$=2, $N_2$=5 である。また、自然数$k$に対して、$N_k$を$k$を用いて表すと$N_k$=$\boxed{\ \ セ\ \ }$である。また、自然数$k$に対して、数列$\left\{a_n\right\}$の初項から第$N_k$項までの和を$k$を用いて表すと$\boxed{\ \ ソ\ \ }$である。
(2)約分することで$a_n$=$\frac{1}{4}$ を満たす自然数$n$のうち、$k$番目に小さいものを$M_k$で表す。例えば$M_1$=11, $M_2$=$\boxed{\ \ タ\ \ }$である。このとき、自然数$k$に対して、$M_k$を$k$を用いて表すと$M_k$=$\boxed{\ \ チ\ \ }$である。
(3)$a_{200}$を約分した形で表すと$a_{200}$=$\boxed{\ \ ツ\ \ }$である。また数列$\left\{a_n\right\}$の初項から第200項までの和は$\boxed{\ \ テ\ \ }$である。
この動画を見る
$\Large\boxed{3}$ 数列 $\frac{0}{1}$, $\frac{1}{1}$, $\frac{0}{2}$, $\frac{1}{2}$, $\frac{2}{2}$, $\frac{0}{3}$, $\frac{1}{3}$, $\frac{2}{3}$, $\frac{3}{3}$, $\frac{0}{4}$, $\frac{1}{4}$, $\frac{2}{4}$, $\frac{3}{4}$, $\frac{4}{4}$, $\frac{0}{5}$, ...
の第$n$項を$a_n$とする。
(1)約分することで$a_n$=1 を満たす自然数$n$のうち、$k$番目に小さいものを$N_k$で表す。例えば、$N_1$=2, $N_2$=5 である。また、自然数$k$に対して、$N_k$を$k$を用いて表すと$N_k$=$\boxed{\ \ セ\ \ }$である。また、自然数$k$に対して、数列$\left\{a_n\right\}$の初項から第$N_k$項までの和を$k$を用いて表すと$\boxed{\ \ ソ\ \ }$である。
(2)約分することで$a_n$=$\frac{1}{4}$ を満たす自然数$n$のうち、$k$番目に小さいものを$M_k$で表す。例えば$M_1$=11, $M_2$=$\boxed{\ \ タ\ \ }$である。このとき、自然数$k$に対して、$M_k$を$k$を用いて表すと$M_k$=$\boxed{\ \ チ\ \ }$である。
(3)$a_{200}$を約分した形で表すと$a_{200}$=$\boxed{\ \ ツ\ \ }$である。また数列$\left\{a_n\right\}$の初項から第200項までの和は$\boxed{\ \ テ\ \ }$である。
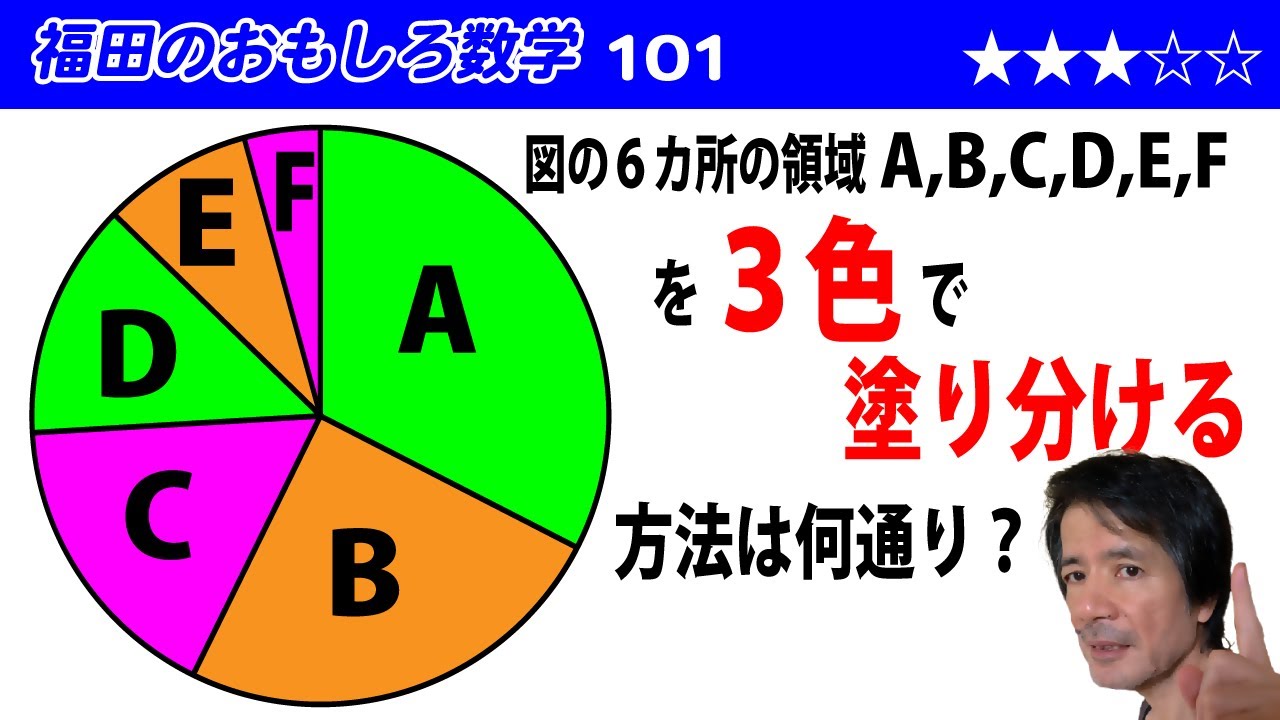
福田のおもしろ数学101〜円の中の領域の塗り分け
福田の数学〜慶應義塾大学2024年看護医療学部第2問(3)〜ルート2が無理数である証明

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ (3)$\sqrt 2$が無理数であることを証明せよ。
この動画を見る
$\Large\boxed{2}$ (3)$\sqrt 2$が無理数であることを証明せよ。
福田のおもしろ数学100〜帰納的に考える方法〜階段の登り方

福田の数学〜慶應義塾大学2024年看護医療学部第2問(2)〜2次方程式の解の存在範囲

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ (2)$m$を実数とする。$x$の2次方程式
$x^2$+$mx$+$m$+3=0
が異なる2つの虚数解をもつような$m$の値の範囲は$\boxed{\ \ シ\ \ }$であり、異なる2つの正の解をもつような$m$の値の範囲は$\boxed{\ \ ス\ \ }$である。
この動画を見る
$\Large\boxed{2}$ (2)$m$を実数とする。$x$の2次方程式
$x^2$+$mx$+$m$+3=0
が異なる2つの虚数解をもつような$m$の値の範囲は$\boxed{\ \ シ\ \ }$であり、異なる2つの正の解をもつような$m$の値の範囲は$\boxed{\ \ ス\ \ }$である。
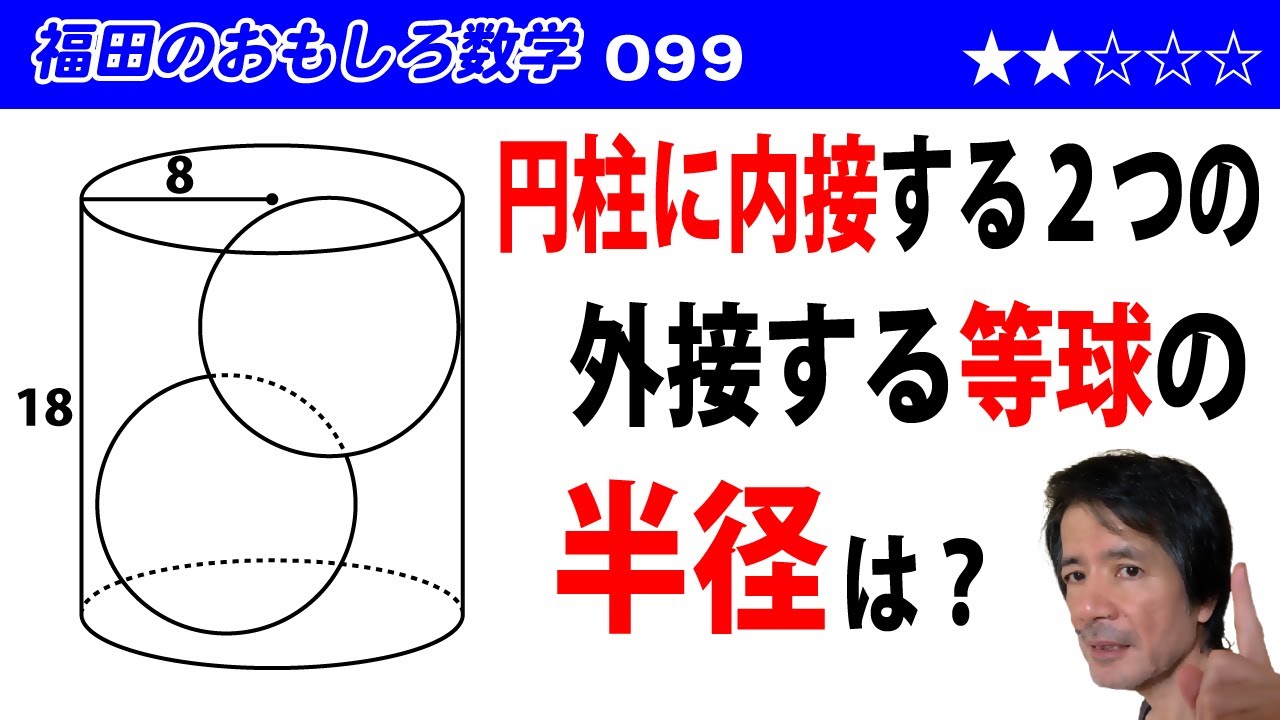
福田のおもしろ数学099〜円柱に内接する2つの球の半径
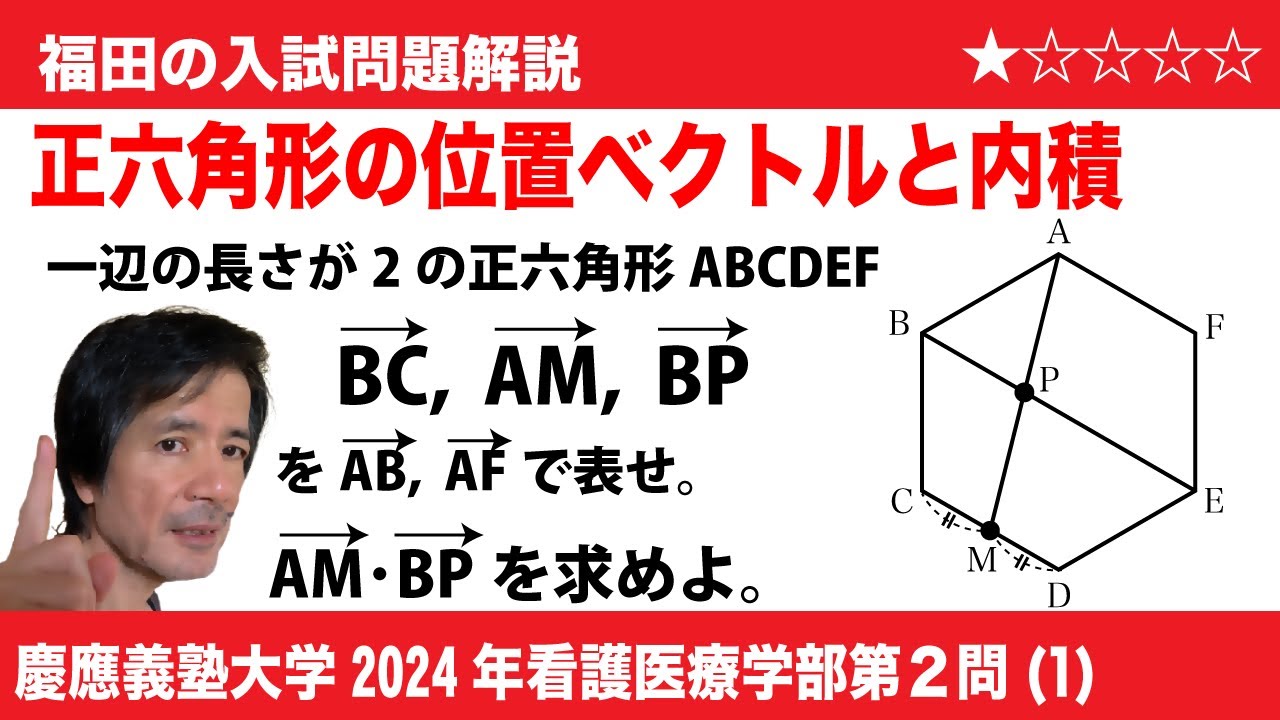
福田の数学〜慶應義塾大学2024年看護医療学部第2問(1)〜正六角形の位置ベクトル
単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ (1)一辺の長さが2の正六角形ABCDEFにおいて、辺CDの中点をMとし、直線BEと直線AMの交点をPとする。このとき、$\overrightarrow{BC}$, $\overrightarrow{AM}$, $\overrightarrow{BP}$をそれぞれ$\overrightarrow{AB}$, $\overrightarrow{AF}$を用いて表すと$\overrightarrow{BC}$=$\boxed{\ \ ク\ \ }$, $\overrightarrow{AM}$=$\boxed{\ \ ケ\ \ }$, $\overrightarrow{BP}$=$\boxed{\ \ コ\ \ }$である。また、$\overrightarrow{AM}$と$\overrightarrow{BP}$の内積$\overrightarrow{AM}・\overrightarrow{BP}$の値は$\boxed{\ \ サ\ \ }$である。
この動画を見る
$\Large\boxed{2}$ (1)一辺の長さが2の正六角形ABCDEFにおいて、辺CDの中点をMとし、直線BEと直線AMの交点をPとする。このとき、$\overrightarrow{BC}$, $\overrightarrow{AM}$, $\overrightarrow{BP}$をそれぞれ$\overrightarrow{AB}$, $\overrightarrow{AF}$を用いて表すと$\overrightarrow{BC}$=$\boxed{\ \ ク\ \ }$, $\overrightarrow{AM}$=$\boxed{\ \ ケ\ \ }$, $\overrightarrow{BP}$=$\boxed{\ \ コ\ \ }$である。また、$\overrightarrow{AM}$と$\overrightarrow{BP}$の内積$\overrightarrow{AM}・\overrightarrow{BP}$の値は$\boxed{\ \ サ\ \ }$である。
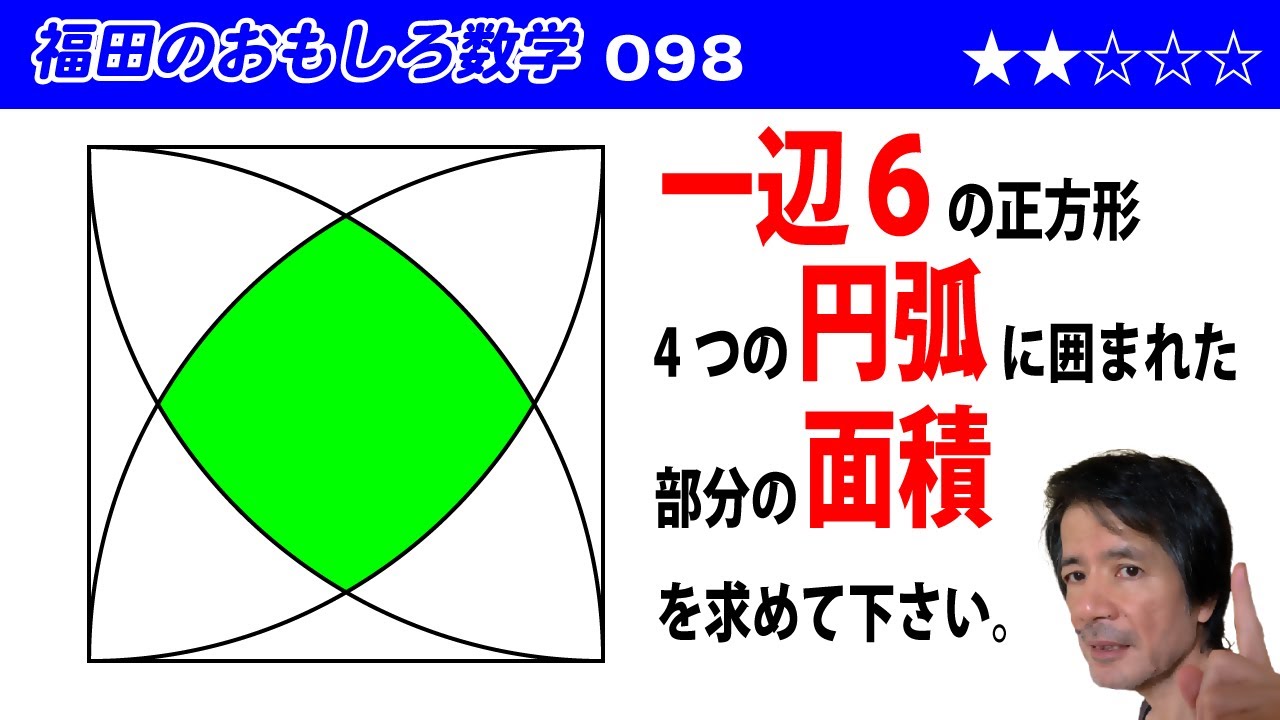
福田のおもしろ数学098〜正方形の中の4つの円弧に囲まれた部分の面積
福田の数学〜慶應義塾大学2024年看護医療学部第1問(4)〜円と接線の長さ

単元:
#数Ⅱ#図形と方程式#円と方程式
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (4)円$x^2$+$y^2$-$4x$+$10y$+11=0 を$C$とするとき、円$C$の中心は$\boxed{\ \ オ\ \ }$であり、半径は$\boxed{\ \ カ\ \ }$である。また、この円$C$には点P(3,2)から2本の接線を引くことができるが、その接点の1つをAとする。このとき、線分APの長さはAP=$\boxed{\ \ キ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (4)円$x^2$+$y^2$-$4x$+$10y$+11=0 を$C$とするとき、円$C$の中心は$\boxed{\ \ オ\ \ }$であり、半径は$\boxed{\ \ カ\ \ }$である。また、この円$C$には点P(3,2)から2本の接線を引くことができるが、その接点の1つをAとする。このとき、線分APの長さはAP=$\boxed{\ \ キ\ \ }$である。
福田のおもしろ数学097〜4変数の不等式の証明の仕方

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a$≧2, $b$≧2, $c$≧2, $d$≧2 のとき、次を証明せよ。
$abcd$>$a$+$b$+$c$+$d$
この動画を見る
$a$≧2, $b$≧2, $c$≧2, $d$≧2 のとき、次を証明せよ。
$abcd$>$a$+$b$+$c$+$d$
福田の数学〜慶應義塾大学2024年看護医療学部第1問(3)〜対数不等式

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (3)不等式$(\log_4x)^2$-$\log_8x^2$+$\frac{1}{3}$<0 を解くと$\boxed{\ \ エ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (3)不等式$(\log_4x)^2$-$\log_8x^2$+$\frac{1}{3}$<0 を解くと$\boxed{\ \ エ\ \ }$である。
福田のおもしろ数学096〜連立方程式が実数解をもつ条件

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a$,$b$が実数のとき、次の連立方程式が実数解をもつための$a$,$b$の条件を求めよ。
$\left\{\begin{array}{1}
x+y+z=a ...①
x^2+y^2+z^2=b ...②
\end{array}\right.$
この動画を見る
$a$,$b$が実数のとき、次の連立方程式が実数解をもつための$a$,$b$の条件を求めよ。
$\left\{\begin{array}{1}
x+y+z=a ...①
x^2+y^2+z^2=b ...②
\end{array}\right.$
福田の数学〜慶應義塾大学2024年看護医療学部第1問(2)〜三角方程式

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (2)0≦$x$<$\pi$のとき、方程式$\cos 3x$+$\cos x$=0 の解は$x$=$\boxed{\ \ イ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (2)0≦$x$<$\pi$のとき、方程式$\cos 3x$+$\cos x$=0 の解は$x$=$\boxed{\ \ イ\ \ }$である。
福田のおもしろ数学095〜素数が並ぶ数列

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
次の数列は全ての項が素数であるかどうか調べよ。
17, 19, 23, 29, 37, 47, 59, 73, 89, ...
この動画を見る
次の数列は全ての項が素数であるかどうか調べよ。
17, 19, 23, 29, 37, 47, 59, 73, 89, ...
福田の数学〜慶應義塾大学2024年看護医療学部第1問(1)〜さいころの目の積が4の倍数になる確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)4個のさいころを同時に投げるとき、出た目の積が偶数になる確率は$\boxed{\ \ ア\ \ }$であり、出た目の積が4の倍数になる確率は$\boxed{\ \ イ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (1)4個のさいころを同時に投げるとき、出た目の積が偶数になる確率は$\boxed{\ \ ア\ \ }$であり、出た目の積が4の倍数になる確率は$\boxed{\ \ イ\ \ }$である。
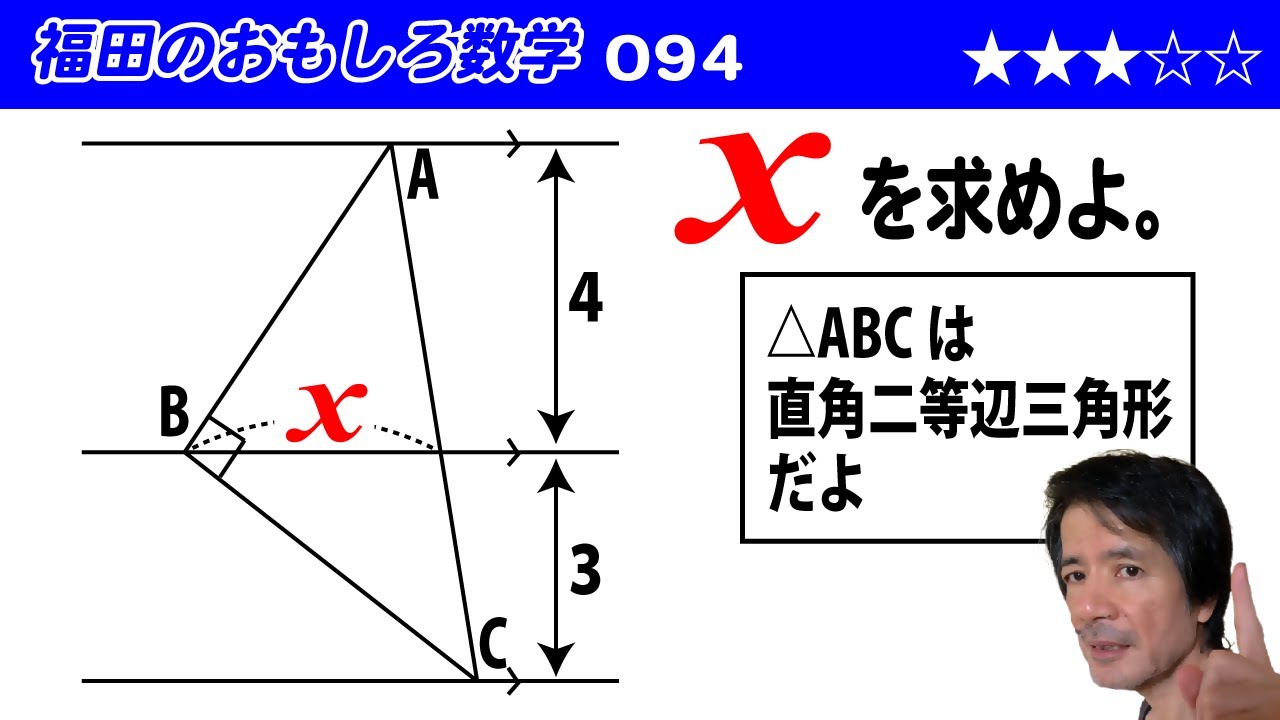
福田のおもしろ数学094〜平行線と直角二等辺三角形
福田の数学〜慶應義塾大学2024年薬学部第3問〜ウイルスの保有と症状に関する条件付き確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 10万人の集団があり、この集団に対してウイルスXとウイルスYの保有及び症状の有無を調べた。
この集団のうち2万人がウイルスXを保有し、ウイルスX保有者の$\frac{1}{4}$、ウイルスX非保有者の$\frac{1}{4}$がウイルスYを保有していた。ウイルスXが原因でみられる症状は発熱のみ、ウイルスYが原因でみられる症状は腹痛のみであり、ウイルスを保有していなくても発熱や腹痛がみられることがある。
過去の研究から、発熱はウイルスX保有者に確率$\frac{3}{4}$、ウイルスX非保有者に確率$\frac{1}{10}$でみられ、腹痛はウイルスY保有者に確率$\frac{9}{10}$、ウイルスY非保有者に確率$\frac{1}{5}$でみられることがわかっている。なお、発熱と腹痛はそれぞれ独立に発症し互いに影響しないものとする。
(1)この集団から無作為に選ばれた1人がウイルスXを保有していないが発熱がみられる確率は$\boxed{\ \ ト\ \ }$である。
(2)この集団から無作為に選ばれた1人がウイルスYを保有していないが発熱がみられる確率は$\boxed{\ \ ナ\ \ }$である。
(3)この集団から無作為に1人を選んでウイルスの保有および症状の有無を調べて集団に戻す試行を3回繰り返した。
(i)3回の試行で選ばれた人のうち、1人のみに腹痛がみられる確率は$\boxed{\ \ ニ\ \ }$である。
(ii)3回の試行で選ばれた人のうち、1人のみに腹痛がみられるとき、選ばれた人のうち少なくとも1人がウイルスYを保有している確率は$\boxed{\ \ ヌ\ \ }$である。
この動画を見る
$\Large\boxed{3}$ 10万人の集団があり、この集団に対してウイルスXとウイルスYの保有及び症状の有無を調べた。
この集団のうち2万人がウイルスXを保有し、ウイルスX保有者の$\frac{1}{4}$、ウイルスX非保有者の$\frac{1}{4}$がウイルスYを保有していた。ウイルスXが原因でみられる症状は発熱のみ、ウイルスYが原因でみられる症状は腹痛のみであり、ウイルスを保有していなくても発熱や腹痛がみられることがある。
過去の研究から、発熱はウイルスX保有者に確率$\frac{3}{4}$、ウイルスX非保有者に確率$\frac{1}{10}$でみられ、腹痛はウイルスY保有者に確率$\frac{9}{10}$、ウイルスY非保有者に確率$\frac{1}{5}$でみられることがわかっている。なお、発熱と腹痛はそれぞれ独立に発症し互いに影響しないものとする。
(1)この集団から無作為に選ばれた1人がウイルスXを保有していないが発熱がみられる確率は$\boxed{\ \ ト\ \ }$である。
(2)この集団から無作為に選ばれた1人がウイルスYを保有していないが発熱がみられる確率は$\boxed{\ \ ナ\ \ }$である。
(3)この集団から無作為に1人を選んでウイルスの保有および症状の有無を調べて集団に戻す試行を3回繰り返した。
(i)3回の試行で選ばれた人のうち、1人のみに腹痛がみられる確率は$\boxed{\ \ ニ\ \ }$である。
(ii)3回の試行で選ばれた人のうち、1人のみに腹痛がみられるとき、選ばれた人のうち少なくとも1人がウイルスYを保有している確率は$\boxed{\ \ ヌ\ \ }$である。
福田のおもしろ数学093〜条件付きの式の証明

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a^2$+$c^2$=1, $b^2$+$d^2$=1, $ab$+$cd$=0 のとき次を示せ。
$a^2$+$b^2$=1, $c^2$+$d^2$=1, $ac$+$bd$=0
この動画を見る
$a^2$+$c^2$=1, $b^2$+$d^2$=1, $ab$+$cd$=0 のとき次を示せ。
$a^2$+$b^2$=1, $c^2$+$d^2$=1, $ac$+$bd$=0
福田の数学〜慶應義塾大学2024年薬学部第2問〜放物線と円が接する条件と面積

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 原点をOとする$xy$平面上に円$x^2$+$y^2$-$12y$=0 があり、円の中心をPとする。
円周上に動点Qがあり、半直線POを始線とする動径PQの回転角を$\theta$とする。
ただし、$\theta$は$-\frac{\pi}{2}$<$\theta$<$\frac{\pi}{2}$を満たす実数とする。
(1)直線PQを表す方程式は、$\theta$=0 のとき$\boxed{\ \ ソ\ \ }$であり、$\theta$≠0 のとき$\boxed{\ \ タ\ \ }$である。
(2)点Qを通る放物線$y$=$ax^2$+$b$ をおく。点Qにおける放物線の接線は、点Qにおける円の接線と一致する。ただし、$a$, $b$は実数であり、$a$は$a$>0 を満たす。
(i)$\theta$≠0 のとき$a$と$b$を$\theta$で表すと、$a$=$\boxed{\ \ チ\ \ }$, $b$=$\boxed{\ \ ツ\ \ }$ である。
(ii)$\theta$=$-\frac{\pi}{3}$ のとき、直線PQと放物線で囲まれる部分の面積は$\boxed{\ \ テ\ \ }$である。
この動画を見る
$\Large\boxed{2}$ 原点をOとする$xy$平面上に円$x^2$+$y^2$-$12y$=0 があり、円の中心をPとする。
円周上に動点Qがあり、半直線POを始線とする動径PQの回転角を$\theta$とする。
ただし、$\theta$は$-\frac{\pi}{2}$<$\theta$<$\frac{\pi}{2}$を満たす実数とする。
(1)直線PQを表す方程式は、$\theta$=0 のとき$\boxed{\ \ ソ\ \ }$であり、$\theta$≠0 のとき$\boxed{\ \ タ\ \ }$である。
(2)点Qを通る放物線$y$=$ax^2$+$b$ をおく。点Qにおける放物線の接線は、点Qにおける円の接線と一致する。ただし、$a$, $b$は実数であり、$a$は$a$>0 を満たす。
(i)$\theta$≠0 のとき$a$と$b$を$\theta$で表すと、$a$=$\boxed{\ \ チ\ \ }$, $b$=$\boxed{\ \ ツ\ \ }$ である。
(ii)$\theta$=$-\frac{\pi}{3}$ のとき、直線PQと放物線で囲まれる部分の面積は$\boxed{\ \ テ\ \ }$である。



