 福田次郎
福田次郎
 福田次郎
福田次郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
2024年共通テスト解答速報〜数学ⅠA第4問整数の性質〜福田の入試問題解説

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
T 3 、 T 4 、 T 6 を次のようなタイマ ー とする。
T3 : 3 進数を 3 桁表示するタイマ ー
T4 : 4 進数を 3 桁表示するタイマ ー
T 6 : 6 進数を 3 裄表示するタイマ ー
なお、第進数とは進法で表された数のことである。これらのタイマ ー は.すべて次の表示方法に従うものとする。
表示方法
(a) スタ ー トした時点でタイマ ー は 000 と表示されている。
(b)タイマ ー は、スタ ー トした後、表示される数が1秒ごとに1ずつ増えていき、3 析で表示できる最大の数が表示された1秒後に.表示が000に戻る。
(c)タイマ ー は表示が 000 に戻った後も(b )と同様に表示される数が 1秒ごとに1ずつ増えていき、3 裄で表示できる最大の数が表示された1秒後に、表示が 000 に戻るという動作を繰り返す。
例えば、 T3 はスタ ー トしてから 3 進数でに$12_{ (3) }$秒後に012 と表示される。その後 222 と表示された1秒後に表示が000に戻り、その$12_{ (3) }$秒後に再び012と表示される。
( 1 ) T6 は、スタ ー トしてから 10 進数で 40 秒後にアイウと表示される。T4 は、スタ ー トしてから 2 進数で$10011_{ (2) }$秒後にエオカと表示される。
( 2 ) T 4 をスタ ー トさせた後、初めて表示が 000 に戻るのは、スタ ー トしてから10 進数でキク秒後であり、その後もキク秒ごとに表示が 000 に戻る。同様の考察を T 6 に対しても行うことにより、 T 4 と T 6 を同時にスタートさせた後、初めて両方の表示が同時に 000 に戻るのは.スタ ー トしてから 10 進でケコサシ秒後であることがわかる。
( 3 ) 0 以上の整数$\ell$に対して、T 4 をスタ ー トさせた$\ell$秒後に T4 が 012と表示されることと
$\ell$をスセで割った余りがソであることは同値である。ただしスセとソは10進法で表されているものとする。T3 についても同様の考察を行うことにより、次のことがわかる。T3 と T4 を同時にスタ ー トさせてから、初めて両方が同時に 012 と表示されるまでの時間をm秒とするとき、mは 10 進法でタチツと表される。
また、 T4とT6 の表示に関する記述として.次の0~3のうち、正しいものはテである。
0 T4 と T6 を同時にスタ ー トさせてから、m秒後より前に初めて両方が同時に 012 と表示される。
1 T4 と T6 を同時にスタ ー トさせてから、ちょうどm秒後に初めて両方が同時に 0 と表示される。
2 T4 と T6 を同時にスタ ー トさせてから、m秒後より後に初めて両方が同時に 012 と表示される。
3 T4 と T6 を同時にスタ一トさせてから、両方が同時に 012 と表示されることはない。
2024共通テスト過去問
この動画を見る
T 3 、 T 4 、 T 6 を次のようなタイマ ー とする。
T3 : 3 進数を 3 桁表示するタイマ ー
T4 : 4 進数を 3 桁表示するタイマ ー
T 6 : 6 進数を 3 裄表示するタイマ ー
なお、第進数とは進法で表された数のことである。これらのタイマ ー は.すべて次の表示方法に従うものとする。
表示方法
(a) スタ ー トした時点でタイマ ー は 000 と表示されている。
(b)タイマ ー は、スタ ー トした後、表示される数が1秒ごとに1ずつ増えていき、3 析で表示できる最大の数が表示された1秒後に.表示が000に戻る。
(c)タイマ ー は表示が 000 に戻った後も(b )と同様に表示される数が 1秒ごとに1ずつ増えていき、3 裄で表示できる最大の数が表示された1秒後に、表示が 000 に戻るという動作を繰り返す。
例えば、 T3 はスタ ー トしてから 3 進数でに$12_{ (3) }$秒後に012 と表示される。その後 222 と表示された1秒後に表示が000に戻り、その$12_{ (3) }$秒後に再び012と表示される。
( 1 ) T6 は、スタ ー トしてから 10 進数で 40 秒後にアイウと表示される。T4 は、スタ ー トしてから 2 進数で$10011_{ (2) }$秒後にエオカと表示される。
( 2 ) T 4 をスタ ー トさせた後、初めて表示が 000 に戻るのは、スタ ー トしてから10 進数でキク秒後であり、その後もキク秒ごとに表示が 000 に戻る。同様の考察を T 6 に対しても行うことにより、 T 4 と T 6 を同時にスタートさせた後、初めて両方の表示が同時に 000 に戻るのは.スタ ー トしてから 10 進でケコサシ秒後であることがわかる。
( 3 ) 0 以上の整数$\ell$に対して、T 4 をスタ ー トさせた$\ell$秒後に T4 が 012と表示されることと
$\ell$をスセで割った余りがソであることは同値である。ただしスセとソは10進法で表されているものとする。T3 についても同様の考察を行うことにより、次のことがわかる。T3 と T4 を同時にスタ ー トさせてから、初めて両方が同時に 012 と表示されるまでの時間をm秒とするとき、mは 10 進法でタチツと表される。
また、 T4とT6 の表示に関する記述として.次の0~3のうち、正しいものはテである。
0 T4 と T6 を同時にスタ ー トさせてから、m秒後より前に初めて両方が同時に 012 と表示される。
1 T4 と T6 を同時にスタ ー トさせてから、ちょうどm秒後に初めて両方が同時に 0 と表示される。
2 T4 と T6 を同時にスタ ー トさせてから、m秒後より後に初めて両方が同時に 012 と表示される。
3 T4 と T6 を同時にスタ一トさせてから、両方が同時に 012 と表示されることはない。
2024共通テスト過去問
福田のおもしろ数学021〜開成中学入試問題だよ〜正六角形と正三角形の面積
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#相似と相似を利用した問題#開成中学
指導講師:
福田次郎
問題文全文(内容文):
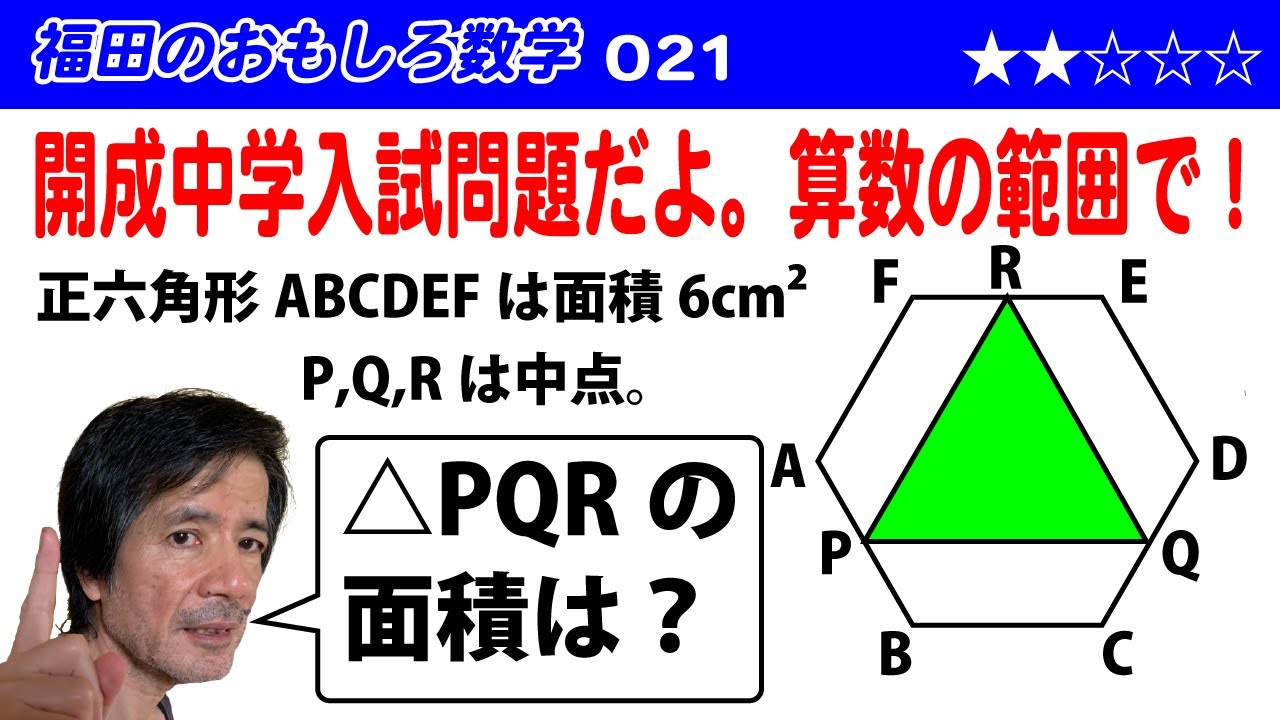
面積が$6cm^2$の正六角形 ABCDEF がある。図のように P, Q, R をそれぞれ辺 AB ,CD, EF の真ん中の点とする。三角形 PQR の面積を求めよ。
開成中過去問
この動画を見る
面積が$6cm^2$の正六角形 ABCDEF がある。図のように P, Q, R をそれぞれ辺 AB ,CD, EF の真ん中の点とする。三角形 PQR の面積を求めよ。
開成中過去問
2024年共通テスト解答速報〜数学ⅠA第3問〜福田の入試問題解説

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
2024共通テスト数学ⅠA第3問解説です
箱の中にカ ー ドが 2 枚以上入っており、それぞれのカ ードにはアルファベットが一文字だけ書かれている。この箱の中からカ ー ドを一枚取り出し、書かれているアルファベットを確認してからもとに戻すという試行をり返し行う。
(1)箱の中にA,Bのカードが 1 枚ずつ全部で 2 枚入っている場合を考える。以下では、2 以上の自然数nに対しn回の試行で A. Bがそろっているとは、n回の試行でA,Bのそれぞれが少なくとも1回は取り出されることを意味する。
(i)2回の試行でA,Bがそろっている確率は$\dfrac{ア}{イ}$である。
(ii)3回の試行でA,Bがそろっている確率を求める。
例えば、3回の試行のうちAを1回、Bを2回取り出す取り出し方は3通りあり、それらを全て挙げると次のようになる。※表は動画内参照
このように考えることにより、3 回の試行で A. B がそろっている取り出し方はウ通りあることがわかる。よって、3 回の試行で A. B がそろっている確率は$\dfrac{ウ}{2^3}$である。
(iii) 4 回の試行で A. B がそろっている取り出し方はエオ通りある。 よって、4 回の試行でA,B がそろっている確率は$\dfrac{カ}{キ}$である。
(2)箱の中にA,B,Cのカ ー ドが一枚ずつ全で 3 枚入っている場合を考える。
以下では、3 以上の自然数nに対しn回目の試行で初めて A. B. C がそろうとn回の試行で A,B,Cのそれぞれが少なくとも1回は取り出されかつA,B.Cのうちいずれか1枚がn回目の試行で初めて取り出されることを意味する。
(i)3 回目の試行で初めて A. B, C がそろう取り出し方はク通りある。よって、3 回目の試行で初めて A. B, C がそろう確率は$\dfrac{ク}{3^3}$である。
(ii) 4 回目の試行で初めて A.B,C がそろう確率を求める。4 回目の試行で初めて A. B. C がそろう取り出し方は.(1)の(ii)を振り返ることにより、3×ウ通りあることがわかる。よって、4 回目の試行で初めて A. B, C がそろう確率は$\dfrac{ケ}{コ}$である。
(iii)5 回目の試行で初めて A. B. C がそろう取り出し方はサシ通りある。よってを 5 回目の試行で初めてA,B,Cがそろう確率は$\dfrac{サシ}{3^3}$である。
太郎さんと花子さんは. 6 回目の試行で初めて A. B, C, D がそろう確率について考えている。
太郎:例えば. 5 回目までにA,B,Cのそれぞれが少なくとも1回は取り出され.かっ 6 回目に初めてDが取り出される場合を考えたら計算できそうだね。
花子:それなら初めて A. B. C だけがそろうのが, 3 回目のとき. 4 回目のとき. 5 回目のときで分けて考えてみてはどうかな。
6 回の試行のうち 3 回目の試行で初めて A. B. C だけがそろう取り出し方がク通りであることに注意すると「 6 回の試行のうち 3 回目の試行で初めて A. B. C だけがそろい、かつ6 回目の試行で初めてDが取り出される取り出し方はスセ通りあることがわかる。同じように考えると6回の試行のうち 4 回目の試行で初めて A, B, C だけがそろい、かっ 6 回目の試行で初めてDが取り出される」取り出し方はソタ通りあることもわかる。以上のように考えることにより, 6 回目の試行で初めて A. B. C, D がそろう確率は$\dfrac{チツ}{テトナ}$であることがわかる。
2024共通テスト過去問
この動画を見る
2024共通テスト数学ⅠA第3問解説です
箱の中にカ ー ドが 2 枚以上入っており、それぞれのカ ードにはアルファベットが一文字だけ書かれている。この箱の中からカ ー ドを一枚取り出し、書かれているアルファベットを確認してからもとに戻すという試行をり返し行う。
(1)箱の中にA,Bのカードが 1 枚ずつ全部で 2 枚入っている場合を考える。以下では、2 以上の自然数nに対しn回の試行で A. Bがそろっているとは、n回の試行でA,Bのそれぞれが少なくとも1回は取り出されることを意味する。
(i)2回の試行でA,Bがそろっている確率は$\dfrac{ア}{イ}$である。
(ii)3回の試行でA,Bがそろっている確率を求める。
例えば、3回の試行のうちAを1回、Bを2回取り出す取り出し方は3通りあり、それらを全て挙げると次のようになる。※表は動画内参照
このように考えることにより、3 回の試行で A. B がそろっている取り出し方はウ通りあることがわかる。よって、3 回の試行で A. B がそろっている確率は$\dfrac{ウ}{2^3}$である。
(iii) 4 回の試行で A. B がそろっている取り出し方はエオ通りある。 よって、4 回の試行でA,B がそろっている確率は$\dfrac{カ}{キ}$である。
(2)箱の中にA,B,Cのカ ー ドが一枚ずつ全で 3 枚入っている場合を考える。
以下では、3 以上の自然数nに対しn回目の試行で初めて A. B. C がそろうとn回の試行で A,B,Cのそれぞれが少なくとも1回は取り出されかつA,B.Cのうちいずれか1枚がn回目の試行で初めて取り出されることを意味する。
(i)3 回目の試行で初めて A. B, C がそろう取り出し方はク通りある。よって、3 回目の試行で初めて A. B, C がそろう確率は$\dfrac{ク}{3^3}$である。
(ii) 4 回目の試行で初めて A.B,C がそろう確率を求める。4 回目の試行で初めて A. B. C がそろう取り出し方は.(1)の(ii)を振り返ることにより、3×ウ通りあることがわかる。よって、4 回目の試行で初めて A. B, C がそろう確率は$\dfrac{ケ}{コ}$である。
(iii)5 回目の試行で初めて A. B. C がそろう取り出し方はサシ通りある。よってを 5 回目の試行で初めてA,B,Cがそろう確率は$\dfrac{サシ}{3^3}$である。
太郎さんと花子さんは. 6 回目の試行で初めて A. B, C, D がそろう確率について考えている。
太郎:例えば. 5 回目までにA,B,Cのそれぞれが少なくとも1回は取り出され.かっ 6 回目に初めてDが取り出される場合を考えたら計算できそうだね。
花子:それなら初めて A. B. C だけがそろうのが, 3 回目のとき. 4 回目のとき. 5 回目のときで分けて考えてみてはどうかな。
6 回の試行のうち 3 回目の試行で初めて A. B. C だけがそろう取り出し方がク通りであることに注意すると「 6 回の試行のうち 3 回目の試行で初めて A. B. C だけがそろい、かつ6 回目の試行で初めてDが取り出される取り出し方はスセ通りあることがわかる。同じように考えると6回の試行のうち 4 回目の試行で初めて A, B, C だけがそろい、かっ 6 回目の試行で初めてDが取り出される」取り出し方はソタ通りあることもわかる。以上のように考えることにより, 6 回目の試行で初めて A. B. C, D がそろう確率は$\dfrac{チツ}{テトナ}$であることがわかる。
2024共通テスト過去問
福田のおもしろ数学019〜ジュニア数学オリンピック本選問題〜直角三角形の斜辺の長さを求める

単元:
#数学(中学生)#中3数学#数A#数学検定・数学甲子園・数学オリンピック等#図形の性質#三平方の定理#三角形の辺の比(内分・外分・二等分線)#数学オリンピック#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
直角三角形の一辺の長さが 18 で、すべての辺の長さが整数のとき、斜辺の長さは?
ジュニア数学オリンピック過去問
この動画を見る
直角三角形の一辺の長さが 18 で、すべての辺の長さが整数のとき、斜辺の長さは?
ジュニア数学オリンピック過去問
2024年共通テスト解答速報〜数学ⅠA第1問(2)〜福田の入試問題解説

単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角形の辺の比(内分・外分・二等分線)#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
図 1 のように、電柱の影の先端は坂の斜面(以下、坂)にあるとする。また、坂には傾斜を表す道路標識が設置されていてをそこには 7 %と表示されているとする。電柱の太さと影の幅は無視して考えるものとする。また。地面と坂は平面であるとし、地面と坂が交わってできる直線を$\ell$とする。電柱の先端を点 A とし、根もとを点 B とする。電柱の影について。地面にある部分を線分 BC とし、坂にある部分を線分 CD とする。線分BC、CDがそれぞれ$\ell$と重直であるとき、電柱の影は坂に向かってまっすぐにのびているということにする。
※図は動画内参照
電柱の影が坂に向かってまっすぐにのびているとする。このとき、 4 点 A.B. C. D を通る平面は$\ell$と重直である。その平面において、図 2 のように、直線 ADと直線BCの交点を P とすると、太陽高度とは $\angle APB$の大きさのことである。
※図は動画内参照
道路標識の 7 %という表示は、この坂をのぼったとき、100m の水平距離に対して 7m の割合で高くなることを示している。nを1以上 9 以下の整数とするとき、坂の傾斜角$\angle DCP$の大きさについて
$n° \lt \angle DCP \lt n°+1°$
を満たすnの値は シ である。
以下では、$\angle DCP$の大きさは、ちょうどシ°であるとする。
ある日、電柱の影が坂に向かってまっすぐにのびていたとき、影の長さを調べたところBC= 7 m、 CD= 4 m であり、太陽高度は $angle\ APB$=45°であった。点 D から直線 AB に重直な直線を引き、直物 AB との交点を E とするとき
BE=ス×セm
であり
DE=(ソ+アタ×チ)m
である。よって電柱の高さは、小数点第2位で四捨五入するとソmであることがわかる。
別の日、電柱の影が坂に向かってまっすぐにのびていたときの太陽高度は刻= 42°であった。電住の高さがわかったので、前回調べた日からの影の長さの変化を知ることができる。電柱の影について、坂にある第分の長さは
$\dfrac{AB-テ×ト}{ナ+ニ×ト}m$
である。AB=ツmとして、これを計算することにより、この日の電柱の陰について、坂にある部分の長さは、前回調べた4mより約1.2mだけ長いことが分かる。
2024共通テスト過去問
この動画を見る
図 1 のように、電柱の影の先端は坂の斜面(以下、坂)にあるとする。また、坂には傾斜を表す道路標識が設置されていてをそこには 7 %と表示されているとする。電柱の太さと影の幅は無視して考えるものとする。また。地面と坂は平面であるとし、地面と坂が交わってできる直線を$\ell$とする。電柱の先端を点 A とし、根もとを点 B とする。電柱の影について。地面にある部分を線分 BC とし、坂にある部分を線分 CD とする。線分BC、CDがそれぞれ$\ell$と重直であるとき、電柱の影は坂に向かってまっすぐにのびているということにする。
※図は動画内参照
電柱の影が坂に向かってまっすぐにのびているとする。このとき、 4 点 A.B. C. D を通る平面は$\ell$と重直である。その平面において、図 2 のように、直線 ADと直線BCの交点を P とすると、太陽高度とは $\angle APB$の大きさのことである。
※図は動画内参照
道路標識の 7 %という表示は、この坂をのぼったとき、100m の水平距離に対して 7m の割合で高くなることを示している。nを1以上 9 以下の整数とするとき、坂の傾斜角$\angle DCP$の大きさについて
$n° \lt \angle DCP \lt n°+1°$
を満たすnの値は シ である。
以下では、$\angle DCP$の大きさは、ちょうどシ°であるとする。
ある日、電柱の影が坂に向かってまっすぐにのびていたとき、影の長さを調べたところBC= 7 m、 CD= 4 m であり、太陽高度は $angle\ APB$=45°であった。点 D から直線 AB に重直な直線を引き、直物 AB との交点を E とするとき
BE=ス×セm
であり
DE=(ソ+アタ×チ)m
である。よって電柱の高さは、小数点第2位で四捨五入するとソmであることがわかる。
別の日、電柱の影が坂に向かってまっすぐにのびていたときの太陽高度は刻= 42°であった。電住の高さがわかったので、前回調べた日からの影の長さの変化を知ることができる。電柱の影について、坂にある第分の長さは
$\dfrac{AB-テ×ト}{ナ+ニ×ト}m$
である。AB=ツmとして、これを計算することにより、この日の電柱の陰について、坂にある部分の長さは、前回調べた4mより約1.2mだけ長いことが分かる。
2024共通テスト過去問
2024年共通テスト速報〜数学ⅠA第1問の(1)〜福田の入試解説

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
$n \lt 2\sqrt{ 13 } \lt n+1$を満たす整数nはアである。
実数a,bを$a=2\sqrt{ 13 }$-ア,b=$\frac{1}{a}$で定める。このとき
$b=\frac{イ+2\sqrt{13}}{ウ}$である。また、$a^2-9b^2=エオカ\sqrt{13}$である。
①(7$\lt 2\sqrt{13} \lt 8$)から$\frac{7}{2} \lt \sqrt{13} \lt 4$が成り立つ。
①と④($b=\frac{7+2\sqrt{13}}{3}$)から$\frac{m}{ウ} \lt b \lt \frac{m+1}{ウ}$を満たすmはキク
よって③($b=\frac{1}{a}$)から$\frac{a}{15} \lt a \lt \frac{ウ}{14}$・・・⑥が成り立つ。
$\sqrt{13}$の整数部分はケであり、②($a=2\sqrt{13}-7$)と⑥から$\sqrt{13}$の小数点第1位の数字はコ、小数点第2位の数字はサである。
2024共通テスト過去問
この動画を見る
$n \lt 2\sqrt{ 13 } \lt n+1$を満たす整数nはアである。
実数a,bを$a=2\sqrt{ 13 }$-ア,b=$\frac{1}{a}$で定める。このとき
$b=\frac{イ+2\sqrt{13}}{ウ}$である。また、$a^2-9b^2=エオカ\sqrt{13}$である。
①(7$\lt 2\sqrt{13} \lt 8$)から$\frac{7}{2} \lt \sqrt{13} \lt 4$が成り立つ。
①と④($b=\frac{7+2\sqrt{13}}{3}$)から$\frac{m}{ウ} \lt b \lt \frac{m+1}{ウ}$を満たすmはキク
よって③($b=\frac{1}{a}$)から$\frac{a}{15} \lt a \lt \frac{ウ}{14}$・・・⑥が成り立つ。
$\sqrt{13}$の整数部分はケであり、②($a=2\sqrt{13}-7$)と⑥から$\sqrt{13}$の小数点第1位の数字はコ、小数点第2位の数字はサである。
2024共通テスト過去問
福田のおもしろ数学018〜1分以内に証明できたら天才〜不等式が常に成り立つ証明

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
どんなxに対しても次の方程式が成り立つことを証明せよ。
$x^{16}-x+1\gt 0$
この動画を見る
どんなxに対しても次の方程式が成り立つことを証明せよ。
$x^{16}-x+1\gt 0$
福田のおもしろ数学017〜中学入試問題に挑戦しよう〜ウォーキングする姉妹が目視できる時間の計算
単元:
#算数(中学受験)#速さ#点の移動・時計算
指導講師:
福田次郎
問題文全文(内容文):
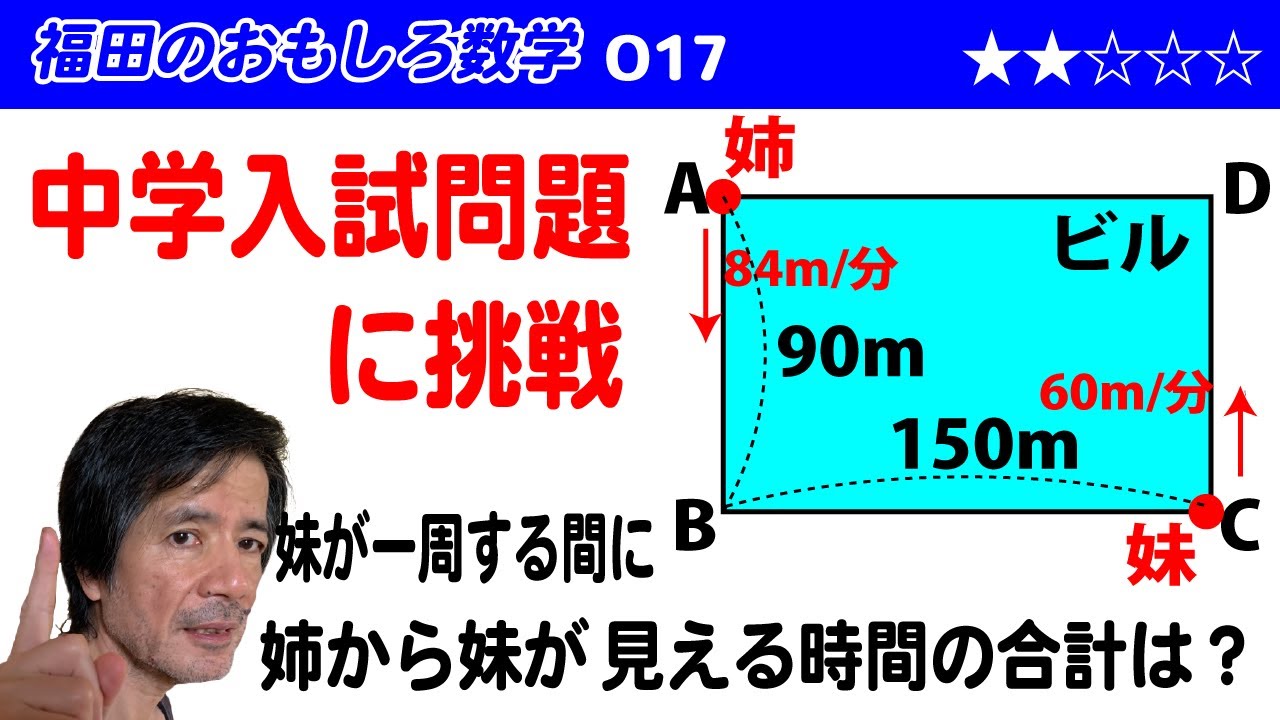
周囲が長方形 ABCD の建物の周りを姉と妹がウォ ー キングする。姉は A 地点から、妹は C 地点から同時に矢印の方向に歩き出した。 AB 間の距離が 90m 、 BC 間の距離が 150m であり、姉の歩く速さは毎分 84m 、妹の歩く速さは毎分 60m である。妹が一周して C 地点に戻るまでに、姉から妹の姿が見えている時間の合計は何分か。
※図は動画内参照
この動画を見る
周囲が長方形 ABCD の建物の周りを姉と妹がウォ ー キングする。姉は A 地点から、妹は C 地点から同時に矢印の方向に歩き出した。 AB 間の距離が 90m 、 BC 間の距離が 150m であり、姉の歩く速さは毎分 84m 、妹の歩く速さは毎分 60m である。妹が一周して C 地点に戻るまでに、姉から妹の姿が見えている時間の合計は何分か。
※図は動画内参照
福田のおもしろ数学016〜ジュニア数学オリンピック予選問題〜正三角形の面積
単元:
#算数(中学受験)#数学(中学生)#中1数学#中2数学#数学検定・数学甲子園・数学オリンピック等#平面図形#角度と面積#平面図形#三角形と四角形#数学オリンピック
指導講師:
福田次郎
問題文全文(内容文):
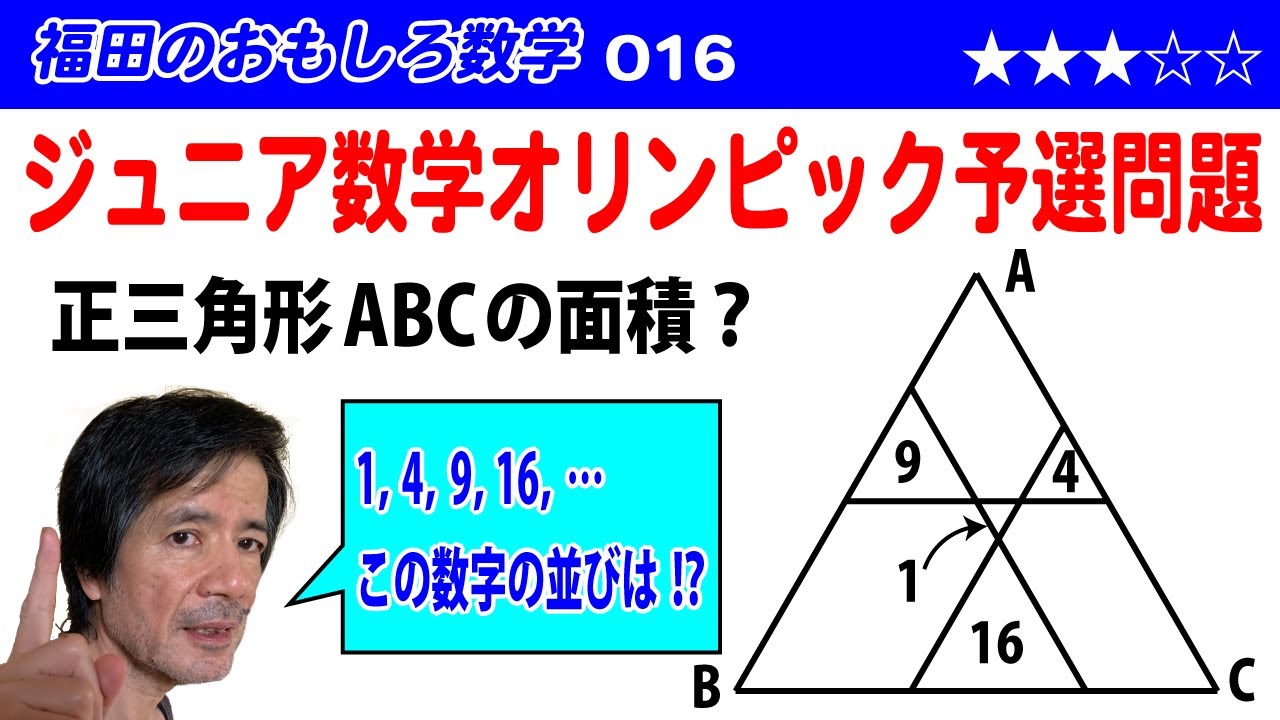
正三角形 ABC を図のように、 3 辺に平行な線分を 1 本ずっ引いて分割した。書かれている数は分割してできた正三角形の面積を表している。このとき、正三角形の面積を求めよ。
※図は動画内参照
ジュニア数学オリンピック過去問
この動画を見る
正三角形 ABC を図のように、 3 辺に平行な線分を 1 本ずっ引いて分割した。書かれている数は分割してできた正三角形の面積を表している。このとき、正三角形の面積を求めよ。
※図は動画内参照
ジュニア数学オリンピック過去問
福田のおもしろ数学015〜ジュニア数学オリンピック本戦問題〜2つの式を満たす4つの自然数を求める

単元:
#数学(中学生)#中2数学#連立方程式#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#数学オリンピック
指導講師:
福田次郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
a+b=cd \\
c+d=ab
\end{array}
\right.
\end{eqnarray}$
を満たす正の整数 $a,b,c,d$は?
ジュニア数学オリンピック過去問
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
a+b=cd \\
c+d=ab
\end{array}
\right.
\end{eqnarray}$
を満たす正の整数 $a,b,c,d$は?
ジュニア数学オリンピック過去問
福田のおもしろ数学014〜恒例10秒チャレンジ〜3変数の連立方程式

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
福田次郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y=4 \\
y+z=3 \\
z+x=5
\end{array}
\right.
\end{eqnarray}$
を解け.
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y=4 \\
y+z=3 \\
z+x=5
\end{array}
\right.
\end{eqnarray}$
を解け.
福田のおもしろ数学013〜ジュニア数学オリンピックから〜条件を満たす6個の変数は

単元:
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学オリンピック#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a,b,c,d,e,f$は相異なる1以上9以下の整数
$ab=cd=e+f$のとき、
$a+b+c+d+e+f$
として考えられる値をすべて求めよ.
ジュニア数学オリンピック過去問
この動画を見る
$a,b,c,d,e,f$は相異なる1以上9以下の整数
$ab=cd=e+f$のとき、
$a+b+c+d+e+f$
として考えられる値をすべて求めよ.
ジュニア数学オリンピック過去問
福田の数学〜2点が動くときはどちらか一方を固定する〜東京大学2018年文系第4問〜平面ベクトルと点の動ける領域

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
4 放物線$y=x^2$ のうち$-1 \leqq x \leqq 1$をみたす部分を C とする。座標平面上の原点Oと点A(1,0)を考える。
( 1 )点 P が C 上を動くとき、$\overrightarrow{OQ}=2\overrightarrow{ OP}$ をみたす点 Q の軌跡を求めよ。
( 2 )点 P が C 上を動き、点 R が線分 OA 上を動くとき$\overrightarrow{ OS }=\overrightarrow{ 2OP }+\overrightarrow{ OR }$をみたす点 S が動く領域を座標平面上に図示し、その面積を求めよ。
2018東京大学文過去問
この動画を見る
4 放物線$y=x^2$ のうち$-1 \leqq x \leqq 1$をみたす部分を C とする。座標平面上の原点Oと点A(1,0)を考える。
( 1 )点 P が C 上を動くとき、$\overrightarrow{OQ}=2\overrightarrow{ OP}$ をみたす点 Q の軌跡を求めよ。
( 2 )点 P が C 上を動き、点 R が線分 OA 上を動くとき$\overrightarrow{ OS }=\overrightarrow{ 2OP }+\overrightarrow{ OR }$をみたす点 S が動く領域を座標平面上に図示し、その面積を求めよ。
2018東京大学文過去問
福田のおもしろ数学020〜わんちゃんの男の子と女の子の比率は〜Google入社試験の類題

単元:
#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#数列の極限#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
わんちゃんの国があります。この国ではどの家庭も男の子が産まれるまで子供を作り続けます。この国の男の子と女の子の比率はどうなりますか.
google入社試験過去問
この動画を見る
わんちゃんの国があります。この国ではどの家庭も男の子が産まれるまで子供を作り続けます。この国の男の子と女の子の比率はどうなりますか.
google入社試験過去問
福田の数学〜3次方程式の解の存在範囲に関する問題〜東京大学2018年文系第3問〜関数の増減と方程式の解

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
a>0とし、f(x)=$x^3-3a^2x$とおく。
( 1 )x$ \geqq 1$でf(x)が単調に増加するための aについての条件を求めよ。
( 2 )次の 2 条件を満たす点(a,b)の動きうる範囲を求め、座標平面上に図示せよ。
条件 1 :方程式f(x)=bは相異なる 3 実数解をもつ。
条件 2 :さらに方程式f(x)=bの解を$\alpha<\beta<\gamma$とすると、$\beta >1$ である。
2018東京大学文過去問
この動画を見る
a>0とし、f(x)=$x^3-3a^2x$とおく。
( 1 )x$ \geqq 1$でf(x)が単調に増加するための aについての条件を求めよ。
( 2 )次の 2 条件を満たす点(a,b)の動きうる範囲を求め、座標平面上に図示せよ。
条件 1 :方程式f(x)=bは相異なる 3 実数解をもつ。
条件 2 :さらに方程式f(x)=bの解を$\alpha<\beta<\gamma$とすると、$\beta >1$ である。
2018東京大学文過去問
福田のおもしろ数学012〜10秒チャレンジ〜重心によって分割される3つの三角形の面積が等しい証明

単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
三角形において、その重心 G で分割された 3 つの三角形の面積は等しいことを証明せよ.
※図は動画内参照
この動画を見る
三角形において、その重心 G で分割された 3 つの三角形の面積は等しいことを証明せよ.
※図は動画内参照
福田の数学〜0と1の間に整数は存在しないなんて当たり前〜東京大学2018年文系第2問〜数列の増減と整数となる条件

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
数列$a_{ 1},a_{ 2 }$,・・・を$a_{ n }=\displaystyle \frac{{}_2n \mathrm{ C }_n}{n!}$(n=1,2,・・・)で定める。
(1)$a_{ 7 }$と1の大小を調べよ。
(2)$n \geqq 2$とする。$\displaystyle \frac{a_{ n }}{a_{ n-1}}<1$を満たすnの範囲を求めよ。
(3)$a_{ n }$が整数となる$n \geqq 1$を全て求めよ。
2018東京大学文過去問
この動画を見る
数列$a_{ 1},a_{ 2 }$,・・・を$a_{ n }=\displaystyle \frac{{}_2n \mathrm{ C }_n}{n!}$(n=1,2,・・・)で定める。
(1)$a_{ 7 }$と1の大小を調べよ。
(2)$n \geqq 2$とする。$\displaystyle \frac{a_{ n }}{a_{ n-1}}<1$を満たすnの範囲を求めよ。
(3)$a_{ n }$が整数となる$n \geqq 1$を全て求めよ。
2018東京大学文過去問
福田のおもしろ数学011〜あけましておめでとうございます〜2024の階乗は末尾に0が何個並ぶか

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
2024 !の末尾に並ぶ 0 の個数を求めよ。
この動画を見る
2024 !の末尾に並ぶ 0 の個数を求めよ。
福田の数学〜不等式の図形的な意味に気づけるか〜東京大学2018年文系第1問(2)〜領域内を動く点が不等式を満たす条件

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
座標平面上に放物線 C を$y=x^2-3x+4$で定め、領域Dを$y \geqq x^2-3x+4$で定める。原点を通る 2 直線l, m は C に接する。
( 2 )次の条件を満たす点 P(p,q)の動きうる範囲を求め、座標平面上に図示せよ。
条件:領域Dのすべての点は(x,y)に対し、不等式$px+qy\leqq 0$が成り立つ。
2018東京大学文過去問
この動画を見る
座標平面上に放物線 C を$y=x^2-3x+4$で定め、領域Dを$y \geqq x^2-3x+4$で定める。原点を通る 2 直線l, m は C に接する。
( 2 )次の条件を満たす点 P(p,q)の動きうる範囲を求め、座標平面上に図示せよ。
条件:領域Dのすべての点は(x,y)に対し、不等式$px+qy\leqq 0$が成り立つ。
2018東京大学文過去問
福田のおもしろ数学010〜10秒で解けるキミは天才〜階乗の和の1の位

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
1 !十 2 !十 3 !十・・・十 2023 !十 2024 !の 1 の位を求めよ。
この動画を見る
1 !十 2 !十 3 !十・・・十 2023 !十 2024 !の 1 の位を求めよ。
福田の数学〜複数の絶対値に対応できるか〜東京大学2018年文系第1問(1)〜絶対値を含む関数の最小

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
座標平面上に放物線 C を$y=x^2-3x+4$ で定め、領域Dを$y \geqq x^2-3x+4$で定める。原点を通る 2 直線l, m は C に接する。
(1) 放物線 C 上を動く点 A と直線l, m の距離をそれぞれL,M とする。$\sqrt{ \mathstrut L } + \sqrt{ \mathstrut M }$が最小値をとるときの点 A の座標を求めよ。
2018東京大学文過去問
この動画を見る
座標平面上に放物線 C を$y=x^2-3x+4$ で定め、領域Dを$y \geqq x^2-3x+4$で定める。原点を通る 2 直線l, m は C に接する。
(1) 放物線 C 上を動く点 A と直線l, m の距離をそれぞれL,M とする。$\sqrt{ \mathstrut L } + \sqrt{ \mathstrut M }$が最小値をとるときの点 A の座標を求めよ。
2018東京大学文過去問
福田のおもしろ数学009〜あなたはネコを見つけられるか〜箱から箱へ移動するネコを見つける方法
単元:
#数A#場合の数と確率#確率#その他#その他#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
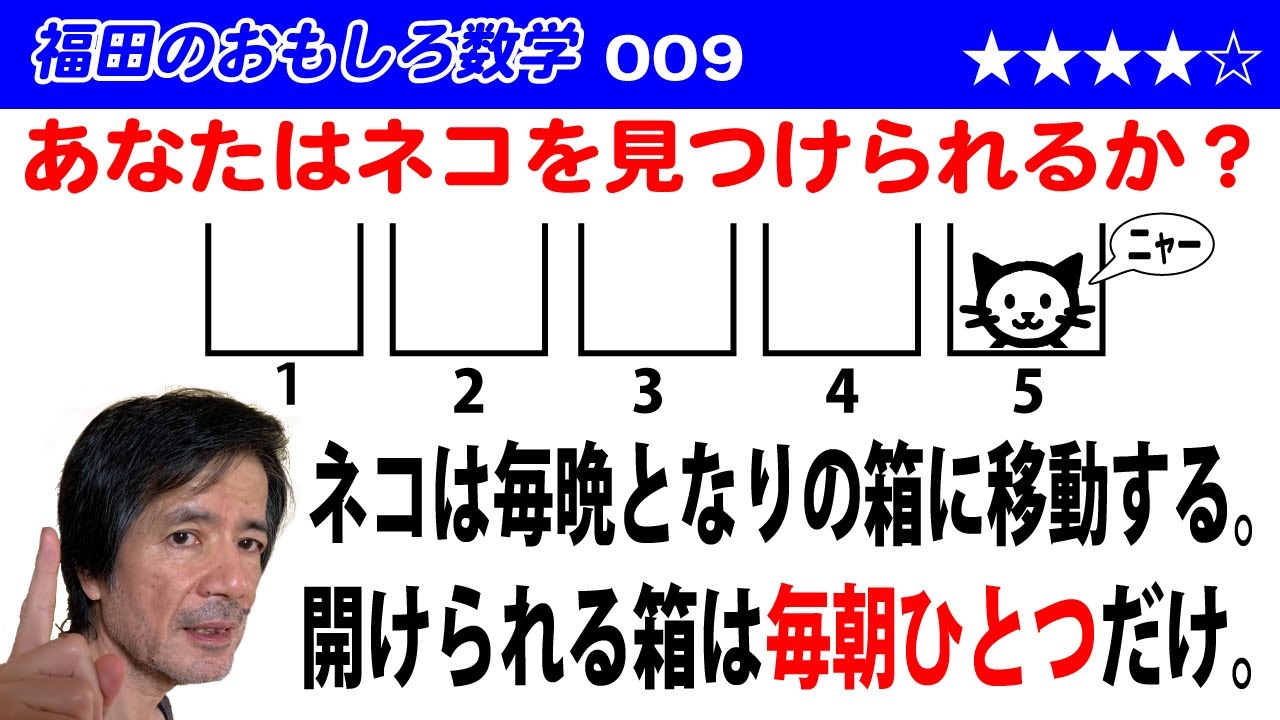
あなたはネコを見つけられるか?
猫は毎晩となりの箱に移動する。
開けられる箱は毎朝ひとつだけ。
この動画を見る
あなたはネコを見つけられるか?
猫は毎晩となりの箱に移動する。
開けられる箱は毎朝ひとつだけ。
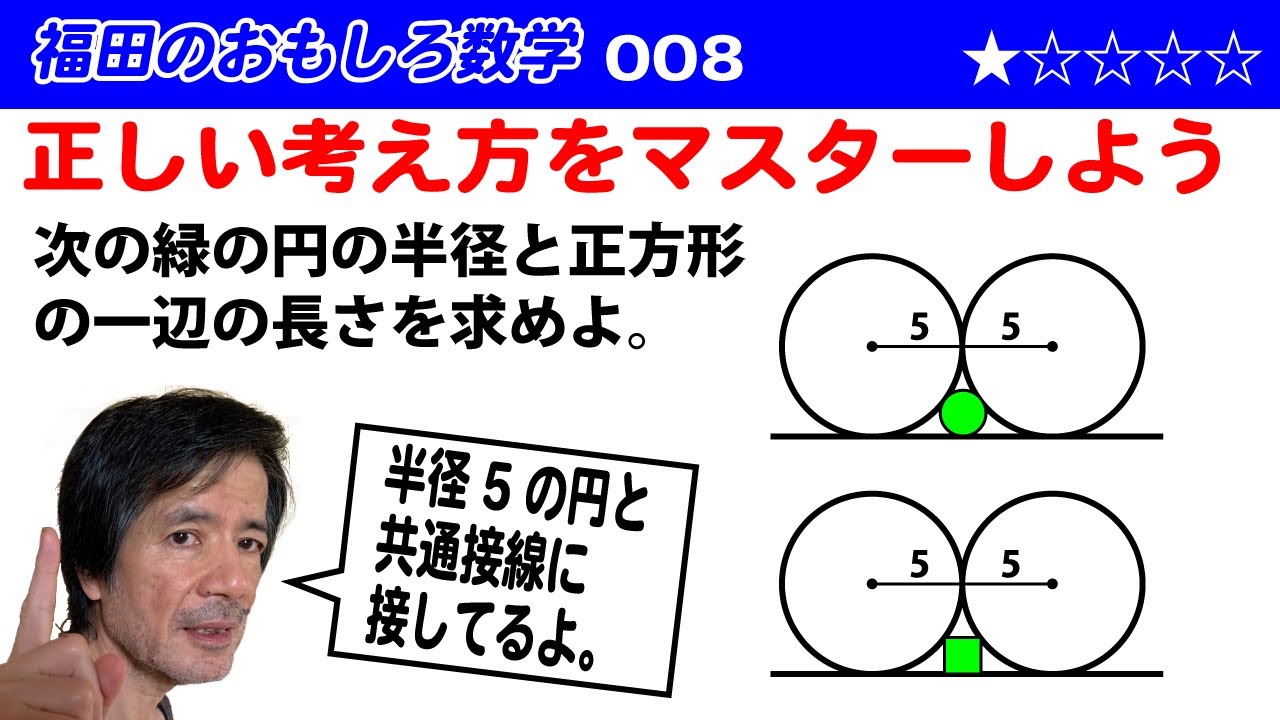
福田のおもしろ数学008〜正しいフォームを身につけよう〜外接する2円と共通接線に接する正方形
単元:
#数学(中学生)#中3数学#数A#図形の性質#三平方の定理#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
次の緑の円の半径と正方形の一片の長さを求めよ
※図は動画内参照
この動画を見る
次の緑の円の半径と正方形の一片の長さを求めよ
※図は動画内参照
福田のおもしろ数学007〜灘中学の入試問題に挑戦〜弧の長さの合計は

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#平面図形その他#灘中学校
指導講師:
福田次郎
問題文全文(内容文):
半径2の円周上に中心をもつ半径1の円が7つ。赤い弧の長さは?
※図は動画内参照
灘中過去問
この動画を見る
半径2の円周上に中心をもつ半径1の円が7つ。赤い弧の長さは?
※図は動画内参照
灘中過去問
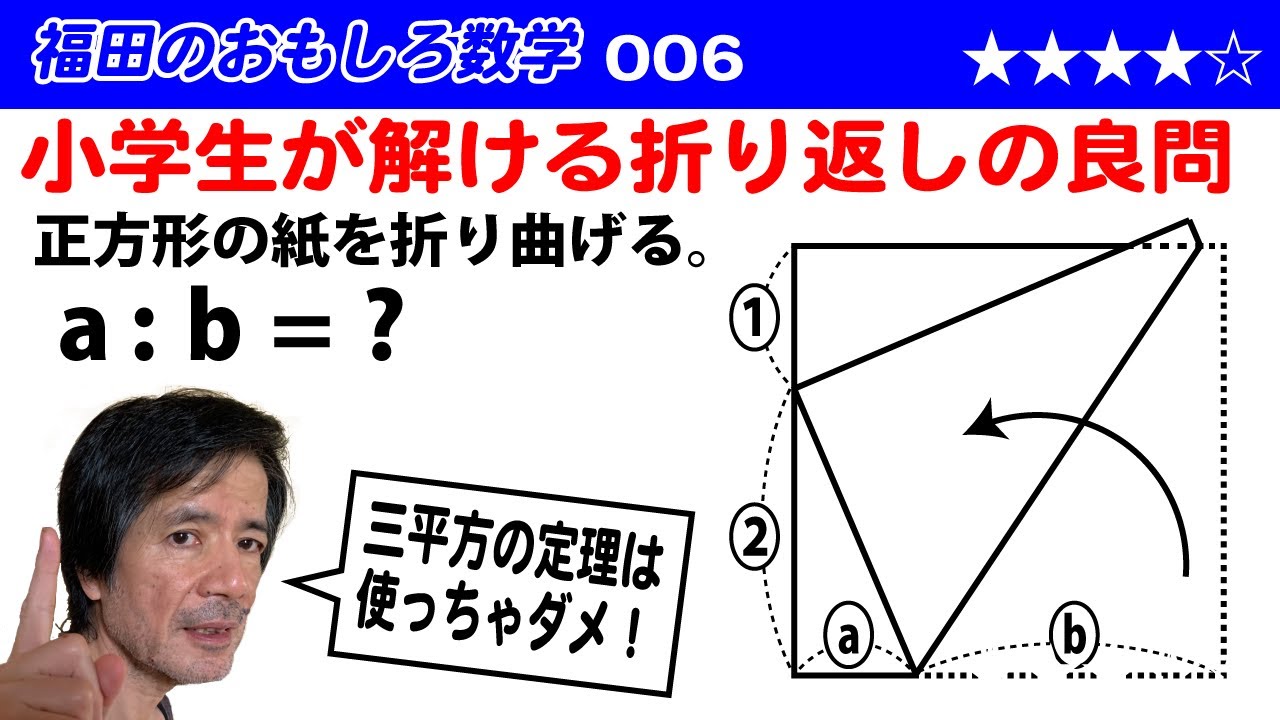
福田のおもしろ数学006〜中学入試の算数に挑戦、三平方の定理を使わない〜正方形の折り返し
福田のおもしろ数学005〜中学入試の算数に挑戦〜台形の面積

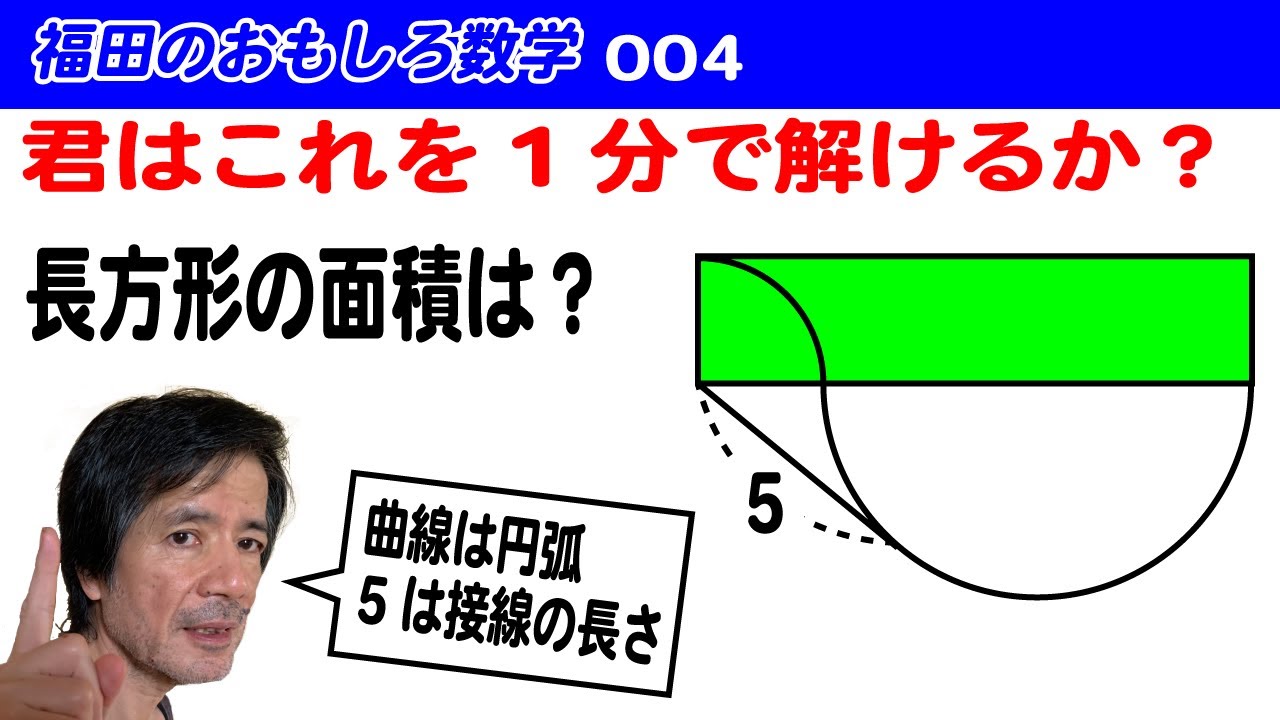
福田のおもしろ数学004〜接線の長さしかわからない〜長方形の面積を求める
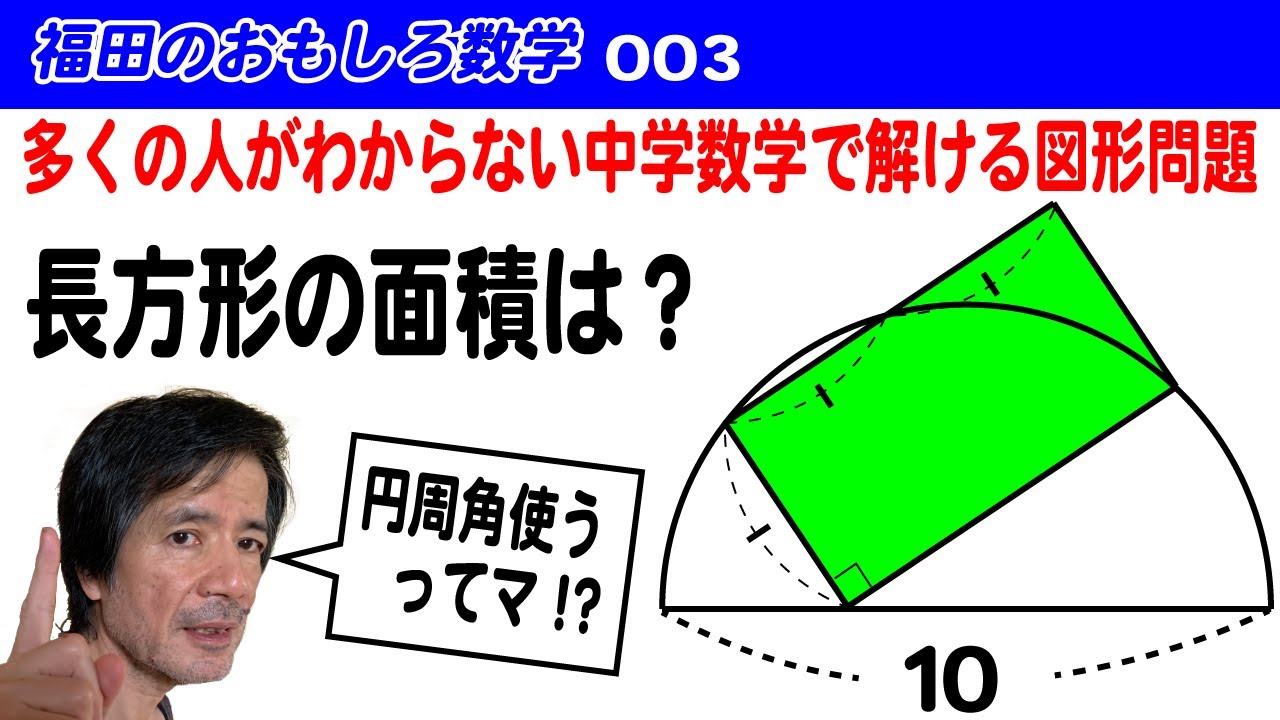
福田のおもしろ数学〜円周角の定理を使うってマ?〜長方形の面積を求める
福田の数学〜空間図形の通過範囲の面積と体積〜杏林大学2023年医学部第3問後編〜空間図形の通過範囲の面積と体積

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#杏林大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$xy$平面上の単位円$C$の$x\geqq 0$に動点$P$が$A$から$B$へ移動するとき、
$P,Q$を通り頂点$T$の放物線$L$と線分$PQ$で囲まれた図形の
通過範囲の体積を求めよ。
ただし$TM=PQ$とする。
この動画を見る
$xy$平面上の単位円$C$の$x\geqq 0$に動点$P$が$A$から$B$へ移動するとき、
$P,Q$を通り頂点$T$の放物線$L$と線分$PQ$で囲まれた図形の
通過範囲の体積を求めよ。
ただし$TM=PQ$とする。
福田の数学〜空間図形の通過範囲の面積と体積〜杏林大学2023年医学部第3問後編〜空間図形の通過範囲の面積と体積

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#杏林大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
座標空間において原点 O を中心とする半径 1 の円 C がxy平面上にあり、x> 0の領域において点 A ( 0 ,- 1 , 0 )から点 B ( 0 , 1,0 )まで移動する C 上の動点を P とする。
(1) 下記の 2 条件を満たす直角二等辺三角形 PQR を考える。
・点 Q は C 上にあり、直線 PQ はx軸に平行である。
・点 R の z 座標は正であり、直線 PR はz軸に平行である。
点 P が点 A から点 B まで移動するとき、三角形 PQR の周および内部が通過してできる立体Vについて、以下の間いに答えよ。
(a) 点 P が点 A から点 B まで移動するとき、線分 PR が通過してできる曲面の展開図は、横軸に弧 AP の長さ、縦軸に線分 PR の長さをとったグラフを考えればよく、アで表される概形となり、その面積はイである。
線分 PQ の中点を M とし、点 M から直線 QR に引いた垂線と線分 QR との交点を H とする。点 H は線分 QR を 1 :ウに内分する点である。点 P の位置に依らず、線分の長さについて$エ×(MH)^2+(OM)^2=1$が成り立つ。点Pが点 A から点 B まで移動するとき、線分 MH が通過する領域の概形はオであり、面積は$\displaystyle \frac{\sqrt{ カ }}{キ}\pi$である。
※ア、オの解答群は動画内参照
(b) 点 P が点 A から点 B まで移動するとき、線分 QR が通過してできる曲面上において、 2 点 A , B を結ぶ最も短い曲線はクが描く曲線である。
クの解答群①点 Q ②点 R ③設間( a )で考えた点 H ④線分 QR とyz平面との交点 ⑤線分 QR を 1 :$\sqrt{ 2 }$に内分する点 ⑥線分 QR を$\sqrt{ 2 }$: 1 に内分する点 ⑦三角形 PQR の重心から線分 QR に引いた垂線と線分 QR との交点
(c) 点 P が点 A から点 B まで移動するとき、線分 PQ を直径とするxz平面に平行な円が通過してできる球の体積は$\displaystyle \frac{ケ}{コ}$である。また△ PQR の面積は、線分 PQを直径とする円の面積の$\displaystyle \frac{サ}{\pi}$倍である。よって、立体Vの体積は$\displaystyle \frac{シ}{ス}$である。
( 2 )$z \geqq 0$ の領域において、yz平面上の点 T を頂点とし、 2 点 P , Q を通る放物線Lを考える。ただし、 Q , T は下記の 2 条件を満たす点とする。
・点 Q は C 上にあり、直線 PQ はx軸に平行である。
・三角形 PQT はxz平面に平行であり、点 T の z 座標は線分 PQ の長さに等しい。点 P が(1,0,0)であるとき、放物線Lを表す式はy=0,$z=セソx^2+タ$(ただし$-1 \leqq x \leqq 1$)であり、この放物線と線分 PQ で囲まれる図形の面積は$\displaystyle \frac{チ}{ツ}$である。
点 P が点 A から点 B まで移動するとき、放物線 L と線分 PQ で囲まれる図形が通過してできる立体の体積は$\displaystyle \frac{テト}{ナ}$である。
点 P が点 A から点 B まで移動するとき、線分 PQ を直径とするxz平面に平行な円が通過してできる球の体積は$\displaystyle \frac{ケ}{コ}\pi$である。また△ PQR の面積は、線分 PQ を直径とする円の面積の$\displaystyle \frac{サ}{\pi}$倍である。よって、立体体積はV の体積は$\displaystyle \frac{シ}{ス}$である。
2023杏林大学過去問
この動画を見る
座標空間において原点 O を中心とする半径 1 の円 C がxy平面上にあり、x> 0の領域において点 A ( 0 ,- 1 , 0 )から点 B ( 0 , 1,0 )まで移動する C 上の動点を P とする。
(1) 下記の 2 条件を満たす直角二等辺三角形 PQR を考える。
・点 Q は C 上にあり、直線 PQ はx軸に平行である。
・点 R の z 座標は正であり、直線 PR はz軸に平行である。
点 P が点 A から点 B まで移動するとき、三角形 PQR の周および内部が通過してできる立体Vについて、以下の間いに答えよ。
(a) 点 P が点 A から点 B まで移動するとき、線分 PR が通過してできる曲面の展開図は、横軸に弧 AP の長さ、縦軸に線分 PR の長さをとったグラフを考えればよく、アで表される概形となり、その面積はイである。
線分 PQ の中点を M とし、点 M から直線 QR に引いた垂線と線分 QR との交点を H とする。点 H は線分 QR を 1 :ウに内分する点である。点 P の位置に依らず、線分の長さについて$エ×(MH)^2+(OM)^2=1$が成り立つ。点Pが点 A から点 B まで移動するとき、線分 MH が通過する領域の概形はオであり、面積は$\displaystyle \frac{\sqrt{ カ }}{キ}\pi$である。
※ア、オの解答群は動画内参照
(b) 点 P が点 A から点 B まで移動するとき、線分 QR が通過してできる曲面上において、 2 点 A , B を結ぶ最も短い曲線はクが描く曲線である。
クの解答群①点 Q ②点 R ③設間( a )で考えた点 H ④線分 QR とyz平面との交点 ⑤線分 QR を 1 :$\sqrt{ 2 }$に内分する点 ⑥線分 QR を$\sqrt{ 2 }$: 1 に内分する点 ⑦三角形 PQR の重心から線分 QR に引いた垂線と線分 QR との交点
(c) 点 P が点 A から点 B まで移動するとき、線分 PQ を直径とするxz平面に平行な円が通過してできる球の体積は$\displaystyle \frac{ケ}{コ}$である。また△ PQR の面積は、線分 PQを直径とする円の面積の$\displaystyle \frac{サ}{\pi}$倍である。よって、立体Vの体積は$\displaystyle \frac{シ}{ス}$である。
( 2 )$z \geqq 0$ の領域において、yz平面上の点 T を頂点とし、 2 点 P , Q を通る放物線Lを考える。ただし、 Q , T は下記の 2 条件を満たす点とする。
・点 Q は C 上にあり、直線 PQ はx軸に平行である。
・三角形 PQT はxz平面に平行であり、点 T の z 座標は線分 PQ の長さに等しい。点 P が(1,0,0)であるとき、放物線Lを表す式はy=0,$z=セソx^2+タ$(ただし$-1 \leqq x \leqq 1$)であり、この放物線と線分 PQ で囲まれる図形の面積は$\displaystyle \frac{チ}{ツ}$である。
点 P が点 A から点 B まで移動するとき、放物線 L と線分 PQ で囲まれる図形が通過してできる立体の体積は$\displaystyle \frac{テト}{ナ}$である。
点 P が点 A から点 B まで移動するとき、線分 PQ を直径とするxz平面に平行な円が通過してできる球の体積は$\displaystyle \frac{ケ}{コ}\pi$である。また△ PQR の面積は、線分 PQ を直径とする円の面積の$\displaystyle \frac{サ}{\pi}$倍である。よって、立体体積はV の体積は$\displaystyle \frac{シ}{ス}$である。
2023杏林大学過去問



