 福田次郎
福田次郎
 福田次郎
福田次郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
福田の数学〜名古屋大学2023年理系第2問〜回転体の体積と関数の増減と最大

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#微分とその応用#積分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#面積、体積#数学(高校生)#名古屋大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 0<b<a とする。xy平面において、原点を中心とする半径rの円Cと点(a, 0)を中心とする半径bの円Dが2点で交わっている。
(1)半径rの満たすべき条件を求めよ。
(2)CとDの交点のうちy座標が正のものをPとする。Pのx座標h(r)を求めよ。
(3)点Q(r, 0)と点R(a-b, 0)をとる。Dの内部にあるCの弧PQ、線分QR、および線分RPで囲まれる図形をAとする。xyz空間においてAをx軸の周りに1回転して得られる立体の体積V(r)を求めよ。ただし答えにh(r)を用いてもよい。
(4)(3)の最大値を与えるrを求めよ。また、そのrをr(a)とおいたとき、
$\displaystyle\lim_{a \to \infty}(r(a)-a)$を求めよ。
2023名古屋大学理系過去問
この動画を見る
$\Large\boxed{2}$ 0<b<a とする。xy平面において、原点を中心とする半径rの円Cと点(a, 0)を中心とする半径bの円Dが2点で交わっている。
(1)半径rの満たすべき条件を求めよ。
(2)CとDの交点のうちy座標が正のものをPとする。Pのx座標h(r)を求めよ。
(3)点Q(r, 0)と点R(a-b, 0)をとる。Dの内部にあるCの弧PQ、線分QR、および線分RPで囲まれる図形をAとする。xyz空間においてAをx軸の周りに1回転して得られる立体の体積V(r)を求めよ。ただし答えにh(r)を用いてもよい。
(4)(3)の最大値を与えるrを求めよ。また、そのrをr(a)とおいたとき、
$\displaystyle\lim_{a \to \infty}(r(a)-a)$を求めよ。
2023名古屋大学理系過去問
福田の数学〜名古屋大学2023年理系第1問〜4次方程式の解と共役な複素数の性質

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#複素数平面#数学(高校生)#名古屋大学#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 実数係数の4次方程式$x^4$$-px^3$$+qx^2$$-rx$$+s$=0 は相異なる複素数$\alpha$, $\bar{\alpha}$, $\beta$, $\bar{\beta}$を解に持ち、点1を中心とする半径1の円周上にあるとする。ただし、$\bar{\alpha}$, $\bar{\beta}$はそれぞれ $\alpha$, $\beta$と共役な複素数を表す。
(1)$\alpha$+$\bar{\alpha}$=$\alpha$$\bar{\alpha}$ を示せ。
(2)$t$=$\alpha$+$\bar{\alpha}$, $u$=$\beta$+$\bar{\beta}$とおく。p, q, r, sをそれぞれtとuで表せ。
(3)座標平面において、点(p, s)のとりうる範囲を図示せよ。
2023名古屋大学理系過去問
この動画を見る
$\Large\boxed{1}$ 実数係数の4次方程式$x^4$$-px^3$$+qx^2$$-rx$$+s$=0 は相異なる複素数$\alpha$, $\bar{\alpha}$, $\beta$, $\bar{\beta}$を解に持ち、点1を中心とする半径1の円周上にあるとする。ただし、$\bar{\alpha}$, $\bar{\beta}$はそれぞれ $\alpha$, $\beta$と共役な複素数を表す。
(1)$\alpha$+$\bar{\alpha}$=$\alpha$$\bar{\alpha}$ を示せ。
(2)$t$=$\alpha$+$\bar{\alpha}$, $u$=$\beta$+$\bar{\beta}$とおく。p, q, r, sをそれぞれtとuで表せ。
(3)座標平面において、点(p, s)のとりうる範囲を図示せよ。
2023名古屋大学理系過去問
福田の数学〜一橋大学2023年文系第5問〜反復試行の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ A, B, Cの3人が、A, B, C, A, B, C, A, ... という順番にさいころを投げ、最初に1を出した人を勝ちとする。だれかが1を出すか、全員が$n$回ずつ投げたら、ゲームを終了する。A, B, Cが勝つ確率$P_A$, $P_B$, $P_C$をそれぞれ求めよ。
2023一橋大学文系過去問
この動画を見る
$\Large\boxed{5}$ A, B, Cの3人が、A, B, C, A, B, C, A, ... という順番にさいころを投げ、最初に1を出した人を勝ちとする。だれかが1を出すか、全員が$n$回ずつ投げたら、ゲームを終了する。A, B, Cが勝つ確率$P_A$, $P_B$, $P_C$をそれぞれ求めよ。
2023一橋大学文系過去問
福田の数学〜一橋大学2023年文系第4問〜群数列

単元:
#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ xy平面上で、x座標とy座標がともに正の整数であるような各点に、下の図のような番号をつける。(※動画参照)点(m, n)につけた番号をf(m, n)とする。
たとえば、$f(1, 1)=1, f(3, 4)=19$ である。
(1)$f(m, n)+f(m+1, n+1)=2f(m, n+1)$
が成り立つことを示せ。
(2)$f(m, n)+f(m+1, n)+f(m, n+1)+f(m+1, n+1)=2023$
となるような整数の組(m, n)を求めよ。
2023一橋大学文系過去問
この動画を見る
$\Large\boxed{4}$ xy平面上で、x座標とy座標がともに正の整数であるような各点に、下の図のような番号をつける。(※動画参照)点(m, n)につけた番号をf(m, n)とする。
たとえば、$f(1, 1)=1, f(3, 4)=19$ である。
(1)$f(m, n)+f(m+1, n+1)=2f(m, n+1)$
が成り立つことを示せ。
(2)$f(m, n)+f(m+1, n)+f(m, n+1)+f(m+1, n+1)=2023$
となるような整数の組(m, n)を求めよ。
2023一橋大学文系過去問
福田の数学〜一橋大学2023年文系第3問〜ベクトルと四面体の体積の最大

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 原点をOとする座標空間内に3点A(-3, 2, 0), B(1, 5, 0), C(4, 5, 1)がある。
Pは|$\overrightarrow{PA}$+3$\overrightarrow{PB}$+2$\overrightarrow{PC}$|≦36 を満たす点である。
4点O, A, B, Pが同一平面上にないとき、四面体OABPの体積の最大値を求めよ。
2023一橋大学文系過去問
この動画を見る
$\Large\boxed{3}$ 原点をOとする座標空間内に3点A(-3, 2, 0), B(1, 5, 0), C(4, 5, 1)がある。
Pは|$\overrightarrow{PA}$+3$\overrightarrow{PB}$+2$\overrightarrow{PC}$|≦36 を満たす点である。
4点O, A, B, Pが同一平面上にないとき、四面体OABPの体積の最大値を求めよ。
2023一橋大学文系過去問
福田の数学〜一橋大学2023年文系第2問〜共通接線が存在する条件

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ aを正の実数とする。2つの曲線$C_1$:y=$x^3$+2$ax^2$ および$C_2$:y=3$ax^2$$-\displaystyle\frac{3}{a}$ の両方に接する直線が存在するようなaの範囲を求めよ。
2023一橋大学文系過去問
この動画を見る
$\Large\boxed{2}$ aを正の実数とする。2つの曲線$C_1$:y=$x^3$+2$ax^2$ および$C_2$:y=3$ax^2$$-\displaystyle\frac{3}{a}$ の両方に接する直線が存在するようなaの範囲を求めよ。
2023一橋大学文系過去問
福田の数学〜一橋大学2023年文系第1問〜コンビネーションの等式を満たす自然数

単元:
#数A#大学入試過去問(数学)#場合の数と確率#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ nを2以上20以下の整数、kを1以上n-1以下の整数とする。
${}_{n+2}C_{k+1}$=2(${}_nC_{k-1}$+${}_nC_{k+1}$)
が成り立つような整数の組(n, k)を求めよ。
2023一橋大学文系過去問
この動画を見る
$\Large\boxed{1}$ nを2以上20以下の整数、kを1以上n-1以下の整数とする。
${}_{n+2}C_{k+1}$=2(${}_nC_{k-1}$+${}_nC_{k+1}$)
が成り立つような整数の組(n, k)を求めよ。
2023一橋大学文系過去問
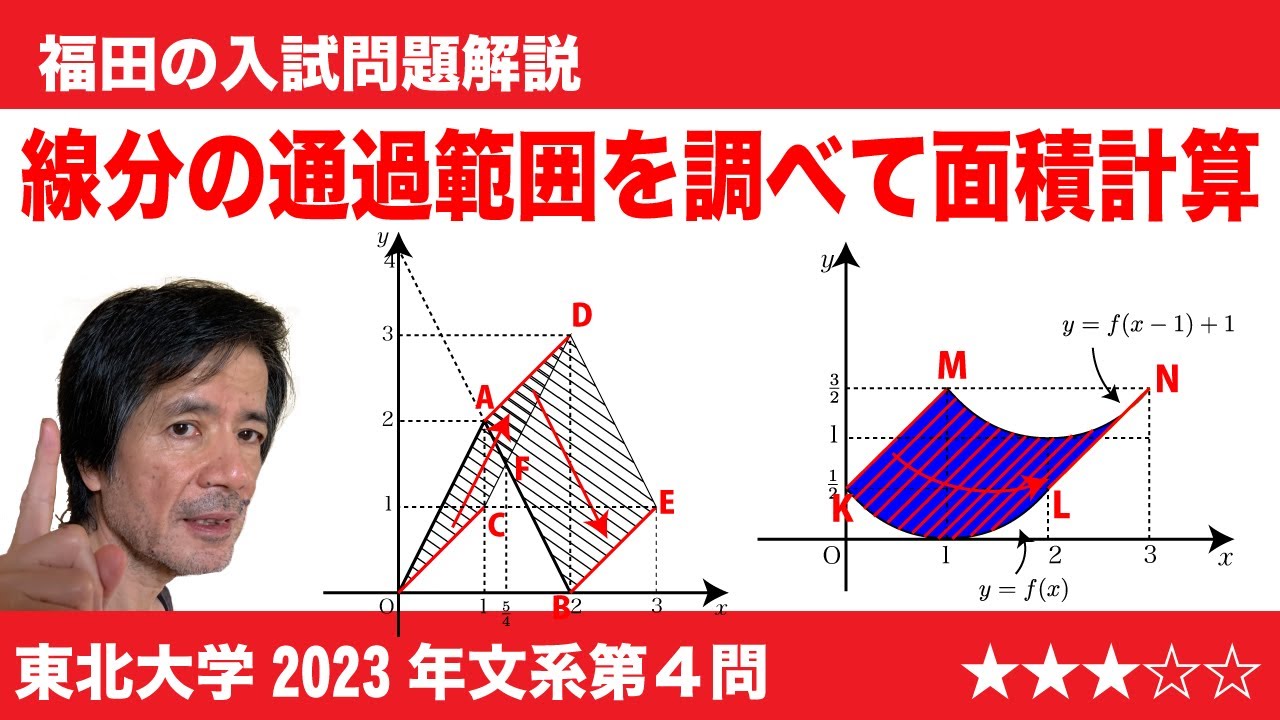
福田の数学〜東北大学2023年文系第4問〜線分の通過範囲の面積
単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#東北大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 関数f(x)に対して、座標平面上の2つの点P(x, f(x)), Q(x+1, f(x)+1)を考える。実数xが0≦x≦2の範囲を動くとき、線分PQがつうかしてできる図形の面積をSとおく。以下の問いに答えよ。
(1)関数f(x)=-2|x-1|+2に 対して、Sの値を求めよ。
(2)関数f(x)=$\frac{1}{2}(x-1)^2$ に対して、曲線y=f(x)の接線で、傾きが1のものの方程式を求めよ。
(3)設問(2)の関数f(x)=$\frac{1}{2}(x-1)^2$ に対して、Sの値を求めよ。
2023東北大学文系過去問
この動画を見る
$\Large\boxed{4}$ 関数f(x)に対して、座標平面上の2つの点P(x, f(x)), Q(x+1, f(x)+1)を考える。実数xが0≦x≦2の範囲を動くとき、線分PQがつうかしてできる図形の面積をSとおく。以下の問いに答えよ。
(1)関数f(x)=-2|x-1|+2に 対して、Sの値を求めよ。
(2)関数f(x)=$\frac{1}{2}(x-1)^2$ に対して、曲線y=f(x)の接線で、傾きが1のものの方程式を求めよ。
(3)設問(2)の関数f(x)=$\frac{1}{2}(x-1)^2$ に対して、Sの値を求めよ。
2023東北大学文系過去問
福田の数学〜東北大学2023年文系第3問〜軸の動く最大最小

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ aを実数とし、2次関数f(x)=$x^2$+2$ax$-3 を考える。実数xがa≦x≦a+3 の範囲を動くときのf(x)の最大値および最小値を、それぞれM(a), m(a)とする。
以下の問いに答えよ。
(1)M(a)をaを用いて表せ。
(2)m(a)をaを用いて表せ。
(3)aがすべての実数を動くとき、m(a)の最小値を求めよ。
2023東北大学文系過去問
この動画を見る
$\Large\boxed{3}$ aを実数とし、2次関数f(x)=$x^2$+2$ax$-3 を考える。実数xがa≦x≦a+3 の範囲を動くときのf(x)の最大値および最小値を、それぞれM(a), m(a)とする。
以下の問いに答えよ。
(1)M(a)をaを用いて表せ。
(2)m(a)をaを用いて表せ。
(3)aがすべての実数を動くとき、m(a)の最小値を求めよ。
2023東北大学文系過去問
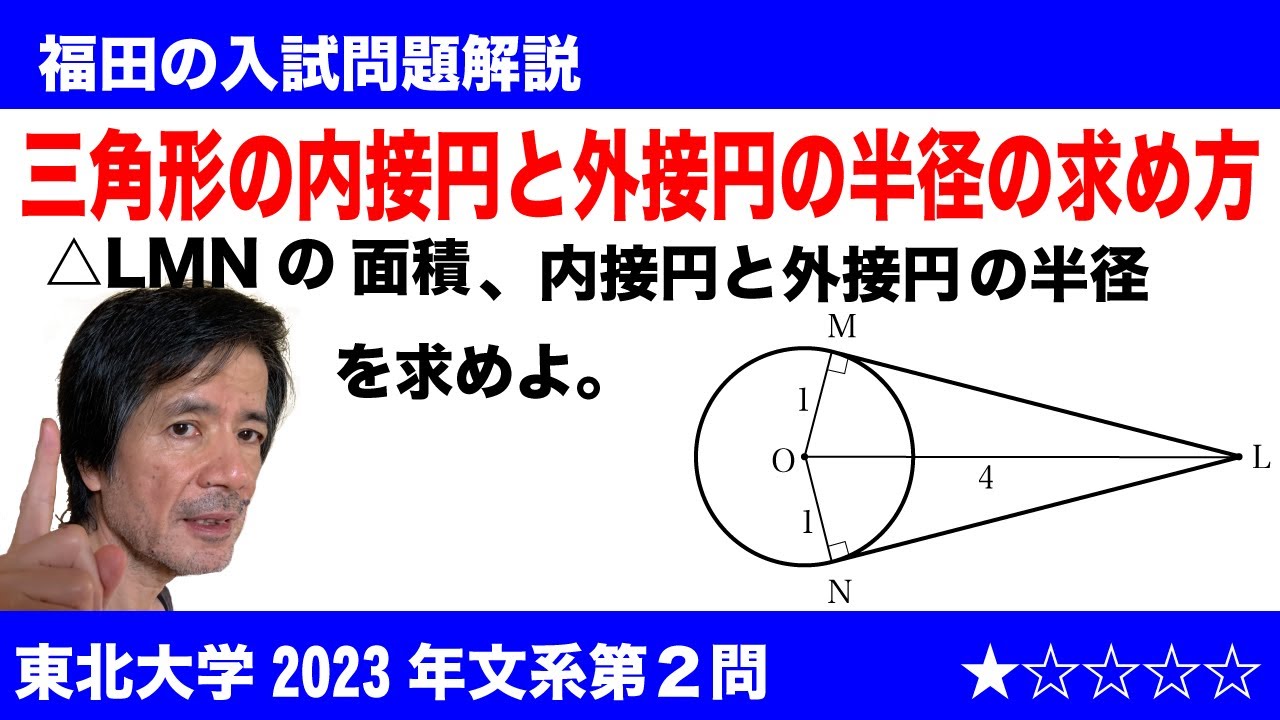
福田の数学〜東北大学2023年文系第1問〜三角形の面積と内接円と外接円の半径
単元:
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#三角形の辺の比(内分・外分・二等分線)#周角と円に内接する四角形・円と接線・接弦定理#三角関数#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 平面上の半径1の円Cの中心Oから距離4だけ離れた点Lをとる。点Lを通る円Cの2本の接線と円Cの接点をそれぞれM、Nとする。以下の問いに答えよ。
(1)三角形LMNの面積を求めよ。
(2)三角形LMNの内接円の半径をrと、三角形LMNの外接円の半径Rをそれぞれ求めよ。
2023東北大学文系過去問
この動画を見る
$\Large\boxed{2}$ 平面上の半径1の円Cの中心Oから距離4だけ離れた点Lをとる。点Lを通る円Cの2本の接線と円Cの接点をそれぞれM、Nとする。以下の問いに答えよ。
(1)三角形LMNの面積を求めよ。
(2)三角形LMNの内接円の半径をrと、三角形LMNの外接円の半径Rをそれぞれ求めよ。
2023東北大学文系過去問
福田の数学〜東北大学2023年理系第6問〜線分の通過範囲の面積

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#微分法#接線と法線・平均値の定理#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{6}$ 関数$f(x)$=$-\frac{1}{2}x$$-\frac{4}{6x+1}$について、以下の問いに答えよ。
(1)曲線y=f(x)の接線で、傾きが1であり、かつ接点のx座標が正であるものの方程式を求めよ。
(2)座標平面上の2点P(x, f(x)), Q(x+1, f(x)+1)を考える。xが0≦x≦2の範囲を動くとき、線分PQが通過してできる図形Sの概形を描け。またSの面積を求めよ。
2023東北大学理系過去問
この動画を見る
$\Large\boxed{6}$ 関数$f(x)$=$-\frac{1}{2}x$$-\frac{4}{6x+1}$について、以下の問いに答えよ。
(1)曲線y=f(x)の接線で、傾きが1であり、かつ接点のx座標が正であるものの方程式を求めよ。
(2)座標平面上の2点P(x, f(x)), Q(x+1, f(x)+1)を考える。xが0≦x≦2の範囲を動くとき、線分PQが通過してできる図形Sの概形を描け。またSの面積を求めよ。
2023東北大学理系過去問
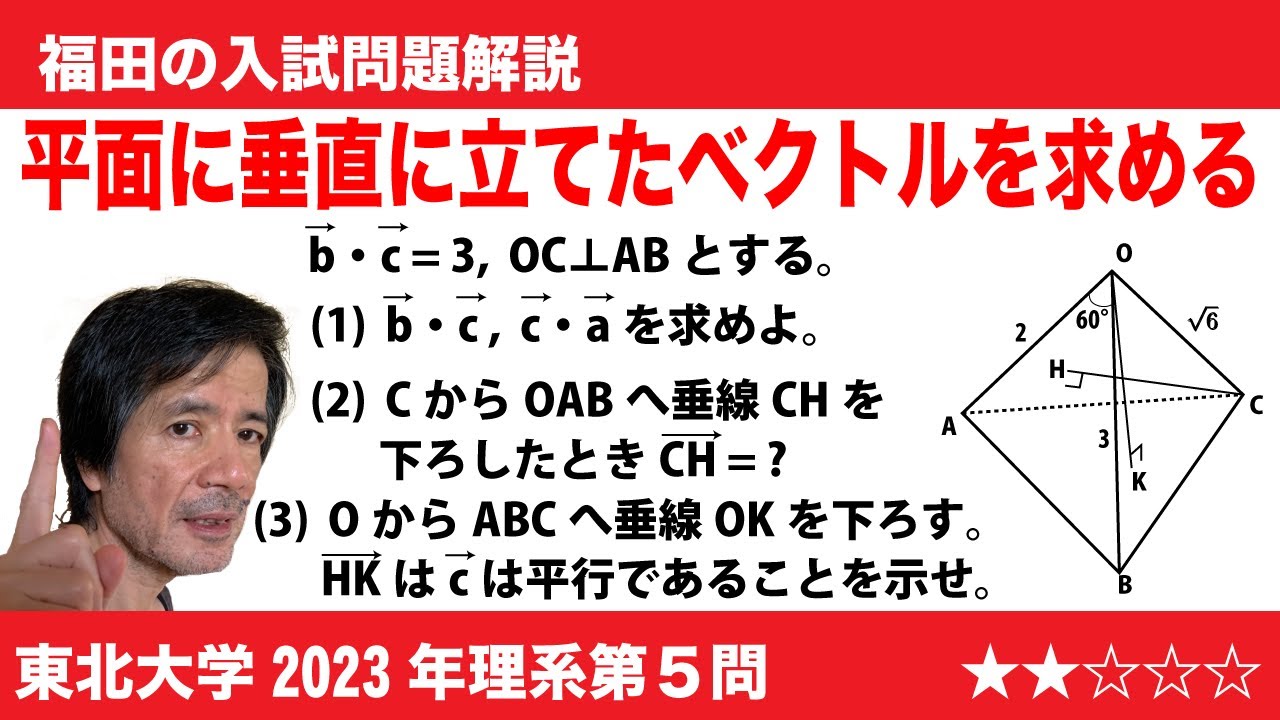
福田の数学〜東北大学2023年理系第5問〜空間ベクトルと内積
単元:
#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 四面体OABCにおいて、$\overrightarrow{a}$=$\overrightarrow{OA}$, $\overrightarrow{b}$=$\overrightarrow{OB}$, $\overrightarrow{c}$=$\overrightarrow{OC}$とおき、次が成り立つとする。
$\angle$AOB=60°, |$\overrightarrow{a}$|=2, |$\overrightarrow{b}$|=3, |$\overrightarrow{c}$|=$\sqrt 6$, $\overrightarrow{b}$・$\overrightarrow{c}$=3
ただし、$\overrightarrow{b}$・$\overrightarrow{c}$は、2つのベクトル$\overrightarrow{b}$と$\overrightarrow{c}$の内積を表す。さらに、線分OCと線分ABは垂直であるとする。点Cから3点O, A, Bを含む平面に下ろした垂線をCHとし、点Oから3点A, B, Cを含む平面に下ろした垂線をOKとする。
(1)$\overrightarrow{a}$・$\overrightarrow{b}$と$\overrightarrow{c}$・$\overrightarrow{a}$を求めよ。
(2)ベクトル$\overrightarrow{OH}$を$\overrightarrow{a}$と$\overrightarrow{b}$を用いて表せ。
(3)ベクトル$\overrightarrow{c}$とベクトル$\overrightarrow{HK}$は平行であることを示せ。
2023東北大学理系過去問
この動画を見る
$\Large\boxed{5}$ 四面体OABCにおいて、$\overrightarrow{a}$=$\overrightarrow{OA}$, $\overrightarrow{b}$=$\overrightarrow{OB}$, $\overrightarrow{c}$=$\overrightarrow{OC}$とおき、次が成り立つとする。
$\angle$AOB=60°, |$\overrightarrow{a}$|=2, |$\overrightarrow{b}$|=3, |$\overrightarrow{c}$|=$\sqrt 6$, $\overrightarrow{b}$・$\overrightarrow{c}$=3
ただし、$\overrightarrow{b}$・$\overrightarrow{c}$は、2つのベクトル$\overrightarrow{b}$と$\overrightarrow{c}$の内積を表す。さらに、線分OCと線分ABは垂直であるとする。点Cから3点O, A, Bを含む平面に下ろした垂線をCHとし、点Oから3点A, B, Cを含む平面に下ろした垂線をOKとする。
(1)$\overrightarrow{a}$・$\overrightarrow{b}$と$\overrightarrow{c}$・$\overrightarrow{a}$を求めよ。
(2)ベクトル$\overrightarrow{OH}$を$\overrightarrow{a}$と$\overrightarrow{b}$を用いて表せ。
(3)ベクトル$\overrightarrow{c}$とベクトル$\overrightarrow{HK}$は平行であることを示せ。
2023東北大学理系過去問
福田の数学〜東北大学2023年理系第4問〜1の5乗根

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#複素数平面#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#複素数平面#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 実数a=$\frac{\sqrt5-1}{2}$に対して、整式f(x)=$x^2$-$ax$+1を考える。
(1)整式$x^4$+$x^3$+$x^2$+$x$+1 はf(x)で割り切れることを示せ。
(2)方程式f(x)=0の虚数解であって虚部が正のものを$\alpha$とする。$\alpha$を極形式で表せ。ただし、$r^5$=1を満たす実数rがr=1のみであることは、認めて使用してよい。
(3)設問(2)の虚数$\alpha$に対して、$\alpha^{2023}$+$\alpha^{-2023}$の値を求めよ。
2023東北大学理系過去問
この動画を見る
$\Large\boxed{4}$ 実数a=$\frac{\sqrt5-1}{2}$に対して、整式f(x)=$x^2$-$ax$+1を考える。
(1)整式$x^4$+$x^3$+$x^2$+$x$+1 はf(x)で割り切れることを示せ。
(2)方程式f(x)=0の虚数解であって虚部が正のものを$\alpha$とする。$\alpha$を極形式で表せ。ただし、$r^5$=1を満たす実数rがr=1のみであることは、認めて使用してよい。
(3)設問(2)の虚数$\alpha$に対して、$\alpha^{2023}$+$\alpha^{-2023}$の値を求めよ。
2023東北大学理系過去問
福田の数学〜東北大学2023年理系第3問〜漸化式と数列の和

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ sを実数とし、数列$\left\{a_n\right\}$を
$a_1$=s, (n+2)$a_{n+1}$=n$a_n$+2 (n=1,2,3,...)
で定める。以下の問いに答えよ。
(1)$a_n$をnとsを用いて表せ。
(2)ある正の整数$m$に対して、$\displaystyle\sum_{n=1}^ma_n$=0が成り立つとする。sをmを用いて表せ。
2023東北大学理系過去問
この動画を見る
$\Large\boxed{3}$ sを実数とし、数列$\left\{a_n\right\}$を
$a_1$=s, (n+2)$a_{n+1}$=n$a_n$+2 (n=1,2,3,...)
で定める。以下の問いに答えよ。
(1)$a_n$をnとsを用いて表せ。
(2)ある正の整数$m$に対して、$\displaystyle\sum_{n=1}^ma_n$=0が成り立つとする。sをmを用いて表せ。
2023東北大学理系過去問
福田の数学〜東北大学2023年理系第2問〜三角方程式の解の個数とその極限

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#三角関数#円と方程式#三角関数とグラフ#関数と極限#微分とその応用#関数の極限#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 関数f(x)=$\sin3x$+$\sin x$について、以下の問いに答えよ。
(1)f(x)=0 を満たす正の実数$x$のうち、最小のものを求めよ。
(2)正の整数$m$に対して、f(x)=0を満たす正の実数$x$のうち、$m$以下のものの個数を$p(m)$とする。極限値$\displaystyle\lim_{m \to \infty}\frac{p(m)}{m}$ を求めよ。
2023東北大学理系過去問
この動画を見る
$\Large\boxed{2}$ 関数f(x)=$\sin3x$+$\sin x$について、以下の問いに答えよ。
(1)f(x)=0 を満たす正の実数$x$のうち、最小のものを求めよ。
(2)正の整数$m$に対して、f(x)=0を満たす正の実数$x$のうち、$m$以下のものの個数を$p(m)$とする。極限値$\displaystyle\lim_{m \to \infty}\frac{p(m)}{m}$ を求めよ。
2023東北大学理系過去問
福田の数学〜東北大学2023年理系第1問〜確率の基本性質

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 赤玉4個と白玉5個の入った、中の見えない袋がある。玉はすべて、色が区別できる他には違いはないものとする。A,Bの2人が、Aから交互に、袋から玉を1個ずつ取り出すゲームを行う。ただし取り出した玉は袋の中に戻さない。Aが赤玉を取り出したらAの勝ちとし、その時点でゲームを終了する。Bが白玉を取り出したらBの勝ちとし、その時点でゲームを終了する。袋から玉がなくなったら引き分けとし、ゲームを終了する。
(1)このゲームが引き分けとなる確率を求めよ。
(2)このゲームにAが勝つ確率を求めよ。
2023東北大学理系過去問
この動画を見る
$\Large\boxed{1}$ 赤玉4個と白玉5個の入った、中の見えない袋がある。玉はすべて、色が区別できる他には違いはないものとする。A,Bの2人が、Aから交互に、袋から玉を1個ずつ取り出すゲームを行う。ただし取り出した玉は袋の中に戻さない。Aが赤玉を取り出したらAの勝ちとし、その時点でゲームを終了する。Bが白玉を取り出したらBの勝ちとし、その時点でゲームを終了する。袋から玉がなくなったら引き分けとし、ゲームを終了する。
(1)このゲームが引き分けとなる確率を求めよ。
(2)このゲームにAが勝つ確率を求めよ。
2023東北大学理系過去問
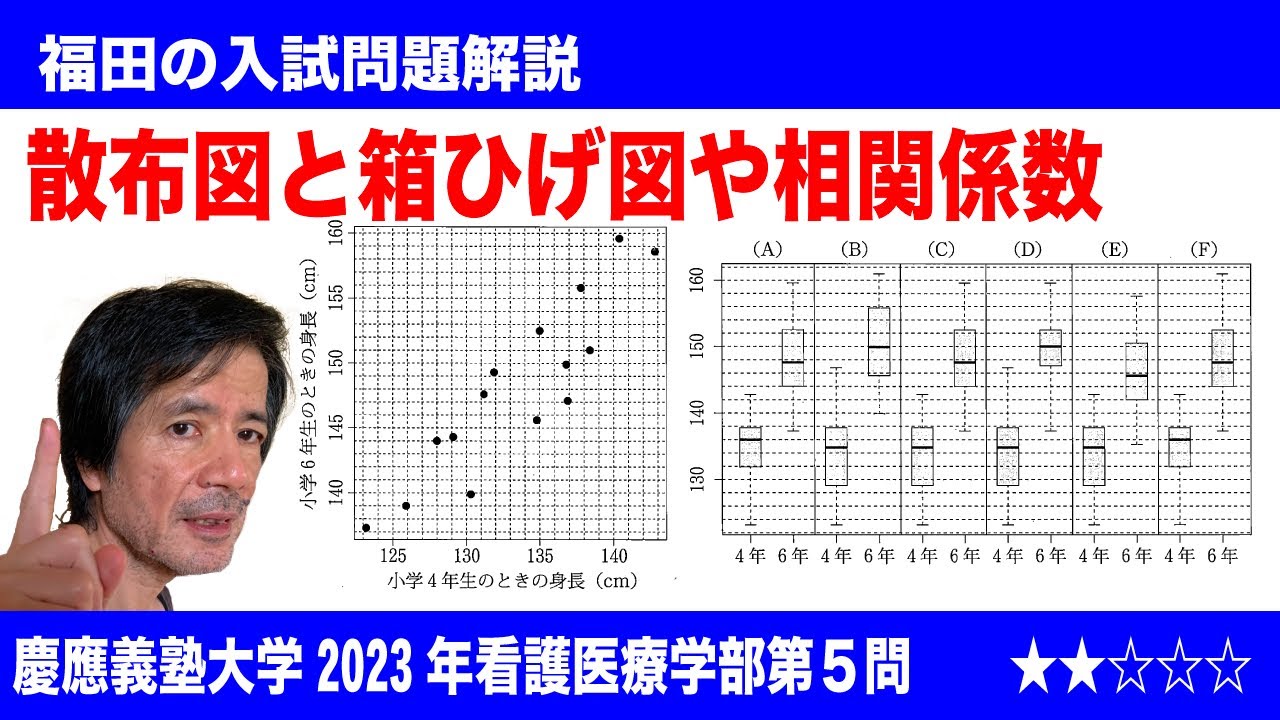
福田の数学〜慶應義塾大学2023年看護医療学部第5問〜散布図と箱ひげ図の関係と相関係数
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#データの分析#データの分析#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 以下の図は、ある小学校の15人の女子児童の4年生の4月に計測した身長を横軸に、5年生の4月に計測した身長を縦軸にとった散布図である。(※動画参照)
と表すことができる。よってS(a)を最小にするaはa=$\boxed{\ \ ミ\ \ }$である。
S(a)の最小値は、女子児童の4年生のときと6年生のときの身長の相関係数rと$s_y^2$を用いて$\boxed{\ \ ム\ \ }$と表せる。
また、左の散布図で示した女子児童の計測値を計算すると
$s_x^2$=29.00, $s_y^2$=42.65, $s_{xy}$=31.69
であった。これらを用いてS(a)を最小にするaを計算し、小数第4位を四捨五入すると$\boxed{\ \ メ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{5}$ 以下の図は、ある小学校の15人の女子児童の4年生の4月に計測した身長を横軸に、5年生の4月に計測した身長を縦軸にとった散布図である。(※動画参照)
と表すことができる。よってS(a)を最小にするaはa=$\boxed{\ \ ミ\ \ }$である。
S(a)の最小値は、女子児童の4年生のときと6年生のときの身長の相関係数rと$s_y^2$を用いて$\boxed{\ \ ム\ \ }$と表せる。
また、左の散布図で示した女子児童の計測値を計算すると
$s_x^2$=29.00, $s_y^2$=42.65, $s_{xy}$=31.69
であった。これらを用いてS(a)を最小にするaを計算し、小数第4位を四捨五入すると$\boxed{\ \ メ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
福田の数学〜慶應義塾大学2023年看護医療学部第4問〜絶対値の付いた関数と領域における最大最小
単元:
#大学入試過去問(数学)#図形と方程式#軌跡と領域#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
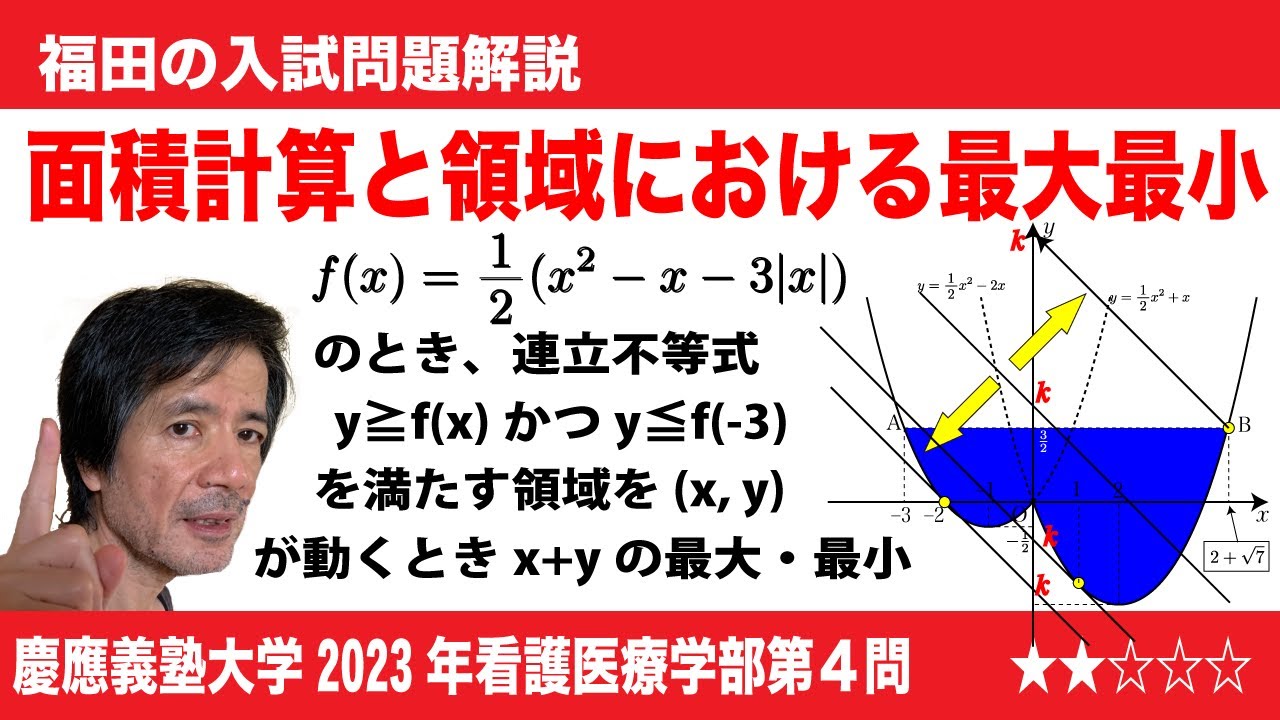
$\Large\boxed{4}$ 関数f(x)をf(x)=$\frac{1}{2}$($x^2$-$x$-3|$x$|)で定める。以下に答えなさい。
(1)y=f(x)のグラフをかきなさい。
(2)曲線y=f(x)上の点A(-3, f(-3))を通り、点Aにおける接線に垂直な直線lの方程式はy=$\boxed{\ \ ニ\ \ }$である。また、曲線と直線lは2つの共有点をもつが点Aとは異なる共有点の座標は$\boxed{\ \ ヌ\ \ }$である。さらに、曲線y=f(x)と直線lで囲まれた図形の面積は$\boxed{\ \ ネ\ \ }$である。
(3)連立不等式y≧f(x), y≦f(-3)の表す領域をDとする。点(x,y)がこの領域Dを動くとき、x+yは(x,y)=$\boxed{\ \ ノ\ \ }$のとき最大値$\boxed{\ \ ハ\ \ }$をとり、
(x,y)=$\boxed{\ \ ヒ\ \ }$のうち最小値$\boxed{\ \ フ\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{4}$ 関数f(x)をf(x)=$\frac{1}{2}$($x^2$-$x$-3|$x$|)で定める。以下に答えなさい。
(1)y=f(x)のグラフをかきなさい。
(2)曲線y=f(x)上の点A(-3, f(-3))を通り、点Aにおける接線に垂直な直線lの方程式はy=$\boxed{\ \ ニ\ \ }$である。また、曲線と直線lは2つの共有点をもつが点Aとは異なる共有点の座標は$\boxed{\ \ ヌ\ \ }$である。さらに、曲線y=f(x)と直線lで囲まれた図形の面積は$\boxed{\ \ ネ\ \ }$である。
(3)連立不等式y≧f(x), y≦f(-3)の表す領域をDとする。点(x,y)がこの領域Dを動くとき、x+yは(x,y)=$\boxed{\ \ ノ\ \ }$のとき最大値$\boxed{\ \ ハ\ \ }$をとり、
(x,y)=$\boxed{\ \ ヒ\ \ }$のうち最小値$\boxed{\ \ フ\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
福田の数学〜慶應義塾大学2023年看護医療学部第3問〜三角比と図形の計量
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
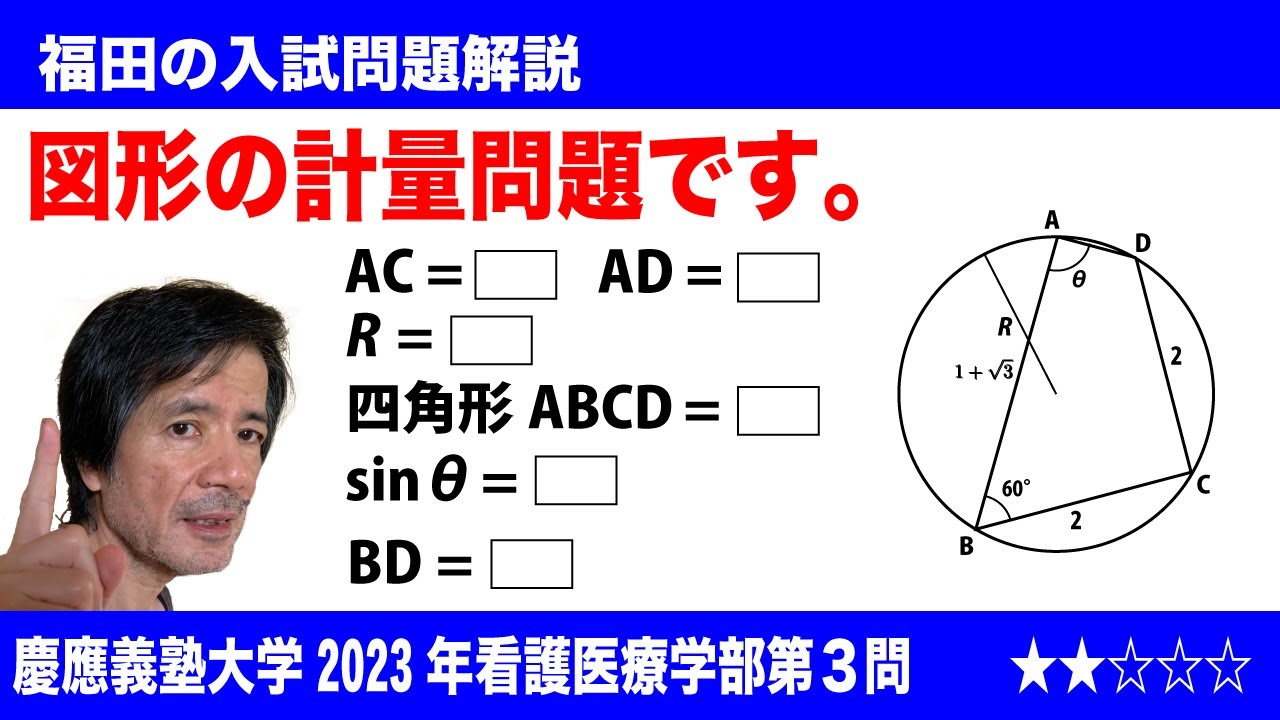
$\Large\boxed{3}$ 半径Rの円に内接する四角形ABCDにおいて
AB=1+$\sqrt3$, BC=CD=2, $\angle$ABC=60°
であるとき、$\angle$ADCの大きさは$\angle$ADC=$\boxed{\ \ ソ\ \ }$であり、AC,AD,Rの長さはそれぞれAC=$\boxed{\ \ タ\ \ }$, AD=$\boxed{\ \ チ\ \ }$, R=$\boxed{\ \ ツ\ \ }$である。
また、四角形ABCDの面積は$\boxed{\ \ テ\ \ }$である。さらに、θ=$\angle$DABとするとき、$\sin\theta$=$\boxed{\ \ ト\ \ }$であり、BDの長さはBD=$\boxed{\ \ ナ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{3}$ 半径Rの円に内接する四角形ABCDにおいて
AB=1+$\sqrt3$, BC=CD=2, $\angle$ABC=60°
であるとき、$\angle$ADCの大きさは$\angle$ADC=$\boxed{\ \ ソ\ \ }$であり、AC,AD,Rの長さはそれぞれAC=$\boxed{\ \ タ\ \ }$, AD=$\boxed{\ \ チ\ \ }$, R=$\boxed{\ \ ツ\ \ }$である。
また、四角形ABCDの面積は$\boxed{\ \ テ\ \ }$である。さらに、θ=$\angle$DABとするとき、$\sin\theta$=$\boxed{\ \ ト\ \ }$であり、BDの長さはBD=$\boxed{\ \ ナ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
福田の数学〜慶應義塾大学2023年看護医療学部第2問(3)〜推定して数学的帰納法

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#数学的帰納法#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ (3) 次の条件によって定められる数列$\left\{a_n\right\}$がある。
$a_1$=1, $a_{n+1}$=$\sqrt{a_n^2+1}$ ($n$=1,2,3,...)
(i)$a_2$=$\boxed{\ \ シ\ \ }$, $a_3$=$\boxed{\ \ ス\ \ }$であり、一般項$a_n$を推定すると$a_n$=$\boxed{\ \ セ\ \ }$である。
(ii)一般項$a_n$が$a_n$=$\boxed{\ \ セ\ \ }$であることの数学的帰納法による証明を述べよ。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{2}$ (3) 次の条件によって定められる数列$\left\{a_n\right\}$がある。
$a_1$=1, $a_{n+1}$=$\sqrt{a_n^2+1}$ ($n$=1,2,3,...)
(i)$a_2$=$\boxed{\ \ シ\ \ }$, $a_3$=$\boxed{\ \ ス\ \ }$であり、一般項$a_n$を推定すると$a_n$=$\boxed{\ \ セ\ \ }$である。
(ii)一般項$a_n$が$a_n$=$\boxed{\ \ セ\ \ }$であることの数学的帰納法による証明を述べよ。
2023慶應義塾大学看護医療学部過去問
福田の数学〜慶應義塾大学2023年看護医療学部第2問(2)〜ルートが自然数になる条件

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#整数の性質#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ (2)$n$を自然数とする。$\sqrt{\frac{200}{\sqrt n}}$が自然数となるような$n$をすべて求めると$n$=$\boxed{\ \ サ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{2}$ (2)$n$を自然数とする。$\sqrt{\frac{200}{\sqrt n}}$が自然数となるような$n$をすべて求めると$n$=$\boxed{\ \ サ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
福田の数学〜慶應義塾大学2023年看護医療学部第2問(1)〜三角方程式

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#三角関数#円と方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ (1)0≦x≦π のとき、$\sqrt3\sin x$+$\cos x$=$\sqrt2$を解くと$x$=$\boxed{\ \ コ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{2}$ (1)0≦x≦π のとき、$\sqrt3\sin x$+$\cos x$=$\sqrt2$を解くと$x$=$\boxed{\ \ コ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
福田の数学〜慶應義塾大学2023年看護医療学部第1問(5)〜整式の割り算の余り

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (5)整式P(x)を
P(x)=$\displaystyle\sum_{n=1}^{20}nx^n$=20$x^{20}$+19$x^{19}$+18$x^{18}$+...+2$x^2$+$x$
と定める。このとき、P(x)をx-1で割った時の余りは$\boxed{\ \ ク\ \ }$である。
また、P(x)を$x^2$-1で割った時の余りは$\boxed{\ \ ケ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{1}$ (5)整式P(x)を
P(x)=$\displaystyle\sum_{n=1}^{20}nx^n$=20$x^{20}$+19$x^{19}$+18$x^{18}$+...+2$x^2$+$x$
と定める。このとき、P(x)をx-1で割った時の余りは$\boxed{\ \ ク\ \ }$である。
また、P(x)を$x^2$-1で割った時の余りは$\boxed{\ \ ケ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
福田の数学〜慶應義塾大学2023年看護医療学部第1問(4)〜対数方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#指数関数と対数関数#剰余の定理・因数定理・組み立て除法と高次方程式#対数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (4)($\log_29$)($\log_3x$)-$\log_25$=2 を解くとx=$\boxed{\ \ キ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{1}$ (4)($\log_29$)($\log_3x$)-$\log_25$=2 を解くとx=$\boxed{\ \ キ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
福田の数学〜慶應義塾大学2023年看護医療学部第1問(3)〜解と係数の関係

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (3)2次方程式$x^2$+$x$+3=0 の2つの解を$\alpha$、$\beta$とするとき、
$\frac{\beta}{\alpha}$+$\frac{\alpha}{\beta}$=$\boxed{\ \ オ\ \ }$であり、$\frac{\beta^2}{\alpha}$+$\frac{\alpha^2}{\beta}$=$\boxed{\ \ カ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{1}$ (3)2次方程式$x^2$+$x$+3=0 の2つの解を$\alpha$、$\beta$とするとき、
$\frac{\beta}{\alpha}$+$\frac{\alpha}{\beta}$=$\boxed{\ \ オ\ \ }$であり、$\frac{\beta^2}{\alpha}$+$\frac{\alpha^2}{\beta}$=$\boxed{\ \ カ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
福田の数学〜慶應義塾大学2023年看護医療学部第1問(2)〜同じものを含む順列

単元:
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#確率#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (2)k a n g o g a k u の9文字すべてを並べてできる文字列の種類は全部で$\boxed{\ \ ウ\ \ }$通りであり、このうち子音と母音が交互に並ぶものは$\boxed{\ \ エ\ \ }$通りである。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{1}$ (2)k a n g o g a k u の9文字すべてを並べてできる文字列の種類は全部で$\boxed{\ \ ウ\ \ }$通りであり、このうち子音と母音が交互に並ぶものは$\boxed{\ \ エ\ \ }$通りである。
2023慶應義塾大学看護医療学部過去問
福田の数学〜慶應義塾大学2023年看護医療学部第1問(1)〜交点の位置ベクトル
単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
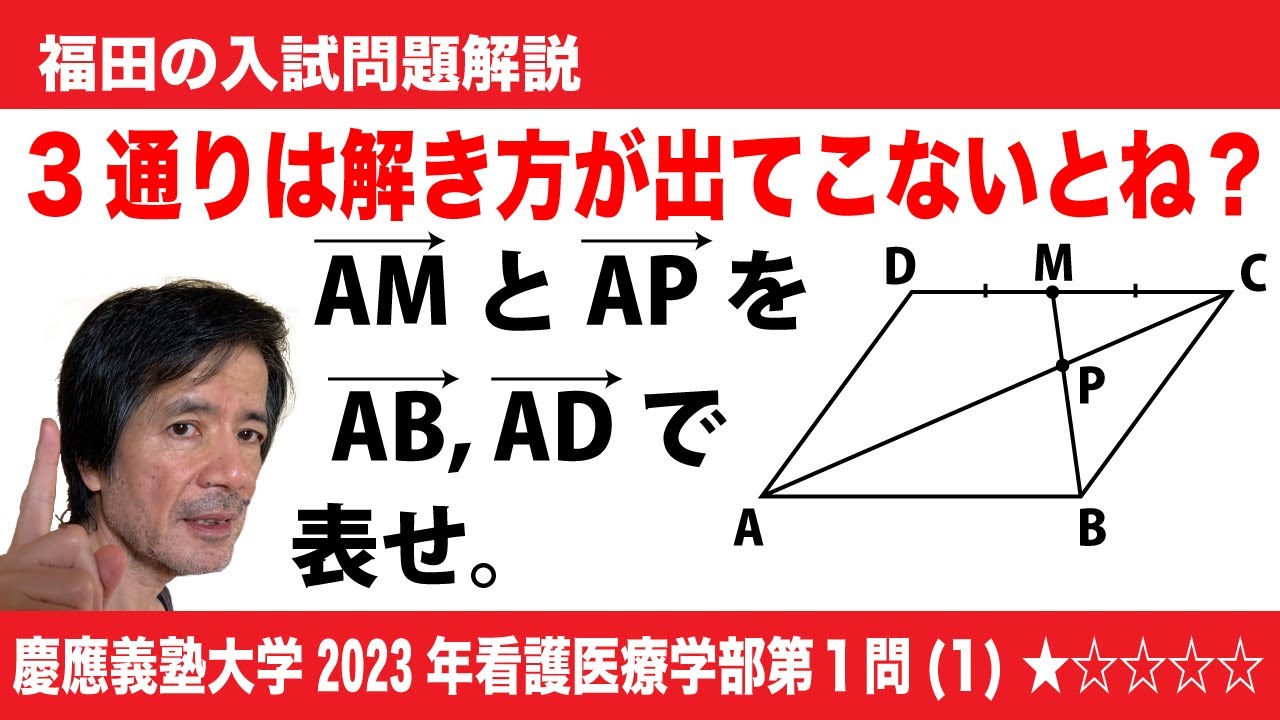
問題文全文(内容文):
$\Large\boxed{1}$ (1)平行四辺形ABCDにおいて、辺CDの中点をMとし、直線ACと直線BMの交点をPとする。このとき、$\overrightarrow{AM}$, $\overrightarrow{AP}$をそれぞれ$\overrightarrow{AB}$, $\overrightarrow{AD}$を用いて表すと
$\overrightarrow{AM}$=$\boxed{\ \ ア\ \ }$, $\overrightarrow{AP}$=$\boxed{\ \ イ\ \ }$
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{1}$ (1)平行四辺形ABCDにおいて、辺CDの中点をMとし、直線ACと直線BMの交点をPとする。このとき、$\overrightarrow{AM}$, $\overrightarrow{AP}$をそれぞれ$\overrightarrow{AB}$, $\overrightarrow{AD}$を用いて表すと
$\overrightarrow{AM}$=$\boxed{\ \ ア\ \ }$, $\overrightarrow{AP}$=$\boxed{\ \ イ\ \ }$
2023慶應義塾大学看護医療学部過去問
福田の数学〜慶應義塾大学2023年医学部第4問PART2〜円に内接する円の性質
単元:
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
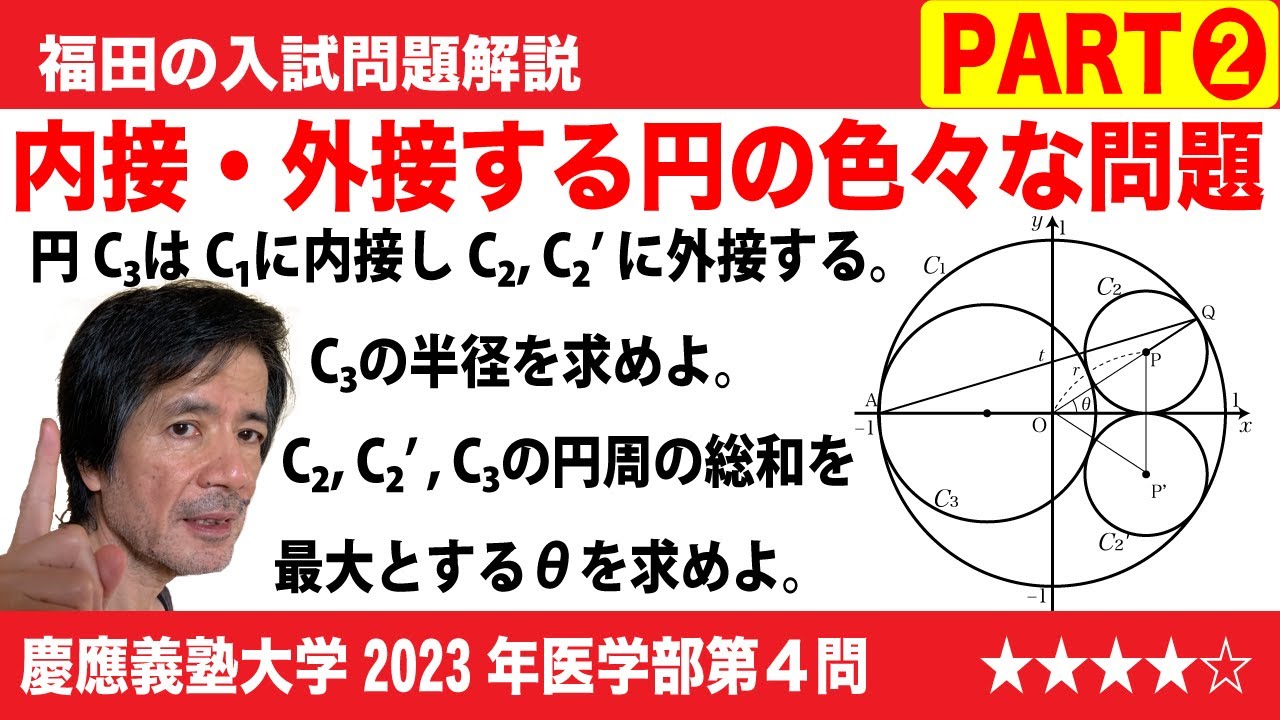
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
福田の数学〜慶應義塾大学2023年医学部第4問PART1〜円に内接する円の性質
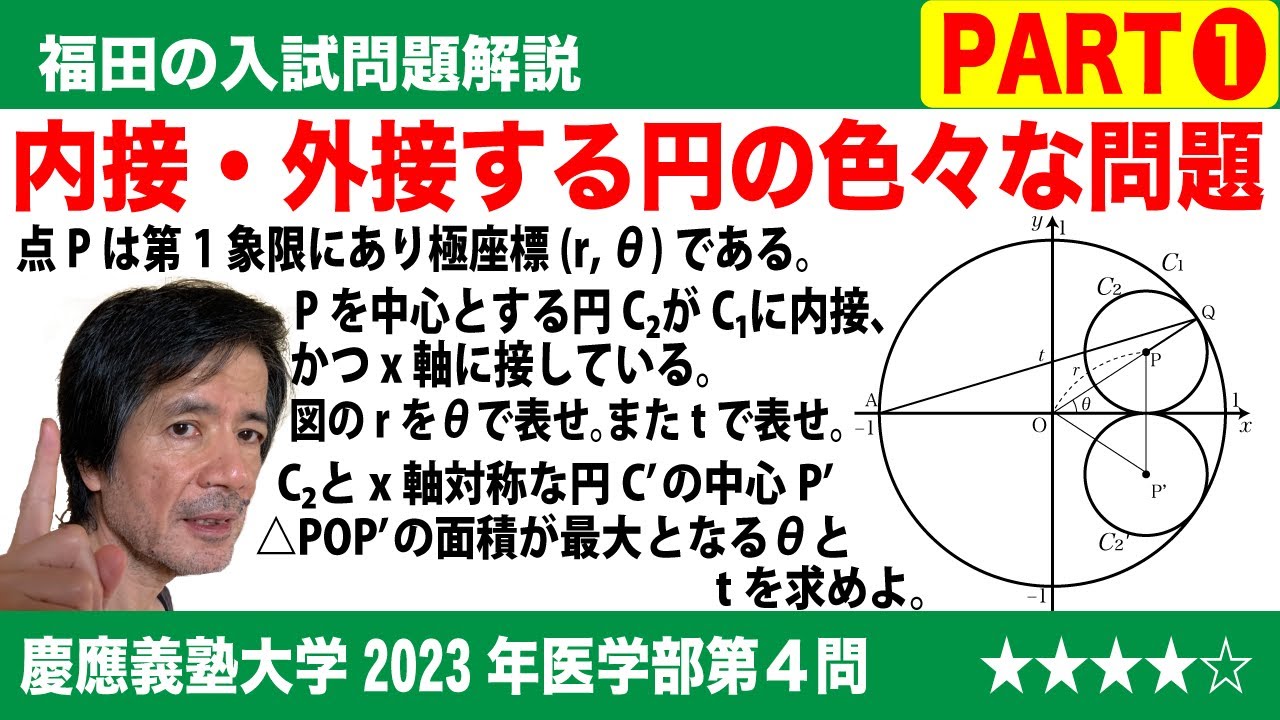
単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#複素数平面#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#円と方程式#微分とその応用#複素数平面#図形への応用#微分法#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
福田の数学〜慶應義塾大学2023年医学部第3問〜接線が作る三角形

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#三角形の辺の比(内分・外分・二等分線)#図形と方程式#微分法と積分法#軌跡と領域#接線と増減表・最大値・最小値#関数と極限#微分とその応用#積分とその応用#数列の極限#微分法#定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 座標平面上の曲線y=$\frac{1}{x^2}$ (x $\ne$ 0)をCとする。$a_1$を正の実数とし、点$A_1$$\left(a_1, \frac{1}{a_1^2}\right)$におけるCの接線を$l_1$とする。$l_1$とCの交点で$A_1$と異なるものを$A_2$$\left(a_2, \frac{1}{a_2^2}\right)$とする。次に点$A_2$におけるCの接線を$l_2$とCの交点で$A_2$と異なるものを$A_3$$\left(a_3, \frac{1}{a_3^2}\right)$とする。以下、同様にしてn=3,4,5,...に対して、$A_n$$\left(a_n, \frac{1}{a_n^2}\right)$におけるCの接線を$l_n$とし、$l_n$とCの交点で$A_n$と異なるものを$A_{n+1}$$\left(a_{n+1}, \frac{1}{a_{n+1}^2}\right)$とする。
(1)$\frac{a_2}{a_1}$=$\boxed{\ \ あ\ \ }$であり、$\frac{a_3}{a_1}$=$\boxed{\ \ い\ \ }$である。
(2)$a_n$を$a_1$で表すと$a_n$=$\boxed{\ \ う\ \ }$である。無限級数$\displaystyle\sum_{n=1}^{\infty}a_n$の和をTを$a_1$を用いて表すとT=$\boxed{\ \ え\ \ }$である。
(3)$a_1$を正の実数すべてにわたって動かすとき、三角形$A_1A_2A_3$の重心が描く軌跡の方程式をy=f(x)の形で求めるとf(x)=$\boxed{\ \ お\ \ }$となる。
(4)三角形$A_1A_2A_3$が鋭角三角形になるための条件は$\boxed{\ \ か\ \ }$<$a_1$<$\boxed{\ \ き\ \ }$である。
(5)x軸上に2点$A'_1$($a_1$, 0), $A'_2$($a_2$, 0)をとり、台形$A_1A_2A'_2A'_1$の面積を$S_1$とする。また、点$A_1$から点$A_3$にいたる曲線Cの部分、および線分$A_3A_2$と$A_2A_1$で囲まれた図形の面積を$S_2$とする。このとき、$S_1$:$S_2$=$\boxed{\ \ く\ \ }$:$\boxed{\ \ け\ \ }$である。ただし、$\boxed{\ \ く\ \ }$と$\boxed{\ \ け\ \ }$は互いに素な自然数である。
2023慶應義塾大学医学部過去問
この動画を見る
$\Large\boxed{3}$ 座標平面上の曲線y=$\frac{1}{x^2}$ (x $\ne$ 0)をCとする。$a_1$を正の実数とし、点$A_1$$\left(a_1, \frac{1}{a_1^2}\right)$におけるCの接線を$l_1$とする。$l_1$とCの交点で$A_1$と異なるものを$A_2$$\left(a_2, \frac{1}{a_2^2}\right)$とする。次に点$A_2$におけるCの接線を$l_2$とCの交点で$A_2$と異なるものを$A_3$$\left(a_3, \frac{1}{a_3^2}\right)$とする。以下、同様にしてn=3,4,5,...に対して、$A_n$$\left(a_n, \frac{1}{a_n^2}\right)$におけるCの接線を$l_n$とし、$l_n$とCの交点で$A_n$と異なるものを$A_{n+1}$$\left(a_{n+1}, \frac{1}{a_{n+1}^2}\right)$とする。
(1)$\frac{a_2}{a_1}$=$\boxed{\ \ あ\ \ }$であり、$\frac{a_3}{a_1}$=$\boxed{\ \ い\ \ }$である。
(2)$a_n$を$a_1$で表すと$a_n$=$\boxed{\ \ う\ \ }$である。無限級数$\displaystyle\sum_{n=1}^{\infty}a_n$の和をTを$a_1$を用いて表すとT=$\boxed{\ \ え\ \ }$である。
(3)$a_1$を正の実数すべてにわたって動かすとき、三角形$A_1A_2A_3$の重心が描く軌跡の方程式をy=f(x)の形で求めるとf(x)=$\boxed{\ \ お\ \ }$となる。
(4)三角形$A_1A_2A_3$が鋭角三角形になるための条件は$\boxed{\ \ か\ \ }$<$a_1$<$\boxed{\ \ き\ \ }$である。
(5)x軸上に2点$A'_1$($a_1$, 0), $A'_2$($a_2$, 0)をとり、台形$A_1A_2A'_2A'_1$の面積を$S_1$とする。また、点$A_1$から点$A_3$にいたる曲線Cの部分、および線分$A_3A_2$と$A_2A_1$で囲まれた図形の面積を$S_2$とする。このとき、$S_1$:$S_2$=$\boxed{\ \ く\ \ }$:$\boxed{\ \ け\ \ }$である。ただし、$\boxed{\ \ く\ \ }$と$\boxed{\ \ け\ \ }$は互いに素な自然数である。
2023慶應義塾大学医学部過去問



