数学・算数の楽しさを思い出した / Ken
数学・算数の楽しさを思い出した / Ken
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
高校の時に唯一好きだった教科の数学。 その延長で、大学は某大学の数学科に進学。
社会人になり、数学から離れていたが、仕事で数学に触れる機会があり、再度その面白さに魅了されました。
数学・算数の成績が上がるような動画や数学・算数が好きになるような動画配信をしています。
本職はエンジニア。
数学成績アップのための問題解説 ・面白い算数・数学の問題解説 ・入試問題の問題解説 ・高校数学・中学数学の解説を配信中！
難易度表記のあるレベルのわかりやすい動画内容が魅力。難関大学の過去問を中心に数学解説動画を展開中。
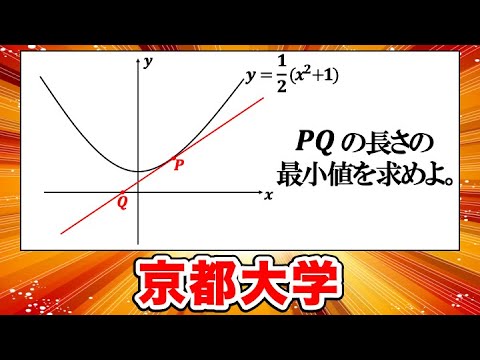
頻出！微分のよく見るような問題【京都大学】【数学 入試問題】
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
曲線y=-1/2(x²+1)上の点Pにおける接線はx軸と交わるとし,その交点をQとおく。線分PQの長さをLとするとき, Lが取りうる値の最小値を求めよ。
京都大過去問
この動画を見る
曲線y=-1/2(x²+1)上の点Pにおける接線はx軸と交わるとし,その交点をQとおく。線分PQの長さをLとするとき, Lが取りうる値の最小値を求めよ。
京都大過去問
東大数学！少しひらめきを求められる問題です（誘導あり）【東京大学】【数学 入試問題】
単元：
#大学入試過去問(数学)#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
(1)実数$x$が$-1<x<1,x \neq 0$を満たすとき,次の不等式を示せ。
$(1-x)^{1-\dfrac{1}{x}}<(1+x)^{\dfrac{1}{x}}$
(2)次の不等式を示せ。
$0.9999^{101}<0.99<0.9999^{100}$
東大過去問
この動画を見る
(1)実数$x$が$-1<x<1,x \neq 0$を満たすとき,次の不等式を示せ。
$(1-x)^{1-\dfrac{1}{x}}<(1+x)^{\dfrac{1}{x}}$
(2)次の不等式を示せ。
$0.9999^{101}<0.99<0.9999^{100}$
東大過去問
数Ⅲ微分！絶対に落としたくない問題です【一橋大学】【数学 入試問題】
単元：
#大学入試過去問(数学)#微分とその応用#微分法#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数Ⅲ
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$x>0$に対して,$(1+x)^{\frac{1}{x}}<e<(1+x)^{\frac{1}{x}+1}$が成り立つことを示せ。
一橋大過去問
この動画を見る
$x>0$に対して,$(1+x)^{\frac{1}{x}}<e<(1+x)^{\frac{1}{x}+1}$が成り立つことを示せ。
一橋大過去問
対数と整数の融合問題！難問です【一橋大学】【数学 入試問題】
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$\log_{y} (6x+y)=x$を満たす正の整数$x,y$の組を求めよ。
一橋大過去問
この動画を見る
$\log_{y} (6x+y)=x$を満たす正の整数$x,y$の組を求めよ。
一橋大過去問
対数と整数の融合問題！難問です【一橋大学】【数学 入試問題】
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$log y (6x+y) =x$
を満たす正の整数の組を求めよ
一橋大過去問
この動画を見る
$log y (6x+y) =x$
を満たす正の整数の組を求めよ
一橋大過去問
２通りで解説！微分を使わなくても解けます【名古屋大学】【数学 入試問題】
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
実数$a,b$が$0<a<b<1$を満たすとき,$\dfrac{2^a-2a}{a-1}$と$\dfrac{2^b-2b}{b-1}$の大小を比較せよ。
名古屋大過去問
この動画を見る
実数$a,b$が$0<a<b<1$を満たすとき,$\dfrac{2^a-2a}{a-1}$と$\dfrac{2^b-2b}{b-1}$の大小を比較せよ。
名古屋大過去問
【中学数学あるある】大小比較せよ #Shorts
単元：
#数学(中学生)#中１数学#正の数・負の数
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$2^{48},3^{36},5^{24}$を大きい順に並べよ。
この動画を見る
$2^{48},3^{36},5^{24}$を大きい順に並べよ。
京大の整数問題！〇〇に注目！【京都大学】【数学 入試問題】
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
二つの奇数$a,b$に対して,$m=11a+b,n=3a+b$とおく。$m,n$がともに平方数であることはないことを証明せよ。
京都大過去問
この動画を見る
二つの奇数$a,b$に対して,$m=11a+b,n=3a+b$とおく。$m,n$がともに平方数であることはないことを証明せよ。
京都大過去問
京大の整数問題！〇〇に注目！【京都大学】【数学 入試問題】
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
2つの奇数a,bに対して、$m=11a+b,n=3a+b$とおく。
$m,n$が平方数でないことを証明しなさい。
京都大過去問
この動画を見る
2つの奇数a,bに対して、$m=11a+b,n=3a+b$とおく。
$m,n$が平方数でないことを証明しなさい。
京都大過去問
【工夫あり】これが本当に京大の入試問題？絶対値を含んだ積分【数学 入試問題】
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#京都大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
定積分$\displaystyle \int_{-1}^{1}\left| x^2-\dfrac{1}{2}x-\dfrac{1}{2} \right | dx$を求めよ。
京都大過去問
この動画を見る
定積分$\displaystyle \int_{-1}^{1}\left| x^2-\dfrac{1}{2}x-\dfrac{1}{2} \right | dx$を求めよ。
京都大過去問
ベクトルの簡単すぎる京大の問題【京都大学】【数学 入試問題】
単元：
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数C
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$\triangle OAB$において$OA=3,OB=2,\angle AOB=90^{ \circ }$とする。$\triangle OAB$の垂心を$H$とするとき,$\overrightarrow{OH}$を$\overrightarrow{OA}$と$\overrightarrow{OB}$を用いて表せ。
京都大過去問
この動画を見る
$\triangle OAB$において$OA=3,OB=2,\angle AOB=90^{ \circ }$とする。$\triangle OAB$の垂心を$H$とするとき,$\overrightarrow{OH}$を$\overrightarrow{OA}$と$\overrightarrow{OB}$を用いて表せ。
京都大過去問
n進法の理解が深まる問題！２通りで解説！【京都大学】【数学 入試問題】
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
10進法で表された6.75を2進法で表せ。
また、この数と、2進法で表された数101.101との積として与えられる数を2進法および4進法で表せ
京都大過去問
この動画を見る
10進法で表された6.75を2進法で表せ。
また、この数と、2進法で表された数101.101との積として与えられる数を2進法および4進法で表せ
京都大過去問
n進法の理解が深まる問題！２通りで解説！【京都大学】【数学 入試問題】
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
10進法で表された数6.75を二進法で表せ。また,この数と２進法で表された数101.0101の積として与えられる数を2進法および4進法で表せ。
この動画を見る
10進法で表された数6.75を二進法で表せ。また,この数と２進法で表された数101.0101の積として与えられる数を2進法および4進法で表せ。
【整数問題】難関大が好きなパターン！範囲を絞り込め！
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$abcd=a+b+c+d$を満たす正の整数$a,b,c,d$をすべて求めよ。
この動画を見る
$abcd=a+b+c+d$を満たす正の整数$a,b,c,d$をすべて求めよ。
【整数問題】難関大が好きなパターン！範囲を絞り込め！
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
abcd=a+b+c+dを満たす正の整数a,b,c,dを求めよ
この動画を見る
abcd=a+b+c+dを満たす正の整数a,b,c,dを求めよ
微分の難問！それぞれの関数の〇〇を比較すればOKです【滋賀大学】【数学 入試問題】
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$a$を$0$以下の定数とする。このとき,$f(x)=2x^3-3(a+2)x^2+8$と$g(x)=-3x^2-6ax$について,次の問いに答えよ。
(1)$x≧0$における$f(x)$の最小値を$m(a)$とする。$m(a)$を$a$の式で表せ。
(2)$s≧0,t≧0$を満たすすべての$s,t$に対して$f(s)≧g(t)$となる$a$の値の範囲を求めよ。
滋賀大過去問
この動画を見る
$a$を$0$以下の定数とする。このとき,$f(x)=2x^3-3(a+2)x^2+8$と$g(x)=-3x^2-6ax$について,次の問いに答えよ。
(1)$x≧0$における$f(x)$の最小値を$m(a)$とする。$m(a)$を$a$の式で表せ。
(2)$s≧0,t≧0$を満たすすべての$s,t$に対して$f(s)≧g(t)$となる$a$の値の範囲を求めよ。
滋賀大過去問
絶対に落としたくない問題です【自治医科大学】【数学 入試問題】
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
関数$f(x)$は,等式$f(x)=3x^2 \displaystyle \int_{-1}^{1} f(t) dt+x+\displaystyle \int_{0}^{1} [{f(t)}]^{2} dt+$
$\displaystyle \int_{0}^{1} f(t) dt$を満たす。
$\displaystyle \int_{0}^{1} f(t) dt \neq 0$とするとき,$f(0)$の値を求めよ。
自治医科大過去問
この動画を見る
関数$f(x)$は,等式$f(x)=3x^2 \displaystyle \int_{-1}^{1} f(t) dt+x+\displaystyle \int_{0}^{1} [{f(t)}]^{2} dt+$
$\displaystyle \int_{0}^{1} f(t) dt$を満たす。
$\displaystyle \int_{0}^{1} f(t) dt \neq 0$とするとき,$f(0)$の値を求めよ。
自治医科大過去問
こういう問題に苦手意識ある人は必見です【甲南大学】【数学 入試問題】
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
次の2つの等式を満たす多項式$(x),g(x)$及び定数$a$を求めよ。
$\displaystyle \int_{1}^{x} f(t) dt=2xg(x)-3x+a $
$g(x)=x^2+x \displaystyle \int_{0}^{1} f(t)dx+1$
甲南大過去問
この動画を見る
次の2つの等式を満たす多項式$(x),g(x)$及び定数$a$を求めよ。
$\displaystyle \int_{1}^{x} f(t) dt=2xg(x)-3x+a $
$g(x)=x^2+x \displaystyle \int_{0}^{1} f(t)dx+1$
甲南大過去問
数Ⅱ微分の良問です【大阪大学】【数学 入試問題】
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$点(0,1)を通り曲線$y=x^3-ax^2$に接する直線がちょうど2本存在するとき,実数$a$の値と2本の接線の方程式を求めよ。
大阪大過去問
この動画を見る
$点(0,1)を通り曲線$y=x^3-ax^2$に接する直線がちょうど2本存在するとき,実数$a$の値と2本の接線の方程式を求めよ。
大阪大過去問
数Ⅱ微分の良問です【大阪大学】【数学 入試問題】
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$点(0,1)を通り曲線$y=x^3-ax^2$に接する直線がちょうど2本存在するとき,実数$a$の値と2本の接線の方程式を求めよ。
大阪大過去問
この動画を見る
$点(0,1)を通り曲線$y=x^3-ax^2$に接する直線がちょうど2本存在するとき,実数$a$の値と2本の接線の方程式を求めよ。
大阪大過去問
３つの整数の最大公約数！解けますか？【京都大学】【数学 入試問題】
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$n$を自然数とする。3つの整数$n^2+2,n^4+2,n^6+2$の最大公約数$A_n$を求めよ。
京都大過去問
この動画を見る
$n$を自然数とする。3つの整数$n^2+2,n^4+2,n^6+2$の最大公約数$A_n$を求めよ。
京都大過去問
３つの整数の最大公約数！解けますか？【京都大学】【数学 入試問題】
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$n$を自然数とする。3つの整数$n^2+2,n^4+2,n^6+2$の最大公約数$A_n$を求めよ。
京都大過去問
この動画を見る
$n$を自然数とする。3つの整数$n^2+2,n^4+2,n^6+2$の最大公約数$A_n$を求めよ。
京都大過去問
難問です！三角関数と整数の融合問題！解けますか？【一橋大学】【数学 入試問題】
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
三角形$ABC$において,$ tanA,tanB,tanC$の値がすべて整数であるとき,それらの値を求めよ。
一橋大過去問
この動画を見る
三角形$ABC$において,$ tanA,tanB,tanC$の値がすべて整数であるとき,それらの値を求めよ。
一橋大過去問
三角関数の基礎問題です！２通りで解説【一橋大学】【数学 入試問題】
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
三角形$ABC$において,$\angle A=60°$であるとする。
(1)$sinB+sinC$の取り得る値の範囲を求めよ。
(2)$sinBsinC$の取り得る値の範囲を求めよ。
一橋大過去問
この動画を見る
三角形$ABC$において,$\angle A=60°$であるとする。
(1)$sinB+sinC$の取り得る値の範囲を求めよ。
(2)$sinBsinC$の取り得る値の範囲を求めよ。
一橋大過去問
三角関数の基礎問題です！２通りで解説【一橋大学】【数学 入試問題】
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
三角形ABCにおいて、$∠A=60°$のとき、
$\sin B+\sin C$と$\sin B \sin C$の取り得る値の範囲を求めよ.
一橋大過去問
この動画を見る
三角形ABCにおいて、$∠A=60°$のとき、
$\sin B+\sin C$と$\sin B \sin C$の取り得る値の範囲を求めよ.
一橋大過去問
整数問題！これ２通りで解けますか？【札幌医科大学】【数学 入試問題】
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#札幌医科大学
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
自然数$n$に対して
$N=(n+2)^3-n(n+1)(n+2)$
が36の倍数になるような$n$をすべて求めよ。
札幌医科大過去問
この動画を見る
自然数$n$に対して
$N=(n+2)^3-n(n+1)(n+2)$
が36の倍数になるような$n$をすべて求めよ。
札幌医科大過去問
n進法に苦手意識ある人必見！難しいことはありません【京都大学】【数学 入試問題】
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$n$を4以上の自然数とする。数2,12,1331がすべて$n$進法で表記されているとして,
$2^{12}=1331$
が成り立っている。このとき$n$はいくつか。十進法で答えよ。
京都大過去問
この動画を見る
$n$を4以上の自然数とする。数2,12,1331がすべて$n$進法で表記されているとして,
$2^{12}=1331$
が成り立っている。このとき$n$はいくつか。十進法で答えよ。
京都大過去問
整数問題の難問！誘導ありでも難しいです【九州大学】【数学 入試問題】
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
自然数$m,n$が、$n^4=1+210m^2$ ･･･①を満たすとき,以下の問いに答えよ。
(1)$\displaystyle \frac{n^2+1}{2},\displaystyle \frac{n^2-1}{2}$は互いに素な整数であることを示せ。
九州大過去問
この動画を見る
自然数$m,n$が、$n^4=1+210m^2$ ･･･①を満たすとき,以下の問いに答えよ。
(1)$\displaystyle \frac{n^2+1}{2},\displaystyle \frac{n^2-1}{2}$は互いに素な整数であることを示せ。
九州大過去問
【算数】小学生すごすぎ！灘中学の入試問題解いてみた【中学受験】 #Shorts
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#灘中学校
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
15÷4=3.75,15÷125=0.12のように15をある正の整数で割るとき、ちょうど小数第2位を求めたところで割り算が終わる。
このような正の整数は4と125を含めて$□$個である。
この動画を見る
15÷4=3.75,15÷125=0.12のように15をある正の整数で割るとき、ちょうど小数第2位を求めたところで割り算が終わる。
このような正の整数は4と125を含めて$□$個である。
【算数】灘中学の整数問題を解いてみた【中学受験】 #Shorts
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#灘中学校
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
異なる４つの整数を小さい方から順に並べ、隣り合った2数の和を求めると、それぞれ28,32,59であった。4つの整数の中で最も大きい数は$□$である。
この動画を見る
異なる４つの整数を小さい方から順に並べ、隣り合った2数の和を求めると、それぞれ28,32,59であった。4つの整数の中で最も大きい数は$□$である。