 ますただ
ますただ
 ますただ
ますただ
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
大学入試問題#664「三角関数or複素平面」 藤田医科大学(2023) 2024年入学

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \sum_{k=1}^4 \cos\displaystyle \frac{2k}{9}\pi$の値を求めよ
出典:2023年藤田医科大学 入試問題
この動画を見る
$\displaystyle \sum_{k=1}^4 \cos\displaystyle \frac{2k}{9}\pi$の値を求めよ
出典:2023年藤田医科大学 入試問題
大学入試問題#663「これは良問」 信州大学(2023) 定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学
指導講師:
ますただ
問題文全文(内容文):
$x \gt 0$
$\displaystyle \int_{-\frac{1}{x}}^{x} \displaystyle \frac{dt}{1+t^2}$
出典:2023年信州大学 入試問題
この動画を見る
$x \gt 0$
$\displaystyle \int_{-\frac{1}{x}}^{x} \displaystyle \frac{dt}{1+t^2}$
出典:2023年信州大学 入試問題
大学入試問題#661「落ち着いて計算」 山梨大学工学部(2022) 定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#山梨大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{2}}^{\frac{3}{4}\pi} (\sqrt{ \sin^2\ x+1 }) \sin2x\ dx$
出典:2022年山梨大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{2}}^{\frac{3}{4}\pi} (\sqrt{ \sin^2\ x+1 }) \sin2x\ dx$
出典:2022年山梨大学 入試問題
大学入試問題#660「合否をわける積分」 日本医科大学(2022) 定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#日本医科大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{1}{2}}^{log2} \displaystyle \frac{dt}{e^t\sqrt{ e^{2t}-1 }}$
出典:2022年日本医科大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{1}{2}}^{log2} \displaystyle \frac{dt}{e^t\sqrt{ e^{2t}-1 }}$
出典:2022年日本医科大学 入試問題
大学入試問題#659「これはなかなか。。。」 名古屋大学(1991) 微積の応用

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学
指導講師:
ますただ
問題文全文(内容文):
$f(t)=\displaystyle \int_{0}^{\frac{\pi}{2}} |\cos\ x-t\sin\ x| dx$
(1)
$0 \lt \theta \lt \displaystyle \frac{\pi}{2},0 \lt t$において
$\cos\ \theta=t\ \sin\theta$のとき、$\cos\theta,\sin\theta$を$t$で表せ
(2)
$f(t)(t \gt 0)$の最小値を求めよ
出典:1991年名古屋大学 入試問題
この動画を見る
$f(t)=\displaystyle \int_{0}^{\frac{\pi}{2}} |\cos\ x-t\sin\ x| dx$
(1)
$0 \lt \theta \lt \displaystyle \frac{\pi}{2},0 \lt t$において
$\cos\ \theta=t\ \sin\theta$のとき、$\cos\theta,\sin\theta$を$t$で表せ
(2)
$f(t)(t \gt 0)$の最小値を求めよ
出典:1991年名古屋大学 入試問題
大学入試問題#658「基本問題」 名古屋大学(1995)

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学
指導講師:
ますただ
問題文全文(内容文):
$f'(x)=\sin\ x+\displaystyle \int_{-\pi}^{\pi} f(t) dt$
$f(0)=0$を満たす$f(x)$を求めよ
出典:1995年名古屋大学 入試問題
この動画を見る
$f'(x)=\sin\ x+\displaystyle \int_{-\pi}^{\pi} f(t) dt$
$f(0)=0$を満たす$f(x)$を求めよ
出典:1995年名古屋大学 入試問題
大学入試問題#657「第一感は微分だけど」 藤田医科大学(2019)

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学
指導講師:
ますただ
問題文全文(内容文):
$0 \neq x$:実数
$16x^2+\displaystyle \frac{1}{8x^4}$の最小値を求めよ
出典:2019年藤田医科大学 入試問題
この動画を見る
$0 \neq x$:実数
$16x^2+\displaystyle \frac{1}{8x^4}$の最小値を求めよ
出典:2019年藤田医科大学 入試問題
大学入試問題#656「これはさすがに」 日本医科大学(2023) 定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#日本医科大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\sqrt{ 3 }-1} \displaystyle \frac{dx}{x^2+2x+4}$
出典:2023年日本医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\sqrt{ 3 }-1} \displaystyle \frac{dx}{x^2+2x+4}$
出典:2023年日本医科大学 入試問題
大学入試問題#655「解き方いろいろ」 千葉大学後期(2018) 整数問題

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \frac{8a+8}{a^2+4a+12}$が整数となるような整数$a$をすべて求めよ
出典:2018年千葉大学 入試問題
この動画を見る
$\displaystyle \frac{8a+8}{a^2+4a+12}$が整数となるような整数$a$をすべて求めよ
出典:2018年千葉大学 入試問題
大学入試問題#654「特に工夫はなし」 青山学院大学(2012) 定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2} (x^2+2x+3)log(x+1) dx$
出典:2012年青山学院大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{2} (x^2+2x+3)log(x+1) dx$
出典:2012年青山学院大学 入試問題
大学入試問題#653「綺麗な問題」 獨協医科大学(2014) 積分方程式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$f(x)$は$x \gt -\displaystyle \frac{1}{3}$で定義され
$f"(x)$をもち
$f(x)=2x+\displaystyle \int_{0}^{x} (4x-7t)f'(t) dx$を満たす$f(x)$を求めよ
出典:2014年獨協医科大学 入試問題
この動画を見る
$f(x)$は$x \gt -\displaystyle \frac{1}{3}$で定義され
$f"(x)$をもち
$f(x)=2x+\displaystyle \int_{0}^{x} (4x-7t)f'(t) dx$を満たす$f(x)$を求めよ
出典:2014年獨協医科大学 入試問題
大学入試問題#652「パット見余裕!」 慶應大学医学部(2001) 整数問題

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\sqrt{ n^2+n+34 }$が整数となるような自然数$n$をすべて求めよ
出典:2001年慶應義塾大学 入試問題
この動画を見る
$\sqrt{ n^2+n+34 }$が整数となるような自然数$n$をすべて求めよ
出典:2001年慶應義塾大学 入試問題
大学入試問題#651「t=tan x/2でいけるはず」 埼玉大学(2004) 不定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{5}{3\sin\ x+4\cos\ x} dx$
出典:2004年埼玉大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{5}{3\sin\ x+4\cos\ x} dx$
出典:2004年埼玉大学 入試問題
大学入試問題#650「3秒クッキング」 藤田医科大学(2020) 定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-3}^{3} x(x+\cos^3x) dx$
出典:2020年藤田医科大学 入試問題
この動画を見る
$\displaystyle \int_{-3}^{3} x(x+\cos^3x) dx$
出典:2020年藤田医科大学 入試問題
大学入試問題#649「慌てない慌てない」 青山学院大(2006) 定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} x(1+x^2\sin\displaystyle \frac{\pi\ x}{2}) dx$
出典:2006年青山学院大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} x(1+x^2\sin\displaystyle \frac{\pi\ x}{2}) dx$
出典:2006年青山学院大学 入試問題
大学入試問題#648「あえてのこう」 静岡大学(2018) 定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#静岡大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$f(x)=\displaystyle \frac{1}{e^x+e^{-x}}$
$x=log(\tan\theta)$とおいて
$\displaystyle \int_{0}^{\frac{1}{2}log3} f(x) dx$を求めよ
出典:2018年静岡大学 入試問題
この動画を見る
$f(x)=\displaystyle \frac{1}{e^x+e^{-x}}$
$x=log(\tan\theta)$とおいて
$\displaystyle \int_{0}^{\frac{1}{2}log3} f(x) dx$を求めよ
出典:2018年静岡大学 入試問題
大学入試問題#647「すっきりした解答がわからない」 東邦大学医学部(2013) 微分の応用

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東邦大学
指導講師:
ますただ
問題文全文(内容文):
$x,y$:実数
$x^2+y^2 \leqq \displaystyle \frac{3}{2}$のとき
$\displaystyle \frac{y}{(x-2)^2}$の最大値を求めよ
出典:2013年東邦大学医学部 入試問題
この動画を見る
$x,y$:実数
$x^2+y^2 \leqq \displaystyle \frac{3}{2}$のとき
$\displaystyle \frac{y}{(x-2)^2}$の最大値を求めよ
出典:2013年東邦大学医学部 入試問題
大学入試問題#646「似てるけど」 京都工芸繊維大学(2011) 定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$0 \lt A \lt \displaystyle \frac{\pi}{2}$
(1)
$\displaystyle \int_{A}^{\frac{\pi}{2}} (\cos\ x)log(\sin\ x) dx$
(2)
$\displaystyle \int_{0}^{A} (\cos\ x)log(\cos\ x) dx$
出典:2011年京都工芸繊維大学後期 入試問題
この動画を見る
$0 \lt A \lt \displaystyle \frac{\pi}{2}$
(1)
$\displaystyle \int_{A}^{\frac{\pi}{2}} (\cos\ x)log(\sin\ x) dx$
(2)
$\displaystyle \int_{0}^{A} (\cos\ x)log(\cos\ x) dx$
出典:2011年京都工芸繊維大学後期 入試問題
大学入試問題#645「もはや盤上この1手」 埼玉大学(2013) 定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉大学
指導講師:
ますただ
問題文全文(内容文):
$a \gt 1$
$\displaystyle \int_{0}^{\pi} \displaystyle \frac{x(a^2-4\cos^2\ x)\sin\ x}{a^2-\cos^2\ x} dx$
出典:2013年埼玉大学 入試問題
この動画を見る
$a \gt 1$
$\displaystyle \int_{0}^{\pi} \displaystyle \frac{x(a^2-4\cos^2\ x)\sin\ x}{a^2-\cos^2\ x} dx$
出典:2013年埼玉大学 入試問題
大学入試問題#644 青山学院大(2022) #積分方程式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$x \gt 0$
$f(x)=\displaystyle \int_{1}^{e} log(xt)f(t) \ dt+x$のとき$f(x)$を求めよ
出典:2022年青山学院大学 入試問題
この動画を見る
$x \gt 0$
$f(x)=\displaystyle \int_{1}^{e} log(xt)f(t) \ dt+x$のとき$f(x)$を求めよ
出典:2022年青山学院大学 入試問題
大学入試問題#643「The ミスれない問題」 藤田医科大学(2023)

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学
指導講師:
ますただ
問題文全文(内容文):
$\sqrt{ x }+\displaystyle \frac{1}{\sqrt{ x }}=\sqrt{ 5 }$のとき
$(x^2-\displaystyle \frac{1}{x^2})^2$の値を求めよ
出典:2023年藤田医科大学 入試問題
この動画を見る
$\sqrt{ x }+\displaystyle \frac{1}{\sqrt{ x }}=\sqrt{ 5 }$のとき
$(x^2-\displaystyle \frac{1}{x^2})^2$の値を求めよ
出典:2023年藤田医科大学 入試問題
大学入試問題#642「問題選択が大変です」 東京電機大学(2022) #不定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東京電機大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e} \displaystyle \frac{log\ x}{x\{1+(log\ x)^2\}} dx$
出典:2022年東京電機大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{e} \displaystyle \frac{log\ x}{x\{1+(log\ x)^2\}} dx$
出典:2022年東京電機大学 入試問題
大学入試問題#641「基本問題」 埼玉大学(2007) #不定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x^3-4x^2-x^2}{x^2-5x+4} dx$
出典:2007年埼玉大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{x^3-4x^2-x^2}{x^2-5x+4} dx$
出典:2007年埼玉大学 入試問題
大学入試問題#640「ミスれない問題」 東邦大学医学部(2013) 剰余の定理

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東邦大学
指導講師:
ますただ
問題文全文(内容文):
$x^9-1$を$x+1$で割ったときの商を$P(x)$とするとき、$P(x)$を$x-2$で割ったときの余りを求めよ。
出典:2013年東邦大学医学部 入試問題
この動画を見る
$x^9-1$を$x+1$で割ったときの商を$P(x)$とするとき、$P(x)$を$x-2$で割ったときの余りを求めよ。
出典:2013年東邦大学医学部 入試問題
大学入試問題#639「参考書に載ってる問題?」 埼玉大学(2013) 定積分 級数
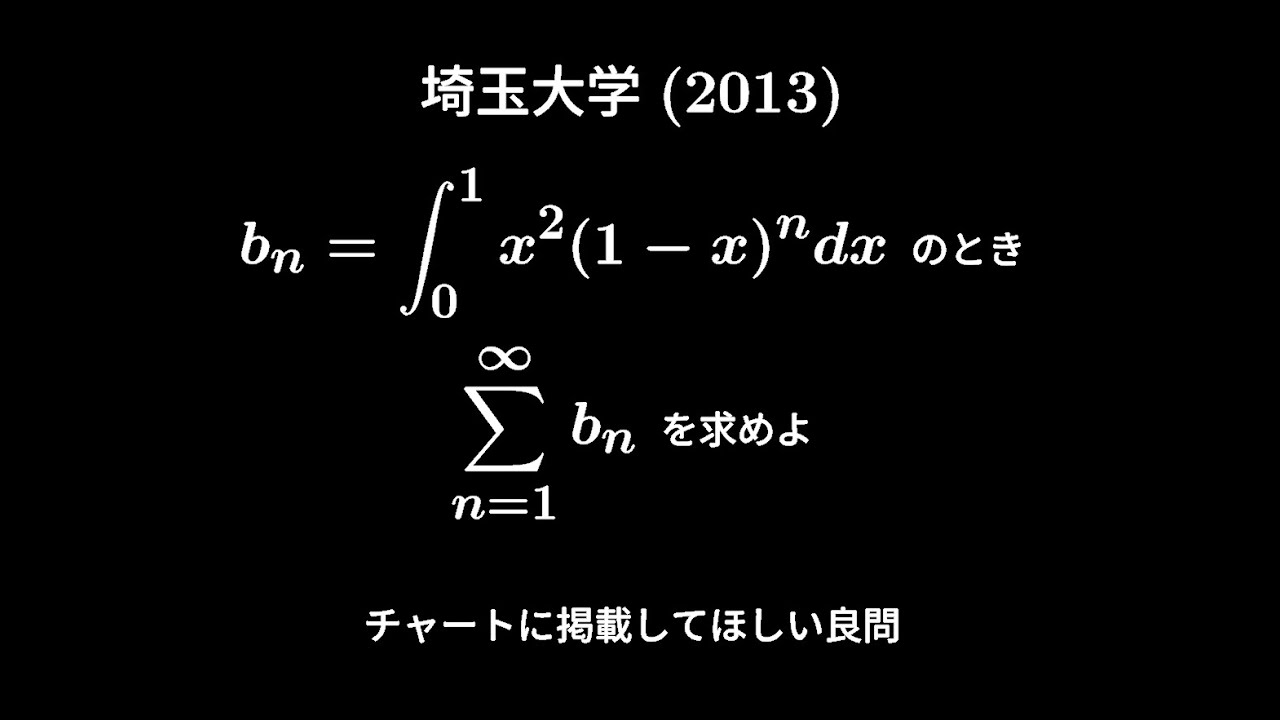
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉大学
指導講師:
ますただ
問題文全文(内容文):
$b_n=\displaystyle \int_{0}^{1} x^2(1-x)^n dx$のとき、$\displaystyle \sum_{n=1}^\infty b_n$を求めよ
出典:2023年埼玉大学 入試問題
この動画を見る
$b_n=\displaystyle \int_{0}^{1} x^2(1-x)^n dx$のとき、$\displaystyle \sum_{n=1}^\infty b_n$を求めよ
出典:2023年埼玉大学 入試問題
#5 回転体の良問 By にっし~Diaryさん

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$f(x)=\displaystyle \frac{1}{xe^x}(x \gt 0)$
(1)$f(x)$は単調減少関数であることを示し、$y=f(x)$のグラフをかけ
(2)曲線$y=f(x)$と2直線$y=\displaystyle \frac{1}{e},\ y=\displaystyle \frac{1}{3e^3},$及び$y$軸で囲まれた図形を$y$軸を中心に一回転してできる立体の体積$V$を求めよ。
この動画を見る
$f(x)=\displaystyle \frac{1}{xe^x}(x \gt 0)$
(1)$f(x)$は単調減少関数であることを示し、$y=f(x)$のグラフをかけ
(2)曲線$y=f(x)$と2直線$y=\displaystyle \frac{1}{e},\ y=\displaystyle \frac{1}{3e^3},$及び$y$軸で囲まれた図形を$y$軸を中心に一回転してできる立体の体積$V$を求めよ。
大学入試問題#638「よくある形」 名古屋市立大学(2021) #数列 #級数

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B#名古屋市立大学
指導講師:
ますただ
問題文全文(内容文):
数列$\{a_n\}$が
$a_1=2,\ \displaystyle \frac{a_{n+1}}{a_n}=\displaystyle \frac{n}{n+2}$を満たすとき
$\displaystyle \sum_{k=1}^\infty a_k$を求めよ
出典:2021年名古屋市立大学 入試問題
この動画を見る
数列$\{a_n\}$が
$a_1=2,\ \displaystyle \frac{a_{n+1}}{a_n}=\displaystyle \frac{n}{n+2}$を満たすとき
$\displaystyle \sum_{k=1}^\infty a_k$を求めよ
出典:2021年名古屋市立大学 入試問題
大学入試問題#637「朝のトーストと一緒にどうぞ!」埼玉大学
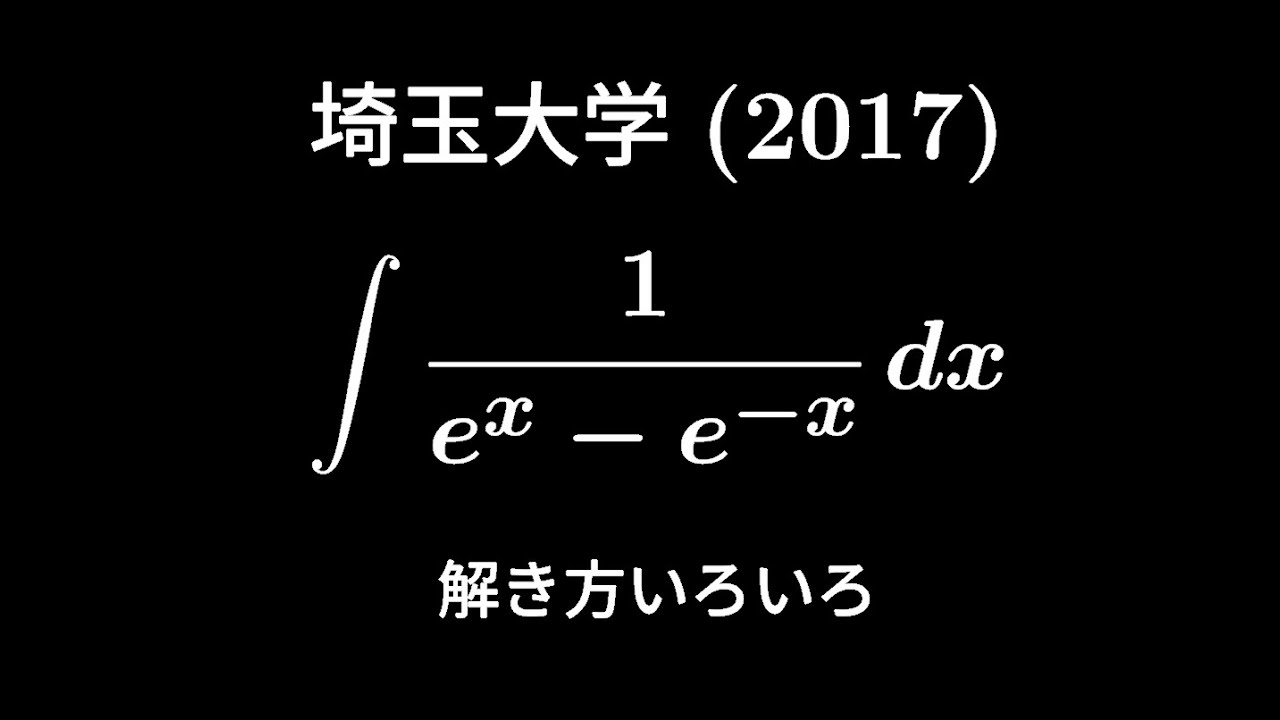
単元:
#大学入試過去問(数学)#不定積分#数学(高校生)#埼玉大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{1}{e^x-e^{-x}} dx$
出典:2017年埼玉大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{1}{e^x-e^{-x}} dx$
出典:2017年埼玉大学 入試問題
大学入試問題#636「ミスなく」 東京電機大学(2020) #不定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#東京電機大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} x^3log(x^2+1) dx$
出典:2020年東京電機大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} x^3log(x^2+1) dx$
出典:2020年東京電機大学 入試問題
大学入試問題#635「意外と簡単」 公立諏訪東京理科大学 #不定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#東京理科大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
(1)$\displaystyle \int e^x\{f'(x)+f(x)\} dx$
(2)$\displaystyle \int e^x \displaystyle \frac{1+\sin\ x}{1+\cos\ x}\ dx$
出典:2023年公立諏訪東京理科大学 入試問題
この動画を見る
(1)$\displaystyle \int e^x\{f'(x)+f(x)\} dx$
(2)$\displaystyle \int e^x \displaystyle \frac{1+\sin\ x}{1+\cos\ x}\ dx$
出典:2023年公立諏訪東京理科大学 入試問題



