ますただ
ますただ
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
大学入試問題をベースに数学の動画を作成しています。大学過去問を多数解説しています。
頻繁に更新していますので是非ご視聴ください！
職業：数学者
職歴：高校非常勤（院生時代）、高専、大学 准教授
趣味：
①将棋 棋力は将棋ウォーズ４段、将棋倶楽部２４はR２０００前後（小学校５，６年のころに頑張ってました）
②麻雀 アカウントは消えましたが、無課金で天鵬で７段まで上がりました。
③ソフトテニス 中学から大学まで、１０年間部活でやっていました。大学時代は４年になってもリーグにでていました。
【解答にミスあり概要欄】大学入試問題#322 慶應義塾大学(2021) #三角関数
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$-\displaystyle \frac{\pi}{2} \leqq \theta \leqq \displaystyle \frac{\pi}{2}$
$4\cos\displaystyle \frac{\theta}{2}(\cos\displaystyle \frac{\theta}{2}+\sin\displaystyle \frac{\theta}{2})$のとき
$\sin\theta$の値を求めよ。
出典：2021年慶應義塾大学 入試問題
この動画を見る
$-\displaystyle \frac{\pi}{2} \leqq \theta \leqq \displaystyle \frac{\pi}{2}$
$4\cos\displaystyle \frac{\theta}{2}(\cos\displaystyle \frac{\theta}{2}+\sin\displaystyle \frac{\theta}{2})$のとき
$\sin\theta$の値を求めよ。
出典：2021年慶應義塾大学 入試問題
大学入試問題#321 甲南大学(2021) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#甲南大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1}\displaystyle \frac{x^2(1-x)^2}{1+x^2}dx$
出典：2021年甲南大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{x^2(1-x)^2}{1+x^2}dx$
出典：2021年甲南大学 入試問題
大学入試問題#320 宮崎大学 改 (2010) #定積分
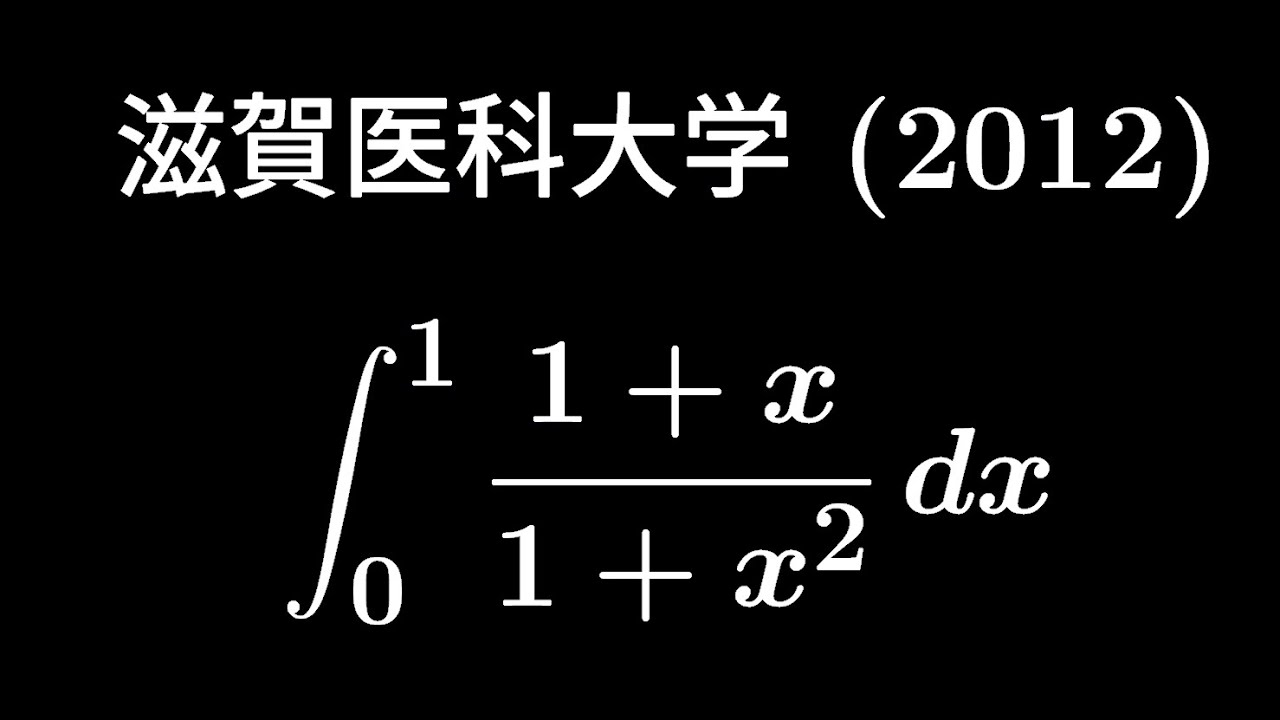
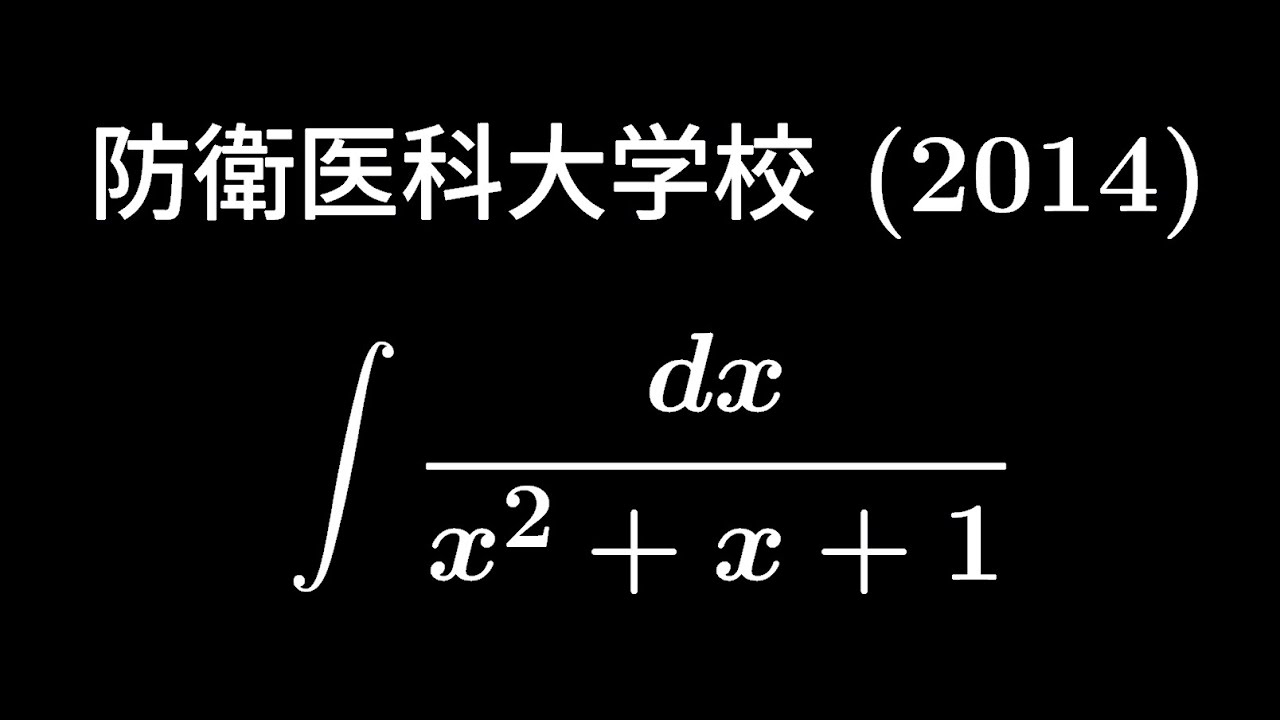
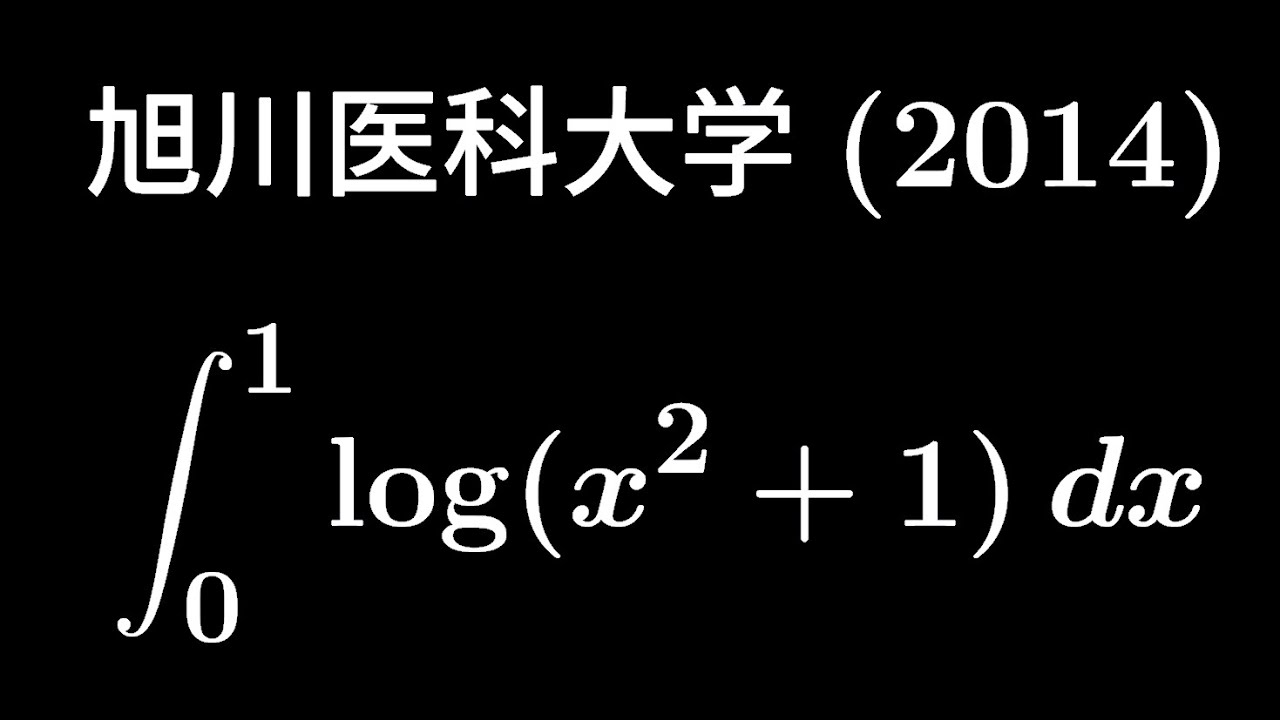
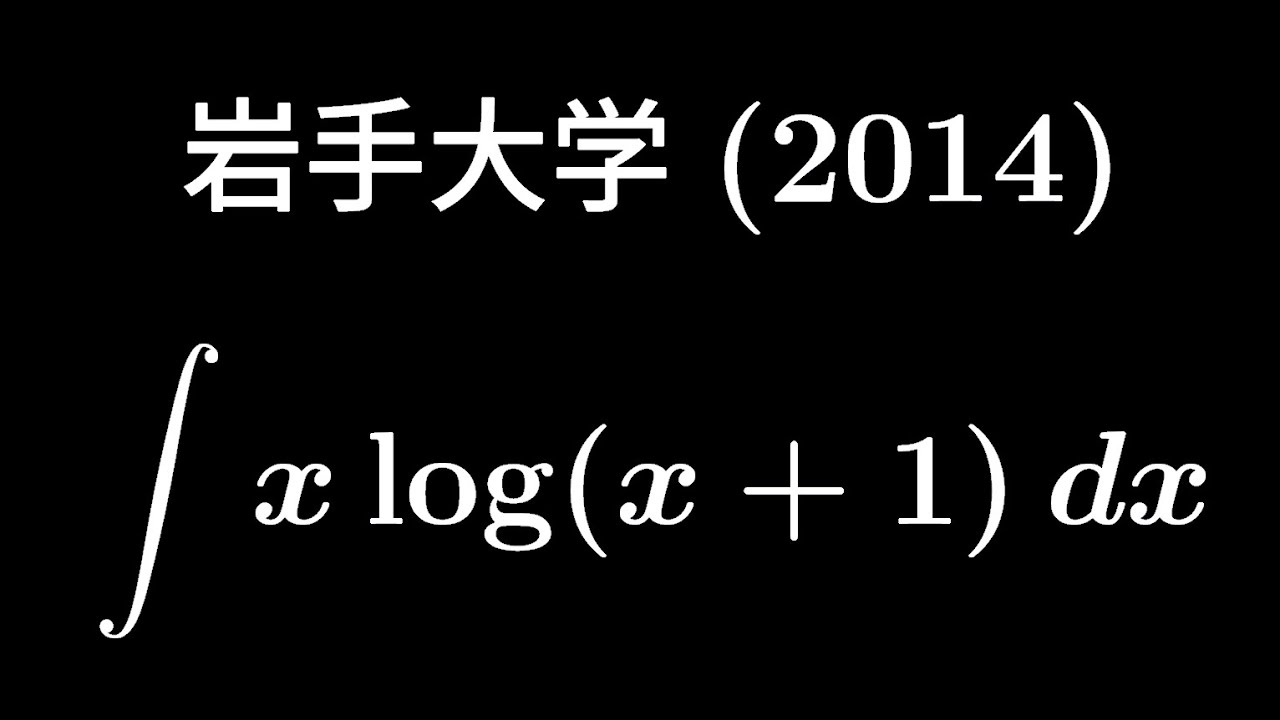
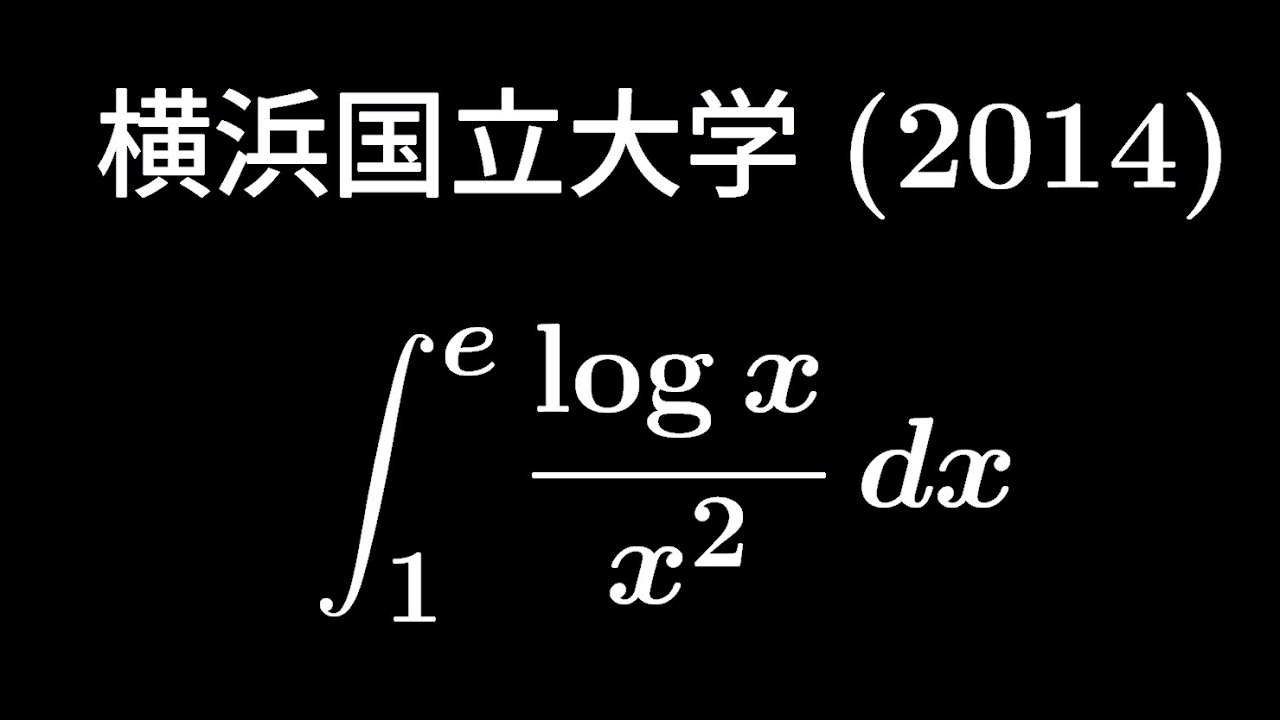
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{log\ \pi}^{log\ 2\pi}e^{2x}\sin(e^x)dx$
出典：2010年宮崎大学 入試問題
この動画を見る
$\displaystyle \int_{log\ \pi}^{log\ 2\pi}e^{2x}\sin(e^x)dx$
出典：2010年宮崎大学 入試問題
大学入試問題#319 電気通信大学(2010) #定積分 #極限
単元：
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#不定積分#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ a \to \infty }\displaystyle \int_{0}^{a}\displaystyle \frac{1}{1+e^x}dx$
出典：2010年電気通信大学 入試問題
この動画を見る
$\displaystyle \lim_{ a \to \infty }\displaystyle \int_{0}^{a}\displaystyle \frac{1}{1+e^x}dx$
出典：2010年電気通信大学 入試問題
大学入試問題#318 立教大学 改 (2021) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{e}\displaystyle \frac{(log\ x)^4}{x^2}dx$
出典：2021年立教大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{e}\displaystyle \frac{(log\ x)^4}{x^2}dx$
出典：2021年立教大学 入試問題
大学入試問題#317 鳥取大学(2010) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#鳥取大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{e}(log\ x)^4dx$
出典：2010年鳥取大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{e}(log\ x)^4dx$
出典：2010年鳥取大学 入試問題
大学入試問題#316 群馬大学(2010) #整数問題
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#群馬大学
指導講師：
ますただ
問題文全文(内容文)：
$2 \leqq p \lt q \lt r$
$\displaystyle \frac{1}{p}+\displaystyle \frac{1}{q}+\displaystyle \frac{1}{r} \geqq 1$をみたす整数の組$(p.g.r)$をすべて求めよ
出典：2010年群馬大学 入試問題
この動画を見る
$2 \leqq p \lt q \lt r$
$\displaystyle \frac{1}{p}+\displaystyle \frac{1}{q}+\displaystyle \frac{1}{r} \geqq 1$をみたす整数の組$(p.g.r)$をすべて求めよ
出典：2010年群馬大学 入試問題
大学入試問題#315 富山県立大学(2010) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#富山県立大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{4}}\tan^3x\ dx$
出典：2010年富山県立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}}\tan^3x\ dx$
出典：2010年富山県立大学 入試問題
大学入試問題#314 弘前大学(2010) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{3}\displaystyle \frac{log(x+1)}{x^2}dx$
出典：2010年広前大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{3}\displaystyle \frac{log(x+1)}{x^2}dx$
出典：2010年広前大学 入試問題
大学入試問題#313 自治医科大学(2021) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#自治医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\cos\ x(1+\sin\ x)}{2+\sin\ x}dx$
出典：2021年自治医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\cos\ x(1+\sin\ x)}{2+\sin\ x}dx$
出典：2021年自治医科大学 入試問題
大学入試問題#312 明治大学2021 #定積分 #極限
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ k \to \infty }\displaystyle \int_{0}^{1}\displaystyle \frac{e^{kx}-1}{e^{kx}+1}$
出典：2021年明治大学 入試問題
この動画を見る
$\displaystyle \lim_{ k \to \infty }\displaystyle \int_{0}^{1}\displaystyle \frac{e^{kx}-1}{e^{kx}+1}$
出典：2021年明治大学 入試問題
数学コンテスト（米国、加奈陀） 2005年 #定積分 #King_property
単元：
Warning: usort() expects parameter 1 to be array, bool given in /home/kaiketsudb/kaiketsu-db.net/public_html/wp-content/themes/lightning-child-sample/taxonomy-teacher.php on line 269
Warning: Invalid argument supplied for foreach() in /home/kaiketsudb/kaiketsu-db.net/public_html/wp-content/themes/lightning-child-sample/taxonomy-teacher.php on line 270
Warning: usort() expects parameter 1 to be array, bool given in /home/kaiketsudb/kaiketsu-db.net/public_html/wp-content/themes/lightning-child-sample/taxonomy-teacher.php on line 269
Warning: Invalid argument supplied for foreach() in /home/kaiketsudb/kaiketsu-db.net/public_html/wp-content/themes/lightning-child-sample/taxonomy-teacher.php on line 270
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1}\displaystyle \frac{log(1+x)}{1+x^2}dx$
出典：数学コンテスト
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{log(1+x)}{1+x^2}dx$
出典：数学コンテスト
大学入試問題#311 杏林大学医学部(2010) #極限
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#杏林大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{\sqrt{ \cos\ 5x }-\sqrt{ \cos\ 3x }}{x^2}$
出典：2010年杏林大学医学部 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{\sqrt{ \cos\ 5x }-\sqrt{ \cos\ 3x }}{x^2}$
出典：2010年杏林大学医学部 入試問題
#55数検準１級１次 過去問 2022年6月 #定積分
単元：
Warning: usort() expects parameter 1 to be array, bool given in /home/kaiketsudb/kaiketsu-db.net/public_html/wp-content/themes/lightning-child-sample/taxonomy-teacher.php on line 269
Warning: Invalid argument supplied for foreach() in /home/kaiketsudb/kaiketsu-db.net/public_html/wp-content/themes/lightning-child-sample/taxonomy-teacher.php on line 270
Warning: usort() expects parameter 1 to be array, bool given in /home/kaiketsudb/kaiketsu-db.net/public_html/wp-content/themes/lightning-child-sample/taxonomy-teacher.php on line 269
Warning: Invalid argument supplied for foreach() in /home/kaiketsudb/kaiketsu-db.net/public_html/wp-content/themes/lightning-child-sample/taxonomy-teacher.php on line 270
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1}\displaystyle \frac{x^3}{1+x^2}dx$
出典：2022年6月数検準一級一次
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{x^3}{1+x^2}dx$
出典：2022年6月数検準一級一次
大学入試問題#310 東京都市大学(2013) #定積分
単元：
Warning: usort() expects parameter 1 to be array, bool given in /home/kaiketsudb/kaiketsu-db.net/public_html/wp-content/themes/lightning-child-sample/taxonomy-teacher.php on line 269
Warning: Invalid argument supplied for foreach() in /home/kaiketsudb/kaiketsu-db.net/public_html/wp-content/themes/lightning-child-sample/taxonomy-teacher.php on line 270
Warning: usort() expects parameter 1 to be array, bool given in /home/kaiketsudb/kaiketsu-db.net/public_html/wp-content/themes/lightning-child-sample/taxonomy-teacher.php on line 269
Warning: Invalid argument supplied for foreach() in /home/kaiketsudb/kaiketsu-db.net/public_html/wp-content/themes/lightning-child-sample/taxonomy-teacher.php on line 270
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{3}}(\cos\ x)log(\sin\ x)dx$
出典：2013年東京都市大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{3}}(\cos\ x)log(\sin\ x)dx$
出典：2013年東京都市大学 入試問題
大学入試問題#309 明治大学 改 (2013) #定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{6}}\cos^5x\ dx$
出典：2013年明治大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{6}}\cos^5x\ dx$
出典：2013年明治大学 入試問題
大学入試問題#308 お茶の水女子大学(2010) #定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#お茶の水女子大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{2}x\ 2^xdx$
出典：2010年お茶の水女子大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{2}x\ 2^xdx$
出典：2010年お茶の水女子大学 入試問題
大学入試問題#307 産業医科大学(2013) #定積分 #King property
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#産業医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\cos\theta}{2\cos^2(\theta-\displaystyle \frac{\pi}{4})}d\theta$
出典：2013年産業医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\cos\theta}{2\cos^2(\theta-\displaystyle \frac{\pi}{4})}d\theta$
出典：2013年産業医科大学 入試問題
大学入試問題#306 早稲田大学2013 #定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1}\displaystyle \frac{\sqrt{ 1-x^2 }}{1+x}dx$
出典：2013年早稲田大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{\sqrt{ 1-x^2 }}{1+x}dx$
出典：2013年早稲田大学 入試問題
大学入試問題#305 明治大学(2013) #極限
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ h \to \infty }\displaystyle \frac{log(1+5h+6h^2)}{h}$
出典：2013年明治大学 入試問題
この動画を見る
$\displaystyle \lim_{ h \to \infty }\displaystyle \frac{log(1+5h+6h^2)}{h}$
出典：2013年明治大学 入試問題
大学入試問題#304 早稲田大学2010 #区分求積法 #極限
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\sqrt[ n ]{ (n+1)(n+2)-(n+n) }$
出典：2010年早稲田大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\sqrt[ n ]{ (n+1)(n+2)-(n+n) }$
出典：2010年早稲田大学 入試問題
大学入試問題#303 横浜市立大学医学部(2011) #積分の応用 #微分方程式
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#横浜市立大学
指導講師：
ますただ
問題文全文(内容文)：
$f(x)$微分可能
$f(x)+\displaystyle \int_{0}^{x}f(t)e^{x-t}dt=\sin\ x$をみたす
$f(0),f'(x),f(x)$を求めよ
出典：2011年横浜市立大学医学部 入試問題
この動画を見る
$f(x)$微分可能
$f(x)+\displaystyle \int_{0}^{x}f(t)e^{x-t}dt=\sin\ x$をみたす
$f(0),f'(x),f(x)$を求めよ
出典：2011年横浜市立大学医学部 入試問題
大学入試問題#302 青山学院大学(2010) #定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{2\pi}|\sin\ x+\cos2x|dx$
出典：2010年青山学院大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{2\pi}|\sin\ x+\cos2x|dx$
出典：2010年青山学院大学 入試問題
大学入試問題#301 旭川医科大学(2011) #定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#旭川医科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$0 \leqq x \lt \displaystyle \frac{\pi}{2}$
$\displaystyle \int_{0}^{x}(\displaystyle \frac{1}{\cos\ t}-\tan\ t)dt$
出典：2011年旭川医科大学 入試問題
この動画を見る
$0 \leqq x \lt \displaystyle \frac{\pi}{2}$
$\displaystyle \int_{0}^{x}(\displaystyle \frac{1}{\cos\ t}-\tan\ t)dt$
出典：2011年旭川医科大学 入試問題
大学入試問題#300 新潟大学2010 #定積分 #極限
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#新潟大学
指導講師：
ますただ
問題文全文(内容文)：
$F(x)=\displaystyle \int_{0}^{x}\sqrt{ 1+e^{2t} }\ dt$のとき
$\displaystyle \lim_{ x \to \infty }\{F(x)-e^x\}$を求めよ
出典：2010年新潟大学 入試問題
この動画を見る
$F(x)=\displaystyle \int_{0}^{x}\sqrt{ 1+e^{2t} }\ dt$のとき
$\displaystyle \lim_{ x \to \infty }\{F(x)-e^x\}$を求めよ
出典：2010年新潟大学 入試問題
大学入試問題#299 信州大学(2001 類題②) #定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{3}\displaystyle \frac{\sqrt{ x }}{\sqrt{ x+1 }-1}dx$
出典：2001年信州大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{3}\displaystyle \frac{\sqrt{ x }}{\sqrt{ x+1 }-1}dx$
出典：2001年信州大学 入試問題
大学入試問題#298 信州大学(2001 類題①) #定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学
指導講師：
ますただ
問題文全文(内容文)：
（1）
$\displaystyle \int_{1}^{3}\displaystyle \frac{x}{\sqrt{ x+1 }-1}dx$
（2）
$\displaystyle \int_{1}^{3}\displaystyle \frac{1}{\sqrt{ x+1 }-1}dx$
出典：2001年信州大学 入試問題
この動画を見る
（1）
$\displaystyle \int_{1}^{3}\displaystyle \frac{x}{\sqrt{ x+1 }-1}dx$
（2）
$\displaystyle \int_{1}^{3}\displaystyle \frac{1}{\sqrt{ x+1 }-1}dx$
出典：2001年信州大学 入試問題
大学入試問題#297 産業医科大学(2010) #極限
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#産業医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{\cos\ x-x^2-1}{x^2}$
出典：2010年産業医科大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{\cos\ x-x^2-1}{x^2}$
出典：2010年産業医科大学 入試問題
大学入試問題#296 電気通信大学(2012) #定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{2}^{4}\displaystyle \frac{dx}{x^2+x-2}$
出典：2012年電気通信大学 入試問題
この動画を見る
$\displaystyle \int_{2}^{4}\displaystyle \frac{dx}{x^2+x-2}$
出典：2012年電気通信大学 入試問題
大学入試問題#295 防衛大学校(2009) #定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#防衛大学校#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{log2}^{log4}\displaystyle \frac{2e^x-2e^{-x}}{e^{2x}+e^{-2x}+1}dx$
出典：2009年防衛大学校
この動画を見る
$\displaystyle \int_{log2}^{log4}\displaystyle \frac{2e^x-2e^{-x}}{e^{2x}+e^{-2x}+1}dx$
出典：2009年防衛大学校