 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【数Ⅲ】極限:次の無限級数の和を求めよう。Σ[n=1~∞](-1/3)^n sin(nπ/2)

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の無限級数の和を求めよう。
$\displaystyle \sum_{n=1}^{\infty}\left(-\dfrac{1}{3}\right)^n \sin\dfrac{n\pi}{2}$
この動画を見る
次の無限級数の和を求めよう。
$\displaystyle \sum_{n=1}^{\infty}\left(-\dfrac{1}{3}\right)^n \sin\dfrac{n\pi}{2}$
【数Ⅲ】極限:次の無限級数の和を求めよう。Σ[n=1~∞](1/3)^n cosnπ

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の無限級数の和を求めよう。
$\displaystyle \sum_{n=1}^{\infty}\left(\dfrac{1}{3}\right)^n \cos n\pi$
この動画を見る
次の無限級数の和を求めよう。
$\displaystyle \sum_{n=1}^{\infty}\left(\dfrac{1}{3}\right)^n \cos n\pi$
【古文】高校入試に必要な基本古文単語テスト

単元:
#国語(中学生)#国語(高校生)#古文#古典的文章#単語
指導講師:
理数個別チャンネル
問題文全文(内容文):
高校受験(私立)に必要な基礎古文単語テストを生徒に解いてもらいました。さあ、生徒はクリアできたのか?そしてあなたもクリアできますか?
古文単語の覚え方も収録しているので要チェック!
この動画を見る
高校受験(私立)に必要な基礎古文単語テストを生徒に解いてもらいました。さあ、生徒はクリアできたのか?そしてあなたもクリアできますか?
古文単語の覚え方も収録しているので要チェック!
【中学数学】2次方程式:x=-5+√19のとき、x²+10x+11の値を求めよ。
【数Ⅱ】複素数と方程式:2x²-6x-3=0の解がα、βのとき、①β²/α+α²/β②(2α²-6α-5)(2β²-6β-1)の値を求めよ。

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$2x^2-6x-3=0$の解が$\alpha,\beta$のとき、
①$\dfrac{\beta^2}{\alpha}+\dfrac{\alpha^2}{\beta}
②$(2\alpha^2-6\alpha-5)(2\beta^2-6\beta-1)$の値を求めよ。
この動画を見る
$2x^2-6x-3=0$の解が$\alpha,\beta$のとき、
①$\dfrac{\beta^2}{\alpha}+\dfrac{\alpha^2}{\beta}
②$(2\alpha^2-6\alpha-5)(2\beta^2-6\beta-1)$の値を求めよ。
【英語】共通テスト第2問を時間をかけずに効率良く満点を取る方法

単元:
#英語(高校生)#大学入試過去問(英語)#共通テスト
指導講師:
理数個別チャンネル
問題文全文(内容文):
共通テスト第2問を時間をかけずに効率良く満点を取る方法に関して解説していきます.
この動画を見る
共通テスト第2問を時間をかけずに効率良く満点を取る方法に関して解説していきます.
【英語】英語共通テスト得点源の第1問AB!英語が苦手な生徒でも分かるように丁寧に解き方を説明してみました。(2018年試行問題)

【数Ⅱ】図形と方程式:x²+y²-2x+4y-11=0はどのような図形を表しているでしょう?

単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
教材:
#高校ゼミスタンダード#高校ゼミスタンダード数Ⅱ#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$x^2+y^2-2x+4y-11=0$はどのような図形を表しているか?
この動画を見る
$x^2+y^2-2x+4y-11=0$はどのような図形を表しているか?
【数Ⅱ】図形と方程式:x²+y²+4x-6y+13=0はどのような図形を表しているでしょう?

単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
教材:
#高校ゼミスタンダード#高校ゼミスタンダード数Ⅱ#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$x^2+y^2+4x-6y+13=0$はどのような図形を表しているか?
この動画を見る
$x^2+y^2+4x-6y+13=0$はどのような図形を表しているか?
【英語】共通テスト:第4問~6問の解き方のコツ!模擬問題から要注意表現も大量紹介!

【国語】⑧現代文:共通テスト(第2問)にも全問挑戦!

単元:
#国語(高校生)#現代文#大学入試過去問(国語)#共通テスト(現代文)
指導講師:
理数個別チャンネル
問題文全文(内容文):
共通テスト国語の第2問「詩とエッセイ」の解き方を詩が苦手な人でも解ける方法を分かりやすく解説しています。
この動画を見る
共通テスト国語の第2問「詩とエッセイ」の解き方を詩が苦手な人でも解ける方法を分かりやすく解説しています。
【受験算数】つるかめ算:つるかめ算をマスターしよう!その5 面積図を利用②:つるとかめが合計8匹います。足の合計が26本です。それぞれ何匹いるでしょう。

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師:
理数個別チャンネル
問題文全文(内容文):
つるとかめが合計8匹います。足の合計が26本です。それぞれ何匹いるでしょう。
この動画を見る
つるとかめが合計8匹います。足の合計が26本です。それぞれ何匹いるでしょう。
【受験算数】つるかめ算:つるかめ算をマスターしよう!その4 面積図を利用①:つるとかめが合計8匹います。足の合計が26本です。それぞれ何匹いるでしょう。

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師:
理数個別チャンネル
問題文全文(内容文):
つるとかめが合計8匹います。足の合計が26本です。それぞれ何匹いるでしょう。
この動画を見る
つるとかめが合計8匹います。足の合計が26本です。それぞれ何匹いるでしょう。
【受験算数】つるかめ算:つるかめ算をマスターしよう!その3 計算を利用:つるとかめが合計8匹います。足の合計が26本です。それぞれ何匹いるでしょう。

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師:
理数個別チャンネル
問題文全文(内容文):
つるとかめが合計8匹います。足の合計が26本です。それぞれ何匹いるでしょう。
この動画を見る
つるとかめが合計8匹います。足の合計が26本です。それぞれ何匹いるでしょう。
【受験算数】つるかめ算:つるかめ算をマスターしよう!その1 表を利用①:つるとかめが合計8匹います。足の合計が26本です。それぞれ何匹いるでしょう。

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師:
理数個別チャンネル
問題文全文(内容文):
つるとかめが合計8匹います。足の合計が26本です。それぞれ何匹いるでしょう。
この動画を見る
つるとかめが合計8匹います。足の合計が26本です。それぞれ何匹いるでしょう。
【受験算数】つるかめ算:つるかめ算をマスターしよう!その2 表を利用②:つるとかめが合計8匹います。足の合計が26本です。それぞれ何匹いるでしょう。

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師:
理数個別チャンネル
問題文全文(内容文):
つるとかめが合計8匹います。足の合計が26本です。それぞれ何匹いるでしょう。
この動画を見る
つるとかめが合計8匹います。足の合計が26本です。それぞれ何匹いるでしょう。
【生物】発生:なぜ卵の発生実験にウニを用いるのか

単元:
#生物#生物#発生#理科(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
共通テストでも聞かれるような、なぜその実験をするのか、なぜ観察対象がそれなのか、などの本質的な質問に対する解説です。
この動画を見る
共通テストでも聞かれるような、なぜその実験をするのか、なぜ観察対象がそれなのか、などの本質的な質問に対する解説です。
⑥現代文:傍線部内の抽象部分を「言い換え」て正解する方法

単元:
#国語(高校生)#現代文#大学入試過去問(国語)#共通テスト(現代文)
指導講師:
理数個別チャンネル
問題文全文(内容文):
この動画は、
①【共通テスト試行問題解説】https://youtu.be/F12KJ9ie8xg
②【本文を読まなくても解ける問題】https://youtu.be/nwLCksLZ_7k
の次の3番目の動画です。(先に上記の2つの動画をご覧ください)
センターの過去問で、抽象→具体を実際に解いて見ていきます!
この動画を見る
この動画は、
①【共通テスト試行問題解説】https://youtu.be/F12KJ9ie8xg
②【本文を読まなくても解ける問題】https://youtu.be/nwLCksLZ_7k
の次の3番目の動画です。(先に上記の2つの動画をご覧ください)
センターの過去問で、抽象→具体を実際に解いて見ていきます!
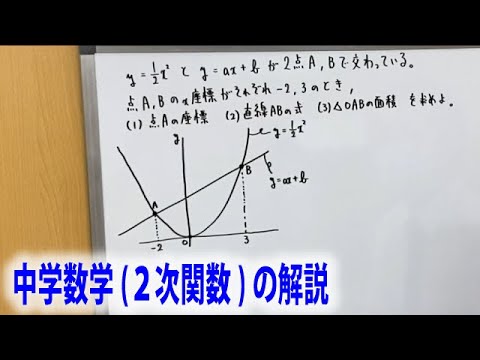
【中学数学】関数y=ax²:y=1/2x²とy=ax+bが2点A,Bで交わっている。点A,Bのx座標がそれぞれ-2,3のとき (1)点Aの座標 (2)直線ABの式 (3)△OABの面積 を求めよ。
単元:
#数学(中学生)#中3数学#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数$y=ax^2:y=\dfrac{1}{2}x^2$と$y=ax+b$が2点A,Bで交わっている。点A,Bのx座標がそれぞれ-2,3のとき
(1)点Aの座標
(2)直線ABの式
(3)△OABの面積
を求めよ。
この動画を見る
関数$y=ax^2:y=\dfrac{1}{2}x^2$と$y=ax+b$が2点A,Bで交わっている。点A,Bのx座標がそれぞれ-2,3のとき
(1)点Aの座標
(2)直線ABの式
(3)△OABの面積
を求めよ。
【数Ⅱ】三角関数:弧度法の考え方② -19π/6って第何象限でどんな形?!

【中学英語】「〜の間」を表す4つの単語 ~during while between amongの違い~

単元:
#英語(中学生)#中3英語#間接疑問文
指導講師:
理数個別チャンネル
問題文全文(内容文):
「〜の間」を表す4つの単語,during while between amongの違いに関して解説していきます.
この動画を見る
「〜の間」を表す4つの単語,during while between amongの違いに関して解説していきます.
【英語】現在完了〈完了〉alreadyとdoneの『意外な』使い方!

単元:
#英語(中学生)#英語(高校生)#英文法#中3英語#時制#現在完了(継続、経験、完了・結果)
指導講師:
理数個別チャンネル
問題文全文(内容文):
現在完了〈完了〉で頻出のalreadyとdoneの『意外な』使い方を解説します!
この動画を見る
現在完了〈完了〉で頻出のalreadyとdoneの『意外な』使い方を解説します!
【国語】③評論文・説明文の精読実践

単元:
#国語(中学受験)#国語(高校生)#現代文#説明文
指導講師:
理数個別チャンネル
問題文全文(内容文):
「【国語】②国語の説明文(評論文)の読み方について話しました。」で話した内容について、
実際の解き方を高校入試の過去問で実践しましたのでご覧ください。
この動画を見る
「【国語】②国語の説明文(評論文)の読み方について話しました。」で話した内容について、
実際の解き方を高校入試の過去問で実践しましたのでご覧ください。
【数Ⅰ】集合と命題:あなたは”命題”が何かわかりますか??共通テストへ向けて言葉の意味も知っておいた方がいい!…かも

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
以下の文章は命題でしょうか?
・3は偶数である。
・0.001は小さい数である。
この動画を見る
以下の文章は命題でしょうか?
・3は偶数である。
・0.001は小さい数である。
【受験算数】日暦算:2020年の1月1日から12月15日までは何日ある??

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
理数個別チャンネル
問題文全文(内容文):
2020年の1月1日から12月15日までは何日ある?
この動画を見る
2020年の1月1日から12月15日までは何日ある?
【中学理科】光・音・力:凸レンズの基本
【数Ⅱ】三角関数:弧度法の考え方①

【国語】②国語の説明文(評論文)の読み方について話しました。

単元:
#国語(中学受験)#国語(中学生)#国語(高校生)#現代文#説明文#説明的文章
指導講師:
理数個別チャンネル
問題文全文(内容文):
神奈川県入試の問題を題材に中学受験、高校受験、大学受験で使える「評論文(説明文」の読み方を「実際の線引き」をしながら解説しています。
この動画を見る
神奈川県入試の問題を題材に中学受験、高校受験、大学受験で使える「評論文(説明文」の読み方を「実際の線引き」をしながら解説しています。
【受験算数】年齢算:父vs子どもチーム? 現在太郎君の父の年齢は39才、太郎君は4才、太郎君の弟は2才、太郎君の妹は1才です。太郎君の父の年齢が、子どもたちの年齢の和の3倍になるのは何年後?

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師:
理数個別チャンネル
問題文全文(内容文):
現在太郎君の父の年齢は39才、太郎君は4才、太郎君の弟は2才、太郎君の妹は1才です。太郎君の父の年齢が、子どもたちの年齢の和の3倍になるのは何年後?
この動画を見る
現在太郎君の父の年齢は39才、太郎君は4才、太郎君の弟は2才、太郎君の妹は1才です。太郎君の父の年齢が、子どもたちの年齢の和の3倍になるのは何年後?
【算数】割合:歩合?百分率?増し?引き?

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例
指導講師:
理数個別チャンネル
問題文全文(内容文):
割合の単元でよく出てくる歩合、百分率、増し、引きについて丁寧に解説します!
この動画を見る
割合の単元でよく出てくる歩合、百分率、増し、引きについて丁寧に解説します!




