 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【中学受験理科】標本調査【毎週日曜日16時更新!】

単元:
#理科(中学受験)#生物分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の問に答えなさい。答えが割り切れないときは四捨五入して整数で答えなさい。
問1 ある草原の一定区域に生息する野ネズミの数を調べるために、区域全体でつかまえた100匹に印をつけて、もう一度放しました。しばらく経った別の日に、区域全体でまた100匹をつかまえると、この中に前に印をつけておいた野ネズミが12匹いました。この草原には、何匹の野ネズミがいると考えられますか。
問2 ある砂浜で、1辺が2mの正方形をつくり、そこに住んでいるある生物の数を調べることにしました。この正方形を64区画に等分し、そのうち8区画だけこの生物の数を調べたところ、それぞれ25,32,36,36,37,40,43,51匹でした。正方形1㎡あたり、この生物は何匹いると考えられますか。
この動画を見る
次の問に答えなさい。答えが割り切れないときは四捨五入して整数で答えなさい。
問1 ある草原の一定区域に生息する野ネズミの数を調べるために、区域全体でつかまえた100匹に印をつけて、もう一度放しました。しばらく経った別の日に、区域全体でまた100匹をつかまえると、この中に前に印をつけておいた野ネズミが12匹いました。この草原には、何匹の野ネズミがいると考えられますか。
問2 ある砂浜で、1辺が2mの正方形をつくり、そこに住んでいるある生物の数を調べることにしました。この正方形を64区画に等分し、そのうち8区画だけこの生物の数を調べたところ、それぞれ25,32,36,36,37,40,43,51匹でした。正方形1㎡あたり、この生物は何匹いると考えられますか。
【数Ⅰ】【2次関数】関数の場合分け ※問題文は概要欄
単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数のグラフをかけ。
(1) y=-x+2 (x<2) , y=x-2 (x≧2)
(2) y=1 (x<0) , y=x+1 (x≧0)
(3) y=x² (x<0) , y=x (0≦x<1) , y=-x²+2x (1≦x)
この動画を見る
次の関数のグラフをかけ。
(1) y=-x+2 (x<2) , y=x-2 (x≧2)
(2) y=1 (x<0) , y=x+1 (x≧0)
(3) y=x² (x<0) , y=x (0≦x<1) , y=-x²+2x (1≦x)
【高校物理】充電されたコンデンサーの接続【定期考査直前 特別企画!】【月・木・土 16時新作公開!】

単元:
#物理#電気#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
10V の電圧で充電された 3.0μF のコンデンサー C₁ に、充電されていない 2.0μF のコンデンサー C₂、スイッチ S、50V の電池を図のように接続し、スイッチ S を閉じた。
(1) C₁、C₂ にたくわえられる電気量はそれぞれいくらか。
(2) C₁、C₂ の両端の電圧はそれぞれいくらか。
この動画を見る
10V の電圧で充電された 3.0μF のコンデンサー C₁ に、充電されていない 2.0μF のコンデンサー C₂、スイッチ S、50V の電池を図のように接続し、スイッチ S を閉じた。
(1) C₁、C₂ にたくわえられる電気量はそれぞれいくらか。
(2) C₁、C₂ の両端の電圧はそれぞれいくらか。
【高校物理】単振動の式【毎週土曜日16時更新!】

単元:
#物理#力学#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
原点Oを中心として、x軸上で単振動をする物体がある。
この単振動の振幅はA〔m〕、振動数はf〔Hz〕である。物体が、原点のOを正の向きに通過する時刻をt=0とする。
(1)角振動数を求めよ。
(2)時刻(>0)における変位x〔m〕を表す式を示せ。
(3)時刻t(>0)における速度〔m/s〕を表す式を示せ。
(4)速さの最大値を求めよ。
(5)加速度の大きさの最大値を求めよ。
この動画を見る
原点Oを中心として、x軸上で単振動をする物体がある。
この単振動の振幅はA〔m〕、振動数はf〔Hz〕である。物体が、原点のOを正の向きに通過する時刻をt=0とする。
(1)角振動数を求めよ。
(2)時刻(>0)における変位x〔m〕を表す式を示せ。
(3)時刻t(>0)における速度〔m/s〕を表す式を示せ。
(4)速さの最大値を求めよ。
(5)加速度の大きさの最大値を求めよ。
【高校化学】エタノールとその誘導体【毎週土曜日16時更新!】

単元:
#化学#有機#有機化合物の特徴と構造#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
図は、エタノールを中心とした有機化合物の関連と反応を示したものである。
図中のA~Hに該当する構造式を記し,下の各問いに答えよ。
*図は動画中で!
(1) 図中の(a)〜(c)に該当する操作を、次の(ア)〜(ウ)から1つずつ選べ。
(ア) ニッケル触媒下で水素を付加する
(イ) リン酸触媒を用いて水を付加する
(ウ) 塩化パラジウム(II)と塩化銅(II)を触媒に用いて酸化する
(2) 図中の①~⑤に該当する反応名を,下の(ア)~(オ)から1つずつ選べ。
(ア)酸化 (イ) 還元 (ウ)中和(エ)付加(オ)脱水
(3) A~Hのうち,次の(ア),(イ)に該当する物質をすべて選べ。
(ア)フェーリング液を還元する。
(イ)炭酸水素ナトリウム水溶液を加えると気体が発生する。
この動画を見る
図は、エタノールを中心とした有機化合物の関連と反応を示したものである。
図中のA~Hに該当する構造式を記し,下の各問いに答えよ。
*図は動画中で!
(1) 図中の(a)〜(c)に該当する操作を、次の(ア)〜(ウ)から1つずつ選べ。
(ア) ニッケル触媒下で水素を付加する
(イ) リン酸触媒を用いて水を付加する
(ウ) 塩化パラジウム(II)と塩化銅(II)を触媒に用いて酸化する
(2) 図中の①~⑤に該当する反応名を,下の(ア)~(オ)から1つずつ選べ。
(ア)酸化 (イ) 還元 (ウ)中和(エ)付加(オ)脱水
(3) A~Hのうち,次の(ア),(イ)に該当する物質をすべて選べ。
(ア)フェーリング液を還元する。
(イ)炭酸水素ナトリウム水溶液を加えると気体が発生する。
【小5算数解説】受験算数 比と割合A4:売買損益 売価は? 【問題文は概要欄】

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例
指導講師:
理数個別チャンネル
問題文全文(内容文):
4800円で仕入れたある品物に、4割増しの定価をつけ、定価の2割引きで売ったら□円になりました。
この動画を見る
4800円で仕入れたある品物に、4割増しの定価をつけ、定価の2割引きで売ったら□円になりました。
【数A】【場合の数】硬貨で支払える金額 ※問題文は概要欄

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#場合の数と確率#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の場合硬貨の一部または全部を使ってちょうど支払うことができる金額は何通りあるか
(1)10円硬貨4枚、50円硬貨1枚、100円硬貨3枚
(2)10円硬貨2枚、50円硬貨3枚、100円硬貨3枚
(3)10円硬貨7枚、50円硬貨1枚、100円硬貨3枚
10円、50円、100円の3種類の硬貨を使ってちょうど250円支払うには何通りの支払いの方法があるか
ただし、どの硬貨も十分な枚数があり、使わない硬貨があっても良いものとする
この動画を見る
次の場合硬貨の一部または全部を使ってちょうど支払うことができる金額は何通りあるか
(1)10円硬貨4枚、50円硬貨1枚、100円硬貨3枚
(2)10円硬貨2枚、50円硬貨3枚、100円硬貨3枚
(3)10円硬貨7枚、50円硬貨1枚、100円硬貨3枚
10円、50円、100円の3種類の硬貨を使ってちょうど250円支払うには何通りの支払いの方法があるか
ただし、どの硬貨も十分な枚数があり、使わない硬貨があっても良いものとする
【数A】【場合の数】樹形図の使い方 ※問題文は概要欄

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#場合の数と確率#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
梨4個、柿2個、桃2個から6個だけ取り出す方法は何通りあるか。
ただし、取り出さない果物があってもよいものとする。
上の図を、Aを出発点として一筆でかく方法は何通りあるか。
この動画を見る
梨4個、柿2個、桃2個から6個だけ取り出す方法は何通りあるか。
ただし、取り出さない果物があってもよいものとする。
上の図を、Aを出発点として一筆でかく方法は何通りあるか。
【数A】【場合の数】余事象の使い方 ※問題文は概要欄

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#場合の数と確率#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
大中小3個のさいころを投げるとき、次のような場合は何通りあるか
(1)目が全て異なる (2)少なくとも2個が同じ目
(3)目の積が3の倍数 (4)目の和が奇数
正四面体の1つの面を下にしておき、1つの辺を軸として3回転がす。2回目
以降、直前にあった場所を通らないようにするとき、次の数を求めよ
(1)転がし方の総数 (2)3回転がした後の正四面体の位置の総数
この動画を見る
大中小3個のさいころを投げるとき、次のような場合は何通りあるか
(1)目が全て異なる (2)少なくとも2個が同じ目
(3)目の積が3の倍数 (4)目の和が奇数
正四面体の1つの面を下にしておき、1つの辺を軸として3回転がす。2回目
以降、直前にあった場所を通らないようにするとき、次の数を求めよ
(1)転がし方の総数 (2)3回転がした後の正四面体の位置の総数
【数A】【場合の数】約数の個数と総和 ※問題文は概要欄

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#場合の数と確率#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題28
次の数の正の約数の個数と、その約数の総和を求めよ。
(1)$5・2^3$ (2)$108$ (3)$540$
問題29
2桁の自然数のうち、各位の数の積が偶数になる自然数は何個あるか。
この動画を見る
問題28
次の数の正の約数の個数と、その約数の総和を求めよ。
(1)$5・2^3$ (2)$108$ (3)$540$
問題29
2桁の自然数のうち、各位の数の積が偶数になる自然数は何個あるか。
【数Ⅰ】【数と式】平方根の式の値 ※問題文は概要欄

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#数と式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$x=\dfrac{\sqrt{ 5 }+2}{\sqrt{ 5 }-2}$ , $y=\dfrac{\sqrt{ 5 }-2}{\sqrt{ 5 }+2}$
のとき, 次の式の値を求めよ。
(1) $x+y$ (2) $xy$ (3) $x^2y+xy^2 $
(4) $x^2+y^2$ (5) $x^3+y^3$
$x=\sqrt{ 2 }-1$
のとき, 次の式の値を求めよ。
(1) $x+\dfrac{1}{x}$ (2) $x^2+\dfrac{1}{x^2}$ (3) $x^3+\dfrac{1}{x^3}$
(4) $x^4+\dfrac{1}{x^4}$ (5) $x^5+\dfrac{1}{x^5}$
この動画を見る
$x=\dfrac{\sqrt{ 5 }+2}{\sqrt{ 5 }-2}$ , $y=\dfrac{\sqrt{ 5 }-2}{\sqrt{ 5 }+2}$
のとき, 次の式の値を求めよ。
(1) $x+y$ (2) $xy$ (3) $x^2y+xy^2 $
(4) $x^2+y^2$ (5) $x^3+y^3$
$x=\sqrt{ 2 }-1$
のとき, 次の式の値を求めよ。
(1) $x+\dfrac{1}{x}$ (2) $x^2+\dfrac{1}{x^2}$ (3) $x^3+\dfrac{1}{x^3}$
(4) $x^4+\dfrac{1}{x^4}$ (5) $x^5+\dfrac{1}{x^5}$
【数A】【場合の数】集合の個数 ※問題文は概要欄

単元:
#数Ⅰ#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
全体集合Uと、その部分集合$A$,$B$に対して${}_{ n }$U = 50,${}_{ n }$($A$$\cup$$B$) = 42,${}_{ n }$($A$$\cap$$B$) = 3, ${}_{ n }$($\overline{A}$$\cap$$B$) = 15であるとき、次の集合の要素の個数を求めよ。
(1) $\overline{A}$$\cap$$\overline{B}$ (2) $A$$\cap$$\overline{B}$ (3) $A$
この動画を見る
全体集合Uと、その部分集合$A$,$B$に対して${}_{ n }$U = 50,${}_{ n }$($A$$\cup$$B$) = 42,${}_{ n }$($A$$\cap$$B$) = 3, ${}_{ n }$($\overline{A}$$\cap$$B$) = 15であるとき、次の集合の要素の個数を求めよ。
(1) $\overline{A}$$\cap$$\overline{B}$ (2) $A$$\cap$$\overline{B}$ (3) $A$
【数Ⅰ】【数と式】平方根の式の値 ※問題文は概要欄

単元:
#数Ⅰ#数と式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$x$=$\cfrac{\sqrt{5}+2}{\sqrt{5}-2}$ , $y$ = $\cfrac{\sqrt{5}-2}{\sqrt{5}+2}$ のとき、次の式の値を求めよ
(1) $x$+$y$ (2)$xy$ (3) $x^2y+xy^2$ (4)$x^2+y^2$ (5)$x^3+y^3$
この動画を見る
$x$=$\cfrac{\sqrt{5}+2}{\sqrt{5}-2}$ , $y$ = $\cfrac{\sqrt{5}-2}{\sqrt{5}+2}$ のとき、次の式の値を求めよ
(1) $x$+$y$ (2)$xy$ (3) $x^2y+xy^2$ (4)$x^2+y^2$ (5)$x^3+y^3$
【数A】【場合の数】集合の文章題 ※問題文は概要欄

単元:
#数A#場合の数と確率#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
海外旅行者100人のうち、75人がカゼ薬を、80人が胃薬を携帯していた。次のような人は、最も多くて何人か。また少なくて何人か。
(1)カゼ薬と胃薬を両方とも携帯した人
(2)カゼ薬と胃薬を両方とも携帯していない人
この動画を見る
海外旅行者100人のうち、75人がカゼ薬を、80人が胃薬を携帯していた。次のような人は、最も多くて何人か。また少なくて何人か。
(1)カゼ薬と胃薬を両方とも携帯した人
(2)カゼ薬と胃薬を両方とも携帯していない人
【数A】【場合の数】3つの集合 ※問題文は概要欄

単元:
#数A#場合の数と確率#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
1から100までの整数のうち、次のような数は何個あるか。
(1)2,3,7の少なくとも1つで割り切れる数
(2)2では割り切れるが、3でも7でも割り切れない数
この動画を見る
1から100までの整数のうち、次のような数は何個あるか。
(1)2,3,7の少なくとも1つで割り切れる数
(2)2では割り切れるが、3でも7でも割り切れない数
【数A】【場合の数】集合の基本、ベン図の使い方 ※問題文は概要欄
単元:
#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
U={ $1$,$2$,$3$,$4$,$5$,$6$,$7$,$8$,$9$ }を全体集合とする。Uの部分集合$A$,$B$について、$A$$\cap$$B$ = { $2$,$4$,$6$,$8$ } , $\overline{ A }$$\cap$$\overline{ B }$ = { $1$,$9$ }であるとき、次の集合を求めよ。
(1)$A$$\cup$$B$ (2)$B$ (3)$A$$\cap$$\overline{B}$
この動画を見る
U={ $1$,$2$,$3$,$4$,$5$,$6$,$7$,$8$,$9$ }を全体集合とする。Uの部分集合$A$,$B$について、$A$$\cap$$B$ = { $2$,$4$,$6$,$8$ } , $\overline{ A }$$\cap$$\overline{ B }$ = { $1$,$9$ }であるとき、次の集合を求めよ。
(1)$A$$\cup$$B$ (2)$B$ (3)$A$$\cap$$\overline{B}$
【数 I】【数と式】平方根の近似値

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\sqrt{2}=1.4142,\ \sqrt{3}=1.7321\ とするとき, \ 分母の有理化を利用して,\ 次の値を求めよ。\\\\$
$(1) \ \frac{10}{\sqrt{3}+\sqrt{2}}\ (2)\ \frac{1}{\sqrt{12}-\sqrt{2}}$
この動画を見る
$\sqrt{2}=1.4142,\ \sqrt{3}=1.7321\ とするとき, \ 分母の有理化を利用して,\ 次の値を求めよ。\\\\$
$(1) \ \frac{10}{\sqrt{3}+\sqrt{2}}\ (2)\ \frac{1}{\sqrt{12}-\sqrt{2}}$
【数Ⅰ】【数と式】平方根の近似値 ※問題文は概要欄

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#数と式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\sqrt{2}=1.4142$, $\sqrt{3}=1.7321$
とするとき, 分母の有理化を利用して, 次の値を求めよ。
(1) $\dfrac{10}{\sqrt{3}+\sqrt{2}}$ (2) $\dfrac{1}{\sqrt{12}-\sqrt{2}}$
$x=1-\sqrt{5}$
のとき, 次の式の値を求めよ。
(1) $x^2-2x-4$ (2) $x^3-2x^2$
この動画を見る
$\sqrt{2}=1.4142$, $\sqrt{3}=1.7321$
とするとき, 分母の有理化を利用して, 次の値を求めよ。
(1) $\dfrac{10}{\sqrt{3}+\sqrt{2}}$ (2) $\dfrac{1}{\sqrt{12}-\sqrt{2}}$
$x=1-\sqrt{5}$
のとき, 次の式の値を求めよ。
(1) $x^2-2x-4$ (2) $x^3-2x^2$
【数Ⅰ】【数と式】平方根の計算 ※問題文は概要欄

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#数と式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の計算をせよ。
(1) $(1+\sqrt{ 2 }-\sqrt{ 3 })^2$
(2)$(3-\sqrt{ 2 }-\sqrt{ 11 })(3-\sqrt{ 2 }+\sqrt{ 11 })$
次の計算をせよ。
(1) $\displaystyle \frac{3\sqrt{ 5 }-5\sqrt{ 3 }}{\sqrt{ 5 }+\sqrt{ 3 }}+\displaystyle \frac{3\sqrt{ 5 }+4\sqrt{ 3 }}{3\sqrt{ 5 }-4\sqrt{ 3 }}$
(2) $\displaystyle \frac{\sqrt{ 2 }-1}{\sqrt{ 2 }+1}+\displaystyle \frac{\sqrt{ 3 }-\sqrt{ 2 }}{\sqrt{ 3 }+\sqrt{ 2 }}+\displaystyle \frac{\sqrt{ 3 }+\sqrt{ 2 }}{2-\sqrt{ 3 }}$
次の計算をせよ。
(1) $\displaystyle \frac{1}{1+\sqrt{ 2 }-\sqrt{ 3 }}$
(2) $\displaystyle \frac{\sqrt{ 5 }+\sqrt{ 3 }+\sqrt{ 2 }}{\sqrt{ 5 }+\sqrt{ 3 }-\sqrt{ 2 }}$
(3) $\displaystyle \frac{\sqrt{ 2 }+\sqrt{ 5 }+\sqrt{ 7 }}{\sqrt{ 2 }+\sqrt{ 5 }-\sqrt{ 7 }}+\displaystyle \frac{\sqrt{ 2 }-\sqrt{ 5 }+\sqrt{ 7 }}{\sqrt{ 2 }-\sqrt{ 5 }-\sqrt{ 7 }}$
この動画を見る
次の計算をせよ。
(1) $(1+\sqrt{ 2 }-\sqrt{ 3 })^2$
(2)$(3-\sqrt{ 2 }-\sqrt{ 11 })(3-\sqrt{ 2 }+\sqrt{ 11 })$
次の計算をせよ。
(1) $\displaystyle \frac{3\sqrt{ 5 }-5\sqrt{ 3 }}{\sqrt{ 5 }+\sqrt{ 3 }}+\displaystyle \frac{3\sqrt{ 5 }+4\sqrt{ 3 }}{3\sqrt{ 5 }-4\sqrt{ 3 }}$
(2) $\displaystyle \frac{\sqrt{ 2 }-1}{\sqrt{ 2 }+1}+\displaystyle \frac{\sqrt{ 3 }-\sqrt{ 2 }}{\sqrt{ 3 }+\sqrt{ 2 }}+\displaystyle \frac{\sqrt{ 3 }+\sqrt{ 2 }}{2-\sqrt{ 3 }}$
次の計算をせよ。
(1) $\displaystyle \frac{1}{1+\sqrt{ 2 }-\sqrt{ 3 }}$
(2) $\displaystyle \frac{\sqrt{ 5 }+\sqrt{ 3 }+\sqrt{ 2 }}{\sqrt{ 5 }+\sqrt{ 3 }-\sqrt{ 2 }}$
(3) $\displaystyle \frac{\sqrt{ 2 }+\sqrt{ 5 }+\sqrt{ 7 }}{\sqrt{ 2 }+\sqrt{ 5 }-\sqrt{ 7 }}+\displaystyle \frac{\sqrt{ 2 }-\sqrt{ 5 }+\sqrt{ 7 }}{\sqrt{ 2 }-\sqrt{ 5 }-\sqrt{ 7 }}$
【数Ⅰ】【数と式】循環小数と絶対値 ※問題文は概要欄

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#数と式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の分数を小数で表したとき、[ ]内の数字を求めよ。
(1) $\frac{11}{101}$ (2) $\frac{9}{41}$
x=-4,-1,2,5 のそれぞれについて、次の式の値を求めよ。
(1)|-x| (2)|x+1| (3)|1-2x|+|x-1|
この動画を見る
次の分数を小数で表したとき、[ ]内の数字を求めよ。
(1) $\frac{11}{101}$ (2) $\frac{9}{41}$
x=-4,-1,2,5 のそれぞれについて、次の式の値を求めよ。
(1)|-x| (2)|x+1| (3)|1-2x|+|x-1|
【数Ⅰ】【集合と論証】背理法の使い方 ※問題文は概要欄

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#数と式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
"$x,y,z$は実数とする。次の▢の中に、「必要十分条件であるが十分条件ではない」「十分条件であるが必要条件ではない」「必要十分条件である」「必要条件でも十分条件でもない」のうち、それぞれどれが適するか。
(1)$(x-y)(y-z)=0$は$x=y=z$であるための$\Box$
(2)$「x\gt 0 $かつ$y\gt 0」$は、$xy\gt 0$であるための$\Box$
(3)$x=y=0$は、$「xy=0$かつ$x+y=0」$であるための$\Box$
(4)$\angle A\lt 90$は$△ABC$が鋭角三角形であるための$\Box$
(5)$△ABC$の3辺$BC,CA,AB$の長さがそれぞれa$,b,c$とする。
$(a-b)(a^2+b^2=c^2)=0$は$△ABC$が直角二等辺三角形であるための$\Box$
$a,b$は実数とする。次の2つの条件$p,q$は同値であることを証明せよ。
$p:a\gt 1$かつ$b\gt 1$ $q:a+b\gt 2$かつ$(a-1)(b-1)\gt 0$
この動画を見る
"$x,y,z$は実数とする。次の▢の中に、「必要十分条件であるが十分条件ではない」「十分条件であるが必要条件ではない」「必要十分条件である」「必要条件でも十分条件でもない」のうち、それぞれどれが適するか。
(1)$(x-y)(y-z)=0$は$x=y=z$であるための$\Box$
(2)$「x\gt 0 $かつ$y\gt 0」$は、$xy\gt 0$であるための$\Box$
(3)$x=y=0$は、$「xy=0$かつ$x+y=0」$であるための$\Box$
(4)$\angle A\lt 90$は$△ABC$が鋭角三角形であるための$\Box$
(5)$△ABC$の3辺$BC,CA,AB$の長さがそれぞれa$,b,c$とする。
$(a-b)(a^2+b^2=c^2)=0$は$△ABC$が直角二等辺三角形であるための$\Box$
$a,b$は実数とする。次の2つの条件$p,q$は同値であることを証明せよ。
$p:a\gt 1$かつ$b\gt 1$ $q:a+b\gt 2$かつ$(a-1)(b-1)\gt 0$
【数Ⅰ】【集合と論証】対偶の使い方 ※問題文は概要欄

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#集合と命題#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
【1問目】
$m,n$は整数とする。次の命題を証明せよ。
(1)$n^2$が5の倍数ならば、$n$は5の倍数である。
(2)$mn$が3の倍数ならば、$m,n$の少なくとも一方は3の倍数である。
【2問目】
$\sqrt6$が無理数であることを用いて、$\sqrt3-\sqrt2$は無理数であることを証明せよ。
この動画を見る
【1問目】
$m,n$は整数とする。次の命題を証明せよ。
(1)$n^2$が5の倍数ならば、$n$は5の倍数である。
(2)$mn$が3の倍数ならば、$m,n$の少なくとも一方は3の倍数である。
【2問目】
$\sqrt6$が無理数であることを用いて、$\sqrt3-\sqrt2$は無理数であることを証明せよ。
【数Ⅰ】【集合と論証】真偽の調べ方 ※問題文は概要欄

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#集合と命題#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$a,b$は実数とする。次の命題の真偽を求めよ。
(1)$ab=0$ならば$a^2+b^2=0$である。
(2)$a^2=4$ならば$|a+1|≧1$である。
(3)$ab$が有理数であるならば、$a,b$はともに有理数である。
(4)$a+b, ab$がともに有理数ならば、$a,b$はともに有理数である。
全体集合を$U$とし、条件$p,q$を満たす全体の集合を、それぞれ$P,Q$とする。
命題$\overline{p}⇒q$が真であるとき、$P,Q$について常に成り立つ事をすべて選べ。
①$P=Q$
②$Q⊂P$
③$\overline{Q}⊂P$
④$P⊂\overline{Q}$
⑤$P∪\overline{Q}=P$
⑥$P∪\overline{Q}=\overline{Q}$
⑦$P∩Q=\varnothing$
⑧$P∪Q=U$
この動画を見る
$a,b$は実数とする。次の命題の真偽を求めよ。
(1)$ab=0$ならば$a^2+b^2=0$である。
(2)$a^2=4$ならば$|a+1|≧1$である。
(3)$ab$が有理数であるならば、$a,b$はともに有理数である。
(4)$a+b, ab$がともに有理数ならば、$a,b$はともに有理数である。
全体集合を$U$とし、条件$p,q$を満たす全体の集合を、それぞれ$P,Q$とする。
命題$\overline{p}⇒q$が真であるとき、$P,Q$について常に成り立つ事をすべて選べ。
①$P=Q$
②$Q⊂P$
③$\overline{Q}⊂P$
④$P⊂\overline{Q}$
⑤$P∪\overline{Q}=P$
⑥$P∪\overline{Q}=\overline{Q}$
⑦$P∩Q=\varnothing$
⑧$P∪Q=U$
【数Ⅰ】【集合と論証】集合:ベン図を利用した問題 ※問題文は概要欄

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#集合と命題#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$U=\{1,2,3,4,5,6,7,8,9\}$を全体集合とする。$U$の部分集合$A,B$について
$A∩B=\{2\}$ $\overline{A}∩B=\{4,6,8\}$ $ \overline{A}∩\overline{B}=\{1,9\}$
であるとき、次の∩を求めよ。
(1)$A∪B$
(2)$B$
(3)$A∩\overline{B}$
$U=\{x|1≦x≦10、xは整数\}$を全体集合とする。$U$の部分集合
$A=\{1,2,3,4,8\} B=\{3,4,5,6\} C=\{2,3,6,7\}$
について、次の集合を求めよ。
(1)$A∩B∩C$
(2)$A∪B∪C$
(3)$A∩B∩\overline{C}$
(4)$\overline{A}∩B∩\overline{C}$
(5)$\overline{(A∩B∩C)}$
(6)$(A∪C)∩\overline{B}$
$A=\{1,3,3a-2\}$ $B=\{-5、a+2、a^2-2a+1\}$ $A∩B=\{1,4\}$のとき
定数$a$の値と和集合$A∪B$を求めよ。
この動画を見る
$U=\{1,2,3,4,5,6,7,8,9\}$を全体集合とする。$U$の部分集合$A,B$について
$A∩B=\{2\}$ $\overline{A}∩B=\{4,6,8\}$ $ \overline{A}∩\overline{B}=\{1,9\}$
であるとき、次の∩を求めよ。
(1)$A∪B$
(2)$B$
(3)$A∩\overline{B}$
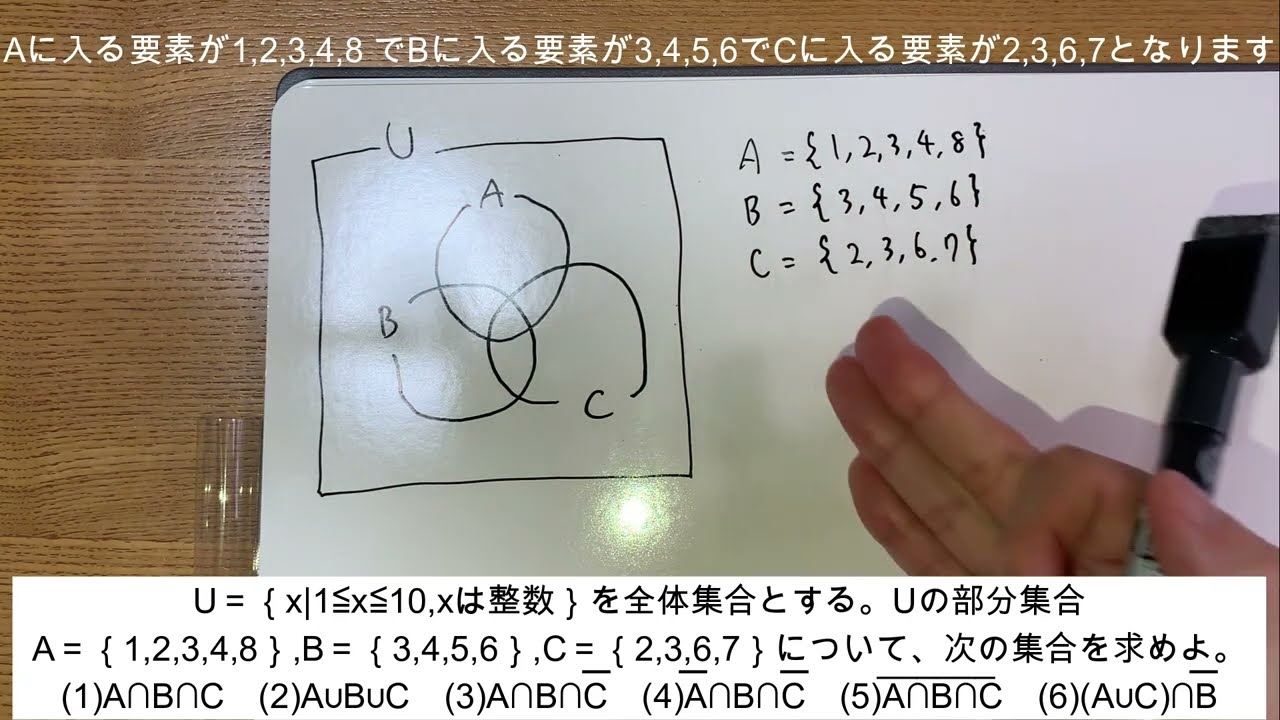
$U=\{x|1≦x≦10、xは整数\}$を全体集合とする。$U$の部分集合
$A=\{1,2,3,4,8\} B=\{3,4,5,6\} C=\{2,3,6,7\}$
について、次の集合を求めよ。
(1)$A∩B∩C$
(2)$A∪B∪C$
(3)$A∩B∩\overline{C}$
(4)$\overline{A}∩B∩\overline{C}$
(5)$\overline{(A∩B∩C)}$
(6)$(A∪C)∩\overline{B}$
$A=\{1,3,3a-2\}$ $B=\{-5、a+2、a^2-2a+1\}$ $A∩B=\{1,4\}$のとき
定数$a$の値と和集合$A∪B$を求めよ。
【数Ⅰ】【数と式】式の展開2 ※問題文は概要欄

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#数と式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
展開せよ
${(a+1)}^3$ ${(x+3y)}^3$
${(2a-1)}^3$ ${(-3a+2b)}^3$
展開せよ
$(a+5)(a^2-5a+25)$ $(3-a)(9+3a+a^2)$
$(2x+y)(4x^2-2xy+y^2)$ $(3a-2b)(9a^2+6ab+4b^2)$
計算せよ
$(x-1)(x-3)(x+1)(x+3)$ $(x+2)(x+5)(x-4)(x-1)$
$(a-b)(a+b)(a+b)(a+b) $ ${(2x-y)}^3{(2x+y)}^3$
${(a+b)}^2{(a-b)}^2{(a+ab+b)}^2{(a-ab+b)}^2$
$(x+2)(x-2)(x^2+2x+4)(x^2-2x+4)$
${(a+b+c)}^2+{(a+b-c)}^2+{(b+c-a)}^2+{(c+a-b)}^2$
この動画を見る
展開せよ
${(a+1)}^3$ ${(x+3y)}^3$
${(2a-1)}^3$ ${(-3a+2b)}^3$
展開せよ
$(a+5)(a^2-5a+25)$ $(3-a)(9+3a+a^2)$
$(2x+y)(4x^2-2xy+y^2)$ $(3a-2b)(9a^2+6ab+4b^2)$
計算せよ
$(x-1)(x-3)(x+1)(x+3)$ $(x+2)(x+5)(x-4)(x-1)$
$(a-b)(a+b)(a+b)(a+b) $ ${(2x-y)}^3{(2x+y)}^3$
${(a+b)}^2{(a-b)}^2{(a+ab+b)}^2{(a-ab+b)}^2$
$(x+2)(x-2)(x^2+2x+4)(x^2-2x+4)$
${(a+b+c)}^2+{(a+b-c)}^2+{(b+c-a)}^2+{(c+a-b)}^2$
【数Ⅰ】【数と式】式の展開1 ※問題文は概要欄

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#数と式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
[ ]内の文字について降べきの順に整理せよ
$ax^2+bx-x^4+ax^2-ab [x]$
$2x^2+y^2-3xy-2y^2+3y+4xy-x^2-2x-5 [y]$
$ax^3+a^2x-2x^2-a^3-3ax^3+4a^3 [a]$
$a^2b+b^3+abc-a^2c-ac^2+bc^2-ab^2+c^3 [a]$
ある多項式から$3x^2-xy+2y^2$を引くところ
を誤って加えたため,答えが$2x^2+xy-y^2$
となった。正しい答えを求めよ
次の式を展開した時の[ ]内の項の係数を
求めよ
$(5a^3-3a^2b+7ab^2-2b^3)(3a^2+2ab-3b^2) [a²b³][a³b²]$
$(x+2y-z)(3x+4y+2z)(-x+y-3z) [xy^2][xyz]$
この動画を見る
[ ]内の文字について降べきの順に整理せよ
$ax^2+bx-x^4+ax^2-ab [x]$
$2x^2+y^2-3xy-2y^2+3y+4xy-x^2-2x-5 [y]$
$ax^3+a^2x-2x^2-a^3-3ax^3+4a^3 [a]$
$a^2b+b^3+abc-a^2c-ac^2+bc^2-ab^2+c^3 [a]$
ある多項式から$3x^2-xy+2y^2$を引くところ
を誤って加えたため,答えが$2x^2+xy-y^2$
となった。正しい答えを求めよ
次の式を展開した時の[ ]内の項の係数を
求めよ
$(5a^3-3a^2b+7ab^2-2b^3)(3a^2+2ab-3b^2) [a²b³][a³b²]$
$(x+2y-z)(3x+4y+2z)(-x+y-3z) [xy^2][xyz]$
【数Ⅰ】【数と式】因数分解4 ※問題文は概要欄

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#数と式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の式を因数分解せよ
(1)$a^2 (b-c)+b^2(c-a)+c^2(a-b)$
(2)$(a+b)(b+c)(c+a)+abc$
次の式を因数分解せよ。
(1)$x^3-5x^2-4x+20$ (2)$8x^3+6x^2+3x+1$
(3)$x^2y+4y^2z-4y^3-x^2z$ (4)$a^4+a^2c-ab^3+abc+b^2c$
この動画を見る
次の式を因数分解せよ
(1)$a^2 (b-c)+b^2(c-a)+c^2(a-b)$
(2)$(a+b)(b+c)(c+a)+abc$
次の式を因数分解せよ。
(1)$x^3-5x^2-4x+20$ (2)$8x^3+6x^2+3x+1$
(3)$x^2y+4y^2z-4y^3-x^2z$ (4)$a^4+a^2c-ab^3+abc+b^2c$
【数Ⅰ】【数と式】因数分解2 ※問題文は概要欄

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#数と式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
因数分解せよ
問1 整理と因数分解
(1) $xy-x-y+1$
(2) $ab+bc-cd-da$
(3) $25-15y+3xy-x^2$
(4) $a^2b+a^2-b-1$
(5) $a^2+b^2+2bc+2ca+2ab$
(6) $2x^2+2xy-3x-4y-2$
問2 たすき掛け
(1) $x^2+(3y+1)x+(y+4)(2y-3)$
(2) $x^2+3xy+2y^2-6x-11y+5$
(3) $x^2-2xy+y^2-x+y-2$
(4) $2x^2+5xy+2y^2+4x-y-6$
(5) $2x^2+xy-y^2+7x-5y-4$
(6) $2x^2+5xy-3y^2-x+11y-6$
この動画を見る
因数分解せよ
問1 整理と因数分解
(1) $xy-x-y+1$
(2) $ab+bc-cd-da$
(3) $25-15y+3xy-x^2$
(4) $a^2b+a^2-b-1$
(5) $a^2+b^2+2bc+2ca+2ab$
(6) $2x^2+2xy-3x-4y-2$
問2 たすき掛け
(1) $x^2+(3y+1)x+(y+4)(2y-3)$
(2) $x^2+3xy+2y^2-6x-11y+5$
(3) $x^2-2xy+y^2-x+y-2$
(4) $2x^2+5xy+2y^2+4x-y-6$
(5) $2x^2+xy-y^2+7x-5y-4$
(6) $2x^2+5xy-3y^2-x+11y-6$
【数Ⅰ】【数と式】因数分解1 ※問題文は概要欄

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#数と式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
因数分解せよ
問1 3次の因数分解①
(1) $8x^3+1$ (2) $64a^3-27$ (3) $27x^3+125y^3$
問2 たすき掛け
(1) $abx^2-(a^2+b^2 )x-ab$ (2) $abx^2+(a^2-b^2 )xy-aby^2$
問3 置き換え
(1) $(x^2-x)^2-14(x^2-x)+24$ (2) $(x^2+2x)(x^2+2x-2)-3$
問4 3次の因数分解②
(1) $x^3+3x^2 y+3xy^2+y^3$ (2) $8a^3-12a^2 b+6ab^2-b^3$
この動画を見る
因数分解せよ
問1 3次の因数分解①
(1) $8x^3+1$ (2) $64a^3-27$ (3) $27x^3+125y^3$
問2 たすき掛け
(1) $abx^2-(a^2+b^2 )x-ab$ (2) $abx^2+(a^2-b^2 )xy-aby^2$
問3 置き換え
(1) $(x^2-x)^2-14(x^2-x)+24$ (2) $(x^2+2x)(x^2+2x-2)-3$
問4 3次の因数分解②
(1) $x^3+3x^2 y+3xy^2+y^3$ (2) $8a^3-12a^2 b+6ab^2-b^3$
【小5算数解説】受験算数 比と割合A3:食塩水を混ぜる 食塩水+食塩水【問題文は概要欄】

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例
指導講師:
理数個別チャンネル
問題文全文(内容文):
6.5%の食塩水500gに、10%の食塩水200gを混ぜると□%の食塩水になります。
この動画を見る
6.5%の食塩水500gに、10%の食塩水200gを混ぜると□%の食塩水になります。




