 高校入試から見た数学の世界「全部入試問題」by しろたん
高校入試から見た数学の世界「全部入試問題」by しろたん
 高校入試から見た数学の世界「全部入試問題」by しろたん
高校入試から見た数学の世界「全部入試問題」by しろたん
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【ソフィー・ジェルマンに感謝して】計算:市川高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#正の数・負の数#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \dfrac{1}{6}\times\dfrac{(4^4+4・3^4)(4^4+4・11^4)(4^4+4・19^4)}{(4^4+4・7^4)(4^4+4・15^4)(4^4+4・23^4)}\times\dfrac{(4^4+4・27^4)(4^4+4・35^4)}{(4^4+4・31^4)(4^4+4・39^4)}$
を計算せよ.
市川高校過去問
この動画を見る
$ \dfrac{1}{6}\times\dfrac{(4^4+4・3^4)(4^4+4・11^4)(4^4+4・19^4)}{(4^4+4・7^4)(4^4+4・15^4)(4^4+4・23^4)}\times\dfrac{(4^4+4・27^4)(4^4+4・35^4)}{(4^4+4・31^4)(4^4+4・39^4)}$
を計算せよ.
市川高校過去問
【一番いいのは考え込まないこと !?】計算:広島大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#正の数・負の数#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ 26\times78\times(-5)^2$を計算せよ.
広大付属高校過去問
この動画を見る
$ 26\times78\times(-5)^2$を計算せよ.
広大付属高校過去問
【得意分野にしよう!】図形:福岡大学附属大濠高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#中3数学#円#三角形と四角形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
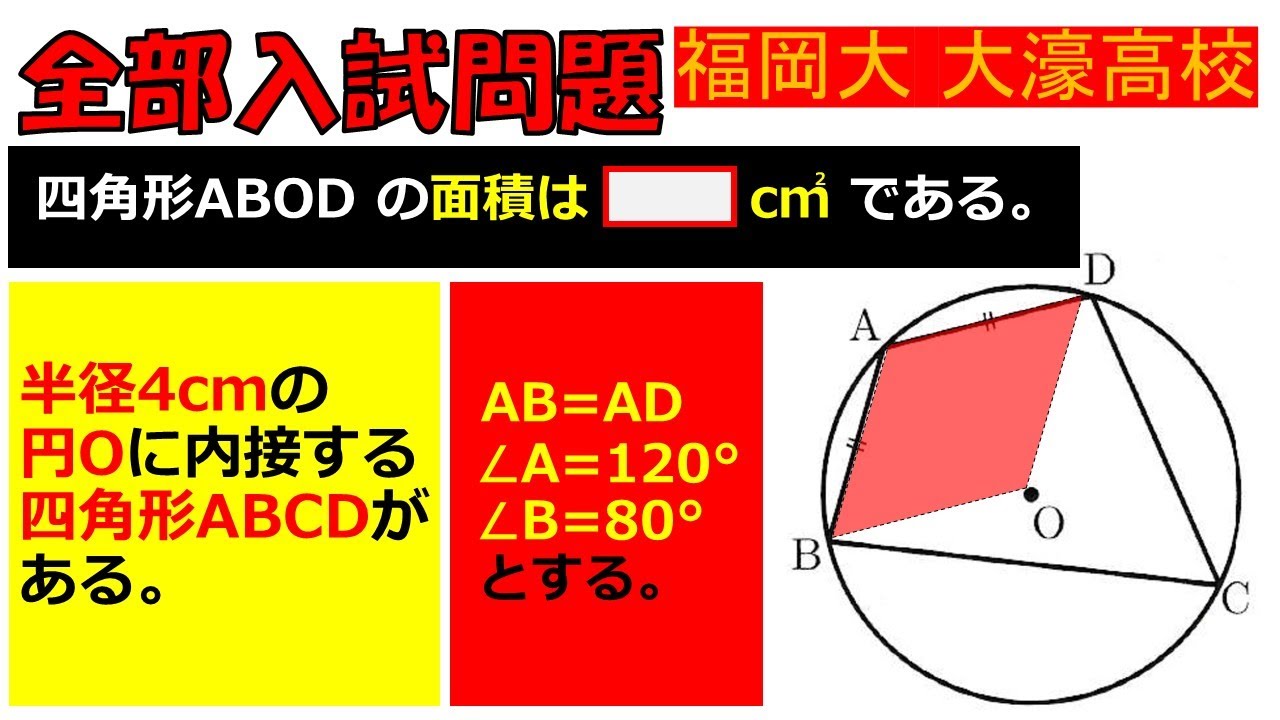
半径4cmの円$O$に内接する四角形$ABCD$がある.
$AB=AD,\angle A=120°,\angle B=80°$とする.
四角形$ABCD$の面積は$\Box cm^2$である.
福岡大学附属大濠高等学校過去問
この動画を見る
半径4cmの円$O$に内接する四角形$ABCD$がある.
$AB=AD,\angle A=120°,\angle B=80°$とする.
四角形$ABCD$の面積は$\Box cm^2$である.
福岡大学附属大濠高等学校過去問
【まず流れを理解しよう!】二次方程式:慶応義塾志木高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x^2-(4t-1)x+4t^2-2t=0$の2解を$\alpha,\beta$とする.
3辺の長さが,$5,\alpha,\beta$である三角形が直角三角形である.
$t$の値を求めよ.
慶応義塾志木高等学校過去問
この動画を見る
$ x^2-(4t-1)x+4t^2-2t=0$の2解を$\alpha,\beta$とする.
3辺の長さが,$5,\alpha,\beta$である三角形が直角三角形である.
$t$の値を求めよ.
慶応義塾志木高等学校過去問
【ケアレスミスをなくすには…!】計算:江戸川学園取手高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#正の数・負の数#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ -144a^4b^2c^3\div(-6a^3b^2c^2)^3\times \left(-\dfrac{3}{2}a^3b^2c\right)^2$を計算しなさい.
江戸川取手高校過去問
この動画を見る
$ -144a^4b^2c^3\div(-6a^3b^2c^2)^3\times \left(-\dfrac{3}{2}a^3b^2c\right)^2$を計算しなさい.
江戸川取手高校過去問
【ひとまず解答してみよう…!】整数:慶応義塾高等学校~全国入試問題解法

単元:
#数学(中学生)#整数の性質#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2つの自然数$m,n$は$2^m-1=(2n+1)(2n+3)$を満たす.
$m=6$のとき,$n$の値を求めよ.
慶應義塾高校過去問
この動画を見る
2つの自然数$m,n$は$2^m-1=(2n+1)(2n+3)$を満たす.
$m=6$のとき,$n$の値を求めよ.
慶應義塾高校過去問
【理解すれば素早く解ける!】関数:和洋国府台女子高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#1次関数#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
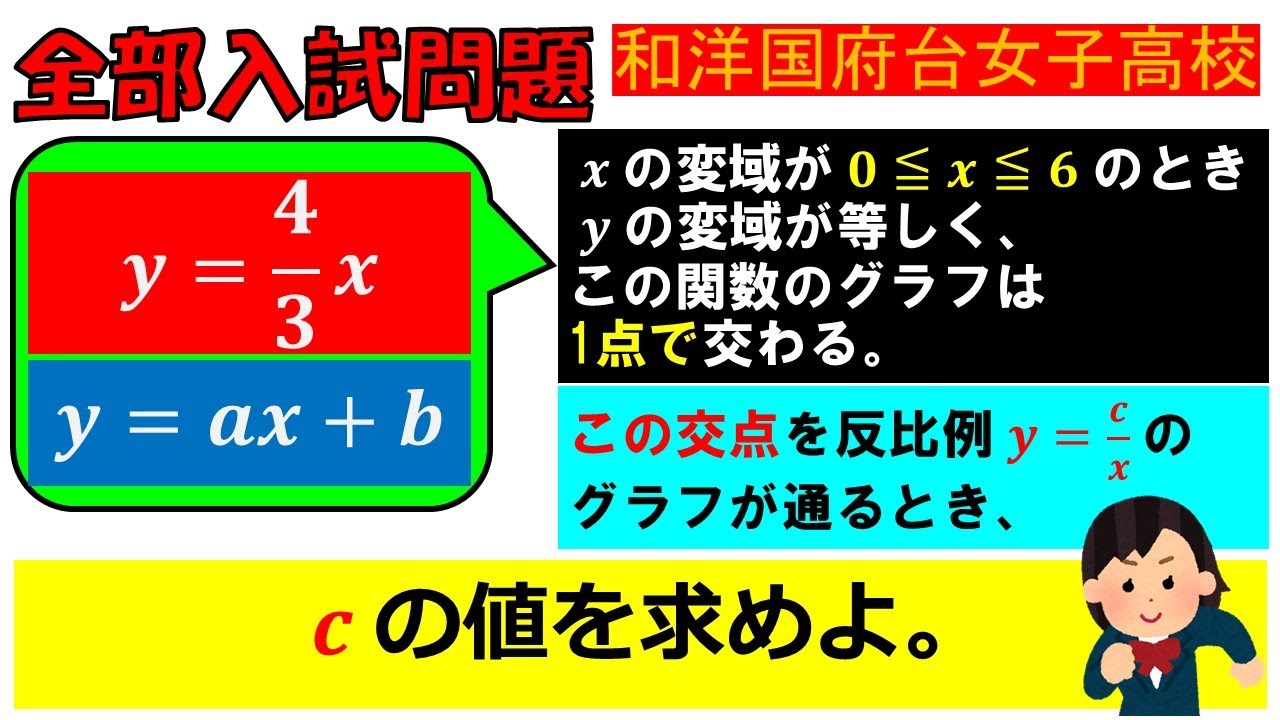
$x$の変域が$0\leqq x\leqq 6$のとき,$y$の変域が等しく,この関数のグラフは1点で交わる.
この交点を反比例$y=\dfrac{c}{x}$のグラフが通るとき,$c$の値を求めよ.
和洋国府台女子高校過去問
この動画を見る
$x$の変域が$0\leqq x\leqq 6$のとき,$y$の変域が等しく,この関数のグラフは1点で交わる.
この交点を反比例$y=\dfrac{c}{x}$のグラフが通るとき,$c$の値を求めよ.
和洋国府台女子高校過去問
難しそうでいて簡単にできそうだけどやっぱり難しい数学~全国入試問題解法 #Shorts #数学 #sound #高校受験

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ (x+1)(x+2)(x+3)(x+4)=x^4+10x^3+9$を解け.
この動画を見る
$ (x+1)(x+2)(x+3)(x+4)=x^4+10x^3+9$を解け.
【見慣れないから出題される!】方程式:明治学院高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
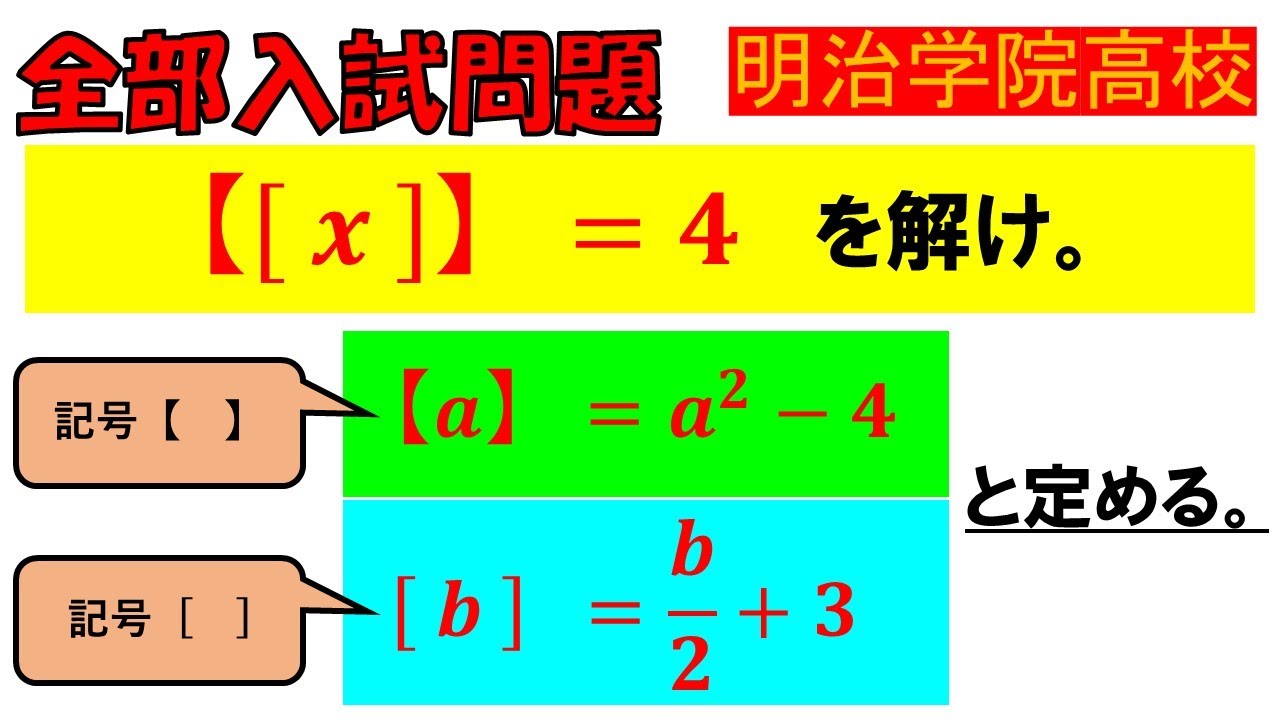
$【[a]】=a^2-4$,$[b]=\dfrac{b}{2}+3$と定める.
$【[x]】=4$を解け.
明治学院高校過去問
この動画を見る
$【[a]】=a^2-4$,$[b]=\dfrac{b}{2}+3$と定める.
$【[x]】=4$を解け.
明治学院高校過去問
【比べてみれば!】因数分解:明治学院高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \dfrac{1}{6}x^2-ax-18$を因数分解すると$\dfrac{1}{6}(x-12)(x+b)$となる.
$a,b$の値を求めよ.
明治学院高校過去問
この動画を見る
$ \dfrac{1}{6}x^2-ax-18$を因数分解すると$\dfrac{1}{6}(x-12)(x+b)$となる.
$a,b$の値を求めよ.
明治学院高校過去問
【条件から導き出されることは…!】整数:灘高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#整数の性質#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$x$を$x-n+a$と表す.
$ x^2+a^2=8$のとき,$n=\Box,x=\Box$である.
灘高校過去問
この動画を見る
$x$を$x-n+a$と表す.
$ x^2+a^2=8$のとき,$n=\Box,x=\Box$である.
灘高校過去問
【分数…同じ部分…!】連立方程式:日本大学第三高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{2x+4}{3}+\dfrac{y+1}{2}=1 \\
2x+4-\dfrac{y+1}{6}=-\dfrac{1}{3}
\end{array}
\right.
\end{eqnarray}$
を解きなさい.
日大第三高校過去問
この動画を見る
連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{2x+4}{3}+\dfrac{y+1}{2}=1 \\
2x+4-\dfrac{y+1}{6}=-\dfrac{1}{3}
\end{array}
\right.
\end{eqnarray}$
を解きなさい.
日大第三高校過去問
【「分かる」と「知ってる」は違う…!】文字式:立命館高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
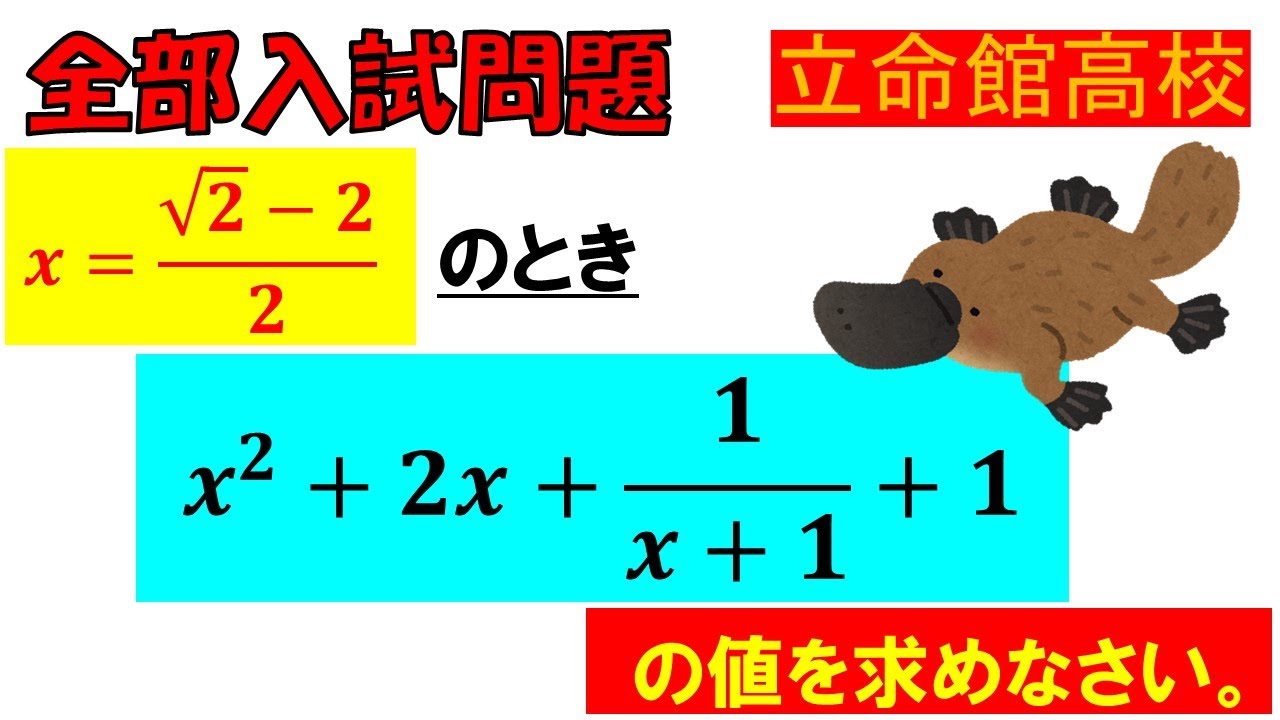
$ x=\dfrac{\sqrt2-2}{2}$のとき,$x^2+2x+\dfrac{1}{x+1}+1$の値を求めなさい.
立命館高校過去問
この動画を見る
$ x=\dfrac{\sqrt2-2}{2}$のとき,$x^2+2x+\dfrac{1}{x+1}+1$の値を求めなさい.
立命館高校過去問
【その解法は「美しい」か !?】確率:同志社高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
7つの区画に色を塗る.隣り合う区画には異なる色を塗る.
同じ色は何度用いてもよい.赤,青,黄,緑の4色をすべて用いる.
色分けの方法は,それぞれ何通りあるか.
同志社高校過去問
この動画を見る
7つの区画に色を塗る.隣り合う区画には異なる色を塗る.
同じ色は何度用いてもよい.赤,青,黄,緑の4色をすべて用いる.
色分けの方法は,それぞれ何通りあるか.
同志社高校過去問
【当たって砕けろ!】連立方程式:法政大学第二高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
解の比$x:y$を最も簡単な整数の比で答えなさい.
連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
37x-53y=2 \\
17x-19y=1
\end{array}
\right.
\end{eqnarray}$
法政大第二高校過去問
この動画を見る
解の比$x:y$を最も簡単な整数の比で答えなさい.
連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
37x-53y=2 \\
17x-19y=1
\end{array}
\right.
\end{eqnarray}$
法政大第二高校過去問
【この考え方が役に立つ!】図形:東京工業大学附属科学技術高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#平面図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
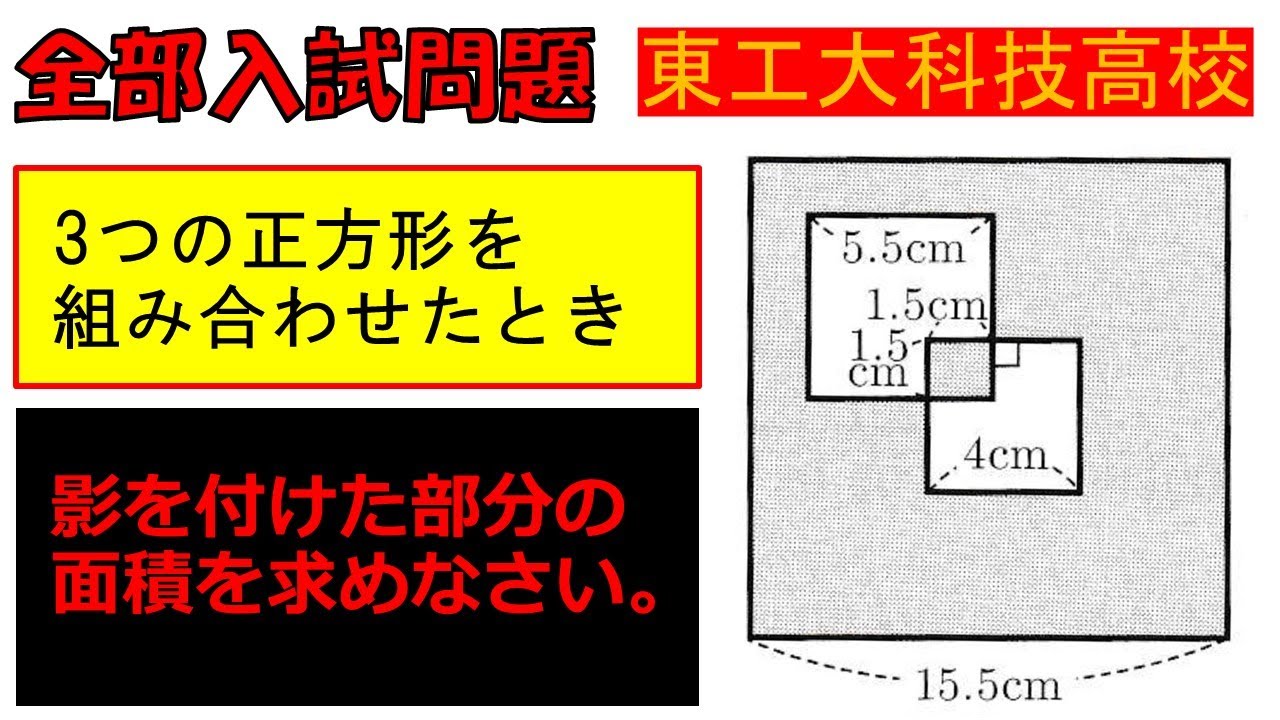
3つの正方形を組み合わせたとき,影を付けた部分の面積を求めなさい.
東工大科技高校過去問
この動画を見る
3つの正方形を組み合わせたとき,影を付けた部分の面積を求めなさい.
東工大科技高校過去問
【いかに論理的に説明するか…!】整数:法政大学高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#整数の性質#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$n$を8で割ったときの余り$r$について$n=7r$が成り立つ.
$n$の値を求めなさい.
法政大高校過去問
この動画を見る
$n$を8で割ったときの余り$r$について$n=7r$が成り立つ.
$n$の値を求めなさい.
法政大高校過去問
【解を代入しても式は1つだけ…!】二次方程式:立命館高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2次方程式$ax^2+2x+b=0$の解が$x=2$のただ1つである.
定数$a,b$の値をそれぞれ求めなさい.
立命館高校過去問
この動画を見る
2次方程式$ax^2+2x+b=0$の解が$x=2$のただ1つである.
定数$a,b$の値をそれぞれ求めなさい.
立命館高校過去問
30秒でまとめた高校入試の必出問題!~全国入試問題解法 #Shorts #sound #mathematics #数学

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
(1)$y-\dfrac{1}{4}x^2$について,$A→B:$変化の割合は?
(2)直線$CD$の式は?
この動画を見る
(1)$y-\dfrac{1}{4}x^2$について,$A→B:$変化の割合は?
(2)直線$CD$の式は?
【考え込むより、まず手を付けよう!】平方根:桐蔭学園高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の$\Box$に最も適する数字を答えよ.
${(\sqrt3+\sqrt2)^2-(\sqrt3-\sqrt2)^2}^2=\Box$である.
桐蔭学園高等学校
この動画を見る
次の$\Box$に最も適する数字を答えよ.
${(\sqrt3+\sqrt2)^2-(\sqrt3-\sqrt2)^2}^2=\Box$である.
桐蔭学園高等学校
30秒にまとめた多分野にまたがる入試問題~全国入試問題解法 #Shorts #数学 #高校受験 #sound
単元:
#数学(中学生)#中2数学#中3数学#式の計算(展開、因数分解)#確率#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$c$のとりうる値は何通りあるか.
$(x+a)(x+b)$
を展開すると
$x^2+cx+12$
となる.
中大杉並高校過去問
この動画を見る
$c$のとりうる値は何通りあるか.
$(x+a)(x+b)$
を展開すると
$x^2+cx+12$
となる.
中大杉並高校過去問
【困難は分解せよ!】平方根:桐朋高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\dfrac{(\sqrt{14}-\sqrt6)(\sqrt7+\sqrt3)}{2}-(\sqrt2+1)^2$を計算せよ.
桐朋高校過去問
この動画を見る
$\dfrac{(\sqrt{14}-\sqrt6)(\sqrt7+\sqrt3)}{2}-(\sqrt2+1)^2$を計算せよ.
桐朋高校過去問
【一度解けば忘れない解法!】空間図形:東海大学附属浦安高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#空間図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
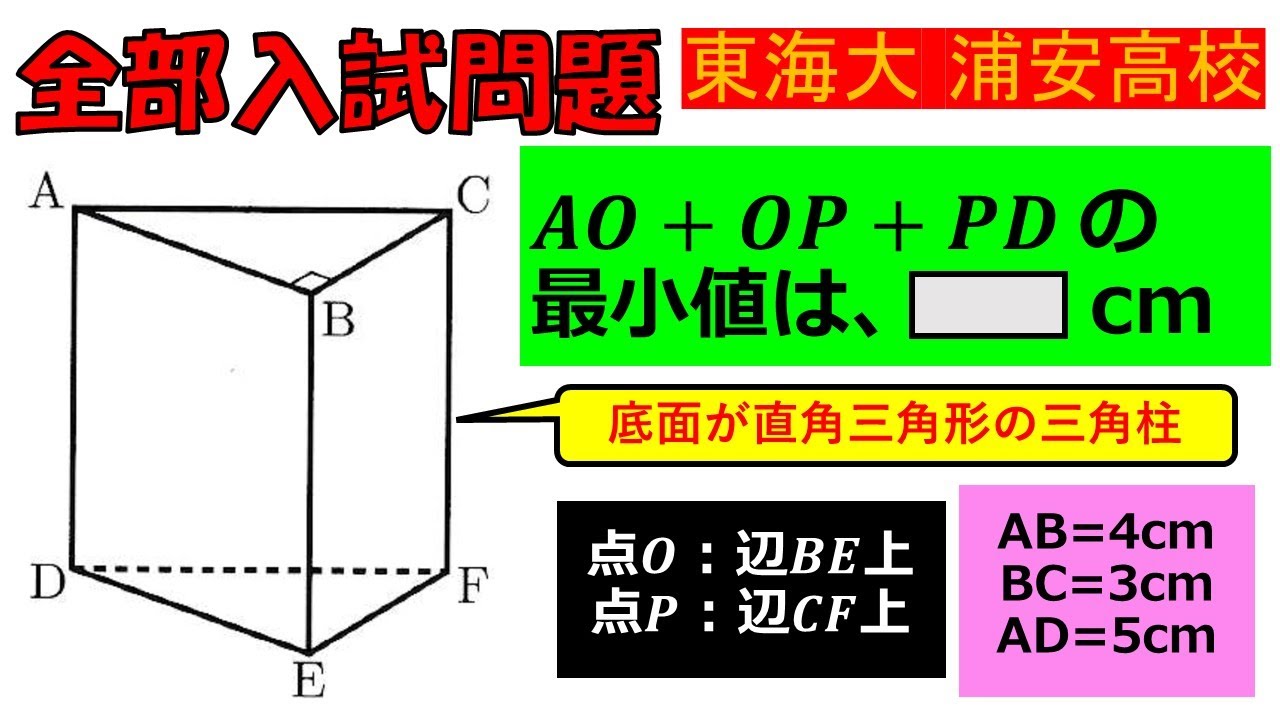
底面が直角三角形の三角柱の$AO+OP+PD$の最小値は,$\Box$cmである.
東海大浦安高校過去問
この動画を見る
底面が直角三角形の三角柱の$AO+OP+PD$の最小値は,$\Box$cmである.
東海大浦安高校過去問
【手がかりを順番に探れ!】二次方程式:日本大学第二高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$x^2-ax+3=0$の解の1つは$x^2-4x+12=0$の小さい方の解に1を加えたものと等しい.
$a$の値を求めよ.
日大第二高校過去問
この動画を見る
$x^2-ax+3=0$の解の1つは$x^2-4x+12=0$の小さい方の解に1を加えたものと等しい.
$a$の値を求めよ.
日大第二高校過去問
【考えて解くか、解きながら考えるか…】計算:大阪教育大学附属高等学校平野校舎~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の計算をし,$\Box$に当てはまる数を答えなさい.
$340^2-337^2-3^2=\Box$
大教大付属高校平野過去問
この動画を見る
次の計算をし,$\Box$に当てはまる数を答えなさい.
$340^2-337^2-3^2=\Box$
大教大付属高校平野過去問
【直前にもう一度見なおしたい!】文章題:専修大学附属高等学校~全国入試問題解法
単元:
#数学(中学生)#文章題#売買損益と食塩水#文章題その他#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
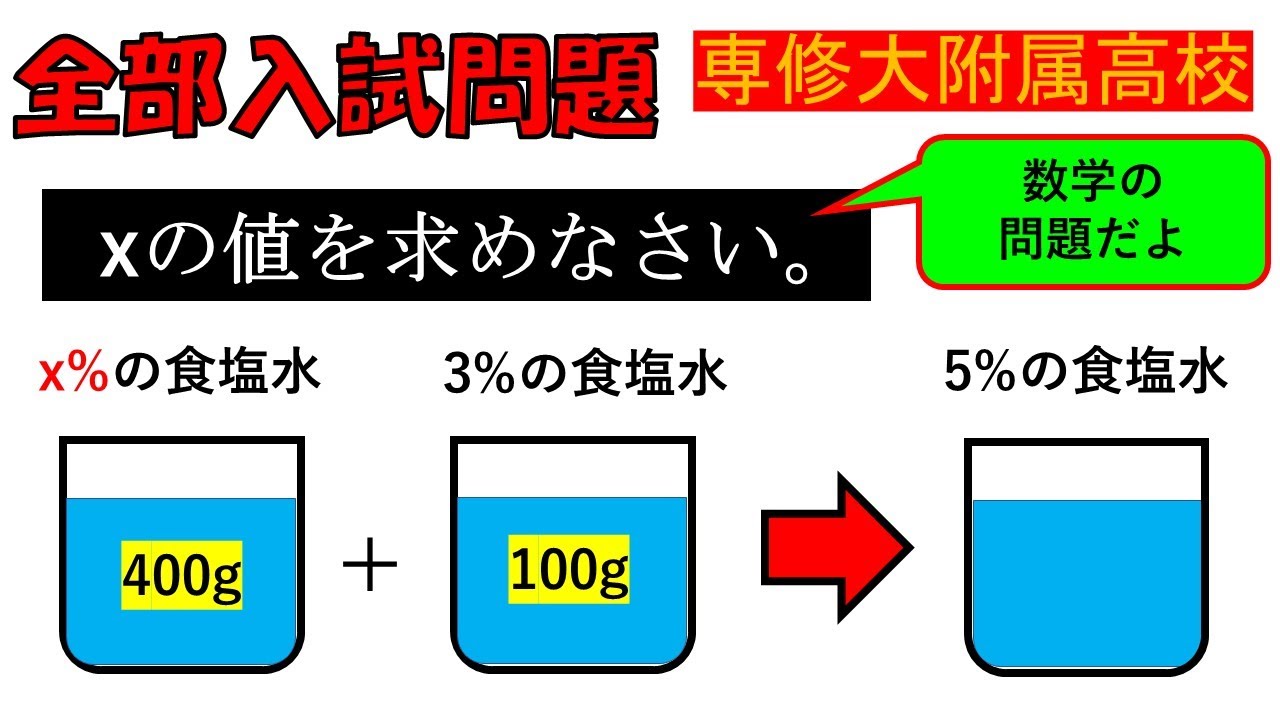
$A$の容器に$x$%の食塩水が400g入っている.
$A$の容器に$3$%の食塩水を100g加え,よくかき混ぜたところ,
$A$の容器の食塩水は$5$%となった.
$x$の値を求めなさい.
専修大学附属高等学校過去問
この動画を見る
$A$の容器に$x$%の食塩水が400g入っている.
$A$の容器に$3$%の食塩水を100g加え,よくかき混ぜたところ,
$A$の容器の食塩水は$5$%となった.
$x$の値を求めなさい.
専修大学附属高等学校過去問
難しい空間図形を解きながら音楽を聞く動画~全国入試問題解法 #Shorts #数学 #高校入試
単元:
#数学(中学生)#中1数学#空間図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
立方体$ABCD-EFGH$は1辺6cmであり,
点$P$は辺$AB$の中点であり,点$O$は辺$AD$の中点である.
この立体を平面$TPHQ$で切ったとき,
$APQ-EFH$の体積を求めなさい.
函館ラサール高校過去問
この動画を見る
立方体$ABCD-EFGH$は1辺6cmであり,
点$P$は辺$AB$の中点であり,点$O$は辺$AD$の中点である.
この立体を平面$TPHQ$で切ったとき,
$APQ-EFH$の体積を求めなさい.
函館ラサール高校過去問
【3分で問題との付き合い方を学ぶ】:中央大学杉並高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$(x+a)(x+b)$を展開すると$x^2+cx+12$となる.
$c$のとりうる値は何通りあるか.
中大杉並高校過去問
この動画を見る
$(x+a)(x+b)$を展開すると$x^2+cx+12$となる.
$c$のとりうる値は何通りあるか.
中大杉並高校過去問
難しい連立方程式だけど音楽が気になる動画~全国入試問題解法 #Shorts #数学 #sound
単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
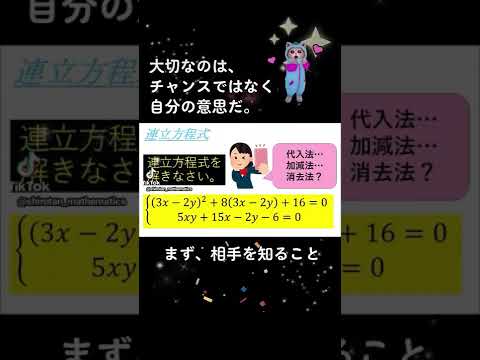
$\begin{eqnarray}
\left\{
\begin{array}{l}
(3x-2y)^2+8(3x-2y)+16=0 \\
5xy+15x-2y-6=0
\end{array}
\right.
\end{eqnarray}$
連立方程式を解きなさい.
渋谷教育幕張高校過去問
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
(3x-2y)^2+8(3x-2y)+16=0 \\
5xy+15x-2y-6=0
\end{array}
\right.
\end{eqnarray}$
連立方程式を解きなさい.
渋谷教育幕張高校過去問
確率の問題は解法が複数存在する30秒~全国入試問題解法 #Shorts #数学 #確率
単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
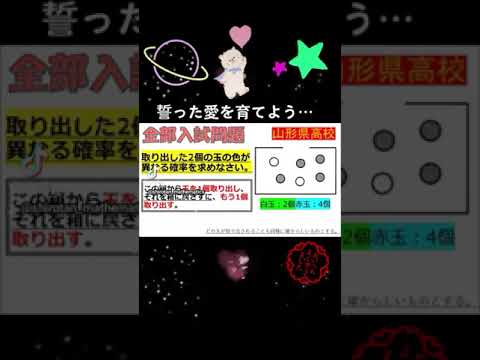
この箱から玉を1個取り出し,それを箱に戻さずに,もう1個取り出す.
取り出した2個の玉の色が異なる確率を求めない.
山形県高校過去問
この動画を見る
この箱から玉を1個取り出し,それを箱に戻さずに,もう1個取り出す.
取り出した2個の玉の色が異なる確率を求めない.
山形県高校過去問



