 高校入試から見た数学の世界「全部入試問題」by しろたん
高校入試から見た数学の世界「全部入試問題」by しろたん
 高校入試から見た数学の世界「全部入試問題」by しろたん
高校入試から見た数学の世界「全部入試問題」by しろたん
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【有理数とは!】平方根(有理数と無理数)前編:教科書順で内容確認~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
平方根(有理数と無理数)に関して解説していきます.
この動画を見る
平方根(有理数と無理数)に関して解説していきます.
【ケアレスミスを減らすために】文字式:江戸川学園取手高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\dfrac{a-5b+2}{5}-\dfrac{4a-3b-2}{3}+2a-1$を計算しなさい.
江戸川学園取手高等学校過去問
この動画を見る
$\dfrac{a-5b+2}{5}-\dfrac{4a-3b-2}{3}+2a-1$を計算しなさい.
江戸川学園取手高等学校過去問
【「分かったつもり」が命取り!】文字式:大阪星光学院高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
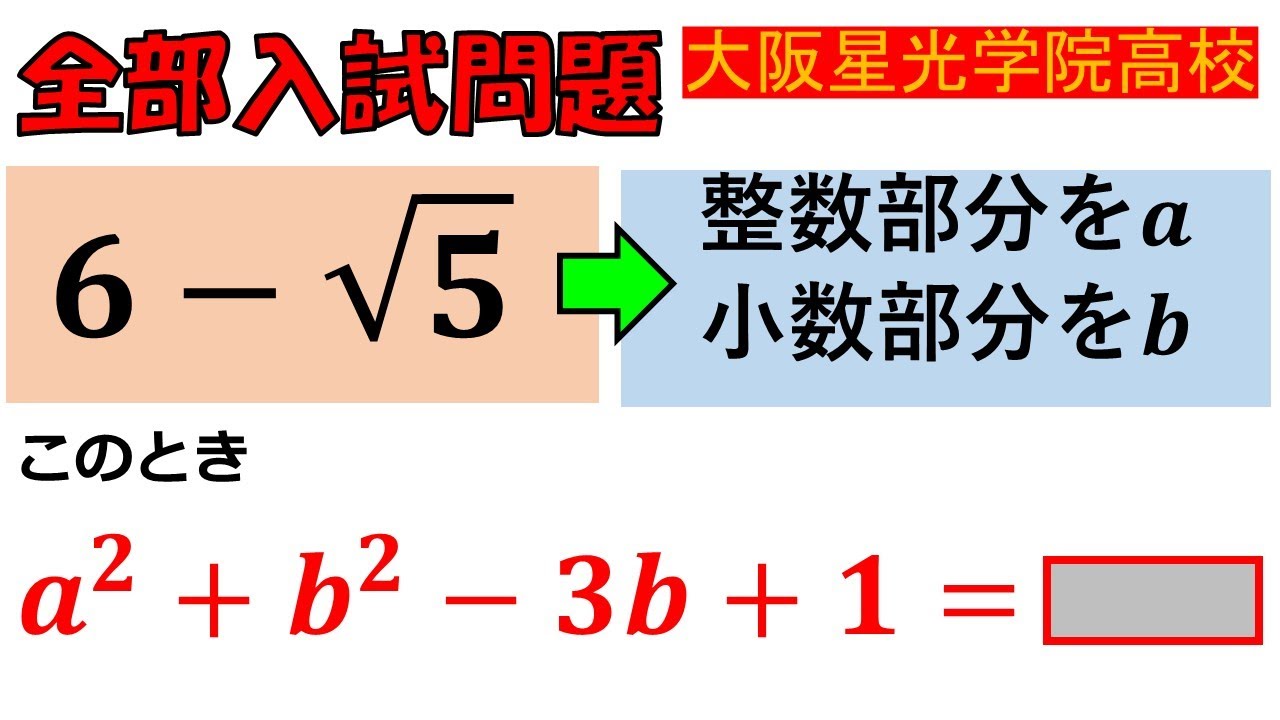
$6-\sqrt5$の整数部分を$a$とし,小数部分を$b$とする.
このとき,$a^2+b^2-3b+1=\Box$である.$\Box$の値を求めよ.
大阪星光学院高等学校過去問
この動画を見る
$6-\sqrt5$の整数部分を$a$とし,小数部分を$b$とする.
このとき,$a^2+b^2-3b+1=\Box$である.$\Box$の値を求めよ.
大阪星光学院高等学校過去問
【ただ一つ言えることは…】連立方程式:城北高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
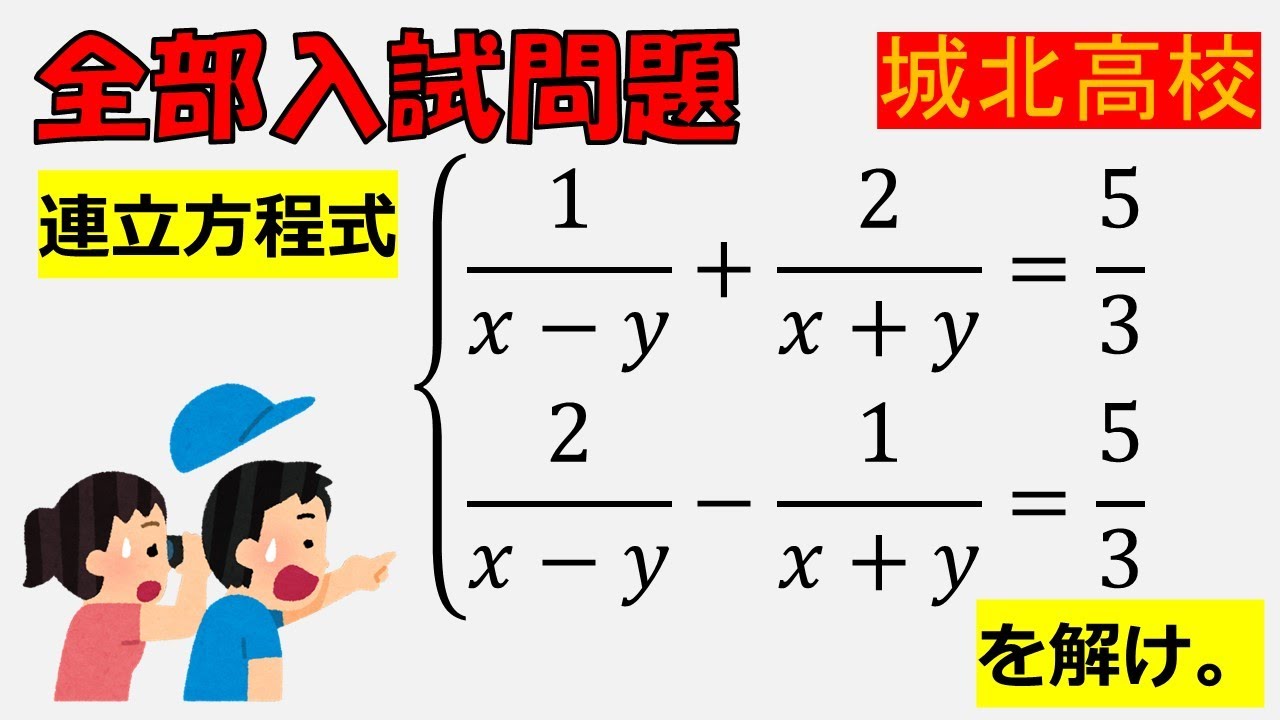
連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{1}{x-y}+\dfrac{2}{x+y}=\dfrac{5}{3} \\
\dfrac{2}{x-y}-\dfrac{1}{x+y}=\dfrac{5}{3}
\end{array}
\right.
\end{eqnarray}$
を解け.
城北高校過去問
この動画を見る
連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{1}{x-y}+\dfrac{2}{x+y}=\dfrac{5}{3} \\
\dfrac{2}{x-y}-\dfrac{1}{x+y}=\dfrac{5}{3}
\end{array}
\right.
\end{eqnarray}$
を解け.
城北高校過去問
【その場で「考える力」を身に付ける!】整数:大阪星光学院高等学校~全国入試問題解法

単元:
#数学(中学生)#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2数$a,b$の最大公約数を$[a\odot b]$と表すと・・・
$[1\odot 2]+[2\odot 3]+[3\odot 4]+・・・+[100\odot 101]=\Box$であり,
$[1\odot 3]+[2\odot 4]+[3\dot 5]+・・・+[99\odot 101]+[100\odot 102]=\box$である.
大阪星光高校過去問
この動画を見る
2数$a,b$の最大公約数を$[a\odot b]$と表すと・・・
$[1\odot 2]+[2\odot 3]+[3\odot 4]+・・・+[100\odot 101]=\Box$であり,
$[1\odot 3]+[2\odot 4]+[3\dot 5]+・・・+[99\odot 101]+[100\odot 102]=\box$である.
大阪星光高校過去問
【この形!どの形?】平方根:渋谷教育学園幕張高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
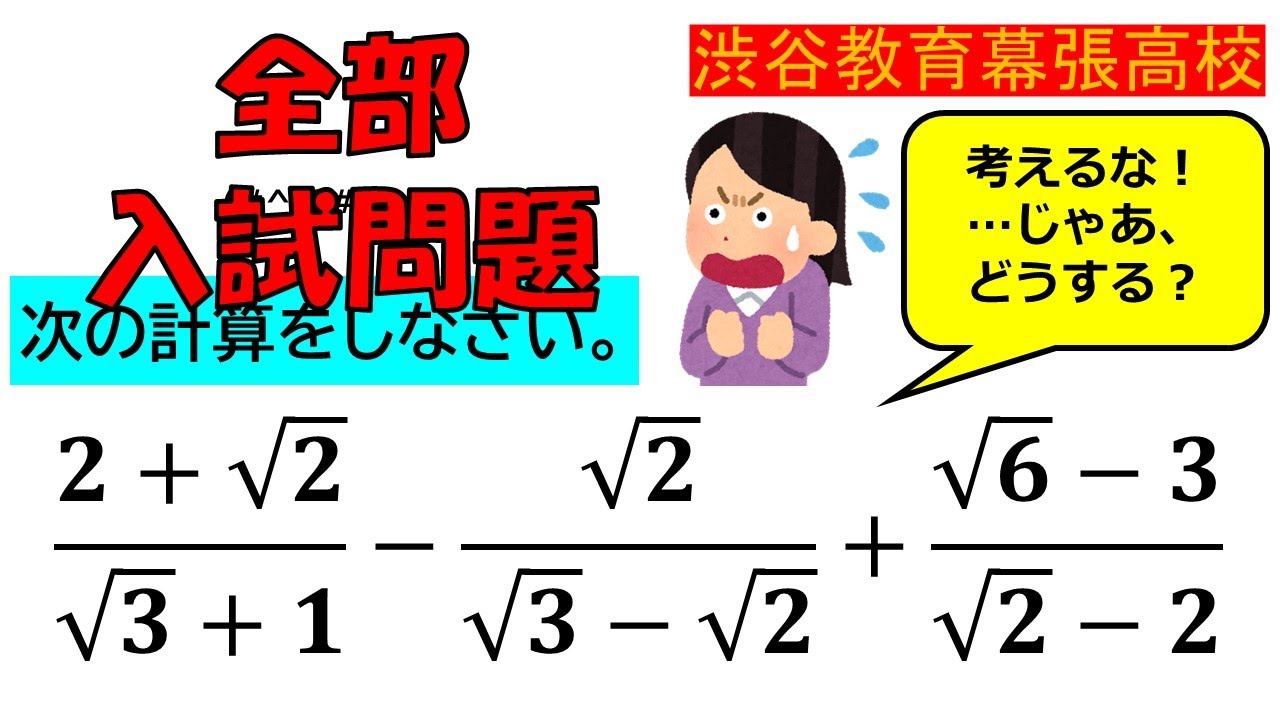
次の計算をしなさい.
$\dfrac{2+\sqrt2}{\sqrt3+1}-\dfrac{\sqrt2}{\sqrt3-\sqrt2}+\dfrac{\sqrt6-3}{\sqrt2-2}$
渋谷教育学園幕張高等学校過去問
この動画を見る
次の計算をしなさい.
$\dfrac{2+\sqrt2}{\sqrt3+1}-\dfrac{\sqrt2}{\sqrt3-\sqrt2}+\dfrac{\sqrt6-3}{\sqrt2-2}$
渋谷教育学園幕張高等学校過去問
数学を動体視力を用いて学ぶツインテール~全国入試問題解法 #Shorts

単元:
#数学(中学生)#中3数学#円
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
点$A,B,C$は,円$O$の円周上の点である.
$\angle x$の大きさを求めなさい.
長野県高校過去問
この動画を見る
点$A,B,C$は,円$O$の円周上の点である.
$\angle x$の大きさを求めなさい.
長野県高校過去問
【一度は解きたい!典型問題!】図形:埼玉県高等学校~全国入試問題解法
単元:
#数学(中学生)#平面図形#平面図形その他#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
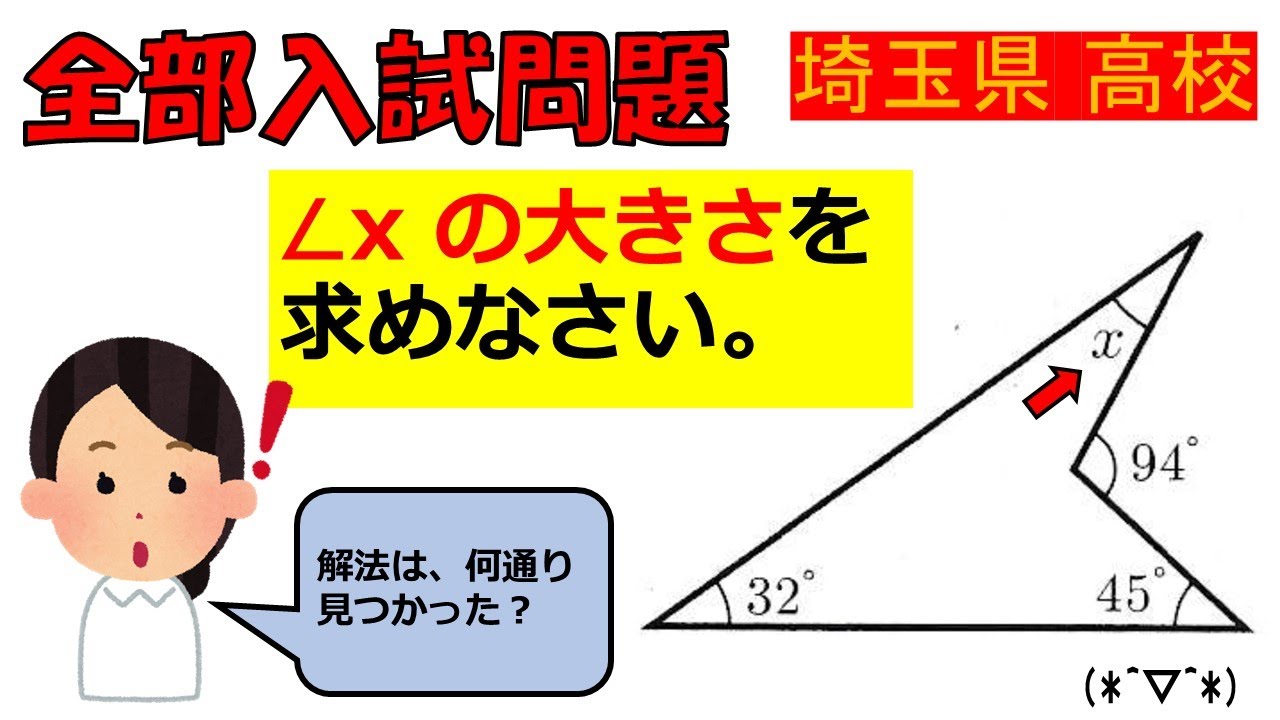
$\angle x$の大きさを求めなさい.
埼玉県高校過去問
この動画を見る
$\angle x$の大きさを求めなさい.
埼玉県高校過去問
【条件を数式に変えよ!】整数:新潟県高等学校~全国入試問題解法

単元:
#数学(中学生)#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
この2つの自然数の積は,この2つの自然数の和より55大きい.
連続する2つの自然数を求めなさい.
新潟県高校過去問
この動画を見る
この2つの自然数の積は,この2つの自然数の和より55大きい.
連続する2つの自然数を求めなさい.
新潟県高校過去問
【1分30秒で大切なものが見える!】図形:新潟県高等学校~全国入試問題解法
単元:
#数学(中学生)#平面図形#平面図形その他#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
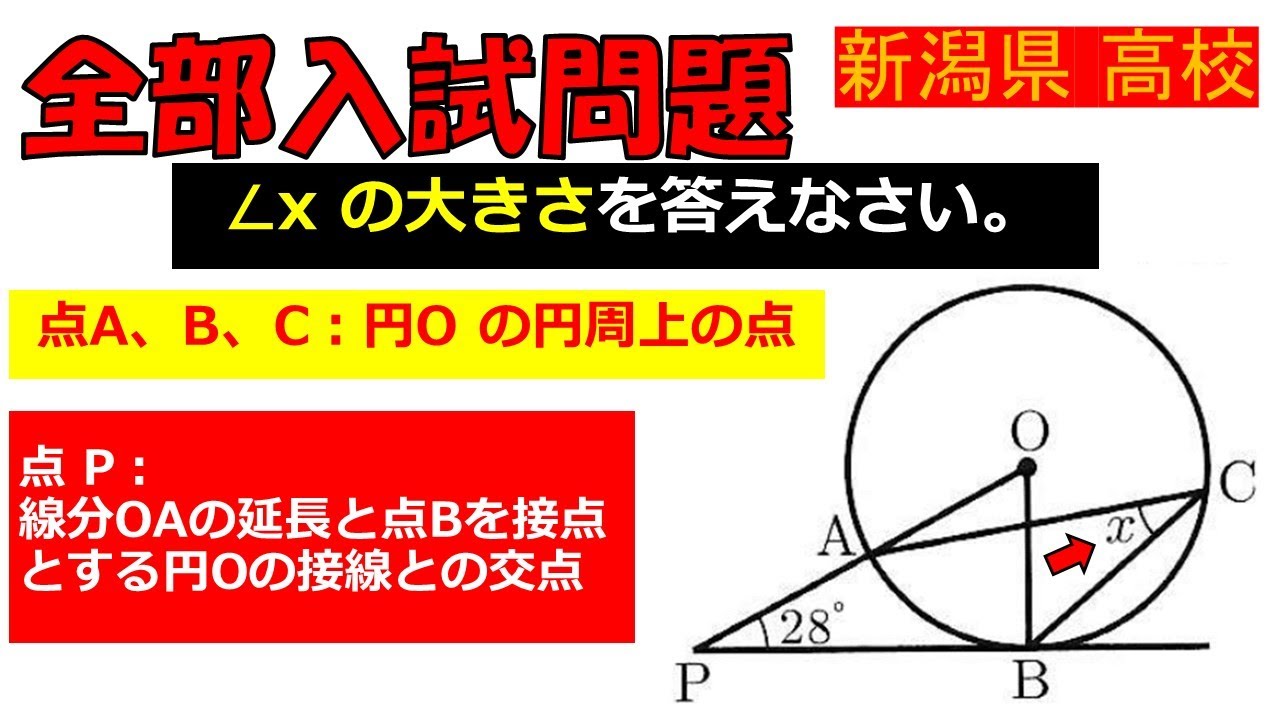
点$A,B,C$は円$O$の円周上の点であり,
点$P$は線分$OA$の延長と点$B$を接点とする円$O$の接線との交点である.
$\angle x$の大きさを求めなさい.
新潟県高校過去問
この動画を見る
点$A,B,C$は円$O$の円周上の点であり,
点$P$は線分$OA$の延長と点$B$を接点とする円$O$の接線との交点である.
$\angle x$の大きさを求めなさい.
新潟県高校過去問
話題の三角関数で加法定理を回転変換して解く~全国入試問題解法 #Shorts

単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
三角関数で加法定理を回転変換して解く解き方に関して解説していきます.
この動画を見る
三角関数で加法定理を回転変換して解く解き方に関して解説していきます.
【簡潔に予習・復習!】平方根(意味と計算):教科書順で内容確認~全国入試問題解法

【高校生になると見方が変わる!】二次方程式:東京都立国立高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の二次方程式を解け.
$2\left(x-\dfrac{1}{4}\right)^2-3=x^2+\dfrac{1}{8}$
都立国立高校過去問
この動画を見る
次の二次方程式を解け.
$2\left(x-\dfrac{1}{4}\right)^2-3=x^2+\dfrac{1}{8}$
都立国立高校過去問
【基礎力は身に付いているのか】計算:和洋国府台女子高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の式を計算せよ.
$\left(\dfrac{1}{3}-\dfrac{1}{2}\right)\div \left(-\dfrac{2^2}{5}+\dfrac{1}{2}\right)$
和洋国府台女子高等学校過去問
この動画を見る
次の式を計算せよ.
$\left(\dfrac{1}{3}-\dfrac{1}{2}\right)\div \left(-\dfrac{2^2}{5}+\dfrac{1}{2}\right)$
和洋国府台女子高等学校過去問
【3分で好きになる!】連立方程式:近畿大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 近畿大学附属高等学校
aの値を求めよ。
【連立方程式】
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x + y = 5a-13 \\
3x - 2y = -2a+1
\end{array}
\right.
\end{eqnarray}$
の解は、$y$が$x$の$2$倍になっている。
この動画を見る
入試問題 近畿大学附属高等学校
aの値を求めよ。
【連立方程式】
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x + y = 5a-13 \\
3x - 2y = -2a+1
\end{array}
\right.
\end{eqnarray}$
の解は、$y$が$x$の$2$倍になっている。
【3分で理解を深める!】二次方程式:東京都立新宿高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
二次方程式$(x+2)(x-3)=(2x+4)(3x-5)$を解け.
都立新宿高校過去問
この動画を見る
二次方程式$(x+2)(x-3)=(2x+4)(3x-5)$を解け.
都立新宿高校過去問
【方針が立っても完答は…!】連立方程式:東京学芸大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$x,y$についての連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
2ax-7y=236 \\
x+2y=\dfrac{a}{7}
\end{array}
\right.
\end{eqnarray}$
の解が$x=3,y=b$である.
このとき,定数$a,b$の値を求めなさい.
東京学芸大高校過去問
この動画を見る
$x,y$についての連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
2ax-7y=236 \\
x+2y=\dfrac{a}{7}
\end{array}
\right.
\end{eqnarray}$
の解が$x=3,y=b$である.
このとき,定数$a,b$の値を求めなさい.
東京学芸大高校過去問
【時間内で楽しむのも数学!】二次方程式:お茶の水女子大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の方程式を解きなさい.
$\dfrac{2}{5}x^2+\dfrac{1}{10}x=\dfrac{3}{4}$
お茶の水附属高校過去問
この動画を見る
次の方程式を解きなさい.
$\dfrac{2}{5}x^2+\dfrac{1}{10}x=\dfrac{3}{4}$
お茶の水附属高校過去問
【正解するのが一番の目的!】平方根:東京都立八王子東高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\left(\dfrac{\sqrt6+2}{\sqrt2}\right)\left(\dfrac{\sqrt2-\sqrt3}{3}\right)$を計算せよ.
都立八王子東高校過去問
この動画を見る
$\left(\dfrac{\sqrt6+2}{\sqrt2}\right)\left(\dfrac{\sqrt2-\sqrt3}{3}\right)$を計算せよ.
都立八王子東高校過去問
【簡潔に予習・復習!】多項式(式の利用):教科書順で内容確認~全国入試問題解法

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
多項式に関して解説していきます.
この動画を見る
多項式に関して解説していきます.
【まずは理解優先!必ず解ける!】図形:鎌倉学園高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#中3数学#円#平面図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
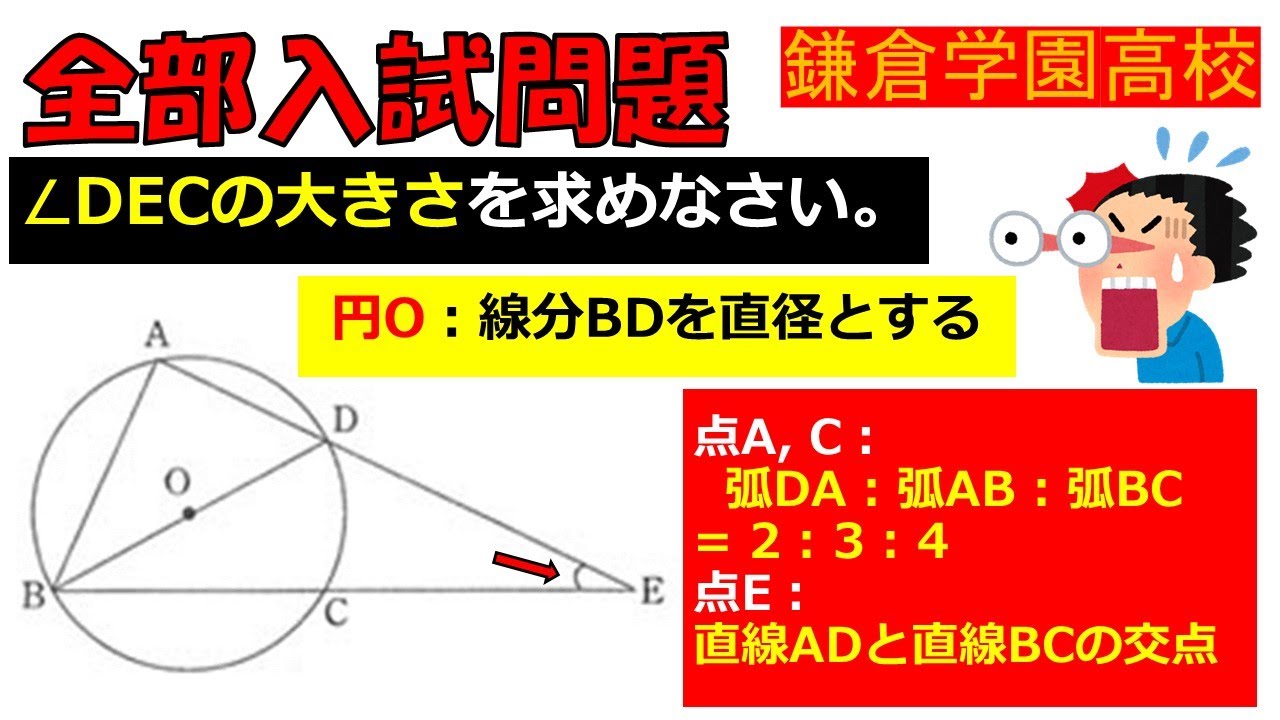
円$O$の線分$BD$を直径とする.
$\angle DEC$の大きさを求めなさい.
鎌倉学園高校過去問
この動画を見る
円$O$の線分$BD$を直径とする.
$\angle DEC$の大きさを求めなさい.
鎌倉学園高校過去問
【簡潔に予習・復習!】多項式(後編):式の展開と因数分解~全国入試問題解法

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
多項式に関して解説していきます.
この動画を見る
多項式に関して解説していきます.
動体視力でイメージする数学と音楽の世界~全国入試問題解法 #Shorts #math

単元:
#数学(中学生)#中3数学#2次方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$a\star b=a^2-b^2+2ab$と定める.
$x\star(x+4)=0$を解きなさい.
立命館高校過去問
この動画を見る
$a\star b=a^2-b^2+2ab$と定める.
$x\star(x+4)=0$を解きなさい.
立命館高校過去問
【簡潔に予習・復習!】多項式(前編):教科書順で内容確認~全国入試問題解法

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
多項式に関して解説していきます.
この動画を見る
多項式に関して解説していきます.
【道は一筋なり!】文章題:明治学院東村山高等学校~全国入試問題解法
単元:
#数学(中学生)#文章題#売買損益と食塩水#文章題その他#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
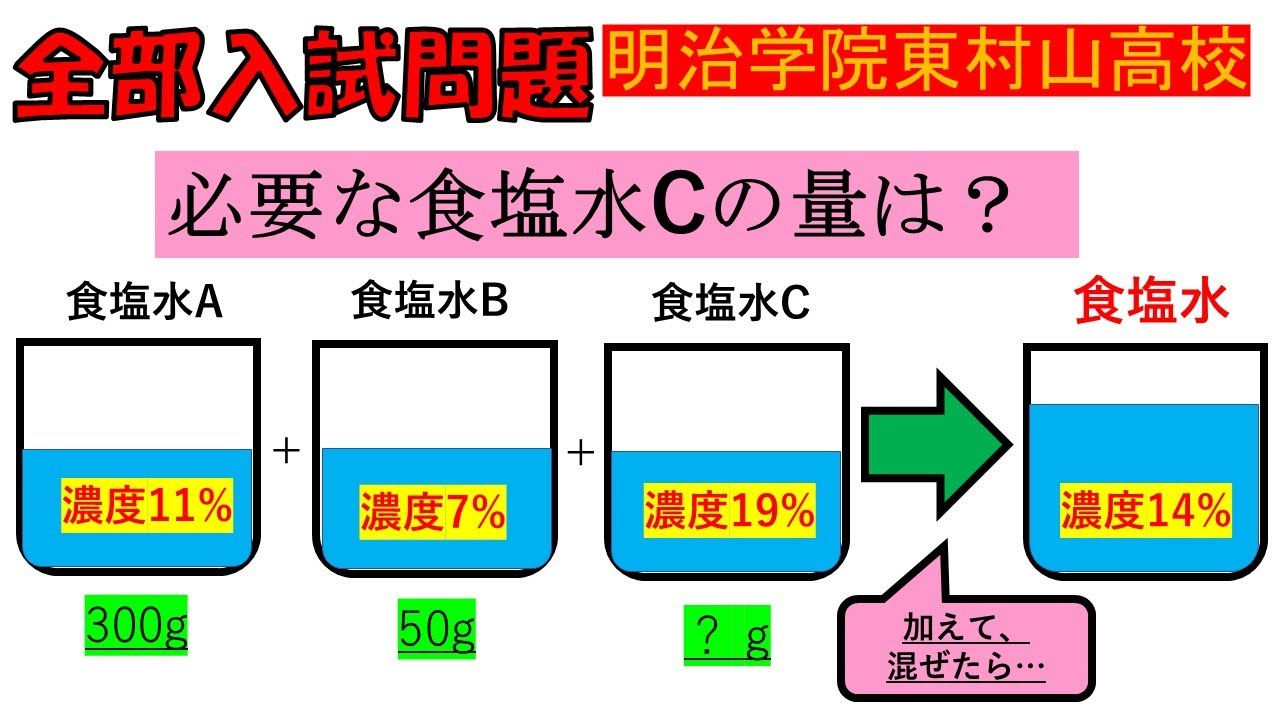
必要な食塩水$C$の量は?
明治学院東村山高等学校過去問
この動画を見る
必要な食塩水$C$の量は?
明治学院東村山高等学校過去問
【何を問われているか理解しているか?】計算:鎌倉学園高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の計算をしなさい.
${{2^3-(-2)^3}}\times{-2^5+(-2)^5}$
鎌倉学園高校過去問
この動画を見る
次の計算をしなさい.
${{2^3-(-2)^3}}\times{-2^5+(-2)^5}$
鎌倉学園高校過去問
【シンプルな問題の実態は…?】整数:大東文化大学第一高等学校~全国入試問題解法

単元:
#数学(中学生)#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$300$を$2$けたの自然数$N$で割ると,商があまりの$2$倍になった.
$N$を求めよ.
大東文化第一高校過去問
この動画を見る
$300$を$2$けたの自然数$N$で割ると,商があまりの$2$倍になった.
$N$を求めよ.
大東文化第一高校過去問
動体視力と数学を鍛えるサウンド~全国入試問題解法 #Shorts

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の$\Box$をうめなさい.
$624^2-623\times625=\Box$
土浦日大高校過去問
この動画を見る
次の$\Box$をうめなさい.
$624^2-623\times625=\Box$
土浦日大高校過去問
【1分で方向性を理解!】確率:大東文化大学第一高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
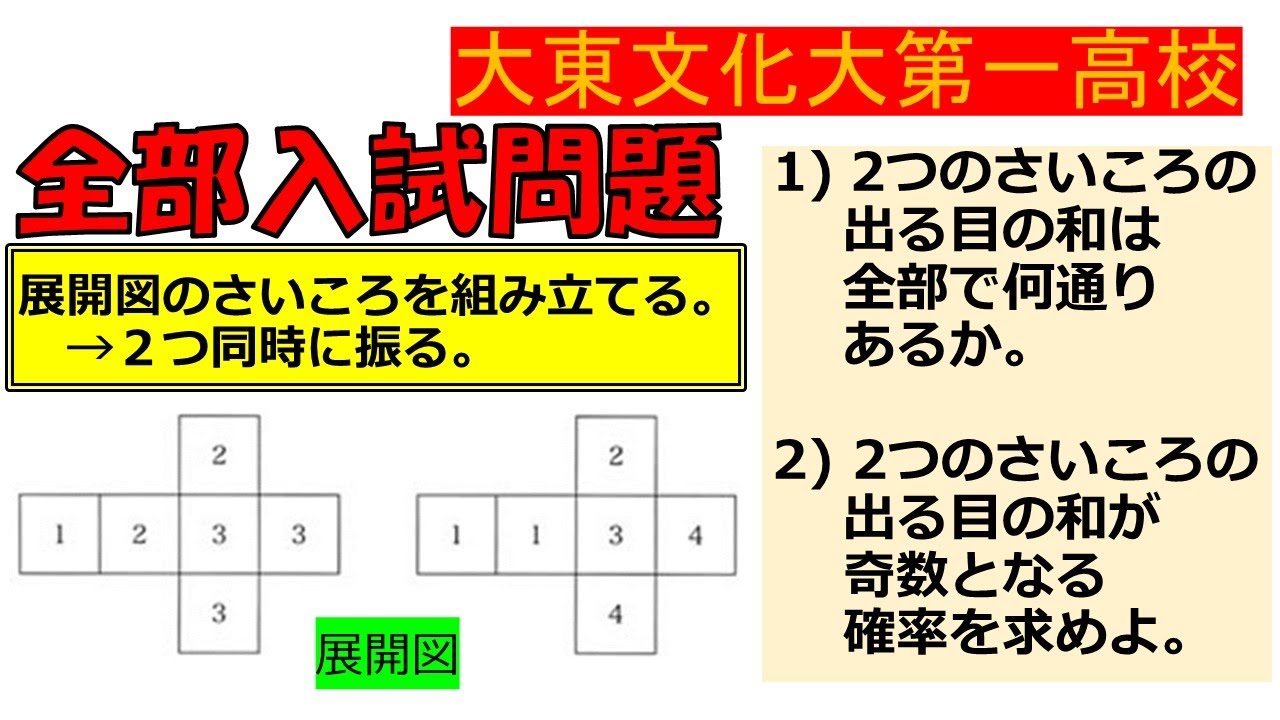
展開図のさいころを組み立て,2つ同時に振る.
(1)2つのさいころの出る目の和は全部で何通りあるか.
(2)2つのさいころの出る目の和が奇数となる確率を求めよ.
大東文化大第一高校過去問
この動画を見る
展開図のさいころを組み立て,2つ同時に振る.
(1)2つのさいころの出る目の和は全部で何通りあるか.
(2)2つのさいころの出る目の和が奇数となる確率を求めよ.
大東文化大第一高校過去問
【時に「習ってない」は言い訳にならない】文字式:明治学院東村山高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$x=\sqrt3+8$のとき,
$2x^2-32x+128$の値を求めなさい.
明治学院東村山高校過去問
この動画を見る
$x=\sqrt3+8$のとき,
$2x^2-32x+128$の値を求めなさい.
明治学院東村山高校過去問



