 鈴木貫太郎
鈴木貫太郎
 鈴木貫太郎
鈴木貫太郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
虚数解の6乗が実数
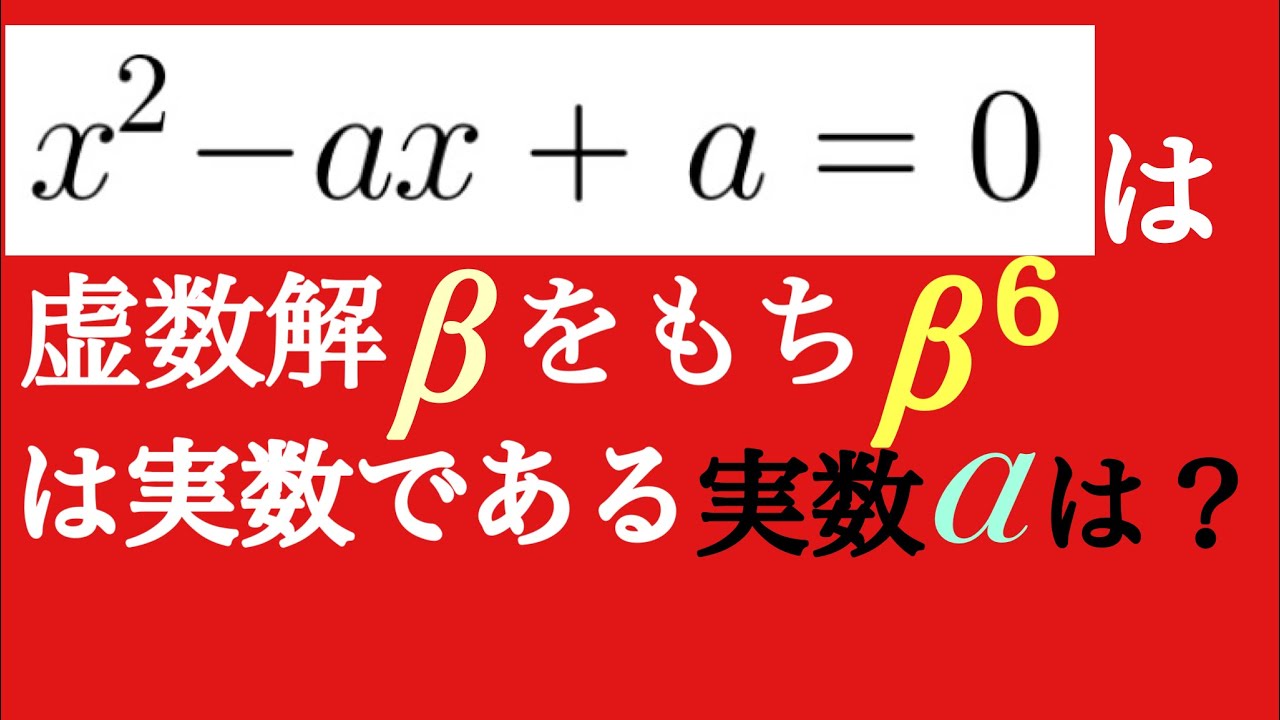
単元:
#数Ⅱ#複素数と方程式#複素数#解と判別式・解と係数の関係
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^2-ax+a=0$は虚数解$\beta$をもち$\beta^6$は実数である.
aの値を求めよ.
この動画を見る
$ x^2-ax+a=0$は虚数解$\beta$をもち$\beta^6$は実数である.
aの値を求めよ.
九州大のナイスな問題

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\alpha=\sqrt5-1+\sqrt{10+2\sqrt5}i$
$\beta=-\sqrt5-1+\sqrt{10-2\sqrt5}i$
(1)$\alpha$を解にもつ実数係数の2次方程式を1つ例示せよ.
(2)$\alpha,\beta$を解にもつ実数係数の4次方程式を1つ例示せよ.
(3)$\beta^5$の値を求めよ.
九州大(類)過去問
この動画を見る
$\alpha=\sqrt5-1+\sqrt{10+2\sqrt5}i$
$\beta=-\sqrt5-1+\sqrt{10-2\sqrt5}i$
(1)$\alpha$を解にもつ実数係数の2次方程式を1つ例示せよ.
(2)$\alpha,\beta$を解にもつ実数係数の4次方程式を1つ例示せよ.
(3)$\beta^5$の値を求めよ.
九州大(類)過去問
どっちがでかい?2通りの解法で

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
a,b,cは正の実数で$a^2+b^2=c^2$を満たす次の大小を比較せよ.
(1)$a^3+b^3,c^3$
(2)$\sqrt a+\sqrt b.\sqrt c$
この動画を見る
a,b,cは正の実数で$a^2+b^2=c^2$を満たす次の大小を比較せよ.
(1)$a^3+b^3,c^3$
(2)$\sqrt a+\sqrt b.\sqrt c$
簡単な指数方程式

単元:
#数Ⅱ#複素数と方程式#指数関数と対数関数#剰余の定理・因数定理・組み立て除法と高次方程式#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 2^x-3^x=\sqrt{6^x-9^x}$
これの実数解を求めよ.
この動画を見る
$ 2^x-3^x=\sqrt{6^x-9^x}$
これの実数解を求めよ.
何乗しても実数にならない数

整数問題やや難

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
m,nを自然数とする.
$2^n+17=m^4$
,これを解け.
この動画を見る
m,nを自然数とする.
$2^n+17=m^4$
,これを解け.
解けるように選ばれた数字で作られた問題
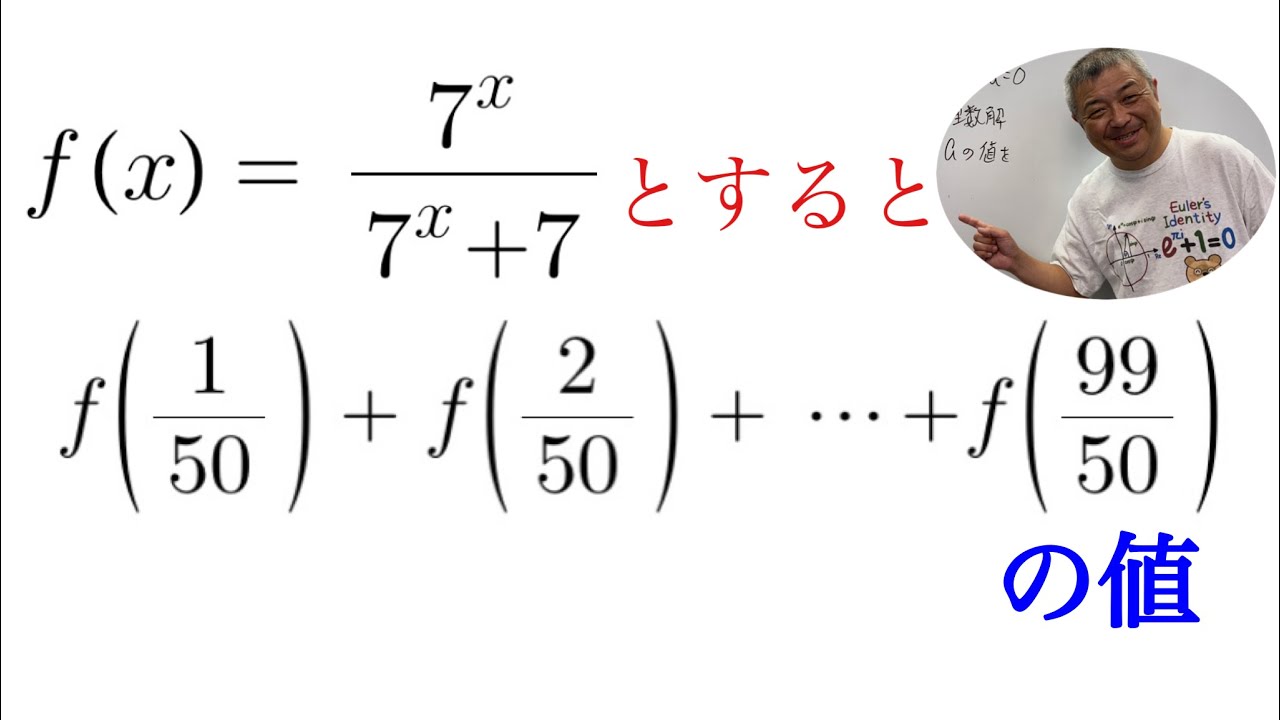
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ f(x)=\dfrac{7^x}{7^x+7}$とする.
$f\left(\frac{1}{50} \right)+f\left(\frac{2}{50} \right)+……f\left(\frac{98}{50} \right)+f\left(\frac{99}{50} \right)$
の値を求めよ.
この動画を見る
$ f(x)=\dfrac{7^x}{7^x+7}$とする.
$f\left(\frac{1}{50} \right)+f\left(\frac{2}{50} \right)+……f\left(\frac{98}{50} \right)+f\left(\frac{99}{50} \right)$
の値を求めよ.
基本問題

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^4-2x^3+3x^2-2x+1=0$のとき,
$\dfrac{x^{2222}}{x^{2224}+1}$の値を求めよ.
この動画を見る
$ x^4-2x^3+3x^2-2x+1=0$のとき,
$\dfrac{x^{2222}}{x^{2224}+1}$の値を求めよ.
早稲田(商)合同式の基本

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
整数a,b,c,dは次の条件(i),(ii),(iii)を満たしている.
(i)$3 \leqq a \lt b \lt c \lt d$
(ii)$a-b,b-c$は3の倍数,
(iii)$c^a-b^d$は3の倍数でない$a+b+c+d$の最小値
この動画を見る
整数a,b,c,dは次の条件(i),(ii),(iii)を満たしている.
(i)$3 \leqq a \lt b \lt c \lt d$
(ii)$a-b,b-c$は3の倍数,
(iii)$c^a-b^d$は3の倍数でない$a+b+c+d$の最小値
整式の剰余

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^{2022}$を$x^6-x^5+x^4-x^3+x^2-x+1$で割った余りを求めよ.
この動画を見る
$x^{2022}$を$x^6-x^5+x^4-x^3+x^2-x+1$で割った余りを求めよ.
ナイスな不定二次方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
x,yは自然数とする.
$x^2(2-y)+y^2(2-x)=-12$を満たす$(x,y)$をすべて求めよ.
この動画を見る
x,yは自然数とする.
$x^2(2-y)+y^2(2-x)=-12$を満たす$(x,y)$をすべて求めよ.
近畿大(理工)整式の剰余

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#近畿大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^{10}-x+1$を$(x-1)^3$で割った余りを求めよ.
近畿大(理工)過去問
この動画を見る
$ x^{10}-x+1$を$(x-1)^3$で割った余りを求めよ.
近畿大(理工)過去問
5乗数を平方の和で
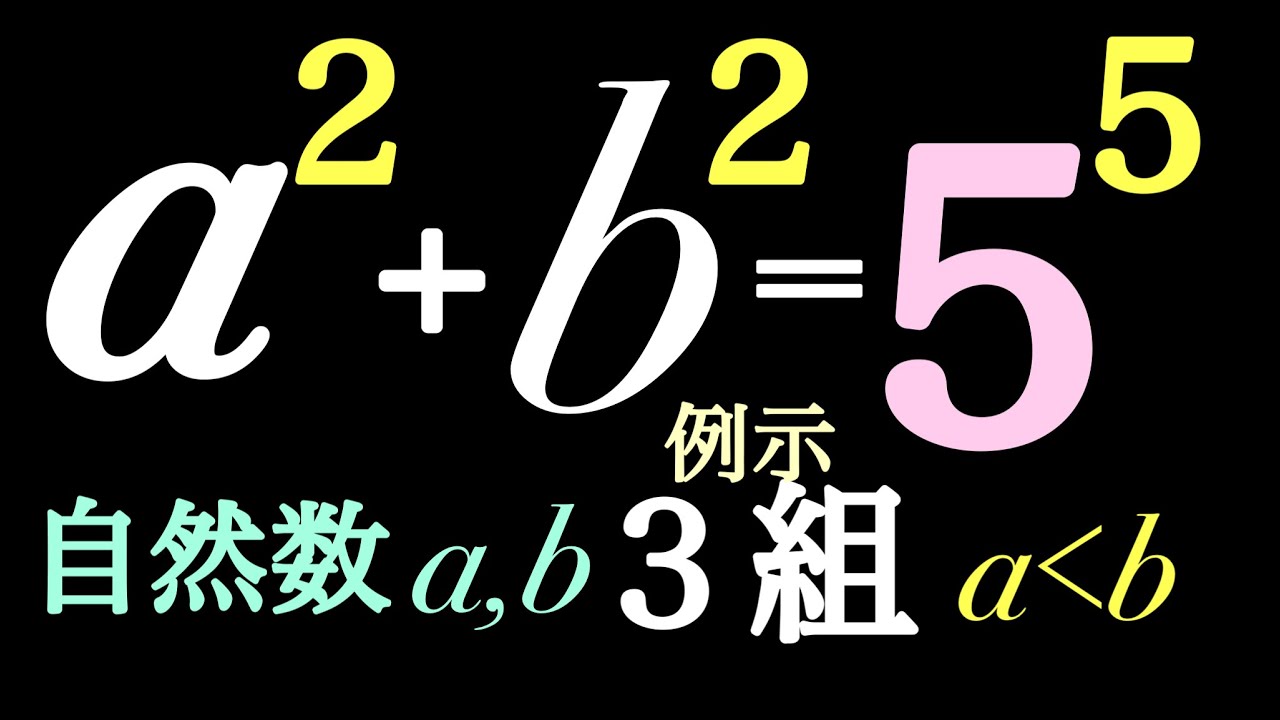
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a^2+b^2=5^5$,$a\lt b$
自然数$(a,b)$を3組例示せよ.
この動画を見る
$a^2+b^2=5^5$,$a\lt b$
自然数$(a,b)$を3組例示せよ.
5乗数を平方の和で
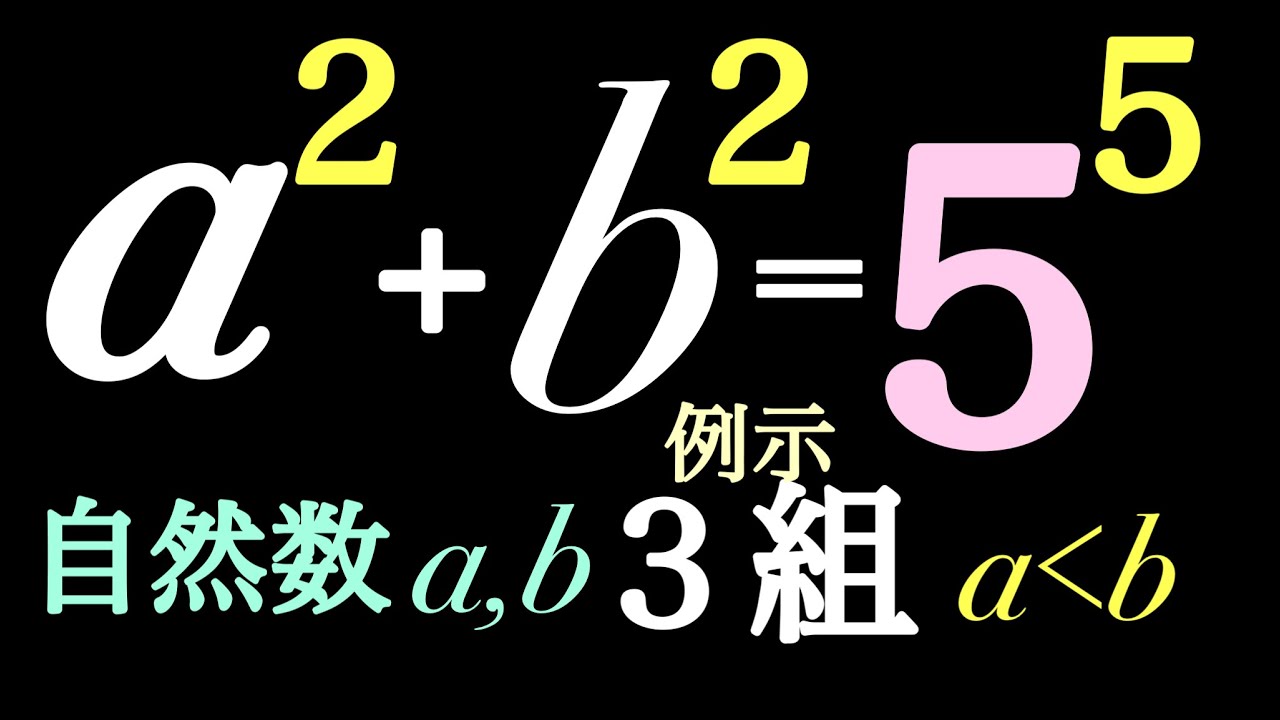
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a^2+b^2=5^5,a \lt b$とする.
自然数(a,b)を3組例示せよ.
この動画を見る
$ a^2+b^2=5^5,a \lt b$とする.
自然数(a,b)を3組例示せよ.
複素数の2次方程式・2通りの解法で
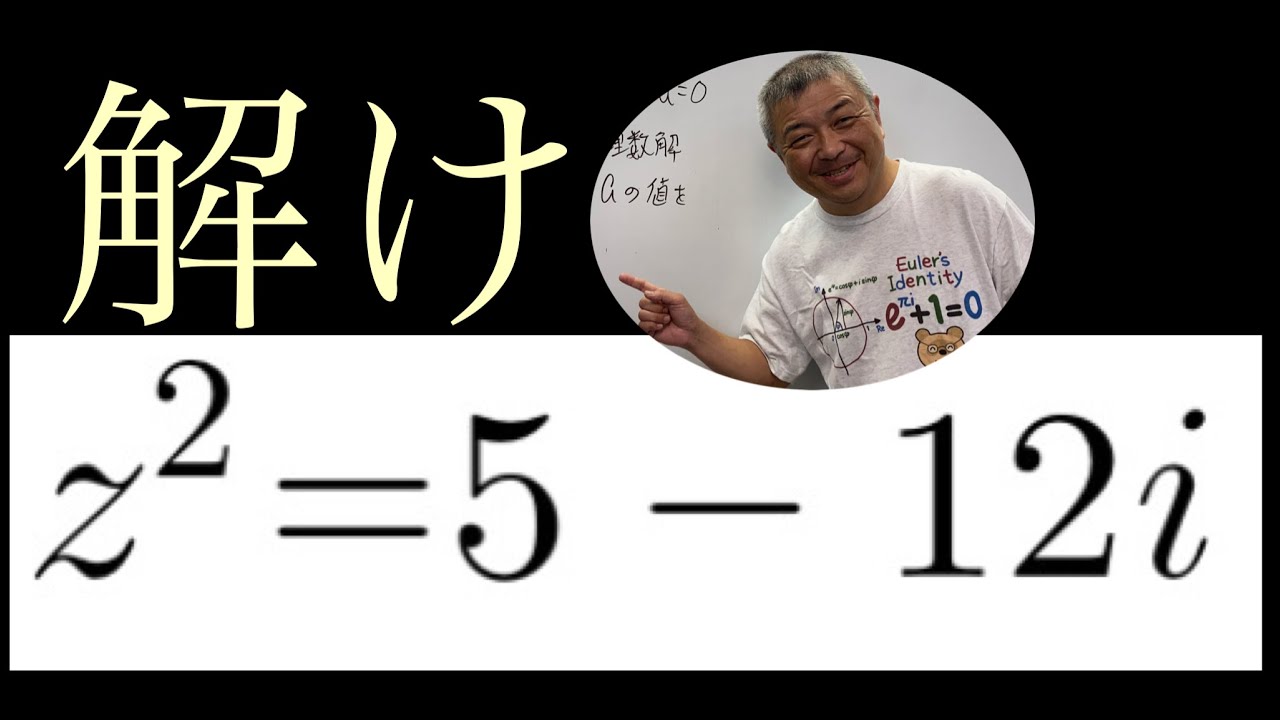
不定三次方程式
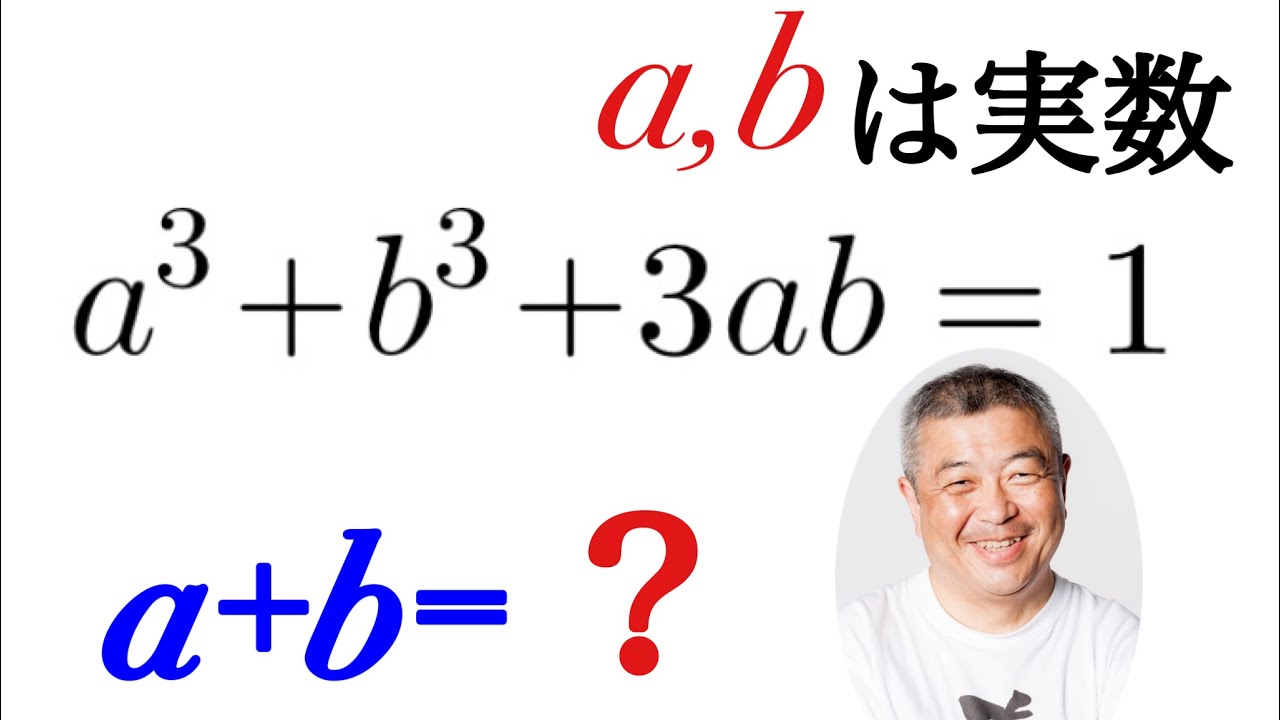
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
a,bを実数とする.
$a^3+b^3+3ab=1,a+b=?$これを解け.
この動画を見る
a,bを実数とする.
$a^3+b^3+3ab=1,a+b=?$これを解け.
ただの計算問題

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \sqrt{101^2+101^2・102^2+102^2}$
これを計算せよ.
この動画を見る
$ \sqrt{101^2+101^2・102^2+102^2}$
これを計算せよ.
ナイスな連立3元2次方程式
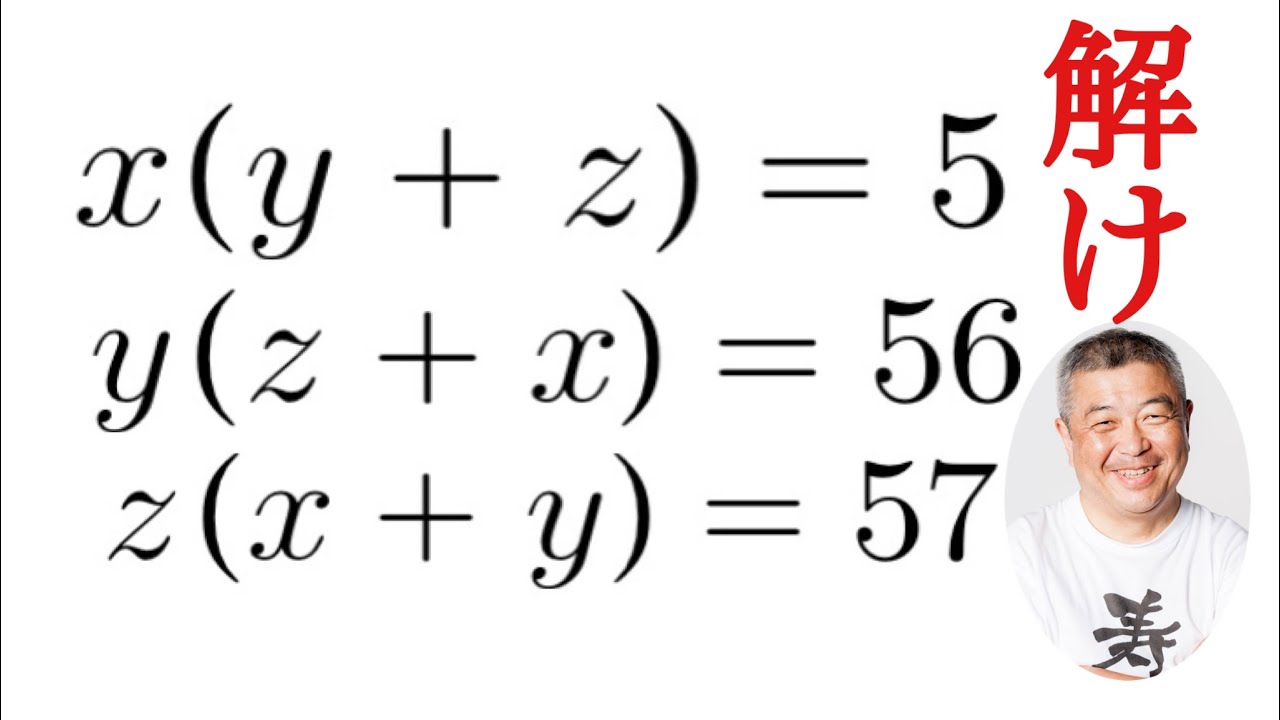
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
x(y+z)=5 \\
y(z+x)=56 \\
z(x+y)=57 \\
\end{array}
\right.
\end{eqnarray}$
これを解け.
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
x(y+z)=5 \\
y(z+x)=56 \\
z(x+y)=57 \\
\end{array}
\right.
\end{eqnarray}$
これを解け.
4次方程式 要工夫

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^4-2\sqrt3 x^2=x-3+\sqrt3$
これを解け.
この動画を見る
$ x^4-2\sqrt3 x^2=x-3+\sqrt3$
これを解け.
高校の宿題をアレンジしてみたその2

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
5Nを7で割ると3余り,6Nを11で割ると4余るようなNで3桁で最小のものを求めよ.
この動画を見る
5Nを7で割ると3余り,6Nを11で割ると4余るようなNで3桁で最小のものを求めよ.
部屋割り問題 東大

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
n個のボールを3つの箱に入れる場合の数,
(1)ボールの色はすべて異なり,箱にも名前有.
(2)ボールは区別できない,箱は区別できる.
(3)ボールは区別,箱は区別しない.
(4)6m区別なし,箱も区別なし.
東大過去問
この動画を見る
n個のボールを3つの箱に入れる場合の数,
(1)ボールの色はすべて異なり,箱にも名前有.
(2)ボールは区別できない,箱は区別できる.
(3)ボールは区別,箱は区別しない.
(4)6m区別なし,箱も区別なし.
東大過去問
部屋割り問題

どうってことない計算

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \dfrac{1}{\log_2 10000}+\dfrac{1}{\log_5 10000}$
これを解け.
この動画を見る
$ \dfrac{1}{\log_2 10000}+\dfrac{1}{\log_5 10000}$
これを解け.
高校の宿題をアレンジしてみた(合同式)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)4Nを5で割ると2余り,3Nを7で割ると3余る.Nを35で割った余りを求めよ.
(2)3Nを5で割ると4余り,3N+1は7で割り切れる.Nを35で割った余りを求めよ.
この動画を見る
(1)4Nを5で割ると2余り,3Nを7で割ると3余る.Nを35で割った余りを求めよ.
(2)3Nを5で割ると4余り,3N+1は7で割り切れる.Nを35で割った余りを求めよ.
4次式の因数分解

できるように作られた因数分解

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 36x^4+24x^3+67x^2+24x+36$
これを因数分解せよ.
この動画を見る
$ 36x^4+24x^3+67x^2+24x+36$
これを因数分解せよ.
東北大文系 虚数のナイスな問題

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#解と判別式・解と係数の関係#数列#漸化式#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
pは0でない実数である.$x^2-px+5p=0$の解を$\alpha,\beta$とする.
(1)$\alpha^5+\beta^5=p\5$となるpを求めよ.
(2)$\alpha$は虚数で$\alpha^5$が実数となるpを求めよ.
東北大文系過去問
この動画を見る
pは0でない実数である.$x^2-px+5p=0$の解を$\alpha,\beta$とする.
(1)$\alpha^5+\beta^5=p\5$となるpを求めよ.
(2)$\alpha$は虚数で$\alpha^5$が実数となるpを求めよ.
東北大文系過去問
さくっと解こう

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
x,y,zは相異なる実数である.
$x+\dfrac{1}{y}=y+\dfrac{1}{z}=z+\dfrac{1}{x}$のとき,
$x^2y^2z^2$の値を求めよ.
この動画を見る
x,y,zは相異なる実数である.
$x+\dfrac{1}{y}=y+\dfrac{1}{z}=z+\dfrac{1}{x}$のとき,
$x^2y^2z^2$の値を求めよ.
福島大 3数の相加相乗平均の応用

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
${\left(\dfrac{1}{3}(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}) \right)}^{-1} \leqq \dfrac{a+b+c}{3},$
a,b,cは正の実数である.これを証明せよ.
この動画を見る
${\left(\dfrac{1}{3}(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}) \right)}^{-1} \leqq \dfrac{a+b+c}{3},$
a,b,cは正の実数である.これを証明せよ.
The 因数分解

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ (a+b-2ab)(a+b-2)+(1-ab)^2$
これを因数分解せよ.
この動画を見る
$ (a+b-2ab)(a+b-2)+(1-ab)^2$
これを因数分解せよ.



