 鈴木貫太郎
鈴木貫太郎
 鈴木貫太郎
鈴木貫太郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
光文社新書「中学の知識でオイラー公式がわかる」Vol.15 複素数の絶対値・かけ算

光文社新書「中学の知識でオイラー公式がわかる」Vol14

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^2=9$
$(x-2)^2=25$
$x^2=5$
$(x+3)^2=2$
この動画を見る
$x^2=9$
$(x-2)^2=25$
$x^2=5$
$(x+3)^2=2$
光文社新書「中学の知識でオイラー公式がわかる」Vol 13 eとは何か後編

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
①$e=\displaystyle \lim_{ n \to \infty } (1+\displaystyle \frac{1}{n})^n \lt 3$
$\displaystyle \lim_{ h \to 0 } (1+h)^{\displaystyle \frac{1}{h}}$
②$y=e^x$ $y^1=e^x$
③$y=e^x$
$(0,1)$における接線の傾きが1
④$(log_ex)^1=\displaystyle \frac{1}{x}$
この動画を見る
①$e=\displaystyle \lim_{ n \to \infty } (1+\displaystyle \frac{1}{n})^n \lt 3$
$\displaystyle \lim_{ h \to 0 } (1+h)^{\displaystyle \frac{1}{h}}$
②$y=e^x$ $y^1=e^x$
③$y=e^x$
$(0,1)$における接線の傾きが1
④$(log_ex)^1=\displaystyle \frac{1}{x}$
光文社新書「中学の知識でオイラー公式がわかる」Vol12 eとは何か前編

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
①$e=\displaystyle \lim_{ n \to \infty } (1+\displaystyle \frac{1}{n})^n$
②$y=e^x$ $y^1=e^x$
③$y=e^x$
$(0,1)$における接線の傾きが1
④$(log_ex)^1=\displaystyle \frac{1}{x}$
この動画を見る
①$e=\displaystyle \lim_{ n \to \infty } (1+\displaystyle \frac{1}{n})^n$
②$y=e^x$ $y^1=e^x$
③$y=e^x$
$(0,1)$における接線の傾きが1
④$(log_ex)^1=\displaystyle \frac{1}{x}$
光文社新書「中学の知識でオイラー公式がわかる」Vol11 sinの微分

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
sinの微分解説動画です
$\displaystyle \lim_{ h \to o } \displaystyle \frac{\sin h}{h} =1$
この動画を見る
sinの微分解説動画です
$\displaystyle \lim_{ h \to o } \displaystyle \frac{\sin h}{h} =1$
光文社新書「中学の知識でオイラー公式がわかる」Vol.10 弧度法を使う理由

光文社新書「中学の知識でオイラー公式がわかる」Vol 9 大きな数の桁数&最上位の数

光文社新書「中学の知識でオイラー公式がわかる」Vol 9 大きな数の桁数&最上位の数

単元:
#計算と数の性質#数の性質その他
指導講師:
鈴木貫太郎
問題文全文(内容文):
光文社新書「中学の知識でオイラー公式がわかる」Vol 9 大きな数の桁数&最上位の数を解説していきます.
この動画を見る
光文社新書「中学の知識でオイラー公式がわかる」Vol 9 大きな数の桁数&最上位の数を解説していきます.
光文社新書「中学の知識でオイラーの公式がわかる」Vol.8対数 log

光文社新書「中学の知識でオイラーの公式がわかる」Vol.7積の微分の公式証明

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#微分とその応用#積分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
積の微分の公式証明解説動画です
この動画を見る
積の微分の公式証明解説動画です
光文社新書「中学の知識でオイラーの公式がわかる」Vol.6 自由落下運動と微分

光文社新書「中学の知識でオイラーの公式がわかる」Vol.5微分て何?

光文社新書「中学の知識でオイラー公式がわかる」Vol 4 加法定理

光文社新書「中学の知識でオイラーの公式がわかる」Vol.3余弦定理

光文社新書「中学の知識でオイラーの公式がわかる」Vol.2三角関数

光文社新書「中学の知識でオイラーの公式がわかる」Vol.1序章

単元:
#数A#図形の性質#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$e^{i\theta}\cos\theta+i\sin\theta$
$\theta=\pi$
$e^{i\pi}=-1$
この動画を見る
$e^{i\theta}\cos\theta+i\sin\theta$
$\theta=\pi$
$e^{i\pi}=-1$
岐阜大 積分 3次方程式の実数解

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#微分法と積分法#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#不定積分・定積分#岐阜大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=2x^3+ax^2-\displaystyle \int_{-2}^{1} x f(t) dt$
$f(x)=0$が異なる3つの実数解をもつ$a$の範囲を求めよ
出典:2013年岐阜大学 過去問
この動画を見る
$f(x)=2x^3+ax^2-\displaystyle \int_{-2}^{1} x f(t) dt$
$f(x)=0$が異なる3つの実数解をもつ$a$の範囲を求めよ
出典:2013年岐阜大学 過去問
変な方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x$の値を求めよ
$(26+15\sqrt{ 3 })^x-3(7+4\sqrt{ 3 })^x$
$-2(2+\sqrt{ 3 })^x+(2-\sqrt{ 3 })^x=3$
この動画を見る
$x$の値を求めよ
$(26+15\sqrt{ 3 })^x-3(7+4\sqrt{ 3 })^x$
$-2(2+\sqrt{ 3 })^x+(2-\sqrt{ 3 })^x=3$
センター試験レベル 指数方程式の解 津田塾大

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#津田塾大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x$の方程式
$9^x+2a・3^x+2a^2+a-6=0$が正と負の解を各1つもつ$a$の範囲を求めよ
出典:2000年津田塾大学 過去問
この動画を見る
$x$の方程式
$9^x+2a・3^x+2a^2+a-6=0$が正と負の解を各1つもつ$a$の範囲を求めよ
出典:2000年津田塾大学 過去問
藤田保健衛生大(医)5乗根の計算

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\sqrt[ 5 ]{ \displaystyle \frac{5\sqrt{ 5 }+11}{2} }-\sqrt[ 5 ]{ \displaystyle \frac{5\sqrt{ 5 }-11}{2} }$
出典:2017年藤田医科大学医学部 過去問
この動画を見る
$\sqrt[ 5 ]{ \displaystyle \frac{5\sqrt{ 5 }+11}{2} }-\sqrt[ 5 ]{ \displaystyle \frac{5\sqrt{ 5 }-11}{2} }$
出典:2017年藤田医科大学医学部 過去問
変わった不等式
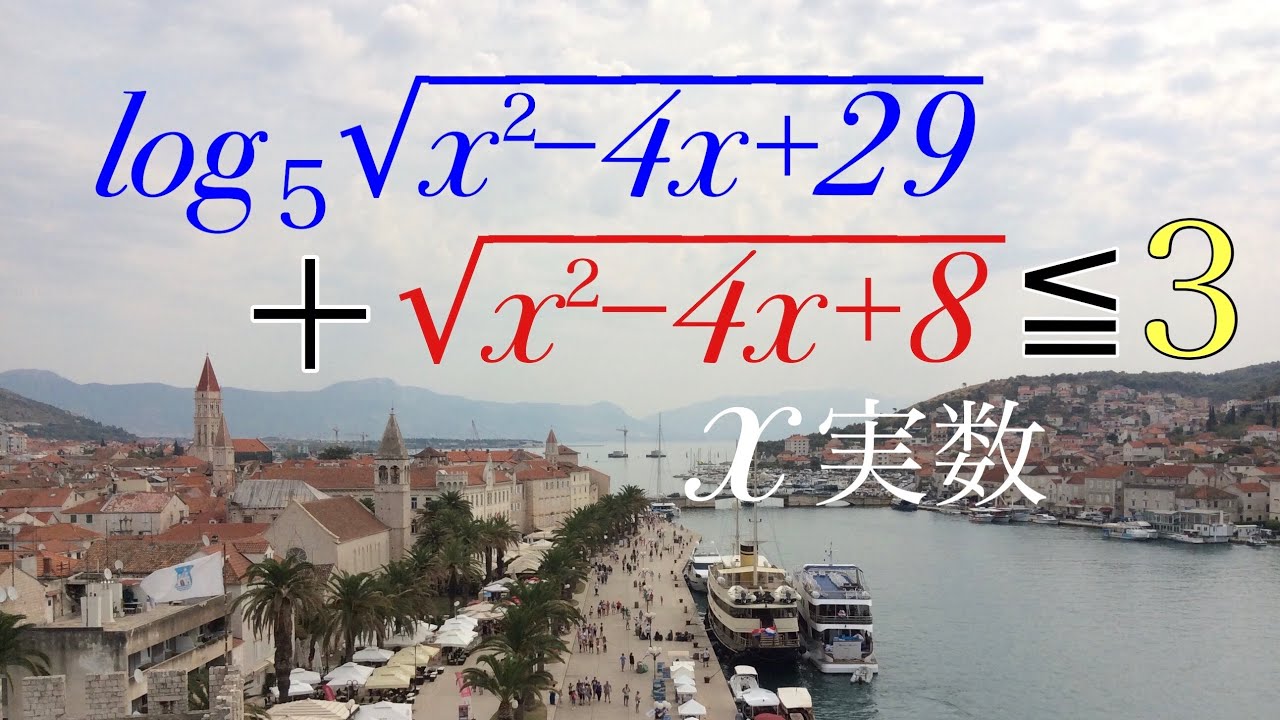
単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ
$log_5\sqrt{ x^2-4x+29 }+\sqrt{ x^2-4x+8 } \leqq 3$
この動画を見る
実数解を求めよ
$log_5\sqrt{ x^2-4x+29 }+\sqrt{ x^2-4x+8 } \leqq 3$
東工大 約数の個数

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
自然数$N$は12個の約数をもち、約数を小さい順に並べると7番目が12である。
$N$をすべて求めよ
出典:東京工業大学 過去問
この動画を見る
自然数$N$は12個の約数をもち、約数を小さい順に並べると7番目が12である。
$N$をすべて求めよ
出典:東京工業大学 過去問
対数の近似値の求め方

奈良女子大 数列の積
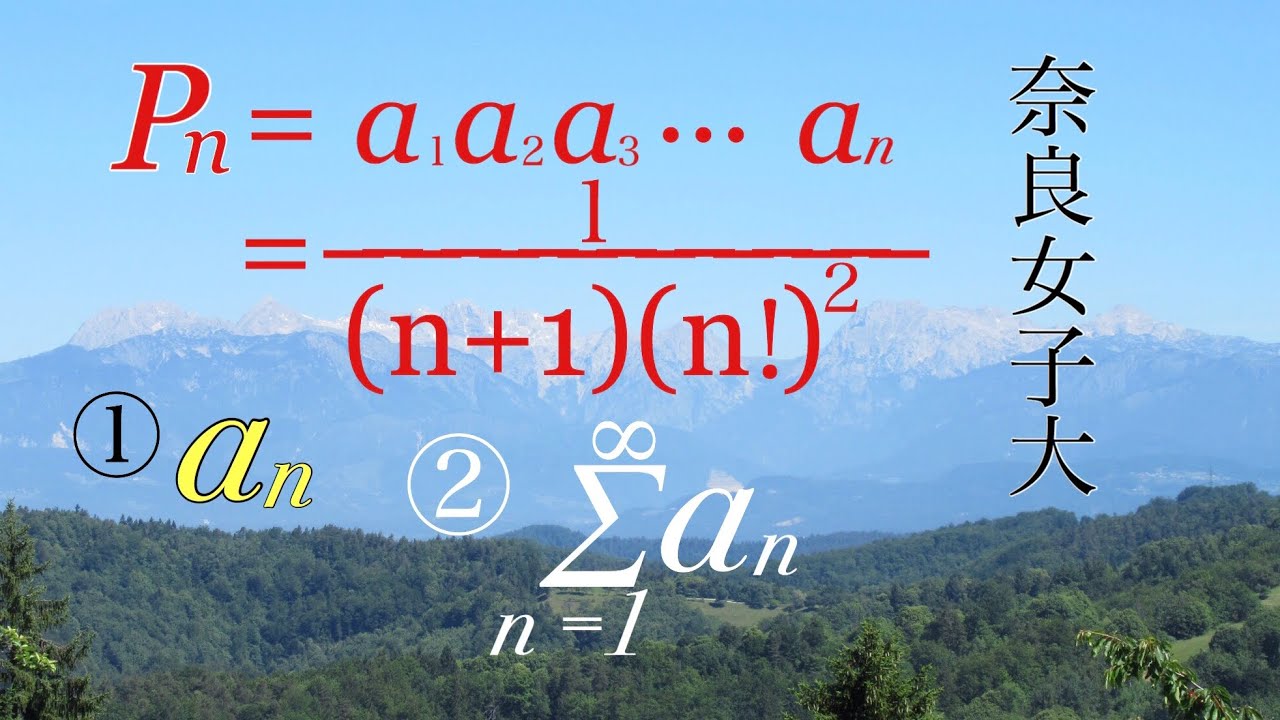
単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#奈良女子大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$P_n=a_1a_2a_3…a_n=\displaystyle \frac{1}{(n+1)(n!)^2}$
(1)
$a_n$を求めよ
(2)
$\displaystyle \sum_{n=1}^\infty a_m$を求めよ
出典:奈良女子大学 過去問
この動画を見る
$P_n=a_1a_2a_3…a_n=\displaystyle \frac{1}{(n+1)(n!)^2}$
(1)
$a_n$を求めよ
(2)
$\displaystyle \sum_{n=1}^\infty a_m$を求めよ
出典:奈良女子大学 過去問
総合問題2020

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(5+\sqrt{ 26 })^{2020}$の1の位の数を求めよ
この動画を見る
$(5+\sqrt{ 26 })^{2020}$の1の位の数を求めよ
京都大 三角関数 4倍角の公式 最大値・最小値

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(\theta)=\cos4\theta-4\sin^2\theta$
$0 \leqq \theta \leqq \displaystyle \frac{3}{4}\pi$における$f(\theta)$の最大値・最小値を求めよ
出典:2004年京都大学 過去問
この動画を見る
$f(\theta)=\cos4\theta-4\sin^2\theta$
$0 \leqq \theta \leqq \displaystyle \frac{3}{4}\pi$における$f(\theta)$の最大値・最小値を求めよ
出典:2004年京都大学 過去問
10万人ありがとうございます。鬼が笑う2021問題

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\sqrt[ 20 ]{ 20! }$と$\sqrt[ 21 ]{ 21! }$ どちらが大きいか求めよ
この動画を見る
$\sqrt[ 20 ]{ 20! }$と$\sqrt[ 21 ]{ 21! }$ どちらが大きいか求めよ
滋賀大 複素数 数列 漸化式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B#滋賀大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_n,b_n$整数
$(3+2i)^n=a_n+b_ni$
$a_n,b_n$の一般項を求めよ
出典:滋賀大学 過去問
この動画を見る
$a_n,b_n$整数
$(3+2i)^n=a_n+b_ni$
$a_n,b_n$の一般項を求めよ
出典:滋賀大学 過去問
大分大 対数の基本

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#大分大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$log_{10}2$の小数第一位を求めよ
$2^{21}$と$5^9$の大小比較
出典:大分大学 過去問
この動画を見る
$log_{10}2$の小数第一位を求めよ
$2^{21}$と$5^9$の大小比較
出典:大分大学 過去問
宇都宮大 漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B#宇都宮大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_n \gt 0,a_1=3$
$S_{n+1}+S_n=\displaystyle \frac{1}{3}(S_{n+1}-S_n)^2$
$a_n,S_n$を求めよ
出典:2013年宇都宮大学 過去問
この動画を見る
$a_n \gt 0,a_1=3$
$S_{n+1}+S_n=\displaystyle \frac{1}{3}(S_{n+1}-S_n)^2$
$a_n,S_n$を求めよ
出典:2013年宇都宮大学 過去問



