北海道大学
北海道大学
福田の数学〜北海道大学2025文系第4問〜関数方程式
単元：
#大学入試過去問(数学)#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{4}$
関数$f(x)$は、
すべての実数$x$およびすべての整数$n$について
$f(nx)={f(x)}^n$を満たし、
さらに$f(1)=2$を満たすとする。
ただし、$f(x)$のとりうる値は$0$でない実数とする。
(1)$f(n) \leqq 100$となるような最大の整数$n$を求めよ。
(2)すべての実数$x$について
$f(x)\gt 0$であることを証明せよ。
(3)$f(0.25)$を求めよ。
(4)$a$が有理数のとき、$f(a)$を$a$で表せ。
$2025$年北海道大学文系過去問題
この動画を見る
$\boxed{4}$
関数$f(x)$は、
すべての実数$x$およびすべての整数$n$について
$f(nx)={f(x)}^n$を満たし、
さらに$f(1)=2$を満たすとする。
ただし、$f(x)$のとりうる値は$0$でない実数とする。
(1)$f(n) \leqq 100$となるような最大の整数$n$を求めよ。
(2)すべての実数$x$について
$f(x)\gt 0$であることを証明せよ。
(3)$f(0.25)$を求めよ。
(4)$a$が有理数のとき、$f(a)$を$a$で表せ。
$2025$年北海道大学文系過去問題
福田の数学〜北海道大学2025文系第3問〜3項間漸化式と数列の和
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$
数列$\{a_n\}$を次のように定める。
$a_1=1,a_2=3,$
$(n+1)a_{n+2}-(2n+3)a_{n+1}+(n+2)a_n=0$
$\qquad (n=1,2,3,･･････)$
(1)$b_n=a_{n-1}-a_n$とおくと、
$b_{n+1}=\dfrac{n+2}{n+1}b_n \quad (n=1,2,3,･･････)$
が成り立つことを示せ。
(2)数列$\{a_n\}$の一般項を求めよ。
(3)$\displaystyle \sum_{n=1}^{225}\dfrac{1}{a_n}$の値を求めよ。
$2025$年北海道大学文系過去問題
この動画を見る
$\boxed{3}$
数列$\{a_n\}$を次のように定める。
$a_1=1,a_2=3,$
$(n+1)a_{n+2}-(2n+3)a_{n+1}+(n+2)a_n=0$
$\qquad (n=1,2,3,･･････)$
(1)$b_n=a_{n-1}-a_n$とおくと、
$b_{n+1}=\dfrac{n+2}{n+1}b_n \quad (n=1,2,3,･･････)$
が成り立つことを示せ。
(2)数列$\{a_n\}$の一般項を求めよ。
(3)$\displaystyle \sum_{n=1}^{225}\dfrac{1}{a_n}$の値を求めよ。
$2025$年北海道大学文系過去問題
福田の数学〜北海道大学2025文系第2問〜数え上げと余弦定理
単元：
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用（正弦・余弦・面積）#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
整数$a,b,c$は条件
$2\leqq a \lt b \lt c \leqq 6$を満たすとする。
(1)不等式$a+b\gt c$を満たすような
$(a+b+c)$をすべて挙げよ。
(2)不等式$a^2+b^2\geqq c^2$を満たすような
$(a+b+c)$をすべて挙げよ。
(3) (2)で求めた$(a,b,c)$について、
頂点$A,B,C$と向かい合う辺の長さがそれぞれ
$a,b,c$で与えられる$\triangle ABC$を考える。
このようなすべての$\triangle ABC$について
$\cos \angle ACB$を求めよ。
$2025$年北海道大学文系過去問題
この動画を見る
$\boxed{2}$
整数$a,b,c$は条件
$2\leqq a \lt b \lt c \leqq 6$を満たすとする。
(1)不等式$a+b\gt c$を満たすような
$(a+b+c)$をすべて挙げよ。
(2)不等式$a^2+b^2\geqq c^2$を満たすような
$(a+b+c)$をすべて挙げよ。
(3) (2)で求めた$(a,b,c)$について、
頂点$A,B,C$と向かい合う辺の長さがそれぞれ
$a,b,c$で与えられる$\triangle ABC$を考える。
このようなすべての$\triangle ABC$について
$\cos \angle ACB$を求めよ。
$2025$年北海道大学文系過去問題
福田の数学〜北海道大学2025文系第1問〜関数の増減と接線の方程式
単元：
#大学入試過去問(数学)#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
関数$f(x)=x^3-6x^2-15x+30$について考える。
$y=f(x)$のグラフを$C$とおく。
(1)$f(x)$が極大値、
極小値をとるような$x$をそれぞれ求め、
$f(x)$の極大値、極小値を求めよ。
(2)$C$上の点$(-3,-6)$を通り、
$C$に接する直線の方程式をすべて求めよ。
$2025$年北海道大学文系過去問題
この動画を見る
$\boxed{1}$
関数$f(x)=x^3-6x^2-15x+30$について考える。
$y=f(x)$のグラフを$C$とおく。
(1)$f(x)$が極大値、
極小値をとるような$x$をそれぞれ求め、
$f(x)$の極大値、極小値を求めよ。
(2)$C$上の点$(-3,-6)$を通り、
$C$に接する直線の方程式をすべて求めよ。
$2025$年北海道大学文系過去問題
福田の数学〜北海道大学2025理系第5問〜条件を満たす3つの整数を選び出す場合の数
単元：
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{5}$
$n$を$3$以上の整数とする。
(1)$k$を整数とする。
$k\lt a\lt b \lt c \leqq k+n$を満たす
整数$a,b,c$の選び方の
総数を$n$の式で表せ。
(2)$1\leqq a \lt b \lt c \leqq 2n$を満たす
整数$a,b,c$のうち、
$a+b \gt c$となる$a,b,c$の選び方の総数を$L$とする。
このとき、$L\gt {}_n \mathrm{ C }_3 $であることを示せ。
この動画を見る
$\boxed{5}$
$n$を$3$以上の整数とする。
(1)$k$を整数とする。
$k\lt a\lt b \lt c \leqq k+n$を満たす
整数$a,b,c$の選び方の
総数を$n$の式で表せ。
(2)$1\leqq a \lt b \lt c \leqq 2n$を満たす
整数$a,b,c$のうち、
$a+b \gt c$となる$a,b,c$の選び方の総数を$L$とする。
このとき、$L\gt {}_n \mathrm{ C }_3 $であることを示せ。
福田の数学〜北海道大学2025理系第3問〜部分積分と極限
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$
実数$a$および自然数$n$に対して、定積分
$I(a,n)=\displaystyle \int_{0}^{2\pi} e^{ax} \sin (nx) dx$
を考える。ここで$e$は自然対数の底である。
(1)$I(a,n)$を求めよ。
(2)$a_n=\dfrac{\log _n}{2\pi} (n=1,2,3,\cdots)$のとき、
極限$\displaystyle \lim_{n\to\infty} I(a_n,n)$を求めよ。
ただし、$\log_n$は$n$の自然対数である。
また、必要ならば$\displaystyle \lim_{n\to\infty}\dfrac{\log_n}{n}=0$である
ことを用いてもよい。
$2025$年北海道大学理系過去問題
この動画を見る
$\boxed{3}$
実数$a$および自然数$n$に対して、定積分
$I(a,n)=\displaystyle \int_{0}^{2\pi} e^{ax} \sin (nx) dx$
を考える。ここで$e$は自然対数の底である。
(1)$I(a,n)$を求めよ。
(2)$a_n=\dfrac{\log _n}{2\pi} (n=1,2,3,\cdots)$のとき、
極限$\displaystyle \lim_{n\to\infty} I(a_n,n)$を求めよ。
ただし、$\log_n$は$n$の自然対数である。
また、必要ならば$\displaystyle \lim_{n\to\infty}\dfrac{\log_n}{n}=0$である
ことを用いてもよい。
$2025$年北海道大学理系過去問題
福田の数学〜北海道大学2025理系第4問〜複素数平面上の点の軌跡と2円が共有点をもつ条件
単元：
#数Ⅱ#大学入試過去問(数学)#複素数平面#図形と方程式#軌跡と領域#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{4}$
$a$を正の実数とする。
(1)$a$が$1$でないとき、複素数$z$についての方程式
$a \vert z-1 \vert = \vert (a-2)z +a \vert$
を考える。
この方程式を満たす$z$全体の集合を
複素数平面上に図示せよ。
$2025$年北海道大学理系過去問題
この動画を見る
$\boxed{4}$
$a$を正の実数とする。
(1)$a$が$1$でないとき、複素数$z$についての方程式
$a \vert z-1 \vert = \vert (a-2)z +a \vert$
を考える。
この方程式を満たす$z$全体の集合を
複素数平面上に図示せよ。
$2025$年北海道大学理系過去問題
福田の数学〜北海道大学2025理系第2問〜円に引いた2本の接線でできる四角形の面積の最大最小
単元：
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
円$C_1:x^2+y^2=1$を考える。
実数$p,q$が$p^2+q^2 \gt 1$を満たすとき、
点$p(p,q)$から$C_1$に引いた$2$本の接線$\ell_1,\ell_2$の
接点をそれぞれ$Q_1(x_1,y_1), Q_2(x_2,y_2)$とする。
また、座標平面上の原点を$O(0,0)$とする。
(1)直線$\ell_1,\ell_2$,線分$OQ_1,OQ_2$で囲まれた
四角形の面積$S$を$p,q$を用いて表せ。
(2)点$P$が楕円
$C_2:\dfrac{x^2}{2}+\dfrac{y^2}{3}=1$
の上を動くとき、
(1)の四角形の面積$S$の最大値と最小値を求めよ。
$2025$年北海道大学理系過去問題
この動画を見る
$\boxed{2}$
円$C_1:x^2+y^2=1$を考える。
実数$p,q$が$p^2+q^2 \gt 1$を満たすとき、
点$p(p,q)$から$C_1$に引いた$2$本の接線$\ell_1,\ell_2$の
接点をそれぞれ$Q_1(x_1,y_1), Q_2(x_2,y_2)$とする。
また、座標平面上の原点を$O(0,0)$とする。
(1)直線$\ell_1,\ell_2$,線分$OQ_1,OQ_2$で囲まれた
四角形の面積$S$を$p,q$を用いて表せ。
(2)点$P$が楕円
$C_2:\dfrac{x^2}{2}+\dfrac{y^2}{3}=1$
の上を動くとき、
(1)の四角形の面積$S$の最大値と最小値を求めよ。
$2025$年北海道大学理系過去問題
福田の数学〜北海道大学2025理系第1問〜指数対数の基本性質と数列
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
$\alpha,r$を$\alpha \gt 1,r \gt 1$を満たす実数とする。
数列$\{a_n\}$を$a_1=\alpha$で公比が$r$の等比数列とする。
数列$\{b_n\}$を
$b_n=\log_{a_{n}} (a_{n+1}) (n=1,2,3,\cdots)$で定める。
(1)$b_n$を$n$と$\log_{\alpha}r$を用いて表せ。
$2025$年北海道大学理系過去問題
この動画を見る
$\boxed{1}$
$\alpha,r$を$\alpha \gt 1,r \gt 1$を満たす実数とする。
数列$\{a_n\}$を$a_1=\alpha$で公比が$r$の等比数列とする。
数列$\{b_n\}$を
$b_n=\log_{a_{n}} (a_{n+1}) (n=1,2,3,\cdots)$で定める。
(1)$b_n$を$n$と$\log_{\alpha}r$を用いて表せ。
$2025$年北海道大学理系過去問題
#北海道大学1957#方程式_65
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#２次関数#一次不等式（不等式・絶対値のある方程式・不等式）#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
ますただ
問題文全文(内容文)：
$\dfrac{10x-10^{-x}}{10x+10^{-x}}=a \ (\vert a \vert \gt 1)$
$x$について解け.
1957北海道大学過去問題
この動画を見る
$\dfrac{10x-10^{-x}}{10x+10^{-x}}=a \ (\vert a \vert \gt 1)$
$x$について解け.
1957北海道大学過去問題
#北海道大学1957#因数分解_64
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
ますただ
問題文全文(内容文)：
$2x^2-xy-y^2-7x+y+6$を因数分解せよ.
1957北海道大学過去問題
この動画を見る
$2x^2-xy-y^2-7x+y+6$を因数分解せよ.
1957北海道大学過去問題
#北海道大学1919#因数分解_63
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
ますただ
問題文全文(内容文)：
$a^4+b^4+c^4-2b^2c^2-2c^2a^2-2a^2b^2$を因数分解せよ.
1919北海道帝国大学過去問題
この動画を見る
$a^4+b^4+c^4-2b^2c^2-2c^2a^2-2a^2b^2$を因数分解せよ.
1919北海道帝国大学過去問題
大学入試問題#899「初めてのベクトルやってみた」 #北海道大学(2024)
単元：
#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#平面上のベクトルと内積#空間ベクトル#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数C
指導講師：
ますただ
問題文全文(内容文)：
三角形$OAB$が
$|\overrightarrow{ OA }|=3,$ $|\overrightarrow{ AB }|=5,$ $\overrightarrow{ OA }.\overrightarrow{ AB }=10$
を満たしているとする。
三角形$OAB$の内接円の中心を$I$とし、この内接円と辺$OA$の接点を$H$とする。
１．辺$OB$の長さを求めよ。
２．$\overrightarrow{ OI }$を$\overrightarrow{ OA }$と$\overrightarrow{ OB }$を用いて表せ。
３．$\overrightarrow{ HI }$を$\overrightarrow{ OA }$と$\overrightarrow{ OB }$を用いて表せ。
出典：2024年北海道大学
この動画を見る
三角形$OAB$が
$|\overrightarrow{ OA }|=3,$ $|\overrightarrow{ AB }|=5,$ $\overrightarrow{ OA }.\overrightarrow{ AB }=10$
を満たしているとする。
三角形$OAB$の内接円の中心を$I$とし、この内接円と辺$OA$の接点を$H$とする。
１．辺$OB$の長さを求めよ。
２．$\overrightarrow{ OI }$を$\overrightarrow{ OA }$と$\overrightarrow{ OB }$を用いて表せ。
３．$\overrightarrow{ HI }$を$\overrightarrow{ OA }$と$\overrightarrow{ OB }$を用いて表せ。
出典：2024年北海道大学
大学入試問題#897「解法の迷走」 #北海道大学(2024)
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \frac{x^2-x+1}{x^2+x+1}$
が整数となるような実数$x$をすべて求めよ。
出典：2024年北海道大学後期
この動画を見る
$\displaystyle \frac{x^2-x+1}{x^2+x+1}$
が整数となるような実数$x$をすべて求めよ。
出典：2024年北海道大学後期
大学入試問題#896「難関大学ではたまにでる？」 #北海道大学(2024)
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
ますただ
問題文全文(内容文)：
関数$f_1(x),f_2(x),f_3(x),…$を次の関係式で定める。
$f_1(x)=3x$
$f_{n+1}(x)=(n+2)x^{n+1}+(\displaystyle \int_{0}^{1} f_n(t) dt)x$
関数$f_n(x)$を$x$と$n$の式で表せ。$(n=1,2,3,…)$
出典：2024年北海道大学
この動画を見る
関数$f_1(x),f_2(x),f_3(x),…$を次の関係式で定める。
$f_1(x)=3x$
$f_{n+1}(x)=(n+2)x^{n+1}+(\displaystyle \int_{0}^{1} f_n(t) dt)x$
関数$f_n(x)$を$x$と$n$の式で表せ。$(n=1,2,3,…)$
出典：2024年北海道大学
福田の数学〜北海道大学2024年理系第3問〜関数方程式の解
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
福田次郎
問題文全文(内容文)：
$\Large{\boxed{3}}$ 次の問いに答えよ。
(1)$\alpha$ を実数とする。次のように定められた数列$\left\{a_n\right\}$ の一般項を求めよ。
$a_1$=$\alpha$, $a_{n+1}$=$\frac{1}{2}a_n$+1 ($n$=1,2,3,...)
(2)関数$f_1(x)$, $f_2(x)$, $f_3(x)$,... を次の関係式で定める。
$f_1(x)$=$3x$
$f_{n+1}(x)$=$(n+2)x^{n+1}$+$\displaystyle\left(\int_0^1f_n(t)dt\right)x$ ($n$=1,2,3,...)
関数$f_n(x)$を$x$と$n$の式で表せ。
この動画を見る
$\Large{\boxed{3}}$ 次の問いに答えよ。
(1)$\alpha$ を実数とする。次のように定められた数列$\left\{a_n\right\}$ の一般項を求めよ。
$a_1$=$\alpha$, $a_{n+1}$=$\frac{1}{2}a_n$+1 ($n$=1,2,3,...)
(2)関数$f_1(x)$, $f_2(x)$, $f_3(x)$,... を次の関係式で定める。
$f_1(x)$=$3x$
$f_{n+1}(x)$=$(n+2)x^{n+1}$+$\displaystyle\left(\int_0^1f_n(t)dt\right)x$ ($n$=1,2,3,...)
関数$f_n(x)$を$x$と$n$の式で表せ。
【高校数学】遂に完結!!北海道大学2024年の積分の問題をその場で解説しながら解いてみた！毎日積分104日目~47都道府県制覇への道~【㊼北海道】【最終回】
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数Ⅲ
指導講師：
理数個別チャンネル
問題文全文(内容文)：
【北海道大学 2024】
関数
$f(x)=xlog(x+2)+1 (x＞-2)$
を考える。$y=f(x)$で表される曲線を$C$とする。$C$の接線のうち傾きが正で原点を通るものを$l$とする。ただし、$logt$は$t$の自然対数である。
(1) 直線$l$の方程式を求めよ。
(2) 曲線$C$は下に凸であることを証明せよ。
(3) $C$と$l$および$y$軸で囲まれた部分の面積を求めよ。
この動画を見る
【北海道大学 2024】
関数
$f(x)=xlog(x+2)+1 (x＞-2)$
を考える。$y=f(x)$で表される曲線を$C$とする。$C$の接線のうち傾きが正で原点を通るものを$l$とする。ただし、$logt$は$t$の自然対数である。
(1) 直線$l$の方程式を求めよ。
(2) 曲線$C$は下に凸であることを証明せよ。
(3) $C$と$l$および$y$軸で囲まれた部分の面積を求めよ。
大学入試問題#755「基本問題」 北海道大学(1970) #微分方程式
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
ますただ
問題文全文(内容文)：
$f(x)$は$x \gt 0$で定義された正の値をとる微分可能な関数で
$\{f(x)\}^2=x+1+\displaystyle \int_{1}^{x} \{f(t)\}^2dt$を満たすものとする。
（1）$y=f(x)$の満たす1階微分方程式を求めよ。
（2）$y=f(x)$を任意定数を含まない形で求めよ。
出典：1970年北海道大学 入試問題
この動画を見る
$f(x)$は$x \gt 0$で定義された正の値をとる微分可能な関数で
$\{f(x)\}^2=x+1+\displaystyle \int_{1}^{x} \{f(t)\}^2dt$を満たすものとする。
（1）$y=f(x)$の満たす1階微分方程式を求めよ。
（2）$y=f(x)$を任意定数を含まない形で求めよ。
出典：1970年北海道大学 入試問題
北海道大学(1970) #定積分 #Shorts
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
ますただ
問題文全文(内容文)：
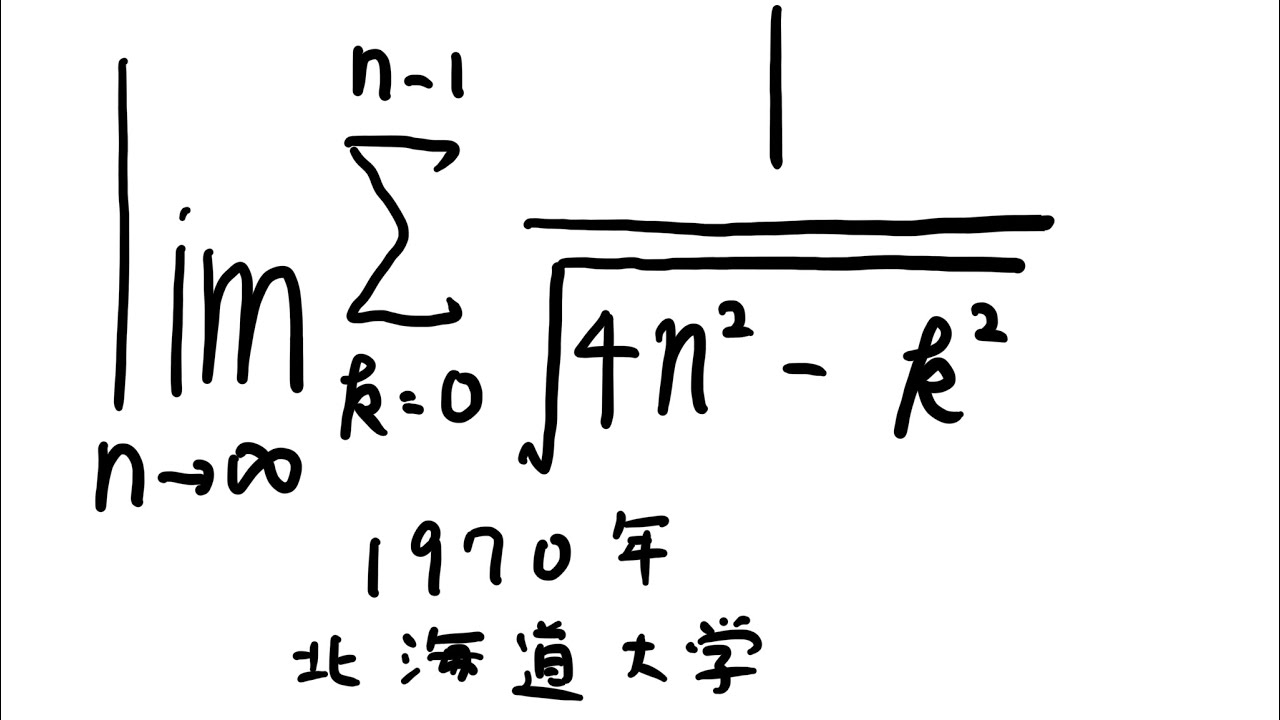
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=0}^{n-1} \displaystyle \frac{1}{\sqrt{ 4n^2-k^2 }}$
出典：1970年北海道大学
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=0}^{n-1} \displaystyle \frac{1}{\sqrt{ 4n^2-k^2 }}$
出典：1970年北海道大学
福田の数学〜北海道大学2023年文系第４問〜円と放物線の共通接線と囲まれる面積
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#北海道大学
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{4}$ qを実数とする。座標平面上に円C：$x^2$+$y^2$=1と放物線P：y=$x^2$+q がある。
(1)CとPに同じ点で接する傾き正の直線が存在するとき、qの値およびその接点の座標を求めよ。
(2)(1)で求めたqの値を$q_1$、接点のy座標を$y_1$とするとき、連立不等式
$\left\{\begin{array}{1}
x^2+y^2≧1\\
y≧x^2+q_1\\
y≦y_1\\
\end{array}\right.$
の表す領域の面積を求めよ。
2023北海道大学文系過去問
この動画を見る
$\Large\boxed{4}$ qを実数とする。座標平面上に円C：$x^2$+$y^2$=1と放物線P：y=$x^2$+q がある。
(1)CとPに同じ点で接する傾き正の直線が存在するとき、qの値およびその接点の座標を求めよ。
(2)(1)で求めたqの値を$q_1$、接点のy座標を$y_1$とするとき、連立不等式
$\left\{\begin{array}{1}
x^2+y^2≧1\\
y≧x^2+q_1\\
y≦y_1\\
\end{array}\right.$
の表す領域の面積を求めよ。
2023北海道大学文系過去問
福田の数学〜北海道大学2023年文系第３問〜絶対値の和の最小値
単元：
#数Ⅰ#数A#大学入試過去問(数学)#数と式#場合の数と確率#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#集合と命題（集合・命題と条件・背理法）#場合の数#確率#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{3}$ nを2以上の自然数とする。1個のさいころをn回投げて出た目の数を順に$a_1$, $a_2$, ...., $a_n$とし、
$K_n$=|1-$a_1$|+|$a_1$-$a_2$|+...+|$a_{n-1}$-$a_n$|+|$a_n$-6|
とおく。また$K_n$のとりうる値の最小値を$q_n$とする。
(1)$K_2$=5 となる確率を求めよ。
(2)$K_3$=5 となる確率を求めよ。
(3)$q_n$を求めよ。また、$K_n$=$q_n$となるための$a_1$, $a_2$, ...., $a_n$に関する必要十分条件を求めよ。
2023北海道大学文系過去問
この動画を見る
$\Large\boxed{3}$ nを2以上の自然数とする。1個のさいころをn回投げて出た目の数を順に$a_1$, $a_2$, ...., $a_n$とし、
$K_n$=|1-$a_1$|+|$a_1$-$a_2$|+...+|$a_{n-1}$-$a_n$|+|$a_n$-6|
とおく。また$K_n$のとりうる値の最小値を$q_n$とする。
(1)$K_2$=5 となる確率を求めよ。
(2)$K_3$=5 となる確率を求めよ。
(3)$q_n$を求めよ。また、$K_n$=$q_n$となるための$a_1$, $a_2$, ...., $a_n$に関する必要十分条件を求めよ。
2023北海道大学文系過去問
福田の数学〜北海道大学2023年文系第２問〜角の２等分線の位置ベクトル
単元：
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{2}$ 三角形OABは辺の長さがOA=3, OB=5, AB=7であるとする。また、$\angle$AOBの2等分線と直線ABとの交点をPとし、頂点Bにおける外角の2等分線と直線OPとの交点をQとする。
(1)$\overrightarrow{ OP }$を$\overrightarrow{ OA }$, $\overrightarrow{ OB }$を用いて表せ。また、|$\overrightarrow{ OP }$|の値を求めよ。
(2)$\overrightarrow{ OQ }$を$\overrightarrow{ OA }$, $\overrightarrow{ OB }$を用いて表せ。また、|$\overrightarrow{ OQ }$|の値を求めよ。
2023北海道大学文系過去問
この動画を見る
$\Large\boxed{2}$ 三角形OABは辺の長さがOA=3, OB=5, AB=7であるとする。また、$\angle$AOBの2等分線と直線ABとの交点をPとし、頂点Bにおける外角の2等分線と直線OPとの交点をQとする。
(1)$\overrightarrow{ OP }$を$\overrightarrow{ OA }$, $\overrightarrow{ OB }$を用いて表せ。また、|$\overrightarrow{ OP }$|の値を求めよ。
(2)$\overrightarrow{ OQ }$を$\overrightarrow{ OA }$, $\overrightarrow{ OB }$を用いて表せ。また、|$\overrightarrow{ OQ }$|の値を求めよ。
2023北海道大学文系過去問
福田の数学〜北海道大学2023年文系第１問〜関数方程式と剰余定理因数定理
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#複素数と方程式#恒等式・等式・不等式の証明#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{5}$ P(x)をxについての整式とし、P(x)P(-x)=P($x^2$)はxについての恒等式であるとする。
(1)P(0)=0またはP(0)=1 であることを示せ。
(2)P(x)がx-1で割り切れないならば、P(x)-1はx+1で割り切れることを示せ。
(3)次数が2であるP(x)を全て求めよ。
2023北海道大学文系過去問
この動画を見る
$\Large\boxed{5}$ P(x)をxについての整式とし、P(x)P(-x)=P($x^2$)はxについての恒等式であるとする。
(1)P(0)=0またはP(0)=1 であることを示せ。
(2)P(x)がx-1で割り切れないならば、P(x)-1はx+1で割り切れることを示せ。
(3)次数が2であるP(x)を全て求めよ。
2023北海道大学文系過去問
福田の数学〜北海道大学2023年理系第５問〜中間値の定理と関数の増減PART2
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{5}$ a,bを$a^2$+$b^2$＜ 1を満たす正の実数とする。また、座標平面上で原点を中心とする半径1の円をCとし、Cの内部になる2点A(a,0), B(0,b)を考える。
0＜θ＜$\frac{\pi}{2}$に対してC上の点P($\cos\theta$, $\sin\theta$)を考え、PにおけるCの接線に関してBと対称な点をDとおく。
(1)$f(\theta)$=ab$\cos2\theta$+a$\sin\theta$-b$\cos\theta$とおく。方程式$f(\theta)$=0の解が0＜θ＜$\frac{\pi}{2}$の範囲に少なくとも一つ存在することを示せ。
(2)Dの座標をa,θを用いて表せ。
(3)θが0＜θ＜$\frac{\pi}{2}$の範囲を動くとき、3点A,P,Dが同一直線上にあるようなθは少なくとも一つ存在することを示せ。また、このようなθはただ一つであることを示せ。
2023北海道大学理系過去問
この動画を見る
$\Large\boxed{5}$ a,bを$a^2$+$b^2$＜ 1を満たす正の実数とする。また、座標平面上で原点を中心とする半径1の円をCとし、Cの内部になる2点A(a,0), B(0,b)を考える。
0＜θ＜$\frac{\pi}{2}$に対してC上の点P($\cos\theta$, $\sin\theta$)を考え、PにおけるCの接線に関してBと対称な点をDとおく。
(1)$f(\theta)$=ab$\cos2\theta$+a$\sin\theta$-b$\cos\theta$とおく。方程式$f(\theta)$=0の解が0＜θ＜$\frac{\pi}{2}$の範囲に少なくとも一つ存在することを示せ。
(2)Dの座標をa,θを用いて表せ。
(3)θが0＜θ＜$\frac{\pi}{2}$の範囲を動くとき、3点A,P,Dが同一直線上にあるようなθは少なくとも一つ存在することを示せ。また、このようなθはただ一つであることを示せ。
2023北海道大学理系過去問
福田の数学〜北海道大学2023年理系第５問〜中間値の定理と関数の増減PART1
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#点と直線#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{5}$ a,bを$a^2$+$b^2$＜1をみたす正の実数とする。また、座標平面上で原点を中心とする半径1の円をCとし、Cの内部にある2点A(a,0), B(0,b)を考える。
0＜θ＜$\frac{\pi}{2}$に対してC上の点P($\cos\theta$, $\sin\theta$)を考え、PにおけるCの接線に関してBと対称な点をDとおく。
(1)f(θ)=ab$\cos2\theta$+a$\sin\theta$-b$\cos\theta$とおく。方程式f(θ)=0の解が0＜θ＜$\frac{\pi}{2}$の範囲に少なくとも1つ存在することを示せ。
(2)Dの座標をa, $\theta$を用いて表せ。
(3)θが0＜θ＜$\frac{\pi}{2}$の範囲を動くとき、3点A,P,Dが同一直線上にあるようなθは少なくとも1つ存在することを示せ。また、このようなθはただ1つであることを示せ。
2023北海道大学理系過去問
この動画を見る
$\Large\boxed{5}$ a,bを$a^2$+$b^2$＜1をみたす正の実数とする。また、座標平面上で原点を中心とする半径1の円をCとし、Cの内部にある2点A(a,0), B(0,b)を考える。
0＜θ＜$\frac{\pi}{2}$に対してC上の点P($\cos\theta$, $\sin\theta$)を考え、PにおけるCの接線に関してBと対称な点をDとおく。
(1)f(θ)=ab$\cos2\theta$+a$\sin\theta$-b$\cos\theta$とおく。方程式f(θ)=0の解が0＜θ＜$\frac{\pi}{2}$の範囲に少なくとも1つ存在することを示せ。
(2)Dの座標をa, $\theta$を用いて表せ。
(3)θが0＜θ＜$\frac{\pi}{2}$の範囲を動くとき、3点A,P,Dが同一直線上にあるようなθは少なくとも1つ存在することを示せ。また、このようなθはただ1つであることを示せ。
2023北海道大学理系過去問
福田の数学〜北海道大学2023年理系第４問〜絶対値の和の最小となる確率
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{4}$ nを2以上の自然数とする。1個のさいころをn回投げて出た目の数を順に$a_1$, $a_2$, ... ,$a_n$とし、
$K_n$=|1-$a_1$|+|$a_1$-$a_2$|+...+|$a_{n-1}$-$a_n$|+|$a_n$-6|
とおく。また$K_n$のとりうる値の最小値を$q_n$とする。
(1)$K_3$=5となる確率を求めよ。
(2)$q_n$を求めよ。また、$K_n$=$q_n$となるための$a_1$, $a_2$,...,$a_n$に関する必要十分条件を求めよ。
(3)nを4以上の自然数とする。$L_n$=$K_n$+|$a_4$-4|とおき、$L_n$のとりうる値の最小値を$r_n$とする。$L_n$=$r_n$となる確率$p_n$を求めよ。
2023北海道大学理系過去問
この動画を見る
$\Large\boxed{4}$ nを2以上の自然数とする。1個のさいころをn回投げて出た目の数を順に$a_1$, $a_2$, ... ,$a_n$とし、
$K_n$=|1-$a_1$|+|$a_1$-$a_2$|+...+|$a_{n-1}$-$a_n$|+|$a_n$-6|
とおく。また$K_n$のとりうる値の最小値を$q_n$とする。
(1)$K_3$=5となる確率を求めよ。
(2)$q_n$を求めよ。また、$K_n$=$q_n$となるための$a_1$, $a_2$,...,$a_n$に関する必要十分条件を求めよ。
(3)nを4以上の自然数とする。$L_n$=$K_n$+|$a_4$-4|とおき、$L_n$のとりうる値の最小値を$r_n$とする。$L_n$=$r_n$となる確率$p_n$を求めよ。
2023北海道大学理系過去問
福田の数学〜北海道大学2023年理系第３問〜指数方程式の解
単元：
#大学入試過去問(数学)#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{3}$ 以下の問いに答えよ。ただし、eは自然対数の底を表す。
(1)kを実数の定数とし、f(x)=$xe^{-x}$とおく。方程式f(x)=kの異なる実数解の個数を求めよ。ただし、$\displaystyle\lim_{x \to \infty}f(x)$=0を用いてもよい。
(2)$xye^{-(x+y)}$=cを満たす正の実数x, yの組がただ1つ存在するときの実数cの値を求めよ。
(3)$xye^{-(x+y)}$=$\frac{3}{e^4}$を満たす正の実数x, yを考えるとき、yのとりうる値の最大値とそのときのxの値を求めよ。
2023北海道大学理系過去問
この動画を見る
$\Large\boxed{3}$ 以下の問いに答えよ。ただし、eは自然対数の底を表す。
(1)kを実数の定数とし、f(x)=$xe^{-x}$とおく。方程式f(x)=kの異なる実数解の個数を求めよ。ただし、$\displaystyle\lim_{x \to \infty}f(x)$=0を用いてもよい。
(2)$xye^{-(x+y)}$=cを満たす正の実数x, yの組がただ1つ存在するときの実数cの値を求めよ。
(3)$xye^{-(x+y)}$=$\frac{3}{e^4}$を満たす正の実数x, yを考えるとき、yのとりうる値の最大値とそのときのxの値を求めよ。
2023北海道大学理系過去問
福田の数学〜北海道大学2023年理系第２問〜球面と平面の交わりと切り取られる弦の長さ
単元：
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{2}$ Oを原点とする座標空間において、3点A(4,2,1), B(1,-4,1), C(2,2,-1)を通る平面を$\alpha$とおく。また、球面Sは半径が9で、Sと$\alpha$の交わりはAを中心としBを通る円であるとする。ただし、Sの中心Pのz座標は正とする。
(1)線分APの長さを求めよ。
(2)Pの座標を求めよ。
(3)Sと直線OCは2点で交わる。その2点間の距離を求めよ。
2023北海道大学理系過去問
この動画を見る
$\Large\boxed{2}$ Oを原点とする座標空間において、3点A(4,2,1), B(1,-4,1), C(2,2,-1)を通る平面を$\alpha$とおく。また、球面Sは半径が9で、Sと$\alpha$の交わりはAを中心としBを通る円であるとする。ただし、Sの中心Pのz座標は正とする。
(1)線分APの長さを求めよ。
(2)Pの座標を求めよ。
(3)Sと直線OCは2点で交わる。その2点間の距離を求めよ。
2023北海道大学理系過去問
福田の数学〜北海道大学2023年理系第１問〜複素数平面上の図形の列
単元：
#大学入試過去問(数学)#複素数平面#関数と極限#複素数平面#図形への応用#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数C#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ 複素数平面上における図形$C_1$, $C_2$, ...,$C_n$, ...は次の条件(A)と(B)を満たすとする。ただし、$i$は虚数単位とする。
(A)$C_1$は原点Oを中心とする半径2の円である。
(B)自然数nに対して、zが$C_n$上を動くとき2w=z+1+$i$で定まるwの描く図形が$C_{n+1}$である。
(1)すべての自然数nに対して、$C_n$は円であることを示し、その中心を表す複素数$\alpha_n$と半径$r_n$を求めよ。
(2)$C_n$上の点とOとの距離の最小値を$d_n$とする。このとき、$d_n$を求めよ。
また、$\displaystyle\lim_{n \to \infty}d_n$を求めよ。
2023北海道大学理系過去問
この動画を見る
$\Large\boxed{1}$ 複素数平面上における図形$C_1$, $C_2$, ...,$C_n$, ...は次の条件(A)と(B)を満たすとする。ただし、$i$は虚数単位とする。
(A)$C_1$は原点Oを中心とする半径2の円である。
(B)自然数nに対して、zが$C_n$上を動くとき2w=z+1+$i$で定まるwの描く図形が$C_{n+1}$である。
(1)すべての自然数nに対して、$C_n$は円であることを示し、その中心を表す複素数$\alpha_n$と半径$r_n$を求めよ。
(2)$C_n$上の点とOとの距離の最小値を$d_n$とする。このとき、$d_n$を求めよ。
また、$\displaystyle\lim_{n \to \infty}d_n$を求めよ。
2023北海道大学理系過去問
福田の1.5倍速演習〜合格する重要問題082〜北海道大学2018年度理系第５問〜不等式の証明と面積
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{5}$ 2つの関数
f(x)=$\cos x$, g(x)=$\displaystyle\sqrt{\frac{\pi^2}{2}-x^2-\frac{\pi}{2}}$
がある。
(1)0≦x≦$\frac{\pi}{2}$のとき、不等式$\frac{2}{\pi}x$≦$\sin x$が成り立つことを示せ。
(2)0≦x≦$\frac{\pi}{2}$のとき、不等式g(x)≦f(x)が成り立つことを示せ。
(3)0≦x≦$\frac{\pi}{2}$の範囲において、2つの曲線y=f(x), y=g(x)およびy軸が囲む部分の面積を求めよ。
2018北海道大学理系過去問
この動画を見る
$\Large\boxed{5}$ 2つの関数
f(x)=$\cos x$, g(x)=$\displaystyle\sqrt{\frac{\pi^2}{2}-x^2-\frac{\pi}{2}}$
がある。
(1)0≦x≦$\frac{\pi}{2}$のとき、不等式$\frac{2}{\pi}x$≦$\sin x$が成り立つことを示せ。
(2)0≦x≦$\frac{\pi}{2}$のとき、不等式g(x)≦f(x)が成り立つことを示せ。
(3)0≦x≦$\frac{\pi}{2}$の範囲において、2つの曲線y=f(x), y=g(x)およびy軸が囲む部分の面積を求めよ。
2018北海道大学理系過去問