 一橋大学
一橋大学
 一橋大学
一橋大学
福田の数学〜一橋大学2025文系第4問〜ベクトル方程式と領域と角を2等分するベクトル

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#図形と方程式#軌跡と領域#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
原点を$O$とする座標空間内の
$2$点$A(0,3,-5),B(5,-2,10)$に対して
$\overrightarrow{OP}=s\left \{ (1-t)\overrightarrow{OA}+t\overrightarrow{OB} \right \},x\geqq 0,\dfrac{1}{5} \leqq t \leqq \dfrac{3}{5}$
で定まる点$P$が存在する範囲を$D$とする。
$D$に含まれる半径$10\sqrt2$の円のうち、
その中心と原点との距離が最小となるものを
$C$とする。
円$C$の中心の座標を求めよ。
$2025$年一橋大学文系過去問題
この動画を見る
$\boxed{4}$
原点を$O$とする座標空間内の
$2$点$A(0,3,-5),B(5,-2,10)$に対して
$\overrightarrow{OP}=s\left \{ (1-t)\overrightarrow{OA}+t\overrightarrow{OB} \right \},x\geqq 0,\dfrac{1}{5} \leqq t \leqq \dfrac{3}{5}$
で定まる点$P$が存在する範囲を$D$とする。
$D$に含まれる半径$10\sqrt2$の円のうち、
その中心と原点との距離が最小となるものを
$C$とする。
円$C$の中心の座標を求めよ。
$2025$年一橋大学文系過去問題
福田の数学〜一橋大学2025文系第3問〜定積分で表された方程式の解の個数

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
等式
$6\displaystyle \int_{0}^{2} \vert x^2-a \vert dx-a^2-2a+k$
が成り立つ実数$a$がちょうど$4$つ存在するような
実数$k$の範囲を求めよ。
$2025$年一橋大学文系過去問題
この動画を見る
$\boxed{3}$
等式
$6\displaystyle \int_{0}^{2} \vert x^2-a \vert dx-a^2-2a+k$
が成り立つ実数$a$がちょうど$4$つ存在するような
実数$k$の範囲を求めよ。
$2025$年一橋大学文系過去問題
福田の数学〜一橋大学2025文系第2問〜円と円の交点を通る直線に対称な点の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
座標平面上に原点を中心とす半径$3$の円$C_1$がある。
また、直線$x=2$上の点$P$を中心とする半径$1$の円を
$C_2$とする。
(1)$C_1$と$C_2$が共有点を$2$つ持つような$P$の
$y$座標の範囲を求めよ。
(2)$C_1$と$C_2$が共有点を$2$つ持つとき、
その$2$つの共有点を通る直線を$\ell$とする。
$\ell$に関して$P$と対称な位置にある点を$Q$とする。
ただし、$P$が$\ell$上にあるときは$Q=P$とする。
$P$の$y$座標が(1)で求めた範囲を動くとき、
点$Q$の軌跡を求め、図示せよ。
$2025$年一橋大学文系過去問題
この動画を見る
$\boxed{2}$
座標平面上に原点を中心とす半径$3$の円$C_1$がある。
また、直線$x=2$上の点$P$を中心とする半径$1$の円を
$C_2$とする。
(1)$C_1$と$C_2$が共有点を$2$つ持つような$P$の
$y$座標の範囲を求めよ。
(2)$C_1$と$C_2$が共有点を$2$つ持つとき、
その$2$つの共有点を通る直線を$\ell$とする。
$\ell$に関して$P$と対称な位置にある点を$Q$とする。
ただし、$P$が$\ell$上にあるときは$Q=P$とする。
$P$の$y$座標が(1)で求めた範囲を動くとき、
点$Q$の軌跡を求め、図示せよ。
$2025$年一橋大学文系過去問題
福田の数学〜一橋大学2025文系第1問〜正の約数の個数と関数の最大値

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
正の整数$n$に対し、$n$の正の約数の個数を
$d(n)$とする。
たとえば、$6$の正の約数は$1,2,3,6$の$4$個なので、
$d(6)=4$である。また、
$f(n)=\dfrac{d(n)}{\sqrt n}$
とする。
(1)$f(2025)$を求めよ。
(2)素数$p$と正の整数$k$の組で
$f(p^k)\leqq f(p^{k+1})$を満たすものを求めよ。
(3)$f(n)$の最大値と、そのときの$n$を求めよ。
$2025$年一橋大学文系過去問題
この動画を見る
$\boxed{1}$
正の整数$n$に対し、$n$の正の約数の個数を
$d(n)$とする。
たとえば、$6$の正の約数は$1,2,3,6$の$4$個なので、
$d(6)=4$である。また、
$f(n)=\dfrac{d(n)}{\sqrt n}$
とする。
(1)$f(2025)$を求めよ。
(2)素数$p$と正の整数$k$の組で
$f(p^k)\leqq f(p^{k+1})$を満たすものを求めよ。
(3)$f(n)$の最大値と、そのときの$n$を求めよ。
$2025$年一橋大学文系過去問題
解ける?一橋大学の整数問題の難問! #Shorts #ずんだもん #勉強 #数学

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
nを2以上20以下の整数、
kを1以上n-1以下の整数とする。
n+2Ck+1=2(nCk-1+nCk+1)
が成り立つような整数の組(n,k)を求めよ。
この動画を見る
nを2以上20以下の整数、
kを1以上n-1以下の整数とする。
n+2Ck+1=2(nCk-1+nCk+1)
が成り立つような整数の組(n,k)を求めよ。
2次方程式の解を四捨五入!?あまり見かけない問題。解ける? #Shorts #ずんだもん #勉強 #数学

単元:
#数Ⅰ#数A#大学入試過去問(数学)#2次関数#2次方程式と2次不等式#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
m,nを正の整数とする。xについての2次方程式 12x^2-mx+n=0 の2つの実数解を小数第2位で四捨五入して0.3および0.7を得た。m,nを求めよ。
この動画を見る
m,nを正の整数とする。xについての2次方程式 12x^2-mx+n=0 の2つの実数解を小数第2位で四捨五入して0.3および0.7を得た。m,nを求めよ。
対数と整数の融合問題!難問です!解ける? #Shorts #ずんだもん #勉強 #数学

単元:
#数A#数Ⅱ#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
logy_(6x+y)=xを満たす正の整数x,yの組を求めよ。
この動画を見る
logy_(6x+y)=xを満たす正の整数x,yの組を求めよ。
三角関数と整数の融合問題!整数問題の大事な考え方が詰まっています

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
三角形ABCにおいて、tanA,tanB,tanCの値がすべて整数のとき、それらの値を求めよ。
この動画を見る
三角形ABCにおいて、tanA,tanB,tanCの値がすべて整数のとき、それらの値を求めよ。
整数問題の良問!どうやって解く? #Shorts #ずんだもん #勉強 #数学

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
直角三角形の3辺の長さがすべて整数のとき、面積は2の整数倍であることを示せ。
この動画を見る
直角三角形の3辺の長さがすべて整数のとき、面積は2の整数倍であることを示せ。
シンプルで難しい整数問題 #Shorts #ずんだもん #勉強 #数学

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
連立方程式
x²=yz+7
y²=zx+7
z²=xy+7
を満たす整数の組(x,y,z)でx<=y<=zとなるものを求めよ。
この動画を見る
連立方程式
x²=yz+7
y²=zx+7
z²=xy+7
を満たす整数の組(x,y,z)でx<=y<=zとなるものを求めよ。
大小比較の難問!どう解く?

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#対数関数#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
e^πとπ^eの大小を比較せよ。
この動画を見る
e^πとπ^eの大小を比較せよ。
意外と差がつく!互いに素の証明!できるようになっておきたい【一橋大学】【数学 入試問題】

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
nは正の整数とする。n^2と2n+1は互いに素であることを示せ。
この動画を見る
nは正の整数とする。n^2と2n+1は互いに素であることを示せ。
大学入試問題#920「工夫しがいがある問題」

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$f(x)=\displaystyle \frac{x^4+x^2+1}{x^3-1}(x \gt 1)$
出典:1963年 一橋大学
この動画を見る
$f(x)=\displaystyle \frac{x^4+x^2+1}{x^3-1}(x \gt 1)$
出典:1963年 一橋大学
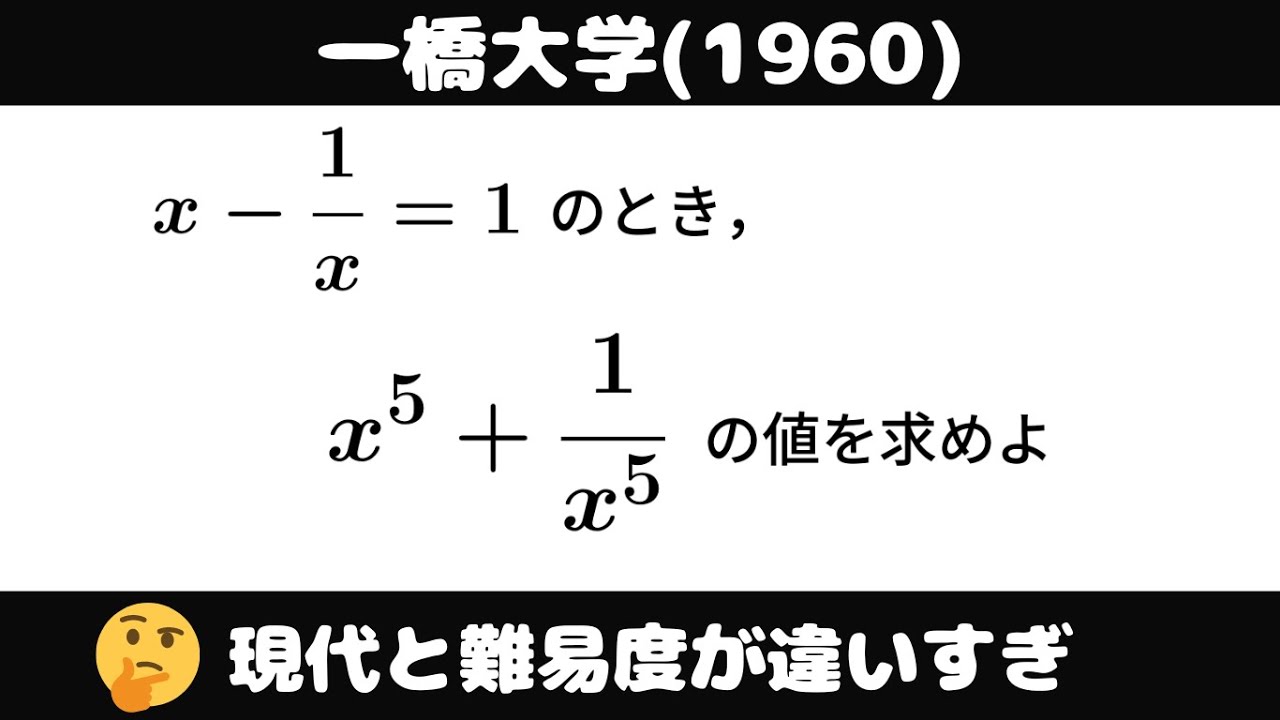
大学入試問題#919「昔は落ち着いた問題」
単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$x-\displaystyle \frac{1}{x}=1$のとき、
$x^5+\displaystyle \frac{1}{x^5}$の値を求めよ。
出典:一橋大(1960)
この動画を見る
$x-\displaystyle \frac{1}{x}=1$のとき、
$x^5+\displaystyle \frac{1}{x^5}$の値を求めよ。
出典:一橋大(1960)
福田のおもしろ数学182〜2x3x5x7x11x13の10乗の桁数

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$(2×3×5×7×11×13)^{10}$ の10進法での桁数を求めよ。
この動画を見る
$(2×3×5×7×11×13)^{10}$ の10進法での桁数を求めよ。
福田の数学〜一橋大学2024年文系第3問〜多項式の商と余り

単元:
#数Ⅱ#剰余の定理・因数定理・組み立て除法と高次方程式#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ $f(x)$は$x$に関する4次方程式で4次の係数は1である。$f(x)$は$(x+1)^2$で割ると1余り、$(x-1)^2$で割ると2余る。$f(x)$を求めよ。
この動画を見る
$\Large\boxed{3}$ $f(x)$は$x$に関する4次方程式で4次の係数は1である。$f(x)$は$(x+1)^2$で割ると1余り、$(x-1)^2$で割ると2余る。$f(x)$を求めよ。
福田の数学〜一橋大学2024年文系第2問〜2つの放物線が共有点で接線直交する条件

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ $a$, $b$を実数とする。曲線$C$:$y$=$x^2$ と曲線$C'$:$y$=$-x^2$+$ax$+$b$はある点を共有しており、その点におけるそれぞれの接線は直交している。$C$と$C'$で囲まれた部分の面積の最小値を求めよ。
この動画を見る
$\Large\boxed{2}$ $a$, $b$を実数とする。曲線$C$:$y$=$x^2$ と曲線$C'$:$y$=$-x^2$+$ax$+$b$はある点を共有しており、その点におけるそれぞれの接線は直交している。$C$と$C'$で囲まれた部分の面積の最小値を求めよ。
福田の数学〜一橋大学2024年文系第1問〜シグマが2024になるような2変数の値

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ $\displaystyle\sum_{k=1}^mk(n-2k)$=2024 を満たす正の整数の組($m$, $n$)を求めよ。
この動画を見る
$\Large\boxed{1}$ $\displaystyle\sum_{k=1}^mk(n-2k)$=2024 を満たす正の整数の組($m$, $n$)を求めよ。
大学入試問題#726「一橋レベルでこれは落とせん」 一橋大学(2021)積分方程式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$f(x)$は微分可能かつ導関数が連続な関数とする。
$f(0)=0$であるとき、
$\displaystyle \frac{d}{dx}(\displaystyle \int_{0}^{x} e^{-t}f(x-t)dt)=\displaystyle \int_{0}^{x} e^{-t}f'(x-t)dt$ を示せ
出典:2021年一橋大学後期 入試問題
この動画を見る
$f(x)$は微分可能かつ導関数が連続な関数とする。
$f(0)=0$であるとき、
$\displaystyle \frac{d}{dx}(\displaystyle \int_{0}^{x} e^{-t}f(x-t)dt)=\displaystyle \int_{0}^{x} e^{-t}f'(x-t)dt$ を示せ
出典:2021年一橋大学後期 入試問題
大学入試問題#723「いつもとタイプが違う」 一橋大学(2023)整数問題

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\sqrt{ m }+\sqrt{ n }=\sqrt{ 2023 }$を満たす自然数の組$(m,n)$の個数を求めよ。
出典:2023年一橋大学後期 入試問題
この動画を見る
$\sqrt{ m }+\sqrt{ n }=\sqrt{ 2023 }$を満たす自然数の組$(m,n)$の個数を求めよ。
出典:2023年一橋大学後期 入試問題
一橋大 確率のふりをした整数問題

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
赤玉x個、白玉x個の中から2個取り出す。
同じ色の玉が出る確率と異なる色の玉が出る確率が等しい(x,y)の組をすべて求めよ。
一橋大学過去問
この動画を見る
赤玉x個、白玉x個の中から2個取り出す。
同じ色の玉が出る確率と異なる色の玉が出る確率が等しい(x,y)の組をすべて求めよ。
一橋大学過去問
【数学A】一橋大学文系2010 確率の問題(解説)

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数B
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
$n$を3以上の自然数とする
サイコロを$n$回投げ、出た目の数をそれぞれ順に$X_1,X_2,$・・・$,X_n$とする
$i=2,3,…n$に対して$Xi=Xi-1$となる事象を$Ai$ことする。
(1)$A_2,A_3,…,A_n$のうち少なくとも1つが起こる確率$pn$は?
(2)$A_2,A_3,…,A_n$少なくとも2つが起こる確率$gn$は?
この動画を見る
$n$を3以上の自然数とする
サイコロを$n$回投げ、出た目の数をそれぞれ順に$X_1,X_2,$・・・$,X_n$とする
$i=2,3,…n$に対して$Xi=Xi-1$となる事象を$Ai$ことする。
(1)$A_2,A_3,…,A_n$のうち少なくとも1つが起こる確率$pn$は?
(2)$A_2,A_3,…,A_n$少なくとも2つが起こる確率$gn$は?
福田の数学〜一橋大学2023年文系第5問〜反復試行の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ A, B, Cの3人が、A, B, C, A, B, C, A, ... という順番にさいころを投げ、最初に1を出した人を勝ちとする。だれかが1を出すか、全員が$n$回ずつ投げたら、ゲームを終了する。A, B, Cが勝つ確率$P_A$, $P_B$, $P_C$をそれぞれ求めよ。
2023一橋大学文系過去問
この動画を見る
$\Large\boxed{5}$ A, B, Cの3人が、A, B, C, A, B, C, A, ... という順番にさいころを投げ、最初に1を出した人を勝ちとする。だれかが1を出すか、全員が$n$回ずつ投げたら、ゲームを終了する。A, B, Cが勝つ確率$P_A$, $P_B$, $P_C$をそれぞれ求めよ。
2023一橋大学文系過去問
福田の数学〜一橋大学2023年文系第4問〜群数列

単元:
#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ xy平面上で、x座標とy座標がともに正の整数であるような各点に、下の図のような番号をつける。(※動画参照)点(m, n)につけた番号をf(m, n)とする。
たとえば、$f(1, 1)=1, f(3, 4)=19$ である。
(1)$f(m, n)+f(m+1, n+1)=2f(m, n+1)$
が成り立つことを示せ。
(2)$f(m, n)+f(m+1, n)+f(m, n+1)+f(m+1, n+1)=2023$
となるような整数の組(m, n)を求めよ。
2023一橋大学文系過去問
この動画を見る
$\Large\boxed{4}$ xy平面上で、x座標とy座標がともに正の整数であるような各点に、下の図のような番号をつける。(※動画参照)点(m, n)につけた番号をf(m, n)とする。
たとえば、$f(1, 1)=1, f(3, 4)=19$ である。
(1)$f(m, n)+f(m+1, n+1)=2f(m, n+1)$
が成り立つことを示せ。
(2)$f(m, n)+f(m+1, n)+f(m, n+1)+f(m+1, n+1)=2023$
となるような整数の組(m, n)を求めよ。
2023一橋大学文系過去問
福田の数学〜一橋大学2023年文系第3問〜ベクトルと四面体の体積の最大

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 原点をOとする座標空間内に3点A(-3, 2, 0), B(1, 5, 0), C(4, 5, 1)がある。
Pは|$\overrightarrow{PA}$+3$\overrightarrow{PB}$+2$\overrightarrow{PC}$|≦36 を満たす点である。
4点O, A, B, Pが同一平面上にないとき、四面体OABPの体積の最大値を求めよ。
2023一橋大学文系過去問
この動画を見る
$\Large\boxed{3}$ 原点をOとする座標空間内に3点A(-3, 2, 0), B(1, 5, 0), C(4, 5, 1)がある。
Pは|$\overrightarrow{PA}$+3$\overrightarrow{PB}$+2$\overrightarrow{PC}$|≦36 を満たす点である。
4点O, A, B, Pが同一平面上にないとき、四面体OABPの体積の最大値を求めよ。
2023一橋大学文系過去問
福田の数学〜一橋大学2023年文系第2問〜共通接線が存在する条件

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ aを正の実数とする。2つの曲線$C_1$:y=$x^3$+2$ax^2$ および$C_2$:y=3$ax^2$$-\displaystyle\frac{3}{a}$ の両方に接する直線が存在するようなaの範囲を求めよ。
2023一橋大学文系過去問
この動画を見る
$\Large\boxed{2}$ aを正の実数とする。2つの曲線$C_1$:y=$x^3$+2$ax^2$ および$C_2$:y=3$ax^2$$-\displaystyle\frac{3}{a}$ の両方に接する直線が存在するようなaの範囲を求めよ。
2023一橋大学文系過去問
福田の数学〜一橋大学2023年文系第1問〜コンビネーションの等式を満たす自然数

単元:
#数A#大学入試過去問(数学)#場合の数と確率#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ nを2以上20以下の整数、kを1以上n-1以下の整数とする。
${}_{n+2}C_{k+1}$=2(${}_nC_{k-1}$+${}_nC_{k+1}$)
が成り立つような整数の組(n, k)を求めよ。
2023一橋大学文系過去問
この動画を見る
$\Large\boxed{1}$ nを2以上20以下の整数、kを1以上n-1以下の整数とする。
${}_{n+2}C_{k+1}$=2(${}_nC_{k-1}$+${}_nC_{k+1}$)
が成り立つような整数の組(n, k)を求めよ。
2023一橋大学文系過去問
整数問題!問題文でかなり範囲が絞られている!?さらに候補を絞り込もう!【一橋大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
nを2以上20以下の整数、kを1以上n-1以下の整数とする。
${}_{n+1} \mathrm{ C }_{k+1}$=$2({}_n \mathrm{ C }_{k-1}+{}_n \mathrm{ C }_{k+1})$
が成り立つような整数の組(n,k)を求めよ。
一橋大過去問
この動画を見る
nを2以上20以下の整数、kを1以上n-1以下の整数とする。
${}_{n+1} \mathrm{ C }_{k+1}$=$2({}_n \mathrm{ C }_{k-1}+{}_n \mathrm{ C }_{k+1})$
が成り立つような整数の組(n,k)を求めよ。
一橋大過去問
2023一橋大 確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
A,B,Cの3人が順番にサイコロを振り,最初に1を出した人が勝ち,
だれかが1を出すか、全員がn回ずつ振ったら終了
A,B,Cそれぞれが勝つ確率$P_A,P_B,P_C$を求めよ.
2023一橋大過去問
この動画を見る
A,B,Cの3人が順番にサイコロを振り,最初に1を出した人が勝ち,
だれかが1を出すか、全員がn回ずつ振ったら終了
A,B,Cそれぞれが勝つ確率$P_A,P_B,P_C$を求めよ.
2023一橋大過去問
極限の難問!答えは予測できるが・・・【一橋大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$\displaystyle \lim_{ x \to \infty }(\cos^2 \sqrt{x+1}+\sin^2\sqrt{x})$を求めよ。
一橋大過去問
この動画を見る
$\displaystyle \lim_{ x \to \infty }(\cos^2 \sqrt{x+1}+\sin^2\sqrt{x})$を求めよ。
一橋大過去問
