 上智大学
上智大学
 上智大学
上智大学
福田の数学〜上智大学2025TEAP利用型文系第1問〜放物線と円の位置関係と面積

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
座標平面上の放物線$C_1:y=x^2$と
円$C_2:x^2+(y-b)^2=a^2$を考える。
ただし、$a,b$は正の実数とする。
(1)$C_1$と$C_2$が共有点をちょうど$3$つもつための
必要十分条件は
$b=\boxed{ア}a$かつ$a\gt \dfrac{\boxed{イ}}{\boxed{ウ}}$である。
(2)$C_1$と$C_2$が異なる$2$点で接するための
必要十分条件は
$b=\boxed{エ}a^2+\dfrac{\boxed{オ}}{\boxed{カ}}$かつ$a\gt \dfrac{\boxed{キ}}{\boxed{ク}}$である。
(ただし、$C_1$と$C_2$が共有点$P$で接するとは、
$P$における$C_1$の接線と$C_"$の接線が等しいことをいう)
また、このとき$2$つの接点のうち$x$座標が
正のものを$A(\alpha,\beta)$とすると、
$\beta=\boxed{ケ}a^2+\dfrac{\boxed{コ}}{\boxed{サ}}$である。
$A$における共通の接線の傾きが$\sqrt3$であるとき、
直線$y=\beta$の下側で、
$C_1$と$C_2$に囲まれた部分の面積は
$\dfrac{\boxed{シ}}{\boxed{ス}}\sqrt{\boxed{セ}}-\dfrac{\pi}{\boxed{ソ}}$である。
$2025$年上智大学TEAP利用型文系過去問題
この動画を見る
$\boxed{1}$
座標平面上の放物線$C_1:y=x^2$と
円$C_2:x^2+(y-b)^2=a^2$を考える。
ただし、$a,b$は正の実数とする。
(1)$C_1$と$C_2$が共有点をちょうど$3$つもつための
必要十分条件は
$b=\boxed{ア}a$かつ$a\gt \dfrac{\boxed{イ}}{\boxed{ウ}}$である。
(2)$C_1$と$C_2$が異なる$2$点で接するための
必要十分条件は
$b=\boxed{エ}a^2+\dfrac{\boxed{オ}}{\boxed{カ}}$かつ$a\gt \dfrac{\boxed{キ}}{\boxed{ク}}$である。
(ただし、$C_1$と$C_2$が共有点$P$で接するとは、
$P$における$C_1$の接線と$C_"$の接線が等しいことをいう)
また、このとき$2$つの接点のうち$x$座標が
正のものを$A(\alpha,\beta)$とすると、
$\beta=\boxed{ケ}a^2+\dfrac{\boxed{コ}}{\boxed{サ}}$である。
$A$における共通の接線の傾きが$\sqrt3$であるとき、
直線$y=\beta$の下側で、
$C_1$と$C_2$に囲まれた部分の面積は
$\dfrac{\boxed{シ}}{\boxed{ス}}\sqrt{\boxed{セ}}-\dfrac{\pi}{\boxed{ソ}}$である。
$2025$年上智大学TEAP利用型文系過去問題
福田の数学〜上智大学2024理工学部第3問〜円の内部を反射しながら進む点の通過範囲

単元:
#大学入試過去問(数学)#平面上のベクトル#数列#平面上のベクトルと内積#漸化式#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数B#数C
指導講師:
福田次郎
問題文全文(内容文):
点$O$を中心とし半径が$1$の円形のビリヤード台がある。台の縁の点$P_1$に大きさが無視できる球$Q$を置き、半径$P_1O$とのなす角が$\frac{\pi}{8}$の方向へ球$Q$を打ち出す。
球$Q$は、ビリヤード台の縁に当たると、図のように入射角と反射角が等しくなるように反射し、一度打ち出されたら止まらないものとする。
$i=1,2,3,\cdots$に対し、点$P_i$の次に球$Q$が縁に当たる点を$P_{i+1}$とし、$\overrightarrow{OP_i}=\overrightarrow{p_i}$とする。
(1)$\overrightarrow{p_3}=\fbox{あ}\overrightarrow{p_1}+\fbox{い}\overrightarrow{p_2},\overrightarrow{p_4}=\fbox{う}\overrightarrow{p_1}+\fbox{え}\overrightarrow{p_2}$である。
(2)$P_i=P_1となるiのうち、 i\geqq 2で最小のものは\fbox{ソ}である。$
(3)$線分P_1P_2とP_3P_4 との交点をA、線分P_1P_2とP_6P_7との交点をBとすると$
$\overrightarrow{OA}=\fbox{お}\overrightarrow{p_1}+\fbox{か}\overrightarrow{p_2},\overrightarrow{OB}=\fbox{き}\overrightarrow{p_1}+\fbox{く}\overrightarrow{p_2}$である。
(4)球$Q$が点$P_1$から打ち出されてから初めて再び点$P_1$に到達するまでに、中心$O$と球$Q$とを結ぶ線分$OQ$がちょうど2回通過する領域の面積は$\fbox{タ}+\fbox{チ}\sqrt{2}$である。
この動画を見る
点$O$を中心とし半径が$1$の円形のビリヤード台がある。台の縁の点$P_1$に大きさが無視できる球$Q$を置き、半径$P_1O$とのなす角が$\frac{\pi}{8}$の方向へ球$Q$を打ち出す。
球$Q$は、ビリヤード台の縁に当たると、図のように入射角と反射角が等しくなるように反射し、一度打ち出されたら止まらないものとする。
$i=1,2,3,\cdots$に対し、点$P_i$の次に球$Q$が縁に当たる点を$P_{i+1}$とし、$\overrightarrow{OP_i}=\overrightarrow{p_i}$とする。
(1)$\overrightarrow{p_3}=\fbox{あ}\overrightarrow{p_1}+\fbox{い}\overrightarrow{p_2},\overrightarrow{p_4}=\fbox{う}\overrightarrow{p_1}+\fbox{え}\overrightarrow{p_2}$である。
(2)$P_i=P_1となるiのうち、 i\geqq 2で最小のものは\fbox{ソ}である。$
(3)$線分P_1P_2とP_3P_4 との交点をA、線分P_1P_2とP_6P_7との交点をBとすると$
$\overrightarrow{OA}=\fbox{お}\overrightarrow{p_1}+\fbox{か}\overrightarrow{p_2},\overrightarrow{OB}=\fbox{き}\overrightarrow{p_1}+\fbox{く}\overrightarrow{p_2}$である。
(4)球$Q$が点$P_1$から打ち出されてから初めて再び点$P_1$に到達するまでに、中心$O$と球$Q$とを結ぶ線分$OQ$がちょうど2回通過する領域の面積は$\fbox{タ}+\fbox{チ}\sqrt{2}$である。
福田の数学〜上智大学2024理工学部第1問(3)〜回路に電流が流れて電球が点灯する確率の最大
単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
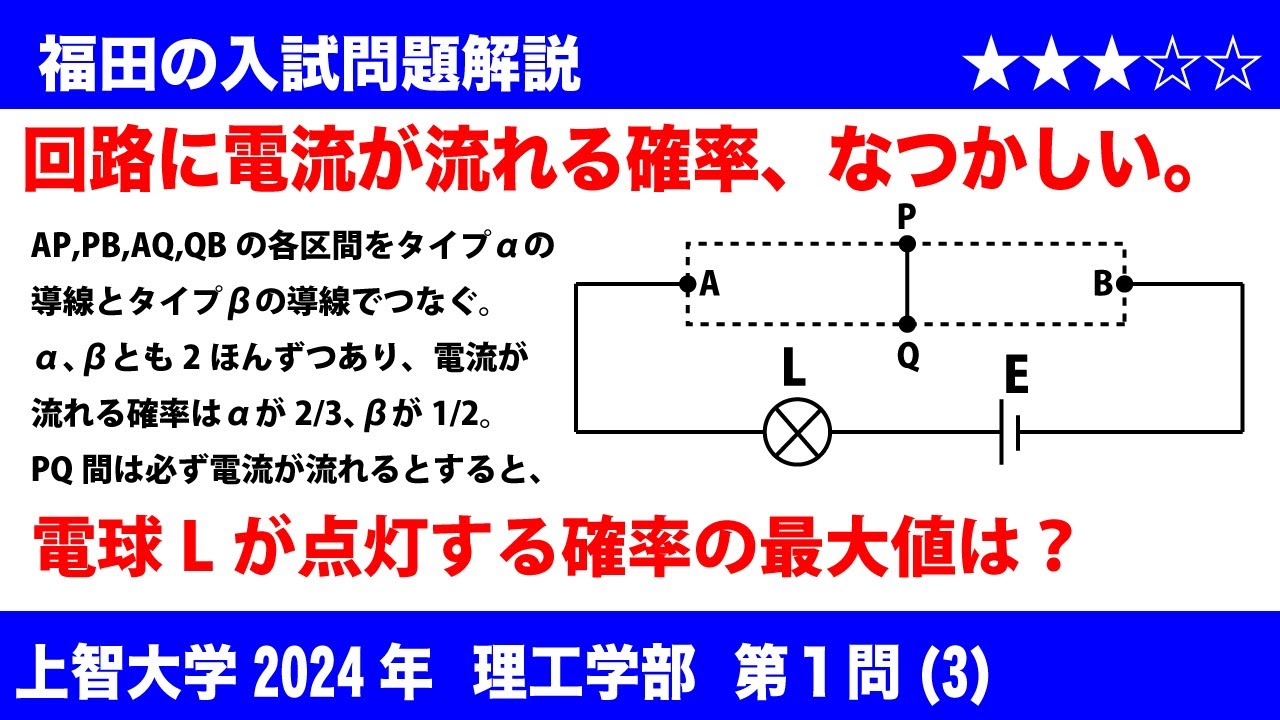
次の図で表される回路は、$\rm AP$間、$\rm AQ$間、$\rm PB$間、$\rm QB$間がつながっておらず、それぞれの区間を1本の導線でつなぐことができる。$\rm P$または$\rm Q$を経由して$\rm AB$間がつながり電流が流れると電球が点灯する。導線にはタイプαが2本、タイプβが2本ある。それぞれの導線に電流が流れる確率はタイプαが$\dfrac23$、タイプβが$\dfrac12$である。
(i) $\rm AP$間、$\rm PB$間を2本のタイプαの導線でそれぞれつなぐとき、$\rm L$が点灯する確率は?
(ii) $\rm AP$間、$\rm AQ$間、$\rm PB$間、$\rm QB$間でそれぞれつなぐすべてのパターンを考える。$\rm L$が点灯する確率が最も大きくなるときの確率は?
(iii) $\rm PQ$間を確実に電流が流れる別の導線でつなぎ、$\rm AP$間、$\rm AQ$間、$\rm PB$間、$\rm QB$間を4本の導線でそれぞれつなぐすべてのパターンを考える。$\rm L$が点灯する確率が最も大きくなるときの確率は?
この動画を見る
次の図で表される回路は、$\rm AP$間、$\rm AQ$間、$\rm PB$間、$\rm QB$間がつながっておらず、それぞれの区間を1本の導線でつなぐことができる。$\rm P$または$\rm Q$を経由して$\rm AB$間がつながり電流が流れると電球が点灯する。導線にはタイプαが2本、タイプβが2本ある。それぞれの導線に電流が流れる確率はタイプαが$\dfrac23$、タイプβが$\dfrac12$である。
(i) $\rm AP$間、$\rm PB$間を2本のタイプαの導線でそれぞれつなぐとき、$\rm L$が点灯する確率は?
(ii) $\rm AP$間、$\rm AQ$間、$\rm PB$間、$\rm QB$間でそれぞれつなぐすべてのパターンを考える。$\rm L$が点灯する確率が最も大きくなるときの確率は?
(iii) $\rm PQ$間を確実に電流が流れる別の導線でつなぎ、$\rm AP$間、$\rm AQ$間、$\rm PB$間、$\rm QB$間を4本の導線でそれぞれつなぐすべてのパターンを考える。$\rm L$が点灯する確率が最も大きくなるときの確率は?
福田の数学〜上智大学2024理工学部第1問(2)〜定積分の計算

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\dfrac{2\sin x}{x^3}dx=-\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\dfrac{\sin x}{x}dx+\fbox{エ}\pi^p+\fbox{オ}\sqrt{\fbox{カ}}\pi^q$
ただし、$p=\fbox{キ},q=\fbox{ク}$である。
この動画を見る
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\dfrac{2\sin x}{x^3}dx=-\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\dfrac{\sin x}{x}dx+\fbox{エ}\pi^p+\fbox{オ}\sqrt{\fbox{カ}}\pi^q$
ただし、$p=\fbox{キ},q=\fbox{ク}$である。
福田の数学〜上智大学2024TEAP利用型理系第1問(3)〜対数不等式を満たす最小の整数

単元:
#大学入試過去問(数学)#指数関数と対数関数#対数関数#微分とその応用#色々な関数の導関数#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
(i) $\log_{10} 2=0.301$とする。このとき、$\log_{10} 1.28=0.\boxed{ウ}$である。
(ii)$n$は$2$以上の整数とする。$n^{100}<1.28^n$となる最小の$n$について、$2^a \leqq n < 2^{a+1}$となる整数$a$は$\boxed{エ}$
この動画を見る
(i) $\log_{10} 2=0.301$とする。このとき、$\log_{10} 1.28=0.\boxed{ウ}$である。
(ii)$n$は$2$以上の整数とする。$n^{100}<1.28^n$となる最小の$n$について、$2^a \leqq n < 2^{a+1}$となる整数$a$は$\boxed{エ}$
福田の数学〜上智大学2024TEAP利用型理系第1問(1)〜不定方程式の解

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}(1)77x+52y=1$を満たす整数$x$、$y$の組のうち、$x$が正で最小の組は$(x,y)=(\boxed{ア},\boxed{イ})$である。
この動画を見る
$\boxed{1}(1)77x+52y=1$を満たす整数$x$、$y$の組のうち、$x$が正で最小の組は$(x,y)=(\boxed{ア},\boxed{イ})$である。
福田の数学〜上智大学2024TEAP利用型文系第3問(4)〜線分の通過範囲の面積

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#軌跡と領域#学校別大学入試過去問解説(数学)#不定積分・定積分#面積、体積#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}(4)$座標平面上で放物線$y=x^2$上の点P$(t,t^2)(0 \leqq t \leqq 1)$における接線$y=-(x+1)^2$の二つの共有点の中点をQとする。ただし、共有点が1つの場合は、その共有点をQとする。Qの座標は$(\boxed{ユ}t+\boxed{ヨ}
,\boxed{ラ}t^2+\boxed{リ}t+\boxed{ル})$である。
tが$0 \leqq t \leqq1$の範囲を動くとき線分PQが動いてできる図形の面積は$\frac{\boxed{レ}}{\boxed{ロ}}$である
この動画を見る
$\boxed{2}(4)$座標平面上で放物線$y=x^2$上の点P$(t,t^2)(0 \leqq t \leqq 1)$における接線$y=-(x+1)^2$の二つの共有点の中点をQとする。ただし、共有点が1つの場合は、その共有点をQとする。Qの座標は$(\boxed{ユ}t+\boxed{ヨ}
,\boxed{ラ}t^2+\boxed{リ}t+\boxed{ル})$である。
tが$0 \leqq t \leqq1$の範囲を動くとき線分PQが動いてできる図形の面積は$\frac{\boxed{レ}}{\boxed{ロ}}$である
福田の数学〜上智大学2024TEAP利用型文系第3問(3)〜直線の回転

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}(3)$座標平面において、直線$y=2x-3$を、原点を中心に反時計回りに45°回転して得られる直線は$y=\boxed{メ}x+\boxed{モ}\sqrt{\boxed{ヤ}}$である。
この動画を見る
$\boxed{3}(3)$座標平面において、直線$y=2x-3$を、原点を中心に反時計回りに45°回転して得られる直線は$y=\boxed{メ}x+\boxed{モ}\sqrt{\boxed{ヤ}}$である。
福田の数学〜上智大学2024TEAP利用型文系第3問(2)〜角の二等分線の長さを求める
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
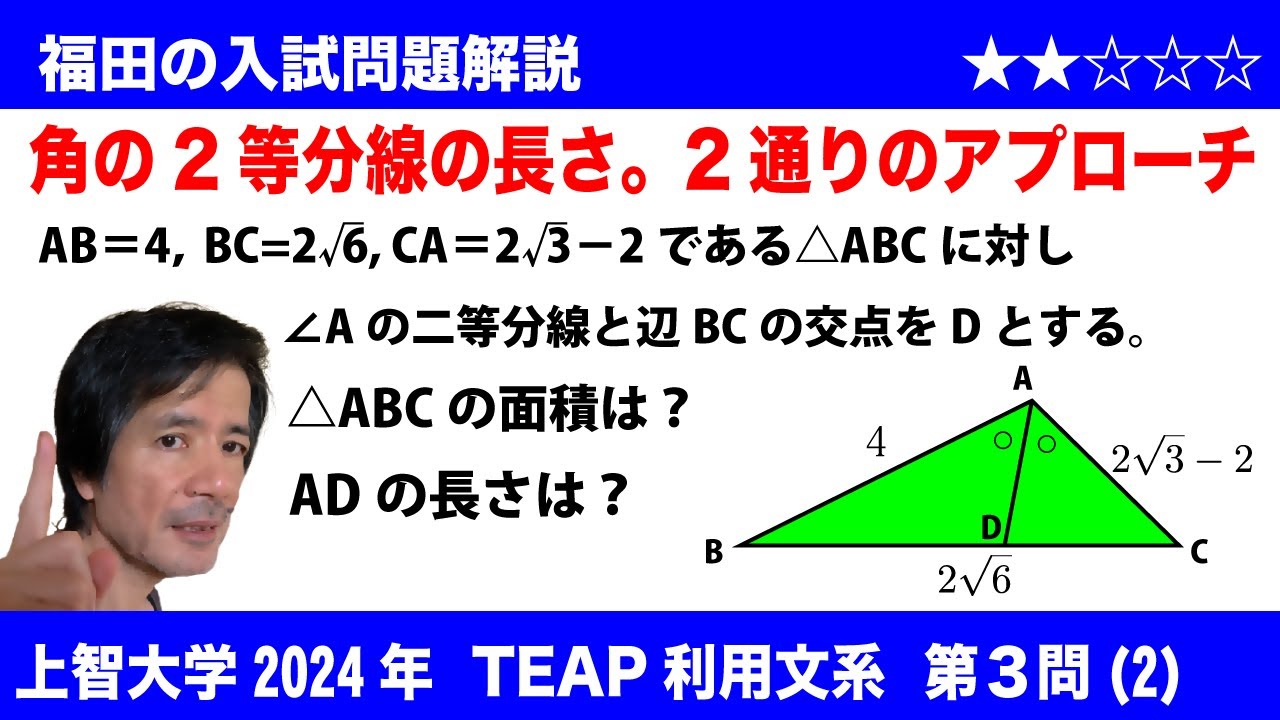
$\boxed{3}(2)AB=4,BC=2\sqrt{6},CA=2\sqrt{3}-2$の$\triangle ABC$がある。$\angle A$の二等分線と辺BCの交点をDとする。このとき、$\triangle ABC$の面積は$\boxed{フ}+\boxed{ヘ}\sqrt{\boxed{ホ}}$であり、$AD=\boxed{マ}+\boxed{ミ}\sqrt{\boxed{ム}}$である。
この動画を見る
$\boxed{3}(2)AB=4,BC=2\sqrt{6},CA=2\sqrt{3}-2$の$\triangle ABC$がある。$\angle A$の二等分線と辺BCの交点をDとする。このとき、$\triangle ABC$の面積は$\boxed{フ}+\boxed{ヘ}\sqrt{\boxed{ホ}}$であり、$AD=\boxed{マ}+\boxed{ミ}\sqrt{\boxed{ム}}$である。
福田の数学〜上智大学2024TEAP利用型文系第3問(1)〜対数指数不等式と領域に含まれる格子点の個数

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}(1)$整数の組$(x,y)$で条件\begin{eqnarray}
\left\{
\begin{array}{l}
\log_{ \frac{π}{4} } y \lt log_{\frac{1}{2}}(x-1) \\
2^{y-1} \lt 8^x
\end{array}
\right.
\end{eqnarray}
を満たすものは全部で$\boxed{ヒ}$個ある。
この動画を見る
$\boxed{3}(1)$整数の組$(x,y)$で条件\begin{eqnarray}
\left\{
\begin{array}{l}
\log_{ \frac{π}{4} } y \lt log_{\frac{1}{2}}(x-1) \\
2^{y-1} \lt 8^x
\end{array}
\right.
\end{eqnarray}
を満たすものは全部で$\boxed{ヒ}$個ある。
福田の数学〜上智大学2024TEAP利用型文系第2問〜2点の移動に関する確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
表と裏が出る確率がそれぞれ $\frac{1}{2}$ である硬貨がある。座標平面において、原点 $(0,0)$ に置かれた点 $\mathrm{A}$ および座標 $(1,0)$ に置かれた点 $\mathrm{B}$ を、硬貨を $1$ 回投げるごとに以下の規則 $(R)$ に従って動かし、 $n$ 回硬貨を投げた直後における点 $\mathrm{A,B}$ の位置について考える。
規則 $(R)$:
・表が出たとき、 $\mathrm{A}$ は動かさず、 $\mathrm{B}$ は $\mathrm{A}$ を中心に反時計回りに $90^{\circ}$ 回転した位置に動かす。
・裏が出たとき、$\mathrm{B}$ は動かさず、 $\mathrm{A}$ は $\mathrm{B}$ を中心に反時計回りに $90^{\circ}$ 回転した位置に動かす。
$(1)$ $n=10$ のとき、$\overrightarrow{\mathrm{AB}}=(\fbox{タ},\fbox{チ})$
$(2)$ $n=3$ のとき、 $\mathrm{A}$ が位置することが可能な座標の総数は $\fbox{ツ}$ である。
$(3)$ $n=4$ のとき、 $\mathrm{A}$ が原点にある確率は $\displaystyle \frac{\fbox{テ}}{\fbox{ト}}$ であり、 $\mathrm{A}$ が $x$ 軸上にある確率は $\displaystyle \frac{\fbox{ナ}}{\fbox{ニ}}$ である。
$(4)$ $n=8$ のとき、 $\mathrm{A}$ が原点にある確率は $\displaystyle \frac{\fbox{ヌ}}{\fbox{ネ}}$ であり、 $\mathrm{A}$ が $x$ 軸上にある確率は $\displaystyle \frac{\fbox{ノ}}{\fbox{ハ}}$ である。
この動画を見る
表と裏が出る確率がそれぞれ $\frac{1}{2}$ である硬貨がある。座標平面において、原点 $(0,0)$ に置かれた点 $\mathrm{A}$ および座標 $(1,0)$ に置かれた点 $\mathrm{B}$ を、硬貨を $1$ 回投げるごとに以下の規則 $(R)$ に従って動かし、 $n$ 回硬貨を投げた直後における点 $\mathrm{A,B}$ の位置について考える。
規則 $(R)$:
・表が出たとき、 $\mathrm{A}$ は動かさず、 $\mathrm{B}$ は $\mathrm{A}$ を中心に反時計回りに $90^{\circ}$ 回転した位置に動かす。
・裏が出たとき、$\mathrm{B}$ は動かさず、 $\mathrm{A}$ は $\mathrm{B}$ を中心に反時計回りに $90^{\circ}$ 回転した位置に動かす。
$(1)$ $n=10$ のとき、$\overrightarrow{\mathrm{AB}}=(\fbox{タ},\fbox{チ})$
$(2)$ $n=3$ のとき、 $\mathrm{A}$ が位置することが可能な座標の総数は $\fbox{ツ}$ である。
$(3)$ $n=4$ のとき、 $\mathrm{A}$ が原点にある確率は $\displaystyle \frac{\fbox{テ}}{\fbox{ト}}$ であり、 $\mathrm{A}$ が $x$ 軸上にある確率は $\displaystyle \frac{\fbox{ナ}}{\fbox{ニ}}$ である。
$(4)$ $n=8$ のとき、 $\mathrm{A}$ が原点にある確率は $\displaystyle \frac{\fbox{ヌ}}{\fbox{ネ}}$ であり、 $\mathrm{A}$ が $x$ 軸上にある確率は $\displaystyle \frac{\fbox{ノ}}{\fbox{ハ}}$ である。
福田の数学〜上智大学2024TEAP利用型文系第1問〜正四面体に関する図形問題
単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
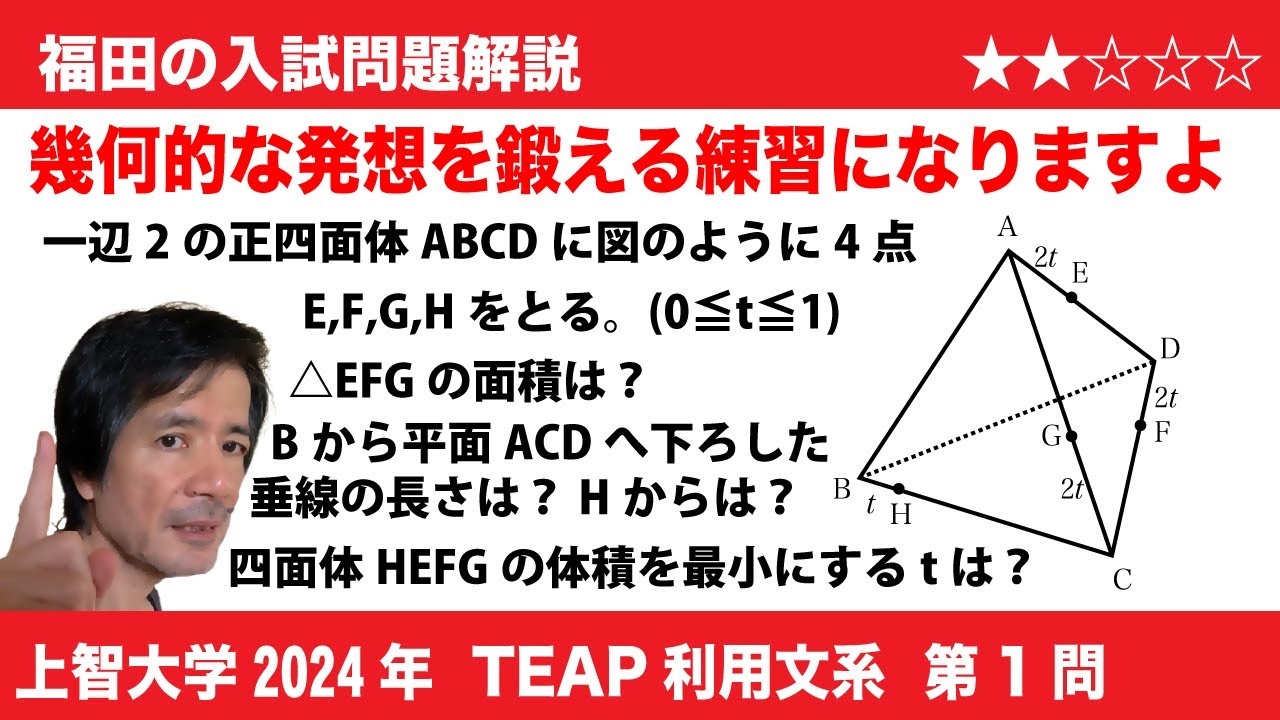
$1$ 辺の長さが $2$ の正四面体 $\mathrm{ABCD}$ において、辺 $\mathrm{AD}$ 上の点 $\mathrm{E}$、辺 $\mathrm{DC}$ 上の点 $\mathrm{F}$、辺 $\mathrm{CA}$ 上の点 $\mathrm{G}$、辺 $\mathrm{BC}$ 上の点 $\mathrm{H}$ を$\mathrm{AE}$$=\mathrm{DF}$$=\mathrm{CG}$$=2t,$ $\mathrm{BH}=t$ となるようにとる。ただし、 $0 \leqq t \leqq 1$ とする。
$(1)$ $\triangle \mathrm{EFG}$ の面積は $\sqrt{\fbox{ア}}(\fbox{イ}t^2$$+\fbox{ウ}t$$+\fbox{エ})$ である。
$(2)$ $\mathrm{B}$ から平面 $\mathrm{ACD}$ に垂線を下ろし、平面 $\mathrm{ACD}$ との交点を $\mathrm{P}$ とするとき、 $\mathrm{BP} = \frac{\fbox{オ}}{\fbox{カ}}\sqrt{\fbox{キ}}$ である。
$(3)$ $\mathrm{H}$ から平面 $\mathrm{EFG}$ に垂線を下ろし、平面 $\mathrm{EFG}$ との交点を $\mathrm{Q}$ とするとき、 $\mathrm{HQ} = \frac{\fbox{ク}}{\fbox{ケ}}\sqrt{\fbox{コ}}(t+\fbox{サ})$ である。
$(4)$ 四面体 $\mathrm{HEFG}$ の体積が最小になるのは
$t=\fbox{シ} + \frac{\fbox{ス}}{\fbox{セ}}\sqrt{\fbox{ソ}}$
この動画を見る
$1$ 辺の長さが $2$ の正四面体 $\mathrm{ABCD}$ において、辺 $\mathrm{AD}$ 上の点 $\mathrm{E}$、辺 $\mathrm{DC}$ 上の点 $\mathrm{F}$、辺 $\mathrm{CA}$ 上の点 $\mathrm{G}$、辺 $\mathrm{BC}$ 上の点 $\mathrm{H}$ を$\mathrm{AE}$$=\mathrm{DF}$$=\mathrm{CG}$$=2t,$ $\mathrm{BH}=t$ となるようにとる。ただし、 $0 \leqq t \leqq 1$ とする。
$(1)$ $\triangle \mathrm{EFG}$ の面積は $\sqrt{\fbox{ア}}(\fbox{イ}t^2$$+\fbox{ウ}t$$+\fbox{エ})$ である。
$(2)$ $\mathrm{B}$ から平面 $\mathrm{ACD}$ に垂線を下ろし、平面 $\mathrm{ACD}$ との交点を $\mathrm{P}$ とするとき、 $\mathrm{BP} = \frac{\fbox{オ}}{\fbox{カ}}\sqrt{\fbox{キ}}$ である。
$(3)$ $\mathrm{H}$ から平面 $\mathrm{EFG}$ に垂線を下ろし、平面 $\mathrm{EFG}$ との交点を $\mathrm{Q}$ とするとき、 $\mathrm{HQ} = \frac{\fbox{ク}}{\fbox{ケ}}\sqrt{\fbox{コ}}(t+\fbox{サ})$ である。
$(4)$ 四面体 $\mathrm{HEFG}$ の体積が最小になるのは
$t=\fbox{シ} + \frac{\fbox{ス}}{\fbox{セ}}\sqrt{\fbox{ソ}}$
#上智大学(2023) #定積分
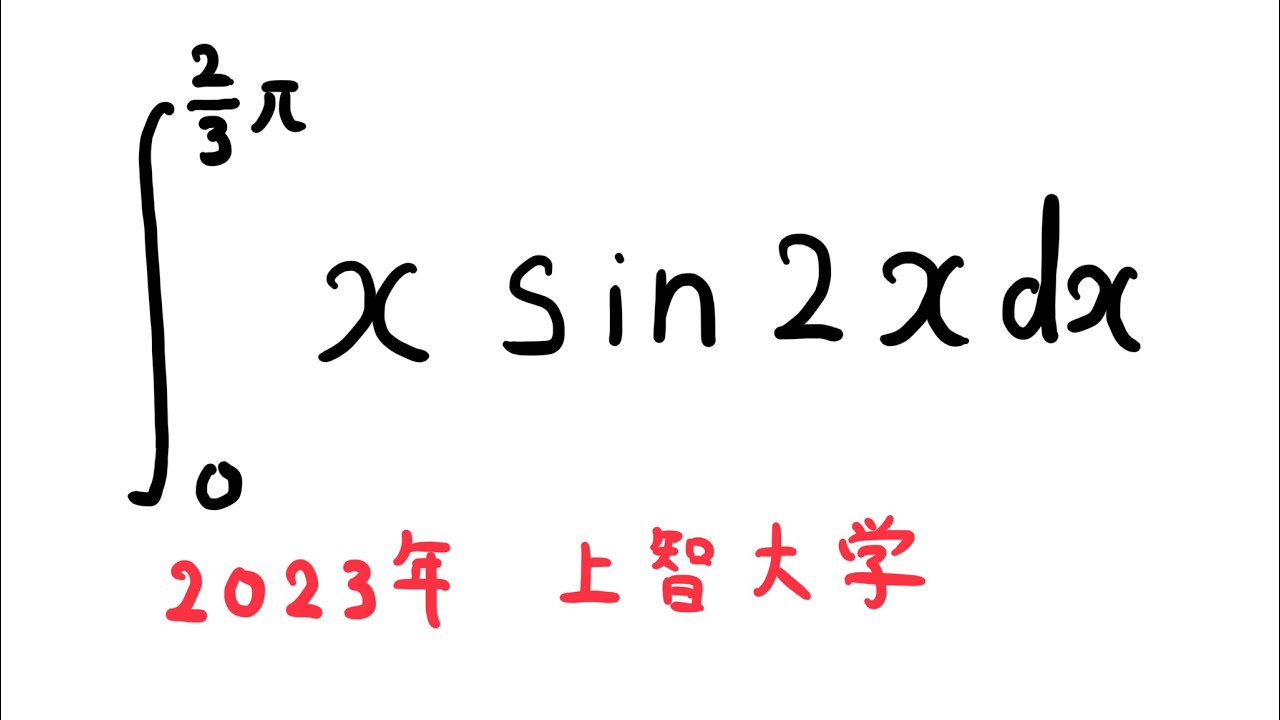
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{2}{3}\pi} x\sin2x\ dx$
出典:2023年上智大学
この動画を見る
$\displaystyle \int_{0}^{\frac{2}{3}\pi} x\sin2x\ dx$
出典:2023年上智大学
大学入試問題#839「解法見えれば余裕!」 #上智大学(2005) #数列

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$a_n=\displaystyle \frac{2n・3^n}{(2n+1)(2n+3)}$のとき、
$S_n=\displaystyle \frac{3^{n+1}}{2(2n+3)}-\displaystyle \frac{1}{2}$であることを示せ。
出典:2005年上智大学
この動画を見る
$a_n=\displaystyle \frac{2n・3^n}{(2n+1)(2n+3)}$のとき、
$S_n=\displaystyle \frac{3^{n+1}}{2(2n+3)}-\displaystyle \frac{1}{2}$であることを示せ。
出典:2005年上智大学
#上智大学(2005) #Shorts

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$f(x)=x^2+x+2\displaystyle \int_{0}^{1} f(t) dt$を満たす関数$f(x)$を求めよ
出典:2005年上智大学
この動画を見る
$f(x)=x^2+x+2\displaystyle \int_{0}^{1} f(t) dt$を満たす関数$f(x)$を求めよ
出典:2005年上智大学
#上智大学(2014) #極限 #Shorts
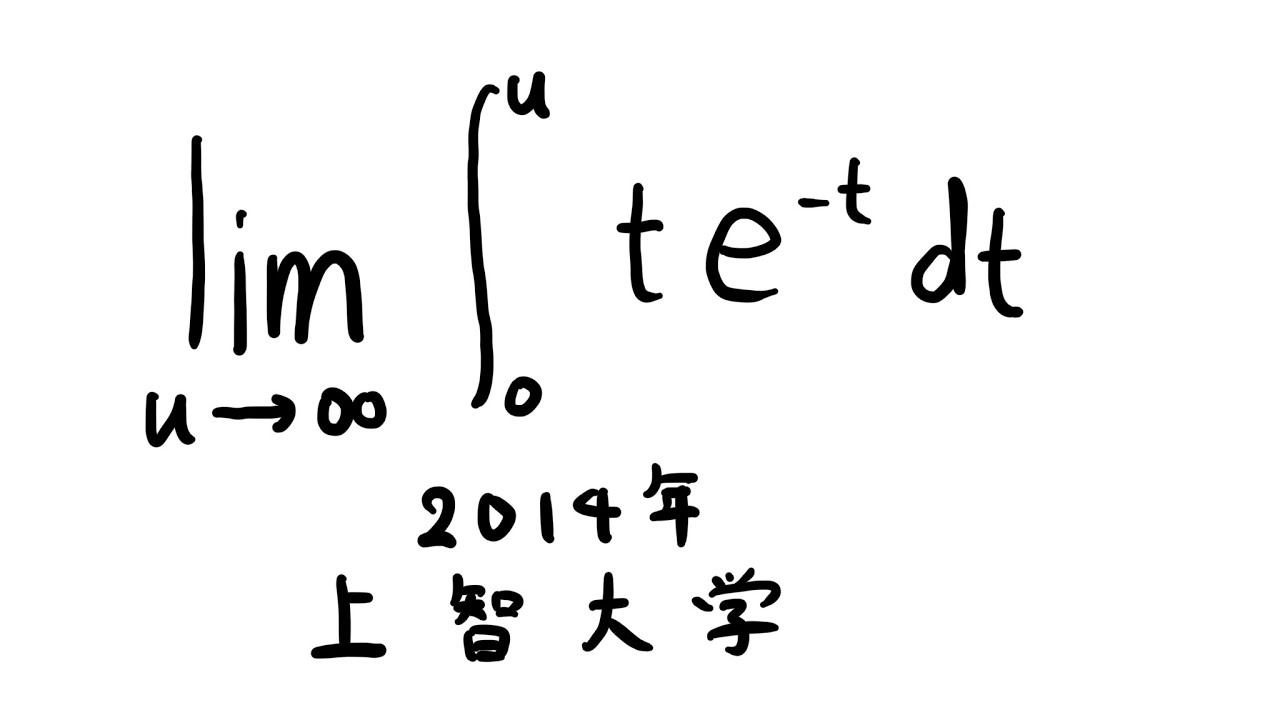
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ u \to \infty } \displaystyle \int_{o}^{u} te^{-t} \ dt$
出典:2014年上智大学
この動画を見る
$\displaystyle \lim_{ u \to \infty } \displaystyle \int_{o}^{u} te^{-t} \ dt$
出典:2014年上智大学
#上智大学(2016) #ウォリス積分 #定積分 #Shorts
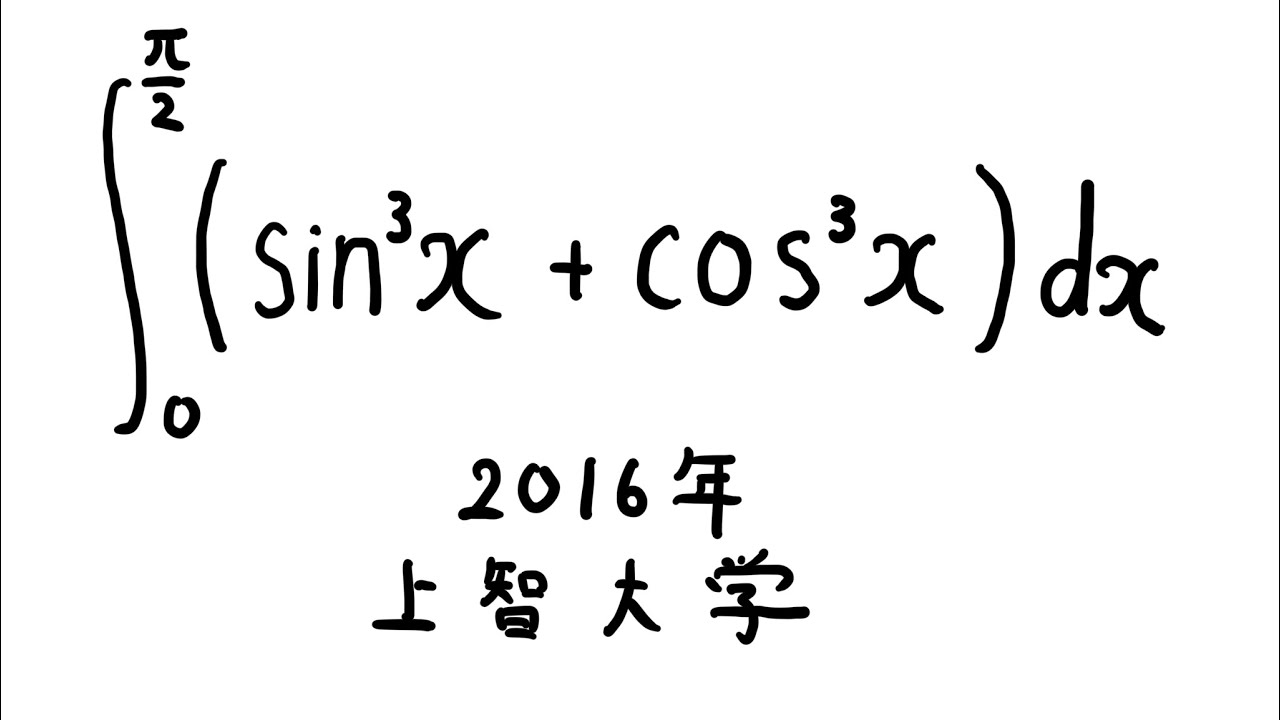
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#上智大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} (\sin^3x+\cos^3x) dx$
出典:2016年上智大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} (\sin^3x+\cos^3x) dx$
出典:2016年上智大学
福田の数学〜上智大学2023年理工学部第3問〜対数関数の積分と数学的帰納法

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#数列#数学的帰納法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ $e$を自然定数の底とする。自然数$n$に対して、
$S_n$=$\displaystyle\int_1^e(\log x)^n dx$
とする。
(1)$S_1$の値を求めよ。
(2)すべての自然数$n$に対して、
$S_n$=$a_n e$+$b_n$, ただし$a_n$, $b_n$はいずれも整数
と表されることを証明せよ。
この動画を見る
$\Large\boxed{3}$ $e$を自然定数の底とする。自然数$n$に対して、
$S_n$=$\displaystyle\int_1^e(\log x)^n dx$
とする。
(1)$S_1$の値を求めよ。
(2)すべての自然数$n$に対して、
$S_n$=$a_n e$+$b_n$, ただし$a_n$, $b_n$はいずれも整数
と表されることを証明せよ。
福田の数学〜上智大学2023年理工学部第2問〜逆関数の微分積分

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{2}}$ 関数$f(x)$=$\sin x$ $\left(0≦x≦\frac{\pi}{2}\right)$の逆関数を$g(x)$とする。
(1)関数$g(x)$の定義域は$\boxed{\ \ え\ \ }$である。
(2)$y$=$g(x)$の$x$=$\frac{4}{5}$における接線の傾きは$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}$である。
(3)$\displaystyle\int_0^{\frac{1}{2}}g(x)dx$=$\displaystyle\frac{\pi}{\boxed{\ \ キ\ \ }}$+$\boxed{\ \ ク\ \ }$+$\displaystyle\frac{\boxed{\ \ ケ\ \ }}{\boxed{\ \ コ\ \ }}\sqrt{\boxed{\ \ サ\ \ }}$である。
(4)$y$=$g(x)$のグラフと$x$=1および$x$軸で囲まれた図形を$x$軸のまわりに1回転させてできる立体の体積は$\displaystyle\frac{\pi^a}{\boxed{\ \ シ\ \ }}$+$\boxed{\ \ ス\ \ }\pi$ ただし$a$=$\boxed{\ \ セ\ \ }$である。
この動画を見る
$\Large{\boxed{2}}$ 関数$f(x)$=$\sin x$ $\left(0≦x≦\frac{\pi}{2}\right)$の逆関数を$g(x)$とする。
(1)関数$g(x)$の定義域は$\boxed{\ \ え\ \ }$である。
(2)$y$=$g(x)$の$x$=$\frac{4}{5}$における接線の傾きは$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}$である。
(3)$\displaystyle\int_0^{\frac{1}{2}}g(x)dx$=$\displaystyle\frac{\pi}{\boxed{\ \ キ\ \ }}$+$\boxed{\ \ ク\ \ }$+$\displaystyle\frac{\boxed{\ \ ケ\ \ }}{\boxed{\ \ コ\ \ }}\sqrt{\boxed{\ \ サ\ \ }}$である。
(4)$y$=$g(x)$のグラフと$x$=1および$x$軸で囲まれた図形を$x$軸のまわりに1回転させてできる立体の体積は$\displaystyle\frac{\pi^a}{\boxed{\ \ シ\ \ }}$+$\boxed{\ \ ス\ \ }\pi$ ただし$a$=$\boxed{\ \ セ\ \ }$である。
福田の数学〜上智大学2023年理工学部第1問(3)〜正四面体を切った断面

単元:
#数A#大学入試過去問(数学)#図形の性質#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (3)一辺の長さが2である正四面体OABCにおいて、辺OAの中点をM、辺BCの中点をNとする。
(i)線分MNの長さは$\boxed{\ \ あ\ \ }$である。
(ii)0<$s$<1とし、線分MNを$s$:$(1-s)$に内分する点をPとする。Pを通りMNに垂直な平面で四面体OABCを切った断面は$\boxed{\ \ い\ \ }$であり、その面積は$\boxed{\ \ う\ \ }$である。
$\boxed{\ \ あ\ \ }$の選択肢
(a)1 (b)$\sqrt 2$ (c)$\sqrt 3$ (d)2 (e)$\frac{1+\sqrt 5}{2}$ (f)$\frac{\sqrt 6}{2}$
$\boxed{\ \ い\ \ }$の選択肢
(a)正三角形 (b)正三角形でない二等辺三角形 (c)二等辺三角形でない三角形 (d)長方形 (e)長方形でない平行四辺形 (f)平行四辺形でない四角形
$\boxed{\ \ う\ \ }$の選択肢
(a)$s^2$ (b)$(1-s)^2$ (c)$s(1-s)$ (d)$s\sqrt{1-s^2}$
(e)$2s^2$ (f)$2(1-s)^2$ (g)$2s(1-s)$ (h)$2s\sqrt{1-s^2}$
(i)$4s^2$ (j)$4(1-s)^2$ (k)$4s(1-s)$ (l)$4s\sqrt{1-s^2}$
この動画を見る
$\Large{\boxed{1}}$ (3)一辺の長さが2である正四面体OABCにおいて、辺OAの中点をM、辺BCの中点をNとする。
(i)線分MNの長さは$\boxed{\ \ あ\ \ }$である。
(ii)0<$s$<1とし、線分MNを$s$:$(1-s)$に内分する点をPとする。Pを通りMNに垂直な平面で四面体OABCを切った断面は$\boxed{\ \ い\ \ }$であり、その面積は$\boxed{\ \ う\ \ }$である。
$\boxed{\ \ あ\ \ }$の選択肢
(a)1 (b)$\sqrt 2$ (c)$\sqrt 3$ (d)2 (e)$\frac{1+\sqrt 5}{2}$ (f)$\frac{\sqrt 6}{2}$
$\boxed{\ \ い\ \ }$の選択肢
(a)正三角形 (b)正三角形でない二等辺三角形 (c)二等辺三角形でない三角形 (d)長方形 (e)長方形でない平行四辺形 (f)平行四辺形でない四角形
$\boxed{\ \ う\ \ }$の選択肢
(a)$s^2$ (b)$(1-s)^2$ (c)$s(1-s)$ (d)$s\sqrt{1-s^2}$
(e)$2s^2$ (f)$2(1-s)^2$ (g)$2s(1-s)$ (h)$2s\sqrt{1-s^2}$
(i)$4s^2$ (j)$4(1-s)^2$ (k)$4s(1-s)$ (l)$4s\sqrt{1-s^2}$
福田の数学〜上智大学2023年理工学部第1問(2)〜関数の集合と条件

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (2)$\left\{x|x>0\right\}$を定義域とする関数$f(x)$の集合Aに対する以下の3つの条件を考える。
(P)関数$f(x)$と$g(x)$が共にAの要素ならば、関数$f(x)+g(x)$もAの要素である。
(Q)関数$f(x)$と$g(x)$が共にAの要素ならば、関数$f(x)g(x)$もAの要素である。
(R)$\alpha$が0でない定数で関数$f(x)$がAの要素ならば、関数$\alpha f(x)$もAの要素である。
Aを以下の(i)~(iv)の集合とするとき、条件(P),(Q),(R)のうち成り立つものをすべて解答欄にマークせよ。
(i)$f(1)$=0 を満たす関数$f(x)$全体の集合
(ii)$f(\alpha)$=0 となる正の実数$\alpha$が存在する関数$f(x)$全体の集合
(iii)全ての正の実数$x$に対して$f(x)$>0 が成り立つ関数$f(x)$全体の集合
(iv)定義域$\left\{x|x>0\right\}$のどこかで連続でない関数$f(x)$全体の集合
この動画を見る
$\Large{\boxed{1}}$ (2)$\left\{x|x>0\right\}$を定義域とする関数$f(x)$の集合Aに対する以下の3つの条件を考える。
(P)関数$f(x)$と$g(x)$が共にAの要素ならば、関数$f(x)+g(x)$もAの要素である。
(Q)関数$f(x)$と$g(x)$が共にAの要素ならば、関数$f(x)g(x)$もAの要素である。
(R)$\alpha$が0でない定数で関数$f(x)$がAの要素ならば、関数$\alpha f(x)$もAの要素である。
Aを以下の(i)~(iv)の集合とするとき、条件(P),(Q),(R)のうち成り立つものをすべて解答欄にマークせよ。
(i)$f(1)$=0 を満たす関数$f(x)$全体の集合
(ii)$f(\alpha)$=0 となる正の実数$\alpha$が存在する関数$f(x)$全体の集合
(iii)全ての正の実数$x$に対して$f(x)$>0 が成り立つ関数$f(x)$全体の集合
(iv)定義域$\left\{x|x>0\right\}$のどこかで連続でない関数$f(x)$全体の集合
福田の数学〜上智大学2023年理工学部第1問(1)〜複素数平面と確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#複素数平面#確率#複素数平面#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (1)次の6つの複素数が1つずつ書かれた6枚のカードがある。
$\frac{1}{2}$, 1, 2, $\cos\frac{\pi}{6}+i\sin\frac{\pi}{6}$, $\cos\frac{\pi}{3}+i\sin\frac{\pi}{3}$, $\cos\frac{\pi}{2}+i\sin\frac{\pi}{2}$
これらから無作為に3枚選び、カードに書かれた3つの複素数を掛けた値に対応する複素数平面上の点をPとする。
(i)点Pが虚軸上にある確率は$\displaystyle\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$である。
(ii)点Pの原点からの距離が1である確率は$\displaystyle\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}$である。
この動画を見る
$\Large{\boxed{1}}$ (1)次の6つの複素数が1つずつ書かれた6枚のカードがある。
$\frac{1}{2}$, 1, 2, $\cos\frac{\pi}{6}+i\sin\frac{\pi}{6}$, $\cos\frac{\pi}{3}+i\sin\frac{\pi}{3}$, $\cos\frac{\pi}{2}+i\sin\frac{\pi}{2}$
これらから無作為に3枚選び、カードに書かれた3つの複素数を掛けた値に対応する複素数平面上の点をPとする。
(i)点Pが虚軸上にある確率は$\displaystyle\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$である。
(ii)点Pの原点からの距離が1である確率は$\displaystyle\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}$である。
福田の数学〜上智大学2023年TEAP利用型理系第4問Part2〜不等式の証明と近似値計算

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#積分とその応用#定積分#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{4}}$ $e$を自然対数の底とする。$e$=2.718...である。
(1)0≦$x$≦1において不等式1+$x$≦$e^x$≦1+2$x$が成り立つことを示せ。
(2)$n$を自然数とするとき、0≦$x$≦1において不等式
$\displaystyle\sum_{k=0}^n\frac{x^k}{k!}$≦$e^x$≦$\displaystyle\sum_{k=0}^n\frac{x^k}{k!}+\frac{x^n}{n!}$
が成り立つことを示せ。
(3)0≦$x$≦1を定義域とする関数$f(x)$を
$f(x)$=$\left\{\begin{array}{1}
1 (x=0)\\
\displaystyle\frac{e^x-1}{x} (0<x≦1)
\end{array}\right.$
と定義する。(2)の不等式を利用して、定積分$\displaystyle\int_0^1f(x)dx$ の近似値を小数第3位まで求め、求めた近似値と真の値との誤差が$10^{-3}$以下である理由を説明せよ。
この動画を見る
$\Large{\boxed{4}}$ $e$を自然対数の底とする。$e$=2.718...である。
(1)0≦$x$≦1において不等式1+$x$≦$e^x$≦1+2$x$が成り立つことを示せ。
(2)$n$を自然数とするとき、0≦$x$≦1において不等式
$\displaystyle\sum_{k=0}^n\frac{x^k}{k!}$≦$e^x$≦$\displaystyle\sum_{k=0}^n\frac{x^k}{k!}+\frac{x^n}{n!}$
が成り立つことを示せ。
(3)0≦$x$≦1を定義域とする関数$f(x)$を
$f(x)$=$\left\{\begin{array}{1}
1 (x=0)\\
\displaystyle\frac{e^x-1}{x} (0<x≦1)
\end{array}\right.$
と定義する。(2)の不等式を利用して、定積分$\displaystyle\int_0^1f(x)dx$ の近似値を小数第3位まで求め、求めた近似値と真の値との誤差が$10^{-3}$以下である理由を説明せよ。
福田の数学〜上智大学2023年TEAP利用型理系第4問Part1〜不等式の証明と近似値計算

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#積分とその応用#定積分#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{4}}$ $e$を自然対数の底とする。$e$=2.718...である。
(1)0≦$x$≦1において不等式1+$x$≦$e^x$≦1+2$x$が成り立つことを示せ。
(2)$n$を自然数とするとき、0≦$x$≦1において不等式
$\displaystyle\sum_{k=0}^n\frac{x^k}{k!}$≦$e^x$≦$\displaystyle\sum_{k=0}^n\frac{x^k}{k!}+\frac{x^n}{n!}$
が成り立つことを示せ。
(3)0≦$x$≦1を定義域とする関数$f(x)$を
$f(x)$=$\left\{\begin{array}{1}
1 (x=0)\\
\displaystyle\frac{e^x-1}{x} (0<x≦1)
\end{array}\right.$
と定義する。(2)の不等式を利用して、定積分$\displaystyle\int_0^1f(x)dx$ の近似値を小数第3位まで求め、求めた近似値と真の値との誤差が$10^{-3}$以下である理由を説明せよ。
この動画を見る
$\Large{\boxed{4}}$ $e$を自然対数の底とする。$e$=2.718...である。
(1)0≦$x$≦1において不等式1+$x$≦$e^x$≦1+2$x$が成り立つことを示せ。
(2)$n$を自然数とするとき、0≦$x$≦1において不等式
$\displaystyle\sum_{k=0}^n\frac{x^k}{k!}$≦$e^x$≦$\displaystyle\sum_{k=0}^n\frac{x^k}{k!}+\frac{x^n}{n!}$
が成り立つことを示せ。
(3)0≦$x$≦1を定義域とする関数$f(x)$を
$f(x)$=$\left\{\begin{array}{1}
1 (x=0)\\
\displaystyle\frac{e^x-1}{x} (0<x≦1)
\end{array}\right.$
と定義する。(2)の不等式を利用して、定積分$\displaystyle\int_0^1f(x)dx$ の近似値を小数第3位まで求め、求めた近似値と真の値との誤差が$10^{-3}$以下である理由を説明せよ。
福田の数学〜上智大学2023年TEAP利用型理系第3問Part2〜容器に水を入れる
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ $\pi$を円周率とする。$f(x)$=$x^2(x^2-1)$とし、$f(x)$の最小値を$m$とする。
(1)$m$=$\displaystyle\frac{\boxed{\ \ シ\ \ }}{\boxed{\ \ ス\ \ }}$ である。
(2)$y$=$f(x)$で表される曲線を$y$軸の周りに1回転させてできる曲面でできた器に、$y$軸方向から静かに水を注ぐ。
(i)水面が$y$=$a$(ただし$m$≦$a$≦0)になったときの水面の面積は$\boxed{\ \ セ\ \ }$である。
(ii)水面が$y$=0になったときの水の体積は$\displaystyle\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}\pi$ である。
(iii)上方から注ぐ水が単位時間あたり一定量であるとする。水面が$y$=0に達するまでは、水面の面積は、水を注ぎ始めてからの時間の$\displaystyle\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}$ 乗に比例して大きくなる。
(iv)水面が$y$=2になったときの水面の面積は$\boxed{\ \ テ\ \ }\pi$であり、水の体積は$\displaystyle\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}\pi$ である。
この動画を見る
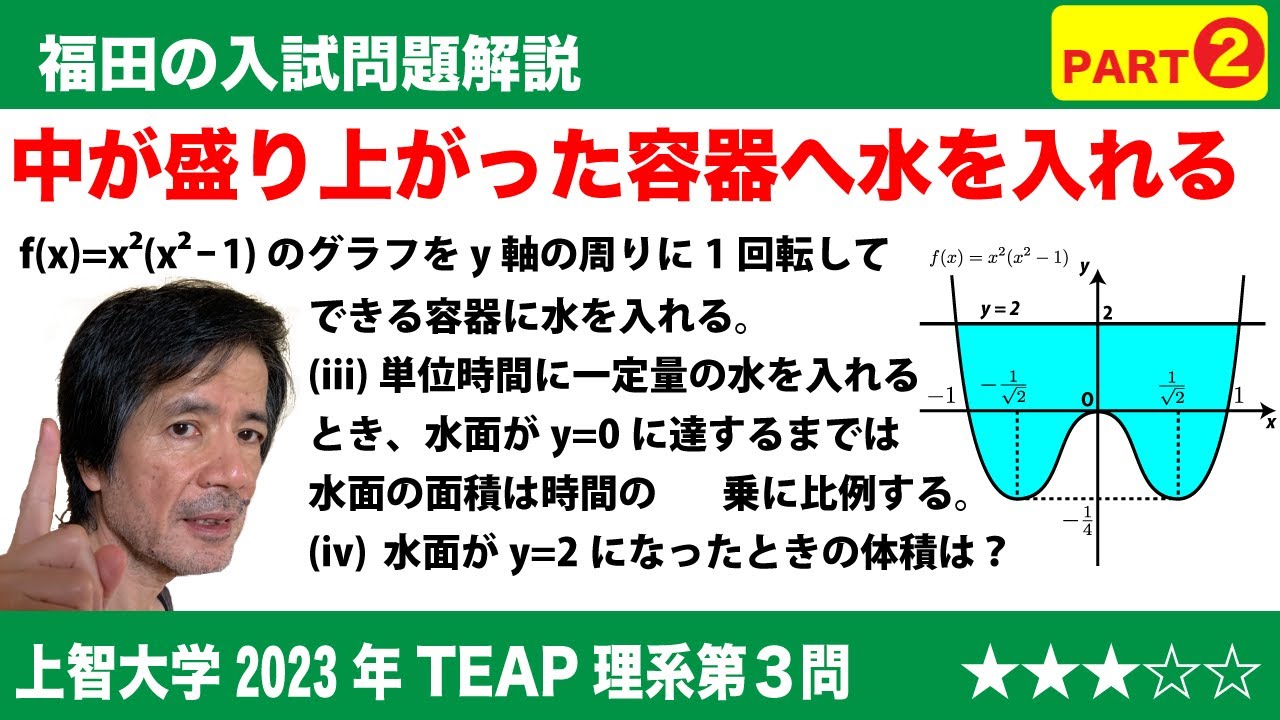
$\Large{\boxed{3}}$ $\pi$を円周率とする。$f(x)$=$x^2(x^2-1)$とし、$f(x)$の最小値を$m$とする。
(1)$m$=$\displaystyle\frac{\boxed{\ \ シ\ \ }}{\boxed{\ \ ス\ \ }}$ である。
(2)$y$=$f(x)$で表される曲線を$y$軸の周りに1回転させてできる曲面でできた器に、$y$軸方向から静かに水を注ぐ。
(i)水面が$y$=$a$(ただし$m$≦$a$≦0)になったときの水面の面積は$\boxed{\ \ セ\ \ }$である。
(ii)水面が$y$=0になったときの水の体積は$\displaystyle\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}\pi$ である。
(iii)上方から注ぐ水が単位時間あたり一定量であるとする。水面が$y$=0に達するまでは、水面の面積は、水を注ぎ始めてからの時間の$\displaystyle\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}$ 乗に比例して大きくなる。
(iv)水面が$y$=2になったときの水面の面積は$\boxed{\ \ テ\ \ }\pi$であり、水の体積は$\displaystyle\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}\pi$ である。
福田の数学〜上智大学2023年TEAP利用型理系第3問Part1〜容器に水を入れる
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
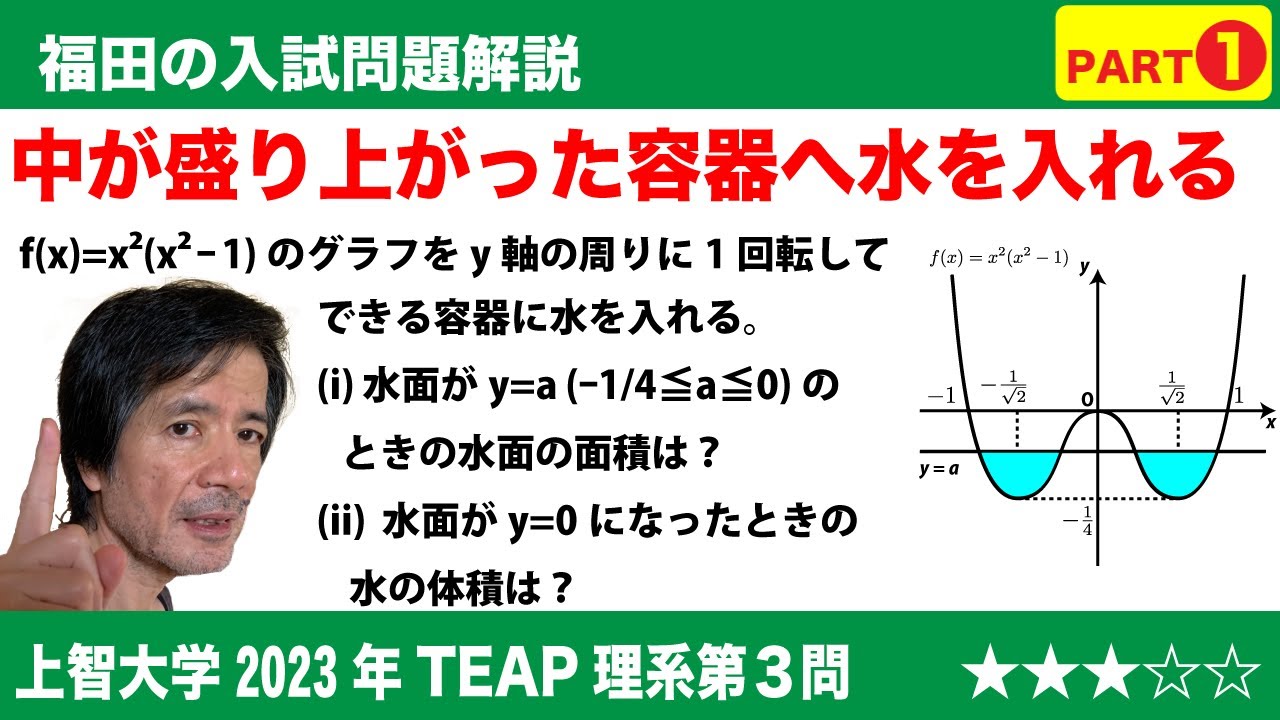
$\Large{\boxed{3}}$ $\pi$を円周率とする。$f(x)$=$x^2(x^2-1)$とし、$f(x)$の最小値を$m$とする。
(1)$m$=$\displaystyle\frac{\boxed{\ \ シ\ \ }}{\boxed{\ \ ス\ \ }}$ である。
(2)$y$=$f(x)$で表される曲線を$y$軸の周りに1回転させてできる曲面でできた器に、$y$軸方向から静かに水を注ぐ。
(i)水面が$y$=$a$(ただし$m$≦$a$≦0)になったときの水面の面積は$\boxed{\ \ セ\ \ }$である。
(ii)水面が$y$=0になったときの水の体積は$\displaystyle\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}\pi$ である。
(iii)上方から注ぐ水が単位時間あたり一定量であるとする。水面が$y$=0に達するまでは、水面の面積は、水を注ぎ始めてからの時間の$\displaystyle\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}$ 乗に比例して大きくなる。
(iv)水面が$y$=2になったときの水面の面積は$\boxed{\ \ テ\ \ }\pi$であり、水の体積は$\displaystyle\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}\pi$ である。
この動画を見る
$\Large{\boxed{3}}$ $\pi$を円周率とする。$f(x)$=$x^2(x^2-1)$とし、$f(x)$の最小値を$m$とする。
(1)$m$=$\displaystyle\frac{\boxed{\ \ シ\ \ }}{\boxed{\ \ ス\ \ }}$ である。
(2)$y$=$f(x)$で表される曲線を$y$軸の周りに1回転させてできる曲面でできた器に、$y$軸方向から静かに水を注ぐ。
(i)水面が$y$=$a$(ただし$m$≦$a$≦0)になったときの水面の面積は$\boxed{\ \ セ\ \ }$である。
(ii)水面が$y$=0になったときの水の体積は$\displaystyle\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}\pi$ である。
(iii)上方から注ぐ水が単位時間あたり一定量であるとする。水面が$y$=0に達するまでは、水面の面積は、水を注ぎ始めてからの時間の$\displaystyle\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}$ 乗に比例して大きくなる。
(iv)水面が$y$=2になったときの水面の面積は$\boxed{\ \ テ\ \ }\pi$であり、水の体積は$\displaystyle\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}\pi$ である。
福田の数学〜上智大学2023年TEAP利用型理系第2問〜立方体の切断と位置ベクトル

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#立体図形#立体切断#上智大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{2}}$ 一辺の長さが2である立方体OADB-CFGEを考える。
$\overrightarrow{OA}$=$\overrightarrow{a}$, $\overrightarrow{OB}$=$\overrightarrow{b}$, $\overrightarrow{OC}$=$\overrightarrow{c}$とおく。辺AFの中点をM、辺BDの中点をNとし、3点O,M,Nを通る平面$\pi$で立方体を切断する。
(1)平面$\pi$は辺AF,BD以外に辺$\boxed{\ \ あ\ \ }$とその両端以外で交わる。
(2)平面$\pi$と辺$\boxed{\ \ あ\ \ }$との交点をPとすると$\overrightarrow{OP}$=$\boxed{\ \ い\ \ } \overrightarrow{a}$+$\boxed{\ \ う\ \ } \overrightarrow{b}$+$\boxed{\ \ え\ \ } \overrightarrow{c}$
(3)断面の面積は$\displaystyle\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ ク\ \ }}\sqrt{\boxed{\ \ ケ\ \ }}$である。
(4)切断されてできる立体のうち、頂点Aを含むものの体積は$\displaystyle\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}$である。
(5)平面$\pi$と線分CDとの交点をQとする。
(i)点Qは線分CDを$\boxed{\ \ お\ \ }$に内分する。
(ii)$\overrightarrow{OQ}$=$\boxed{\ \ か\ \ } \overrightarrow{a}$+$\boxed{\ \ き\ \ } \overrightarrow{b}$+$\boxed{\ \ く\ \ } \overrightarrow{c}$である。
$\boxed{\ \ い\ \ }~\boxed{\ \ え\ \ }$, $\boxed{\ \ か\ \ }~\boxed{\ \ く\ \ }$の選択肢
(a)0 (b)1 (c)$\frac{1}{2}$ (d)$\frac{1}{3}$ (e)$\frac{2}{3}$ (f)$\frac{1}{4}$ (g)$\frac{3}{4}$ (h)$\frac{1}{5}$
(i)$\frac{2}{5}$ (j)$\frac{3}{5}$ (k)$\frac{4}{5}$ (l)$\frac{1}{6}$ (m)$\frac{5}{6}$
$\boxed{\ \ お\ \ }$の選択肢
(a)1:1 (b)2:1 (c)1:2 (d)3:1 (e)1:3 (f)4:1 (g)3:2
(h)2:3 (i)1:4 (j)5:1 (k)1:5
この動画を見る
$\Large{\boxed{2}}$ 一辺の長さが2である立方体OADB-CFGEを考える。
$\overrightarrow{OA}$=$\overrightarrow{a}$, $\overrightarrow{OB}$=$\overrightarrow{b}$, $\overrightarrow{OC}$=$\overrightarrow{c}$とおく。辺AFの中点をM、辺BDの中点をNとし、3点O,M,Nを通る平面$\pi$で立方体を切断する。
(1)平面$\pi$は辺AF,BD以外に辺$\boxed{\ \ あ\ \ }$とその両端以外で交わる。
(2)平面$\pi$と辺$\boxed{\ \ あ\ \ }$との交点をPとすると$\overrightarrow{OP}$=$\boxed{\ \ い\ \ } \overrightarrow{a}$+$\boxed{\ \ う\ \ } \overrightarrow{b}$+$\boxed{\ \ え\ \ } \overrightarrow{c}$
(3)断面の面積は$\displaystyle\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ ク\ \ }}\sqrt{\boxed{\ \ ケ\ \ }}$である。
(4)切断されてできる立体のうち、頂点Aを含むものの体積は$\displaystyle\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}$である。
(5)平面$\pi$と線分CDとの交点をQとする。
(i)点Qは線分CDを$\boxed{\ \ お\ \ }$に内分する。
(ii)$\overrightarrow{OQ}$=$\boxed{\ \ か\ \ } \overrightarrow{a}$+$\boxed{\ \ き\ \ } \overrightarrow{b}$+$\boxed{\ \ く\ \ } \overrightarrow{c}$である。
$\boxed{\ \ い\ \ }~\boxed{\ \ え\ \ }$, $\boxed{\ \ か\ \ }~\boxed{\ \ く\ \ }$の選択肢
(a)0 (b)1 (c)$\frac{1}{2}$ (d)$\frac{1}{3}$ (e)$\frac{2}{3}$ (f)$\frac{1}{4}$ (g)$\frac{3}{4}$ (h)$\frac{1}{5}$
(i)$\frac{2}{5}$ (j)$\frac{3}{5}$ (k)$\frac{4}{5}$ (l)$\frac{1}{6}$ (m)$\frac{5}{6}$
$\boxed{\ \ お\ \ }$の選択肢
(a)1:1 (b)2:1 (c)1:2 (d)3:1 (e)1:3 (f)4:1 (g)3:2
(h)2:3 (i)1:4 (j)5:1 (k)1:5
福田の数学〜上智大学2023年TEAP利用型理系第1問(3)〜連立漸化式と極限

単元:
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (3)$a_1$=0, $b_1$=6とし、
$a_{n+1}$=$\displaystyle\frac{a_n+b_n}{2}$, $b_{n+1}$=$a_n$ ($n$≧1)
で定まる$a_n$, $b_n$を用いて、平面上の点$P_n$($a_n$, $b_n$)($n$=1,2,3,...)を定める。
(i)点$P_n$は常に直線$y$=$\boxed{\ \ ウ\ \ }x$+$\boxed{\ \ エ\ \ }$上にある。
(ii)$n$を限りなく大きくするとき、点$P_n$は点$\left(\boxed{\ \ オ\ \ }, \boxed{\ \ カ\ \ }\right)$に限りなく近づく。
この動画を見る
$\Large{\boxed{1}}$ (3)$a_1$=0, $b_1$=6とし、
$a_{n+1}$=$\displaystyle\frac{a_n+b_n}{2}$, $b_{n+1}$=$a_n$ ($n$≧1)
で定まる$a_n$, $b_n$を用いて、平面上の点$P_n$($a_n$, $b_n$)($n$=1,2,3,...)を定める。
(i)点$P_n$は常に直線$y$=$\boxed{\ \ ウ\ \ }x$+$\boxed{\ \ エ\ \ }$上にある。
(ii)$n$を限りなく大きくするとき、点$P_n$は点$\left(\boxed{\ \ オ\ \ }, \boxed{\ \ カ\ \ }\right)$に限りなく近づく。
福田の数学〜上智大学2023年TEAP利用型理系第1問(2)〜桁数の評価

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (2)$(2・7・11・13)^{20}$の桁数は$\boxed{\ \ イ\ \ }$である。
この動画を見る
$\Large{\boxed{1}}$ (2)$(2・7・11・13)^{20}$の桁数は$\boxed{\ \ イ\ \ }$である。
福田の数学〜上智大学2023年TEAP利用型理系第1問(1)〜ユークリッドの互除法

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (1)44311と43873との最大公約数は$\boxed{\ \ ア\ \ }$である。
この動画を見る
$\Large{\boxed{1}}$ (1)44311と43873との最大公約数は$\boxed{\ \ ア\ \ }$である。
