 立教大学
立教大学
 立教大学
立教大学
福田の数学〜立教大学2023年経済学部第2問〜利息計算と漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 1年目の初めに新規に100万円を預金し、2年目以降の毎年初めに12万円を追加で預金する。ただし、毎年の終わりに、その時点での預金額の8%が利子として預金に加算される。自然数$n$に対して、$n$年目の終わりに利子が加算された後の預金額を$S_n$万円とする。このとき、以下の問いに答えよ。
ただし、$\log_{10}2$=0.3010, $\log_{10}3$=0.4771とする。
(1)$S_1$, $S_2$をそれぞれ求めよ。
(2)$S_{n+1}$を$S_n$を用いて表せ。
(3)$S_n$を$n$を用いて表せ。
(4)$\log_{10}1.08$を求めよ。
(5)$S_n$>513 を満たす最小の自然数$n$を求めよ。
この動画を見る
$\Large\boxed{2}$ 1年目の初めに新規に100万円を預金し、2年目以降の毎年初めに12万円を追加で預金する。ただし、毎年の終わりに、その時点での預金額の8%が利子として預金に加算される。自然数$n$に対して、$n$年目の終わりに利子が加算された後の預金額を$S_n$万円とする。このとき、以下の問いに答えよ。
ただし、$\log_{10}2$=0.3010, $\log_{10}3$=0.4771とする。
(1)$S_1$, $S_2$をそれぞれ求めよ。
(2)$S_{n+1}$を$S_n$を用いて表せ。
(3)$S_n$を$n$を用いて表せ。
(4)$\log_{10}1.08$を求めよ。
(5)$S_n$>513 を満たす最小の自然数$n$を求めよ。
福田の数学〜立教大学2023年経済学部第1問(7)〜集合と座標平面

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (7)座標平面の3つの部分集合
A=$\left\{(x, -2x+2)|xは実数, x<0\right\}$
B=$\left\{(x, 2x+2)|xは実数, x≧0\right\}$
C=$\left\{(x, -x+3)|xは実数\right\}$
に対し、(A$\cup$B)$\cap$C に属する点の座標をすべて求めると$\boxed{\ \ キ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (7)座標平面の3つの部分集合
A=$\left\{(x, -2x+2)|xは実数, x<0\right\}$
B=$\left\{(x, 2x+2)|xは実数, x≧0\right\}$
C=$\left\{(x, -x+3)|xは実数\right\}$
に対し、(A$\cup$B)$\cap$C に属する点の座標をすべて求めると$\boxed{\ \ キ\ \ }$である。
福田の数学〜立教大学2023年経済学部第1問(6)〜関数方程式

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (6)2次式$f(x)$が$f(f(x))$=$f(x)^2$+1 を満たすとき$f(x)$=$\boxed{\ \ カ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (6)2次式$f(x)$が$f(f(x))$=$f(x)^2$+1 を満たすとき$f(x)$=$\boxed{\ \ カ\ \ }$である。
福田の数学〜立教大学2023年経済学部第1問(5)〜共面条件

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (5)$t$を実数とする。座標空間において、3点O(0,0,0), A(1,0,2), B(2,-1,0)の定める平面OAB上に点C($t$+1,$t$,1-$t$)があるとき、$t$=$\boxed{\ \ オ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (5)$t$を実数とする。座標空間において、3点O(0,0,0), A(1,0,2), B(2,-1,0)の定める平面OAB上に点C($t$+1,$t$,1-$t$)があるとき、$t$=$\boxed{\ \ オ\ \ }$である。
福田の数学〜立教大学2023年経済学部第1問(4)〜確率の基本性質

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (4)大小2個のさいころを同時に投げる。大きいサイコロのでた目を$a$、小さいサイコロのでた目を$b$とするとき、$\displaystyle\frac{a}{b}$が整数になる確率は$\boxed{\ \ エ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (4)大小2個のさいころを同時に投げる。大きいサイコロのでた目を$a$、小さいサイコロのでた目を$b$とするとき、$\displaystyle\frac{a}{b}$が整数になる確率は$\boxed{\ \ エ\ \ }$である。
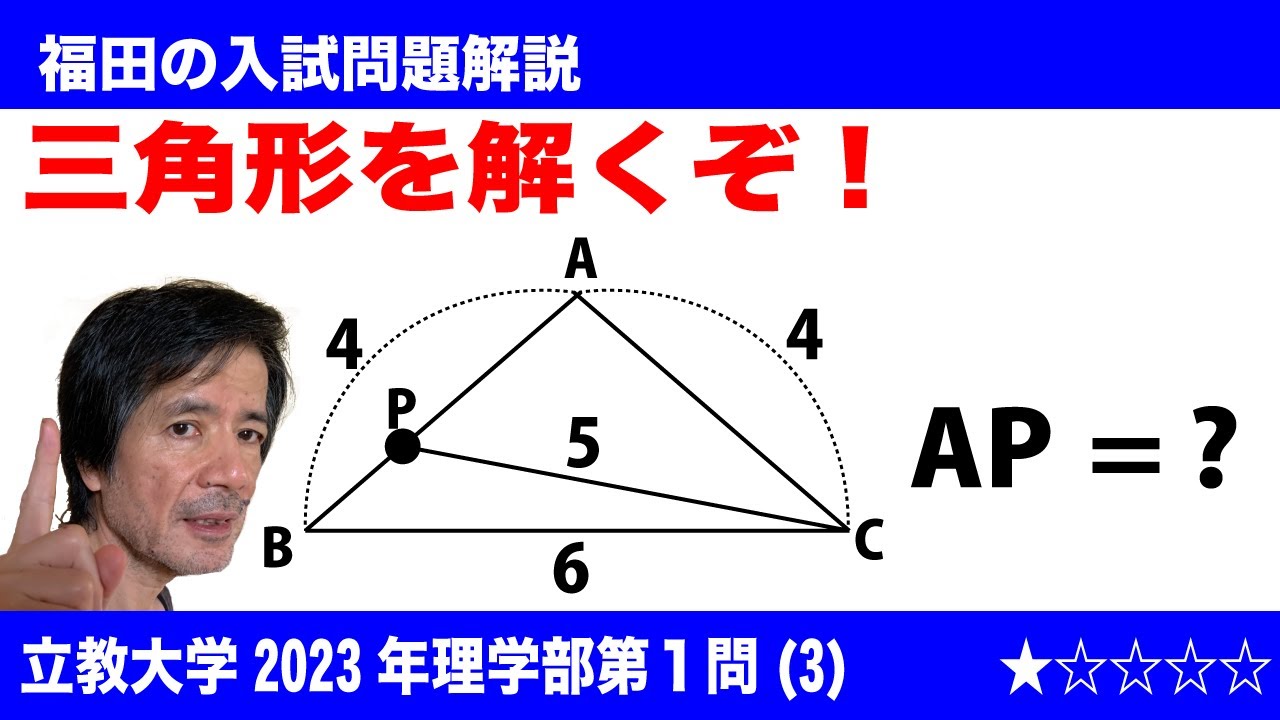
福田の数学〜立教大学2023年経済学部第1問(3)〜三角形を解く
単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#三角形の辺の比(内分・外分・二等分線)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (3)三角形ABCにおいてAB=AC=4, BC=6とする。AB上の点PがCP=5を満たすとき、AP=$\boxed{\ \ ウ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (3)三角形ABCにおいてAB=AC=4, BC=6とする。AB上の点PがCP=5を満たすとき、AP=$\boxed{\ \ ウ\ \ }$である。
福田の数学〜立教大学2023年経済学部第1問(2)〜条件付き最大最小問題

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (2)2つの実数$x$,$y$が$x^2$+$y^2$=1 を満たすとき、$z$=2$x$+$y$のとりうる値の範囲は$\boxed{\ \ イ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (2)2つの実数$x$,$y$が$x^2$+$y^2$=1 を満たすとき、$z$=2$x$+$y$のとりうる値の範囲は$\boxed{\ \ イ\ \ }$である。
福田の数学〜立教大学2023年経済学部第1問(1)〜三角関数の最小値

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#2次関数とグラフ#三角関数#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)関数$y$=4$\cos^2\theta$-$4\sin\theta$-5 の最小値は$\boxed{\ \ ア\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (1)関数$y$=4$\cos^2\theta$-$4\sin\theta$-5 の最小値は$\boxed{\ \ ア\ \ }$である。
福田の数学〜立教大学2023年理学部第4問〜数学的帰納法とはさみうちの原理

単元:
#大学入試過去問(数学)#数列#数学的帰納法#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 正の数列$x_1$,$x_2$,$x_3$,...,$x_n$,... は以下を満たすとする。
$x_1$=8, $x_{n+1}$=$\sqrt{1+x_n}$ ($n$=1,2,3,...)
このとき、次の問いに答えよ。
(1)$x_2$,$x_3$,$x_4$をそれぞれ求めよ。
(2)すべての$n$≧1について($x_{n+1}$-$\alpha$)($x_{n+1}$+$\alpha$)=$x_n$-$\alpha$ となる定数$\alpha$で、
正であるものを求めよ。
(3)$\alpha$を(2)で求めたものとする。すべての$n$≧1について$x_n$>$\alpha$であることを$n$に関する数学的帰納法で示せ。
(4)極限値$\displaystyle\lim_{n \to \infty}x_n$を求めよ。
この動画を見る
$\Large\boxed{4}$ 正の数列$x_1$,$x_2$,$x_3$,...,$x_n$,... は以下を満たすとする。
$x_1$=8, $x_{n+1}$=$\sqrt{1+x_n}$ ($n$=1,2,3,...)
このとき、次の問いに答えよ。
(1)$x_2$,$x_3$,$x_4$をそれぞれ求めよ。
(2)すべての$n$≧1について($x_{n+1}$-$\alpha$)($x_{n+1}$+$\alpha$)=$x_n$-$\alpha$ となる定数$\alpha$で、
正であるものを求めよ。
(3)$\alpha$を(2)で求めたものとする。すべての$n$≧1について$x_n$>$\alpha$であることを$n$に関する数学的帰納法で示せ。
(4)極限値$\displaystyle\lim_{n \to \infty}x_n$を求めよ。
福田の数学〜立教大学2023年理学部第3問〜双曲線と直線の囲む面積

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 座標平面上の曲線Cを
C:$y$=$\frac{3}{x}$-8 ($x$>0)
で定める。また$p$を正の定数とし、点$\left(p, \displaystyle\frac{3}{p}-8\right)$におけるCの接線を$l$とする。
さらに、$a$を実数とし、直線$y$=$ax$を$m$とする。このとき、次の問いに答えよ。
(1)$l$の方程式を求めよ。
(2)$l$が原点を通るとき、$p$の値を求めよ。
(3)Cと$m$が異なる2点P,Qを共有するとき、$a$の値の範囲を求めよ。
(4)(3)のとき、Qの$x$座標$x_0$はPの$x$座標$x_1$よりも大きいとする。$x_0$-$x_1$=1であるときの$a$の値を求めよ。
(5)(4)のとき、Cと直線$m$で囲まれる図形の面積を求めよ。
この動画を見る
$\Large\boxed{3}$ 座標平面上の曲線Cを
C:$y$=$\frac{3}{x}$-8 ($x$>0)
で定める。また$p$を正の定数とし、点$\left(p, \displaystyle\frac{3}{p}-8\right)$におけるCの接線を$l$とする。
さらに、$a$を実数とし、直線$y$=$ax$を$m$とする。このとき、次の問いに答えよ。
(1)$l$の方程式を求めよ。
(2)$l$が原点を通るとき、$p$の値を求めよ。
(3)Cと$m$が異なる2点P,Qを共有するとき、$a$の値の範囲を求めよ。
(4)(3)のとき、Qの$x$座標$x_0$はPの$x$座標$x_1$よりも大きいとする。$x_0$-$x_1$=1であるときの$a$の値を求めよ。
(5)(4)のとき、Cと直線$m$で囲まれる図形の面積を求めよ。
福田の数学〜立教大学2023年理学部第2問〜ベクトルの共面条件と共線条件

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 0<$k$1とする。座標空間内の四面体OABCについて、線分ACの中点をD、線分BCの中点をE、線分DEを1:2に内分する点をPとする。また、
線分OPを$k$:1-$k$に内分する点をQとし、Rを$\overrightarrow{CR}$=$l\overrightarrow{CQ}$を満たす点とする。
$\overrightarrow{a}$=$\overrightarrow{OA}$, $\overrightarrow{b}$=$\overrightarrow{OB}$, $\overrightarrow{c}$=$\overrightarrow{OC}$とおいたとき、次の問いに答えよ。
(1)$\overrightarrow{OD}$, $\overrightarrow{OE}$, $\overrightarrow{OP}$を$\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$を用いて表せ。
(2)$\overrightarrow{OR}$を$\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$, $k$, $l$を用いて表せ。
(3)Rが平面OAB上にあるとき、$l$を$k$を用いて表せ。
(4)線分OAの中点をF、線分OBの中点をGとする。Rが線分FG上にあるときの$k$の値を求めよ。
この動画を見る
$\Large\boxed{2}$ 0<$k$1とする。座標空間内の四面体OABCについて、線分ACの中点をD、線分BCの中点をE、線分DEを1:2に内分する点をPとする。また、
線分OPを$k$:1-$k$に内分する点をQとし、Rを$\overrightarrow{CR}$=$l\overrightarrow{CQ}$を満たす点とする。
$\overrightarrow{a}$=$\overrightarrow{OA}$, $\overrightarrow{b}$=$\overrightarrow{OB}$, $\overrightarrow{c}$=$\overrightarrow{OC}$とおいたとき、次の問いに答えよ。
(1)$\overrightarrow{OD}$, $\overrightarrow{OE}$, $\overrightarrow{OP}$を$\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$を用いて表せ。
(2)$\overrightarrow{OR}$を$\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$, $k$, $l$を用いて表せ。
(3)Rが平面OAB上にあるとき、$l$を$k$を用いて表せ。
(4)線分OAの中点をF、線分OBの中点をGとする。Rが線分FG上にあるときの$k$の値を求めよ。
福田の数学〜立教大学2023年理学部第1問(5)〜反復試行の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (5)表の出る確率が$\frac{2}{3}$、裏の出る確率が$\frac{1}{3}$のコインを投げて、表が出たら+1点を加え、裏が出たら-1点を加える。というルールのゲームを行う。
0点から初めて5回コインを投げ終わった時、得点が3点以上となる確率は$\boxed{\ \ オ\ \ }$である。
2023立教大学理学部過去問
この動画を見る
$\Large\boxed{1}$ (5)表の出る確率が$\frac{2}{3}$、裏の出る確率が$\frac{1}{3}$のコインを投げて、表が出たら+1点を加え、裏が出たら-1点を加える。というルールのゲームを行う。
0点から初めて5回コインを投げ終わった時、得点が3点以上となる確率は$\boxed{\ \ オ\ \ }$である。
2023立教大学理学部過去問
福田の数学〜立教大学2023年理学部第1問(4)〜2次方程式が整数解をもつ条件

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次方程式と2次不等式#2次関数とグラフ#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (4)-1≦$\alpha$≦1 とする。$x$に関する方程式
$x^2$-$\frac{3}{2}x$-$\frac{9}{4}$+$\alpha$=0
が整数解をもつとき、$\alpha$の値は$\boxed{\ \ エ\ \ }$である。
2023立教大学理学部過去問
この動画を見る
$\Large\boxed{1}$ (4)-1≦$\alpha$≦1 とする。$x$に関する方程式
$x^2$-$\frac{3}{2}x$-$\frac{9}{4}$+$\alpha$=0
が整数解をもつとき、$\alpha$の値は$\boxed{\ \ エ\ \ }$である。
2023立教大学理学部過去問
福田の数学〜立教大学2023年理学部第1問(3)〜線分上の格子点の個数

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (3)座標平面上の2点O(0, 0)とP(2023, 1071)について、線分OA上にある点(x, y)でx, yが共に整数であるものの個数は$\boxed{\ \ ウ\ \ }$である。
ただし、線分OPは両端点を含むものとする。
2023立教大学理学部過去問
この動画を見る
$\Large\boxed{1}$ (3)座標平面上の2点O(0, 0)とP(2023, 1071)について、線分OA上にある点(x, y)でx, yが共に整数であるものの個数は$\boxed{\ \ ウ\ \ }$である。
ただし、線分OPは両端点を含むものとする。
2023立教大学理学部過去問
福田の数学〜立教大学2023年理学部第1問(2)〜極値をとる条件

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (2)関数$f(t)$=$a\cos^3t$+$\cos^2t$が$t$=$\frac{\pi}{4}$で極値をとるとき、$a$=$\boxed{\ \ イ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (2)関数$f(t)$=$a\cos^3t$+$\cos^2t$が$t$=$\frac{\pi}{4}$で極値をとるとき、$a$=$\boxed{\ \ イ\ \ }$である。
福田の数学〜立教大学2023年理学部第1問(1)〜指数方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#指数関数と対数関数#剰余の定理・因数定理・組み立て除法と高次方程式#指数関数#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)方程式$2^{x+2}$-$2^{2x+1}$+16=0 を解くと$x$=$\boxed{\ \ ア\ \ }$である。
2023立教大学理学部過去問
この動画を見る
$\Large\boxed{1}$ (1)方程式$2^{x+2}$-$2^{2x+1}$+16=0 を解くと$x$=$\boxed{\ \ ア\ \ }$である。
2023立教大学理学部過去問
立教大のナイスな問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2023立教大学過去問題
$A=\frac{10^{40}-3^{10}}{9997}$,$B=\frac{10^{36}-3^{9}}{9997}$
①Aの1の位の数
②A-3Bを素因数分解
③AとBの最大公約数
この動画を見る
2023立教大学過去問題
$A=\frac{10^{40}-3^{10}}{9997}$,$B=\frac{10^{36}-3^{9}}{9997}$
①Aの1の位の数
②A-3Bを素因数分解
③AとBの最大公約数
大学入試問題#491「綺麗な問題」 立教大学 類題 By 英語orドイツ語シはBかHか さん #不定積分
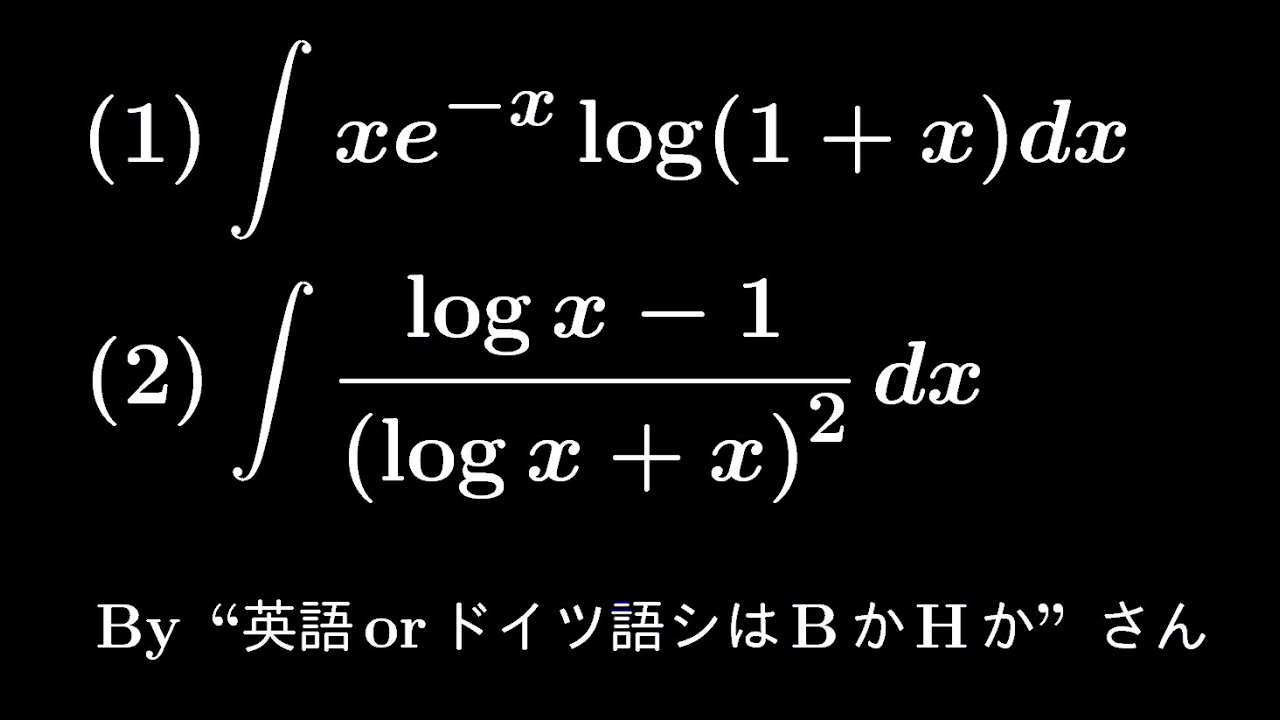
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
(1)
$\displaystyle \int xe^{-x}log(x+1)dx$
(2)
$\displaystyle \int \displaystyle \frac{log\ x-1}{(log\ x+x)^2}dx$
出典:立教大学 入試問題
この動画を見る
(1)
$\displaystyle \int xe^{-x}log(x+1)dx$
(2)
$\displaystyle \int \displaystyle \frac{log\ x-1}{(log\ x+x)^2}dx$
出典:立教大学 入試問題
福田の1.5倍速演習〜合格する重要問題074〜立教大学2019年度経済学部第1問(6)〜最大公約数を求める

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (6)14351と14803の最大公約数は$\boxed{\ \ キ \ \ }$である。
2019立教大学経済学部過去問
この動画を見る
$\Large\boxed{1}$ (6)14351と14803の最大公約数は$\boxed{\ \ キ \ \ }$である。
2019立教大学経済学部過去問
大学入試問題#380「基本に沿って」 立教大学2011 #極限
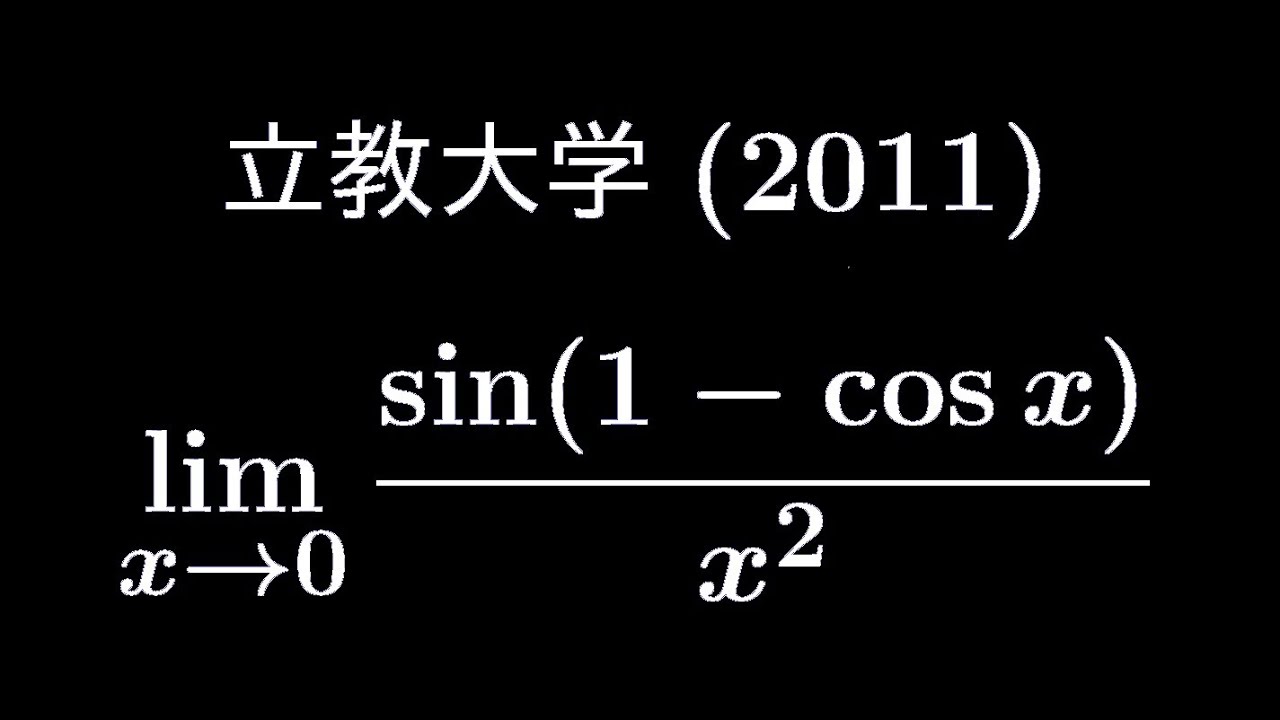
単元:
#大学入試過去問(数学)#関数と極限#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{\sin(1-\cos\ x)}{x^2}$
出典:2011年立教大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{\sin(1-\cos\ x)}{x^2}$
出典:2011年立教大学 入試問題
大学入試問題#341「部分積分の心を・・・」 立教大学 #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int (\sin\ x+x\ \cos\ x)log\ x\ dx$
出典:立教大学 入試問題
この動画を見る
$\displaystyle \int (\sin\ x+x\ \cos\ x)log\ x\ dx$
出典:立教大学 入試問題
福田の数学〜青山学院大学2022年理工学部第1問〜サイコロの目の約数倍数の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
1個のさいころを3回投げるとき、出た目を順にX_1,X_2,X_3とする。
また、$Y=\frac{X_2X_3}{X_1}$とする。
(1)$X_1=2$のとき、Yが整数となる確率は$\frac{\boxed{ア}}{\boxed{イ}}$である。
(2)$X_1=3$のとき、Yが整数となる確率は$\frac{\boxed{ウ}}{\boxed{エ}}\ である。
(3)$X_1=4$のとき、Yが整数となる確率は$\frac{\boxed{オ}}{\boxed{カキ}}$である。
(4)Yが整数となる確率は$\frac{\boxed{クケ}}{\boxed{コサ}}$である。
2022青山学院大学理工学部過去問
この動画を見る
1個のさいころを3回投げるとき、出た目を順にX_1,X_2,X_3とする。
また、$Y=\frac{X_2X_3}{X_1}$とする。
(1)$X_1=2$のとき、Yが整数となる確率は$\frac{\boxed{ア}}{\boxed{イ}}$である。
(2)$X_1=3$のとき、Yが整数となる確率は$\frac{\boxed{ウ}}{\boxed{エ}}\ である。
(3)$X_1=4$のとき、Yが整数となる確率は$\frac{\boxed{オ}}{\boxed{カキ}}$である。
(4)Yが整数となる確率は$\frac{\boxed{クケ}}{\boxed{コサ}}$である。
2022青山学院大学理工学部過去問
福田の数学〜立教大学2022年経済学部第3問〜放物線と円と直線で囲まれた面積

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#微分法と積分法#円と方程式#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
Oを原点とする座標平面上の放物線$C:y=x^2$とC上の点P$(\frac{\sqrt3}{2}, \ \frac{3}{4})$がある。
PにおけるCの接線をlとし、また、Pを通りlと直交する直線をmとする。
さらに、mとx軸の交点をQとする。このとき、次の問いに答えよ。
(1)mの方程式を$y=px+q$とするとき、定数p,qの値を求めよ。
(2)Qの座標を$(a,\ 0)$とするとき、aの値を求めよ。
(3)Qを中心とする半径rの円Dがlとただ1つの共有点を持つとき、rの値を求めよ。
(4)(1)で定めたp,qの値に対して、次の連立不等式の表す領域の面積S_1を求めよ。
$x \geqq 0,\ \ \ y \geqq 0,\ \ \ y \leqq px+q,\ \ \ y \leqq x^2$
(5)(2)で定めたaの値と(3)で定めたrの値に対して、次の連立不等式の表す領域
の面積S_2を求めよ。
$0 \leqq x \leqq \frac{\sqrt3}{2},\ \ \ y \geqq 0,\ \ \ y \leqq x^2,\ \ \ (x-a)^2+y^2 \geqq r^2$
2022立教学部経済学部過去問
この動画を見る
Oを原点とする座標平面上の放物線$C:y=x^2$とC上の点P$(\frac{\sqrt3}{2}, \ \frac{3}{4})$がある。
PにおけるCの接線をlとし、また、Pを通りlと直交する直線をmとする。
さらに、mとx軸の交点をQとする。このとき、次の問いに答えよ。
(1)mの方程式を$y=px+q$とするとき、定数p,qの値を求めよ。
(2)Qの座標を$(a,\ 0)$とするとき、aの値を求めよ。
(3)Qを中心とする半径rの円Dがlとただ1つの共有点を持つとき、rの値を求めよ。
(4)(1)で定めたp,qの値に対して、次の連立不等式の表す領域の面積S_1を求めよ。
$x \geqq 0,\ \ \ y \geqq 0,\ \ \ y \leqq px+q,\ \ \ y \leqq x^2$
(5)(2)で定めたaの値と(3)で定めたrの値に対して、次の連立不等式の表す領域
の面積S_2を求めよ。
$0 \leqq x \leqq \frac{\sqrt3}{2},\ \ \ y \geqq 0,\ \ \ y \leqq x^2,\ \ \ (x-a)^2+y^2 \geqq r^2$
2022立教学部経済学部過去問
福田の数学〜立教大学2022年経済学部第2問〜平面ベクトルの直交条件

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
tを正の実数とする。$OA=1,\ OB=t$である三角形OABにおいて、$\overrightarrow{ a }=\overrightarrow{ OA }$
$\overrightarrow{ b }=\overrightarrow{ OB },\angle AOB=θ$とする。ただし、$0 \lt θ \lt \frac{\pi}{2}$とする。また、辺OAの中点
をM、辺OBを1:2に内分する点をNとする。次の問いに答えよ。
(1)$\overrightarrow{ AN }$と$\overrightarrow{ BM }$を$\overrightarrow{ a }$と$\overrightarrow{ b }$を用いて表せ。
(2)内積$\overrightarrow{ AN }・\overrightarrow{ BM }$を$t$と$\cos θ$を用いて表せ。
(3)$\overrightarrow{ AN }∟\overrightarrow{ BM }$であるとき、$\cos θ$を$t$を用いて表せ。
(4)$\overrightarrow{ AN }∟\overrightarrow{ BM }$であるとき、$\cos θ$の最小値とそれを与えるtの値をそれぞれ求めよ。
(5)$\overrightarrow{ AN }∟\overrightarrow{ BM }$となるθが存在するtの値の範囲を求めよ。
2022立教大学経済学部過去問
この動画を見る
tを正の実数とする。$OA=1,\ OB=t$である三角形OABにおいて、$\overrightarrow{ a }=\overrightarrow{ OA }$
$\overrightarrow{ b }=\overrightarrow{ OB },\angle AOB=θ$とする。ただし、$0 \lt θ \lt \frac{\pi}{2}$とする。また、辺OAの中点
をM、辺OBを1:2に内分する点をNとする。次の問いに答えよ。
(1)$\overrightarrow{ AN }$と$\overrightarrow{ BM }$を$\overrightarrow{ a }$と$\overrightarrow{ b }$を用いて表せ。
(2)内積$\overrightarrow{ AN }・\overrightarrow{ BM }$を$t$と$\cos θ$を用いて表せ。
(3)$\overrightarrow{ AN }∟\overrightarrow{ BM }$であるとき、$\cos θ$を$t$を用いて表せ。
(4)$\overrightarrow{ AN }∟\overrightarrow{ BM }$であるとき、$\cos θ$の最小値とそれを与えるtの値をそれぞれ求めよ。
(5)$\overrightarrow{ AN }∟\overrightarrow{ BM }$となるθが存在するtの値の範囲を求めよ。
2022立教大学経済学部過去問
大学入試問題#318 立教大学 改 (2021) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e}\displaystyle \frac{(log\ x)^4}{x^2}dx$
出典:2021年立教大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{e}\displaystyle \frac{(log\ x)^4}{x^2}dx$
出典:2021年立教大学 入試問題
福田の数学〜立教大学2022年経済学部第1問(5)〜群数列

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
自然数n が 2n-1 個続く、初項が1の次のような数列がある。
1,2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 5,…
このとき、自然数 m が初めて現れるのは第何項か。
また第 2022項はいくつか。
2022立教学部経済学部過去問
この動画を見る
自然数n が 2n-1 個続く、初項が1の次のような数列がある。
1,2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 5,…
このとき、自然数 m が初めて現れるのは第何項か。
また第 2022項はいくつか。
2022立教学部経済学部過去問
福田の数学〜立教大学2022年経済学部第1問(6)〜平均と分散

単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$(6)$n$個の値からなるデータがあり,データの値の総和が4,データの値の2乗の総和が26,データの分散が3であるとする.このとき,データの個数$n$は$\boxed{キ}$である.
2022立教大学経済学部過去問
この動画を見る
$\boxed{1}$(6)$n$個の値からなるデータがあり,データの値の総和が4,データの値の2乗の総和が26,データの分散が3であるとする.このとき,データの個数$n$は$\boxed{キ}$である.
2022立教大学経済学部過去問
福田の数学〜立教大学2022年経済学部第1問(4)〜表が連続して出ない確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
コインを5回投げるとき、表が連続して2回以上出ない確率を求めよ。
ただし、コインを1回投げたとき、 表が出る確率および裏が出る確率はそれぞれ1/2であるとする。
2022立教大学経済学部過去問
この動画を見る
コインを5回投げるとき、表が連続して2回以上出ない確率を求めよ。
ただし、コインを1回投げたとき、 表が出る確率および裏が出る確率はそれぞれ1/2であるとする。
2022立教大学経済学部過去問
福田の数学〜立教大学2022年経済学部第1問(3)〜整式の割り算と余り

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
aを定数とする。
3次式 $F(x)=x^3-6x+a$を2次式$G(x)=x^2 -3x+2$で割った余りを$R(x)$ とする。
G(x)がR(x)で割り切れるようなaの値をすべて求めよ。
2022立教大学経済学部過去問
この動画を見る
aを定数とする。
3次式 $F(x)=x^3-6x+a$を2次式$G(x)=x^2 -3x+2$で割った余りを$R(x)$ とする。
G(x)がR(x)で割り切れるようなaの値をすべて求めよ。
2022立教大学経済学部過去問
福田の数学〜立教大学2022年経済学部第1問(2)〜絶対の付いた方程式の解

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$|X-|X-2||=1$の解をすべて求めよ
2022立教大学経済学部過去問
この動画を見る
$|X-|X-2||=1$の解をすべて求めよ
2022立教大学経済学部過去問
