 信州大学
信州大学
 信州大学
信州大学
大学入試問題#908「正確に対応するだけ」 #信州大学理学部(2024) #積分方程式

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
次の等式を満たす関数$f(x)$を求めよ
$f(x)=x+\displaystyle \int_{0}^{\pi} f(t) \cos(x+t) dt$
出典:2024年信州大学理学部
この動画を見る
次の等式を満たす関数$f(x)$を求めよ
$f(x)=x+\displaystyle \int_{0}^{\pi} f(t) \cos(x+t) dt$
出典:2024年信州大学理学部
大学入試問題#907「チャートに掲載されてる?」 #信州大学理学部(2024) #極限

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to a } \displaystyle \frac{x^3-x^2+(2a-3)x+b}{x^2-(a-1)x-a}=3$
が成り立つように定数$a$と$b$の値を求めよ。
出典:2024年信州大学理学部
この動画を見る
$\displaystyle \lim_{ x \to a } \displaystyle \frac{x^3-x^2+(2a-3)x+b}{x^2-(a-1)x-a}=3$
が成り立つように定数$a$と$b$の値を求めよ。
出典:2024年信州大学理学部
大学入試問題#905「基本変形の王道」 #信州大学教育学部(2024) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} (\cos x\cos 2x-\cos3x\sin4x) dx$
出典:2024年信州大学教育学部
この動画を見る
$\displaystyle \int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} (\cos x\cos 2x-\cos3x\sin4x) dx$
出典:2024年信州大学教育学部
大学入試問題#903「記述の仕方が問われる」 #信州大学後期(2024)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学
指導講師:
ますただ
問題文全文(内容文):
$a_1=3$とする
$\displaystyle \frac{1}{4}a_n+\displaystyle \frac{3}{2} \lt a_n+1 \lt \displaystyle \frac{1}{3}a_n+\displaystyle \frac{4}{3}$
を満たすとき、$\displaystyle \lim_{ n \to \infty } a_n$を求めよ
出典:2024年信州大学後期
この動画を見る
$a_1=3$とする
$\displaystyle \frac{1}{4}a_n+\displaystyle \frac{3}{2} \lt a_n+1 \lt \displaystyle \frac{1}{3}a_n+\displaystyle \frac{4}{3}$
を満たすとき、$\displaystyle \lim_{ n \to \infty } a_n$を求めよ
出典:2024年信州大学後期
大学入試問題#893「難易度クソ高め」 #信州大学(2015)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \displaystyle \int_{2}^{x} \displaystyle \frac{t^2}{(t^2-1)^2}dt$
出典:2015年信州大学後期
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \int_{2}^{x} \displaystyle \frac{t^2}{(t^2-1)^2}dt$
出典:2015年信州大学後期
大学入試問題#891「まだこのタイプの問題残ってた」 #信州大学(2023) #キングプロパティ

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#信州大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\pi}^{ \pi } \displaystyle \frac{1}{1+e^{-2\sin x}} dx$
出典:2023年信州大学
この動画を見る
$\displaystyle \int_{-\pi}^{ \pi } \displaystyle \frac{1}{1+e^{-2\sin x}} dx$
出典:2023年信州大学
#信州大学#不定積分#ますただ
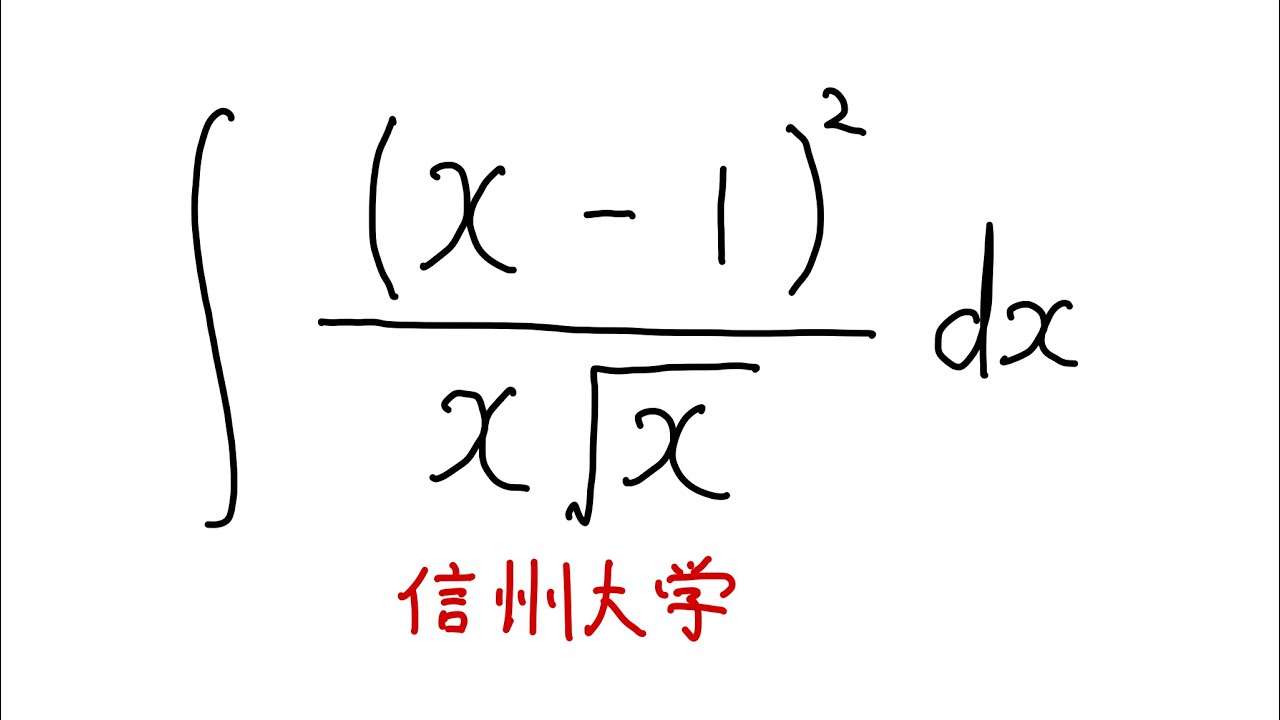
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{(x-1)^2}{x\sqrt{ x }} dx$
出典:信州大学
この動画を見る
$\displaystyle \int \displaystyle \frac{(x-1)^2}{x\sqrt{ x }} dx$
出典:信州大学
#信州大学 #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{1}{x\sqrt{ x+1 }} dx$
出典:信州大学
この動画を見る
$\displaystyle \int \displaystyle \frac{1}{x\sqrt{ x+1 }} dx$
出典:信州大学
#信州大学 #不定積分
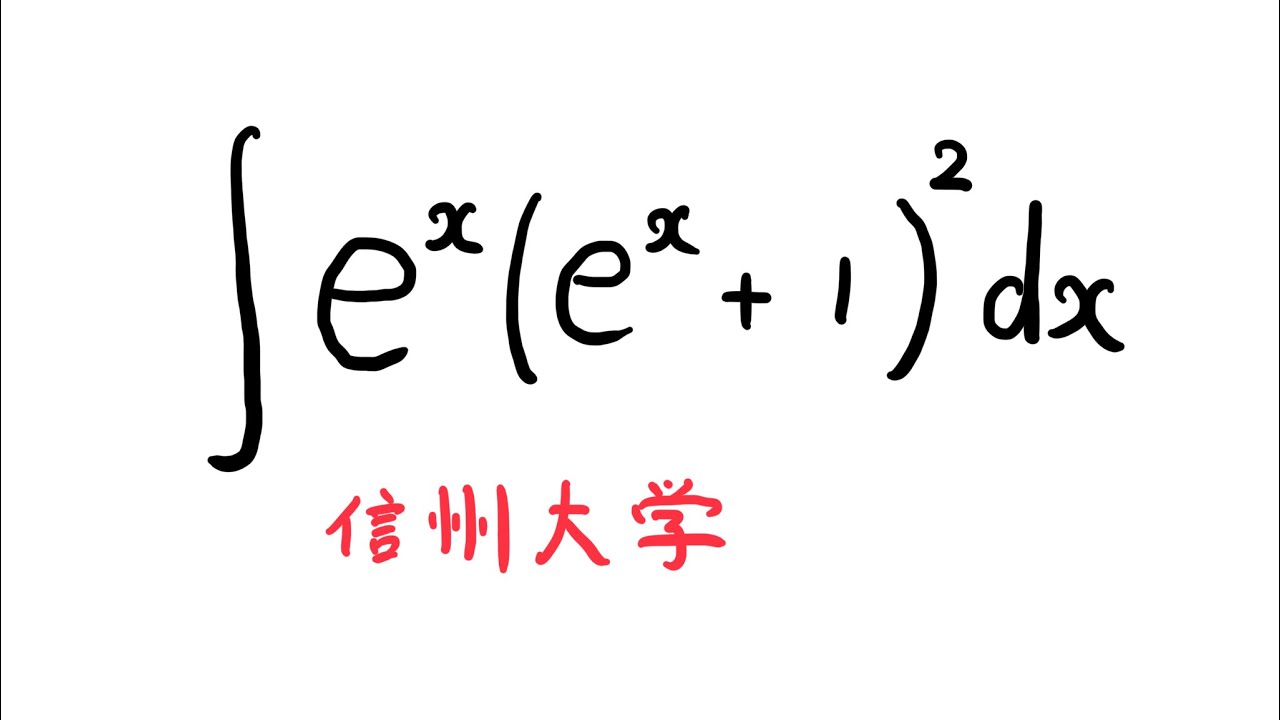
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学
指導講師:
ますただ
問題文全文(内容文):
以下の不定積分を解け
$\displaystyle \int e^x(e^x+1)^2 dx$
出典:信州大学
この動画を見る
以下の不定積分を解け
$\displaystyle \int e^x(e^x+1)^2 dx$
出典:信州大学
【高校数学】信州大学2023年の積分の問題をその場で解説しながら解いてみた!毎日積分88日目~47都道府県制覇への道~【㉛長野】【毎日17時投稿】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
【信州大学 2023】
tを実数とし、座標空間内の2点$P(0,0,t^2-1), Q(t,1,e^t+e^{-t}-e-e^{-1})$を考える。tを$-1≦t≦1$の範囲で動かすとき、線分PQが通過してできる曲面および2平面$y=1,z=0$で囲まれてできる立体の体積を求めよ。
この動画を見る
【信州大学 2023】
tを実数とし、座標空間内の2点$P(0,0,t^2-1), Q(t,1,e^t+e^{-t}-e-e^{-1})$を考える。tを$-1≦t≦1$の範囲で動かすとき、線分PQが通過してできる曲面および2平面$y=1,z=0$で囲まれてできる立体の体積を求めよ。
大学入試問題#663「これは良問」 信州大学(2023) 定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学
指導講師:
ますただ
問題文全文(内容文):
$x \gt 0$
$\displaystyle \int_{-\frac{1}{x}}^{x} \displaystyle \frac{dt}{1+t^2}$
出典:2023年信州大学 入試問題
この動画を見る
$x \gt 0$
$\displaystyle \int_{-\frac{1}{x}}^{x} \displaystyle \frac{dt}{1+t^2}$
出典:2023年信州大学 入試問題
信州大 連立漸化式
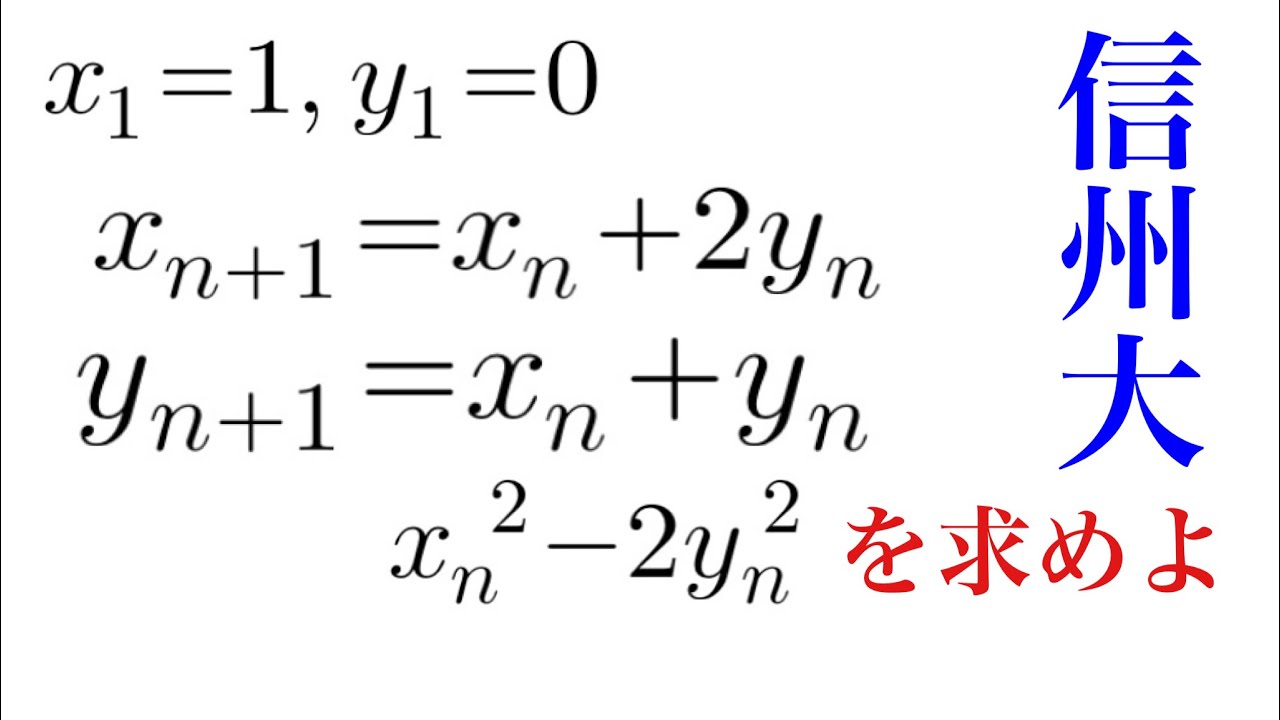
単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x_1=1,y_1=0$
$x_{n+1}=x_n+2y_n$
$y_{n+1}=x_n+y_n$
このとき、${x_n}^2-2{y_n}^2$を求めよ.
信州大過去問
この動画を見る
$x_1=1,y_1=0$
$x_{n+1}=x_n+2y_n$
$y_{n+1}=x_n+y_n$
このとき、${x_n}^2-2{y_n}^2$を求めよ.
信州大過去問
信州大(医)整数問題の基本

単元:
#整数の性質#信州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
2023信州大学過去問題
3つの自然数P,P+10,P+20がすべて素数となるようなPがただ1つ存在することを示せ
この動画を見る
2023信州大学過去問題
3つの自然数P,P+10,P+20がすべて素数となるようなPがただ1つ存在することを示せ
あれを使ってスッキリ解こう❗️信州大
大学入試問題#533「もはや3分で1級の詰将棋」 信州大学1999 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\pi} \displaystyle \frac{x\ \sin\ x}{3+\sin^2\ x} dx$
出典:1999年信州大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\pi} \displaystyle \frac{x\ \sin\ x}{3+\sin^2\ x} dx$
出典:1999年信州大学 入試問題
大学入試問題#530「定石どおり」 信州大学(2000) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} e^{\sin\ x}\sin2x\ dx$
出典:2000年信州大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} e^{\sin\ x}\sin2x\ dx$
出典:2000年信州大学 入試問題
大学入試問題#523「落とせない積分」 信州大学(2001) #定積分
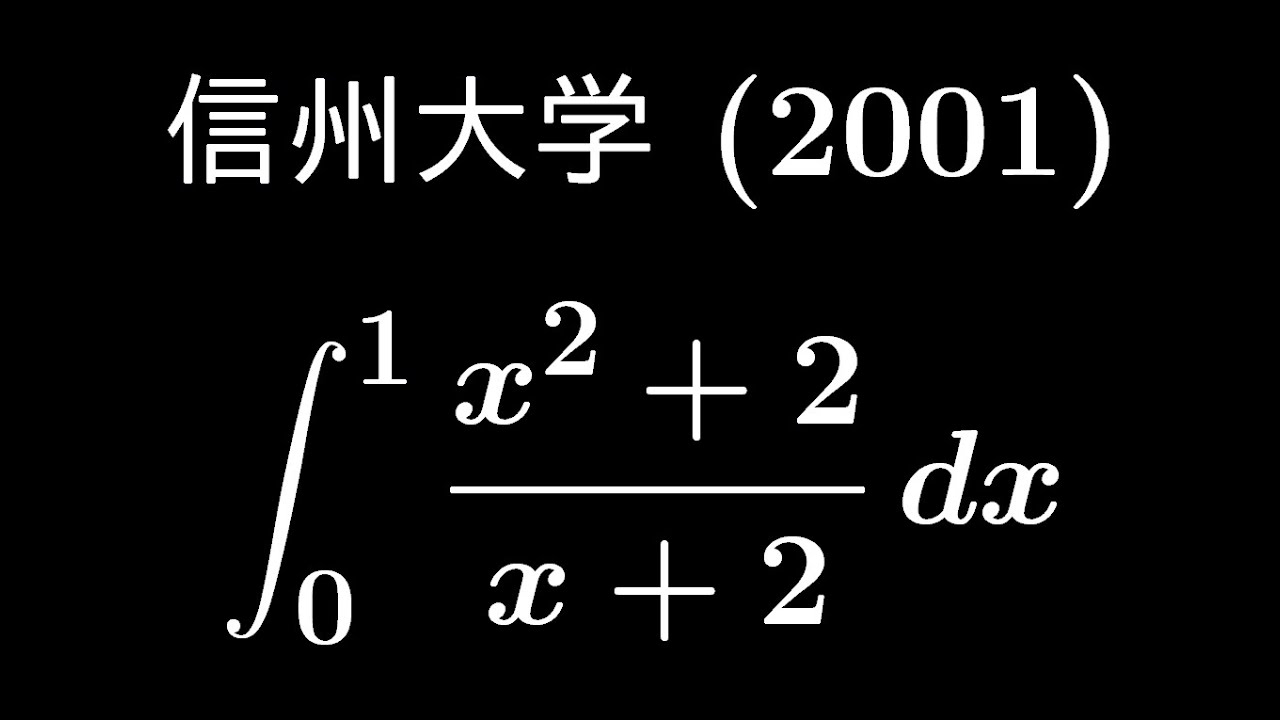
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{x^2+2}{x+2} dx$
出典:2001年信州大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{x^2+2}{x+2} dx$
出典:2001年信州大学 入試問題
大学入試問題#522「これ初見はきつそう」 信州大学2001 #面積

単元:
#大学入試過去問(数学)#平面上の曲線#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#数学(高校生)#信州大学#数C
指導講師:
ますただ
問題文全文(内容文):
$0 \leqq \theta \leqq 2\pi$
曲線
$x=\cos^3\theta,\ y=\sin^3\theta$で囲まれた面積を求めよ
出典:2001年信州大学後期 入試問題
この動画を見る
$0 \leqq \theta \leqq 2\pi$
曲線
$x=\cos^3\theta,\ y=\sin^3\theta$で囲まれた面積を求めよ
出典:2001年信州大学後期 入試問題
大学入試問題#521「部分積分もあるかもしれない」 信州大学(2004) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{2} (x+2)\sqrt{ 4-x^2 }\ dx$
出典:2004年信州大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{2} (x+2)\sqrt{ 4-x^2 }\ dx$
出典:2004年信州大学 入試問題
大学入試問題#499「見た目以上に計算量が多い」 信州大学後期(2015) #広義積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ s \to +0 } \displaystyle \int_{s}^{\frac{\pi}{2}} (\displaystyle \frac{1}{\sin\ x}-\displaystyle \frac{1}{x}) dx$
出典:2015年信州大学後期 入試問題
この動画を見る
$\displaystyle \lim_{ s \to +0 } \displaystyle \int_{s}^{\frac{\pi}{2}} (\displaystyle \frac{1}{\sin\ x}-\displaystyle \frac{1}{x}) dx$
出典:2015年信州大学後期 入試問題
大学入試問題#498「類題はたくさん」 信州大学後期2011 #不定積分3
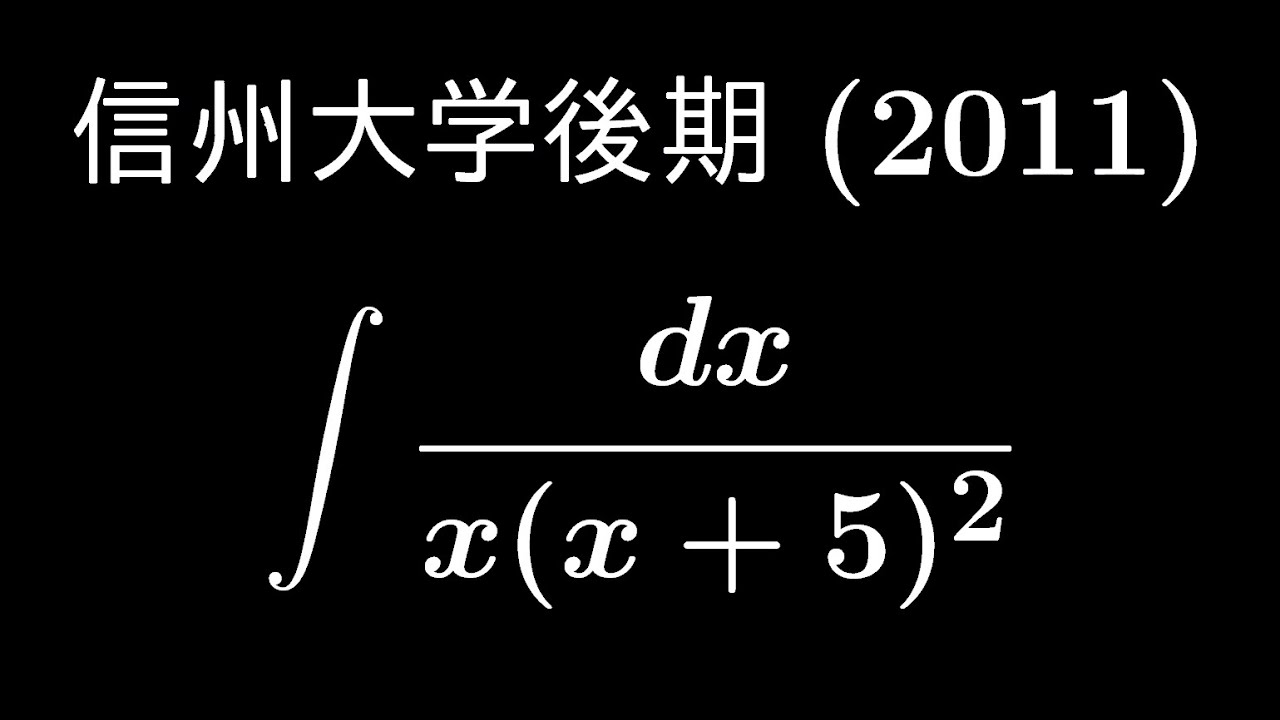
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{dx}{x(x+5)^2}$
出典:2011年信州大学後期 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{dx}{x(x+5)^2}$
出典:2011年信州大学後期 入試問題
大学入試問題#494「基本問題」 信州大学後期(2011) #不定積分
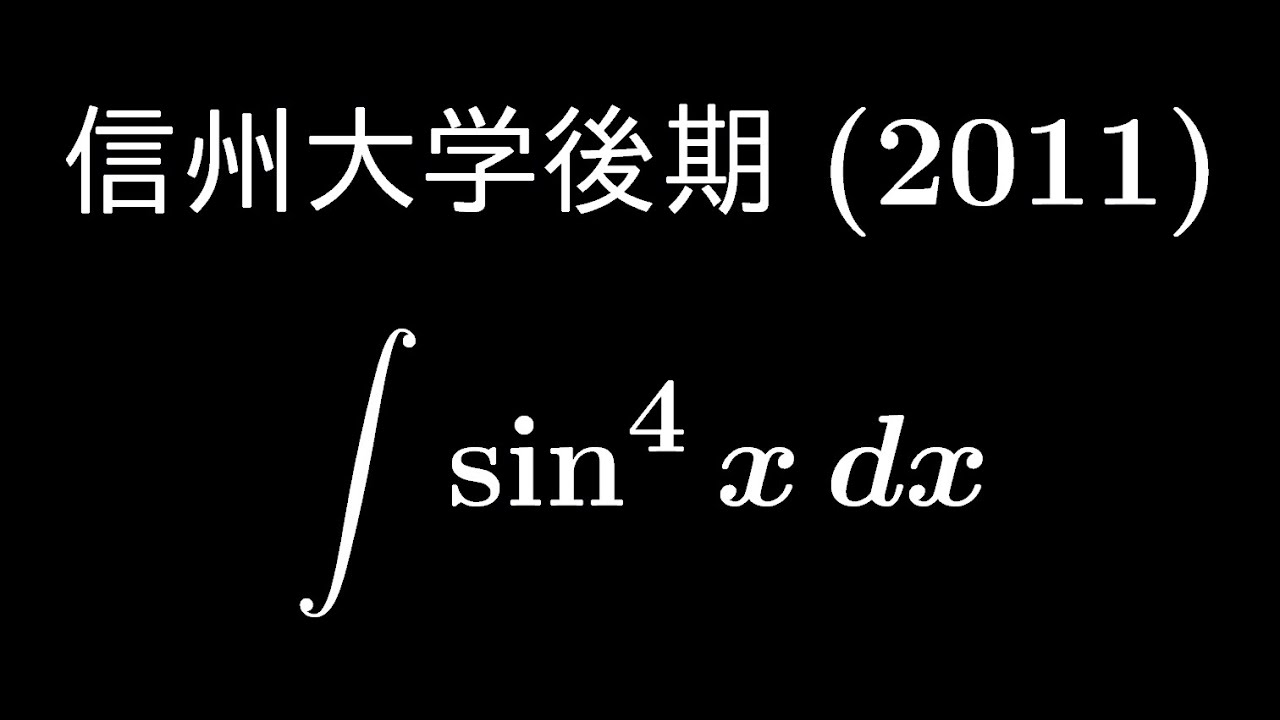
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \sin^4x\ dx$
出典:2011年信州大学後期 入試問題
この動画を見る
$\displaystyle \int \sin^4x\ dx$
出典:2011年信州大学後期 入試問題
大学入試問題#492「置換方法はいろいろ」 信州大学後期(2018) #広義積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \displaystyle \int_{2}^{n} \displaystyle \frac{dx}{\sqrt{ x^5+x^2 }}$
出典:2018年信州大学後期 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \int_{2}^{n} \displaystyle \frac{dx}{\sqrt{ x^5+x^2 }}$
出典:2018年信州大学後期 入試問題
大学入試問題#490「よくみる形」 信州大学後期(2015) #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ#大阪市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int x(log\ x)^2 dx$
出典:2015年信州大学後期 入試問題
この動画を見る
$\displaystyle \int x(log\ x)^2 dx$
出典:2015年信州大学後期 入試問題
大学入試問題#476「むむむ!」 信州大学(2010) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a \gt 0$
$\displaystyle \int_{0}^{a} \displaystyle \frac{x}{1+\sqrt{ a^2-x^2 }} dx$
出典:2010年信州大学 入試問題
この動画を見る
$a \gt 0$
$\displaystyle \int_{0}^{a} \displaystyle \frac{x}{1+\sqrt{ a^2-x^2 }} dx$
出典:2010年信州大学 入試問題
大学入試問題#474「沼にはまりがち」 信州大学後期(2011) #不定積分
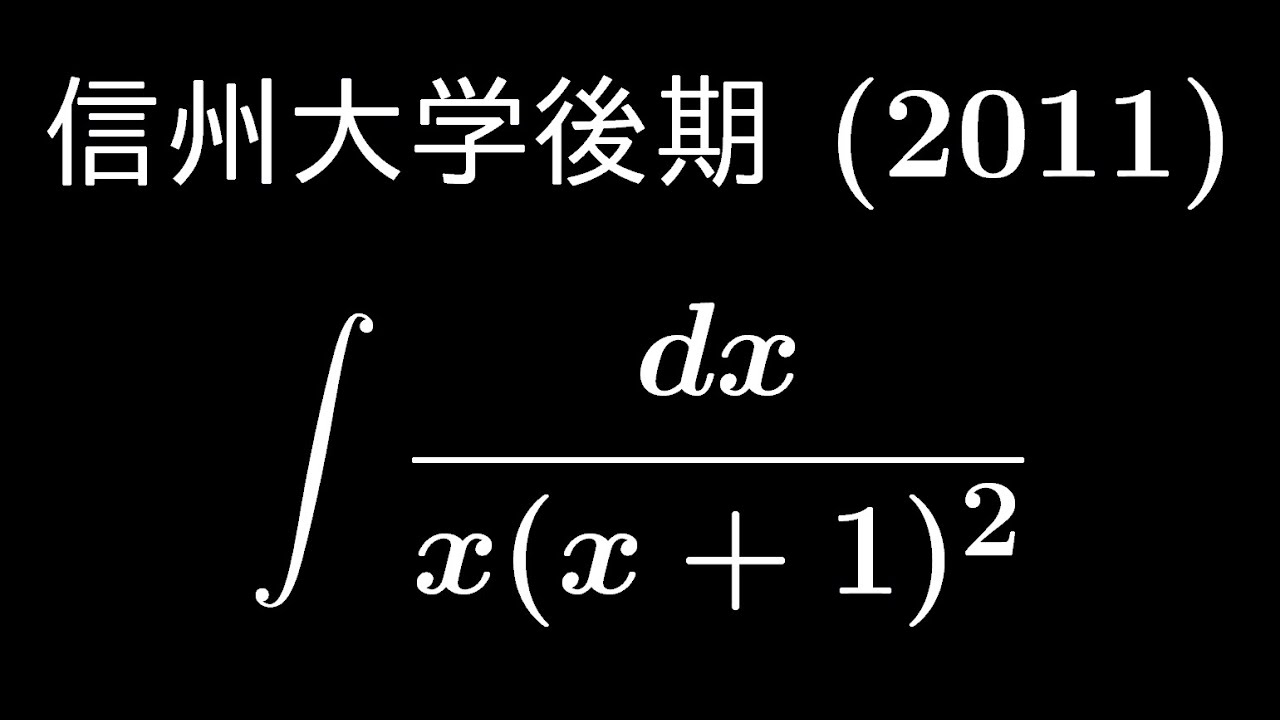
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{dx}{x(x+1)^2}$
出典:2011年信州大学後期 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{dx}{x(x+1)^2}$
出典:2011年信州大学後期 入試問題
大学入試問題#473「計算は大変かもしれない」 信州大学 理・医 (2011) #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int log(1+\sqrt{ x }) dx$
出典:2011年信州大学 入試問題
この動画を見る
$\displaystyle \int log(1+\sqrt{ x }) dx$
出典:2011年信州大学 入試問題
大学入試問題#471「深夜1時でストック0」 信州大学後期(2013) 不定積分
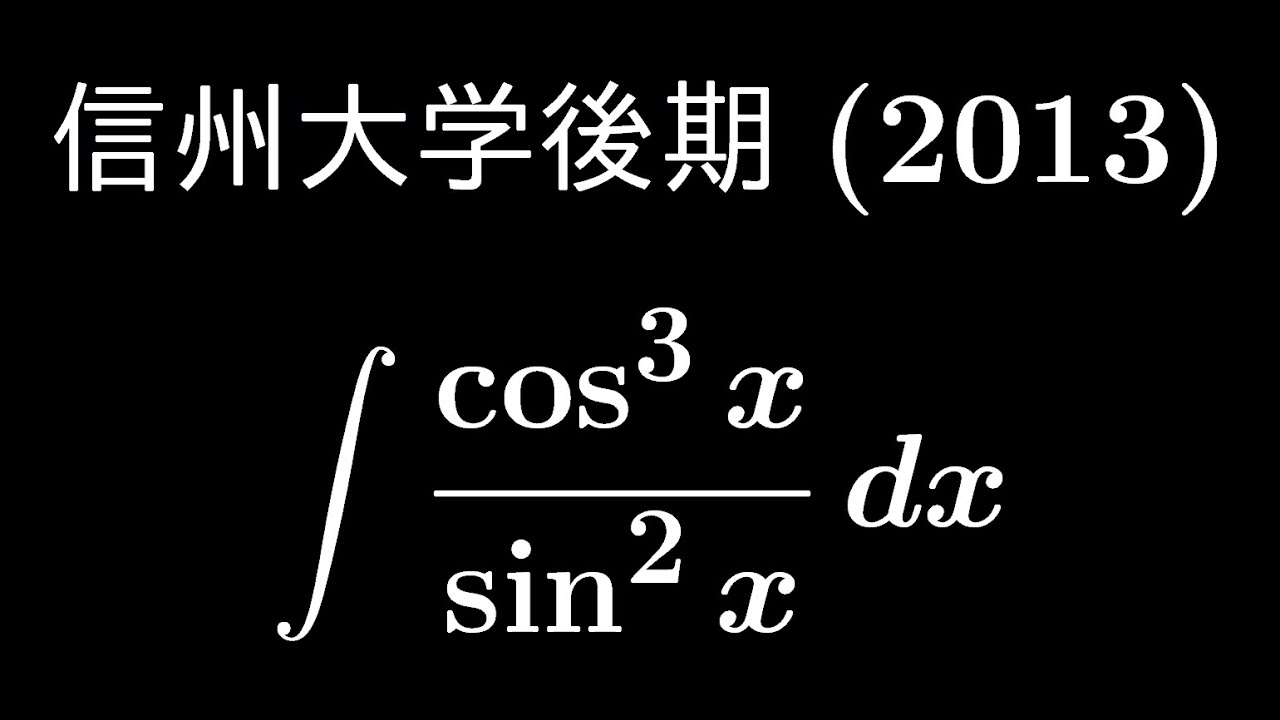
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{\cos^3\ x}{\sin^2\ x} dx$
出典:2013年信州大学後期 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{\cos^3\ x}{\sin^2\ x} dx$
出典:2013年信州大学後期 入試問題
大学入試問題#470「誘導なくてもどうにかできそう」 信州大学 理・医学部(2021) #微積の応用

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#関数の極限#色々な関数の導関数#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\forall\ a,b$
$f(a+b)=f(a)+f(b)+4ab$
$f'(0)=2$
(1)
$f(0)$を求めよ
(2)
$f(x)$は微分可能を示せ
$f(x)$を求めよ
(3)
$\displaystyle \lim_{ x \to \infty } \displaystyle \int_{1}^{x} \displaystyle \frac{1}{f(t)}dt(x \gt 1)$
出典:2021年信州大学 入試問題
この動画を見る
$\forall\ a,b$
$f(a+b)=f(a)+f(b)+4ab$
$f'(0)=2$
(1)
$f(0)$を求めよ
(2)
$f(x)$は微分可能を示せ
$f(x)$を求めよ
(3)
$\displaystyle \lim_{ x \to \infty } \displaystyle \int_{1}^{x} \displaystyle \frac{1}{f(t)}dt(x \gt 1)$
出典:2021年信州大学 入試問題
大学入試問題#463「ええ問題や~~」 信州大学 理・医 (2016) #積分の応用

単元:
#大学入試過去問(数学)#数学的帰納法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} (1-x^2)^n dx$
$=\displaystyle \frac{4^n(n!)^2}{(2n+1)!}$を示せ
出典:2016年信州大学医学部 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} (1-x^2)^n dx$
$=\displaystyle \frac{4^n(n!)^2}{(2n+1)!}$を示せ
出典:2016年信州大学医学部 入試問題
