 早稲田大学
早稲田大学
 早稲田大学
早稲田大学
福田の数学〜早稲田大学2025商学部第3問〜三角形を一辺を軸として回転させたときの回転体の体積の最大

単元:
#数A#大学入試過去問(数学)#図形の性質#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
空間内の異なる$4$点
$A,B,C,D$が$AD=BC=2$、
$AB=CD=1$を満たし、線分$AD$と線分$BC$が
点$P$のみで交わり、$P$は$AD$と$BC$をそれぞれ
$AP:PD=s:(1-s),$
$BP:PC=t:(1-t) \ (0\lt s \lt t,0\lt t \lt 1)$
に内分しているとする。次の問いに答えよ。
(1)$s$を$t$を用いて表せ。
(2)$t$のとりうる値の範囲を求めよ。
(3)線分$BC$を軸にして$\triangle ABP$を$1$回転させるとき、
$\triangle ABP$の辺と内部が通過する部分の体積を
$V$とする。$V$の最大値を求めよ。
$2025$年早稲田大学商学部過去問題
この動画を見る
$\boxed{3}$
空間内の異なる$4$点
$A,B,C,D$が$AD=BC=2$、
$AB=CD=1$を満たし、線分$AD$と線分$BC$が
点$P$のみで交わり、$P$は$AD$と$BC$をそれぞれ
$AP:PD=s:(1-s),$
$BP:PC=t:(1-t) \ (0\lt s \lt t,0\lt t \lt 1)$
に内分しているとする。次の問いに答えよ。
(1)$s$を$t$を用いて表せ。
(2)$t$のとりうる値の範囲を求めよ。
(3)線分$BC$を軸にして$\triangle ABP$を$1$回転させるとき、
$\triangle ABP$の辺と内部が通過する部分の体積を
$V$とする。$V$の最大値を求めよ。
$2025$年早稲田大学商学部過去問題
福田の数学〜早稲田大学2025商学部第2問〜x軸に関する対称移動とy=√3xに関する対称移動の組合せで決まる点列

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
$a,b$を実数とする。
座標平面上の点$P_1,P_2,P_3,\cdots $は
以下の条件を満たしている。
すべての正の奇数$n$に対して、$P_n$と$P_{n+1}$は
$x$軸に関して対称な位置にある。
ただし、$P_n$が$x$軸上にあるときは$P_n=P_{n+1}$で
あるとする。
また、すべての正の偶数$n$に対して、
$P_n$と$P_{n+1}$は直線$y=ax+b$に関して対称な
位置にある。
ただし、$P_n$が直線$y=ax+b$上にあるときは
$P_n=P_{n+1}$であるとする。
(1)$a=0,b=1,P_1(0,0)$であるとき、
$P_{2025}$の座標を求めよ。
(2)$a=1,b=0,P_1(2,1)$であるとき、
$P_{2025}$の座標を求めよ。
(3)$a=\sqrt3,b=0,P_1(1,1)$であるとする。
$m,n$を正の整数とする。
$P_m$と$P_n$の距離の最大値を求めよ。
$2025$年早稲田大学商学部過去問題
この動画を見る
$\boxed{2}$
$a,b$を実数とする。
座標平面上の点$P_1,P_2,P_3,\cdots $は
以下の条件を満たしている。
すべての正の奇数$n$に対して、$P_n$と$P_{n+1}$は
$x$軸に関して対称な位置にある。
ただし、$P_n$が$x$軸上にあるときは$P_n=P_{n+1}$で
あるとする。
また、すべての正の偶数$n$に対して、
$P_n$と$P_{n+1}$は直線$y=ax+b$に関して対称な
位置にある。
ただし、$P_n$が直線$y=ax+b$上にあるときは
$P_n=P_{n+1}$であるとする。
(1)$a=0,b=1,P_1(0,0)$であるとき、
$P_{2025}$の座標を求めよ。
(2)$a=1,b=0,P_1(2,1)$であるとき、
$P_{2025}$の座標を求めよ。
(3)$a=\sqrt3,b=0,P_1(1,1)$であるとする。
$m,n$を正の整数とする。
$P_m$と$P_n$の距離の最大値を求めよ。
$2025$年早稲田大学商学部過去問題
福田の数学〜早稲田大学2025商学部第1問(4)〜正九角形の頂点を結んでできる正三角形の個数

単元:
#数A#大学入試過去問(数学)#場合の数と確率#図形の性質#確率#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(4)$P$を平面上の正九角形とする。
$P$の異なる$2$つの頂点を通る直線をすべて考える。
これら$36$本の直線のうちの$3$本により平面上で
囲まれてできる正三角形の総数は$\boxed{エ}$である。
ただし、互いに合同でも位置の異なるものは
異なる三角形として数える。
$2025$年早稲田大学商学部過去問題
この動画を見る
$\boxed{1}$
(4)$P$を平面上の正九角形とする。
$P$の異なる$2$つの頂点を通る直線をすべて考える。
これら$36$本の直線のうちの$3$本により平面上で
囲まれてできる正三角形の総数は$\boxed{エ}$である。
ただし、互いに合同でも位置の異なるものは
異なる三角形として数える。
$2025$年早稲田大学商学部過去問題
福田の数学〜早稲田大学2025商学部第1問(3)〜定積分で表された関数方程式

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(3)$m,n$を正の整数とする。
$n$次関数$f(x)$が次の等式を満たしているとき、
$f(x)=\boxed{ウ}$である。
$\displaystyle \int_{0}^{x} {f(t)}^{m-1} dt=(2x)^m f(x)$
$2025$年早稲田大学商学部過去問題
この動画を見る
$\boxed{1}$
(3)$m,n$を正の整数とする。
$n$次関数$f(x)$が次の等式を満たしているとき、
$f(x)=\boxed{ウ}$である。
$\displaystyle \int_{0}^{x} {f(t)}^{m-1} dt=(2x)^m f(x)$
$2025$年早稲田大学商学部過去問題
福田の数学〜早稲田大学2025商学部第1問(2)〜3項間漸化式の解法

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(2)数列$\{a_n\}$が次の条件を満たしている。
$a_1=a_{2025}=0,a_{n+1}-2a_n+a_{n-1}=-1 \ (n=2,3,4,\cdots)$
このとき、一般項$a_n$は$a_n=\boxed{イ}$である。
$2025$年早稲田大学商学部過去問題
この動画を見る
$\boxed{1}$
(2)数列$\{a_n\}$が次の条件を満たしている。
$a_1=a_{2025}=0,a_{n+1}-2a_n+a_{n-1}=-1 \ (n=2,3,4,\cdots)$
このとき、一般項$a_n$は$a_n=\boxed{イ}$である。
$2025$年早稲田大学商学部過去問題
福田の数学〜早稲田大学2025商学部第1問(1)〜方程式の実数解の個数

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(1)正の実数$a$に対して、円$x^2+(y-a)^2=a^2$と
曲線$y=x^3$がちょうど$2$つの共有点をもつとき、
$a=\boxed{ア}$である。
$2025$年早稲田大学商学部過去問
この動画を見る
$\boxed{1}$
(1)正の実数$a$に対して、円$x^2+(y-a)^2=a^2$と
曲線$y=x^3$がちょうど$2$つの共有点をもつとき、
$a=\boxed{ア}$である。
$2025$年早稲田大学商学部過去問
福田の数学〜早稲田大学2025教育学部第4問〜共有点の個数と面積計算

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
$k$は実数とする。
曲線$C:y=(x^3-x+2)e^{-x}$と直線$y=k$との
共有点の偶数を$f(k)$で表す。次の問いに答えよ。
ただし、必要ならば自然数$n$に対し
$\displaystyle \lim_{x\to\infty} x^n e^{-x}=0$が成り立つことは
説明なしに用いてもよい。
(1)$k$が実数全体を動くとき、
$f(k)$の最大値の最小値を求めよ。
(2)$f(k)=2$を満たす$k$の値の範囲を求めよ。
(3)$\alpha$を正の実数とする。
曲線$C,x$軸,$y$軸,および直線$x=\alpha$で囲まれる
部分の面積を$\alpha$を用いて表せ。
$2025$年早稲田大学教育学部過去問題
この動画を見る
$\boxed{4}$
$k$は実数とする。
曲線$C:y=(x^3-x+2)e^{-x}$と直線$y=k$との
共有点の偶数を$f(k)$で表す。次の問いに答えよ。
ただし、必要ならば自然数$n$に対し
$\displaystyle \lim_{x\to\infty} x^n e^{-x}=0$が成り立つことは
説明なしに用いてもよい。
(1)$k$が実数全体を動くとき、
$f(k)$の最大値の最小値を求めよ。
(2)$f(k)=2$を満たす$k$の値の範囲を求めよ。
(3)$\alpha$を正の実数とする。
曲線$C,x$軸,$y$軸,および直線$x=\alpha$で囲まれる
部分の面積を$\alpha$を用いて表せ。
$2025$年早稲田大学教育学部過去問題
福田の数学〜早稲田大学2025教育学部第3問〜楕円と接線

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
座標平面上で、
点$H(0,2\sqrt2)$から楕円$C:x^2+2y^2=8$へ引いた
$2$つの接線を$L_1,L_2$とし、$L_1,L_2$と$C$との
共有点をそれぞれ$P_1,P_2$とする。
ただし、$P_1$の$x$座標は正であるとする。
次の問いに答えよ。
(1)直線$L_1$と$L_2$それぞれの傾きを求めよ。
(2)$2$点$P_1,P_2$を通る直線を$L_3$とする。
直線$L_3$と楕円$C$で囲まれた$2$つの部分のうち、
直線$L_3$の上側にある方の面積を求めよ。
$2025$年早稲田大学教育学部過去問題
この動画を見る
$\boxed{3}$
座標平面上で、
点$H(0,2\sqrt2)$から楕円$C:x^2+2y^2=8$へ引いた
$2$つの接線を$L_1,L_2$とし、$L_1,L_2$と$C$との
共有点をそれぞれ$P_1,P_2$とする。
ただし、$P_1$の$x$座標は正であるとする。
次の問いに答えよ。
(1)直線$L_1$と$L_2$それぞれの傾きを求めよ。
(2)$2$点$P_1,P_2$を通る直線を$L_3$とする。
直線$L_3$と楕円$C$で囲まれた$2$つの部分のうち、
直線$L_3$の上側にある方の面積を求めよ。
$2025$年早稲田大学教育学部過去問題
福田の数学〜早稲田大学2025教育学部第2問〜組合せと確率の基本的な性質

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
$n$を自然数とする。
$1$から$n$mでの数字がもれなく一つずつ記入された
$n$枚の赤色のカードと$1$から$n$までの数字がもれなく
一つずつ記入された$n$枚の白色のカードがある。
この$2n$枚のカードの中から同時に$2$枚を取り出し、
カードに記入された数字を確認した後にもとに戻す、
という試行を$2$回行う。次の問いに答えよ。
(1)$1$回目に取り出した$2$枚のカードに記入された
数字が同じであり、かつ$1$回目に取り出した$2$枚の
カードに記入された数字と$2$回目に取り出した$2$枚の
カードに記入された数字の間に共通の数字が
存在しない取り出し方の総数を$n$を用いて表せ。
(2)$1$回目に取り出した$2$枚のカードに記入された
数字が異なり、かつ$1$回目に取り出した$2$枚の
カードに記入された数字と$2$回目に取り出した
$2$枚のカードに記入された数字の間に共通の数字が
存在しない取り出し方の総数を$n$を用いて表せ。
(3)$1$回目に取り出した$2$枚のカードに記入された数字と
$2$回目に取り出した$2$枚のカードに記入された
数字の間に共通の数字が存在する確率を
$n$を用いて表せ。
$2025$年早稲田大学教育学部過去問題
この動画を見る
$\boxed{2}$
$n$を自然数とする。
$1$から$n$mでの数字がもれなく一つずつ記入された
$n$枚の赤色のカードと$1$から$n$までの数字がもれなく
一つずつ記入された$n$枚の白色のカードがある。
この$2n$枚のカードの中から同時に$2$枚を取り出し、
カードに記入された数字を確認した後にもとに戻す、
という試行を$2$回行う。次の問いに答えよ。
(1)$1$回目に取り出した$2$枚のカードに記入された
数字が同じであり、かつ$1$回目に取り出した$2$枚の
カードに記入された数字と$2$回目に取り出した$2$枚の
カードに記入された数字の間に共通の数字が
存在しない取り出し方の総数を$n$を用いて表せ。
(2)$1$回目に取り出した$2$枚のカードに記入された
数字が異なり、かつ$1$回目に取り出した$2$枚の
カードに記入された数字と$2$回目に取り出した
$2$枚のカードに記入された数字の間に共通の数字が
存在しない取り出し方の総数を$n$を用いて表せ。
(3)$1$回目に取り出した$2$枚のカードに記入された数字と
$2$回目に取り出した$2$枚のカードに記入された
数字の間に共通の数字が存在する確率を
$n$を用いて表せ。
$2025$年早稲田大学教育学部過去問題
福田の数学〜早稲田大学2025教育学部第1問(4)〜2変数関数の最大

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(4)$4$つの辺$AB,BC,CD,DA$の長さが$1$である
四面体$ABCD$を考える。
そのような四面体の体積の最大値を求めよ。
$2025$年早稲田大学教育学部過去問題
この動画を見る
$\boxed{1}$
(4)$4$つの辺$AB,BC,CD,DA$の長さが$1$である
四面体$ABCD$を考える。
そのような四面体の体積の最大値を求めよ。
$2025$年早稲田大学教育学部過去問題
福田の数学〜早稲田大学2025教育学部第1問(3)〜5角柱の10個の点から同一平面上にある4点を選ぶ確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(3)底面が正五角形である$5$角柱の頂点から相異なる
$4$点を選ぶとき、
$4$点が同一平面上にある確率を求めよ。
ただし、$4$点の選び方は同様に確からしいとする。
$2025$年早稲田大学教育学部過去問題
この動画を見る
$\boxed{1}$
(3)底面が正五角形である$5$角柱の頂点から相異なる
$4$点を選ぶとき、
$4$点が同一平面上にある確率を求めよ。
ただし、$4$点の選び方は同様に確からしいとする。
$2025$年早稲田大学教育学部過去問題
福田の数学〜早稲田大学2025教育学部第1問(2)〜三角形の外心と垂心と点の回転

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(2)座標平面上の$3$点
$A(1,0),B(0,-1),C(-1,1)$を
頂点とする三角形$ABC$を考える。
三角形$ABC$をその外心を中心として反時計回りに
$\dfrac{\pi}{3}$だけ回転することで得られる三角形の
垂心の座標を求めよ。
なお、三角形の$3$頂点から対辺または
その延長に下ろした$3$本の垂線は一点で交わり、
その交点を三角形の垂心という。
$2025$年早稲田大学教育学部第1問過去問題
この動画を見る
$\boxed{1}$
(2)座標平面上の$3$点
$A(1,0),B(0,-1),C(-1,1)$を
頂点とする三角形$ABC$を考える。
三角形$ABC$をその外心を中心として反時計回りに
$\dfrac{\pi}{3}$だけ回転することで得られる三角形の
垂心の座標を求めよ。
なお、三角形の$3$頂点から対辺または
その延長に下ろした$3$本の垂線は一点で交わり、
その交点を三角形の垂心という。
$2025$年早稲田大学教育学部第1問過去問題
福田の数学〜早稲田大学2025教育学部第1問(1)〜シグマ計算

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(1)$k$を自然数とする。次の数
$-1^2+2^2-3^2+4^2-5^2+6^2- \cdots -(2k-1)^2+(2k)^2$
を$k$を用いて表せ。
$2025$年早稲田大学教育学部過去問題
この動画を見る
$\boxed{1}$
(1)$k$を自然数とする。次の数
$-1^2+2^2-3^2+4^2-5^2+6^2- \cdots -(2k-1)^2+(2k)^2$
を$k$を用いて表せ。
$2025$年早稲田大学教育学部過去問題
福田の数学〜早稲田大学2025社会科学部第3問〜三角関数の最大最小と三角方程式の解の個数

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#三角関数#円と方程式#三角関数とグラフ#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
$\theta$の関数
$f(\theta)=\cos 2\theta-\sqrt3 \sin 2\theta+4\cos\dfrac{\theta}{2}\left(\sin\dfrac{\theta}{2}-\sqrt3 \cos\dfrac{\theta}{2}\right)+2\sqrt3$
を考える。
ただし、$0\leqq \theta \leqq \pi$とする。次の問いに答えよ。
(1)$k=\sin\theta-\sqrt3 \cos \theta$とおくとき、
$f(\theta)$を$k$の関数で表せ。
(2)$f(\theta)$の最大値、最小値を求めよ。
また、そのときの$\theta$の値を求めよ。
(3) (1)の$k$に対して、$\theta$の方程式
$f(\theta)=ak$の解の個数を求めよ。
ただし、定数$a$は$0\lt a \leqq 3$とする。
$2025$年早稲田大学社会科学部過去問題
この動画を見る
$\boxed{3}$
$\theta$の関数
$f(\theta)=\cos 2\theta-\sqrt3 \sin 2\theta+4\cos\dfrac{\theta}{2}\left(\sin\dfrac{\theta}{2}-\sqrt3 \cos\dfrac{\theta}{2}\right)+2\sqrt3$
を考える。
ただし、$0\leqq \theta \leqq \pi$とする。次の問いに答えよ。
(1)$k=\sin\theta-\sqrt3 \cos \theta$とおくとき、
$f(\theta)$を$k$の関数で表せ。
(2)$f(\theta)$の最大値、最小値を求めよ。
また、そのときの$\theta$の値を求めよ。
(3) (1)の$k$に対して、$\theta$の方程式
$f(\theta)=ak$の解の個数を求めよ。
ただし、定数$a$は$0\lt a \leqq 3$とする。
$2025$年早稲田大学社会科学部過去問題
福田の数学〜早稲田大学2025社会科学部第2問〜階差数列

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
数列$\{a_n\}$の階差数列を$\{b_n\}$、すなわち
$b_n=a_{n+1}-a_n \quad (n=1,2,3,\cdots)$
とする。次の問いに答えよ。
(1)$a_n=-\dfrac{1}{n}$のとき、
$b_n$を$n$の式で表す。
(2)$b_n=\dfrac{1}{n(n+1)}$のとき、
$a_n$を$n$の式で表せ。ただし、$a_1=1$とする。
(3)数列$\{b_n\}$が以下を満たすとき、
$a_n$を$n$の式で表せ。ただし、$a_1=1$とする。
$\begin{eqnarray}
\left\{
\begin{array}{l}
b_1=1 \\
b_n=n(n+1) \quad (n\geqq 2)
\end{array}
\right.
\end{eqnarray}$
$2025$念早稲田大学社会科学部過去問題
この動画を見る
$\boxed{2}$
数列$\{a_n\}$の階差数列を$\{b_n\}$、すなわち
$b_n=a_{n+1}-a_n \quad (n=1,2,3,\cdots)$
とする。次の問いに答えよ。
(1)$a_n=-\dfrac{1}{n}$のとき、
$b_n$を$n$の式で表す。
(2)$b_n=\dfrac{1}{n(n+1)}$のとき、
$a_n$を$n$の式で表せ。ただし、$a_1=1$とする。
(3)数列$\{b_n\}$が以下を満たすとき、
$a_n$を$n$の式で表せ。ただし、$a_1=1$とする。
$\begin{eqnarray}
\left\{
\begin{array}{l}
b_1=1 \\
b_n=n(n+1) \quad (n\geqq 2)
\end{array}
\right.
\end{eqnarray}$
$2025$念早稲田大学社会科学部過去問題
福田の数学〜早稲田大学2025社会科学部第1問〜n^pの1の位

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
自然数$n,p$に対して、$n^p$の$1$の位の数を
$f_p(n)$で表す。次の問いに答えよ。
(1)$f_2(n)$の取りうる値をすべて求めよ。
(2)$f_5(n)-f_1(n)$の値を求めよ。
(3)$f_{100}(n)$の取りうる値をすべて求めよ。
$2025$年早稲田大学社会科学部過去問題
この動画を見る
$\boxed{1}$
自然数$n,p$に対して、$n^p$の$1$の位の数を
$f_p(n)$で表す。次の問いに答えよ。
(1)$f_2(n)$の取りうる値をすべて求めよ。
(2)$f_5(n)-f_1(n)$の値を求めよ。
(3)$f_{100}(n)$の取りうる値をすべて求めよ。
$2025$年早稲田大学社会科学部過去問題
福田の数学〜早稲田大学2025人間科学部第5問〜接線と面積
単元:
#大学入試過去問(数学)#微分とその応用#接線と法線・平均値の定理#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
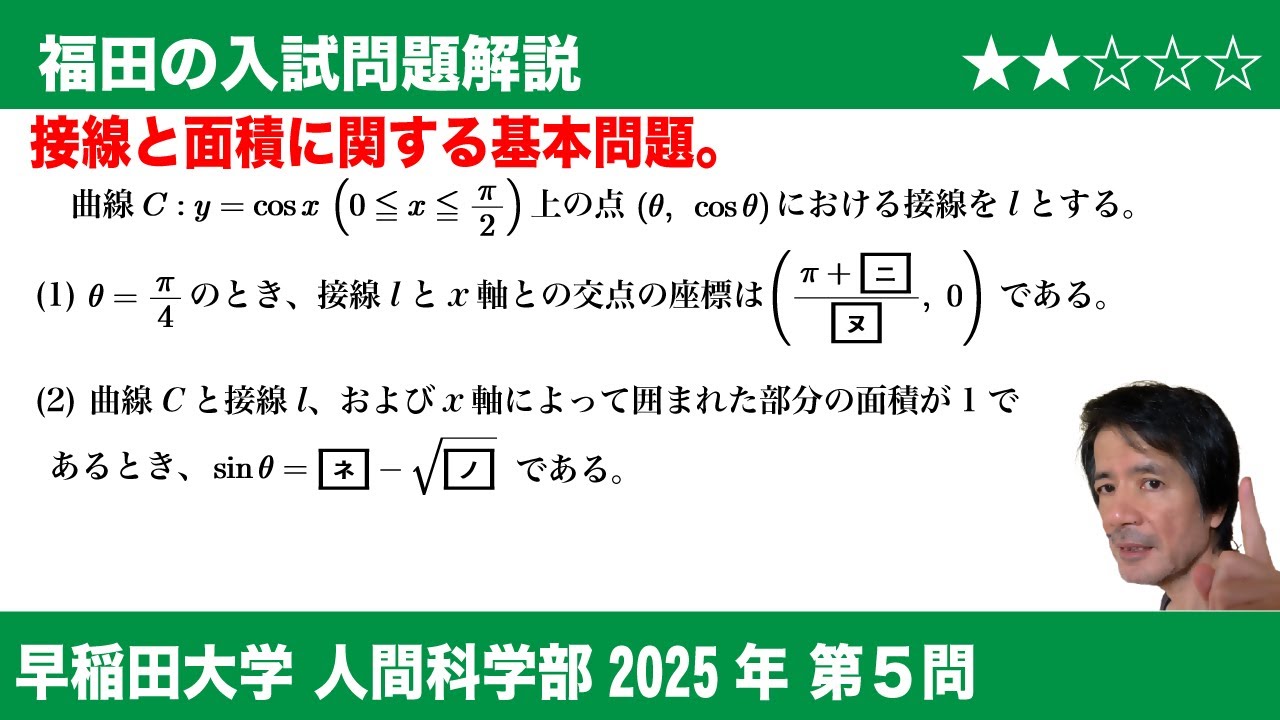
$\boxed{5}$
曲線$C:y=\cos x\left(0\leqq x \leqq \dfrac{\pi}{2}\right)$上の点
$(\theta,\cos\theta)$における接線を$l$とする。
(1)$\theta=\dfrac{\pi}{4}$のとき、接線$l$と
$x$軸との交点の座標は$\left(\dfrac{\pi+\boxed{二}}{\boxed{ヌ}},0\right)$である。
(2)曲線$C$と接線$l$、および$x$軸によって
囲まれた部分の面積が$1$であるとき、
$\sin\theta=\boxed{ネ}-\sqrt{\boxed{ノ}}$である。
$2025$年早稲田大学人間科学部過去問題
この動画を見る
$\boxed{5}$
曲線$C:y=\cos x\left(0\leqq x \leqq \dfrac{\pi}{2}\right)$上の点
$(\theta,\cos\theta)$における接線を$l$とする。
(1)$\theta=\dfrac{\pi}{4}$のとき、接線$l$と
$x$軸との交点の座標は$\left(\dfrac{\pi+\boxed{二}}{\boxed{ヌ}},0\right)$である。
(2)曲線$C$と接線$l$、および$x$軸によって
囲まれた部分の面積が$1$であるとき、
$\sin\theta=\boxed{ネ}-\sqrt{\boxed{ノ}}$である。
$2025$年早稲田大学人間科学部過去問題
福田の数学〜早稲田大学2025人間科学部第4問〜3次方程式の解が直角三角形を作る条件

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
$k$を実数の定数となる。
$z$についての方程式
$z^3-5z^2+kz-5=0$の$3$つの解は
複素数平面上で斜辺$2$の直角三角形の頂点となる。
このとき、$k=\boxed{ト}$であり、
この直角三角形の面積は$\boxed{ナ}$である。
$2025$年早稲田大学人間科学部過去問題
この動画を見る
$\boxed{4}$
$k$を実数の定数となる。
$z$についての方程式
$z^3-5z^2+kz-5=0$の$3$つの解は
複素数平面上で斜辺$2$の直角三角形の頂点となる。
このとき、$k=\boxed{ト}$であり、
この直角三角形の面積は$\boxed{ナ}$である。
$2025$年早稲田大学人間科学部過去問題
福田の数学〜早稲田大学2025人間科学部第3問〜外心と内心の位置ベクトル
単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
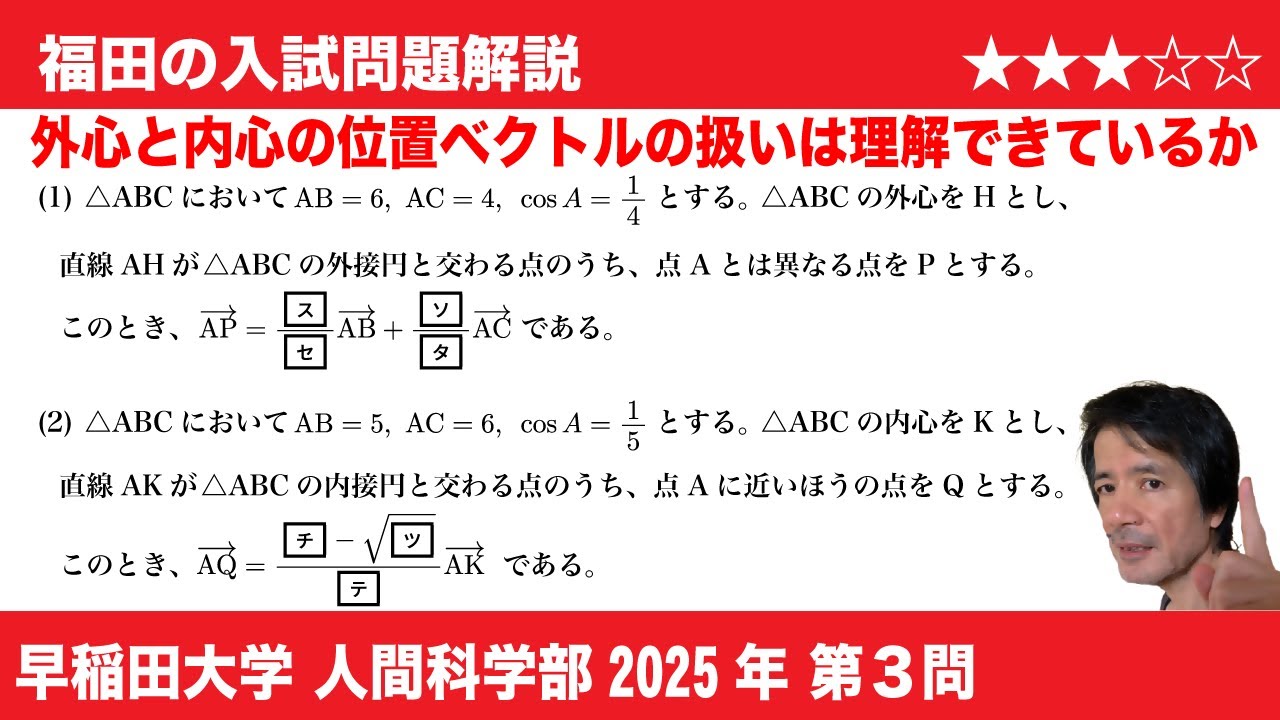
$\boxed{3}$
(1)$\triangle ABC$において$AB=6,AC=4,$
$\cos A=\dfrac{1}{4}$とする。
$\triangle ABC$の外心を$H$とし、直線$AH$が
$\triangle ABC$の外接円と交わる点のうち、
点$A$とは異なる点を$P$とする。
このとき、$\overrightarrow{AP}=\dfrac{\boxed{ス}}{\boxed{セ}}\overrightarrow{AB}+\dfrac{\boxed{ソ}}{\boxed{タ}}\overrightarrow{AC}$である。
(2)$\triangle ABC$において$AB=5,AC=6,$
$\cos A=\dfrac{1}{5}$とする。
$\triangle ABC$の内心を$K$とし、
直線$AK$が$\triangle ABC$の内接円と
交わる点のうち、点$A$に近いほうの点を
$Q$とする。
このとき、$\overrightarrow{AQ}=\dfrac{\boxed{チ}-\sqrt{\boxed{ツ}}}{\boxed{テ}}\overrightarrow{AK}$である。
$2025$年早稲田大学人間科学部過去問題
この動画を見る
$\boxed{3}$
(1)$\triangle ABC$において$AB=6,AC=4,$
$\cos A=\dfrac{1}{4}$とする。
$\triangle ABC$の外心を$H$とし、直線$AH$が
$\triangle ABC$の外接円と交わる点のうち、
点$A$とは異なる点を$P$とする。
このとき、$\overrightarrow{AP}=\dfrac{\boxed{ス}}{\boxed{セ}}\overrightarrow{AB}+\dfrac{\boxed{ソ}}{\boxed{タ}}\overrightarrow{AC}$である。
(2)$\triangle ABC$において$AB=5,AC=6,$
$\cos A=\dfrac{1}{5}$とする。
$\triangle ABC$の内心を$K$とし、
直線$AK$が$\triangle ABC$の内接円と
交わる点のうち、点$A$に近いほうの点を
$Q$とする。
このとき、$\overrightarrow{AQ}=\dfrac{\boxed{チ}-\sqrt{\boxed{ツ}}}{\boxed{テ}}\overrightarrow{AK}$である。
$2025$年早稲田大学人間科学部過去問題
福田の数学〜早稲田大学2025人間科学部第2問〜絶対値の付いた関数の最小

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
$a\lt b \lt c$を満たす実数の定数に対して、
すべての実数を定義域とする$x$の関数
$f(x)=\vert x-a \vert + \vert x-b \vert + \vert x-c \vert $を定める。
このとき、$5x+4f(x)$の最小値は
$\boxed{ク}a + \boxed{ケ}b + \boxed{コ}c$である。
また、$f(x)$の最小値が$20$で、
$f(c)=28$かつ$f(10)=31$を満たす$a$の値は
$\boxed{サ}$と$\boxed{シ}$である。
ただし、$\boxed{サ} \lt \boxed{シ}$とする。
$2025$年早稲田大学人間科学部過去問題
この動画を見る
$\boxed{2}$
$a\lt b \lt c$を満たす実数の定数に対して、
すべての実数を定義域とする$x$の関数
$f(x)=\vert x-a \vert + \vert x-b \vert + \vert x-c \vert $を定める。
このとき、$5x+4f(x)$の最小値は
$\boxed{ク}a + \boxed{ケ}b + \boxed{コ}c$である。
また、$f(x)$の最小値が$20$で、
$f(c)=28$かつ$f(10)=31$を満たす$a$の値は
$\boxed{サ}$と$\boxed{シ}$である。
ただし、$\boxed{サ} \lt \boxed{シ}$とする。
$2025$年早稲田大学人間科学部過去問題
福田の数学〜早稲田大学2025人間科学部第1問(3)〜球面が平面から切り取る領域の面積

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(3)座標空間における$2$点
$\left(\dfrac{\sqrt{35}}{2},5,10\right),\left(-\dfrac{\sqrt{35}}{2},10,-4\right)$
を直径の両端とする球面$S$がある。
球面$S$が$xy$平面を切り取る領域の面積は
$\boxed{カ}\pi$である。
また、球面$S$が$z$軸を切り取る線分の長さは
$\sqrt{\boxed{キ}}$である。
$2025$年早稲田大学人間科学部過去問題
この動画を見る
$\boxed{1}$
(3)座標空間における$2$点
$\left(\dfrac{\sqrt{35}}{2},5,10\right),\left(-\dfrac{\sqrt{35}}{2},10,-4\right)$
を直径の両端とする球面$S$がある。
球面$S$が$xy$平面を切り取る領域の面積は
$\boxed{カ}\pi$である。
また、球面$S$が$z$軸を切り取る線分の長さは
$\sqrt{\boxed{キ}}$である。
$2025$年早稲田大学人間科学部過去問題
福田の数学〜早稲田大学2025人間科学部第1問(2)〜ルートの2個ある無理方程式の解法

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(2)方程式
$\sqrt{x+510}+\sqrt{x+822}=52$
の解は$x=\boxed{オ}$である。
$2025$年早稲田大学人間科学部過去問題
この動画を見る
$\boxed{1}$
(2)方程式
$\sqrt{x+510}+\sqrt{x+822}=52$
の解は$x=\boxed{オ}$である。
$2025$年早稲田大学人間科学部過去問題
福田の数学〜早稲田大学2025人間科学部第1問(1)〜4次式の因数分解と未定係数法

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(1)整式$x^4-13x^2+18x-5$を整数係数の
範囲で因数分解すると
$(x^2+\boxed{ア} x+\boxed{イ})(x^2+\boxed{ウ}x+\boxed{エ})$
となる。
ただし、$\boxed{ア}\lt \boxed{ウ}$とする。
$2025$年早稲田大学人間科学部過去問題
この動画を見る
$\boxed{1}$
(1)整式$x^4-13x^2+18x-5$を整数係数の
範囲で因数分解すると
$(x^2+\boxed{ア} x+\boxed{イ})(x^2+\boxed{ウ}x+\boxed{エ})$
となる。
ただし、$\boxed{ア}\lt \boxed{ウ}$とする。
$2025$年早稲田大学人間科学部過去問題
福田の数学〜早稲田大学理工学部2025第5問〜無理関数のグラフ上に無数の有理点が存在する証明

単元:
#大学入試過去問(数学)#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{5}$
$xy$平面上の曲線$C:y=\sqrt[3]{x^2+2}$と考え、
$C$上の$(0,\sqrt[3]{2})$以外の点$P(a,b)$における接線を
$\ell : y = kx +c$と表す。$C$と$\ell$の方程式から
$x$を消去して得られる$y$についての$3$次方程式
$f(y)=0$は$b$を重解としてもつので、もう$1$つの解を
$b'$とする。
ただし、$b'$が$3$重解のときは$b'=b$とみなす。
次の問いに答えよ。
(1)$2b+b'$を$k$のみの分数式で表せ。
(2)$b'$を$b$のみの分数式で表せ。
(3)$C$と$\ell$の共有点で、その$y$座標が$b'$であるものを
$P'(a',b')$とする。
$a$と$b$が有理数ならば、$a'$と$b'$も有理数であることを
示せ。
(4)$b$が奇数$p,q$と負でない整数$r$を用いて
$b=\dfrac{p}{2^r q}$で与えられるとする。
有理数$b'$を奇数$p',q'$と整数$s$を用いて$b'=\dfrac{p'}{2^s q'}$と
表すとき、$s$を$r$の式で表せ。
(5)$P(5,3)$が曲線$C$上の点であることを利用して、
$C$上に$x$座標と$y$座標がともに有理数であるような点が
無数に存在することを示せ。
$2025$年早稲田大学理工学部過去問題
この動画を見る
$\boxed{5}$
$xy$平面上の曲線$C:y=\sqrt[3]{x^2+2}$と考え、
$C$上の$(0,\sqrt[3]{2})$以外の点$P(a,b)$における接線を
$\ell : y = kx +c$と表す。$C$と$\ell$の方程式から
$x$を消去して得られる$y$についての$3$次方程式
$f(y)=0$は$b$を重解としてもつので、もう$1$つの解を
$b'$とする。
ただし、$b'$が$3$重解のときは$b'=b$とみなす。
次の問いに答えよ。
(1)$2b+b'$を$k$のみの分数式で表せ。
(2)$b'$を$b$のみの分数式で表せ。
(3)$C$と$\ell$の共有点で、その$y$座標が$b'$であるものを
$P'(a',b')$とする。
$a$と$b$が有理数ならば、$a'$と$b'$も有理数であることを
示せ。
(4)$b$が奇数$p,q$と負でない整数$r$を用いて
$b=\dfrac{p}{2^r q}$で与えられるとする。
有理数$b'$を奇数$p',q'$と整数$s$を用いて$b'=\dfrac{p'}{2^s q'}$と
表すとき、$s$を$r$の式で表せ。
(5)$P(5,3)$が曲線$C$上の点であることを利用して、
$C$上に$x$座標と$y$座標がともに有理数であるような点が
無数に存在することを示せ。
$2025$年早稲田大学理工学部過去問題
福田の数学〜早稲田大学理工学部2025第4問〜4つの互いに外接する球面の中心が作る四面体の体積

単元:
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#体積・表面積・回転体・水量・変化のグラフ#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
空間内に原点$O$を中心とする半径$r$の球面$S$がある。
さらに、半径が$1,2,3$の球面$S_1,S_2,S_3$があり、
これら$4$つの球面のうち
どの$2$つの球面も互いに外接している。
$S_1,S_2,S_3$中心を順に$P_1,P_2,P_3$とし、
$O,P_1,P_2,P_3$は同一平面上にないとする。
さらに、球面$S$が球面$S_1,S_2,S_3$と
接する$3$つの点と、
$\overrightarrow{OQ}=\dfrac{1}{4}(\overrightarrow{OP_1}+\overrightarrow{OP_2}+\overrightarrow{OP_3})$
により定まる点$Q$は、同一平面上にあるとする。
次の問いに答えよ。
(1)$r$の値を求めよ。
(2)四面体$OP_1P_2P_3$の体積を求めよ。
$2025$年早稲田大学理工学部過去問題
この動画を見る
$\boxed{4}$
空間内に原点$O$を中心とする半径$r$の球面$S$がある。
さらに、半径が$1,2,3$の球面$S_1,S_2,S_3$があり、
これら$4$つの球面のうち
どの$2$つの球面も互いに外接している。
$S_1,S_2,S_3$中心を順に$P_1,P_2,P_3$とし、
$O,P_1,P_2,P_3$は同一平面上にないとする。
さらに、球面$S$が球面$S_1,S_2,S_3$と
接する$3$つの点と、
$\overrightarrow{OQ}=\dfrac{1}{4}(\overrightarrow{OP_1}+\overrightarrow{OP_2}+\overrightarrow{OP_3})$
により定まる点$Q$は、同一平面上にあるとする。
次の問いに答えよ。
(1)$r$の値を求めよ。
(2)四面体$OP_1P_2P_3$の体積を求めよ。
$2025$年早稲田大学理工学部過去問題
福田の数学〜早稲田大学理工学部2025第3問〜完全順列と漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
$1$から$n$までの異なる自然数が$1$つずつ書かれた
$n$枚のカードが一列に並んでいる。
このとき、
どのカードも現在とは異なる位置に移動するよう
並べ替えてできる順列の総数を$a_n$で表し、
並べ方の総数$n!$に閉める$a_n$の割合を$p_n$で表す。
例えば、$a_1=0,p_1=0,a_2=1,p_2=\dfrac{1}{2},$
$a_3=2,p_3=\dfrac{1}{3}$である。
(1)$a_4$の値を求めよ。
(2)$n\geqq 3$のとき、$a_n$を$a_{n-1}$と
$a_{n-2}$を用いて表せ。
(3)$n\geqq 2$のとき、$p_n-p_{n-1}$を
$n$を用いて表せ。
$2025$年早稲田大学理工学部過去問題
この動画を見る
$\boxed{3}$
$1$から$n$までの異なる自然数が$1$つずつ書かれた
$n$枚のカードが一列に並んでいる。
このとき、
どのカードも現在とは異なる位置に移動するよう
並べ替えてできる順列の総数を$a_n$で表し、
並べ方の総数$n!$に閉める$a_n$の割合を$p_n$で表す。
例えば、$a_1=0,p_1=0,a_2=1,p_2=\dfrac{1}{2},$
$a_3=2,p_3=\dfrac{1}{3}$である。
(1)$a_4$の値を求めよ。
(2)$n\geqq 3$のとき、$a_n$を$a_{n-1}$と
$a_{n-2}$を用いて表せ。
(3)$n\geqq 2$のとき、$p_n-p_{n-1}$を
$n$を用いて表せ。
$2025$年早稲田大学理工学部過去問題
福田の数学〜早稲田大学理工学部2025第2問〜領域に含まれる三角形の面積の最大値

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
$xy$平面上で、
連立不等式
$0\lt x \leqq 1,0\leqq y \leqq \log\dfrac{1}{x}$
で定まる領域と$y$軸の
$y\geqq 0$の部分を合わせた図形を$D$とする。
$D$に含まれる三角形の最大値を求めよ。
$2025$年早稲田大学理工学部過去問題
この動画を見る
$\boxed{2}$
$xy$平面上で、
連立不等式
$0\lt x \leqq 1,0\leqq y \leqq \log\dfrac{1}{x}$
で定まる領域と$y$軸の
$y\geqq 0$の部分を合わせた図形を$D$とする。
$D$に含まれる三角形の最大値を求めよ。
$2025$年早稲田大学理工学部過去問題
福田の数学〜早稲田大学理工学部2025第1問〜複素数平面上の点の軌跡と面積

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
複素数平面上で、複素数$z$が円$\vert z \vert=1$の上の点を動くとき、
$w=\left(\dfrac{1+\sqrt2}{2}\right)z+\left(\dfrac{1-\sqrt2}{2}\right)\dfrac{1}{z}$
を満たす点$w$の軌跡を$C$とする。
次の問いに答えよ。
(1)$C$はどのような図形か。複素数平面上に図示せよ。
(2)$C$と円$\left \vert z-\dfrac{2+\sqrt2}{2}\right \vert =\sqrt2$の共有点を求めよ。
(3)$C$で囲まれる領域と$\left \vert z-\dfrac{2+\sqrt2}{2}\right \vert \leqq \sqrt2$の
表す領域の共通部分の面積を求めよ。
$2025$年早稲田大学理工学部過去問題
この動画を見る
$\boxed{1}$
複素数平面上で、複素数$z$が円$\vert z \vert=1$の上の点を動くとき、
$w=\left(\dfrac{1+\sqrt2}{2}\right)z+\left(\dfrac{1-\sqrt2}{2}\right)\dfrac{1}{z}$
を満たす点$w$の軌跡を$C$とする。
次の問いに答えよ。
(1)$C$はどのような図形か。複素数平面上に図示せよ。
(2)$C$と円$\left \vert z-\dfrac{2+\sqrt2}{2}\right \vert =\sqrt2$の共有点を求めよ。
(3)$C$で囲まれる領域と$\left \vert z-\dfrac{2+\sqrt2}{2}\right \vert \leqq \sqrt2$の
表す領域の共通部分の面積を求めよ。
$2025$年早稲田大学理工学部過去問題
【祝早稲田合格】和男の勉強法と参考書を紹介【大学受験プロジェクト】新メンバーも募集

単元:
#大学入試過去問(数学)#化学#学校別大学入試過去問解説(数学)#大学入試過去問(化学)#英語(高校生)#大学入試過去問(英語)#学校別大学入試過去問解説(英語)#早稲田大学#数学(高校生)#理科(高校生)#早稲田大学#早稲田大学
指導講師:
Morite2 English Channel
問題文全文(内容文):
衝撃スクープ!浪人を経てついに**早稲田合格**を勝ち取った**かず(和男)**の壮絶な裏側が暴露されるぞ!
藤川天のネガキャンで荒れ果てたチャンネルを、かずさんの合格がなんとか回復させたらしい。モリテツ先生が、合格祝いとして**早稲田大学の入学金20万円**を札束で直接手渡しする、生々しいシーンから動画がスタートだ。
かずさんの受験は波乱万丈だ。現役時代、**12月という超直前期**に塾に駆け込み、短期間でやれることだけを進捗管理してもらい、立教大学に合格。しかし進学はせず浪人を選んだ。
浪人中は、計画は**自分で組み**、川井先生に定期的に進捗確認や「本当に理解しているのか」を問う**質疑形式**でサポートを受けていた。数学に関してはレベルが高すぎて、もはや先生と**議論**するほどだったという。
使っていた参考書は、新しく買ったものはほとんどなく、浪人までにやったものを**クオリティを上げる作業**が中心だった。
* **単語帳**は『パス単』の1級レベルまで仕上げた。
* **数学**は『チャート』や『プラチカ』のハイレベルな部分で取りこぼしていたところを埋めた。
* **国語**(古文・漢文)は『古文上達 基礎編』や『漢文ヤマのヤマ』といった、**ド基礎**を時間をかけて染み込ませることに注力した。
そして最大の衝撃事実!かずさんは親に**内緒で受験**しており、なんと**合格発表の前日**までバレていなかった。親が心配で大学の入試情報を調べていたところ、息子がYouTubeに登場しているのを発見したという爆笑エピソードも飛び出した。
ついに始まる早稲田生活。入学式は**富山キャンパスの早稲田アリーナ**で行われるという。モリテツ先生とのTOEICプロジェクト始動の可能性 や、サークルは**テニサーではなく剣道を見に行く**という宣言にも注目だ。
この動画を見る
衝撃スクープ!浪人を経てついに**早稲田合格**を勝ち取った**かず(和男)**の壮絶な裏側が暴露されるぞ!
藤川天のネガキャンで荒れ果てたチャンネルを、かずさんの合格がなんとか回復させたらしい。モリテツ先生が、合格祝いとして**早稲田大学の入学金20万円**を札束で直接手渡しする、生々しいシーンから動画がスタートだ。
かずさんの受験は波乱万丈だ。現役時代、**12月という超直前期**に塾に駆け込み、短期間でやれることだけを進捗管理してもらい、立教大学に合格。しかし進学はせず浪人を選んだ。
浪人中は、計画は**自分で組み**、川井先生に定期的に進捗確認や「本当に理解しているのか」を問う**質疑形式**でサポートを受けていた。数学に関してはレベルが高すぎて、もはや先生と**議論**するほどだったという。
使っていた参考書は、新しく買ったものはほとんどなく、浪人までにやったものを**クオリティを上げる作業**が中心だった。
* **単語帳**は『パス単』の1級レベルまで仕上げた。
* **数学**は『チャート』や『プラチカ』のハイレベルな部分で取りこぼしていたところを埋めた。
* **国語**(古文・漢文)は『古文上達 基礎編』や『漢文ヤマのヤマ』といった、**ド基礎**を時間をかけて染み込ませることに注力した。
そして最大の衝撃事実!かずさんは親に**内緒で受験**しており、なんと**合格発表の前日**までバレていなかった。親が心配で大学の入試情報を調べていたところ、息子がYouTubeに登場しているのを発見したという爆笑エピソードも飛び出した。
ついに始まる早稲田生活。入学式は**富山キャンパスの早稲田アリーナ**で行われるという。モリテツ先生とのTOEICプロジェクト始動の可能性 や、サークルは**テニサーではなく剣道を見に行く**という宣言にも注目だ。
2025年高校別早稲田大学合格者数ランキング #shorts

単元:
#大学入試過去問(数学)#化学#学校別大学入試過去問解説(数学)#大学入試過去問(化学)#英語(高校生)#大学入試過去問(英語)#学校別大学入試過去問解説(英語)#早稲田大学#数学(高校生)#理科(高校生)#早稲田大学#早稲田大学
指導講師:
Morite2 English Channel
問題文全文(内容文):
2025年版!高校別早稲田大学合格者数ランキング速報がヤバい!
早稲田大学合格者数の2025年版!高校別早稲田大学合格者数ランキング速報がヤバい!
早稲田大学合格者数の高校別ランキング上位20位が判明したぞ。
栄えある第1位は、今年も**早稲田高校**で、なんと**250人**合格という圧倒的な強さを見せつけた。東大のモデルにしているところが賢いらしい。
第2位は**栄東高校**(埼玉)で228人。所沢キャンパスが近くにあるのも影響しているようだ。
そして、東大でもめちゃくちゃ伸びた**横浜翠嵐高校**(神奈川)が第3位にランクインし、171人を合格させている。第4位は**聖光学院**(神奈川)の170人、第5位は早稲田合格者数で有名な**市川高校**で164人だ。
その他の注目校は以下の通り!
* 第6位:本郷 (145人)
* 第7位:洗足学園 (神奈川, 136人)
* 第8位:千葉県立千葉 (123人)
* 第10位:**渋渋(渋谷教育学園渋谷)**が120人で、今年も強い。
* 第14位:**県立船橋**(千葉)が111人で、公立校も食い込んでいる。
このランキングを見れば、早稲田を目指すならどこに行くべきか一目瞭然だ!
この動画を見る
2025年版!高校別早稲田大学合格者数ランキング速報がヤバい!
早稲田大学合格者数の2025年版!高校別早稲田大学合格者数ランキング速報がヤバい!
早稲田大学合格者数の高校別ランキング上位20位が判明したぞ。
栄えある第1位は、今年も**早稲田高校**で、なんと**250人**合格という圧倒的な強さを見せつけた。東大のモデルにしているところが賢いらしい。
第2位は**栄東高校**(埼玉)で228人。所沢キャンパスが近くにあるのも影響しているようだ。
そして、東大でもめちゃくちゃ伸びた**横浜翠嵐高校**(神奈川)が第3位にランクインし、171人を合格させている。第4位は**聖光学院**(神奈川)の170人、第5位は早稲田合格者数で有名な**市川高校**で164人だ。
その他の注目校は以下の通り!
* 第6位:本郷 (145人)
* 第7位:洗足学園 (神奈川, 136人)
* 第8位:千葉県立千葉 (123人)
* 第10位:**渋渋(渋谷教育学園渋谷)**が120人で、今年も強い。
* 第14位:**県立船橋**(千葉)が111人で、公立校も食い込んでいる。
このランキングを見れば、早稲田を目指すならどこに行くべきか一目瞭然だ!
