 大学入試過去問(数学)
大学入試過去問(数学)
 大学入試過去問(数学)
大学入試過去問(数学)
大学入試問題#113 一橋大学(2011) 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$1 \lt x \lt y$
$(1+\displaystyle \frac{1}{x})(1+\displaystyle \frac{1}{y})=\displaystyle \frac{5}{3}$を満たす自然数の組$(x,y)$をすべて求めよ。
出典:2011年一橋大学 入試問題
この動画を見る
$1 \lt x \lt y$
$(1+\displaystyle \frac{1}{x})(1+\displaystyle \frac{1}{y})=\displaystyle \frac{5}{3}$を満たす自然数の組$(x,y)$をすべて求めよ。
出典:2011年一橋大学 入試問題
大学入試問題#112 琉球大学(1989) 不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#琉球大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$-1 \neq \alpha$:定数
$\displaystyle \int \displaystyle \frac{(log\ x)^\alpha}{x}\ log(\log\ x)dx$を計算せよ。
出典:1989年琉球大学 入試問題
この動画を見る
$-1 \neq \alpha$:定数
$\displaystyle \int \displaystyle \frac{(log\ x)^\alpha}{x}\ log(\log\ x)dx$を計算せよ。
出典:1989年琉球大学 入試問題
東京大学 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
n,a,b,c,dは0または正の整数
$
\begin{eqnarray}
\left\{
\begin{array}{l}
a^2+b^2+c^2+d^2 = n^2 -6 \\
a+b+c+d = n \\
a \geqq b \geqq c \geqq d
\end{array}
\right.
\end{eqnarray}
$
を満たす(n,a,b,c,d)数の組を全て求めよ
1980年代東京大学
この動画を見る
n,a,b,c,dは0または正の整数
$
\begin{eqnarray}
\left\{
\begin{array}{l}
a^2+b^2+c^2+d^2 = n^2 -6 \\
a+b+c+d = n \\
a \geqq b \geqq c \geqq d
\end{array}
\right.
\end{eqnarray}
$
を満たす(n,a,b,c,d)数の組を全て求めよ
1980年代東京大学
2022久留米大(医)約数の個数

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#久留米大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 2\lt n \gt ^2-9\lt n \gt-7・\lt 81 \gt=0$
を満たす3桁の自然数nを求めよ
2022年久留米大学医学部過去問
この動画を見る
$ 2\lt n \gt ^2-9\lt n \gt-7・\lt 81 \gt=0$
を満たす3桁の自然数nを求めよ
2022年久留米大学医学部過去問
順天堂(医)確率 基本
単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#順天堂大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
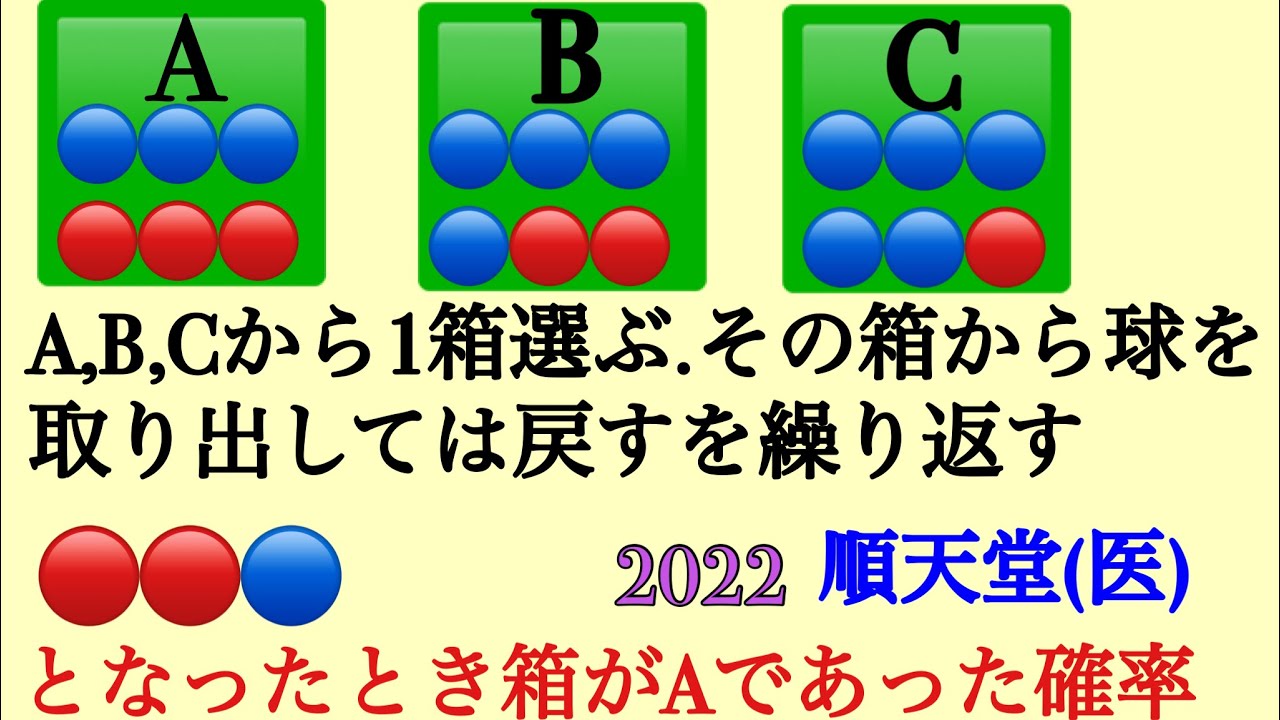
ある1つの箱から とり出して戻すを3回行ったら
●●○となった
箱がAである確率を求めよ
2022年順天堂医学大学 過去問
この動画を見る
ある1つの箱から とり出して戻すを3回行ったら
●●○となった
箱がAである確率を求めよ
2022年順天堂医学大学 過去問
大学入試問題#111 早稲田大学(2021) 次数下げ
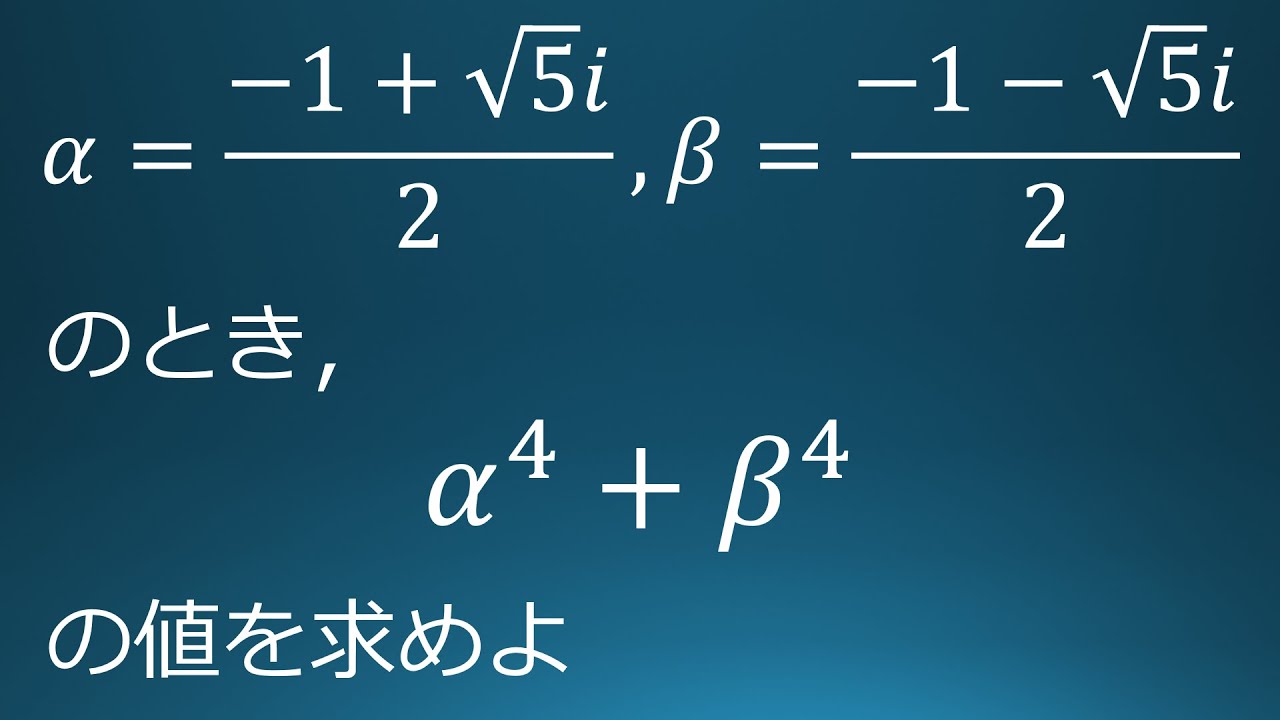
単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\alpha=\displaystyle \frac{-1+\sqrt{ 5 }i}{2}$
$\beta=\displaystyle \frac{-1-\sqrt{ 5 }i}{2}$のとき
$\alpha^4+\beta^4$の値を求めよ。
出典:2021年早稲田大学 入試問題
この動画を見る
$\alpha=\displaystyle \frac{-1+\sqrt{ 5 }i}{2}$
$\beta=\displaystyle \frac{-1-\sqrt{ 5 }i}{2}$のとき
$\alpha^4+\beta^4$の値を求めよ。
出典:2021年早稲田大学 入試問題
大学入試問題#110 産業医科大学(2019) 定積分②
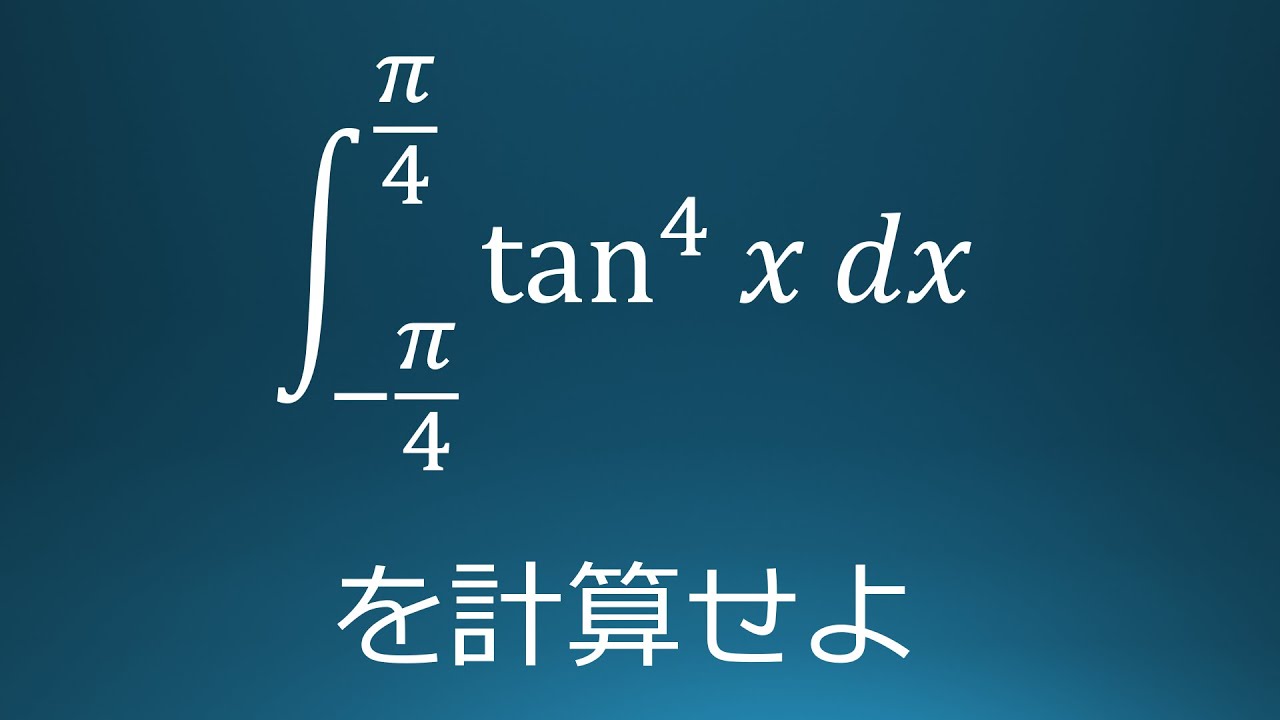
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#産業医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{\pi}{4}}^{\frac{\pi}{4}}\ \tan^4x\ dx$を計算せよ。
出典:2019年産業医科大学 入試問題
この動画を見る
$\displaystyle \int_{-\frac{\pi}{4}}^{\frac{\pi}{4}}\ \tan^4x\ dx$を計算せよ。
出典:2019年産業医科大学 入試問題
大学入試問題#109 大阪府立大学(2010) 無限級数

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#大阪府立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a_1=1$
$a_{n+1}=\displaystyle \frac{n}{n+5}\ a_n$のとき
$\displaystyle \sum_{n=1}^\infty\ a_n$を求めよ
出典:2010年大阪府立大学 入試問題
この動画を見る
$a_1=1$
$a_{n+1}=\displaystyle \frac{n}{n+5}\ a_n$のとき
$\displaystyle \sum_{n=1}^\infty\ a_n$を求めよ
出典:2010年大阪府立大学 入試問題
大学入試問題#108 弘前大学(2018) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a \gt 0$
$\displaystyle \int_{0}^{1}\displaystyle \frac{dx}{(e^{2x}+a)(e^{-2x}+a)}\ $を計算せよ。
出典:2018年弘前大学 入試問題
この動画を見る
$a \gt 0$
$\displaystyle \int_{0}^{1}\displaystyle \frac{dx}{(e^{2x}+a)(e^{-2x}+a)}\ $を計算せよ。
出典:2018年弘前大学 入試問題
知ってれば一瞬!! 名城大学附属2022入試問題解説31問目
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
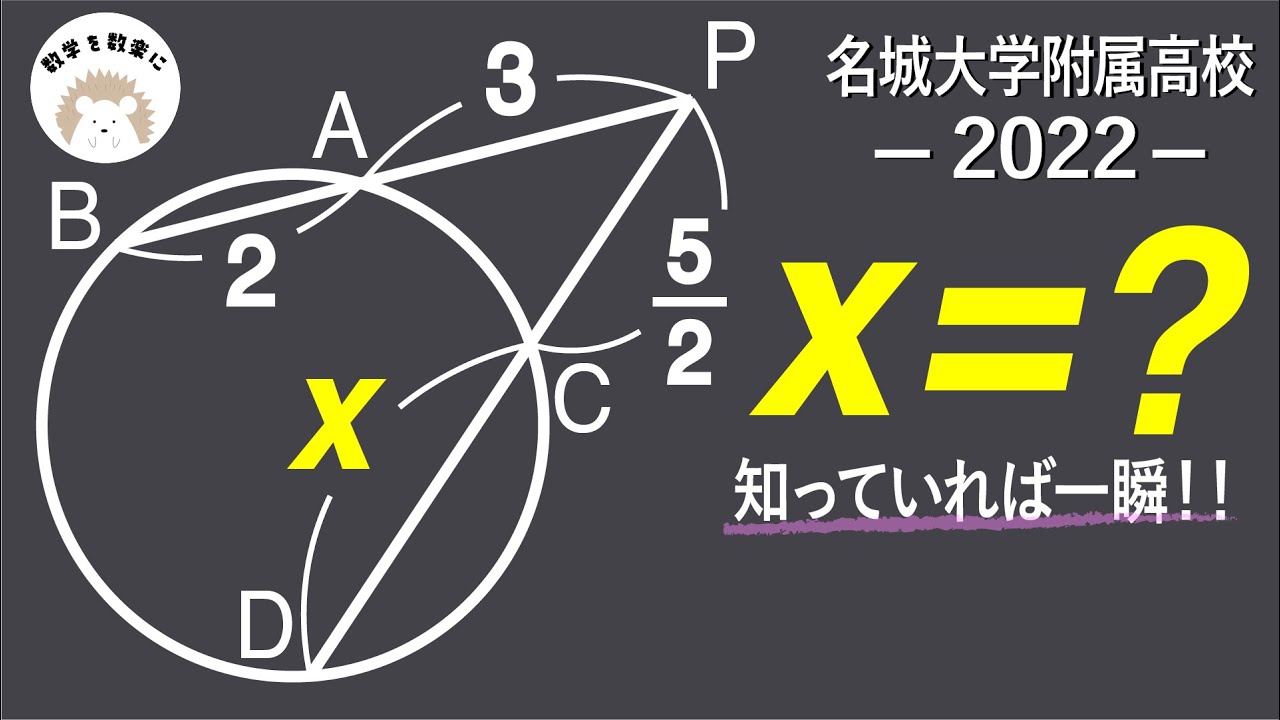
x=?
*図は動画内参照
2022名城大学附属高等学校
この動画を見る
x=?
*図は動画内参照
2022名城大学附属高等学校
大学入試問題#107 産業医科大学(2019) 定積分①

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#産業医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{99}^{101}\sqrt{ (x-99)(101-x) }\ dx\ $を計算せよ。
出典:2019年産業医科大学 入試問題
この動画を見る
$\displaystyle \int_{99}^{101}\sqrt{ (x-99)(101-x) }\ dx\ $を計算せよ。
出典:2019年産業医科大学 入試問題
共通テストの誘導はこういうことだったのね

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
7で割って3余り,9で割って2余り,11で割って1余る最小の自然数を求めよ.
この動画を見る
7で割って3余り,9で割って2余り,11で割って1余る最小の自然数を求めよ.
共通テスト追試ムズイぞ整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
共通テスト追試数学整数問題
この動画を見る
共通テスト追試数学整数問題
共通テスト追試ムズイぞ整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
共通テスト追試の整数問題を解説していきます.
この動画を見る
共通テスト追試の整数問題を解説していきます.
篠原京大塾:2021年(文系数学)過去問解説【篠原好】

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
2021年(文系数学)過去問解説
この動画を見る
2021年(文系数学)過去問解説
2022藤田医科大 等差数列の超基本問題

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
公差が0でない整数の等差数列$a_n$がある
$\sum_{ }^{ } a_n$はn=7で
最大値119 $a_n$を求めよ。
藤田医学科大学
この動画を見る
公差が0でない整数の等差数列$a_n$がある
$\sum_{ }^{ } a_n$はn=7で
最大値119 $a_n$を求めよ。
藤田医学科大学
大学入試問題#105 京都大学(2003) 数列
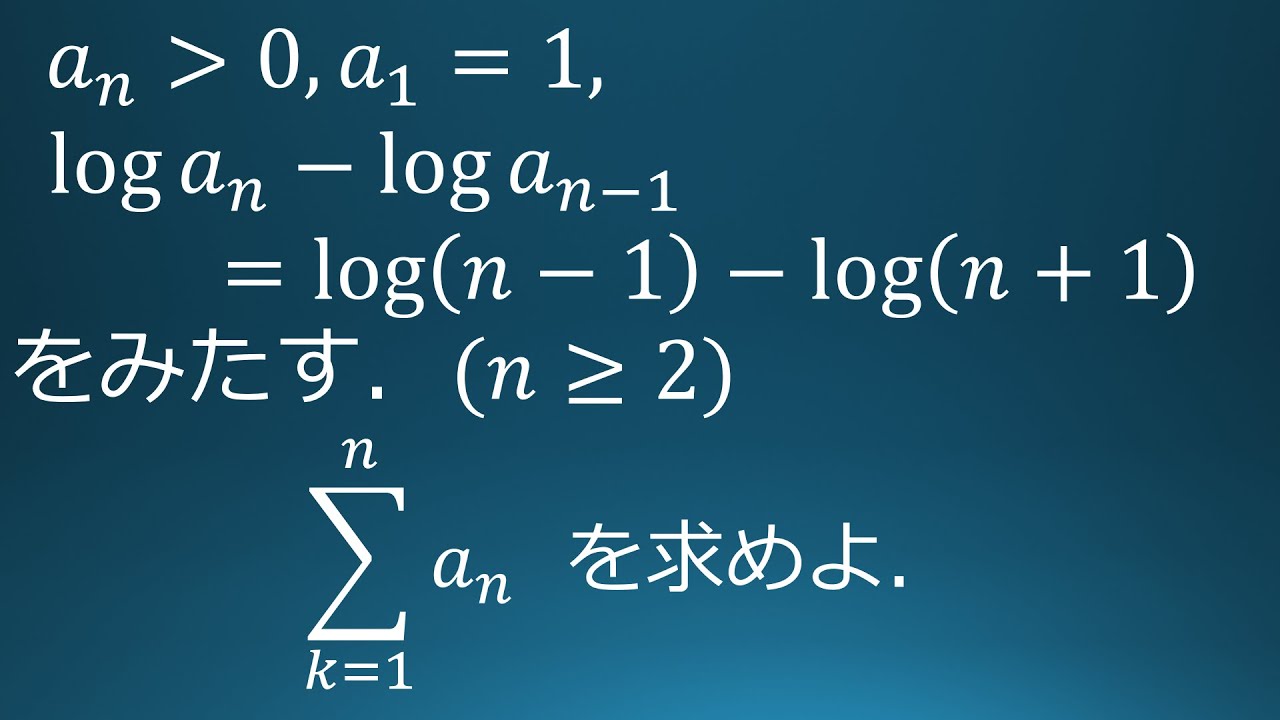
単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数B
指導講師:
ますただ
問題文全文(内容文):
$a_n \gt 0,\ a_1=1$
$n \geqq 2$のとき
$log\ a_n-log\ a_{n-1}=log(n-1)-log(n+1)$である。
$\displaystyle \sum_{k=1}^n a_k$を求めよ
出典:2003年京都大学 入試問題
この動画を見る
$a_n \gt 0,\ a_1=1$
$n \geqq 2$のとき
$log\ a_n-log\ a_{n-1}=log(n-1)-log(n+1)$である。
$\displaystyle \sum_{k=1}^n a_k$を求めよ
出典:2003年京都大学 入試問題
2022関西医科 超基本問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#関西医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x=\displaystyle \frac{6x^2+17x+10}{3x-2}$
(1)$f(x) \gt 0$を解け
(2)$f(n)$の値が自然数となる整数$n$
を求めよ。
2022年 関西医科過去問
この動画を見る
$x=\displaystyle \frac{6x^2+17x+10}{3x-2}$
(1)$f(x) \gt 0$を解け
(2)$f(n)$の値が自然数となる整数$n$
を求めよ。
2022年 関西医科過去問
大学入試問題#104 一橋大学(2006) ベクトル

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$|\vec{ a }|=5,|\vec{ b }|=3,|\vec{ c }|=1$
$\vec{ Z }=\vec{ a }+\vec{ b }+\vec{ c }$
(1)$|\vec{ Z }|$の最大値、最小値
(2)$\vec{ a }・\vec{ Z }=20$
をみたすとき
$|\vec{ Z }|$の最大値、最小値を求めよ
出典:2006年一橋大学 入試問題
この動画を見る
$|\vec{ a }|=5,|\vec{ b }|=3,|\vec{ c }|=1$
$\vec{ Z }=\vec{ a }+\vec{ b }+\vec{ c }$
(1)$|\vec{ Z }|$の最大値、最小値
(2)$\vec{ a }・\vec{ Z }=20$
をみたすとき
$|\vec{ Z }|$の最大値、最小値を求めよ
出典:2006年一橋大学 入試問題
整数問題 千葉大(医)類題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
整数$k,n$を
$k^2=3^n+360$
全て求めよ。
千葉大(医)過去問
この動画を見る
整数$k,n$を
$k^2=3^n+360$
全て求めよ。
千葉大(医)過去問
9で割り切れるのはなぜ?京都大(改)

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$n^9 - n^3$は9で割り切れるのはなぜ?(n:整数)
京都大学
この動画を見る
$n^9 - n^3$は9で割り切れるのはなぜ?(n:整数)
京都大学
大学入試問題#103 東海大学医学部(2017) 二項定理
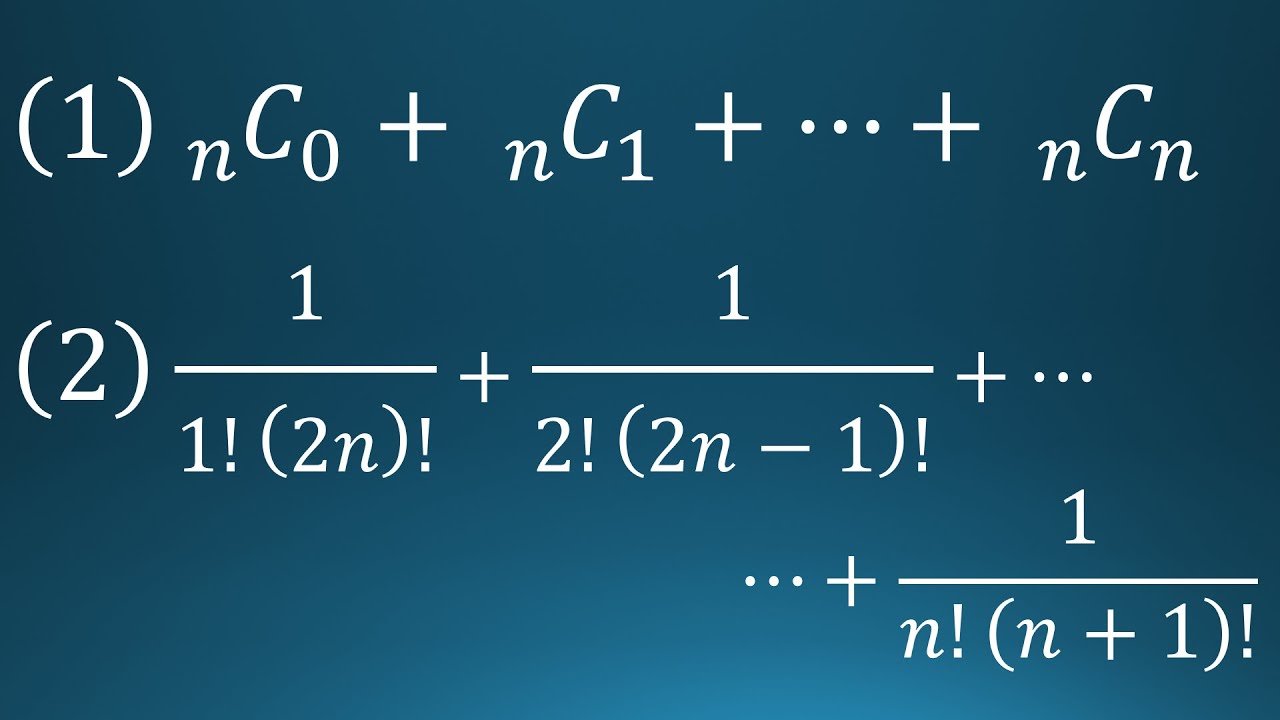
単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)#東海大学
指導講師:
ますただ
問題文全文(内容文):
次の和を求めよ。
(1)
${}_{ n }C_0+{}_{ n }C_1+・・・+{}_{ n }C_n$
(2)
$\displaystyle \frac{1}{1!(2n)!}+\displaystyle \frac{1}{2(2n-1)!}+・・・+\displaystyle \frac{1}{n!(n+1)!}$
出典:2017年東海大学医学部 入試問題
この動画を見る
次の和を求めよ。
(1)
${}_{ n }C_0+{}_{ n }C_1+・・・+{}_{ n }C_n$
(2)
$\displaystyle \frac{1}{1!(2n)!}+\displaystyle \frac{1}{2(2n-1)!}+・・・+\displaystyle \frac{1}{n!(n+1)!}$
出典:2017年東海大学医学部 入試問題
【高校数学】時間内で誰ができるねん~共通テスト数学ⅠA第4問解説~【大学受験】

単元:
#数A#大学入試過去問(数学)#整数の性質#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(4) $11^4$を$2^4$で割ったときの余りは1に等しい。不定方程式
$11^5x-2^5y=1$
の整数解のうち、$x$が正の整数で最小になるのは、$x=$テト, $y=$ナニヌネノである
この動画を見る
(4) $11^4$を$2^4$で割ったときの余りは1に等しい。不定方程式
$11^5x-2^5y=1$
の整数解のうち、$x$が正の整数で最小になるのは、$x=$テト, $y=$ナニヌネノである
大学入試問題#101 東海大学医学部(2017) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東海大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}x^3(1-x^2)^8dx$を計算せよ。
出典:2017年東海大学医学部 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}x^3(1-x^2)^8dx$を計算せよ。
出典:2017年東海大学医学部 入試問題
2022近畿大(医)場合の数

単元:
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#学校別大学入試過去問解説(数学)#近畿大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$人を区別のある 部屋に入れます。
0人部屋はダメ
(1)2部屋 (2)3部屋 (3)4部屋
何通りか求めよ。
2022年 近畿大学医学部 過去問
この動画を見る
$n$人を区別のある 部屋に入れます。
0人部屋はダメ
(1)2部屋 (2)3部屋 (3)4部屋
何通りか求めよ。
2022年 近畿大学医学部 過去問
大学入試問題#100 東京大学(1954) 軌跡・領域

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
点($x,y$)が原点を中心とする半径1の円の内部を動くとき
点($x+y,xy$)の動く範囲を図示せよ。
出典:1954年東京大学 入試問題
この動画を見る
点($x,y$)が原点を中心とする半径1の円の内部を動くとき
点($x+y,xy$)の動く範囲を図示せよ。
出典:1954年東京大学 入試問題
2022藤田医科大 出題意図は「瞬殺せよ」なのかな?

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_1=5,$
$a_{n+1}=3a_n+2$
$\displaystyle \frac{a_{16}-a_{13}}{a_{12}-a_9}$
の値を求めよ。
2022年藤田医科大学 過去問
この動画を見る
$a_1=5,$
$a_{n+1}=3a_n+2$
$\displaystyle \frac{a_{16}-a_{13}}{a_{12}-a_9}$
の値を求めよ。
2022年藤田医科大学 過去問
大学入試問題#99 慶應義塾大学2004 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$x^2+y^2 \lt 9$
$x^2 \leqq y^2$をみたす整数の組$x,y$の個数を求めよ。
出典:2004年慶應義塾大学 入試問題
この動画を見る
$x^2+y^2 \lt 9$
$x^2 \leqq y^2$をみたす整数の組$x,y$の個数を求めよ。
出典:2004年慶應義塾大学 入試問題
大学入試問題#98 千葉大学医学部(2018) 積分・極限
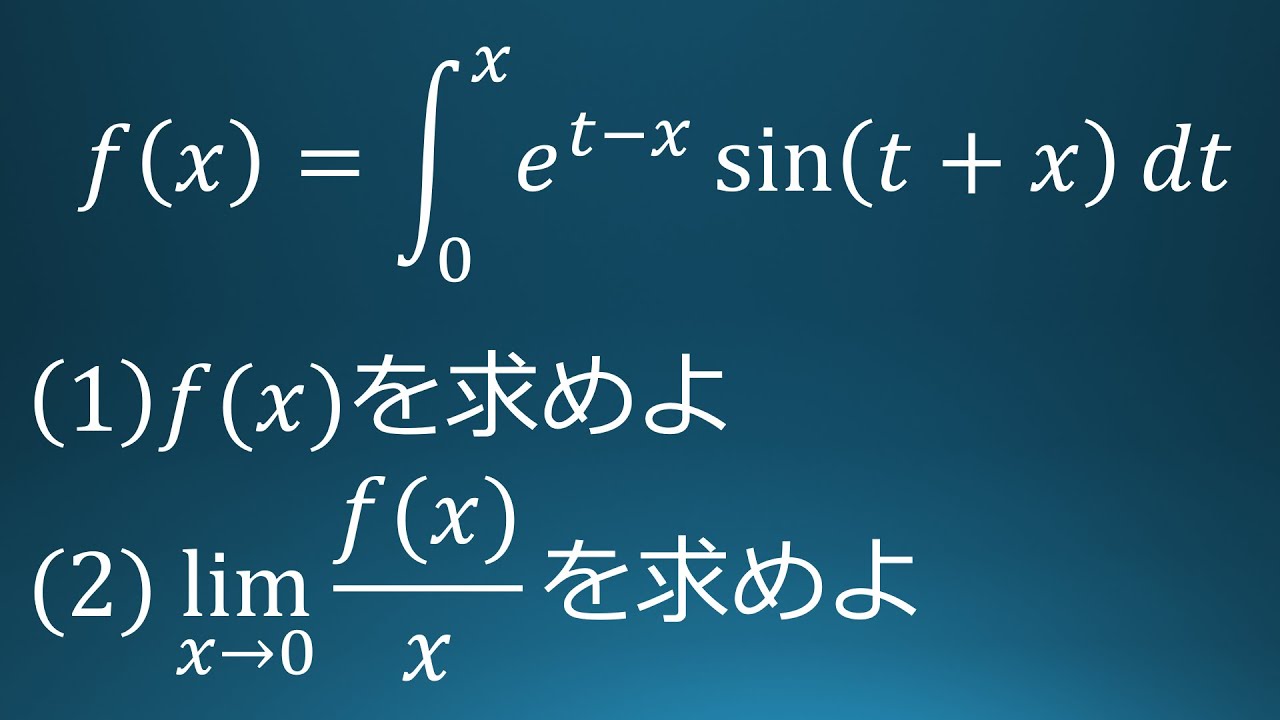
単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#不定積分#定積分#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
(1)
$f(x)=\displaystyle \int_{0}^{x}e^{t-x}\sin(t+x)dt$を求めよ。
(2)
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{f(x)}{x}$を求めよ。
出典:2018年千葉大学 入試問題
この動画を見る
(1)
$f(x)=\displaystyle \int_{0}^{x}e^{t-x}\sin(t+x)dt$を求めよ。
(2)
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{f(x)}{x}$を求めよ。
出典:2018年千葉大学 入試問題
大学入試問題#97 学習院大学(2003) 整数問題 帰納法

単元:
#大学入試過去問(数学)#数列#数学的帰納法#学校別大学入試過去問解説(数学)#数学(高校生)#数B#学習院大学
指導講師:
ますただ
問題文全文(内容文):
$n$:自然数
$11^{n+1}+12^{2n-1}$は$19$で割り切れることを示せ
出典:2003年学習院大学 入試問題
この動画を見る
$n$:自然数
$11^{n+1}+12^{2n-1}$は$19$で割り切れることを示せ
出典:2003年学習院大学 入試問題
