その他
その他
【数学】時間内に間に合わない人_速くするコツ教えます【共通テスト】
【共通テスト】数学1A・2Bのおすすめ参考書・問題集紹介＆レビュー・勉強法【篠原好】
単元：
#その他#勉強法#数学(高校生)#数学#共通テスト
指導講師：
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文)：
「共通テスト数学1A・2Bのおすすめ参考書・問題集」について紹介しています。
この動画を見る
「共通テスト数学1A・2Bのおすすめ参考書・問題集」について紹介しています。
【数学】分かりやすい講義系参考書・問題集はどれがおすすめか？独学数学勉強法【篠原好】
【共通テスト】数学1A 第1問が見るだけで解けるようになる魔法の動画
【数学】数学伸びない人_全員集合【共通テスト】【2次試験】【勉強法】
紙折ったら月届くん？
03東京都教員採用試験（数学：1-(4) 解の個数）
単元：
#数Ⅱ#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$x^2-x-k=2|x-1|$が異なる3個の解をもつとき、$k$の値を求めよ。
出典：東京都教員採用試験
この動画を見る
$x^2-x-k=2|x-1|$が異なる3個の解をもつとき、$k$の値を求めよ。
出典：東京都教員採用試験
05東京都教員採用試験（数学：4番 極小値の総和）
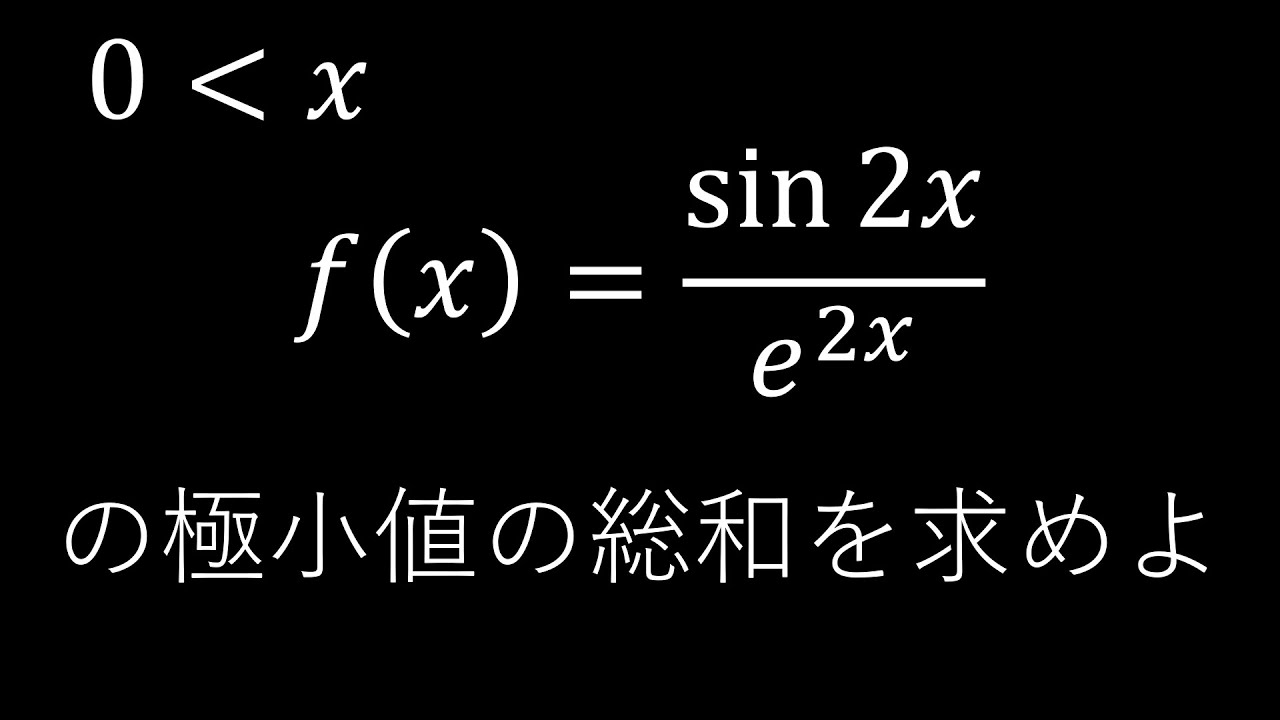
単元：
#微分とその応用#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$x \gt 0$
$f(x)=\displaystyle \frac{e^{2x}}{\sin\ 2x}$の極小値の総和$S$を求めよ。
この動画を見る
$x \gt 0$
$f(x)=\displaystyle \frac{e^{2x}}{\sin\ 2x}$の極小値の総和$S$を求めよ。
14東京都教員採用試験（数学：4番 y軸回転体 バームクーヘンの定理）
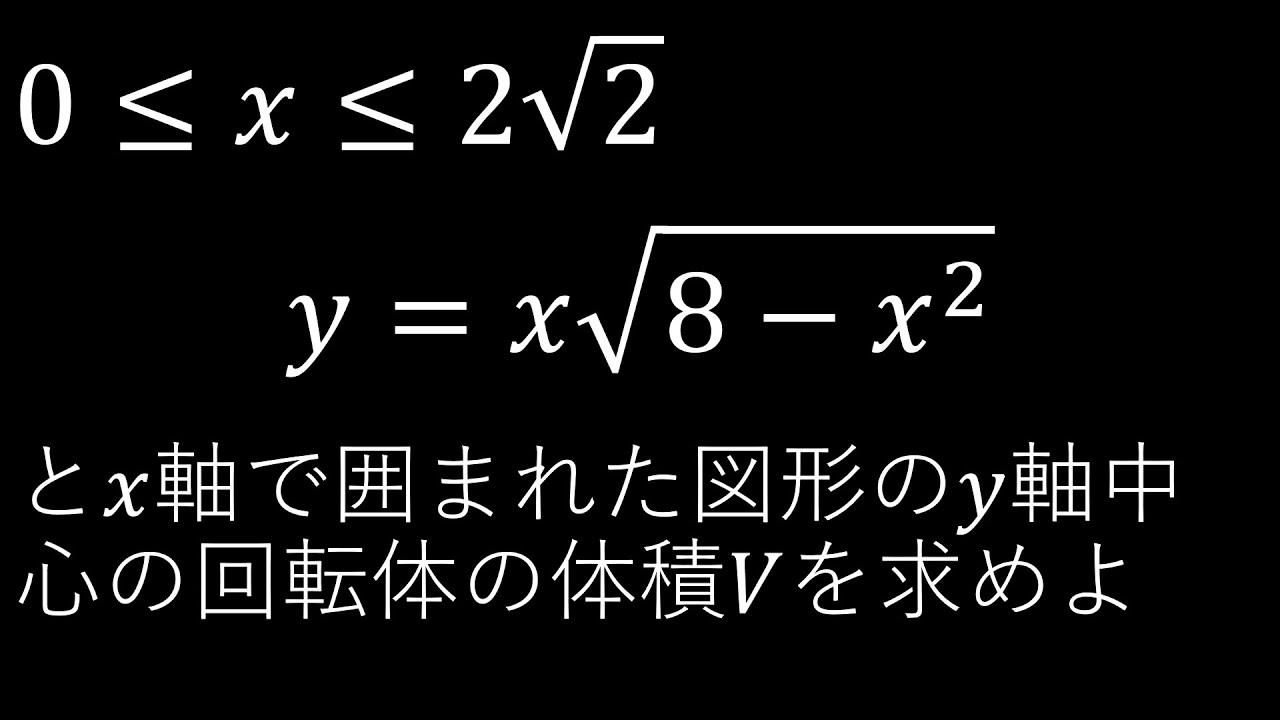
単元：
#積分とその応用#面積・体積・長さ・速度#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$0 \leqq x \leqq 2\sqrt{ 2 }$
$y=x\sqrt{ 8-x^2 }$
のグラフと$x$軸で囲まれた部分を$y$軸のまわりに1回転してできる回転体の体積$V$を求めよ。
出典：東京都教員採用試験
この動画を見る
$0 \leqq x \leqq 2\sqrt{ 2 }$
$y=x\sqrt{ 8-x^2 }$
のグラフと$x$軸で囲まれた部分を$y$軸のまわりに1回転してできる回転体の体積$V$を求めよ。
出典：東京都教員採用試験
練習問題47 東京理科大学 部分積分 数検準1級 教員採用試験
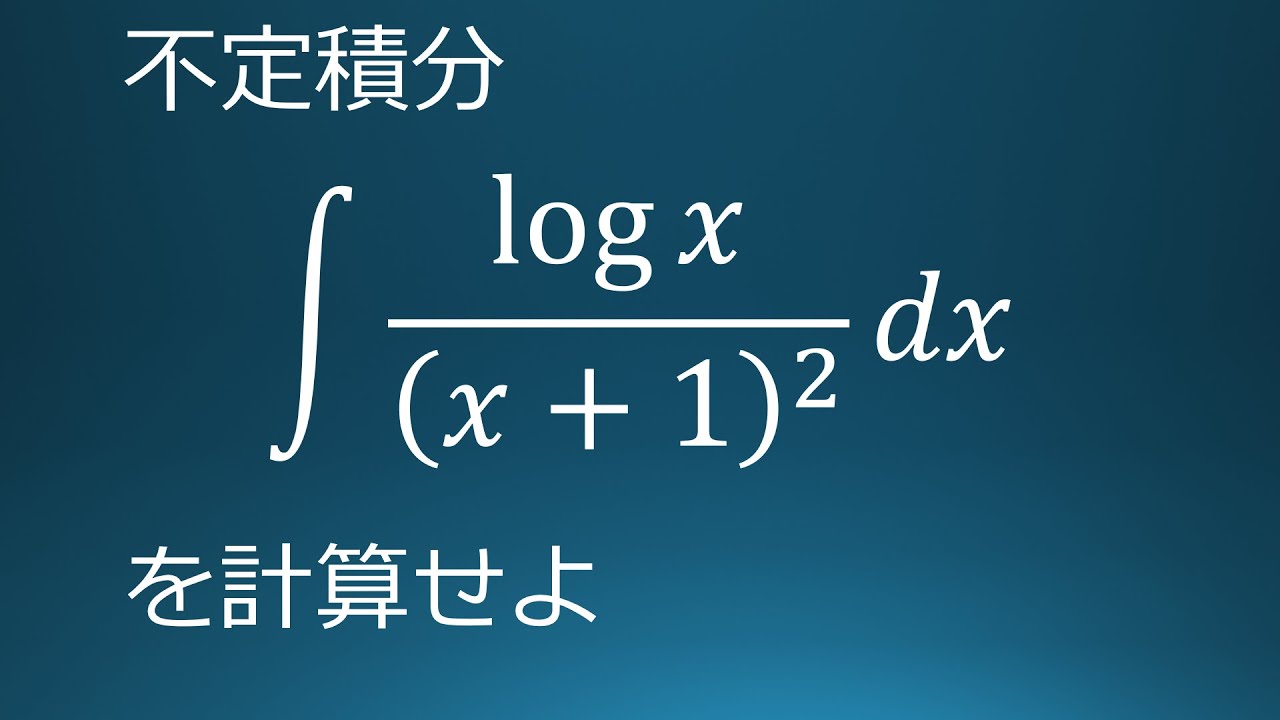
単元：
#大学入試過去問(数学)#数学検定・数学甲子園・数学オリンピック等#積分とその応用#学校別大学入試過去問解説(数学)#その他#数学検定#数学検定準1級#東京理科大学#数学(高校生)#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{log\ x}{(x+1)^2}\ dx$を計算せよ。
出典：東京理科大学
この動画を見る
$\displaystyle \int \displaystyle \frac{log\ x}{(x+1)^2}\ dx$を計算せよ。
出典：東京理科大学
練習問題46 岡山大学 対数の性質を利用した不等式の証明 数検準１級 教員採用試験
単元：
#数Ⅱ#大学入試過去問(数学)#数学検定・数学甲子園・数学オリンピック等#指数関数と対数関数#対数関数#微分とその応用#学校別大学入試過去問解説(数学)#その他#数学検定#数学検定準1級#数学(高校生)#岡山大学#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
実数$a,b,$は
$0 \lt a \lt b$をみたしているとき
$(b+1)^a \lt (a+1)^b$が成り立つことを表せ。
出典：岡山大学
この動画を見る
実数$a,b,$は
$0 \lt a \lt b$をみたしているとき
$(b+1)^a \lt (a+1)^b$が成り立つことを表せ。
出典：岡山大学
数学・理科の『標準問題精講』の使い方・注意点・勉強法【篠原好】
単元：
#化学#その他#勉強法#その他・勉強法#数学(高校生)#理科(高校生)
指導講師：
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文)：
「数学・理科の『標準問題精講』の使い方・注意点・勉強法」についてお話しています。
この動画を見る
「数学・理科の『標準問題精講』の使い方・注意点・勉強法」についてお話しています。
練習問題45 北海道大学 微分と積分 教員採用試験 数検準1級
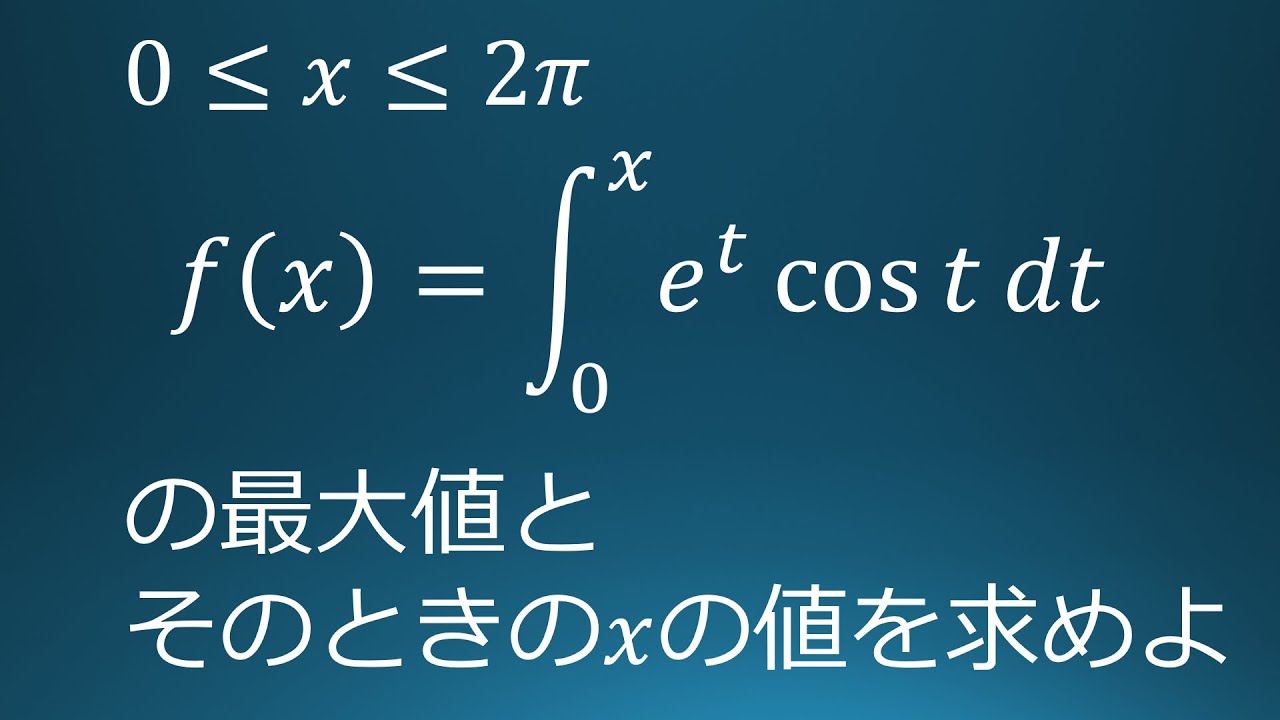
単元：
#大学入試過去問(数学)#数学検定・数学甲子園・数学オリンピック等#微分とその応用#積分とその応用#学校別大学入試過去問解説(数学)#その他#数学検定#数学検定準1級#数学(高校生)#北海道大学#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$0 \leqq x \leqq 2\pi$
関数
$f(x)=\displaystyle \int_{0}^{x}e^t\ cos\ t\ dt$の最大値とそのときの$x$の値を求めよ。
出典：北海道大学 教員採用試験
この動画を見る
$0 \leqq x \leqq 2\pi$
関数
$f(x)=\displaystyle \int_{0}^{x}e^t\ cos\ t\ dt$の最大値とそのときの$x$の値を求めよ。
出典：北海道大学 教員採用試験
練習問題44 東京工業大学 極限値 数検1級 教員採用試験（数学）
単元：
#数学検定・数学甲子園・数学オリンピック等#関数と極限#数列の極限#その他#数学検定#数学検定1級#数学(高校生)#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty }(\displaystyle \frac{{}_{ 3n } C_n}{{}_{ 2n } C_n})^\frac{1}{n}$の極限値を求めよ。
$\displaystyle \int_{0}^{1}f(x)dx=\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\displaystyle \sum_{k=1}^n f(\displaystyle \frac{k}{n})$
出典：東京工業大学 練習問題
この動画を見る
$\displaystyle \lim_{ n \to \infty }(\displaystyle \frac{{}_{ 3n } C_n}{{}_{ 2n } C_n})^\frac{1}{n}$の極限値を求めよ。
$\displaystyle \int_{0}^{1}f(x)dx=\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\displaystyle \sum_{k=1}^n f(\displaystyle \frac{k}{n})$
出典：東京工業大学 練習問題
練習問題43 区分求積法 数検１級１次 教員採用試験
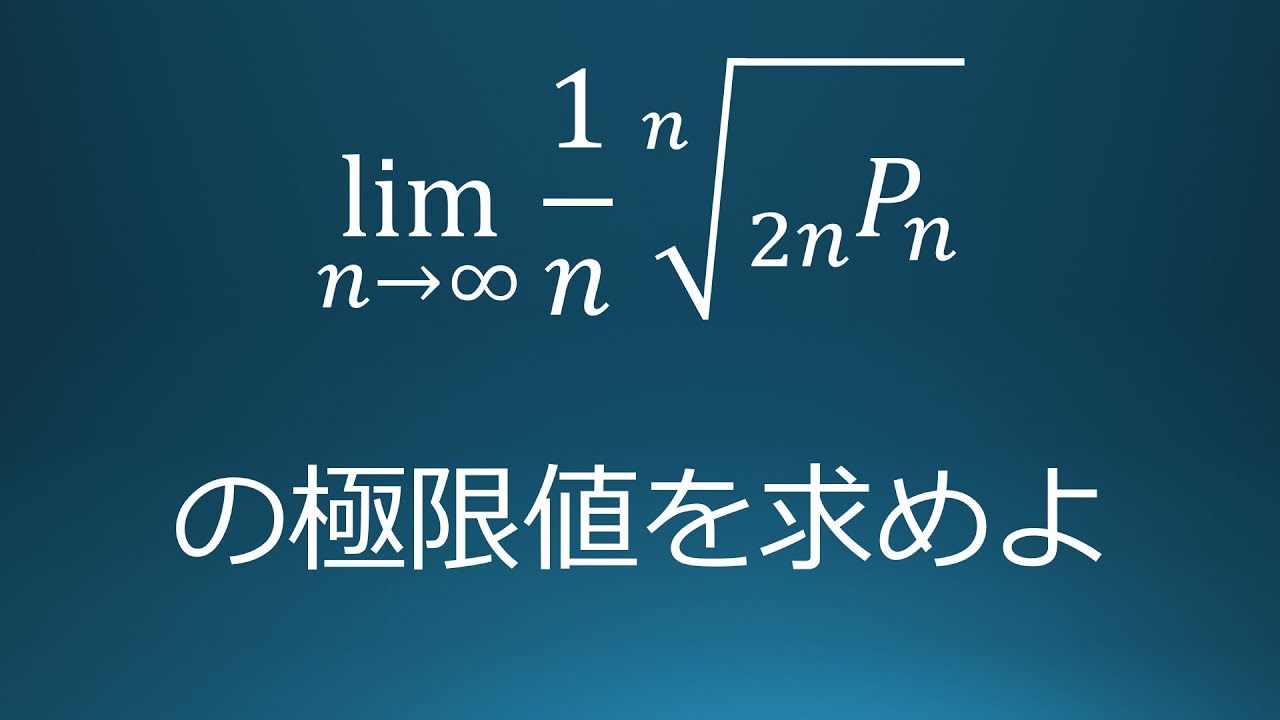
単元：
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#定積分#その他#数学検定#数学検定1級#数学(高校生)#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\sqrt[ n ]{ {}_{ 2n } P_n }$の極限値を求めよ。
$\displaystyle \int_{0}^{1}f(x)dx=\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\displaystyle \sum_{k=1}^n f(\displaystyle \frac{k}{n})$
この動画を見る
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\sqrt[ n ]{ {}_{ 2n } P_n }$の極限値を求めよ。
$\displaystyle \int_{0}^{1}f(x)dx=\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\displaystyle \sum_{k=1}^n f(\displaystyle \frac{k}{n})$
練習問題42 早稲田大学 定積分 数学検定1級 教員採用試験
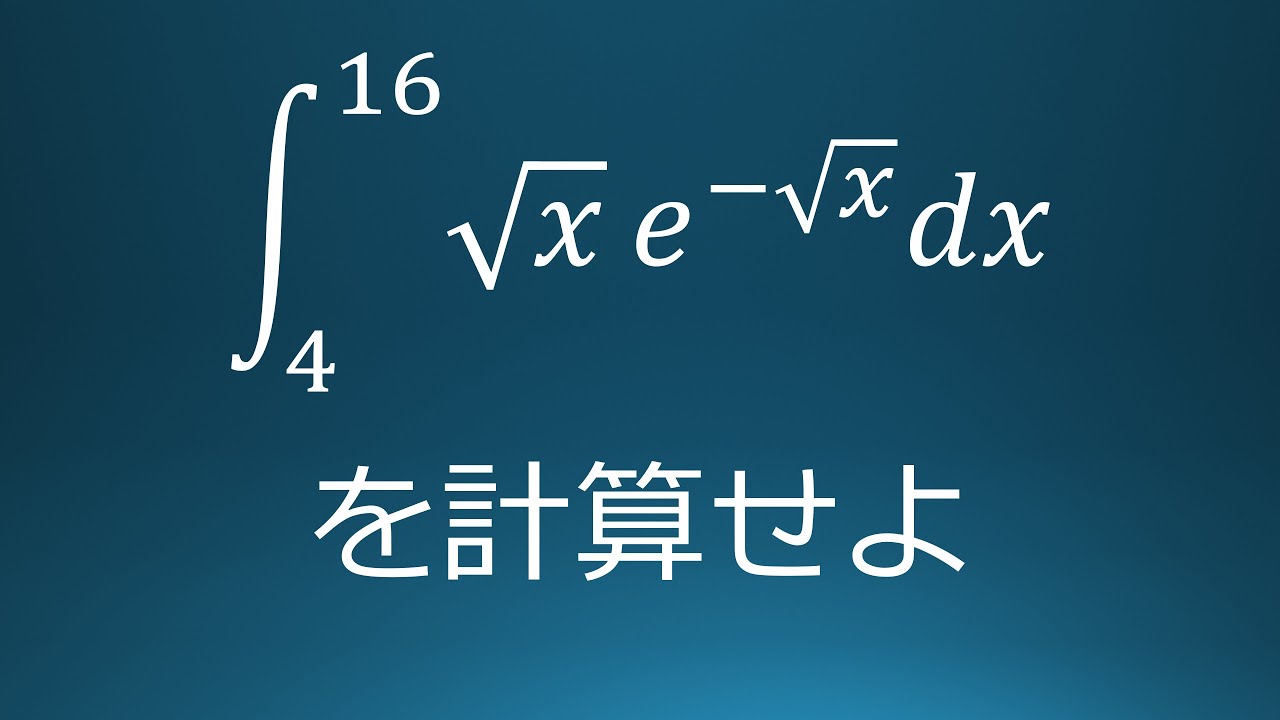
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#その他#早稲田大学#数学(高校生)#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{4}^{16}\sqrt{ x }\ e^{-\sqrt{ x }}\ dx$
出典：早稲田大学 教員採用試験
この動画を見る
$\displaystyle \int_{4}^{16}\sqrt{ x }\ e^{-\sqrt{ x }}\ dx$
出典：早稲田大学 教員採用試験
07和歌山県教員採用試験（数学：３番 解の個数）
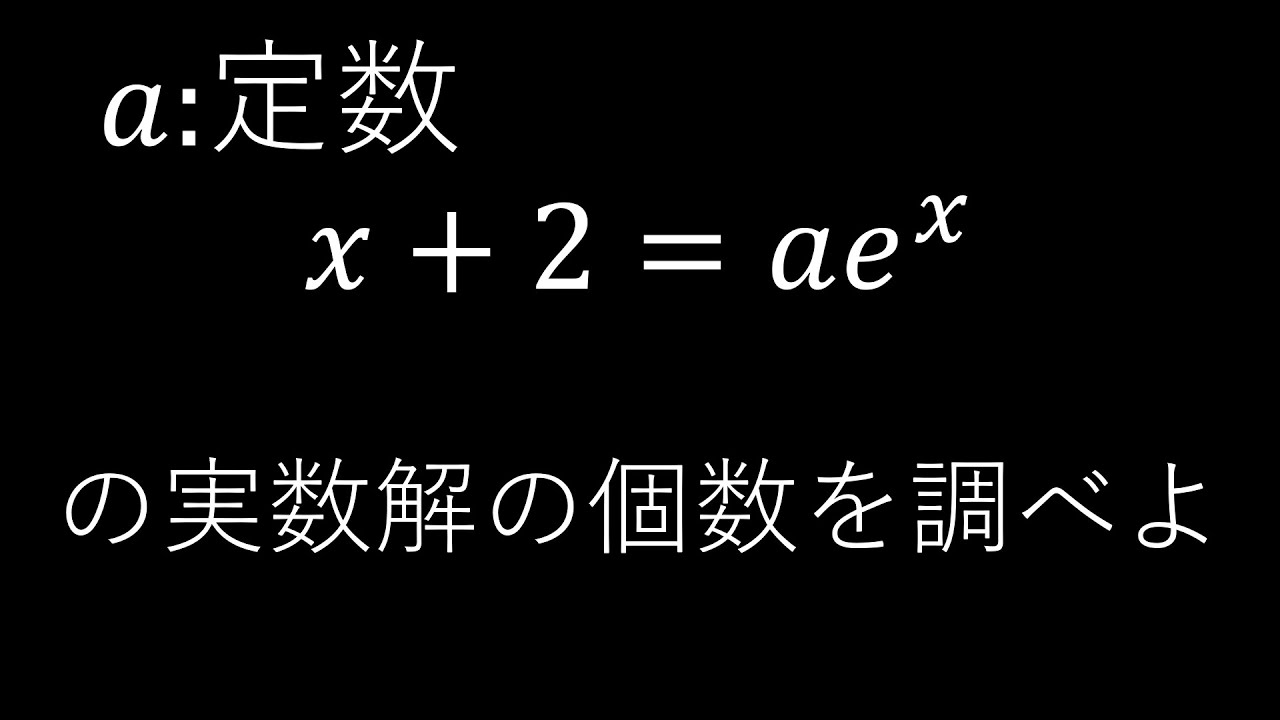
13和歌山県教員採用試験（数学：３番 三角関数）
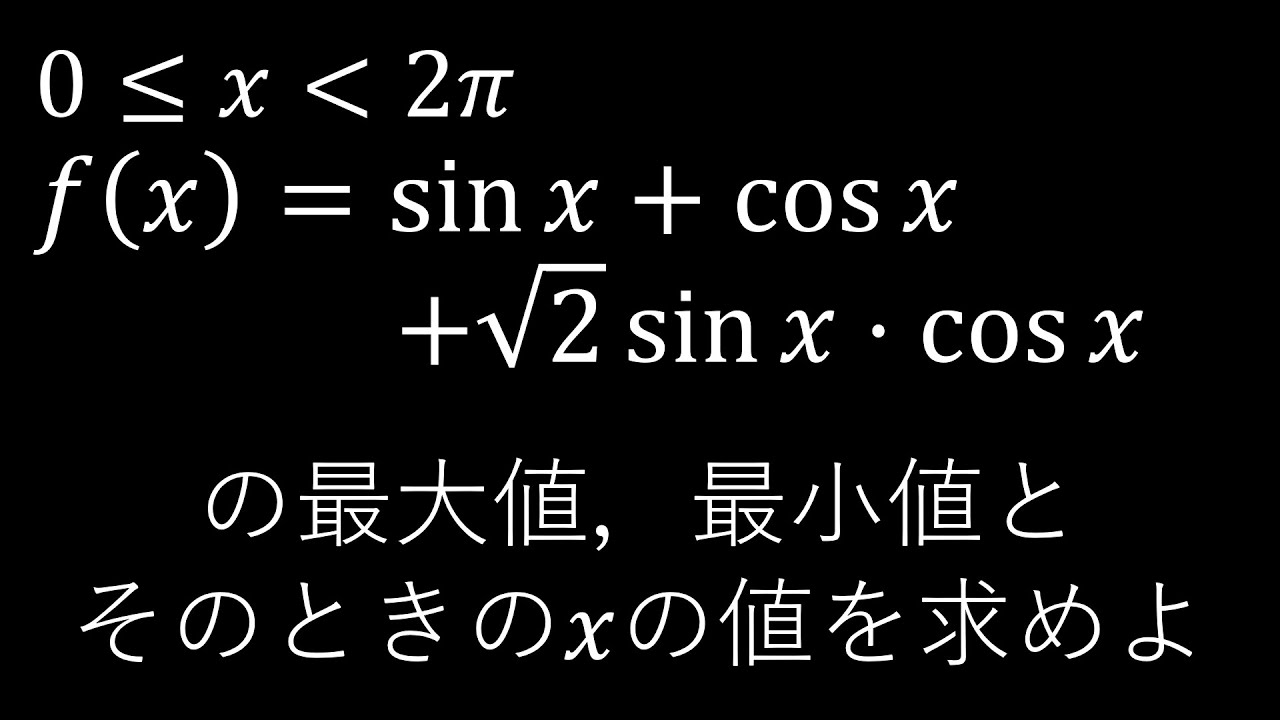
単元：
#数Ⅱ#三角関数#三角関数とグラフ#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{3}$
$0\leqq x\lt 2\pi$である.
$f(x)=\sin x+\cos x+\sqrt 2 \sin x \cos x$の
最大値,最小値とそのときの$x$の値を求めよ.
この動画を見る
$\boxed{3}$
$0\leqq x\lt 2\pi$である.
$f(x)=\sin x+\cos x+\sqrt 2 \sin x \cos x$の
最大値,最小値とそのときの$x$の値を求めよ.
数学『一対一対応』の使い方・注意点・勉強法～偏差値65確定の参考書【篠原好】
単元：
#その他#勉強法#数学(高校生)
指導講師：
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文)：
偏差値65確定の参考書
「数学『一対一対応』の使い方・注意点・勉強法」についてお話しています。
この動画を見る
偏差値65確定の参考書
「数学『一対一対応』の使い方・注意点・勉強法」についてお話しています。
07高知県教員採用試験（数学：2番 対数，解の個数）
単元：
#数Ⅱ#複素数と方程式#指数関数と対数関数#解と判別式・解と係数の関係#対数関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{2}$
$a$:定数である.
$\log_3 (x-1)^2+\log_3 (x+2)=a$において
異なる2つの正の解と1つの負の解をもつように
定数$a$の値の範囲を求めよ.
この動画を見る
$\boxed{2}$
$a$:定数である.
$\log_3 (x-1)^2+\log_3 (x+2)=a$において
異なる2つの正の解と1つの負の解をもつように
定数$a$の値の範囲を求めよ.
練習問題41 微分方程式（数研1級1次 高専数学 教員採用試験）
単元：
#数学検定・数学甲子園・数学オリンピック等#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#その他#数学検定#数学検定1級#数学(高校生)#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$(1-x)y+(1+y)x\dfrac{dy}{dx}=0$の
一般解を求めよ.
この動画を見る
$(1-x)y+(1+y)x\dfrac{dy}{dx}=0$の
一般解を求めよ.
03兵庫県教員採用試験（数学：5-(2) 共有点の個数）
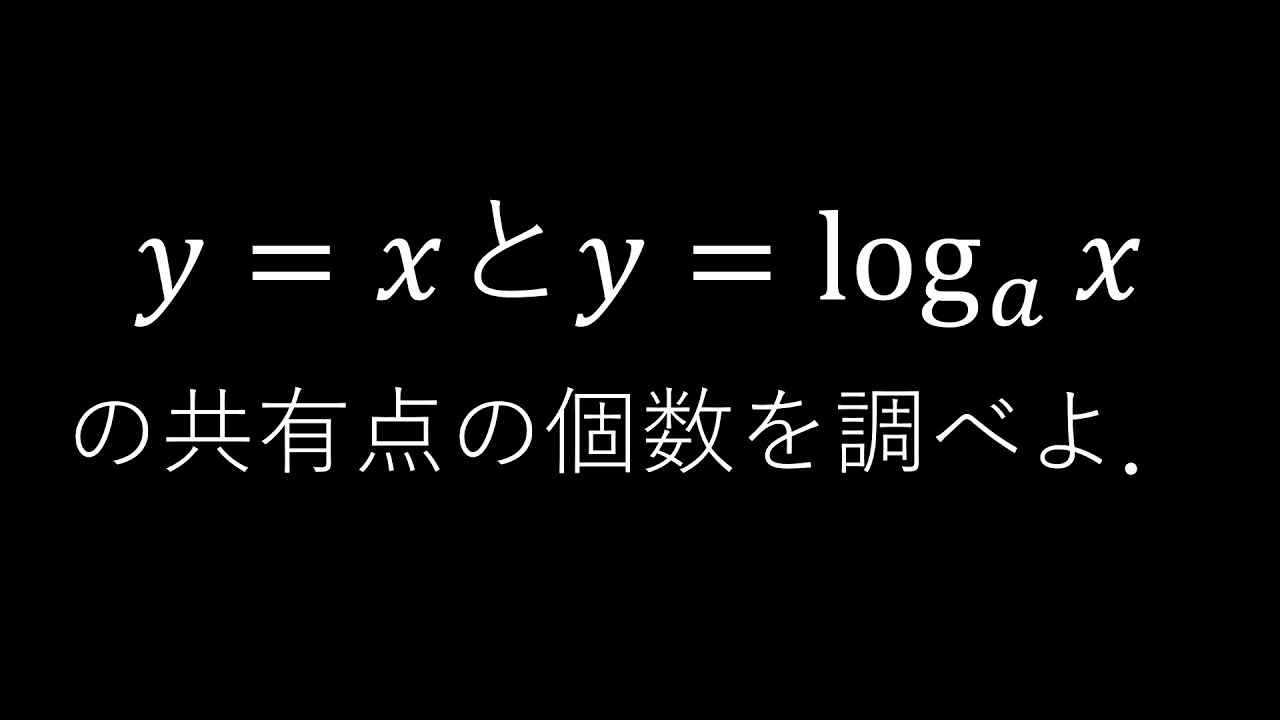
単元：
#数Ⅱ#指数関数と対数関数#対数関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{5}(2)$
直線$y=x$と曲線$y=\log_a x$との
共有点の個数を調べよ.
この動画を見る
$\boxed{5}(2)$
直線$y=x$と曲線$y=\log_a x$との
共有点の個数を調べよ.
11三重県教員採用試験（数学：5-(2) 極限値）
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{5}(2)$
$\displaystyle \lim_{x\to\infty} (2-3x)\sin \left\{\log(2x+2)-\log(2x+1)\right\}$の
極限値を求めよ.
この動画を見る
$\boxed{5}(2)$
$\displaystyle \lim_{x\to\infty} (2-3x)\sin \left\{\log(2x+2)-\log(2x+1)\right\}$の
極限値を求めよ.
07三重県教員採用試験（数学：9番 球面，点と平面の距離）
単元：
#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#その他#数学(高校生)#数C#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{9}$
球面$S:x^2+y^2+z^2-4x+8z=k$の平面
$\alpha:x-2y-z=-6$による切り口の面積が
$6\pi$のとき,$k$の値を求めよ.
この動画を見る
$\boxed{9}$
球面$S:x^2+y^2+z^2-4x+8z=k$の平面
$\alpha:x-2y-z=-6$による切り口の面積が
$6\pi$のとき,$k$の値を求めよ.
07三重県教員採用試験（数学：11番 積分）
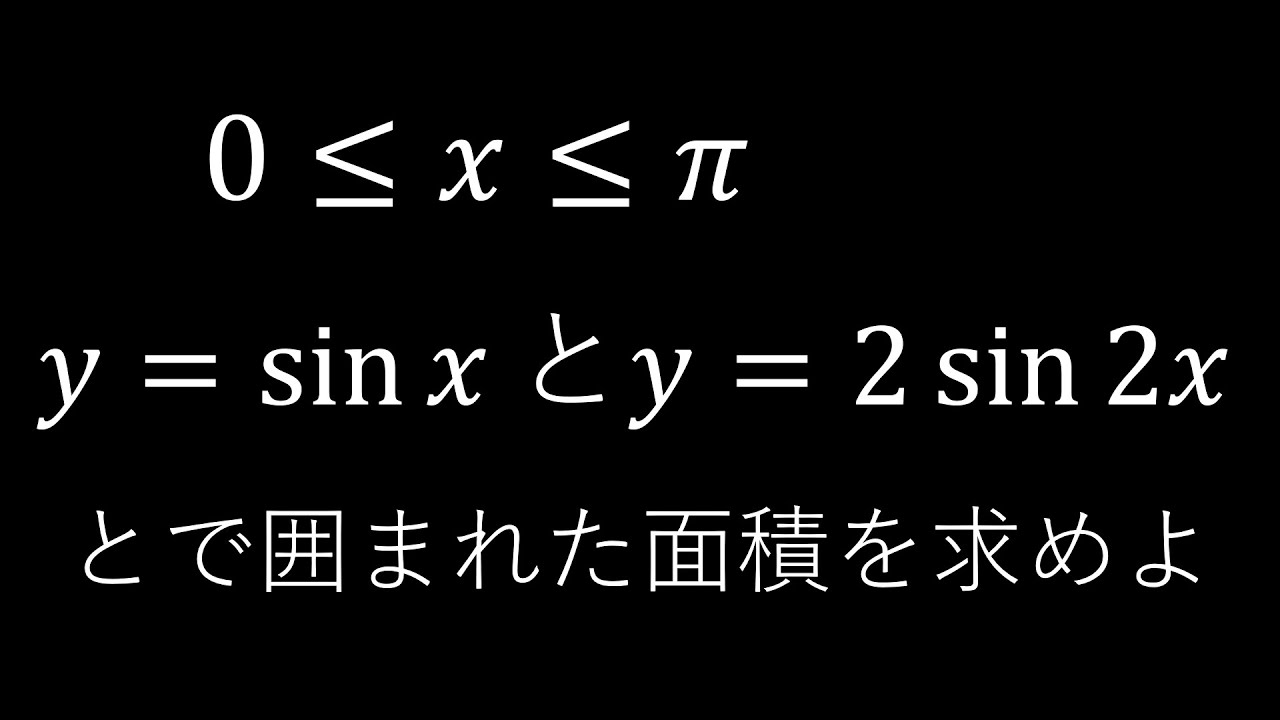
単元：
#数Ⅱ#微分法と積分法#その他#不定積分・定積分#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{11}$
$0\leqq x\leqq \pi$である.
$y=\sin x$と$y=2\sin 2x$とで囲まれた図形の
面積を求めよ.
この動画を見る
$\boxed{11}$
$0\leqq x\leqq \pi$である.
$y=\sin x$と$y=2\sin 2x$とで囲まれた図形の
面積を求めよ.
07三重県教員採用試験（数学：10番 不等式）
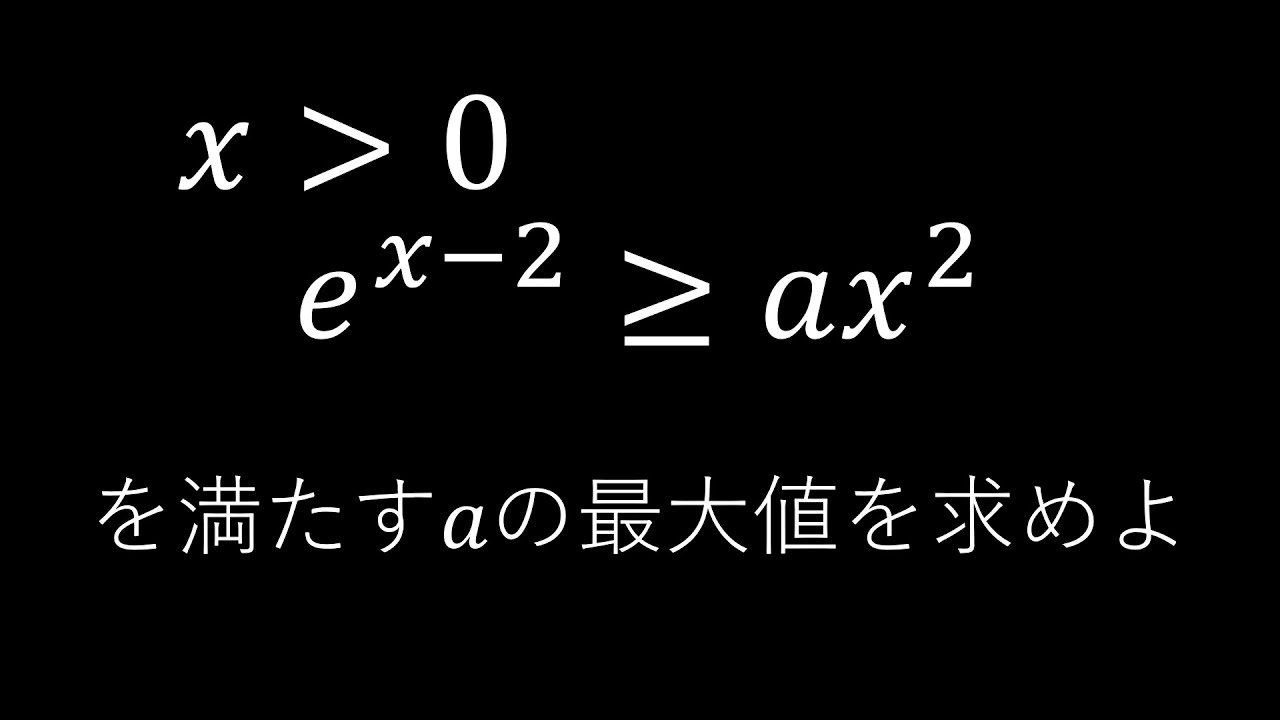
単元：
#数Ⅰ#数と式#一次不等式（不等式・絶対値のある方程式・不等式）#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{10}$
$x\gt 0$である.
$e^{x-2} \geqq ax^2$が成り立つ$a$の値の
最大値を求めよ.
この動画を見る
$\boxed{10}$
$x\gt 0$である.
$e^{x-2} \geqq ax^2$が成り立つ$a$の値の
最大値を求めよ.
俺が使った参考書・問題集（数学編）：これで京大、受かりました！偏差値８４．９の勉強法【篠原好】
単元：
#その他#勉強法#数学(高校生)
指導講師：
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文)：
これで京大、受かりました！
「俺が使った参考書・問題集（数学編）」について紹介しています。
この動画を見る
これで京大、受かりました！
「俺が使った参考書・問題集（数学編）」について紹介しています。
09高知県教員採用試験（数学：1-(4) 不定形の極限）
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{1}-(4)$
$\displaystyle \lim_{x\to 3}\dfrac{ax+b}{\sqrt{x+1}-2}=4$のとき,
定数$a,b$の値を求めよ.
この動画を見る
$\boxed{1}-(4)$
$\displaystyle \lim_{x\to 3}\dfrac{ax+b}{\sqrt{x+1}-2}=4$のとき,
定数$a,b$の値を求めよ.
【数学】高校生でもわかる写像の考え方
単元：
#数学検定・数学甲子園・数学オリンピック等#その他#その他#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
高校生でもわかる写像の考え方に関して解説していきます.
この動画を見る
高校生でもわかる写像の考え方に関して解説していきます.
15和歌山県教員採用試験（数学：４番 帰納法）
単元：
#数列#数学的帰納法#その他#数学(高校生)#数B#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{4}$
$n \gets IN$
$3^n$と$5n+2$の大小を比較せよ.
この動画を見る
$\boxed{4}$
$n \gets IN$
$3^n$と$5n+2$の大小を比較せよ.