数と式
数と式
福田のおもしろ数学500〜循環形式の連立方程式を解こう
単元：
#連立方程式#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x-1)(y^2+6)=y(x^2+1) \\
(y-1)(x^2+6)=x(y^2+1)
\end{array}
\right.
\end{eqnarray}$
を満たす実数$x,y$をすべて求めて下さい。
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x-1)(y^2+6)=y(x^2+1) \\
(y-1)(x^2+6)=x(y^2+1)
\end{array}
\right.
\end{eqnarray}$
を満たす実数$x,y$をすべて求めて下さい。
【保存版】たすき掛けの因数分解の考え方
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
因数分解しなさい。
$5x^{ 2 }-11x+2$
この動画を見る
因数分解しなさい。
$5x^{ 2 }-11x+2$
この因数分解できますか？
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
因数分解しなさい。
$ab(a+b)+bc(b+c)+ca(c+a)+2abc$
この動画を見る
因数分解しなさい。
$ab(a+b)+bc(b+c)+ca(c+a)+2abc$
福田のおもしろ数学494〜3乗根の付いた数の大小比較
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
大小を比較せよ。
$\sqrt[3]{4(2197+2025)}$
VS
$13+\sqrt[3]{2025}$
この動画を見る
大小を比較せよ。
$\sqrt[3]{4(2197+2025)}$
VS
$13+\sqrt[3]{2025}$
福田のおもしろ数学490〜3乗根混じりの2重根号を解消
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\sqrt[3]{1342\sqrt{167}+2005}$
の$2$重根号を解消せよ。
この動画を見る
$\sqrt[3]{1342\sqrt{167}+2005}$
の$2$重根号を解消せよ。
これ知ってた？
単元：
#中３数学#式の計算（展開、因数分解）#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
$(x+a)^{ 2 }=x^{ 2 }+2ax+a^{ 2 }$の考え方
この動画を見る
$(x+a)^{ 2 }=x^{ 2 }+2ax+a^{ 2 }$の考え方
福田のおもしろ数学486〜1分チャレンジ！無理数の計算
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x=\dfrac{\sqrt6+\sqrt2+\sqrt3+2}{\sqrt6-\sqrt2+\sqrt3-2},$
$y=\dfrac{\sqrt6+\sqrt2-\sqrt3-2}{\sqrt6-\sqrt2-\sqrt3+2}$
のとき$x^5+y^5$の値を求めて下さい。
この動画を見る
$x=\dfrac{\sqrt6+\sqrt2+\sqrt3+2}{\sqrt6-\sqrt2+\sqrt3-2},$
$y=\dfrac{\sqrt6+\sqrt2-\sqrt3-2}{\sqrt6-\sqrt2-\sqrt3+2}$
のとき$x^5+y^5$の値を求めて下さい。
福田の数学〜慶應義塾大学看護医療学部2025第1問(1)〜分母の有理化
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
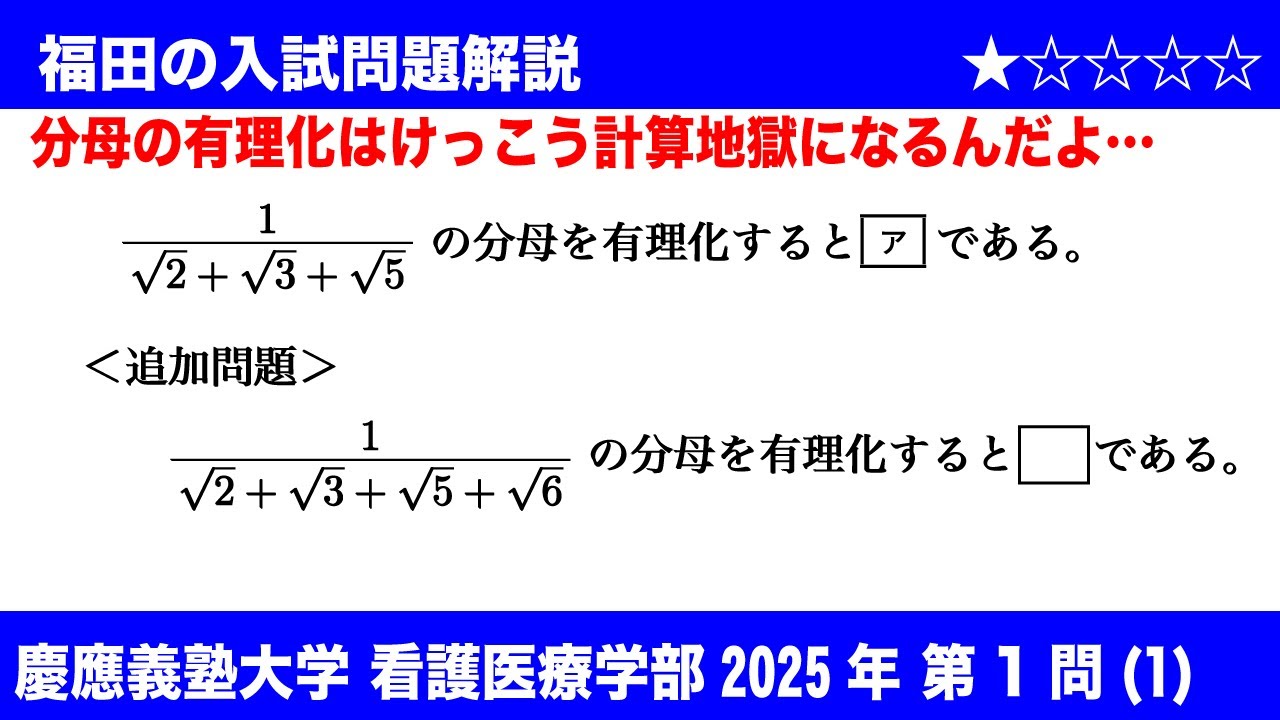
(1)$\dfrac{1}{\sqrt2+\sqrt3+\sqrt5}$の分母を有理化すると
$\boxed{ア}$である。
〈追加問題〉
$\dfrac{1}{\sqrt2+\sqrt3+\sqrt5+\sqrt6}$の分母を有理化すると
$\Box$である。
$2025$年慶應義塾大学看護医療学部過去問題
この動画を見る
$\boxed{1}$
(1)$\dfrac{1}{\sqrt2+\sqrt3+\sqrt5}$の分母を有理化すると
$\boxed{ア}$である。
〈追加問題〉
$\dfrac{1}{\sqrt2+\sqrt3+\sqrt5+\sqrt6}$の分母を有理化すると
$\Box$である。
$2025$年慶應義塾大学看護医療学部過去問題
福田の数学〜早稲田大学理工学部2025第2問〜領域に含まれる三角形の面積の最大値
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#一次不等式（不等式・絶対値のある方程式・不等式）#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
$xy$平面上で、
連立不等式
$0\lt x \leqq 1,0\leqq y \leqq \log\dfrac{1}{x}$
で定まる領域と$y$軸の
$y\geqq 0$の部分を合わせた図形を$D$とする。
$D$に含まれる三角形の最大値を求めよ。
$2025$年早稲田大学理工学部過去問題
この動画を見る
$\boxed{2}$
$xy$平面上で、
連立不等式
$0\lt x \leqq 1,0\leqq y \leqq \log\dfrac{1}{x}$
で定まる領域と$y$軸の
$y\geqq 0$の部分を合わせた図形を$D$とする。
$D$に含まれる三角形の最大値を求めよ。
$2025$年早稲田大学理工学部過去問題
福田のおもしろ数学474〜3変数の関係からa+b+cの値を求める
単元：
#連立方程式#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
実数$a,b,c$が次の条件を満たしている。
$\begin{eqnarray}
\left\{
\begin{array}{l}
a^2+b^2+c^2=1 \\
a^3+b^3+c^3=1
\end{array}
\right.
\end{eqnarray}$
$a+b+c$の値を求めよ。
この動画を見る
実数$a,b,c$が次の条件を満たしている。
$\begin{eqnarray}
\left\{
\begin{array}{l}
a^2+b^2+c^2=1 \\
a^3+b^3+c^3=1
\end{array}
\right.
\end{eqnarray}$
$a+b+c$の値を求めよ。
福田の数学〜京都大学2025理系第4問〜平面が定点を通過する条件
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題（集合・命題と条件・背理法）#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{4}$
座標空間の$4$点$O,A,B,C$は同一平面上にないとする。
$s,t,u$は$0$でない実数とする。
直線$OA$上の点$L$、
直線$OB$上の点$M$、直線$OC$上の点$N$を
$\overrightarrow{ OL }=s\overrightarrow{ OA },\overrightarrow{ OM }=t\overrightarrow{ OB },\overrightarrow{ ON }=u\overrightarrow{ OC }$が
成り立つようにとる。
(1)$s,t,u$が$\dfrac{1}{s}+\dfrac{2}{t}+\dfrac{3}{u}=4$を満たす範囲で
あらゆる値をとるとき、
$3$点$L,M,N$の定める平面$LMN$は、
$s,t,u$の値に無関係な一定の点$P$を通ることを示せ。
さらに、そのような点$P$はただ一つに定まることを示せ。
$2025$年京都大学理系過去問題
この動画を見る
$\boxed{4}$
座標空間の$4$点$O,A,B,C$は同一平面上にないとする。
$s,t,u$は$0$でない実数とする。
直線$OA$上の点$L$、
直線$OB$上の点$M$、直線$OC$上の点$N$を
$\overrightarrow{ OL }=s\overrightarrow{ OA },\overrightarrow{ OM }=t\overrightarrow{ OB },\overrightarrow{ ON }=u\overrightarrow{ OC }$が
成り立つようにとる。
(1)$s,t,u$が$\dfrac{1}{s}+\dfrac{2}{t}+\dfrac{3}{u}=4$を満たす範囲で
あらゆる値をとるとき、
$3$点$L,M,N$の定める平面$LMN$は、
$s,t,u$の値に無関係な一定の点$P$を通ることを示せ。
さらに、そのような点$P$はただ一つに定まることを示せ。
$2025$年京都大学理系過去問題
福田のおもしろ数学430〜整式を満たす整数解の性質
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
整数係数の整式$P(x)$に対して
$P(x)=1$と$P(x)＝3＄がともに整数解をもつとき、
$P(x)=2$
は異なる$2$つの整数解をもてるか？
この動画を見る
整数係数の整式$P(x)$に対して
$P(x)=1$と$P(x)＝3＄がともに整数解をもつとき、
$P(x)=2$
は異なる$2$つの整数解をもてるか？
福田のおもしろ数学428〜√n+1-√n-1が有理数になるような整数nが存在するかどうかを考える
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\sqrt{n+1}-\sqrt{n-1}$が有理数となる
整数$n$は存在するか？
この動画を見る
$\sqrt{n+1}-\sqrt{n-1}$が有理数となる
整数$n$は存在するか？
福田の数学〜東京大学2025理系第4問〜関数の値が平方数となる条件
単元：
#数Ⅰ#数A#大学入試過去問(数学)#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{4}$
この問いでは、
$0$以上の整数の$2$乗になる数を平方数と呼ぶ。
$a$を正の整数とし、
$f_a (x) = x^2+x-a$とおく。
(1)$n$を正の整数とする。
$f_a(n)$は平方数ならば、$n\leqq a$であることを示せ。
(2)$f_a (n)$が平方数となる正の整数$n$の個数を
$N_a$とおく。
次の条件$(i),(ii)$が同値であることを示せ。
$(i)\quad N_a=1$である。
$(ii)\quad 4a+1$は素数である。
$2025$年東京大学理系過去問題
この動画を見る
$\boxed{4}$
この問いでは、
$0$以上の整数の$2$乗になる数を平方数と呼ぶ。
$a$を正の整数とし、
$f_a (x) = x^2+x-a$とおく。
(1)$n$を正の整数とする。
$f_a(n)$は平方数ならば、$n\leqq a$であることを示せ。
(2)$f_a (n)$が平方数となる正の整数$n$の個数を
$N_a$とおく。
次の条件$(i),(ii)$が同値であることを示せ。
$(i)\quad N_a=1$である。
$(ii)\quad 4a+1$は素数である。
$2025$年東京大学理系過去問題
福田のおもしろ数学410〜条件を満たすKの最大値
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
次の貢献を満たす実数$k$の最大値は？
「$a+b+c\leqq K$を満たす任意の正の実数
$a,b,c$に対して$abc \leqq K$が成り立つ」
この動画を見る
次の貢献を満たす実数$k$の最大値は？
「$a+b+c\leqq K$を満たす任意の正の実数
$a,b,c$に対して$abc \leqq K$が成り立つ」
【解法は1つでない…！】連立方程式：東京工業大学附属科学技術高等学校～全国入試問題解法
福田のおもしろ数学400〜2項展開の係数と次数に関する個数
単元：
#数Ⅰ#数A#数と式#式の計算（整式・展開・因数分解）#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\left(\sqrt x+\dfrac{1}{2\sqrt[4]{x}}\right)^n$の展開式を降順に並べたとき、
最初の3項の$x$の係数が等差数列になった。
この展開式の中に$x$の次数が整数となる
項は何個あるか？
この動画を見る
$\left(\sqrt x+\dfrac{1}{2\sqrt[4]{x}}\right)^n$の展開式を降順に並べたとき、
最初の3項の$x$の係数が等差数列になった。
この展開式の中に$x$の次数が整数となる
項は何個あるか？
【理解度が試される…！】平方根：同志社高等学校～全国入試問題解法
単元：
#数学(中学生)#数と式#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$\frac{(1+\sqrt{2}+\sqrt{3})(1+\sqrt{2}-\sqrt{3})}{\sqrt{(-2)^2}}$
この動画を見る
$\frac{(1+\sqrt{2}+\sqrt{3})(1+\sqrt{2}-\sqrt{3})}{\sqrt{(-2)^2}}$
福田のおもしろ数学396〜和が0のn個の実数に対して隣接2項の積の総和が0以下となるnは
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$n\geqq 3$のとき、
$a_1+a_2+\cdots+a_n=0$を
満たすすべての実数$a_1,a_2\cdots a_n$について
$a_1a_2+a_2a_3+\cdots+a_{n-1}a_n+a_na_1 \leqq 0$
が成り立つような整数$n$をすべて求めよ。
この動画を見る
$n\geqq 3$のとき、
$a_1+a_2+\cdots+a_n=0$を
満たすすべての実数$a_1,a_2\cdots a_n$について
$a_1a_2+a_2a_3+\cdots+a_{n-1}a_n+a_na_1 \leqq 0$
が成り立つような整数$n$をすべて求めよ。
平方根と式の値 2025昭和学院秀英
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
a = 2025 b = 118のとき √a²+b²+2ab+4a+4b+4 = ？
この動画を見る
a = 2025 b = 118のとき √a²+b²+2ab+4a+4b+4 = ？
福田のおもしろ数学393〜半径1の円板上の点を3つに分類して距離1離れた2点が同じ部分集合に属さないようにできるか
単元：
#数Ⅰ#数と式#集合と命題（集合・命題と条件・背理法）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
半径1の円板(周も含む)上の点を3つの部分集合に分割し、
それぞれの部分集合において、
距離が1離れた2点を含まないようにすることは可能か？
この動画を見る
半径1の円板(周も含む)上の点を3つの部分集合に分割し、
それぞれの部分集合において、
距離が1離れた2点を含まないようにすることは可能か？
平方根 最大の整数 香川誠陵
単元：
#数学(中学生)#中３数学#平方根#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
${3\sqrt{2} }$以下の実数のうち、最大の整数を求めよ
この動画を見る
${3\sqrt{2} }$以下の実数のうち、最大の整数を求めよ
福田のおもしろ数学388〜条件付き最小問題
単元：
#数Ⅰ#数と式#一次不等式（不等式・絶対値のある方程式・不等式）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
正の実数$x,y,z$が次を満たしている。
$x\sqrt{yz}+y\sqrt{zx}+z\sqrt{xy} \geqq 1$
このとき、$x+y+z$の最小値を求めよ。
この動画を見る
正の実数$x,y,z$が次を満たしている。
$x\sqrt{yz}+y\sqrt{zx}+z\sqrt{xy} \geqq 1$
このとき、$x+y+z$の最小値を求めよ。
福田のおもしろ数学384〜整数部分と小数部分を含む連立方程式
単元：
#数Ⅰ#数と式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
[a]はaの整数部分、{a}はaの小数部分
連立方程式
x+[y]+{z}=2025.1… ①
[x]+{y}+z=2025.2… ②
{x}+y+[z]=2025.3… ③
を解いて下さい。
この動画を見る
[a]はaの整数部分、{a}はaの小数部分
連立方程式
x+[y]+{z}=2025.1… ①
[x]+{y}+z=2025.2… ②
{x}+y+[z]=2025.3… ③
を解いて下さい。
福田のおもしろ数学373〜4変数の連立方程式と循環形式
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
\begin{eqnarray}
\left\{
\begin{array}{l}
abc+ab+bc+ca+a+b+c=2 \\
bcd+bc+cd+db+b+c+d=0 \\
cda+cd+da+ac+c+d+a=2 \\
dab+da+ab+bd+d+a+b=5
\end{array}
\right.
\end{eqnarray}
を満たす実数$a,b,c,d$を求めよ。
この動画を見る
\begin{eqnarray}
\left\{
\begin{array}{l}
abc+ab+bc+ca+a+b+c=2 \\
bcd+bc+cd+db+b+c+d=0 \\
cda+cd+da+ac+c+d+a=2 \\
dab+da+ab+bd+d+a+b=5
\end{array}
\right.
\end{eqnarray}
を満たす実数$a,b,c,d$を求めよ。
福田のおもしろ数学372〜絶対値の付いた式に関する証明
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
整数$a,b,c,d$は$|ac+bd|=|ad+bc|=1$を満たしている。このとき、次を示せ。
$|a|=|b|=1$ or $|c|=|d|=1$
この動画を見る
整数$a,b,c,d$は$|ac+bd|=|ad+bc|=1$を満たしている。このとき、次を示せ。
$|a|=|b|=1$ or $|c|=|d|=1$
square root : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study #test
単元：
#数学(中学生)#中３数学#数と式
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
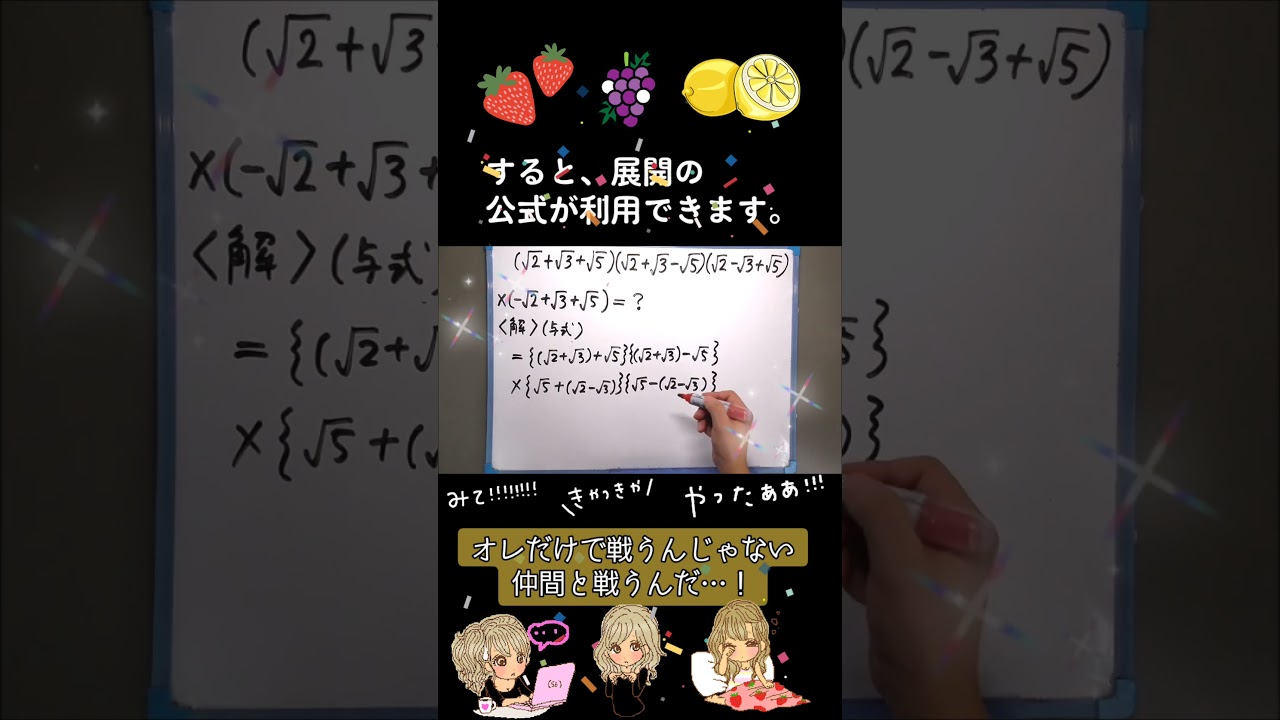
$(\sqtr{2}+\sqrt{3}+\sqrt{5})(\sqtr{2}+\sqrt{3}-\sqrt{5})×(\sqtr{2}-\sqrt{3}+\sqrt{5})(-\sqtr{2}+\sqrt{3}+\sqrt{5})=\boxed{ }$
この動画を見る
$(\sqtr{2}+\sqrt{3}+\sqrt{5})(\sqtr{2}+\sqrt{3}-\sqrt{5})×(\sqtr{2}-\sqrt{3}+\sqrt{5})(-\sqtr{2}+\sqrt{3}+\sqrt{5})=\boxed{ }$
"2025"を含む予想問題(4)：入試予想問題～全国入試問題解法
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#数Ⅰ#数と式#数学(高校生)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$x = \sqrt{2025}のとき$
$x^2 - 87x + 1890$を求めよ
この動画を見る
$x = \sqrt{2025}のとき$
$x^2 - 87x + 1890$を求めよ
"2025"を含む予想問題(3)：入試予想問題～全国入試問題解法
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$(5-2\sqrt{6})^{2025}×(5+2\sqrt{6})^{2026}×(4-\sqrt{6})$
$を計算せよ。$
この動画を見る
$(5-2\sqrt{6})^{2025}×(5+2\sqrt{6})^{2026}×(4-\sqrt{6})$
$を計算せよ。$
"2025"を含む予想問題(1)：入試予想問題～全国入試問題解法
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#数Ⅰ#数と式#数学(高校生)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$2025×2024-2024×2023$
$+2025×2026-2026×2027$
この動画を見る
$2025×2024-2024×2023$
$+2025×2026-2026×2027$