２次関数
２次関数
福田のわかった数学〜高校２年生059〜対称式と領域(1)
単元：
#数Ⅰ#数Ⅱ#２次関数#2次方程式と2次不等式#図形と方程式#軌跡と領域#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{II}$対称式と領域(1)
実数$x,\ yがx^2+y^2 \leqq 1$を
満たしながら動くとき、
次の点の存在範囲を図示せよ。
(1)$P(x+y,\ x-y) (2)Q(x+y,\ xy)$
この動画を見る
数学$\textrm{II}$対称式と領域(1)
実数$x,\ yがx^2+y^2 \leqq 1$を
満たしながら動くとき、
次の点の存在範囲を図示せよ。
(1)$P(x+y,\ x-y) (2)Q(x+y,\ xy)$
【数Ⅰ】区間が動く2次関数の最大最小【丁寧に場合分け】
単元：
#数Ⅰ#２次関数#数学(高校生)
指導講師：
めいちゃんねる
問題文全文(内容文)：
$ aを定数とする.a \leqq x \leqq a+2における関数f(x)=x^2-2x+4の最大値および最小値を求めよ.$
この動画を見る
$ aを定数とする.a \leqq x \leqq a+2における関数f(x)=x^2-2x+4の最大値および最小値を求めよ.$
【数Ⅰ】軸が動く2次関数の最大最小【図を動かしながら場合分け】
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
めいちゃんねる
問題文全文(内容文)：
$ y=x^2-4ax+a(0 \leqq x \leqq 2)
の最小値および最大値を求めよ.$
この動画を見る
$ y=x^2-4ax+a(0 \leqq x \leqq 2)
の最小値および最大値を求めよ.$
福田の数学〜明治大学2021年全学部統一入試IⅡAB第２問〜2つのグラフの共有点の個数と面積
単元：
#数Ⅰ#数Ⅱ#２次関数#2次関数とグラフ#微分法と積分法#数学(高校生)#大学入試解答速報#数学#明治大学
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{2}}$$a,k$を実数とし、xの関数$f(x),\ g(x)$を次のようにする。
$f(x)=x^3-ax, g(x)=|x|+k$
(1)$a=4,\ k=0$のとき、曲線$y=f(x)$と$y=g(x)$は3個の異なる共有点をもつ。
それぞれの交点のx座標は$-\sqrt{\boxed{\ \ ア\ \ }},\ 0,\ \sqrt{\boxed{\ \ イ\ \ }}$である。
(2)$k=0$のとき、曲線$y=f(x)$と$y=g(x)$がちょうど2個の異なる共有点をもつ
aの範囲は$\boxed{\ \ ウ\ \ }$かつ$\boxed{\ \ エ\ \ }$である。
(3)$a=4$のとき、曲線$y=f(x)$と$y=g(x)$が3個の異なる共有点をもつkの範囲は
$-\frac{\boxed{\ \ オカ\ \ }\sqrt{\boxed{\ \ キク\ \ }}}{\boxed{\ \ ケ\ \ }} \lt k \lt \boxed{\ \ コ\ \ }$である。
(4)$a=4,\ k=\boxed{\ \ コ\ \ }$のとき、曲線$y=f(x)$と$y=g(x)$の共有点のx座標は$-\boxed{\ \ サ\ \ }$
と$\boxed{\ \ シ\ \ }+\sqrt{\boxed{\ \ ス\ \ }}$であり、$y=f(x)$と$y=g(x)$で囲まれる図形の面積は
$\boxed{\ \ セ\ \ }+\boxed{\ \ ソ\ \ }\sqrt{\boxed{\ \ タ\ \ }}$である。
$\boxed{\ \ ウ\ \ }$の解答群
$⓪-2 \lt a ①-2 \leqq a ②-1 \lt a ③-1 \leqq a ④0 \lt a$
$⑤0 \leqq a ⑥1 \lt a ⑦1 \leqq a ⑧2 \lt a ⑨2 \leqq a$
$\boxed{\ \ エ\ \ }$の解答群
$⓪a \lt -2 ①a \leqq -2 ②a \lt -1 ③a \leqq -1 ④a \lt 0$
$⑤a \leqq 0 ⑥a \lt 1 ⑦a \leqq 1 ⑧a \lt 2 ⑨a \leqq 2$
2021明治大学全統過去問
この動画を見る
${\Large\boxed{2}}$$a,k$を実数とし、xの関数$f(x),\ g(x)$を次のようにする。
$f(x)=x^3-ax, g(x)=|x|+k$
(1)$a=4,\ k=0$のとき、曲線$y=f(x)$と$y=g(x)$は3個の異なる共有点をもつ。
それぞれの交点のx座標は$-\sqrt{\boxed{\ \ ア\ \ }},\ 0,\ \sqrt{\boxed{\ \ イ\ \ }}$である。
(2)$k=0$のとき、曲線$y=f(x)$と$y=g(x)$がちょうど2個の異なる共有点をもつ
aの範囲は$\boxed{\ \ ウ\ \ }$かつ$\boxed{\ \ エ\ \ }$である。
(3)$a=4$のとき、曲線$y=f(x)$と$y=g(x)$が3個の異なる共有点をもつkの範囲は
$-\frac{\boxed{\ \ オカ\ \ }\sqrt{\boxed{\ \ キク\ \ }}}{\boxed{\ \ ケ\ \ }} \lt k \lt \boxed{\ \ コ\ \ }$である。
(4)$a=4,\ k=\boxed{\ \ コ\ \ }$のとき、曲線$y=f(x)$と$y=g(x)$の共有点のx座標は$-\boxed{\ \ サ\ \ }$
と$\boxed{\ \ シ\ \ }+\sqrt{\boxed{\ \ ス\ \ }}$であり、$y=f(x)$と$y=g(x)$で囲まれる図形の面積は
$\boxed{\ \ セ\ \ }+\boxed{\ \ ソ\ \ }\sqrt{\boxed{\ \ タ\ \ }}$である。
$\boxed{\ \ ウ\ \ }$の解答群
$⓪-2 \lt a ①-2 \leqq a ②-1 \lt a ③-1 \leqq a ④0 \lt a$
$⑤0 \leqq a ⑥1 \lt a ⑦1 \leqq a ⑧2 \lt a ⑨2 \leqq a$
$\boxed{\ \ エ\ \ }$の解答群
$⓪a \lt -2 ①a \leqq -2 ②a \lt -1 ③a \leqq -1 ④a \lt 0$
$⑤a \leqq 0 ⑥a \lt 1 ⑦a \leqq 1 ⑧a \lt 2 ⑨a \leqq 2$
2021明治大学全統過去問
17滋賀県教員採用試験（数学：4番 実数解の個数）
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$k:$定数
方程式$k(x-1)^2=|x|$の異なる実数解の個数を調べよ。
出典：滋賀県教員採用試験
この動画を見る
$k:$定数
方程式$k(x-1)^2=|x|$の異なる実数解の個数を調べよ。
出典：滋賀県教員採用試験
【数Ⅰ】2次関数：2次不等式 解から定数の決定
単元：
#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
2次不等式$ax^2+8x+b＞0$の解が、$-1＜x＜5$のとき、a,bの値を求めよう。
この動画を見る
2次不等式$ax^2+8x+b＞0$の解が、$-1＜x＜5$のとき、a,bの値を求めよう。
【数Ⅰ】2次関数：2変数関数の最大最小
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$x\geqq 0,y\geqq 0,x+y=4$のとき、次の問いに答えよう。
(1)xのとりうる値の範囲を求めよう。
(2)$x^2+y^2$の最小値と、最小値をとるx,yの値を求めよう。
(3)$x^2+y^2$の最大値と、最大値をとるx,yの値を求めよう。
この動画を見る
$x\geqq 0,y\geqq 0,x+y=4$のとき、次の問いに答えよう。
(1)xのとりうる値の範囲を求めよう。
(2)$x^2+y^2$の最小値と、最小値をとるx,yの値を求めよう。
(3)$x^2+y^2$の最大値と、最大値をとるx,yの値を求めよう。
福田の数学〜中央大学2021年経済学部第１問(3)〜三角関数の最大
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#2次関数とグラフ#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{1}} (3)-\frac{\pi}{2} \leqq x \leqq \frac{\pi}{2}$
のとき、次の関数が最大値をとるときのxの値を求めよ。
$y=\sin x+\cos^2x$
2021中央大経済学部過去問
この動画を見る
${\Large\boxed{1}} (3)-\frac{\pi}{2} \leqq x \leqq \frac{\pi}{2}$
のとき、次の関数が最大値をとるときのxの値を求めよ。
$y=\sin x+\cos^2x$
2021中央大経済学部過去問
【数Ⅰ】高2生必見!! 2019年度8月 第2回 K塾高2模試 大問2-1_2次関数
単元：
#数Ⅰ#大学入試過去問(数学)#２次関数#2次方程式と2次不等式#全統模試(河合塾)#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
実数xについての2つの不等式$ (x-a^2)(x-2a+2)\leqq 0$・・・①$\vert 2x-1\vert\leqq 2$・・・② がある。ただし、aは実数の定数とする。
(1)$a=0$のとき、①を解け。
(2)②を解け。
(3)①かつ②を満たす整数xがちょうど1個だけ存在するようなaの値の範囲を求めよ。
この動画を見る
実数xについての2つの不等式$ (x-a^2)(x-2a+2)\leqq 0$・・・①$\vert 2x-1\vert\leqq 2$・・・② がある。ただし、aは実数の定数とする。
(1)$a=0$のとき、①を解け。
(2)②を解け。
(3)①かつ②を満たす整数xがちょうど1個だけ存在するようなaの値の範囲を求めよ。
福田の数学〜中央大学2021年経済学部第１問(1)〜2次方程式の解
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#複素数と方程式#2次方程式と2次不等式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$(1)次の2次方程式において,1つの解が$x=\dfrac{3}{2}-i$であるとき,
実数$a,b$の値を求めよ.ただし,$i$は虚数単位とする.
$-x^2+ax+b=0$
2021中央大経済学部過去問
この動画を見る
$\boxed{1}$(1)次の2次方程式において,1つの解が$x=\dfrac{3}{2}-i$であるとき,
実数$a,b$の値を求めよ.ただし,$i$は虚数単位とする.
$-x^2+ax+b=0$
2021中央大経済学部過去問
【数Ⅰ】高2生必見!!2020年度 第2回 K塾高2模試 大問2-1_2次関数
単元：
#数Ⅰ#大学入試過去問(数学)#２次関数#2次方程式と2次不等式#全統模試(河合塾)#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
実数xについての2つの不等式$ ax^2+2ax-2a+1\leqq 0$・・・①
$\vert x-2\vert \leqq 1$・・・② がある。
ただし、aは0でない実数の定数とする。
(1)$a=-1$のとき、①を解け。
(2)②を解け。
(3)②を満たすすべてのxが①を満たすようなaの値の範囲を求めよ。
この動画を見る
実数xについての2つの不等式$ ax^2+2ax-2a+1\leqq 0$・・・①
$\vert x-2\vert \leqq 1$・・・② がある。
ただし、aは0でない実数の定数とする。
(1)$a=-1$のとき、①を解け。
(2)②を解け。
(3)②を満たすすべてのxが①を満たすようなaの値の範囲を求めよ。
福田の数学〜慶應義塾大学2021年看護医療学部第２問(3)〜絶対値の付いた2次不等式の解
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#２次関数#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{2}}$(3)aを正の定数とし、不等式
$|x^2-ax+3| \leqq 1$
の解を実数の範囲で考える。
0 $\lt a \lt \boxed{\ \ ナ\ \ }$のとき、この不等式の解は存在しない。
$\boxed{\ \ ナ\ \ } \leqq a \leqq \boxed{\ \ ニ\ \ }$のとき、この不等式の解は
ある実数$p,q$によって$p \leqq x \leqq q$と表される。
$a \gt \boxed{\ \ ニ\ \ }$のときこの不等式の解は$\boxed{\ \ ヌ\ \ }$である。
2021慶應義塾大学看護医療学部過去問
この動画を見る
${\Large\boxed{2}}$(3)aを正の定数とし、不等式
$|x^2-ax+3| \leqq 1$
の解を実数の範囲で考える。
0 $\lt a \lt \boxed{\ \ ナ\ \ }$のとき、この不等式の解は存在しない。
$\boxed{\ \ ナ\ \ } \leqq a \leqq \boxed{\ \ ニ\ \ }$のとき、この不等式の解は
ある実数$p,q$によって$p \leqq x \leqq q$と表される。
$a \gt \boxed{\ \ ニ\ \ }$のときこの不等式の解は$\boxed{\ \ ヌ\ \ }$である。
2021慶應義塾大学看護医療学部過去問
【数学Ⅰ】2次不等式（解なし、全ての実数など）
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
【ゼロから理解できる】高校数学・物理
問題文全文(内容文)：
次の2次不等式を解け。
（1）
$x^2-6x+9 \gt 0$
（2）
$x^2+4x+4 \lt 0$
（3）
$-x^2+2x-1 \leqq 0$
（4）
$x^2+3x+4 \gt 0$
（5）
$-x^2+6x-10 \geqq 0$
この動画を見る
次の2次不等式を解け。
（1）
$x^2-6x+9 \gt 0$
（2）
$x^2+4x+4 \lt 0$
（3）
$-x^2+2x-1 \leqq 0$
（4）
$x^2+3x+4 \gt 0$
（5）
$-x^2+6x-10 \geqq 0$
【数学Ⅰ】2次不等式の解き方（基礎）
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
【ゼロから理解できる】高校数学・物理
問題文全文(内容文)：
次の2次不等式を解け。
（1）$x^2-5x+6 \gt 0$
（2）$2x^2-5x+2 \lt 0$
（3）$x^2-4x-3 \leqq 0$
この動画を見る
次の2次不等式を解け。
（1）$x^2-5x+6 \gt 0$
（2）$2x^2-5x+2 \lt 0$
（3）$x^2-4x-3 \leqq 0$
【よく出る】数学Ⅰ 2次関数の係数の符号決定
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
【ゼロから理解できる】高校数学・物理
問題文全文(内容文)：
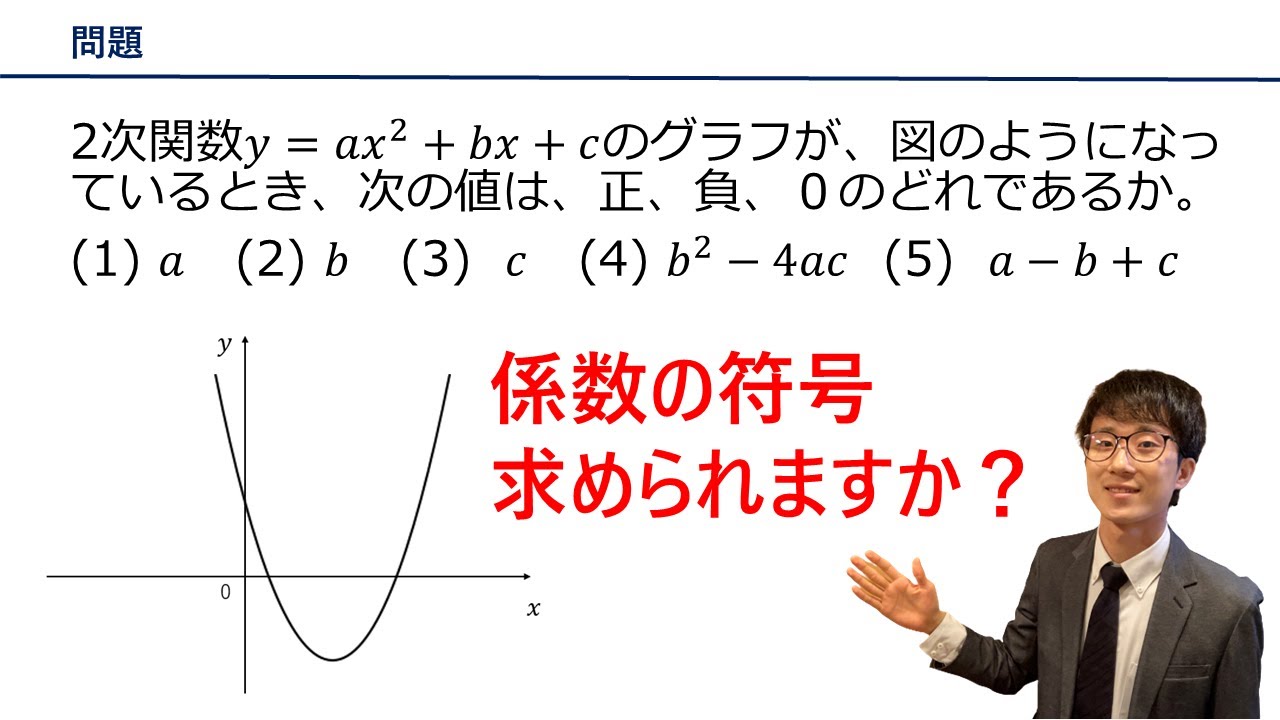
2次関数$y=ax^2+bx+c$のグラフが、図のようになっているとき、次の値は、正、負、$0$のどれであるか。
（1）$a$
（2）$b$
（3）$c$
（4）$b^2-4ac$
（5）$a-b+c$
この動画を見る
2次関数$y=ax^2+bx+c$のグラフが、図のようになっているとき、次の値は、正、負、$0$のどれであるか。
（1）$a$
（2）$b$
（3）$c$
（4）$b^2-4ac$
（5）$a-b+c$
【中学数学】2次方程式の解の公式の証明～中３以上はできないとヤバい～ 3-2【中３数学】
単元：
#数学(中学生)#中３数学#数Ⅰ#２次関数#2次関数#2次方程式と2次不等式#2次関数とグラフ#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
2次方程式の解の公式の証明
この動画を見る
2次方程式の解の公式の証明
【2次不等式は図で解く！】2次不等式を2次関数でイメージする方法を解説！【高校数学 数学】
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
3rd School
問題文全文(内容文)：
（1）$x^2+3x-4 \lt 0$
（2）$-x^2-2x+4 \geqq 0$
この動画を見る
（1）$x^2+3x-4 \lt 0$
（2）$-x^2-2x+4 \geqq 0$
福田の数学〜慶應義塾大学2021年医学部第１問(3)〜集合の要素の個数と2次方程式の解
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#複素数と方程式#集合と命題（集合・命題と条件・背理法）#2次方程式と2次不等式#複素数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{1}}$
(3)整数$k$に対して、$x$の2次方程式$x^2+kx+k+35=0$の解を$\alpha_k,\beta_k$とおく。
ただし、方程式が重解をもつときは$\alpha_k=\beta_k$である。また$U=\left\{k|kは整数、かつ|k| \leqq 100 \right\}$を全体集合とし、その部分集合$A=\{k|k \in U$かつ$\alpha_k,\beta_k$はともに実数で$\alpha_k\neq \beta_k\}$
$B=\{k|k \in U$かつ$\alpha_k,\beta_k$の実数はともに2より大きい$\}$
$C=\{k|k \in U$かつ$\alpha_k,\beta_k$の実部と虚部はすべて整数$\}$
を考える。このとき$n(A)=\boxed{\ \ (か)\ \ },$$n(A \cap B)=\boxed{\ \ (き)\ \ },$$n(\bar{ A } \cap B)=\boxed{\ \ (く)\ \ },$
$n(A \cap C)=\boxed{\ \ (け)\ \ },$$n(\bar{ A } \cap C)=\boxed{\ \ (こ)\ \ }$である。ただし有限集合$X$に対してその要素の個数を$n(X)$で表す。また$\bar{ A }$は$A$の補集合である。
2021慶應義塾大学医学部過去問
この動画を見る
${\Large\boxed{1}}$
(3)整数$k$に対して、$x$の2次方程式$x^2+kx+k+35=0$の解を$\alpha_k,\beta_k$とおく。
ただし、方程式が重解をもつときは$\alpha_k=\beta_k$である。また$U=\left\{k|kは整数、かつ|k| \leqq 100 \right\}$を全体集合とし、その部分集合$A=\{k|k \in U$かつ$\alpha_k,\beta_k$はともに実数で$\alpha_k\neq \beta_k\}$
$B=\{k|k \in U$かつ$\alpha_k,\beta_k$の実数はともに2より大きい$\}$
$C=\{k|k \in U$かつ$\alpha_k,\beta_k$の実部と虚部はすべて整数$\}$
を考える。このとき$n(A)=\boxed{\ \ (か)\ \ },$$n(A \cap B)=\boxed{\ \ (き)\ \ },$$n(\bar{ A } \cap B)=\boxed{\ \ (く)\ \ },$
$n(A \cap C)=\boxed{\ \ (け)\ \ },$$n(\bar{ A } \cap C)=\boxed{\ \ (こ)\ \ }$である。ただし有限集合$X$に対してその要素の個数を$n(X)$で表す。また$\bar{ A }$は$A$の補集合である。
2021慶應義塾大学医学部過去問
よく間違える二次不等式
数I 2次関数の最大に関する問題 （他の問題の解説もあり）
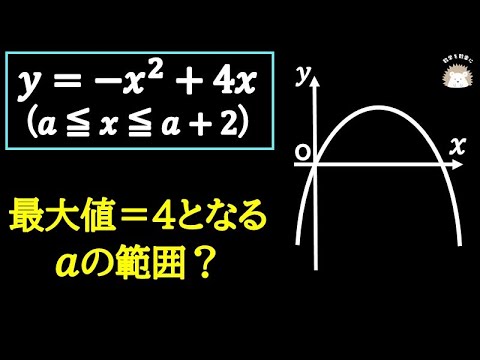
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$y=-x^2+4x (a \leqq x \leqq a+2)$
(1)最大値=3となるaの値=?
(2)最大値=4となるaの範囲は?
この動画を見る
$y=-x^2+4x (a \leqq x \leqq a+2)$
(1)最大値=3となるaの値=?
(2)最大値=4となるaの範囲は?
15岡山県教員採用試験（数学：2次方程式）
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$kx^2-4x+k-3=0$が異なる2つの実数解をもつ.
$k$の値の範囲を求めよ.
この動画を見る
$kx^2-4x+k-3=0$が異なる2つの実数解をもつ.
$k$の値の範囲を求めよ.
福田のわかった数学〜高校１年生029〜いろいろなグラフ(3)
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
\begin{eqnarray}
数学\textrm{I} いろいろなグラフ(3)\\
0 \leqq x \leqq 16の範囲で、\\
y=x[\sqrt x] のグラフを描け。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{I} いろいろなグラフ(3)\\
0 \leqq x \leqq 16の範囲で、\\
y=x[\sqrt x] のグラフを描け。
\end{eqnarray}
【2次関数の応用問題はこう解く！】最大値と最小値の応用問題を図でイメージする方法を解説！【高校数学 数学】
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
3rd School
問題文全文(内容文)：
①
$a \gt 0$のとき、$y=x^2-4x+3(0 \leqq x \leqq a)$の最小値を求めよ
②
$a \gt 0$のとき、$y=-x^2+2ax-a^2+2$の$0 \leqq x \leqq 2$での最大値を求めよ
この動画を見る
①
$a \gt 0$のとき、$y=x^2-4x+3(0 \leqq x \leqq a)$の最小値を求めよ
②
$a \gt 0$のとき、$y=-x^2+2ax-a^2+2$の$0 \leqq x \leqq 2$での最大値を求めよ
福田のわかった数学〜高校１年生028〜いろいろなグラフ(2)
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
\begin{eqnarray}
数学\textrm{I} いろいろなグラフ(2)\\
-2 \leqq x \leqq 4の範囲で\\
\\
y=[x]-x\\
\\
のグラフを描け。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{I} いろいろなグラフ(2)\\
-2 \leqq x \leqq 4の範囲で\\
\\
y=[x]-x\\
\\
のグラフを描け。
\end{eqnarray}
福田のわかった数学〜高校１年生027〜いろいろなグラフ(1)
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{I}$ いろいろなグラフ(1)
$f(x)=\left\{\begin{array}{1}
2x (0 \leqq x \leqq \frac{1}{2})\\
2-2x (\frac{1}{2} \leqq x \leqq 1)\\
\end{array}\right.$
(1)$y=f(x)$のグラフを描け。
(2)$y=f(f(x))$のグラフを描け。
この動画を見る
数学$\textrm{I}$ いろいろなグラフ(1)
$f(x)=\left\{\begin{array}{1}
2x (0 \leqq x \leqq \frac{1}{2})\\
2-2x (\frac{1}{2} \leqq x \leqq 1)\\
\end{array}\right.$
(1)$y=f(x)$のグラフを描け。
(2)$y=f(f(x))$のグラフを描け。
福田のわかった数学〜高校１年生026〜グラフの対称性と平行移動の概念(2)
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{I}$ 対称性、平行移動の概念
次の式の表すグラフを描け。
$y=||x^2-4|-3|$
この動画を見る
数学$\textrm{I}$ 対称性、平行移動の概念
次の式の表すグラフを描け。
$y=||x^2-4|-3|$
知っていれば一瞬！！ これぞ受験テクニック
福田のわかった数学〜高校１年生024〜共通解の考え方
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{I}$ 共通解の考え方
$\left\{\begin{array}{1}
x^2+2x+a=0\\
x^2+ax+2=0\\
\end{array}\right.$
が実数の共通解をもつように
定数$a$の値を求めよ。
この動画を見る
数学$\textrm{I}$ 共通解の考え方
$\left\{\begin{array}{1}
x^2+2x+a=0\\
x^2+ax+2=0\\
\end{array}\right.$
が実数の共通解をもつように
定数$a$の値を求めよ。
福田のわかった数学〜高校１年生023〜連立２次不等式の整数解の個数
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{I}$ 連立2次不等式
$\left\{\begin{array}{1}
x^2-2x-3 \gt 0\\
x^2-(a+1)x+a \lt 0\\
\end{array}\right.$
をともに満たす整数がただ1つとなる
ようなaの値の範囲を求めよ。
この動画を見る
数学$\textrm{I}$ 連立2次不等式
$\left\{\begin{array}{1}
x^2-2x-3 \gt 0\\
x^2-(a+1)x+a \lt 0\\
\end{array}\right.$
をともに満たす整数がただ1つとなる
ようなaの値の範囲を求めよ。
福田のわかった数学〜高校１年生022〜２次方程式の解の分離
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#2次関数とグラフ#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{I}$ 2次方程式の解の分離
$a \geqq 0$のとき、
$x^2-(a+1)x-a=0$
の実数解の取り得る値の範囲を求めよ。
この動画を見る
数学$\textrm{I}$ 2次方程式の解の分離
$a \geqq 0$のとき、
$x^2-(a+1)x-a=0$
の実数解の取り得る値の範囲を求めよ。