図形の性質
図形の性質
福田の数学〜早稲田大学2025商学部第3問〜三角形を一辺を軸として回転させたときの回転体の体積の最大
単元：
#数A#大学入試過去問(数学)#図形の性質#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$
空間内の異なる$4$点
$A,B,C,D$が$AD=BC=2$、
$AB=CD=1$を満たし、線分$AD$と線分$BC$が
点$P$のみで交わり、$P$は$AD$と$BC$をそれぞれ
$AP:PD=s:(1-s),$
$BP:PC=t:(1-t) \ (0\lt s \lt t,0\lt t \lt 1)$
に内分しているとする。次の問いに答えよ。
(1)$s$を$t$を用いて表せ。
(2)$t$のとりうる値の範囲を求めよ。
(3)線分$BC$を軸にして$\triangle ABP$を$1$回転させるとき、
$\triangle ABP$の辺と内部が通過する部分の体積を
$V$とする。$V$の最大値を求めよ。
$2025$年早稲田大学商学部過去問題
この動画を見る
$\boxed{3}$
空間内の異なる$4$点
$A,B,C,D$が$AD=BC=2$、
$AB=CD=1$を満たし、線分$AD$と線分$BC$が
点$P$のみで交わり、$P$は$AD$と$BC$をそれぞれ
$AP:PD=s:(1-s),$
$BP:PC=t:(1-t) \ (0\lt s \lt t,0\lt t \lt 1)$
に内分しているとする。次の問いに答えよ。
(1)$s$を$t$を用いて表せ。
(2)$t$のとりうる値の範囲を求めよ。
(3)線分$BC$を軸にして$\triangle ABP$を$1$回転させるとき、
$\triangle ABP$の辺と内部が通過する部分の体積を
$V$とする。$V$の最大値を求めよ。
$2025$年早稲田大学商学部過去問題
福田の数学〜千葉大学2024年理系第8問〜4つの円の位置関係と極限
単元：
#数A#図形の性質#関数と極限#数列の極限#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
図は動画参照
半径$1$、中心$O$の円$C$がある。2つの円$C_1$と$C_2$が次の2つの条件を満たすとする。
・$C_1$と$C_2$はどちらも$C$に内接する。
・$C_1$と$C_2$は互いに外接する。
円$C_1,\ C_2$の中心をそれぞれ$D,\ E$とし、半径をそれぞれ$p,\ q$とする。$\theta= \angle{DOE}$とおく。
(1) $q$を$p$と$\theta$を用いて表せ。
(2) $p$を固定する。$\theta$が$0$に近づくとき、$\dfrac{q}{theta^2}$の極限値を求めよ。
(3) $p= \sqrt{2}-1$のとき、$q$の値を求めよ。
(4) $\theta$が$0$に近づくとき、$\dfrac{q}{p}$の極限値を求めよ。
この動画を見る
図は動画参照
半径$1$、中心$O$の円$C$がある。2つの円$C_1$と$C_2$が次の2つの条件を満たすとする。
・$C_1$と$C_2$はどちらも$C$に内接する。
・$C_1$と$C_2$は互いに外接する。
円$C_1,\ C_2$の中心をそれぞれ$D,\ E$とし、半径をそれぞれ$p,\ q$とする。$\theta= \angle{DOE}$とおく。
(1) $q$を$p$と$\theta$を用いて表せ。
(2) $p$を固定する。$\theta$が$0$に近づくとき、$\dfrac{q}{theta^2}$の極限値を求めよ。
(3) $p= \sqrt{2}-1$のとき、$q$の値を求めよ。
(4) $\theta$が$0$に近づくとき、$\dfrac{q}{p}$の極限値を求めよ。
福田の数学〜早稲田大学2025商学部第1問(4)〜正九角形の頂点を結んでできる正三角形の個数
単元：
#数A#大学入試過去問(数学)#場合の数と確率#図形の性質#確率#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(4)$P$を平面上の正九角形とする。
$P$の異なる$2$つの頂点を通る直線をすべて考える。
これら$36$本の直線のうちの$3$本により平面上で
囲まれてできる正三角形の総数は$\boxed{エ}$である。
ただし、互いに合同でも位置の異なるものは
異なる三角形として数える。
$2025$年早稲田大学商学部過去問題
この動画を見る
$\boxed{1}$
(4)$P$を平面上の正九角形とする。
$P$の異なる$2$つの頂点を通る直線をすべて考える。
これら$36$本の直線のうちの$3$本により平面上で
囲まれてできる正三角形の総数は$\boxed{エ}$である。
ただし、互いに合同でも位置の異なるものは
異なる三角形として数える。
$2025$年早稲田大学商学部過去問題
福田のおもしろ数学559〜3Xnのタイルを2つの図形で覆うことができるためのnの条件
単元：
#数A#図形の性質#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
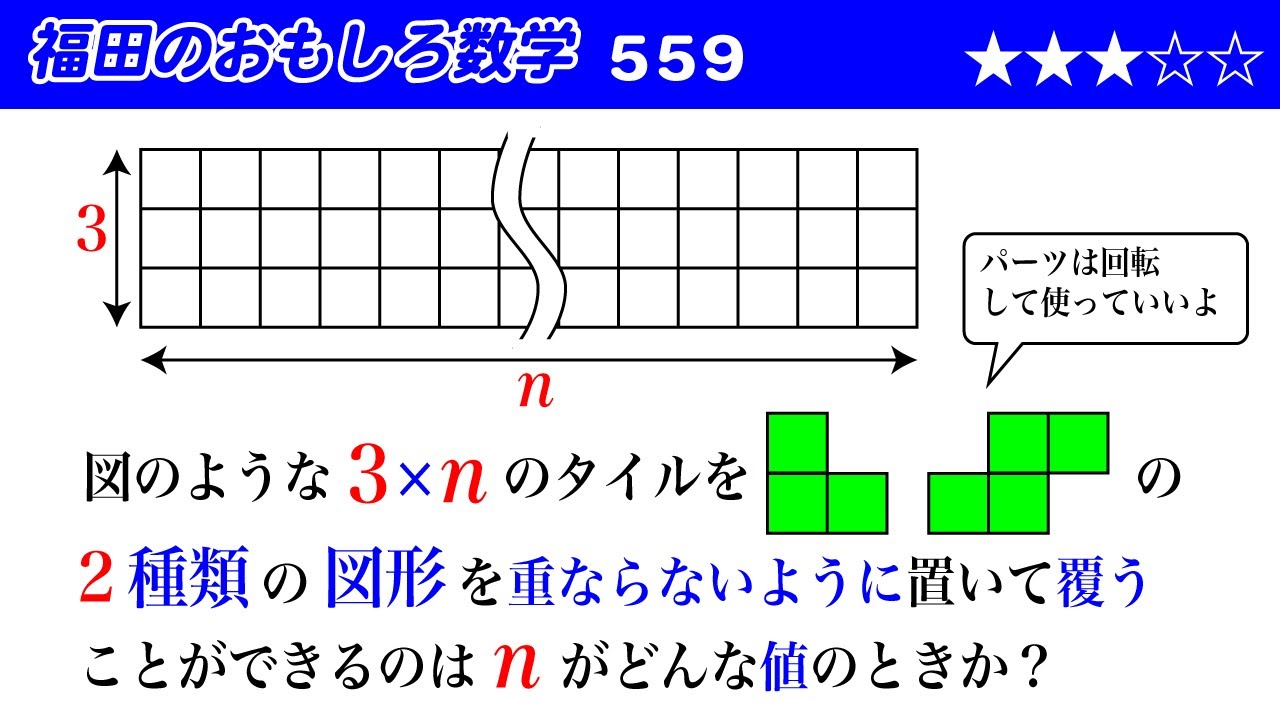
図のような$3\times n$のタイルを(動画を参照)の
$2$種類の図形を重ならないように置いて覆う
ことができるのは$n$がどんな値のときか？
図は動画内参照
この動画を見る
図のような$3\times n$のタイルを(動画を参照)の
$2$種類の図形を重ならないように置いて覆う
ことができるのは$n$がどんな値のときか？
図は動画内参照
福田のおもしろ数学558〜長方形を面積の等しい5個の長方形に分割すると合同な長方形が含まれている証明
単元：
#数A#図形の性質#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
ある長方形を面積の等しい$5$個の長方形に
分割する。
このとき、少なくとも$2$個は
合同であることを証明せよ。
この動画を見る
ある長方形を面積の等しい$5$個の長方形に
分割する。
このとき、少なくとも$2$個は
合同であることを証明せよ。
福田のおもしろ数学556〜直角三角形の内接円の接点が斜辺を分ける長さと面積
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
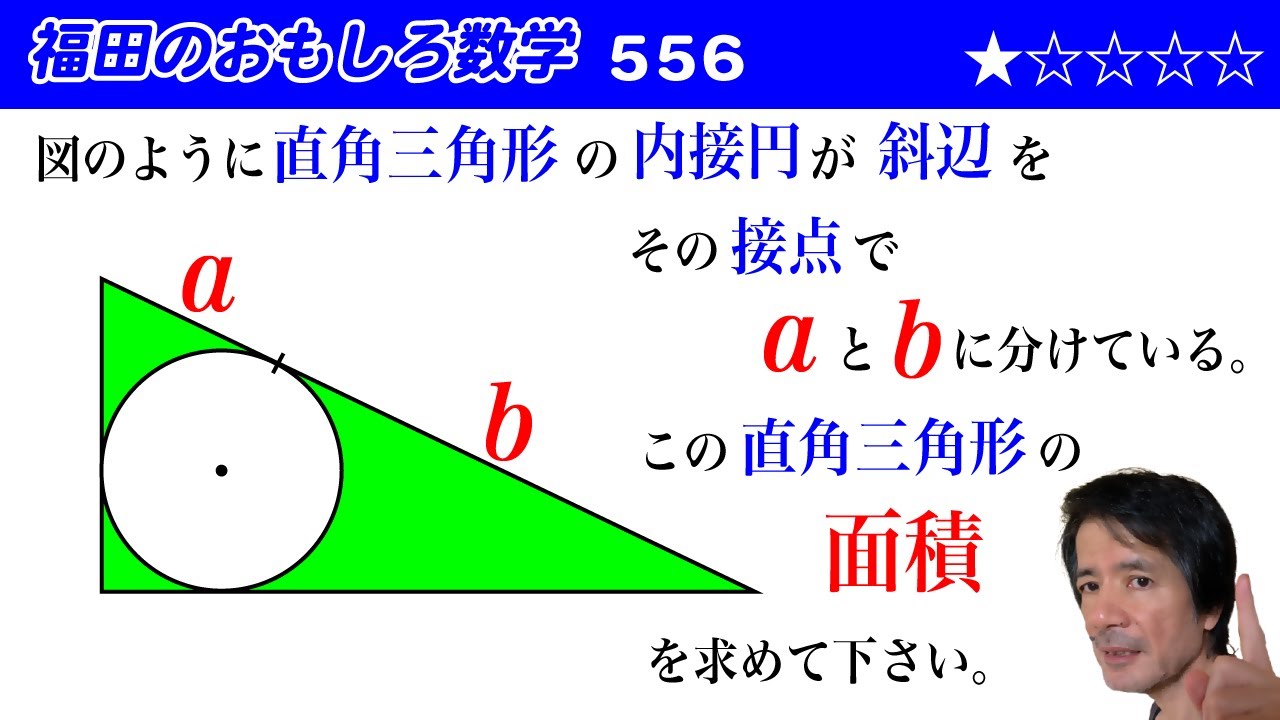
図のような直角三角形の内接円が斜辺を
その接点で$a$と$b$に分けている。
この直角三角形の面積を求めて下さい。
図は動画内参照
この動画を見る
図のような直角三角形の内接円が斜辺を
その接点で$a$と$b$に分けている。
この直角三角形の面積を求めて下さい。
図は動画内参照
福田の数学〜九州大学2025理系第4問〜平面幾何の証明
単元：
#数A#図形の性質#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{4}$
半径$1$の円周上に反時計回りに
点$A,B,C,D$を順にとり、
線分$AD$は直径で、$AC=CD$、
$AB=BC$が成り立つとする。
(1)$\angle ACB$を求めよ。
(2)$BC$を求めよ。
(3)線分$AC$と線分$BD$の交点を$E$とするとき、
三角形$BCE$の面積を求めよ。
$2025$年九州大学理系過去問題
この動画を見る
$\boxed{4}$
半径$1$の円周上に反時計回りに
点$A,B,C,D$を順にとり、
線分$AD$は直径で、$AC=CD$、
$AB=BC$が成り立つとする。
(1)$\angle ACB$を求めよ。
(2)$BC$を求めよ。
(3)線分$AC$と線分$BD$の交点を$E$とするとき、
三角形$BCE$の面積を求めよ。
$2025$年九州大学理系過去問題
福田の数学〜神戸大学2025理系第4問〜空間ベクトルと三角形の面積の最小
単元：
#数A#大学入試過去問(数学)#図形の性質#空間ベクトル#三角形の辺の比（内分・外分・二等分線）#空間ベクトル#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{4}$
$s,t$を実数とする。座標空間に$3$点
$A(-4,-1,0),B(-3,0,-1),P(s,t,-2s+t-1)$がある。
以下の問いに答えよ。
(1)$3$点$A,B,P$は一直線上にないことを示せ。
(2)点$P$から直線$AB$に下ろした垂線を$PH$とする。
点$H$の座標を$s$を用いて表せ。
(3)$s,t$が変化するとき、
三角形$ABP$の面積の最小値を求めよ。
$2025$年神戸大学理系過去問題
この動画を見る
$\boxed{4}$
$s,t$を実数とする。座標空間に$3$点
$A(-4,-1,0),B(-3,0,-1),P(s,t,-2s+t-1)$がある。
以下の問いに答えよ。
(1)$3$点$A,B,P$は一直線上にないことを示せ。
(2)点$P$から直線$AB$に下ろした垂線を$PH$とする。
点$H$の座標を$s$を用いて表せ。
(3)$s,t$が変化するとき、
三角形$ABP$の面積の最小値を求めよ。
$2025$年神戸大学理系過去問題
福田のおもしろ数学533〜凸四角形の性質に関する証明
単元：
#数A#数Ⅱ#図形の性質#式と証明#周角と円に内接する四角形・円と接線・接弦定理#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
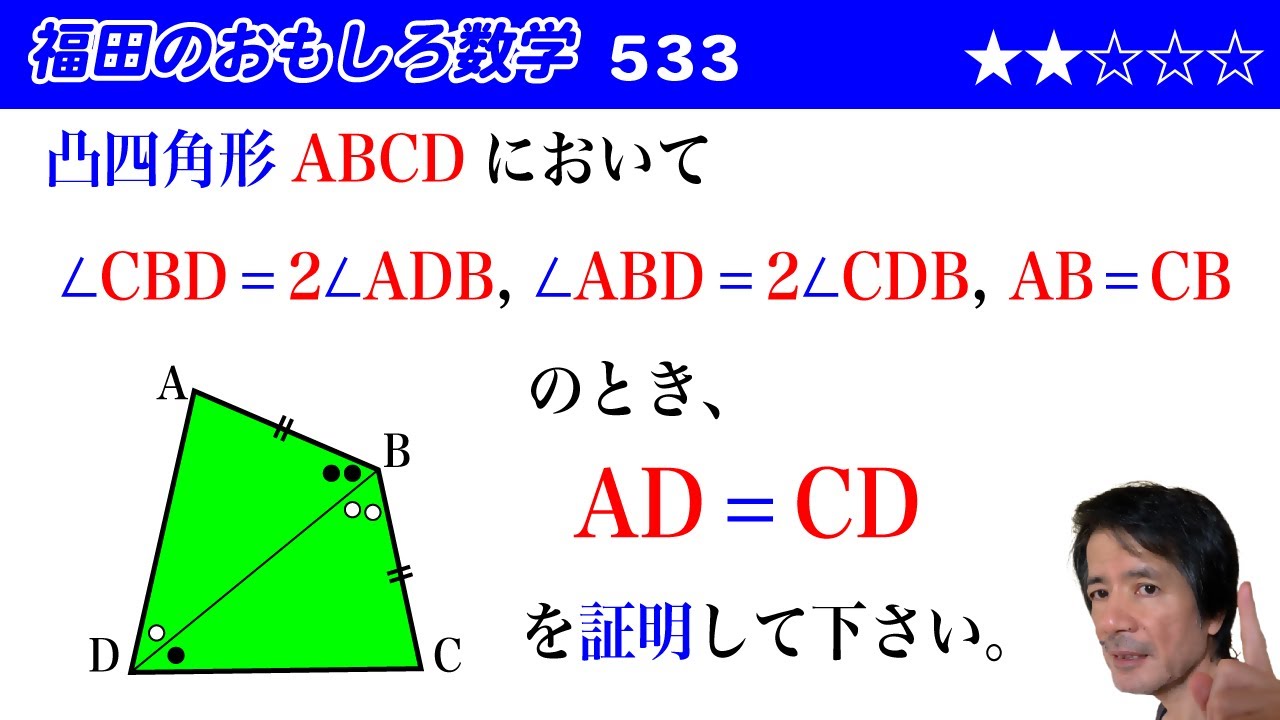
凸四角形$ABCD$において
$\angle CBD = 2\angle ADB,\angle ABD = 2\angle CDB,AB=CB$
のとき、
$AD=CD$を証明して下さい。
図は動画内参照
この動画を見る
凸四角形$ABCD$において
$\angle CBD = 2\angle ADB,\angle ABD = 2\angle CDB,AB=CB$
のとき、
$AD=CD$を証明して下さい。
図は動画内参照
福田のおもしろ数学531〜三角形に関する命題とその逆
単元：
#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
左の三角形$ABC$において
$\angle A=3\angle B$
$\Rightarrow (a^2-b^2)(a-b)=bc^2$
が成り立つことを示せ。
また、逆は成り立つか？
図は動画内参照
この動画を見る
左の三角形$ABC$において
$\angle A=3\angle B$
$\Rightarrow (a^2-b^2)(a-b)=bc^2$
が成り立つことを示せ。
また、逆は成り立つか？
図は動画内参照
福田のおもしろ数学507〜三角形の面がm個ありどの頂点にも4本の辺が集まる多面体
単元：
#数A#図形の性質#空間における垂直と平行と多面体（オイラーの法則）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
ある凸多面体において、
三角形の面が$m$枚あり、
(他の形の面も含まれている可能性がある)
すべての頂点にはちょうど$4$枚の辺が集まって
いるとする。
このとき、$m$の最小値を求めて下さい。
この動画を見る
ある凸多面体において、
三角形の面が$m$枚あり、
(他の形の面も含まれている可能性がある)
すべての頂点にはちょうど$4$枚の辺が集まって
いるとする。
このとき、$m$の最小値を求めて下さい。
福田の数学〜慶應義塾大学2025経済学部第1問(1)〜三角形の面積と線分の長さ
単元：
#数A#大学入試過去問(数学)#図形の性質#三角形の辺の比（内分・外分・二等分線）#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(1)$\sin \alpha=\dfrac{3}{5},\cos \alpha=\dfrac{4}{5}$とする。
座標平面上の$4$点$O,A,B,C$を、
$O(0,0),A(5,0),B(5\cos\alpha,5\sin\alpha),$
$C(5\cos3\alpha,5\sin3\alpha)$とする。
(a)$\triangle OAB$の面積は$\dfrac{\boxed{アイ}}{\boxed{ウ}}$、
辺$AB$の長さは$\sqrt{\boxed{エオ}}$である。
(b)$\triangle OBC$の面積は$\boxed{カキ}$、辺$AB$の長さは$\boxed{ク}$である。
(c)線分$AC$の長さは$\dfrac{\boxed{ケコ}}{\boxed{サ}}\sqrt{\boxed{シス}}$
$2025$年慶應義塾大学経済学部過去問題
この動画を見る
$\boxed{1}$
(1)$\sin \alpha=\dfrac{3}{5},\cos \alpha=\dfrac{4}{5}$とする。
座標平面上の$4$点$O,A,B,C$を、
$O(0,0),A(5,0),B(5\cos\alpha,5\sin\alpha),$
$C(5\cos3\alpha,5\sin3\alpha)$とする。
(a)$\triangle OAB$の面積は$\dfrac{\boxed{アイ}}{\boxed{ウ}}$、
辺$AB$の長さは$\sqrt{\boxed{エオ}}$である。
(b)$\triangle OBC$の面積は$\boxed{カキ}$、辺$AB$の長さは$\boxed{ク}$である。
(c)線分$AC$の長さは$\dfrac{\boxed{ケコ}}{\boxed{サ}}\sqrt{\boxed{シス}}$
$2025$年慶應義塾大学経済学部過去問題
福田の数学〜慶應義塾大学看護医療学部2025第4問〜放物線と接線の囲む面積と内積の最小値
単元：
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#点と直線#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{4}$
$k$を実数の定数とし、
座標平面上に$2$点$A(1,-3),B(-1,k)$をとる。
また、放物線$y=x^2$を$C$とする。
以下に答えなさい。
(1)点$A$から曲線$C$に引いた$2$本の接線のうち、
傾きが正の接線を$\ell_1$とし、
傾きが負の接線を$\ell_2$とするとき、
直線$\ell_1$の方程式は$y=\boxed{テ}$であり、
直線$\ell_2$の方程式は$y=\boxed{ト}$である。
また、$2$直線$\ell_1,\ell_2$のなす角を$\theta$とすると、
$\tan\theta=\boxed{ナ}$である。
ただし、$0\lt\theta\lt\dfrac{\pi}{2}$とする。
さらに、曲線$C$と$2$直線$\ell_1,\ell_2$で囲まれた
図形の面積は$\boxed{ニ}$である。
(2)点$P$が曲線$C$全体を動くときの
$\overrightarrow{PA}･\overrightarrow{PB}$の最小値を$m$とする。
このとき、$m$を$k$を用いて表すと、
$k\geqq \boxed{ヌ}$のときは$m=\boxed{ネ}$であり、
$k\lt \boxed{ヌ}$のときは、$m=\boxed{ノ}$である。
$2025$年慶應義塾大学看護医療学部過去問題
この動画を見る
$\boxed{4}$
$k$を実数の定数とし、
座標平面上に$2$点$A(1,-3),B(-1,k)$をとる。
また、放物線$y=x^2$を$C$とする。
以下に答えなさい。
(1)点$A$から曲線$C$に引いた$2$本の接線のうち、
傾きが正の接線を$\ell_1$とし、
傾きが負の接線を$\ell_2$とするとき、
直線$\ell_1$の方程式は$y=\boxed{テ}$であり、
直線$\ell_2$の方程式は$y=\boxed{ト}$である。
また、$2$直線$\ell_1,\ell_2$のなす角を$\theta$とすると、
$\tan\theta=\boxed{ナ}$である。
ただし、$0\lt\theta\lt\dfrac{\pi}{2}$とする。
さらに、曲線$C$と$2$直線$\ell_1,\ell_2$で囲まれた
図形の面積は$\boxed{ニ}$である。
(2)点$P$が曲線$C$全体を動くときの
$\overrightarrow{PA}･\overrightarrow{PB}$の最小値を$m$とする。
このとき、$m$を$k$を用いて表すと、
$k\geqq \boxed{ヌ}$のときは$m=\boxed{ネ}$であり、
$k\lt \boxed{ヌ}$のときは、$m=\boxed{ノ}$である。
$2025$年慶應義塾大学看護医療学部過去問題
福田のおもしろ数学485〜三角形の内部の点から下ろした垂線の長さと最小値
単元：
#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
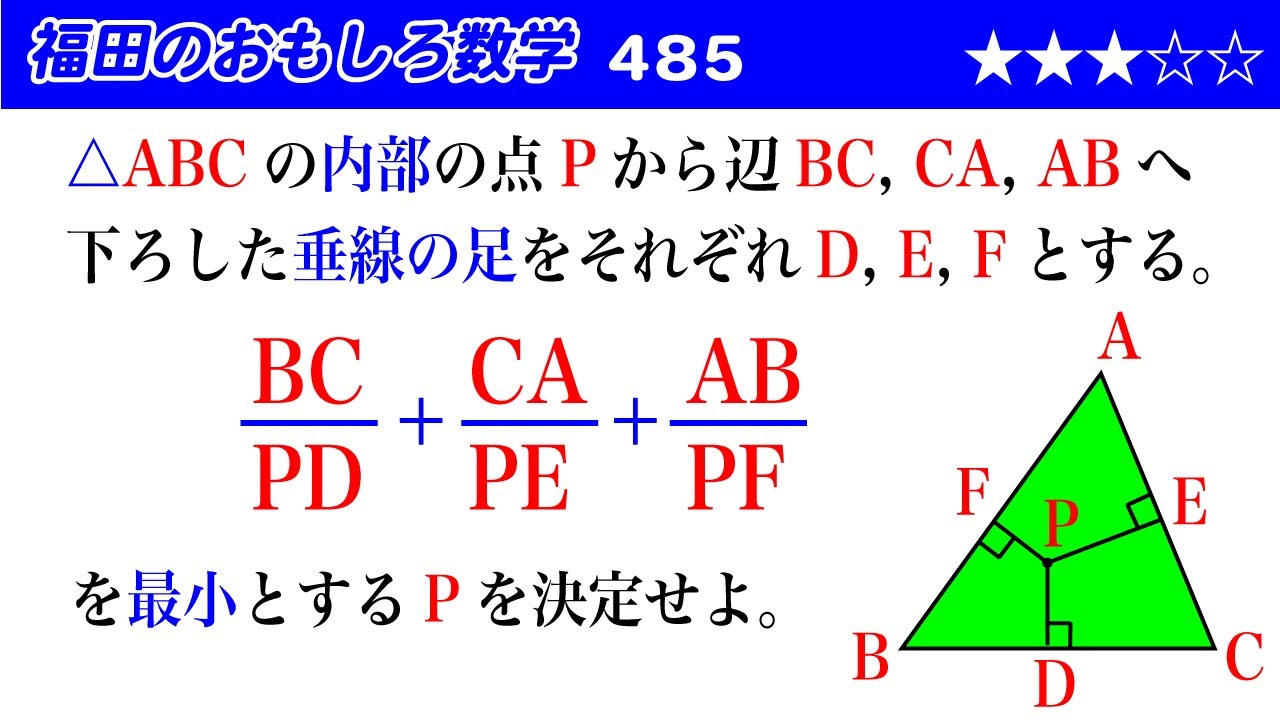
$\triangle ABC$の内部の点$P$から辺$BC,CA,AB$へ
下ろした垂線の足をそれぞれ$D,E,F$とする。
$\dfrac{BC}{PD}+\dfrac{CA}{PE}+\dfrac{AB}{PF}$
を最小とする$P$を決定せよ。
図は動画内参照
この動画を見る
$\triangle ABC$の内部の点$P$から辺$BC,CA,AB$へ
下ろした垂線の足をそれぞれ$D,E,F$とする。
$\dfrac{BC}{PD}+\dfrac{CA}{PE}+\dfrac{AB}{PF}$
を最小とする$P$を決定せよ。
図は動画内参照
福田のおもしろ数学483〜直角に曲がった廊下を曲がれる棒の長さの最大値
単元：
#数Ⅰ#数A#図形の性質#図形と計量#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
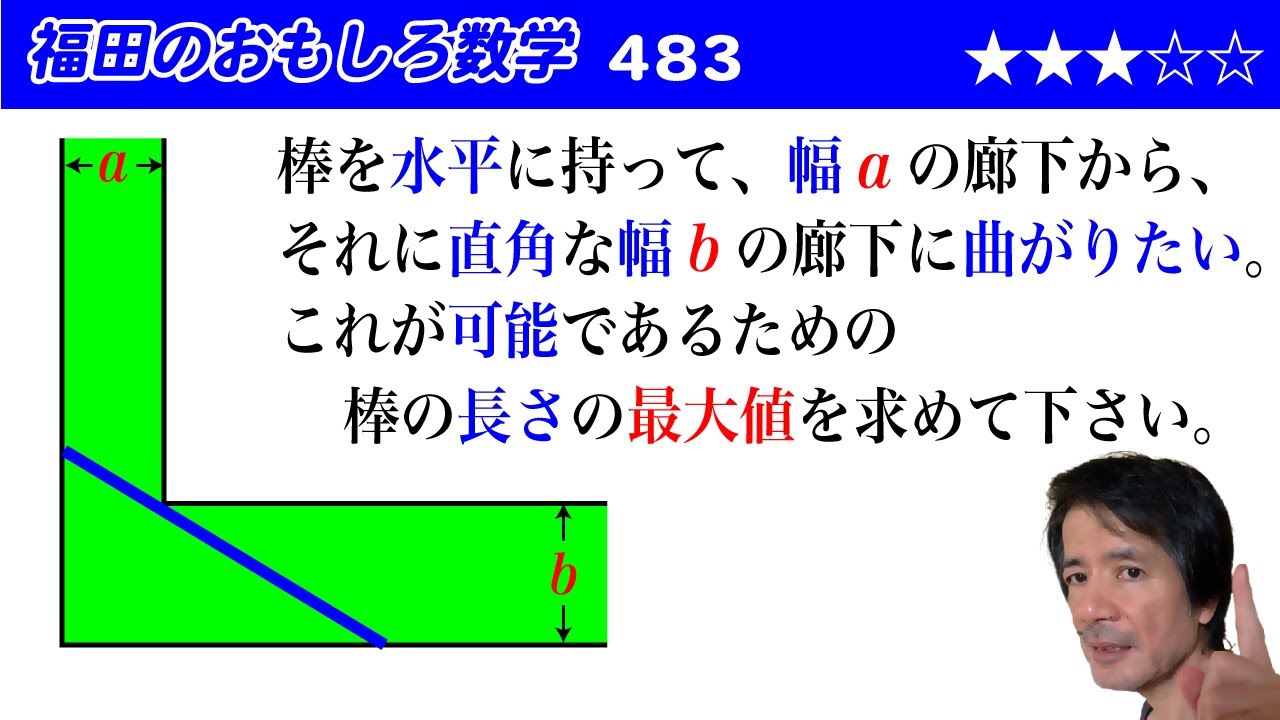
棒を水平に持って、幅$a$の廊下から、
それに直角な幅$b$の廊下に曲がりたい。
これが可能であるための
棒の長さの最大値を求めて下さい。
図は動画内参照
この動画を見る
棒を水平に持って、幅$a$の廊下から、
それに直角な幅$b$の廊下に曲がりたい。
これが可能であるための
棒の長さの最大値を求めて下さい。
図は動画内参照
福田の数学〜早稲田大学理工学部2025第4問〜4つの互いに外接する球面の中心が作る四面体の体積
単元：
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#体積・表面積・回転体・水量・変化のグラフ#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{4}$
空間内に原点$O$を中心とする半径$r$の球面$S$がある。
さらに、半径が$1,2,3$の球面$S_1,S_2,S_3$があり、
これら$4$つの球面のうち
どの$2$つの球面も互いに外接している。
$S_1,S_2,S_3$中心を順に$P_1,P_2,P_3$とし、
$O,P_1,P_2,P_3$は同一平面上にないとする。
さらに、球面$S$が球面$S_1,S_2,S_3$と
接する$3$つの点と、
$\overrightarrow{OQ}=\dfrac{1}{4}(\overrightarrow{OP_1}+\overrightarrow{OP_2}+\overrightarrow{OP_3})$
により定まる点$Q$は、同一平面上にあるとする。
次の問いに答えよ。
(1)$r$の値を求めよ。
(2)四面体$OP_1P_2P_3$の体積を求めよ。
$2025$年早稲田大学理工学部過去問題
この動画を見る
$\boxed{4}$
空間内に原点$O$を中心とする半径$r$の球面$S$がある。
さらに、半径が$1,2,3$の球面$S_1,S_2,S_3$があり、
これら$4$つの球面のうち
どの$2$つの球面も互いに外接している。
$S_1,S_2,S_3$中心を順に$P_1,P_2,P_3$とし、
$O,P_1,P_2,P_3$は同一平面上にないとする。
さらに、球面$S$が球面$S_1,S_2,S_3$と
接する$3$つの点と、
$\overrightarrow{OQ}=\dfrac{1}{4}(\overrightarrow{OP_1}+\overrightarrow{OP_2}+\overrightarrow{OP_3})$
により定まる点$Q$は、同一平面上にあるとする。
次の問いに答えよ。
(1)$r$の値を求めよ。
(2)四面体$OP_1P_2P_3$の体積を求めよ。
$2025$年早稲田大学理工学部過去問題
福田の数学〜慶應義塾大学薬学部2025第1問(2)〜正八面体に内接する立方体の体積
単元：
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#立体図形#立体切断#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(2)$a$は$a\gt 0$を満たす実数とする。
$xyz$空間に$6$点$(a,0,0),(0,a,0),(0,0,a),$
$(-a,0,0)(0,-a,0)(0,0,-a)$を頂点とする多面体
$S$がある。
(i)$S$の体積は$\boxed{オ}$である。
(ii)立方体$U$のすべての頂点が$S$の辺上にあるとき、
$U$の体積は$\boxed{カ}$である。
$2025$年慶應義塾大学薬学部過去問題
この動画を見る
$\boxed{1}$
(2)$a$は$a\gt 0$を満たす実数とする。
$xyz$空間に$6$点$(a,0,0),(0,a,0),(0,0,a),$
$(-a,0,0)(0,-a,0)(0,0,-a)$を頂点とする多面体
$S$がある。
(i)$S$の体積は$\boxed{オ}$である。
(ii)立方体$U$のすべての頂点が$S$の辺上にあるとき、
$U$の体積は$\boxed{カ}$である。
$2025$年慶應義塾大学薬学部過去問題
福田の数学〜北海道大学2025理系第2問〜円に引いた2本の接線でできる四角形の面積の最大最小
単元：
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
円$C_1:x^2+y^2=1$を考える。
実数$p,q$が$p^2+q^2 \gt 1$を満たすとき、
点$p(p,q)$から$C_1$に引いた$2$本の接線$\ell_1,\ell_2$の
接点をそれぞれ$Q_1(x_1,y_1), Q_2(x_2,y_2)$とする。
また、座標平面上の原点を$O(0,0)$とする。
(1)直線$\ell_1,\ell_2$,線分$OQ_1,OQ_2$で囲まれた
四角形の面積$S$を$p,q$を用いて表せ。
(2)点$P$が楕円
$C_2:\dfrac{x^2}{2}+\dfrac{y^2}{3}=1$
の上を動くとき、
(1)の四角形の面積$S$の最大値と最小値を求めよ。
$2025$年北海道大学理系過去問題
この動画を見る
$\boxed{2}$
円$C_1:x^2+y^2=1$を考える。
実数$p,q$が$p^2+q^2 \gt 1$を満たすとき、
点$p(p,q)$から$C_1$に引いた$2$本の接線$\ell_1,\ell_2$の
接点をそれぞれ$Q_1(x_1,y_1), Q_2(x_2,y_2)$とする。
また、座標平面上の原点を$O(0,0)$とする。
(1)直線$\ell_1,\ell_2$,線分$OQ_1,OQ_2$で囲まれた
四角形の面積$S$を$p,q$を用いて表せ。
(2)点$P$が楕円
$C_2:\dfrac{x^2}{2}+\dfrac{y^2}{3}=1$
の上を動くとき、
(1)の四角形の面積$S$の最大値と最小値を求めよ。
$2025$年北海道大学理系過去問題
福田のおもしろ数学440〜正五角形10個でできる図形の内接円と外接円の面積の関係
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
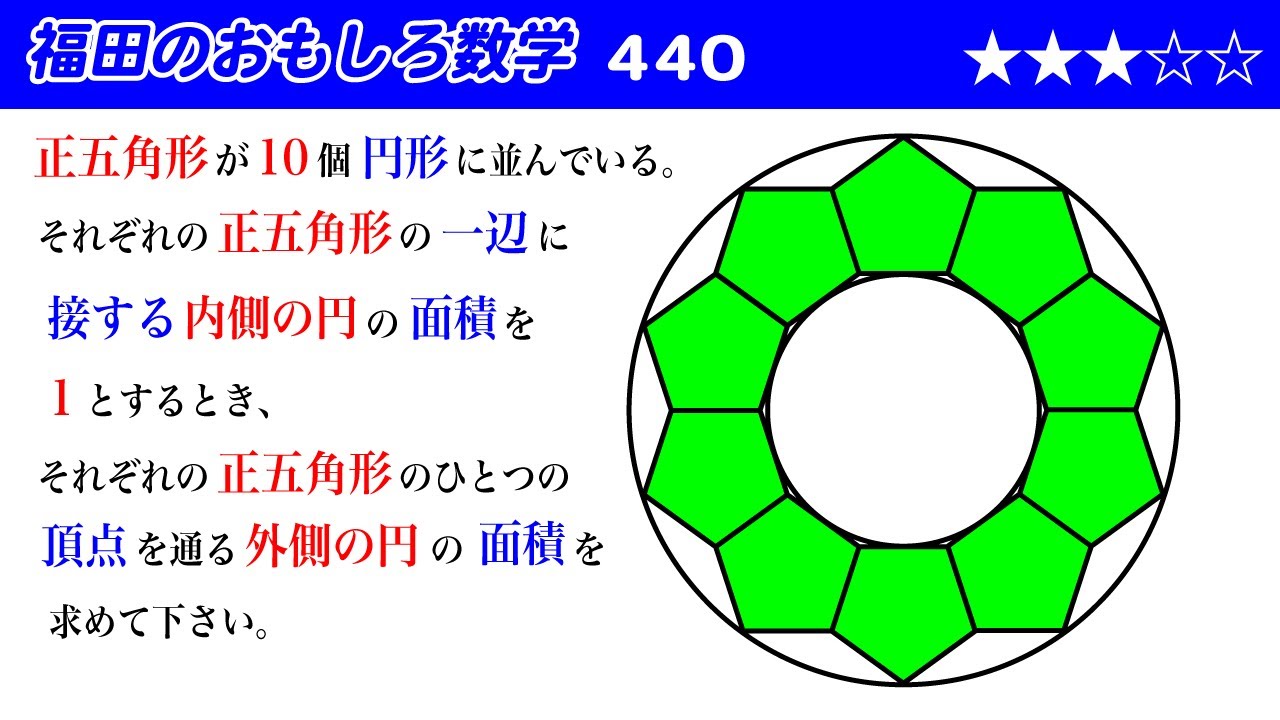
正五角形が$10$個円形に並んでいる。
それぞれの正五角形に一辺に
接する内側の円の面積を$1$とするとき、
それぞれの正五角形のひとつの
頂点を通る外側の円の面積を求めて下さい。
図は動画内参照
この動画を見る
正五角形が$10$個円形に並んでいる。
それぞれの正五角形に一辺に
接する内側の円の面積を$1$とするとき、
それぞれの正五角形のひとつの
頂点を通る外側の円の面積を求めて下さい。
図は動画内参照
福田のおもしろ数学435〜正三角形の内部の点の位置から面積を求める
単元：
#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
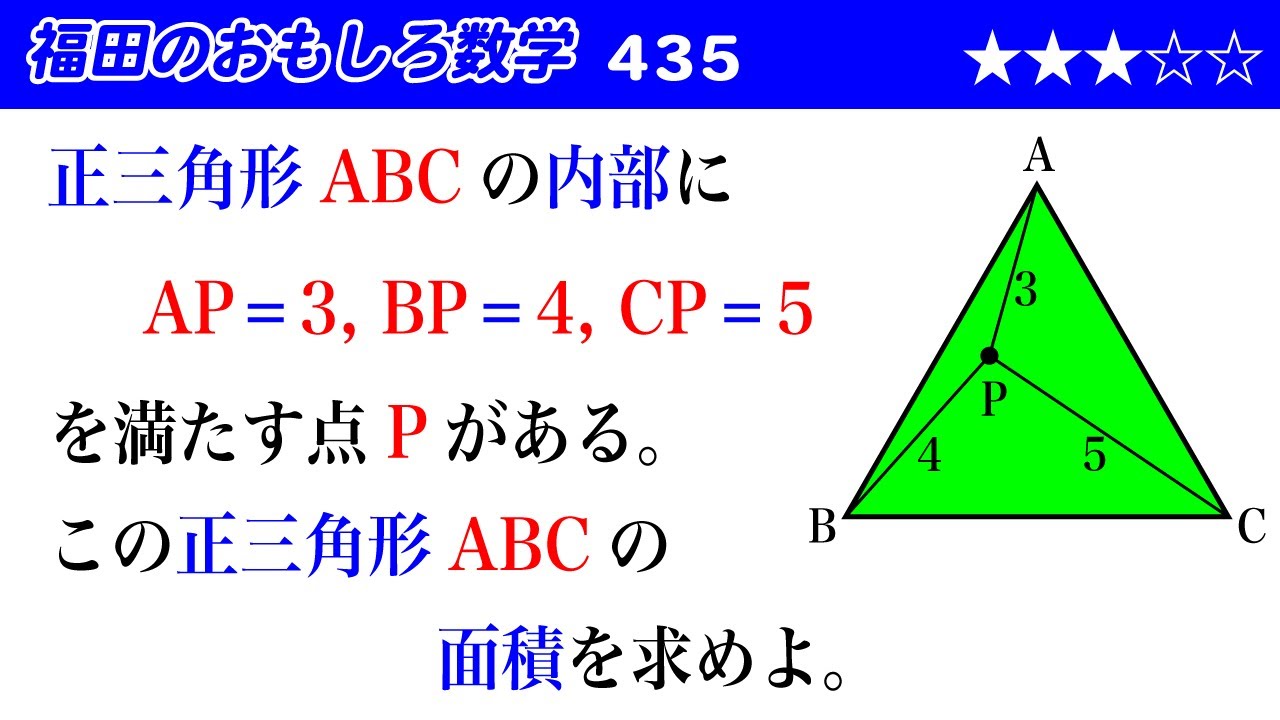
正三角形$ABC$の内部に
$AP=3,BP=4,CP=5$を満たす点$P$がある。
この正三角形$ABC$の面積を求めよ。
図は動画内参照
この動画を見る
正三角形$ABC$の内部に
$AP=3,BP=4,CP=5$を満たす点$P$がある。
この正三角形$ABC$の面積を求めよ。
図は動画内参照
福田のおもしろ数学433〜四面体に関する計量問題
単元：
#数A#図形の性質#空間における垂直と平行と多面体（オイラーの法則）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
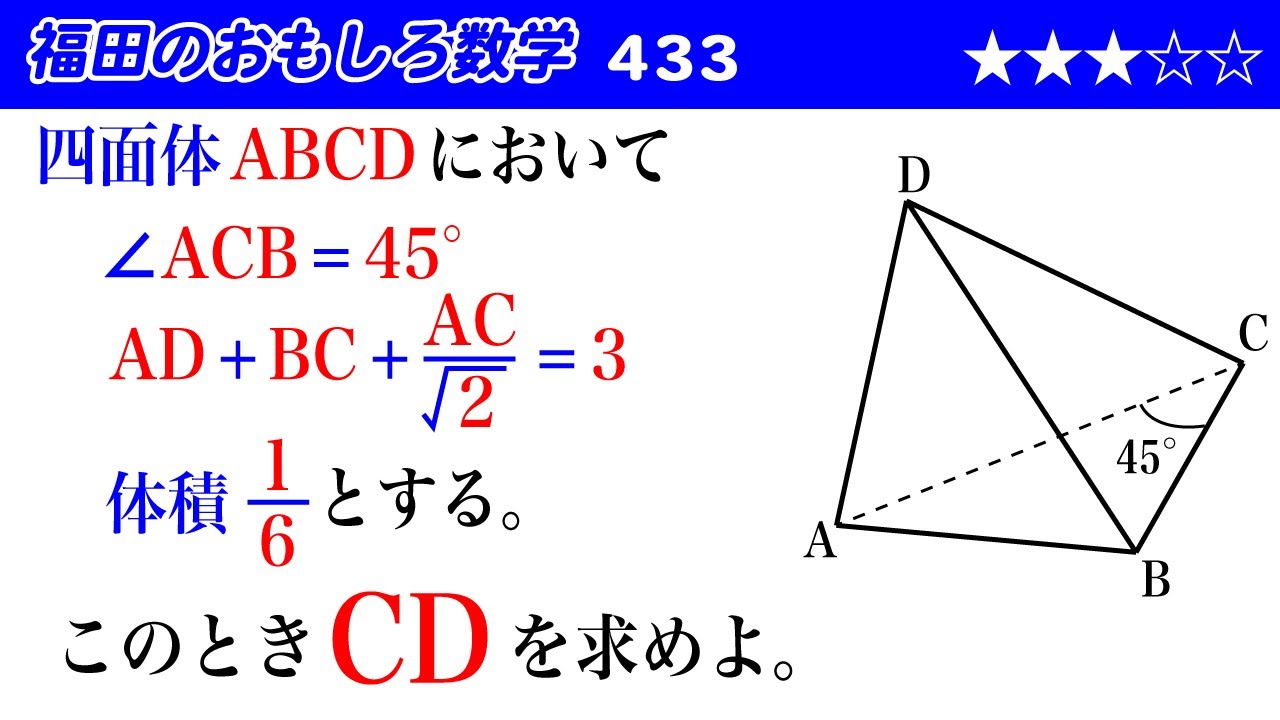
四面体$ABCD$において
$\angle ACB=45°$
$AD+BC+\dfrac{AC}{\sqrt2}=3$
体積$\dfrac{1}{6}$とする。
このとき$CD$を求めよ。
図は動画内参照
この動画を見る
四面体$ABCD$において
$\angle ACB=45°$
$AD+BC+\dfrac{AC}{\sqrt2}=3$
体積$\dfrac{1}{6}$とする。
このとき$CD$を求めよ。
図は動画内参照
【数A】【図形の性質】空間図形の応用3 ※問題文は概要欄
単元：
#数A#図形の性質#方べきの定理と２つの円の関係#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形の性質#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
立方体の各面の対角線の交点を頂点とし、
隣り合った面どうしの頂点を結ぶことによって、
立方体の中に正八面体ができる。
このとき、次の場合について、
正八面体の体積を求めよ。
(1) 立方体の1辺の長さが 10
(2) 正八面体の1辺の長さが6
一辺の長さが５の正八角形について、
次のものを求めよ。
(1) 正八角形の体積V
(2) 正八角形に内接する球の半径ｒ
この動画を見る
立方体の各面の対角線の交点を頂点とし、
隣り合った面どうしの頂点を結ぶことによって、
立方体の中に正八面体ができる。
このとき、次の場合について、
正八面体の体積を求めよ。
(1) 立方体の1辺の長さが 10
(2) 正八面体の1辺の長さが6
一辺の長さが５の正八角形について、
次のものを求めよ。
(1) 正八角形の体積V
(2) 正八角形に内接する球の半径ｒ
【数A】【図形の性質】空間図形の応用2 ※問題文は概要欄
単元：
#数A#図形の性質#方べきの定理と２つの円の関係#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形の性質#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
四面体ABCD において，辺AB と辺CDが垂直ならば，頂点Aから平面BCDに下ろした垂線AHと，頂点Bから平面CDAに下ろした垂線BKは交わることを示せ。ただし，HとB，KとAはそれぞれ一致しないものとする。
直方体 ABCD-EFGHにおいて，
辺AB，AD，AEの長さをそれぞれa，b，cとする。
また，頂点Aから直線FHに下ろした垂線をAK とする。
このとき，次の問いに答えよ。
(1) EK⊥FHであることを証明せよ。
(2) 垂線AKの長さを求めよ。
この動画を見る
四面体ABCD において，辺AB と辺CDが垂直ならば，頂点Aから平面BCDに下ろした垂線AHと，頂点Bから平面CDAに下ろした垂線BKは交わることを示せ。ただし，HとB，KとAはそれぞれ一致しないものとする。
直方体 ABCD-EFGHにおいて，
辺AB，AD，AEの長さをそれぞれa，b，cとする。
また，頂点Aから直線FHに下ろした垂線をAK とする。
このとき，次の問いに答えよ。
(1) EK⊥FHであることを証明せよ。
(2) 垂線AKの長さを求めよ。
【数A】【図形の性質】空間図形の応用1 ※問題文は概要欄
単元：
#数A#図形の性質#方べきの定理と２つの円の関係#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形の性質#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
空間内の異なる2つの直線ℓ 、m と異なる2つの平面α,βについて，
次の記述は常に正しいか。
(1) ℓ⊥α、ｍ⊥αならば、ℓ⊥ｍである。
(2) ℓ⊥α、ｍ⊥αならば、α//βである。
(3) ℓ//α、ｍ//αならば、ℓ//ｍである。
(4) ℓ//α、ｍ⊥αならば、ℓと並行でｍと垂直な直線がある。
正六角柱を底面に
平行でない1つの平面で切ったものである。
六角形ABCDEF について，
辺AB と平行な辺を答えよ。
立方体について、次の問いに答えよ。
(1) 辺BF と垂直な面をすべて答えよ。
(2) 平面 BFHD と平行な辺をすべて答えよ。
(3) この立方体に，平行な位置関係にある面は何組あるか。
(4) 平面ABGHと垂直な面をすべて答えよ。
この動画を見る
空間内の異なる2つの直線ℓ 、m と異なる2つの平面α,βについて，
次の記述は常に正しいか。
(1) ℓ⊥α、ｍ⊥αならば、ℓ⊥ｍである。
(2) ℓ⊥α、ｍ⊥αならば、α//βである。
(3) ℓ//α、ｍ//αならば、ℓ//ｍである。
(4) ℓ//α、ｍ⊥αならば、ℓと並行でｍと垂直な直線がある。
正六角柱を底面に
平行でない1つの平面で切ったものである。
六角形ABCDEF について，
辺AB と平行な辺を答えよ。
立方体について、次の問いに答えよ。
(1) 辺BF と垂直な面をすべて答えよ。
(2) 平面 BFHD と平行な辺をすべて答えよ。
(3) この立方体に，平行な位置関係にある面は何組あるか。
(4) 平面ABGHと垂直な面をすべて答えよ。
【数A】【図形の性質】作図の応用 ※問題文は概要欄
単元：
#数A#図形の性質#方べきの定理と２つの円の関係#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形の性質#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
線分ABが与えられたとき, 線分ABを斜辺とし, ∠BAC=60° である直角三角形ABC を作図せよ。
右の図のような円があり,その周上に点Aがある。
Aを頂点の1つとし、他の5つの頂点がいずれもこの円周上にあるような正六角形を作図せよ。
右の図のように,直線と円Oおよびその中心が与えられている。
直線lに平行な円Oの接線を作図せよ。
この動画を見る
線分ABが与えられたとき, 線分ABを斜辺とし, ∠BAC=60° である直角三角形ABC を作図せよ。
右の図のような円があり,その周上に点Aがある。
Aを頂点の1つとし、他の5つの頂点がいずれもこの円周上にあるような正六角形を作図せよ。
右の図のように,直線と円Oおよびその中心が与えられている。
直線lに平行な円Oの接線を作図せよ。
【数A】【図形の性質】円の位置関係 ※問題文は概要欄
単元：
#数A#図形の性質#方べきの定理と２つの円の関係#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形の性質#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
図のように，数直線上の原点を中心とする半径3の円Oと、
この数直線上を動く点Pを中心とする半径2の円Pがある。
Pの座標をtとするとき,次の件を満たすとの値,またはtの値の範囲を求めよ。
(1) 2円O，Pの共通接線が4本引ける。
(2) 2円O，Pの共有点が1個である。
(3) 2円O，Pの共通接線が、座標が6である数直線上の点Aを通る。
図のように，半径3の外接する2円A, B
が、半径8の円Oに内接している。2円A, B
に外接し，円Oに内接する円Cの半径を求めよ。
この動画を見る
図のように，数直線上の原点を中心とする半径3の円Oと、
この数直線上を動く点Pを中心とする半径2の円Pがある。
Pの座標をtとするとき,次の件を満たすとの値,またはtの値の範囲を求めよ。
(1) 2円O，Pの共通接線が4本引ける。
(2) 2円O，Pの共有点が1個である。
(3) 2円O，Pの共通接線が、座標が6である数直線上の点Aを通る。
図のように，半径3の外接する2円A, B
が、半径8の円Oに内接している。2円A, B
に外接し，円Oに内接する円Cの半径を求めよ。
福田のおもしろ数学424〜直角二等辺三角形の斜辺を1：2：√3に内分する点がAと作る角が45°になる証明
単元：
#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
直角二等辺三角形$ABC$で
斜辺$BC$を$1:2:\sqrt3$に
分ける点を順に$D,E$とする。
$\angle DAE=45°$
であることを証明せよ。
図は動画内参照
この動画を見る
直角二等辺三角形$ABC$で
斜辺$BC$を$1:2:\sqrt3$に
分ける点を順に$D,E$とする。
$\angle DAE=45°$
であることを証明せよ。
図は動画内参照
【数A】【図形の性質】円に内接する図形 ※問題文は概要欄
単元：
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形の性質#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
円oにおいて、平行な2つの弦をAA´、BB´とし、AB´とA´Bが円の内部の点Pで交わっている。このとき、∠APB＝∠AOBであることを証明せよ。
鋭角三角形ABCの垂心をHとし、AHがBCと交わる点をD、△ABCの外接円と交わる点をEとする。このとき、Dは線分HEの中点であることを証明せよ。
下の図において、角θを求めよ。
この動画を見る
円oにおいて、平行な2つの弦をAA´、BB´とし、AB´とA´Bが円の内部の点Pで交わっている。このとき、∠APB＝∠AOBであることを証明せよ。
鋭角三角形ABCの垂心をHとし、AHがBCと交わる点をD、△ABCの外接円と交わる点をEとする。このとき、Dは線分HEの中点であることを証明せよ。
下の図において、角θを求めよ。
【数A】【図形の性質】三角形の関係証明 ※問題文は概要欄
単元：
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形の性質#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
△ABCの内部の1点をPとするとき、AP＋BP＋CP＞1/2（AB＋BC＋CA）を証明せよ。
上の図において、点Pが線分CD上を動くとき、線分の和AP＋PBの最小値とそのときの点Pの位置を求めよ。
この動画を見る
△ABCの内部の1点をPとするとき、AP＋BP＋CP＞1/2（AB＋BC＋CA）を証明せよ。
上の図において、点Pが線分CD上を動くとき、線分の和AP＋PBの最小値とそのときの点Pの位置を求めよ。
【数A】【図形の性質】三角形の辺と角 ※問題文は概要欄
単元：
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形の性質#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
∠B＝90度の直角三角形ABCの辺BC上に頂点と異なる点Pを取る時、AB＜AP＜ACであることを証明せよ。
△ABCにおいて、AB＞ACとする。∠Aの二等分線と辺BCの交点をPとする時、次の①～④のうちで常に成り立つものを全て選べ。
①BP＝PC ②AB＞AP ③AC＞AP ④AC＞CP
次の長さの線分を3辺とする三角形が存在するようなXの値の範囲を求めよ。
(1)X、２、６ (2)３X、X＋４、X＋２
この動画を見る
∠B＝90度の直角三角形ABCの辺BC上に頂点と異なる点Pを取る時、AB＜AP＜ACであることを証明せよ。
△ABCにおいて、AB＞ACとする。∠Aの二等分線と辺BCの交点をPとする時、次の①～④のうちで常に成り立つものを全て選べ。
①BP＝PC ②AB＞AP ③AC＞AP ④AC＞CP
次の長さの線分を3辺とする三角形が存在するようなXの値の範囲を求めよ。
(1)X、２、６ (2)３X、X＋４、X＋２