図形の性質
図形の性質
【高校数学】 数Ａ－５２ 方べきの定理②
単元：
#数A#図形の性質#方べきの定理と２つの円の関係#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①半径上の円に内接する四角形$ABCD$において,
辺$BC$がこの円の直径である.
対角線$AC$と$BD$の交点を$E$とし,$E$から$BC$に垂線$EF$を下ろす.
$BF:FC=m: n$とするとき,$BE･BD$を$r,m,n$を用いて表そう.
図は動画内参照
この動画を見る
①半径上の円に内接する四角形$ABCD$において,
辺$BC$がこの円の直径である.
対角線$AC$と$BD$の交点を$E$とし,$E$から$BC$に垂線$EF$を下ろす.
$BF:FC=m: n$とするとき,$BE･BD$を$r,m,n$を用いて表そう.
図は動画内参照
【高校数学】 数A－５１ 方べきの定理①
単元：
#数A#図形の性質#方べきの定理と２つの円の関係#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
点Pを通る2直線が,円$O$とそれそれ 2点$A,B$と
2点$C,D$で交わるとき,$①=①$が成り立つ.
点$P$を通る2直線の一方が,
円$O$と2点$A,B$で交わり,もう一方が点$T$で接するとき,
$②=②$が成り立つ.
下の図で$x$を求めよう.
ただし,$T$は接点とする.
③
④
図は動画内参照
この動画を見る
点Pを通る2直線が,円$O$とそれそれ 2点$A,B$と
2点$C,D$で交わるとき,$①=①$が成り立つ.
点$P$を通る2直線の一方が,
円$O$と2点$A,B$で交わり,もう一方が点$T$で接するとき,
$②=②$が成り立つ.
下の図で$x$を求めよう.
ただし,$T$は接点とする.
③
④
図は動画内参照
【高校数学】 数A－５０ 接弦定理
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
下の図において,$\angle x,\angle y$を求めよう.
ただし,直線$\ell,m$は円の接線とする.
①
②
③
④
図は動画内参照
この動画を見る
下の図において,$\angle x,\angle y$を求めよう.
ただし,直線$\ell,m$は円の接線とする.
①
②
③
④
図は動画内参照
【高校数学】 数A－４９ トレミーの定理
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
円に内接する四角形$ABCD$について
$AC･BD=①$である.
②$\triangle ABC$の外接円と$\angle BAC$の
二等分線との交点を$M$とするとき,
$MA=MB+MC$ならば,$AB+AC=2BC$であることを,
トレミーの定理を用いて証明しよう.
図は動画内参照
この動画を見る
円に内接する四角形$ABCD$について
$AC･BD=①$である.
②$\triangle ABC$の外接円と$\angle BAC$の
二等分線との交点を$M$とするとき,
$MA=MB+MC$ならば,$AB+AC=2BC$であることを,
トレミーの定理を用いて証明しよう.
図は動画内参照
【高校数学】 数A－４８ 円に内接する四角形②
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$\triangle ABC$の頂点$A$から,辺$BC$に垂線$AD$を引き,
点$D$から辺$AB,AC$にそれぞれ垂線$DE,DF$を引くと,
4点$E,B,C,F$は同一円周上にあることを証明しよう.
図は動画内参照
この動画を見る
①$\triangle ABC$の頂点$A$から,辺$BC$に垂線$AD$を引き,
点$D$から辺$AB,AC$にそれぞれ垂線$DE,DF$を引くと,
4点$E,B,C,F$は同一円周上にあることを証明しよう.
図は動画内参照
【高校数学】 数A－４７ 円に内接する四角形①
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
下の図で$\angle x$の大きさを求めよう.
①
②
③次の四角形$ABCD$のうち,円に内接するものはどれか.
$\boxed{I}$
$\boxed{II}$
$\boxed{III}$
図は動画内参照
この動画を見る
下の図で$\angle x$の大きさを求めよう.
①
②
③次の四角形$ABCD$のうち,円に内接するものはどれか.
$\boxed{I}$
$\boxed{II}$
$\boxed{III}$
図は動画内参照
【高校数学】 数A－４６ 円周角の定理②
単元：
#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①右の図で,$L,M,N$はそれぞれ,円に内接する四角形$ABCD$の
辺$AB,BCAD$の中点である.
また,直線$ML$と直線$DA$の交点を$P$,
直線$NL$と直線$CB$の交点を$Q$とする.
このとき,4点$M,N, P,Q$は1つの円周上にあることを証明しよう.
図は動画内参照
この動画を見る
①右の図で,$L,M,N$はそれぞれ,円に内接する四角形$ABCD$の
辺$AB,BCAD$の中点である.
また,直線$ML$と直線$DA$の交点を$P$,
直線$NL$と直線$CB$の交点を$Q$とする.
このとき,4点$M,N, P,Q$は1つの円周上にあることを証明しよう.
図は動画内参照
【高校数学】 数A－４５ 円周角の定理①
単元：
#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
下の図について,$\angle x$の大きさを求めよう.
①
②
③
④
⑤
⑥
図は動画内参照
この動画を見る
下の図について,$\angle x$の大きさを求めよう.
①
②
③
④
⑤
⑥
図は動画内参照
【高校数学】 数A－４４ 三角形の辺と角の大小関係
単元：
#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
問題1
3辺の長さが次のような三角形は存在するかどうか調べよう.
①$2,3,6$
②$3,4,6$
③$5,7,12$
問題2
次のような三角形$ABC$について,
3つの角$\angle A,\angle B,\angle C$の大小を調べよう.
④$a=7,b=4,c=5$
⑤$a=3,b=5,c=3$
⑥$\angle A=90°,a=4,c=2$
問題3
$\triangle ABC$において,それぞれの長さが次の場合のとき,
$x$のとる値の範囲を求めよう.
⑦$a=6,b=8,c=x$
⑧$a=5,b=x,c=9$
この動画を見る
問題1
3辺の長さが次のような三角形は存在するかどうか調べよう.
①$2,3,6$
②$3,4,6$
③$5,7,12$
問題2
次のような三角形$ABC$について,
3つの角$\angle A,\angle B,\angle C$の大小を調べよう.
④$a=7,b=4,c=5$
⑤$a=3,b=5,c=3$
⑥$\angle A=90°,a=4,c=2$
問題3
$\triangle ABC$において,それぞれの長さが次の場合のとき,
$x$のとる値の範囲を求めよう.
⑦$a=6,b=8,c=x$
⑧$a=5,b=x,c=9$
【高校数学】 数A－４３ メネラウスの定理②
単元：
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図の$\triangle ABC$において,
$AM:MB=2:5,AN:NC=4:3$,$BN$と$CM$との交点を$P$,
$AP$の延長と$BC$との交点を$Q$とする.
①$BP:PN$を求めよう.
②$BQ:QC$を求めよう.
図は動画内参照
この動画を見る
右の図の$\triangle ABC$において,
$AM:MB=2:5,AN:NC=4:3$,$BN$と$CM$との交点を$P$,
$AP$の延長と$BC$との交点を$Q$とする.
①$BP:PN$を求めよう.
②$BQ:QC$を求めよう.
図は動画内参照
【高校数学】 数A－４２ メネラウスの定理①
単元：
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
ある直線が$\triangle ABC$の辺$BC,CA,AB,$またはその延長と,
それぞれ点$P,Q,R$で交わるとき,$①=1$である.
下の図において,$x$を求めよう.
②
③
図は動画内参照
この動画を見る
ある直線が$\triangle ABC$の辺$BC,CA,AB,$またはその延長と,
それぞれ点$P,Q,R$で交わるとき,$①=1$である.
下の図において,$x$を求めよう.
②
③
図は動画内参照
【高校数学】 数A－４１ チェバの定理②
単元：
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
次の図において,$AR:RB$を求めよう.
①
②
図は動画内参照
この動画を見る
次の図において,$AR:RB$を求めよう.
①
②
図は動画内参照
【高校数学】 数A－４０ チェバの定理①
単元：
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
$\triangle ABC$の辺$BC,CA,AB$上にそれぞれ点$P,Q,R$があり,
3直線$AP,BQ,CR$が1点で交わるとき,
$①=1$である.
下の図において,$x$を求めよう.
②
③
図は動画内参照
この動画を見る
$\triangle ABC$の辺$BC,CA,AB$上にそれぞれ点$P,Q,R$があり,
3直線$AP,BQ,CR$が1点で交わるとき,
$①=1$である.
下の図において,$x$を求めよう.
②
③
図は動画内参照
【高校数学】 数A－３９ 傍心と傍接円
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と２つの円の関係#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
三角形の1つの①の①と,他の2つの頂点における
②の②は1点で交わる.この点を傍心という.
③$\triangle ABC$の頂点$A$における内角の二等分線と直線$B,C$
それぞれにおける外角の二等分線は1点で交わることを証明しよう.
図は動画内参照
この動画を見る
三角形の1つの①の①と,他の2つの頂点における
②の②は1点で交わる.この点を傍心という.
③$\triangle ABC$の頂点$A$における内角の二等分線と直線$B,C$
それぞれにおける外角の二等分線は1点で交わることを証明しよう.
図は動画内参照
【高校数学】 数A－３８ 三角形の内心・外心・重心・垂心④
単元：
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$\triangle ABC$の内心を$I$とし,
直線$AI$と辺$BC$の交点を$D$とする.
$AB=6,BC=%,CA=3$であるとき,$AI:ID$を求めよう.
②平行四辺形$ABCD$において,
辺$BC$の中点を$M$とし,
$AM$と$BD$の交点を$E$とする.
このとき,$\triangle BME$の面積と平行四辺形$ABCD$の
面積の比を求めよう.
図は動画内参照
この動画を見る
①$\triangle ABC$の内心を$I$とし,
直線$AI$と辺$BC$の交点を$D$とする.
$AB=6,BC=%,CA=3$であるとき,$AI:ID$を求めよう.
②平行四辺形$ABCD$において,
辺$BC$の中点を$M$とし,
$AM$と$BD$の交点を$E$とする.
このとき,$\triangle BME$の面積と平行四辺形$ABCD$の
面積の比を求めよう.
図は動画内参照
【高校数学】 数A－３７ 三角形の内心・外心・重心・垂心③
単元：
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$\triangle ABC$の$\angle A$の二等分線と
対辺$BC$との交点を$D$とすると,
$AB:AC=BD:DC$が成り立つことを証明しよう.
②平行四辺形$ABCD$において,辺$BC$の中点を$M$とし,
$AM$と$BD$の交点を$P$とする.
このとき,点$P$は$\triangle ABC$の重心であることを証明しよう.
図は動画内参照
この動画を見る
①$\triangle ABC$の$\angle A$の二等分線と
対辺$BC$との交点を$D$とすると,
$AB:AC=BD:DC$が成り立つことを証明しよう.
②平行四辺形$ABCD$において,辺$BC$の中点を$M$とし,
$AM$と$BD$の交点を$P$とする.
このとき,点$P$は$\triangle ABC$の重心であることを証明しよう.
図は動画内参照
【高校数学】 数A－３６ 三角形の内心・外心・重心・垂心②
単元：
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
点$I$を$\triangle ABC$の内心,点$O$を$\triangle ABC$の外心とするとき,
角$x,y$を求めよう.
①
②
③
④
図は動画内参照
この動画を見る
点$I$を$\triangle ABC$の内心,点$O$を$\triangle ABC$の外心とするとき,
角$x,y$を求めよう.
①
②
③
④
図は動画内参照
【高校数学】 数A－３５ 三角形の内心・外心・重心・垂心①
単元：
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
三角形の3つの①の①は1点で交わる.
(この点$I$を中心として,3辺に接する円をかくことができ,
この円を②といい,中心$I$を三角形に内心という.)
三角形の3つの③の③は1点で交わる.
(この点$O$を中心として,3つの頂点を通る円をかくことができ,
この円を④といい,中心$O$を三角形の外心という.)
三角形の3本の⑤は1点で交わる.
(その交点は,それぞれの⑤を⑥に内分する.)
図は動画内参照
この動画を見る
三角形の3つの①の①は1点で交わる.
(この点$I$を中心として,3辺に接する円をかくことができ,
この円を②といい,中心$I$を三角形に内心という.)
三角形の3つの③の③は1点で交わる.
(この点$O$を中心として,3つの頂点を通る円をかくことができ,
この円を④といい,中心$O$を三角形の外心という.)
三角形の3本の⑤は1点で交わる.
(その交点は,それぞれの⑤を⑥に内分する.)
図は動画内参照
【高校数学】 数A－３４ 内分と外分②
単元：
#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
$△ABC$の$\angle A$の二等分線と辺$BC$の交点を$P$とする.
→$AB:AC=①$
$△ABC(AB\neq AC)$の$\angle A$の外角の二等分線と
辺BCの延長との交点を$Q$とする.
→$AB:AC=②$
$AB=8,BC=6,CA=4$である$△ABC$において,
$\angle A$および外角の二等分線と,
直線$BC$との交点をそれぞれ$D,E$とする.
③線分$BD$の長さを求めよう.
④線分$BE$の長さを求めよう.
図は動画内参照
この動画を見る
$△ABC$の$\angle A$の二等分線と辺$BC$の交点を$P$とする.
→$AB:AC=①$
$△ABC(AB\neq AC)$の$\angle A$の外角の二等分線と
辺BCの延長との交点を$Q$とする.
→$AB:AC=②$
$AB=8,BC=6,CA=4$である$△ABC$において,
$\angle A$および外角の二等分線と,
直線$BC$との交点をそれぞれ$D,E$とする.
③線分$BD$の長さを求めよう.
④線分$BE$の長さを求めよう.
図は動画内参照
【高校数学】 数A－３３ 内分・外分①
単元：
#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
線分$AB$において,次の点を記入しよう.
①$3:1$に内分する点$P$
②$1:2$に内分する点$Q$
③$3:1$に外分する点$R$
④$1:4$に外分する点$S$
図は動画内参照
この動画を見る
線分$AB$において,次の点を記入しよう.
①$3:1$に内分する点$P$
②$1:2$に内分する点$Q$
③$3:1$に外分する点$R$
④$1:4$に外分する点$S$
図は動画内参照
【高校数学】 数Ⅰ－１００ 立体に内接する球
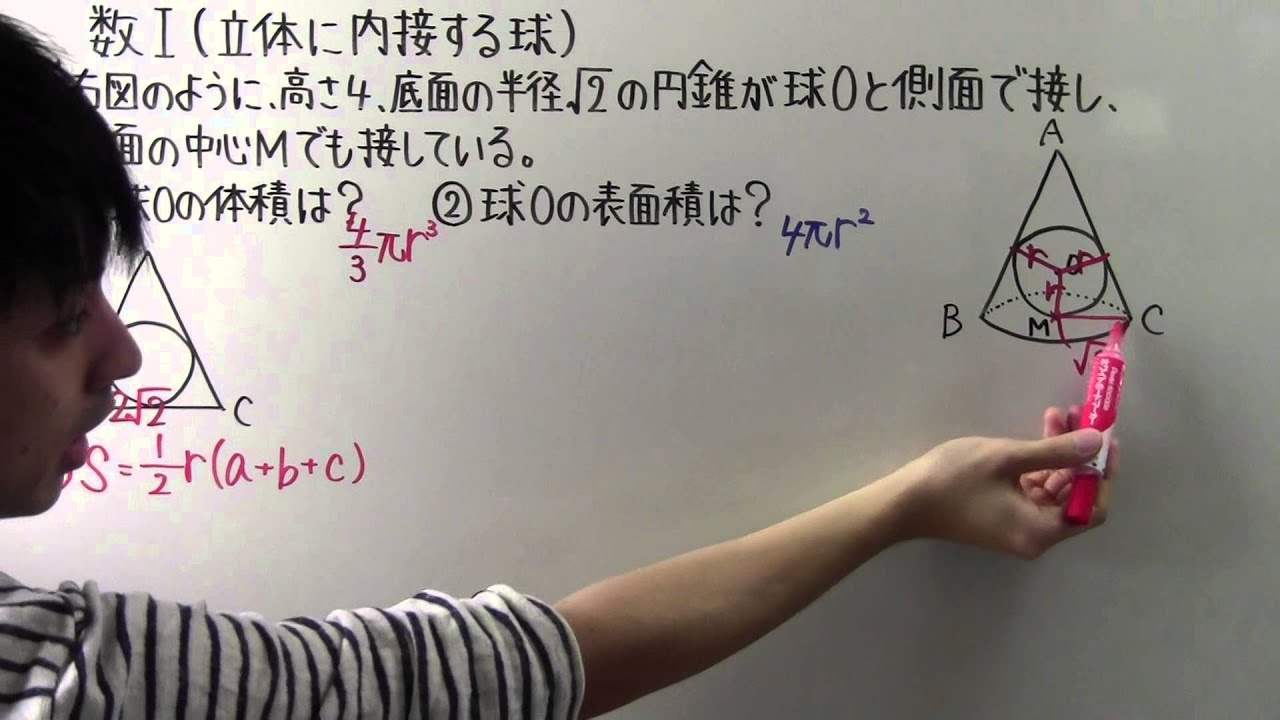
単元：
#数Ⅰ#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎右図のように、高さ4、底面の半径$\sqrt{ 2 }$の円錐球Oと側面で接し、底面の中心Mでも接している。
①球Oの体積は？
②球Oの表面積は？
※図は動画内参照
この動画を見る
◎右図のように、高さ4、底面の半径$\sqrt{ 2 }$の円錐球Oと側面で接し、底面の中心Mでも接している。
①球Oの体積は？
②球Oの表面積は？
※図は動画内参照
【高校数学】 数Ⅰ－９９ 正四面体の切り口
単元：
#数A#図形の性質#空間における垂直と平行と多面体（オイラーの法則）#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎1辺の長さが6の正四面体OABCがある。
OAの中点をL、辺OBを2:1に分ける点をM、辺OC上で2ON=NCを満たす点をNとする。
①$LM$の長さは？
②$\cos \angle MLN$の値は？
③$△LMN$の面積は？
この動画を見る
◎1辺の長さが6の正四面体OABCがある。
OAの中点をL、辺OBを2:1に分ける点をM、辺OC上で2ON=NCを満たす点をNとする。
①$LM$の長さは？
②$\cos \angle MLN$の値は？
③$△LMN$の面積は？
【高校数学】 数Ⅰ－９８ 三角形の内角の二等分線
単元：
#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎$\angle A=60°, AB=4.AC=3$である△ABCの$\angle A$の二等分線が辺BCと交わる点をDとするとき、線分ADの長さを求めよう。
この動画を見る
◎$\angle A=60°, AB=4.AC=3$である△ABCの$\angle A$の二等分線が辺BCと交わる点をDとするとき、線分ADの長さを求めよう。
【高校数学】 数Ⅰ－９７ 内接円と外接円の半径
単元：
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎AB=7,BC=8,CA=5の△ABCについて。
①外接円の半径Rは？
②内接円の半径rは？
この動画を見る
◎AB=7,BC=8,CA=5の△ABCについて。
①外接円の半径Rは？
②内接円の半径rは？
【高校数学】 数Ⅰ－９６ 円に内接する四角形
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
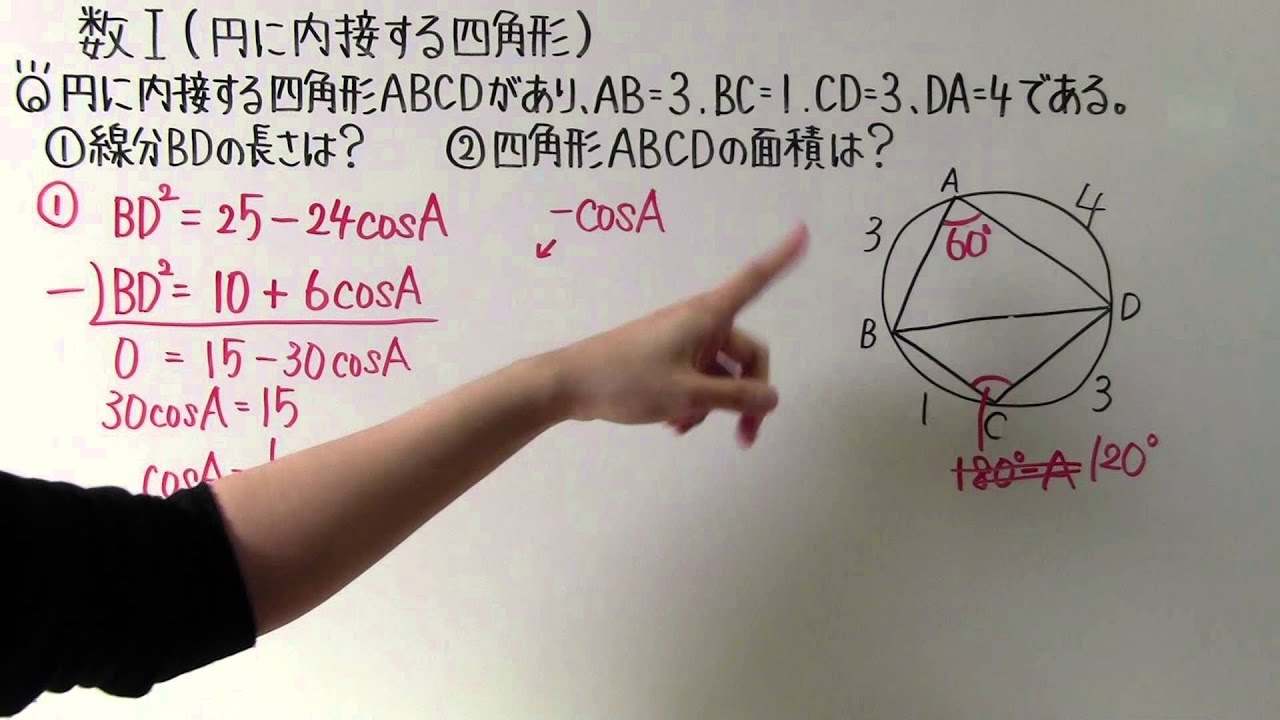
◎円に内接する四角形ABCDがあり、AB=3,BC=1,DA=4である。
①線分BDの長さは？
②四角形ABCDの面積は？
この動画を見る
◎円に内接する四角形ABCDがあり、AB=3,BC=1,DA=4である。
①線分BDの長さは？
②四角形ABCDの面積は？