 ユークリッド互除法と不定方程式・N進法
ユークリッド互除法と不定方程式・N進法
 ユークリッド互除法と不定方程式・N進法
ユークリッド互除法と不定方程式・N進法
指数方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$5^{2x^2-1}-3・5^{(x+1)(x+2)}-2・5^{6(x+1)}=0$
この動画を見る
実数解を求めよ.
$5^{2x^2-1}-3・5^{(x+1)(x+2)}-2・5^{6(x+1)}=0$
変な方程式 指数タワー
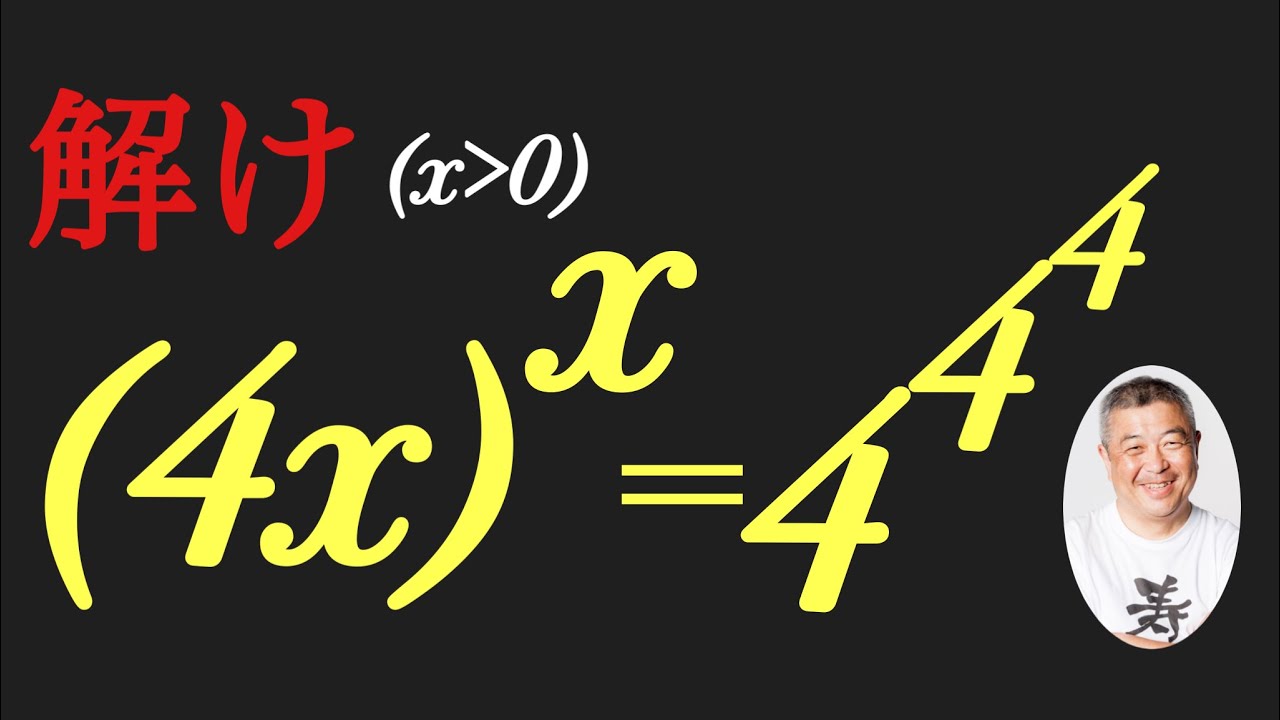
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け. $x\gt 0$
$(4x)^x=4^{4^4}$
この動画を見る
これを解け. $x\gt 0$
$(4x)^x=4^{4^4}$
変な指数方程式
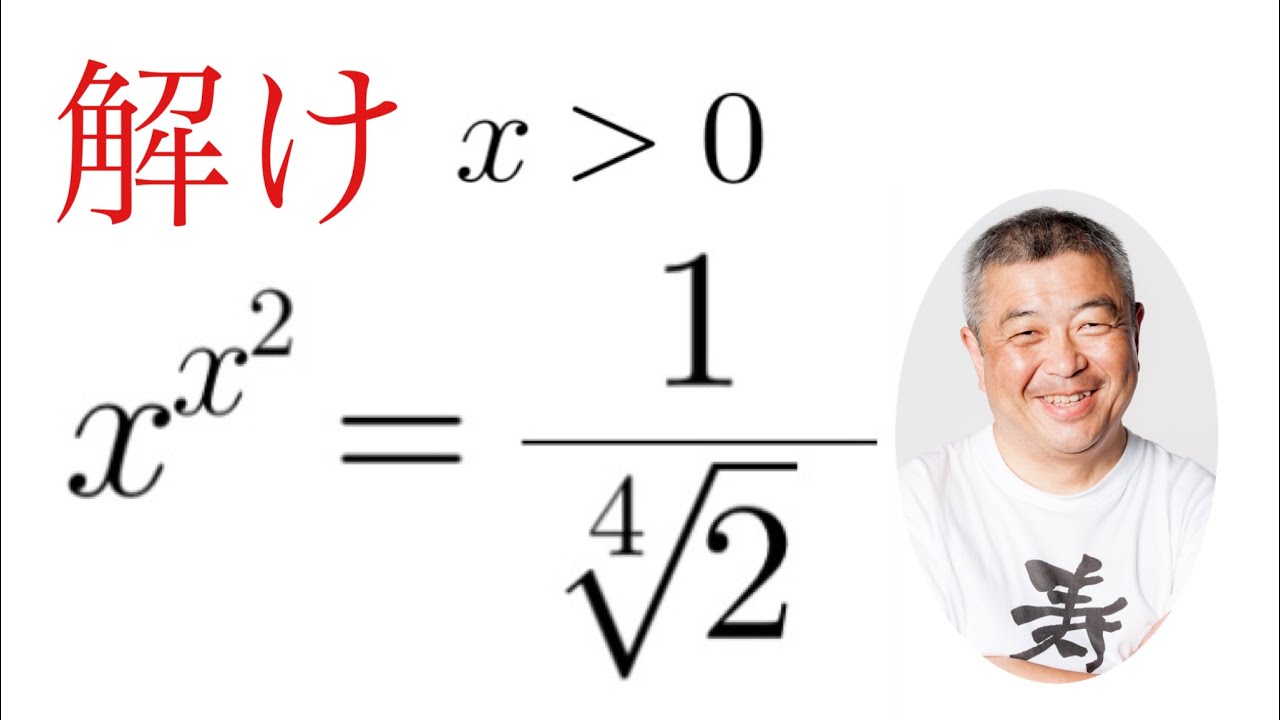
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.$x\gt 0$
$x^{x^2}=\dfrac{1}{\sqrt[4]{2}}$
この動画を見る
これを解け.$x\gt 0$
$x^{x^2}=\dfrac{1}{\sqrt[4]{2}}$
指数方程式 答えは1つじゃないよ

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
すべての解を求めよ.
$5^x・8^{\frac{x}{x+1}}=100$
この動画を見る
すべての解を求めよ.
$5^x・8^{\frac{x}{x+1}}=100$
方程式
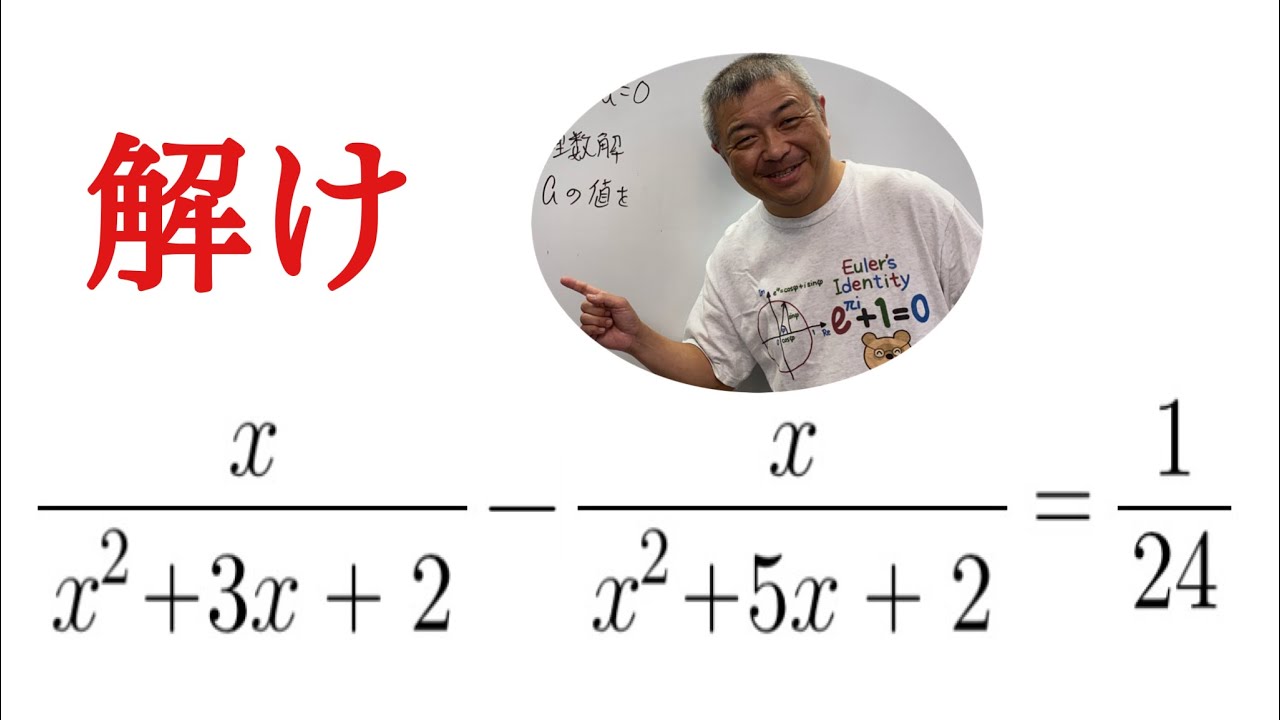
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\dfrac{x}{x^2+3x+2}-\dfrac{x}{x^2+5x+2}=\dfrac{1}{24}$
この動画を見る
これを解け.
$\dfrac{x}{x^2+3x+2}-\dfrac{x}{x^2+5x+2}=\dfrac{1}{24}$
未知数2で式1つの方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これの実数解を求めよ.
$x^2+y^2+15=\sqrt 6(x-3y)$
この動画を見る
これの実数解を求めよ.
$x^2+y^2+15=\sqrt 6(x-3y)$
4乗根の方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$\sqrt[4]{97-x}+\sqrt[4]{x-15}=4$
この動画を見る
実数解を求めよ.
$\sqrt[4]{97-x}+\sqrt[4]{x-15}=4$
指数方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$6^{2x-3}-217・6^{x-2}+36=0$
この動画を見る
これを解け.
$6^{2x-3}-217・6^{x-2}+36=0$
ただの三次方程式
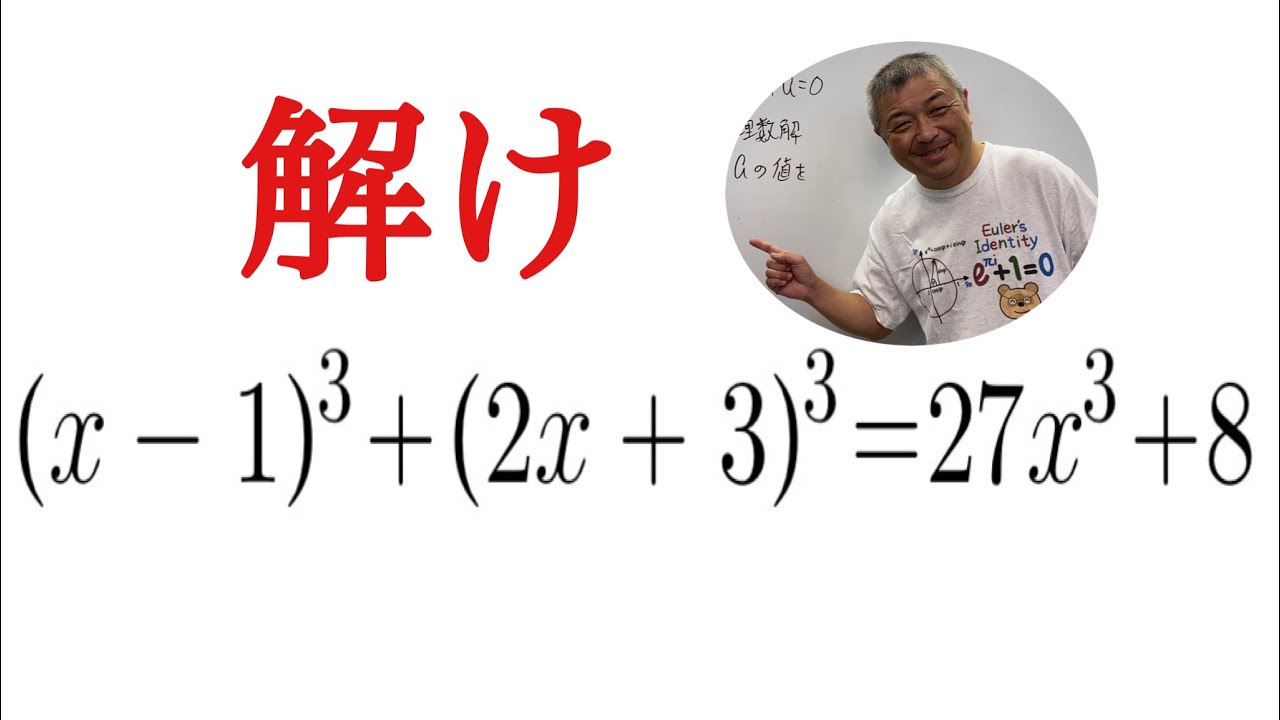
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$(x-1)^3+(2x+3)^3=27x^3+8$
この動画を見る
これを解け.
$(x-1)^3+(2x+3)^3=27x^3+8$
変な指数方程式
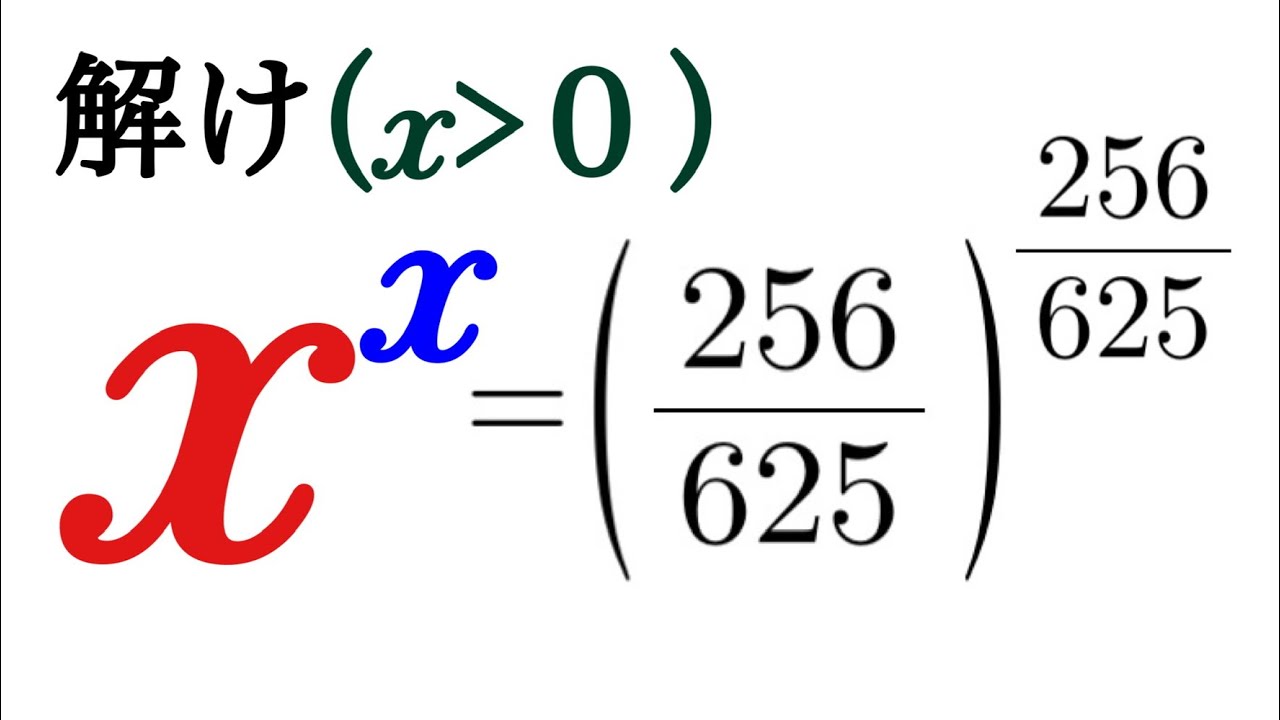
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.$(x\gt 0)$
$x^x=\left(\dfrac{256}{625}\right)^{\frac{256}{625}}$
この動画を見る
これを解け.$(x\gt 0)$
$x^x=\left(\dfrac{256}{625}\right)^{\frac{256}{625}}$
指数方程式 解は1つではない

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$3^x・2^{\frac{6}{x}}=72$
この動画を見る
実数解を求めよ.
$3^x・2^{\frac{6}{x}}=72$
見掛け倒しの対数方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\log_{\log_6(x-3)}81=4$
この動画を見る
これを解け.
$\log_{\log_6(x-3)}81=4$
不思議な方程式。優秀な視聴者様!疑問に答えて!
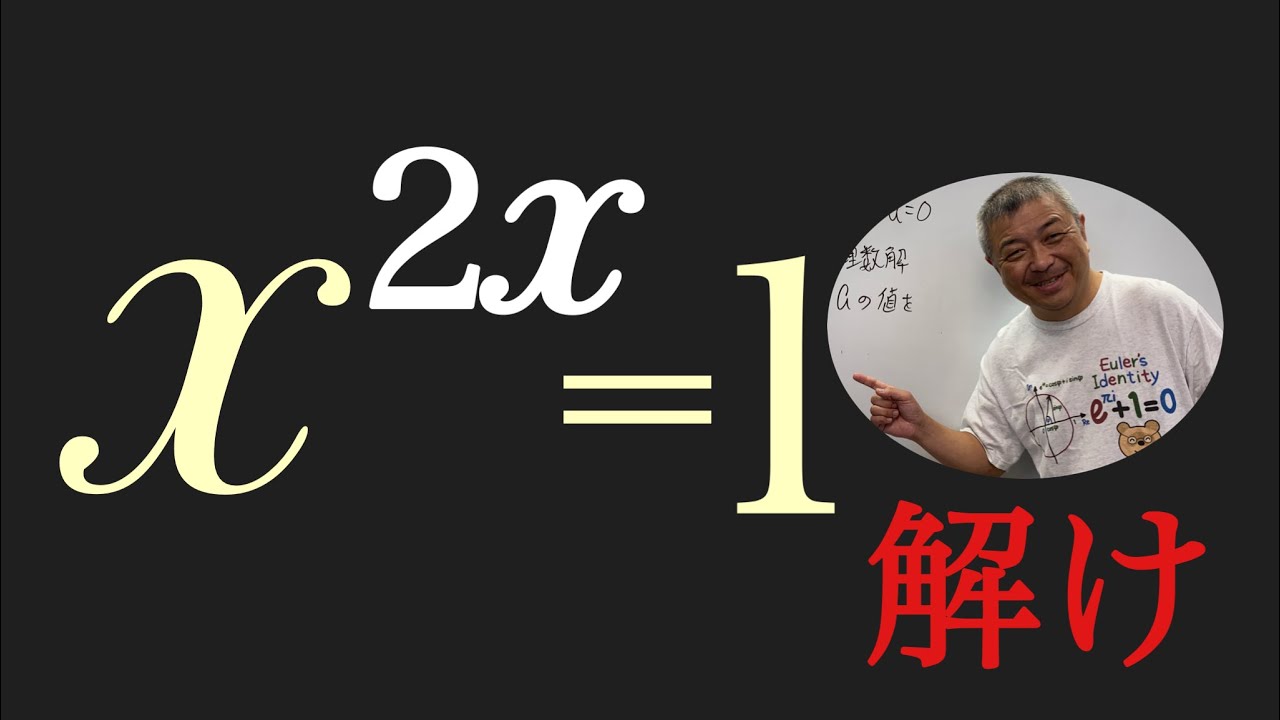
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.$x$は実数である.
$x^{2x}=1$
この動画を見る
これを解け.$x$は実数である.
$x^{2x}=1$
指数方程式だよ
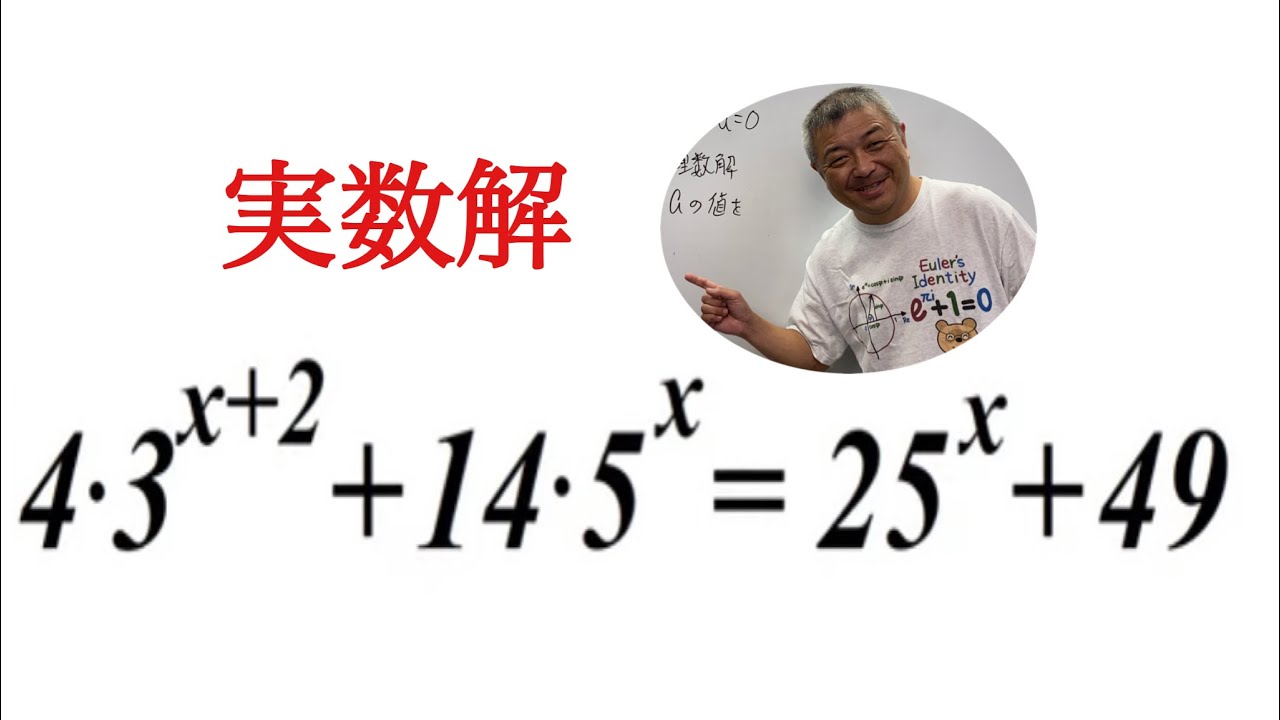
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解$x$を求めよ.
$4・3^{x+2}+14・5^x~25^x+49$
この動画を見る
実数解$x$を求めよ.
$4・3^{x+2}+14・5^x~25^x+49$
解けるようにできた方程式
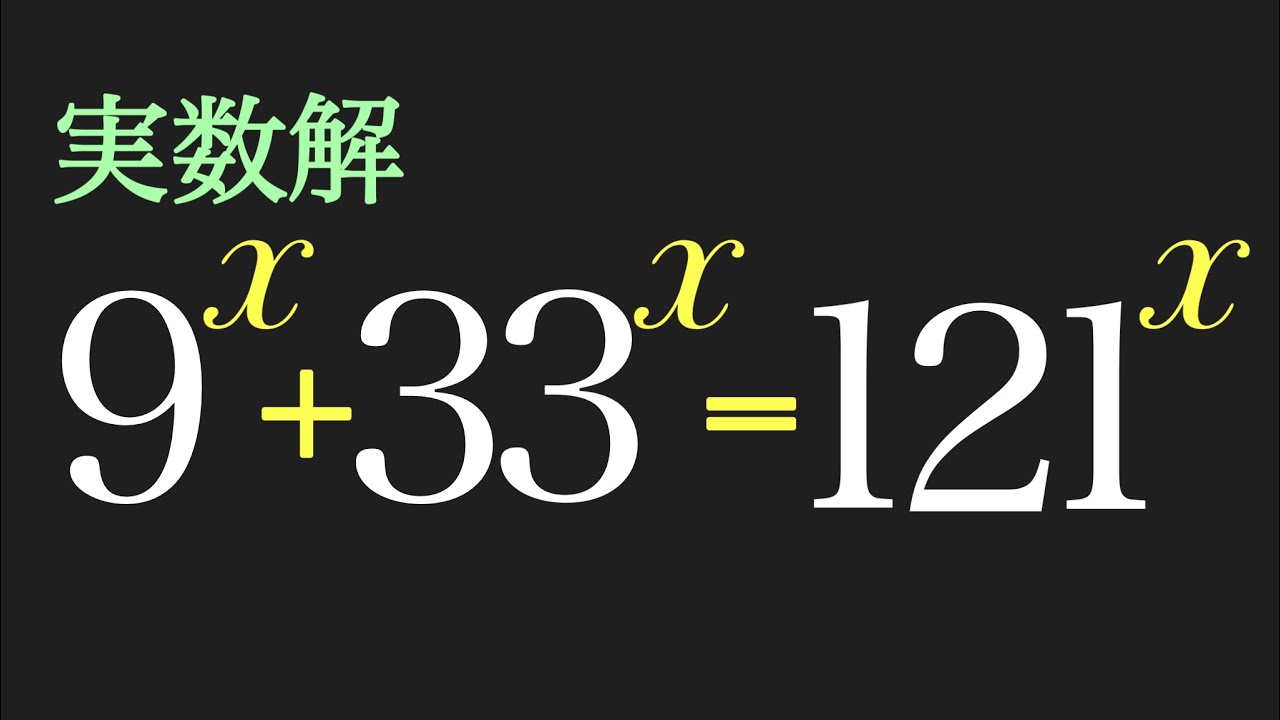
地道にやれば出るよね。パッと出す方法もいろいろありそう

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^4+x^3+x^2+x+1=0$のとき,
$\dfrac{x}{1+x^2}+\dfrac{x^2}{1+x^4}+\dfrac{x^3}{1+x}+\dfrac{x^4}{1+x^3}$の値を求めよ.
この動画を見る
$x^4+x^3+x^2+x+1=0$のとき,
$\dfrac{x}{1+x^2}+\dfrac{x^2}{1+x^4}+\dfrac{x^3}{1+x}+\dfrac{x^4}{1+x^3}$の値を求めよ.
見掛け倒しの方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$(2+\sqrt3)^{x^2-2x+1}+(2-\sqrt3)^{x^2-2x-1}=$
$\dfrac{2}{2-\sqrt3}$
この動画を見る
これを解け.
$(2+\sqrt3)^{x^2-2x+1}+(2-\sqrt3)^{x^2-2x-1}=$
$\dfrac{2}{2-\sqrt3}$
ちょっとした方程式 x^e=e^x
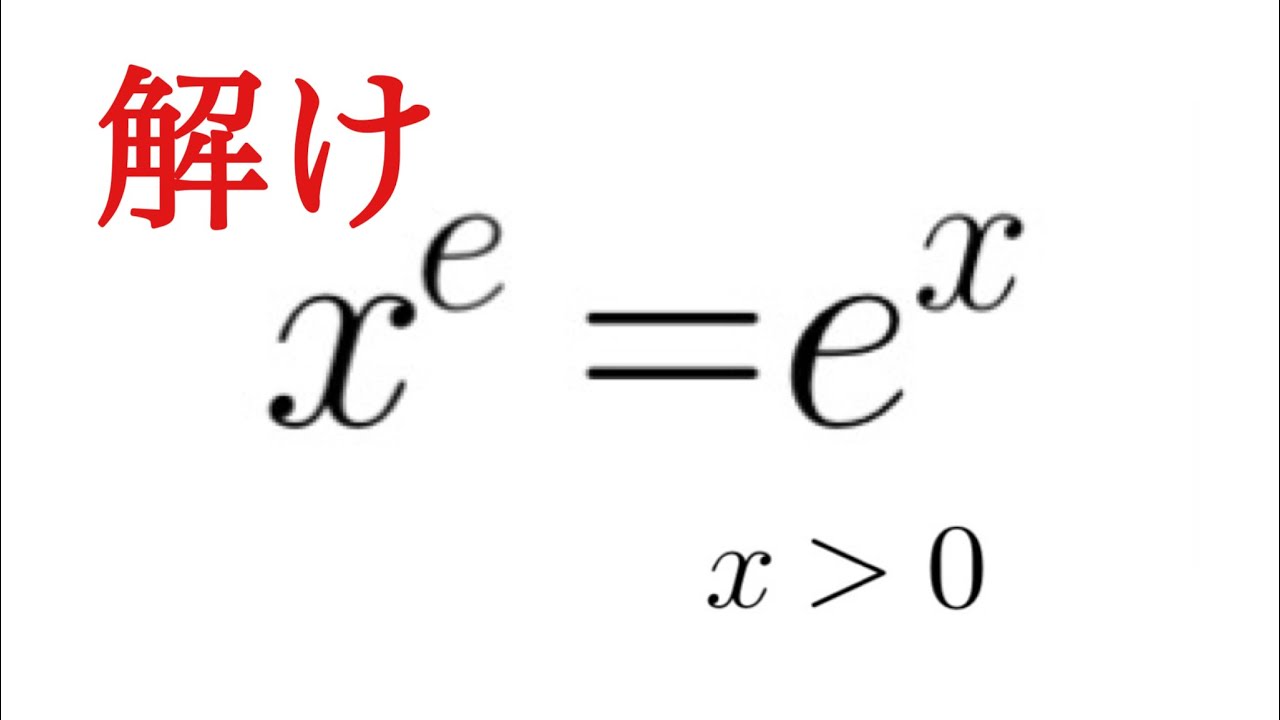
福田の数学〜上智大学2021年TEAP利用理系第1問(2)〜n進法

単元:
#計算と数の性質#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#規則性(周期算・方陣算・数列・日暦算・N進法)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(2)nを20以上の整数とする。n進法で表したとき、$n^3$の位の数が$1,n^2$の位の数が2,
$n^1$の位の数が$3,n^0$の位の数が0である数$1230_{(n)}$を$n+1$進法で表すと$(n+1)^2$の位
の数は$\boxed{\ \ あ\ \ }$であり、$(n+1)^1$の位の数は$\boxed{\ \ い\ \ }$であり、$(n+1)^0$の位の数は$\boxed{\ \ う\ \ }$である。
$\boxed{\ \ あ\ \ }\ ~\ \boxed{\ \ う\ \ }$の選択肢:
$(\textrm{a})0 (\textrm{b})1 (\textrm{c})2 (\textrm{d})3$
$(\textrm{e})n-2 (\textrm{f})n-3 (\textrm{g})n-1 (\textrm{g})n$
2021上智大学理系過去問
この動画を見る
${\Large\boxed{1}}$(2)nを20以上の整数とする。n進法で表したとき、$n^3$の位の数が$1,n^2$の位の数が2,
$n^1$の位の数が$3,n^0$の位の数が0である数$1230_{(n)}$を$n+1$進法で表すと$(n+1)^2$の位
の数は$\boxed{\ \ あ\ \ }$であり、$(n+1)^1$の位の数は$\boxed{\ \ い\ \ }$であり、$(n+1)^0$の位の数は$\boxed{\ \ う\ \ }$である。
$\boxed{\ \ あ\ \ }\ ~\ \boxed{\ \ う\ \ }$の選択肢:
$(\textrm{a})0 (\textrm{b})1 (\textrm{c})2 (\textrm{d})3$
$(\textrm{e})n-2 (\textrm{f})n-3 (\textrm{g})n-1 (\textrm{g})n$
2021上智大学理系過去問
ただの方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$\dfrac{4x}{4x^2-8x+7}+\dfrac{3x}{4x^2-10x+7}=1$
この動画を見る
実数解を求めよ.
$\dfrac{4x}{4x^2-8x+7}+\dfrac{3x}{4x^2-10x+7}=1$
【数A】高2生必見!!2020年度 第2回 K塾高2模試 大問4_整数の性質

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#全統模試(河合塾)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)x,zは0以上の整数とする。
(i)$z=0,1,2,3,4,5,6,7,8,9,10$について、$2^z$を7で割ったときの余りを順に書き 並べよ。ただし、$2^0=1$とする。
(ii)x,zは等式$ 7x=2^z+3$・・・① を満たしている。$0\leqq z\leqq 10$のとき、等式①を満たすx,zの組(x,z)をすべて求めよ。
(2)0以上の整数x,y,zが、等式 $(4x+3y)(x-y)=2^z$・・・② を満たしている。
(i)xが奇数、yが偶数、$z=5$のとき、等式②を満たすx,yの組(x,y)をすべて求めよ。
(ii)xが奇数、yが偶数、$0\leqq z\leqq 20$のとき、等式②を満たすx,y,zの組(x,y,z)の個数 を求めよ。
(iii)$z=100$で、xとyは偶奇を問わないとき、等式②を満たすx,yの組(x,y)の個数 を求めよ。
この動画を見る
(1)x,zは0以上の整数とする。
(i)$z=0,1,2,3,4,5,6,7,8,9,10$について、$2^z$を7で割ったときの余りを順に書き 並べよ。ただし、$2^0=1$とする。
(ii)x,zは等式$ 7x=2^z+3$・・・① を満たしている。$0\leqq z\leqq 10$のとき、等式①を満たすx,zの組(x,z)をすべて求めよ。
(2)0以上の整数x,y,zが、等式 $(4x+3y)(x-y)=2^z$・・・② を満たしている。
(i)xが奇数、yが偶数、$z=5$のとき、等式②を満たすx,yの組(x,y)をすべて求めよ。
(ii)xが奇数、yが偶数、$0\leqq z\leqq 20$のとき、等式②を満たすx,y,zの組(x,y,z)の個数 を求めよ。
(iii)$z=100$で、xとyは偶奇を問わないとき、等式②を満たすx,yの組(x,y)の個数 を求めよ。
ただの連立3元2次方程式
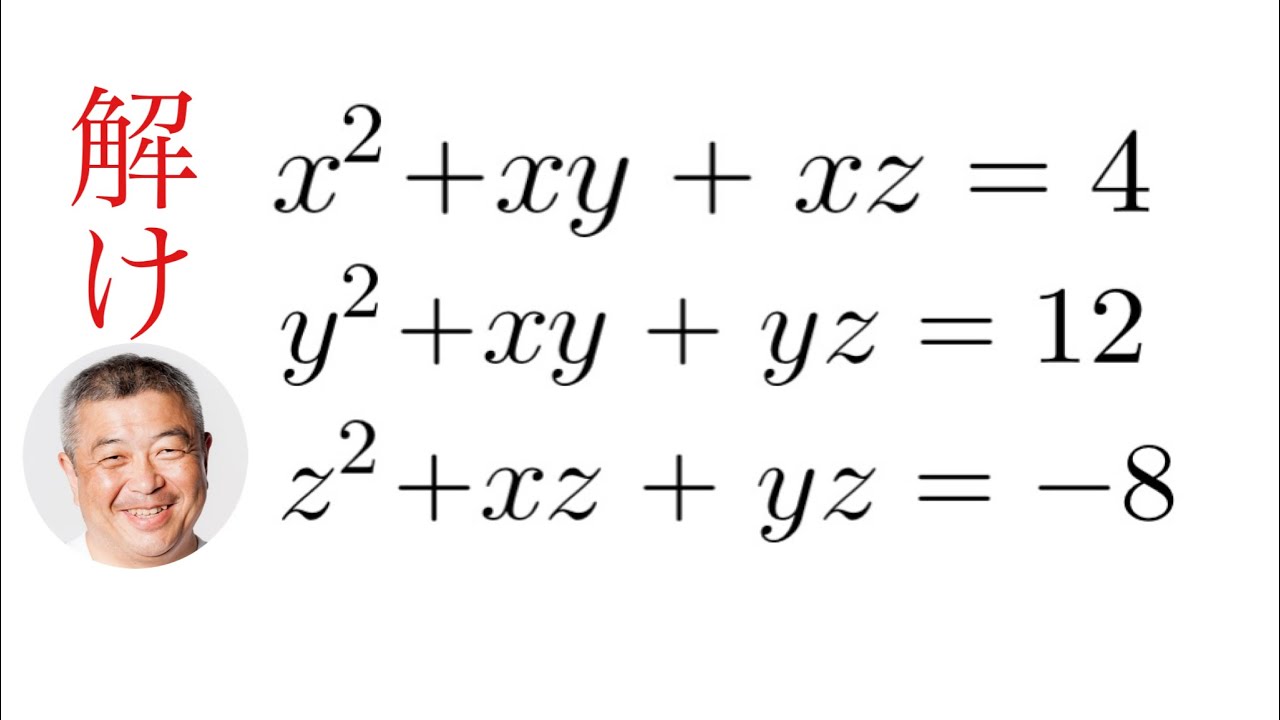
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2+xy+xz=4 \\
y^2+xy+yz=12 \\
z^2+xz+yz=-8 \\
\end{array}
\right.
\end{eqnarray}$
この動画を見る
これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2+xy+xz=4 \\
y^2+xy+yz=12 \\
z^2+xz+yz=-8 \\
\end{array}
\right.
\end{eqnarray}$
3乗根の方程式
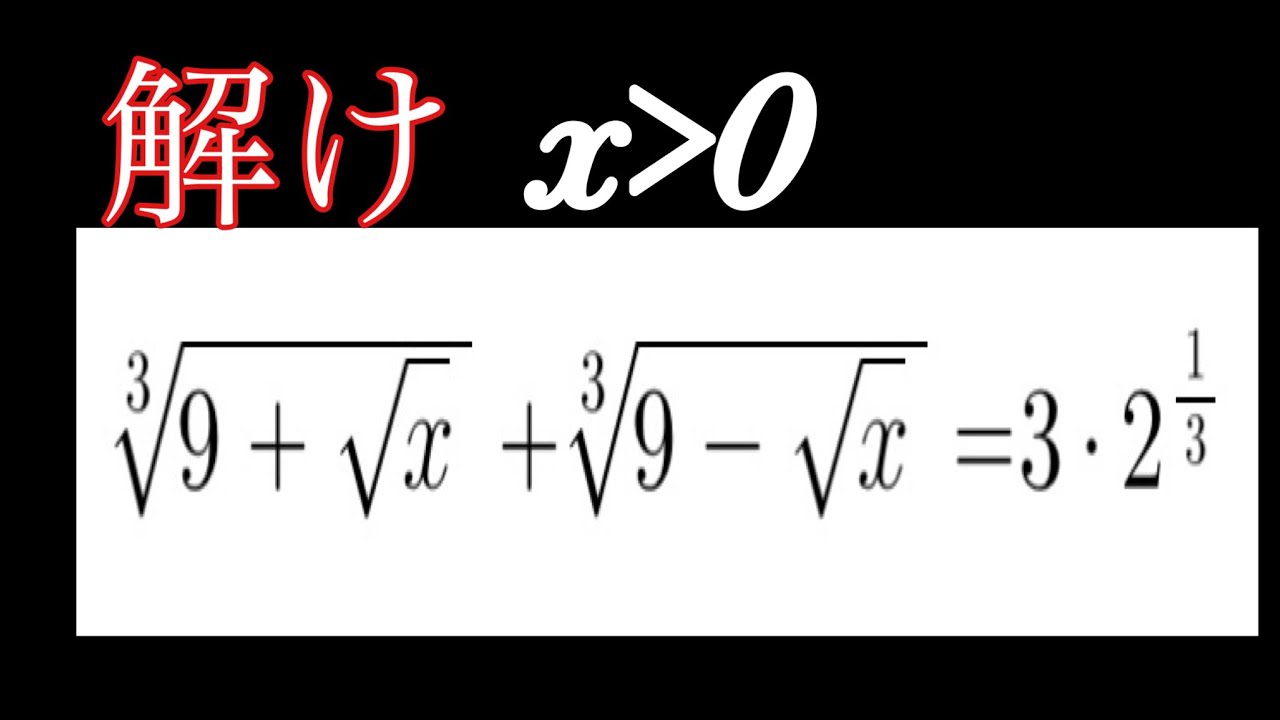
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.$(x\gt 0)$
$\sqrt[3]{9+\sqrt x}+\sqrt[3]{9-\sqrt x}=3・2^{\frac{1}{3}}$
この動画を見る
これを解け.$(x\gt 0)$
$\sqrt[3]{9+\sqrt x}+\sqrt[3]{9-\sqrt x}=3・2^{\frac{1}{3}}$
慶應義塾大(薬)n進法の基本

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\overbrace{210210210・・・・・・210_{(3)} }^{3n桁}$
$3$進法で表記された$210$を繰り返す$3n$桁の数を$十$進法にして$n$の式で表せ.
2021慶應(薬)過去問
この動画を見る
$\overbrace{210210210・・・・・・210_{(3)} }^{3n桁}$
$3$進法で表記された$210$を繰り返す$3n$桁の数を$十$進法にして$n$の式で表せ.
2021慶應(薬)過去問
福田の数学〜慶應義塾大学2021年薬学部第1問(5)〜n進法と等比数列

単元:
#計算と数の性質#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#規則性(周期算・方陣算・数列・日暦算・N進法)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(5)3進法で表された3n桁の整数
$\overbrace{ 210210\cdots210_{(3)}}^{ 3n桁 }$
がある(ただし、nは自然数とする)。この数は、$1 \leqq k \leqq n$を満たす全て
の自然数$k$に対して、最小の位から数えて3k番目の位の数が$2、3k-1$番目の位
の数が$1、3k-2$番目の位の数が0である。この数を10進法で表した数を$a_n$
とおく。
$(\textrm{i})a_2=\boxed{\ \ ク\ \ }$である。
2021慶應義塾大学薬学部過去問
$(\textrm{ii})a_n$をnの式で表すと、$\boxed{\ \ ケ\ \ }$である。
この動画を見る
${\Large\boxed{1}}$(5)3進法で表された3n桁の整数
$\overbrace{ 210210\cdots210_{(3)}}^{ 3n桁 }$
がある(ただし、nは自然数とする)。この数は、$1 \leqq k \leqq n$を満たす全て
の自然数$k$に対して、最小の位から数えて3k番目の位の数が$2、3k-1$番目の位
の数が$1、3k-2$番目の位の数が0である。この数を10進法で表した数を$a_n$
とおく。
$(\textrm{i})a_2=\boxed{\ \ ク\ \ }$である。
2021慶應義塾大学薬学部過去問
$(\textrm{ii})a_n$をnの式で表すと、$\boxed{\ \ ケ\ \ }$である。
【n進数をテンプレ化!】n進数の変換のテンプレをすべて解説!【高校数学 数学】

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
(1)次の数を10進数で表せ
$10010_{(2)}$
(2)次の数を2進数で表せ
$10_{(10)}$
この動画を見る
(1)次の数を10進数で表せ
$10010_{(2)}$
(2)次の数を2進数で表せ
$10_{(10)}$
【n進数をテンプレ化!】n進数の変換のテンプレをすべて解説!【高校数学 数学】

変な方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x\gt 0$であり実数であるとき,これを解け.
$x^{x^4}=64$
この動画を見る
$x\gt 0$であり実数であるとき,これを解け.
$x^{x^4}=64$
【確実に解ける鉄則!】不定方程式とユークリッドの互除法をまとめて解説!

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
①
754と273の最大公約数を求めよ
②
$3x+2y=17$をみたす自然数$x,y$を求めよ
③
$5x+3y=2$をみたす整数$x,y$をすべて求めよ
この動画を見る
①
754と273の最大公約数を求めよ
②
$3x+2y=17$をみたす自然数$x,y$を求めよ
③
$5x+3y=2$をみたす整数$x,y$をすべて求めよ
3乗根の方程式
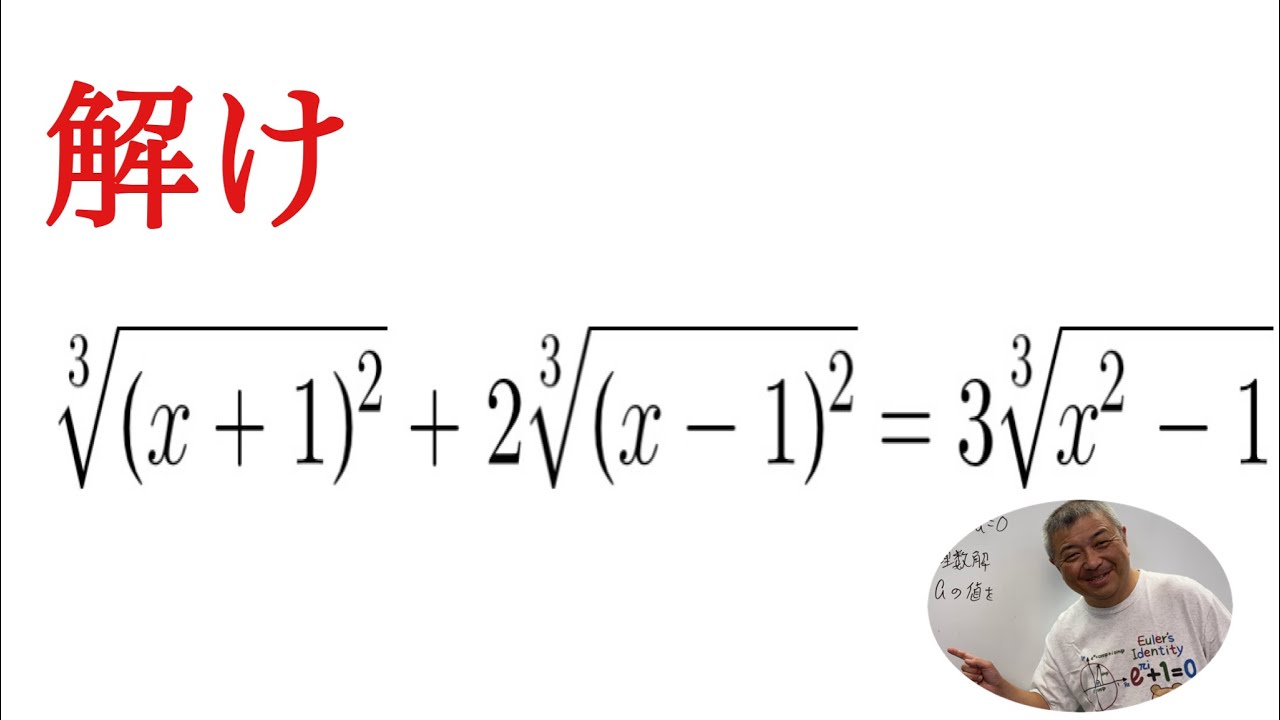
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\sqrt[3]{(x+1)^2}+2\sqrt[3]{(x-1)^2}=3\sqrt[3]{x^2-1}$
この動画を見る
これを解け.
$\sqrt[3]{(x+1)^2}+2\sqrt[3]{(x-1)^2}=3\sqrt[3]{x^2-1}$
