 整数の性質
整数の性質
 整数の性質
整数の性質
Q:鳩の巣原理の解説して下さい

2022九州大 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
自然数m,nは$ n^4=1+210m^2 $を満たす.
(1)$\dfrac{n^2+1}{2},\dfrac{n^2-1}{2}$は互いに素な整数であることを示せ.
(2)$ n^2-1 $は168の倍数であることを示せ.
(3)(m,n)を1組求めよ.
2022九州大過去問
この動画を見る
自然数m,nは$ n^4=1+210m^2 $を満たす.
(1)$\dfrac{n^2+1}{2},\dfrac{n^2-1}{2}$は互いに素な整数であることを示せ.
(2)$ n^2-1 $は168の倍数であることを示せ.
(3)(m,n)を1組求めよ.
2022九州大過去問
素数

単元:
#数Ⅰ#数A#数と式#式の計算(整式・展開・因数分解)#整数の性質#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ n^4-11n^2+49 $が素数となる整数 $ n$を求めよ.
この動画を見る
$ n^4-11n^2+49 $が素数となる整数 $ n$を求めよ.
素数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n^4-11n^2+49$が素数となる整数$n$を求めよ.
この動画を見る
$n^4-11n^2+49$が素数となる整数$n$を求めよ.
大学入試問題#145 自治医科大(2004) 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#自治医科大学
指導講師:
ますただ
問題文全文(内容文):
$x^2-3ax+2a-3=0$が2つの整数解をもつように$a$が定まっている。
$a^2+3$の値を求めよ。
出典:2004年自治医科大学 入試問題
この動画を見る
$x^2-3ax+2a-3=0$が2つの整数解をもつように$a$が定まっている。
$a^2+3$の値を求めよ。
出典:2004年自治医科大学 入試問題
整数問題
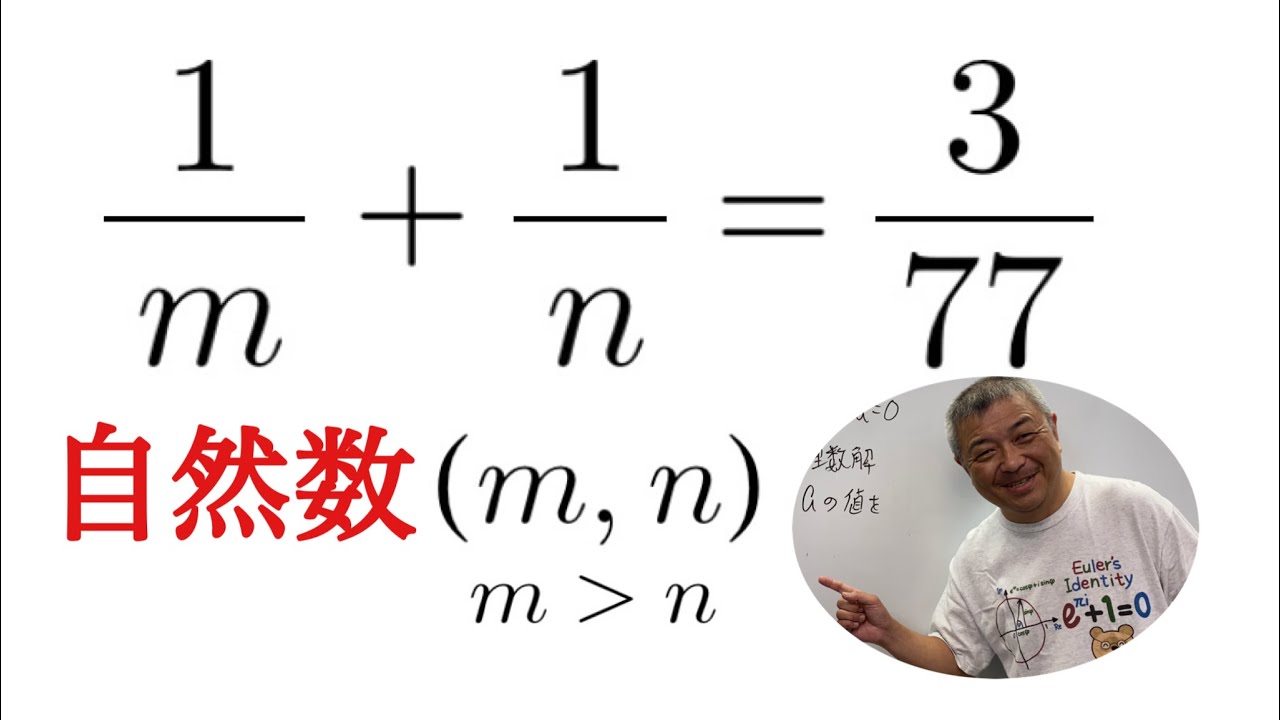
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
自然数$ m,n(m \gt n)$を求めよ.
$ \dfrac{1}{m}+\dfrac{1}{n}=\dfrac{3}{77}$
この動画を見る
自然数$ m,n(m \gt n)$を求めよ.
$ \dfrac{1}{m}+\dfrac{1}{n}=\dfrac{3}{77}$
福田の数学・入試問題解説〜東北大学2022年理系第1問〜不定方程式の整数解の個数

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
Kを3より大きい奇数とし、$l+m+n=K$を満たす正の奇数の組(l,m,n)
の個数Nを考える。ただし、例えば、$K=5$のとき、$(l,m,n)=(1,1,3)$
と$(l,m,n)=(1,3,1)$とは異なる組とみなす。
(1)$K=99$のとき、Nを求めよ。
(2)$K=99$のとき、l,m,nの中に同じ奇数を2つ以上含む組(l,m,n)の個数を
求めよ。
(3)$N \gt K$を満たす最小のKを求めよ。
2022東北大学理系過去問
この動画を見る
Kを3より大きい奇数とし、$l+m+n=K$を満たす正の奇数の組(l,m,n)
の個数Nを考える。ただし、例えば、$K=5$のとき、$(l,m,n)=(1,1,3)$
と$(l,m,n)=(1,3,1)$とは異なる組とみなす。
(1)$K=99$のとき、Nを求めよ。
(2)$K=99$のとき、l,m,nの中に同じ奇数を2つ以上含む組(l,m,n)の個数を
求めよ。
(3)$N \gt K$を満たす最小のKを求めよ。
2022東北大学理系過去問
素数判定
整数問題 一橋大 令和四年

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$2^a3^b+2^c3^d = 2022$を満たす0以上の整数a,b,c,dの組を求めよ。
2022一橋大学
この動画を見る
$2^a3^b+2^c3^d = 2022$を満たす0以上の整数a,b,c,dの組を求めよ。
2022一橋大学
雑問

単元:
#数A#数Ⅱ#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 25^{63}\times 63^{25}$の下3桁を求めよ.
この動画を見る
$ 25^{63}\times 63^{25}$の下3桁を求めよ.
明治学院 令和4年度 2022 入試問題100題解説85問目!

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a,bは整数とする。
$ab^2+2ab+a=50$
a+bの最小値は?
2022明治学院高等学校
この動画を見る
a,bは整数とする。
$ab^2+2ab+a=50$
a+bの最小値は?
2022明治学院高等学校
ニャンニャン問題2022

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 222.......22$のようにすべての桁の数が$2$である整数の中には
必ず$2022$の倍数があることを示せ.
この動画を見る
$ 222.......22$のようにすべての桁の数が$2$である整数の中には
必ず$2022$の倍数があることを示せ.
【糸口を探せ!】整数:同志社国際高等学校~全国入試問題解法

単元:
#数学(中学生)#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\sqrt{24n}$と$\sqrt{n+27}$がともに整数になるような最小の自然数$n$の値を求めよ.
同志社国際高校過去問
この動画を見る
$\sqrt{24n}$と$\sqrt{n+27}$がともに整数になるような最小の自然数$n$の値を求めよ.
同志社国際高校過去問
福田の数学〜京都大学2022年理系第3問〜3つの数の最大公約数

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
nを自然数とする。3つの整数$n^2+2,n^4+2,n^6+2$の最大公約数$A_n$を求めよ。
2022京都大学理系過去問
この動画を見る
nを自然数とする。3つの整数$n^2+2,n^4+2,n^6+2$の最大公約数$A_n$を求めよ。
2022京都大学理系過去問
無題

単元:
#数Ⅰ#数A#数と式#式の計算(整式・展開・因数分解)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ n^2-331n-2022$が$101$の倍数となる
$ 2$桁の自然数$ n$を$1$つ見つけよ.
この動画を見る
$ n^2-331n-2022$が$101$の倍数となる
$ 2$桁の自然数$ n$を$1$つ見つけよ.
大学入試問題#127 関西大学(1991) 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師:
ますただ
問題文全文(内容文):
$l,m,n$:正の整数
$l^2mn=64$を満たす組($l,m,n$)の個数を求めよ。
出典:1991年関西大学 入試問題
この動画を見る
$l,m,n$:正の整数
$l^2mn=64$を満たす組($l,m,n$)の個数を求めよ。
出典:1991年関西大学 入試問題
一橋大学2022整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 2^a3^b+2^c3^d=2022$を満たす$0$以上の整数$(a,b,c,d)$を求めよ.
2022一橋大過去問
この動画を見る
$ 2^a3^b+2^c3^d=2022$を満たす$0$以上の整数$(a,b,c,d)$を求めよ.
2022一橋大過去問
福田の入試問題解説〜東京大学2022年理系第2問〜約数と倍数と最大公約数

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数列$\left\{a_n\right\}$を次のように定める。
$a_1=1, a_{n+1}=a_n^2+1 (n=1,2,3,\ldots)$
(1)正の整数nが3の倍数のとき、$a_n$は5の倍数となることを示せ。
(2)k,nを正の整数とする。$a_n$が$a_k$の倍数となるための必要十分条件をk,nを
用いて表せ。
(3)$a_{2022}$と$(a_{8091})^2$の最大公約数を求めよ。
2022東京大学理系過去問
この動画を見る
数列$\left\{a_n\right\}$を次のように定める。
$a_1=1, a_{n+1}=a_n^2+1 (n=1,2,3,\ldots)$
(1)正の整数nが3の倍数のとき、$a_n$は5の倍数となることを示せ。
(2)k,nを正の整数とする。$a_n$が$a_k$の倍数となるための必要十分条件をk,nを
用いて表せ。
(3)$a_{2022}$と$(a_{8091})^2$の最大公約数を求めよ。
2022東京大学理系過去問
ざ・見掛け倒しだよ

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+……+\dfrac{32}{33}=\dfrac{a}{33!}$
$a$を$17$で割った余りを求めよ.
この動画を見る
$ \dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+……+\dfrac{32}{33}=\dfrac{a}{33!}$
$a$を$17$で割った余りを求めよ.
福田の数学〜東京慈恵会医科大学2022年医学部第3問〜約数と倍数の性質

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
mは3以上の奇数とし、mの全ての正の約数を$a_1,a_2,\ldots,a_k$と並べる。
ただし、$a_1 \lt a_2 \lt \ldots \lt a_k$とする。
以下の2つの条件$(\textrm{i}),(\textrm{ii})$を満たすmについて考える。
$(\textrm{i})m$は素数ではない。
$(\textrm{ii})i \leqq j,1 \lt i \lt k ,1 \lt j \lt k$を満たす全ての整数i,jについて$a_j-a_i \leqq 3$が
成り立つ。
このとき、次の問いに答えよ。
(1)kは3または4であることを示し、mを$a_2$を用いて表せ。
(2)$k=3$となるとき、全ての正の整数nについて$(a_2n+1)^{a_2}-1$は
mの倍数であることを示せ。
2022東京慈恵会医科大学医学部過去問
この動画を見る
mは3以上の奇数とし、mの全ての正の約数を$a_1,a_2,\ldots,a_k$と並べる。
ただし、$a_1 \lt a_2 \lt \ldots \lt a_k$とする。
以下の2つの条件$(\textrm{i}),(\textrm{ii})$を満たすmについて考える。
$(\textrm{i})m$は素数ではない。
$(\textrm{ii})i \leqq j,1 \lt i \lt k ,1 \lt j \lt k$を満たす全ての整数i,jについて$a_j-a_i \leqq 3$が
成り立つ。
このとき、次の問いに答えよ。
(1)kは3または4であることを示し、mを$a_2$を用いて表せ。
(2)$k=3$となるとき、全ての正の整数nについて$(a_2n+1)^{a_2}-1$は
mの倍数であることを示せ。
2022東京慈恵会医科大学医学部過去問
大学入試問題#125 広島修道大学(2015) 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$n$:自然数
$2n-1$と$2n+1$は互いに素であることを示せ
出典:2015年広島修道大学 入試問題
この動画を見る
$n$:自然数
$2n-1$と$2n+1$は互いに素であることを示せ
出典:2015年広島修道大学 入試問題
不定方程式
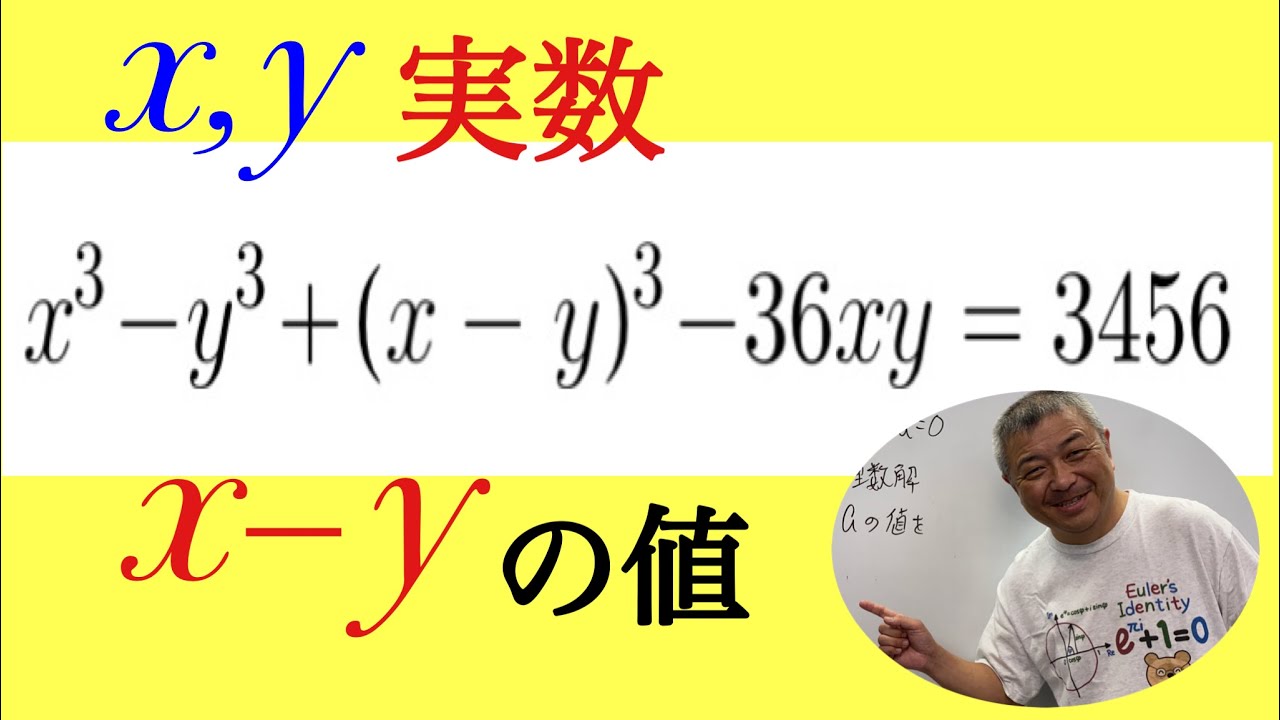
単元:
#数A#複素数と方程式#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x,y$を実数とする.
$ x^3-y^3+(x-y)^3-36xy=3456$のとき,$ x-y$の値を求めよ.
この動画を見る
$x,y$を実数とする.
$ x^3-y^3+(x-y)^3-36xy=3456$のとき,$ x-y$の値を求めよ.
2022都立入試 整数問題証明(11の倍数)

単元:
#数学(中学生)#数A#数Ⅱ#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#恒等式・等式・不等式の証明#数列#数列とその和(等差・等比・階差・Σ)#高校入試過去問(数学)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
2022都立入試 整数問題証明に関して解説していきます.
この動画を見る
2022都立入試 整数問題証明に関して解説していきます.
大学入試問題#117 大分大学(2007) 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#大分大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$x,y,z$:自然数
$x \leqq y \leqq z$
$7(x+y+z)=2(xy+yz+zx)$をみたす組$(x,y,z)$をすべて求めよ。
出典:2007年大分大学 入試問題
この動画を見る
$x,y,z$:自然数
$x \leqq y \leqq z$
$7(x+y+z)=2(xy+yz+zx)$をみたす組$(x,y,z)$をすべて求めよ。
出典:2007年大分大学 入試問題
【題意をつかもう!数学の意味を知ろう!】整数:沖縄県公立高等学校~全国入試問題解法

単元:
#数学(中学生)#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
「ある2桁の自然数$X$と,その数の十の位の数と一の位の数を入れ替えてできる数$Y$との和が$132$になる.」
もとの自然数$X$として考えられる数をすべて求めなさい.
※もとの自然数$X$は,十の位の数が一の位の数より大きいものとする.
沖縄県高校過去問
この動画を見る
「ある2桁の自然数$X$と,その数の十の位の数と一の位の数を入れ替えてできる数$Y$との和が$132$になる.」
もとの自然数$X$として考えられる数をすべて求めなさい.
※もとの自然数$X$は,十の位の数が一の位の数より大きいものとする.
沖縄県高校過去問
整数問題 須磨学園(改) 2022年入試問題100問解説の53問目

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2+6xy+10y^2+6y=9$を満たす整数の組(x,y)をすべて求めよ。
2022須磨学園高等学校
この動画を見る
$x^2+6xy+10y^2+6y=9$を満たす整数の組(x,y)をすべて求めよ。
2022須磨学園高等学校
2022年の整数問題!この問題好きです❤️ 早稲田大学高等学院2022年入試問題解説49問目
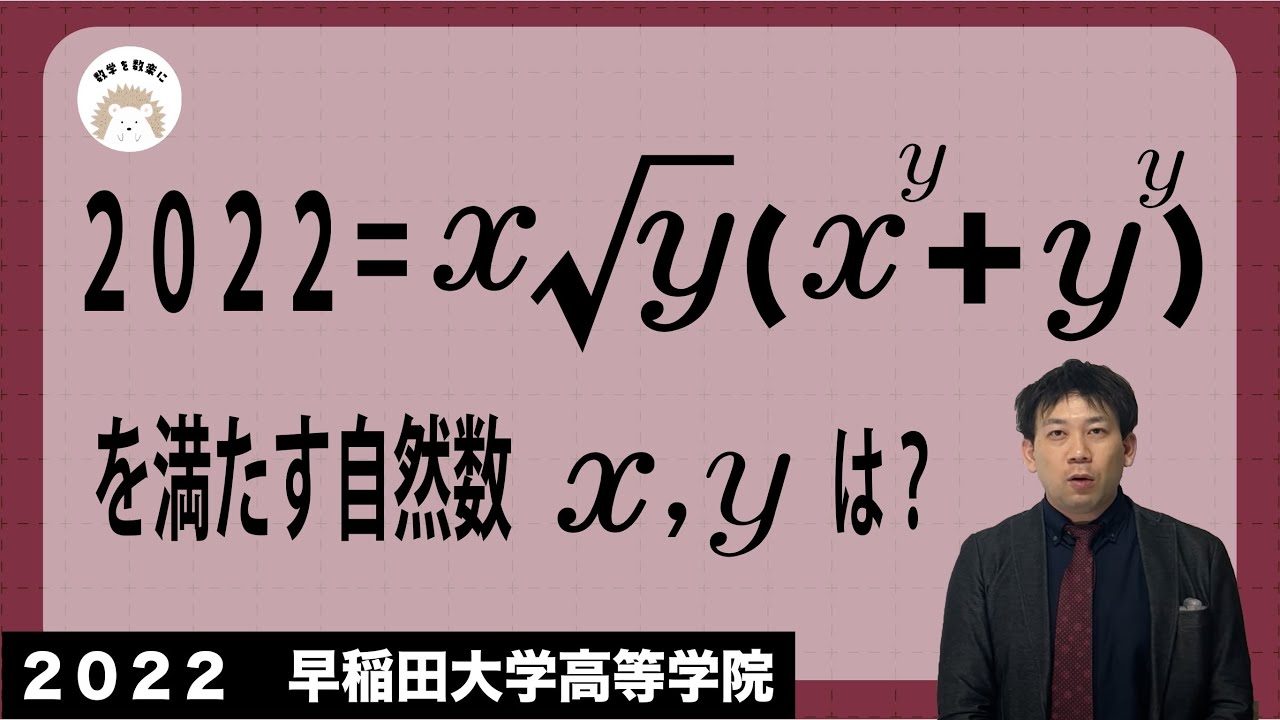
単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$2022=x \sqrt y (x^y+y^y)$
を満たす自然数x,yは?
2022早稲田大学高等学院
この動画を見る
$2022=x \sqrt y (x^y+y^y)$
を満たす自然数x,yは?
2022早稲田大学高等学院
【数学A/整数】 n進法→10進法(小数)

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の数を10進法の小数で表せ。
(1)$0.101_{(2)}$
(2)$0.24_{(5)}$
この動画を見る
次の数を10進法の小数で表せ。
(1)$0.101_{(2)}$
(2)$0.24_{(5)}$
【数学A/整数】10進法をn進法で表す

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の10進法を[ ]内の表し方で表せ。
(1)57 [2進法]
(2)83 [5進法]
この動画を見る
次の10進法を[ ]内の表し方で表せ。
(1)57 [2進法]
(2)83 [5進法]
大学入試問題#113 一橋大学(2011) 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$1 \lt x \lt y$
$(1+\displaystyle \frac{1}{x})(1+\displaystyle \frac{1}{y})=\displaystyle \frac{5}{3}$を満たす自然数の組$(x,y)$をすべて求めよ。
出典:2011年一橋大学 入試問題
この動画を見る
$1 \lt x \lt y$
$(1+\displaystyle \frac{1}{x})(1+\displaystyle \frac{1}{y})=\displaystyle \frac{5}{3}$を満たす自然数の組$(x,y)$をすべて求めよ。
出典:2011年一橋大学 入試問題
