 数A
数A
 数A
数A
福田の数学〜2023年共通テスト速報〜数学IIB第1問三角関数と対数〜三角不等式と対数が有理数とならない条件

単元:
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#整数の性質#ユークリッド互除法と不定方程式・N進法#三角関数#指数関数と対数関数#三角関数とグラフ#指数関数#対数関数#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
第一問
[ 1 ] 三角関数の値の大小関係について考えよう。
(1) $x=\displaystyle\frac{\pi}{6}$のとき$\sin x\boxed{\boxed{\ \ ア\ \ }}\sin 2x$であり、$x=\frac{2}{3}\pi$のとき$\sin x\boxed{\boxed{\ \ イ\ \ }}\sin 2x$である。
$\boxed{\boxed{\ \ ア\ \ }}$, $\boxed{\boxed{\ \ イ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪< ①= ②>
(2) $\sin x$と$\sin 2x$の値の大小関係を詳しく調べよう。
$\sin 2x$-$\sin x$=$\sin 2x\left(\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ }\right)$
であるから、$\sin 2x$-$\sin x$>0が成り立つことは
「$\sin x$>0かつ $\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ } \gt 0$」... ①
「$\sin x$<0かつ $\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ } \lt 0$」... ②
が成り立つことと同値である。$0 \leqq x \leqq 2\pi$のとき、①が成り立つようなxの値の範囲は
$0 \lt x \lt \displaystyle\frac{\pi}{\boxed{\ \ オ\ \ }}$
であり、②が成り立つようなxの値の範囲は
$\pi \lt x \lt \displaystyle\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}\pi$
である。よって、$0 \leqq x \leqq 2\pi$のとき、$\sin 2x \gt \sin x$が成り立つようなxの値の範囲は
$0 \lt x \lt \displaystyle\frac{\pi}{\boxed{\ \ オ\ \ }}, \pi \lt x \lt \displaystyle\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}\pi$
である。
(3)$\sin 3x$と$\sin 4x$の値の大小関係を調べよう。
三角関数の加法定理を用いると、等式
$\sin(\alpha+\beta)$-$\sin(\alpha-\beta)$=$2\cos\alpha\sin\beta$...③
が得られる。$\alpha+\beta=4x$, $\alpha-\beta=3x$を満たす$\alpha$, $\beta$に対して③を用いることにより、$\sin 4x-\sin 3x \gt 0$が成り立つことは
「$\cos\boxed{\boxed{\ \ ク\ \ }} \gt 0$ かつ $\sin\boxed{\boxed{\ \ ケ\ \ }} \gt 0$」...④
または
「$\cos\boxed{\boxed{\ \ ク\ \ }} \lt 0$ かつ $\sin\boxed{\boxed{\ \ ケ\ \ }} \lt 0$」...⑤
が成り立つことと同値であることがわかる。
$0 \leqq x \leqq \pi$のとき、④,⑤により、$\sin 4x$>$\sin 3x$が成り立つようなxの値の範囲は
$0 \leqq x \leqq \displaystyle\frac{\pi}{\boxed{\ \ コ\ \ }}$, $\displaystyle\frac{\boxed{\ \ サ\ \ }}{\boxed{\ \ シ\ \ }}\pi \lt x \lt \frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi$
である。
$\boxed{\boxed{\ \ ク\ \ }}$, $\boxed{\boxed{\ \ ケ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪0 ①x ②2x ③3x
④4x ⑤5x ⑥6x ⑦$\frac{x}{2}$
⑧$\frac{3}{2}x$ ⑨$\frac{5}{2}x$ ⓐ$\frac{7}{2}x$ ⓑ$\frac{9}{2}x$
(4)(2), (3)の考察から、$0 \leqq x \leqq \pi$のとき、$\sin 3x \gt \sin 4x \gt \sin 2x$が成り立つようなxの値の範囲は
$\displaystyle\frac{\pi}{\boxed{\ \ コ\ \ }}$ $\lt$ $\displaystyle\frac{\pi}{\boxed{\ \ ソ\ \ }}$, $\displaystyle\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi \lt x \lt \frac{\boxed{\ \ タ\ \ }}{\boxed{\ \ チ\ \ }}\pi$
であることがわかる。
[ 2 ]
(1)$a \gt 0$, $a \ne 1$, $b \gt 0$のとき、$\log_ab=x$とおくと、$\boxed{\boxed{\ \ ツ\ \ }}$が成り立つ。
$\boxed{\boxed{\ \ ツ\ \ }}$の解答群
⓪$x^a=b$ ①$x^b=a$ ②$a^x=b$
③$b^x=a$ ④$a^b=x$ ⑤$b^a=x$
(2)様々な対数の値が有理数か無理数かについて考えよう。
(i)$\log_5 25=\boxed{\ \ テ\ \ }$, $\log_9 27=\displaystyle\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}$であり、どちらも有理数である。
(ii)$\log_2 3$が有理数と無理数のどちらかであるかを考えよう。
$\log_2 3$が有理数であると仮定すると、$\log_2 3$>0であるので、二つの自然数p, qを用いて$\log_2 3=\displaystyle\frac{p}{q}$と表すことができる。このとき、(1)により$\log_2 3=\displaystyle\frac{p}{q}$は$\boxed{\boxed{\ \ ニ\ \ }}$と変形できる。いま、2は偶数であり3は奇数であるので、$\boxed{\boxed{\ \ ニ\ \ }}$を満たす自然数p, qは存在しない。
したがって、$\log_2 3$は無理数であることがわかる。
(iii)a, bを2以上の自然数とするとき、(ii)と同様に考えると、「$\boxed{\boxed{\ \ ヌ\ \ }}$ならば$\log_a b$は常に無理数である」ことがわかる。
$\boxed{\boxed{\ \ ヌ\ \ }}$の解答群
⓪aが偶数 ①bが偶数 ②aが奇数
③bが奇数 ④aとbがともに偶数、またはaとbがともに奇数 ⑤aとbのいずれか一方が偶数で、もう一方が奇数
2023共通テスト過去問
この動画を見る
第一問
[ 1 ] 三角関数の値の大小関係について考えよう。
(1) $x=\displaystyle\frac{\pi}{6}$のとき$\sin x\boxed{\boxed{\ \ ア\ \ }}\sin 2x$であり、$x=\frac{2}{3}\pi$のとき$\sin x\boxed{\boxed{\ \ イ\ \ }}\sin 2x$である。
$\boxed{\boxed{\ \ ア\ \ }}$, $\boxed{\boxed{\ \ イ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪< ①= ②>
(2) $\sin x$と$\sin 2x$の値の大小関係を詳しく調べよう。
$\sin 2x$-$\sin x$=$\sin 2x\left(\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ }\right)$
であるから、$\sin 2x$-$\sin x$>0が成り立つことは
「$\sin x$>0かつ $\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ } \gt 0$」... ①
「$\sin x$<0かつ $\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ } \lt 0$」... ②
が成り立つことと同値である。$0 \leqq x \leqq 2\pi$のとき、①が成り立つようなxの値の範囲は
$0 \lt x \lt \displaystyle\frac{\pi}{\boxed{\ \ オ\ \ }}$
であり、②が成り立つようなxの値の範囲は
$\pi \lt x \lt \displaystyle\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}\pi$
である。よって、$0 \leqq x \leqq 2\pi$のとき、$\sin 2x \gt \sin x$が成り立つようなxの値の範囲は
$0 \lt x \lt \displaystyle\frac{\pi}{\boxed{\ \ オ\ \ }}, \pi \lt x \lt \displaystyle\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}\pi$
である。
(3)$\sin 3x$と$\sin 4x$の値の大小関係を調べよう。
三角関数の加法定理を用いると、等式
$\sin(\alpha+\beta)$-$\sin(\alpha-\beta)$=$2\cos\alpha\sin\beta$...③
が得られる。$\alpha+\beta=4x$, $\alpha-\beta=3x$を満たす$\alpha$, $\beta$に対して③を用いることにより、$\sin 4x-\sin 3x \gt 0$が成り立つことは
「$\cos\boxed{\boxed{\ \ ク\ \ }} \gt 0$ かつ $\sin\boxed{\boxed{\ \ ケ\ \ }} \gt 0$」...④
または
「$\cos\boxed{\boxed{\ \ ク\ \ }} \lt 0$ かつ $\sin\boxed{\boxed{\ \ ケ\ \ }} \lt 0$」...⑤
が成り立つことと同値であることがわかる。
$0 \leqq x \leqq \pi$のとき、④,⑤により、$\sin 4x$>$\sin 3x$が成り立つようなxの値の範囲は
$0 \leqq x \leqq \displaystyle\frac{\pi}{\boxed{\ \ コ\ \ }}$, $\displaystyle\frac{\boxed{\ \ サ\ \ }}{\boxed{\ \ シ\ \ }}\pi \lt x \lt \frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi$
である。
$\boxed{\boxed{\ \ ク\ \ }}$, $\boxed{\boxed{\ \ ケ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪0 ①x ②2x ③3x
④4x ⑤5x ⑥6x ⑦$\frac{x}{2}$
⑧$\frac{3}{2}x$ ⑨$\frac{5}{2}x$ ⓐ$\frac{7}{2}x$ ⓑ$\frac{9}{2}x$
(4)(2), (3)の考察から、$0 \leqq x \leqq \pi$のとき、$\sin 3x \gt \sin 4x \gt \sin 2x$が成り立つようなxの値の範囲は
$\displaystyle\frac{\pi}{\boxed{\ \ コ\ \ }}$ $\lt$ $\displaystyle\frac{\pi}{\boxed{\ \ ソ\ \ }}$, $\displaystyle\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi \lt x \lt \frac{\boxed{\ \ タ\ \ }}{\boxed{\ \ チ\ \ }}\pi$
であることがわかる。
[ 2 ]
(1)$a \gt 0$, $a \ne 1$, $b \gt 0$のとき、$\log_ab=x$とおくと、$\boxed{\boxed{\ \ ツ\ \ }}$が成り立つ。
$\boxed{\boxed{\ \ ツ\ \ }}$の解答群
⓪$x^a=b$ ①$x^b=a$ ②$a^x=b$
③$b^x=a$ ④$a^b=x$ ⑤$b^a=x$
(2)様々な対数の値が有理数か無理数かについて考えよう。
(i)$\log_5 25=\boxed{\ \ テ\ \ }$, $\log_9 27=\displaystyle\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}$であり、どちらも有理数である。
(ii)$\log_2 3$が有理数と無理数のどちらかであるかを考えよう。
$\log_2 3$が有理数であると仮定すると、$\log_2 3$>0であるので、二つの自然数p, qを用いて$\log_2 3=\displaystyle\frac{p}{q}$と表すことができる。このとき、(1)により$\log_2 3=\displaystyle\frac{p}{q}$は$\boxed{\boxed{\ \ ニ\ \ }}$と変形できる。いま、2は偶数であり3は奇数であるので、$\boxed{\boxed{\ \ ニ\ \ }}$を満たす自然数p, qは存在しない。
したがって、$\log_2 3$は無理数であることがわかる。
(iii)a, bを2以上の自然数とするとき、(ii)と同様に考えると、「$\boxed{\boxed{\ \ ヌ\ \ }}$ならば$\log_a b$は常に無理数である」ことがわかる。
$\boxed{\boxed{\ \ ヌ\ \ }}$の解答群
⓪aが偶数 ①bが偶数 ②aが奇数
③bが奇数 ④aとbがともに偶数、またはaとbがともに奇数 ⑤aとbのいずれか一方が偶数で、もう一方が奇数
2023共通テスト過去問
立命館大 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 55x^2+2xy+y^2=2007$をみたす整数(x,y)をすべて求めよ.
立命館大過去問
この動画を見る
$ 55x^2+2xy+y^2=2007$をみたす整数(x,y)をすべて求めよ.
立命館大過去問
こんなに楽しい方程式はこの世に存在しない 東工大附属
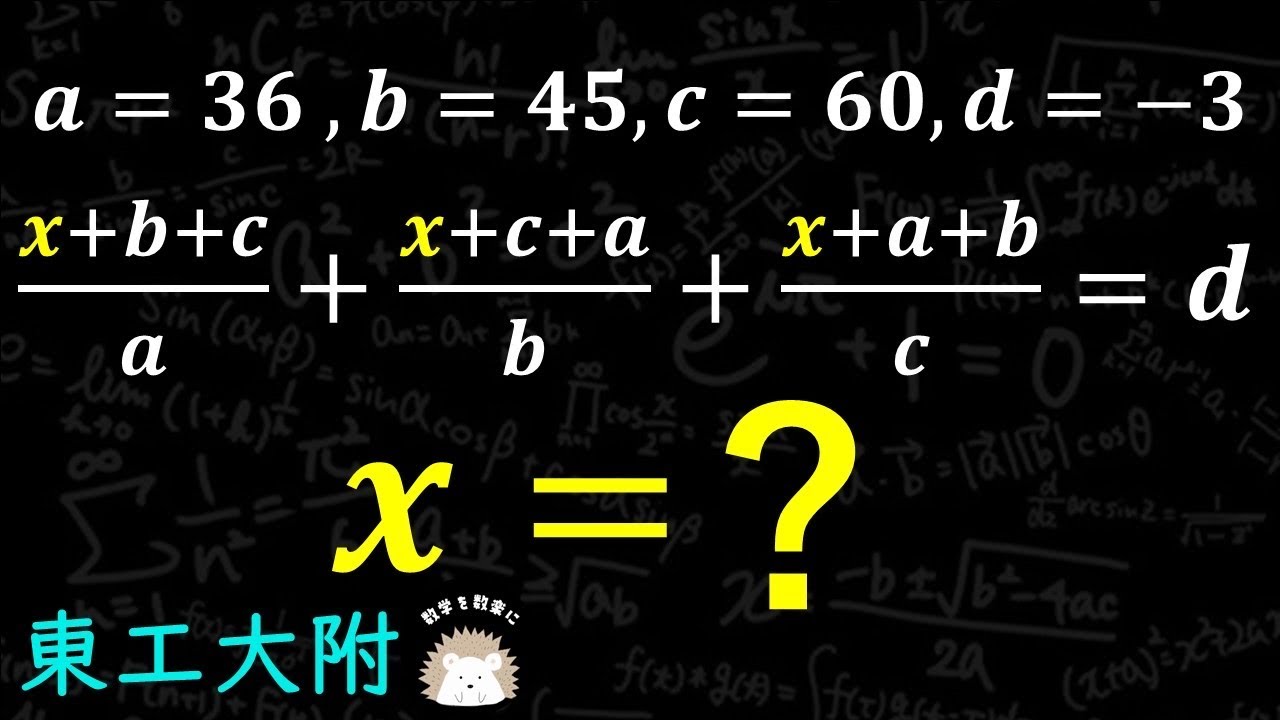
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a=36,b=45,c=60,d=-3$
$\frac{x+b+c}{a} + \frac{x+c+a}{b} + \frac{x+a+b}{c} = d$
x=?
東京工業大学附属科学技術高等学校
この動画を見る
$a=36,b=45,c=60,d=-3$
$\frac{x+b+c}{a} + \frac{x+c+a}{b} + \frac{x+a+b}{c} = d$
x=?
東京工業大学附属科学技術高等学校
福田の1.5倍速演習〜合格する重要問題074〜立教大学2019年度経済学部第1問(6)〜最大公約数を求める

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (6)14351と14803の最大公約数は$\boxed{\ \ キ \ \ }$である。
2019立教大学経済学部過去問
この動画を見る
$\Large\boxed{1}$ (6)14351と14803の最大公約数は$\boxed{\ \ キ \ \ }$である。
2019立教大学経済学部過去問
図形×整数問題!差がつく問題です【一橋大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
直角三角形の3辺の長さがすべて整数のとき、面積は2の整数倍であることを示せ。
一橋大過去問
この動画を見る
直角三角形の3辺の長さがすべて整数のとき、面積は2の整数倍であることを示せ。
一橋大過去問
2023高校入試解説24問目 二乗の和で表せ③ 昭和学院秀英(改)

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
7225は4つの自然数で2乗の和で表せる。
例を1つあげよ。
2023昭和学院秀英高等学校
この動画を見る
7225は4つの自然数で2乗の和で表せる。
例を1つあげよ。
2023昭和学院秀英高等学校
2023高校入試解説18問目 約数の個数が3個 西武文理

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
自然数nの約数は3個その和は57
n=?
2023西部学園文理高等学校
この動画を見る
自然数nの約数は3個その和は57
n=?
2023西部学園文理高等学校
勘で英検合格する確率は?

単元:
#数A#場合の数と確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
全部勘で英検やって合格する確率ってどれくらいですか?
この動画を見る
下記質問の解説動画です
全部勘で英検やって合格する確率ってどれくらいですか?
2023高校入試解説17問目 3つの内接円 渋谷教育学園幕張
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
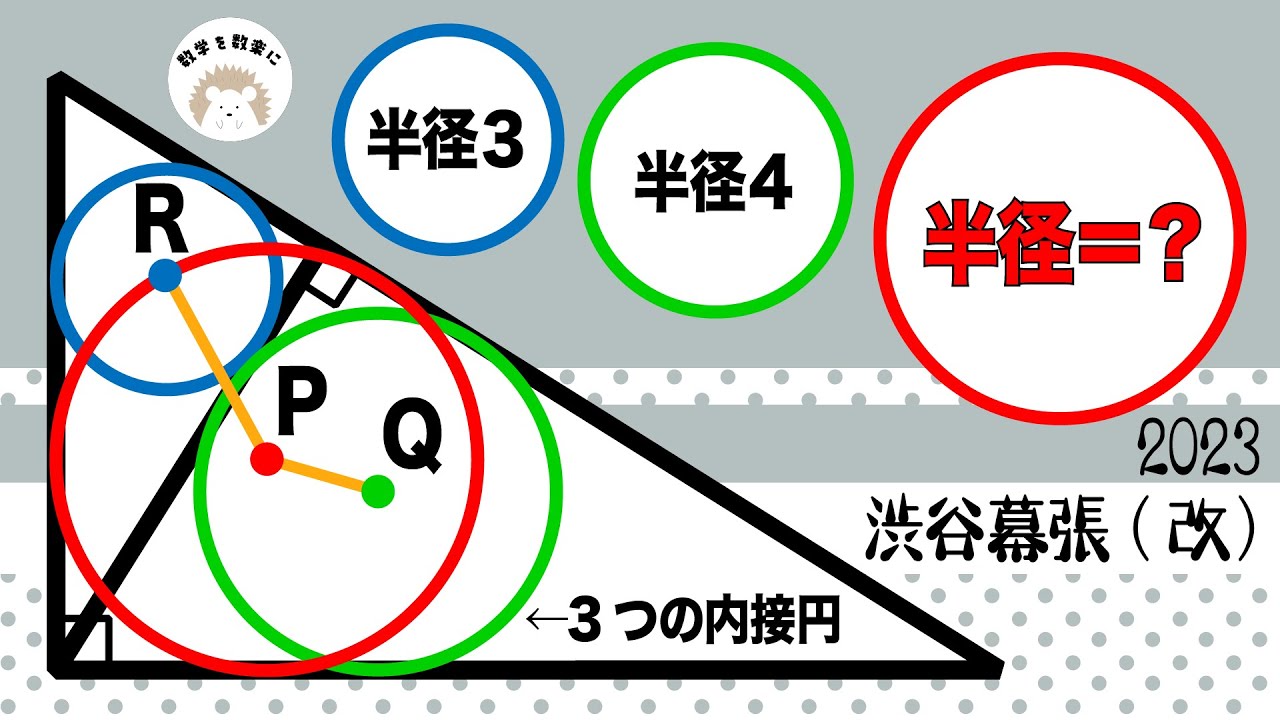
青○:半径3
緑○:半径4
赤○:半径=?
*図は動画内参照
2023渋谷教育学園幕張高等学校(改)
この動画を見る
青○:半径3
緑○:半径4
赤○:半径=?
*図は動画内参照
2023渋谷教育学園幕張高等学校(改)
福田の1.5倍速演習〜合格する重要問題067〜九州大学2017年度文系第4問〜最大公約数

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{4}}$ 以下の問いに答えよ。
(1) 2017と225の最大公約数を求めよ。
(2) 225との最大公約数が15となる2017以下の自然数の個数を求めよ。
(3) 225との最大公約数が15であり、かつ1998との最大公約数が111となる2017以下の自然数を全て求めよ。
2017九州大学文系過去問
この動画を見る
$\Large{\boxed{4}}$ 以下の問いに答えよ。
(1) 2017と225の最大公約数を求めよ。
(2) 225との最大公約数が15となる2017以下の自然数の個数を求めよ。
(3) 225との最大公約数が15であり、かつ1998との最大公約数が111となる2017以下の自然数を全て求めよ。
2017九州大学文系過去問
2023高校入試解説15問目 3種類の4ケタの数 渋谷教育学園幕張 コメントに別解多数あり!!

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
1000~9999の4ケタの整数について2023のようにちょうど3種類の数字が用いられている整数は何個?
2023渋谷教育学園幕張高等学校
この動画を見る
1000~9999の4ケタの整数について2023のようにちょうど3種類の数字が用いられている整数は何個?
2023渋谷教育学園幕張高等学校
見掛け倒しの「どっちがでかい?」

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
どちらが大きいか?
$P_{2022} vs P_{2023}$
$P_n$はサイコロをn回ふって出た目の和が7の倍数になる確率を求めよ.
この動画を見る
どちらが大きいか?
$P_{2022} vs P_{2023}$
$P_n$はサイコロをn回ふって出た目の和が7の倍数になる確率を求めよ.
福田の数学〜2023年共通テスト速報〜数学IA第5問図形の性質〜作図によって描いた図形の性質

単元:
#数A#図形の性質#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
【第5問】
(1) 円Oに対して、次の手順1で作図を行う。
[手順1]
(Step 1) 円Oと異なる2点で交わり、中心Oを通らない直線lを引く。円Oと直線lとの交点をA, Bとし、線分ABの中点Cをとる。
(Step 2) 円Oの周上に、点Dを$\angle COD$が鈍角となるようにとる。直線CDを引き、円Oとの交点でDとは異なる点をEとする。
(Step 3) 点Dを通り直線OCに垂直な直線を引き、直線OCとの交点をFとし、円Oとの交点でDとは異なる点をGとする。
(Step 4) 点Gにおける円Oの接線を引き、直線lとの交点をHとする。
このとき、直線lと点Dの位置によらず、直線EHは円Oの接線である。このことは、次の構想に基づいて、後のように説明できる。
[構想]
直線EHが円Oの接線であることを証明するためには、$\angle OEH=\boxed{\ \ アイ\ \ }°$であることを示せばよい。
手順1の(Step 1)と(Step 4)により、4点C, G, H, $\boxed{\boxed{\ \ ウ\ \ }}$は同一円周上にあることがわかる。よって、$\angle CHG=\boxed{\boxed{\ \ エ\ \ }}$である。一方、点Eは円Oの周上にあることから、$\boxed{\boxed{\ \ エ\ \ }}=\boxed{\boxed{\ \ オ\ \ }}$がわかる。よって、$\angle CHG=\boxed{\boxed{\ \ オ\ \ }}$であるので、4点C, G, H, $\boxed{\boxed{\ \ カ\ \ }}$は同一円周上にある。この円が点$\boxed{\boxed{\ \ ウ\ \ }}$を通ることにより、$\angle OEH=\boxed{\ \ アイ\ \ }°$を示すことができる。
$\boxed{\boxed{\ \ ウ\ \ }}$の解答群
⓪B ①D ②F ③O
$\boxed{\boxed{\ \ エ\ \ }}$の解答群
⓪$\angle AFC$ ①$\angle CDF$ ②$\angle CGH$ ③$\angle CBO$ ④$\angle FOG$
$\boxed{\boxed{\ \ オ\ \ }}$の解答群
⓪$\angle AED$ ①$\angle ADE$ ②$\angle BOE$ ③$\angle DEG$ ④$\angle EOH$
$\boxed{\boxed{\ \ カ\ \ }}$の解答群
⓪A ①D ②E ③F
(2) 円Oに対して、(1)の手順1とは直線lの引き方を変え、次の手順2で作図を行う。
[手順2]
(Step 1) 円Oと共有点をもたない直線lを引く。中心Oから直線lに垂直な直線を引き、直線lとの交点をPとする。
(Step 2) 円Oの周上に、点Qを$\angle POQ$が鈍角となるようにとる。直線PQを引き、円Oとの交点でQとは異なる点をRとする。
(Step 3) 点Qを通り直線OPに垂直な直線を引き、円Oとの交点でQとは異なる点をSとする。
(Step 4) 点Sにおける円Oの接線を引き、直線lとの交点をTとする。
このとき、$\angle PTS=\boxed{\boxed{\ \ キ\ \ }}$である。
円Oの半径が$\sqrt 5$で、OT=$3\sqrt 6$であったとすると、3点O, P, Rを通る円の半径は$\frac{\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}}{\boxed{\ \ コ\ \ }}$であり、RT=$\boxed{\ \ サ\ \ }$である。
$\boxed{\boxed{\ \ キ\ \ }}$の解答群
⓪$\angle PQS$ ①$\angle PST$ ②$\angle QPS$ ③$\angle QRS$ ④$\angle SRT$
2023共通テスト過去問
この動画を見る
【第5問】
(1) 円Oに対して、次の手順1で作図を行う。
[手順1]
(Step 1) 円Oと異なる2点で交わり、中心Oを通らない直線lを引く。円Oと直線lとの交点をA, Bとし、線分ABの中点Cをとる。
(Step 2) 円Oの周上に、点Dを$\angle COD$が鈍角となるようにとる。直線CDを引き、円Oとの交点でDとは異なる点をEとする。
(Step 3) 点Dを通り直線OCに垂直な直線を引き、直線OCとの交点をFとし、円Oとの交点でDとは異なる点をGとする。
(Step 4) 点Gにおける円Oの接線を引き、直線lとの交点をHとする。
このとき、直線lと点Dの位置によらず、直線EHは円Oの接線である。このことは、次の構想に基づいて、後のように説明できる。
[構想]
直線EHが円Oの接線であることを証明するためには、$\angle OEH=\boxed{\ \ アイ\ \ }°$であることを示せばよい。
手順1の(Step 1)と(Step 4)により、4点C, G, H, $\boxed{\boxed{\ \ ウ\ \ }}$は同一円周上にあることがわかる。よって、$\angle CHG=\boxed{\boxed{\ \ エ\ \ }}$である。一方、点Eは円Oの周上にあることから、$\boxed{\boxed{\ \ エ\ \ }}=\boxed{\boxed{\ \ オ\ \ }}$がわかる。よって、$\angle CHG=\boxed{\boxed{\ \ オ\ \ }}$であるので、4点C, G, H, $\boxed{\boxed{\ \ カ\ \ }}$は同一円周上にある。この円が点$\boxed{\boxed{\ \ ウ\ \ }}$を通ることにより、$\angle OEH=\boxed{\ \ アイ\ \ }°$を示すことができる。
$\boxed{\boxed{\ \ ウ\ \ }}$の解答群
⓪B ①D ②F ③O
$\boxed{\boxed{\ \ エ\ \ }}$の解答群
⓪$\angle AFC$ ①$\angle CDF$ ②$\angle CGH$ ③$\angle CBO$ ④$\angle FOG$
$\boxed{\boxed{\ \ オ\ \ }}$の解答群
⓪$\angle AED$ ①$\angle ADE$ ②$\angle BOE$ ③$\angle DEG$ ④$\angle EOH$
$\boxed{\boxed{\ \ カ\ \ }}$の解答群
⓪A ①D ②E ③F
(2) 円Oに対して、(1)の手順1とは直線lの引き方を変え、次の手順2で作図を行う。
[手順2]
(Step 1) 円Oと共有点をもたない直線lを引く。中心Oから直線lに垂直な直線を引き、直線lとの交点をPとする。
(Step 2) 円Oの周上に、点Qを$\angle POQ$が鈍角となるようにとる。直線PQを引き、円Oとの交点でQとは異なる点をRとする。
(Step 3) 点Qを通り直線OPに垂直な直線を引き、円Oとの交点でQとは異なる点をSとする。
(Step 4) 点Sにおける円Oの接線を引き、直線lとの交点をTとする。
このとき、$\angle PTS=\boxed{\boxed{\ \ キ\ \ }}$である。
円Oの半径が$\sqrt 5$で、OT=$3\sqrt 6$であったとすると、3点O, P, Rを通る円の半径は$\frac{\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}}{\boxed{\ \ コ\ \ }}$であり、RT=$\boxed{\ \ サ\ \ }$である。
$\boxed{\boxed{\ \ キ\ \ }}$の解答群
⓪$\angle PQS$ ①$\angle PST$ ②$\angle QPS$ ③$\angle QRS$ ④$\angle SRT$
2023共通テスト過去問
福田の1.5倍速演習〜合格する重要問題066〜九州大学2017年度理系第3問〜等差数列の7の倍数になる項の個数

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ 初項$a_1=1$, 公差4の等差数列$\left\{a_n\right\}$を考える。以下の問いに答えよ。
(1) $\left\{a_n\right\}$の初項から第600項のうち、7の倍数である項の個数を求めよ。
(2) $\left\{a_n\right\}$の初項から第600項のうち、$7^2$の倍数である項の個数を求めよ。
(3) 初項から第n項までの積$a_1a_2\cdots a_n$が$7^{45}$の倍数となる最小の自然数nを求めよ。
2017九州大学理系過去問
この動画を見る
$\Large{\boxed{3}}$ 初項$a_1=1$, 公差4の等差数列$\left\{a_n\right\}$を考える。以下の問いに答えよ。
(1) $\left\{a_n\right\}$の初項から第600項のうち、7の倍数である項の個数を求めよ。
(2) $\left\{a_n\right\}$の初項から第600項のうち、$7^2$の倍数である項の個数を求めよ。
(3) 初項から第n項までの積$a_1a_2\cdots a_n$が$7^{45}$の倍数となる最小の自然数nを求めよ。
2017九州大学理系過去問
2023高校入試解説12問目 台形と半円 解き方2通り 日大習志野(改)

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$AD=\frac{9}{4}$
半円Oの面積=?
*図は動画内参照
2023日本大学習志野高等学校
この動画を見る
$AD=\frac{9}{4}$
半円Oの面積=?
*図は動画内参照
2023日本大学習志野高等学校
福田の1.5倍速演習〜合格する重要問題065〜中央大学2019年度理工学部第3問〜反復試行と確率漸化式

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$ Oを原点とする平面上の動点Rが$R_0$(1, 0)から出発して、単位円の周上を1秒ごとに反時計周りに移動する。移動するときの動径ORの回転角は、確率$\frac{1}{2}$で$\frac{\pi}{6}$、確率$\frac{1}{2}$で$\frac{\pi}{3}$である。n秒後のRの位置を$R_n$とする。以下の問いに答えよ。
(1)$R_5$が(-1, 0)である確率を求めよ。
(2)$R_9$がx軸上にある確率を求めよ。
次に、$R_n$がx軸上またはy軸上にある確率を$p_n$(n≧1)とする。
(3)$p_{n+1}$を$p_n$を用いて表せ。
(4)$p_n$を求めよ。
2019中央大学理工学部過去問
この動画を見る
$\boxed{3}$ Oを原点とする平面上の動点Rが$R_0$(1, 0)から出発して、単位円の周上を1秒ごとに反時計周りに移動する。移動するときの動径ORの回転角は、確率$\frac{1}{2}$で$\frac{\pi}{6}$、確率$\frac{1}{2}$で$\frac{\pi}{3}$である。n秒後のRの位置を$R_n$とする。以下の問いに答えよ。
(1)$R_5$が(-1, 0)である確率を求めよ。
(2)$R_9$がx軸上にある確率を求めよ。
次に、$R_n$がx軸上またはy軸上にある確率を$p_n$(n≧1)とする。
(3)$p_{n+1}$を$p_n$を用いて表せ。
(4)$p_n$を求めよ。
2019中央大学理工学部過去問
福田の数学〜2023年共通テスト速報〜数学IA第4問整数〜長方形のタイルを並べて長方形を作る

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
第4問
色のついた長方形を並べて正方形や長方形を作ることを考える。色のついた長方形は、向きを変えずにすき間なく並べることとし、色のついた長方形は十分あるものとする。
(1)横の長さが462で縦の長さが110である赤い長方形を、図1(※動画参照)のように並べて正方形や長方形を作ることを考える。
462と110の両方を割り切る素数のうち最大のものは$\boxed{\ \ アイ\ \ }$である。
赤い長方形を並べて作ることができる正方形のうち、辺の長さが最小であるものは、一辺の長さが$\boxed{\ \ ウエオカ\ \ }$のものである。
また、赤い長方形を並べて正方形ではない長方形を作るとき、横の長さと縦の長さの差の絶対値が最小になるのは、462の約数と110の約数を考えると、差の絶対値が$\boxed{\ \ キク\ \ }$になるときであることがわかる。
縦の長さが横の長さより$\boxed{\ \ キク\ \ }$長い長方形のうち、横の長さが最小であるものは、横の長さが$\boxed{\ \ ケコサシ\ \ }$のものである。
(2)花子さんと太郎さんは、(1)で用いた赤い長方形を1枚以上並べて長方形を作り、その右側に横の長さが363で縦の長さが154である青い長方形を1枚以上並べて、図2(※動画参照)のような正方形や長方形を作ることを考えている。
このとき、赤い長方形を並べてできる長方形の縦の長さと、青い長方形を並べてできる長方形の縦の長さは等しい。よって、図2のような長方形のうち、縦の長さが最小のものは、縦の長さが$\boxed{\ \ スセソ\ \ }$のものであり、図2のような長方形は縦の長さが$\boxed{\ \ スセソ\ \ }$の倍数である。
二人は、次のように話している。
花子:赤い長方形と青い長方形を図2のように並べて正方形を作ってみようよ。
太郎:赤い長方形の横の長さが462で青い長方形の横の長さが363だから、図2のような正方形の横の長さは462と363を組み合わせて作ることができる長さでないといけないね。
花子:正方形だから、横の長さは$\boxed{\ \ スセソ\ \ }$の倍数でもないといけないね。
462と363の最大公約数は$\boxed{\ \ タチ\ \ }$であり、$\boxed{\ \ タチ\ \ }$の倍数のうちで$\boxed{\ \ スセソ\ \ }$の倍数でもある最小の正の整数は$\boxed{\ \ ツテトナ\ \ }$である。
これらのことと、使う長方形の枚数が赤い長方形も青い長方形も1枚以上であることから、図2のような正方形のうち、辺の長さが最小であるものは、一辺の長さが$\boxed{\ \ ニヌネノ\ \ }$のものであることがわかる。
2023共通テスト過去問
この動画を見る
第4問
色のついた長方形を並べて正方形や長方形を作ることを考える。色のついた長方形は、向きを変えずにすき間なく並べることとし、色のついた長方形は十分あるものとする。
(1)横の長さが462で縦の長さが110である赤い長方形を、図1(※動画参照)のように並べて正方形や長方形を作ることを考える。
462と110の両方を割り切る素数のうち最大のものは$\boxed{\ \ アイ\ \ }$である。
赤い長方形を並べて作ることができる正方形のうち、辺の長さが最小であるものは、一辺の長さが$\boxed{\ \ ウエオカ\ \ }$のものである。
また、赤い長方形を並べて正方形ではない長方形を作るとき、横の長さと縦の長さの差の絶対値が最小になるのは、462の約数と110の約数を考えると、差の絶対値が$\boxed{\ \ キク\ \ }$になるときであることがわかる。
縦の長さが横の長さより$\boxed{\ \ キク\ \ }$長い長方形のうち、横の長さが最小であるものは、横の長さが$\boxed{\ \ ケコサシ\ \ }$のものである。
(2)花子さんと太郎さんは、(1)で用いた赤い長方形を1枚以上並べて長方形を作り、その右側に横の長さが363で縦の長さが154である青い長方形を1枚以上並べて、図2(※動画参照)のような正方形や長方形を作ることを考えている。
このとき、赤い長方形を並べてできる長方形の縦の長さと、青い長方形を並べてできる長方形の縦の長さは等しい。よって、図2のような長方形のうち、縦の長さが最小のものは、縦の長さが$\boxed{\ \ スセソ\ \ }$のものであり、図2のような長方形は縦の長さが$\boxed{\ \ スセソ\ \ }$の倍数である。
二人は、次のように話している。
花子:赤い長方形と青い長方形を図2のように並べて正方形を作ってみようよ。
太郎:赤い長方形の横の長さが462で青い長方形の横の長さが363だから、図2のような正方形の横の長さは462と363を組み合わせて作ることができる長さでないといけないね。
花子:正方形だから、横の長さは$\boxed{\ \ スセソ\ \ }$の倍数でもないといけないね。
462と363の最大公約数は$\boxed{\ \ タチ\ \ }$であり、$\boxed{\ \ タチ\ \ }$の倍数のうちで$\boxed{\ \ スセソ\ \ }$の倍数でもある最小の正の整数は$\boxed{\ \ ツテトナ\ \ }$である。
これらのことと、使う長方形の枚数が赤い長方形も青い長方形も1枚以上であることから、図2のような正方形のうち、辺の長さが最小であるものは、一辺の長さが$\boxed{\ \ ニヌネノ\ \ }$のものであることがわかる。
2023共通テスト過去問
整数問題

単元:
#数Ⅰ#数A#数と式#式の計算(整式・展開・因数分解)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
nを自然数とする.
$(4n-1)^{2n+1}+(4n+1)^{2n-1}$は$32n^2$で割り切れることを示せ.
この動画を見る
nを自然数とする.
$(4n-1)^{2n+1}+(4n+1)^{2n-1}$は$32n^2$で割り切れることを示せ.
福田の数学〜2023年共通テスト速報〜数学IA第3問場合の数

単元:
#数A#場合の数と確率#場合の数#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
第3問
番号によって区別された複数の球が、何本かのひもでつながれている。ただし、各ひもはその両端で二つの球をつなぐものとする。次の条件を満たす球の塗り分け方(以下、球の塗り方)を考える。
【条件】
・それぞれの球を、用意した5色(赤、青、黄、緑、紫)のうちのいずれか1色で塗る。
・1本のひもでつながれた二つの球は異なる色になるようにする。
・同じ色を何回使ってもよく、また使わない色があってもよい。
例えば図A(※動画参照)では、三つの球が2本のひもでつながれている。この三つの球を塗るとき、球1の塗り方が5通りあり、球1を塗った後、球2の塗り方は4通りあり、さらに球3の塗り方は4通りある。したがって、球の塗り方の総数は80である。
(1)図B(※動画参照)において、球の塗り方は$\boxed{\ \ アイウ\ \ }$通りある。
(2)図C(※動画参照)において、球の塗り方は$\boxed{\ \ エオ\ \ }$通りある。
(3)図D(※動画参照)における球の塗り方のうち、赤をちょうど2回使う塗り方は$\boxed{\ \ カキ\ \ }$通りある。
(4)図E(※動画参照)における球の塗り方のうち、赤をちょうど3回使い、かつ青をちょうど2回使う塗り方は$\boxed{\ \ クケ\ \ }$通りある。
(5)図Dにおいて、球の塗り方の総数を求める。
そのために、次の構想を立てる。
【構想】
図Dと図Fを比較する。
図Fでは球3と球4が同色になる球の塗り方が可能であるため、図Dよりも図Fの球の塗り方の総数の方が大きい。
図Fにおける球の塗り方は、図Bにおける球の塗り方と同じであるため、全部で$\boxed{\ \ アイウ\ \ }$通りある。そのうち球3と球4が同色になる球の塗り方の総数と一致する図として、後の⓪~④のうち、正しいものは$\boxed{\boxed{\ \ コ\ \ }}$である。したがって、図Dにおける球の塗り方は$\boxed{\ \ サシス\ \ }$通りある。
$\boxed{\boxed{\ \ コ\ \ }}$の解答群
(解答群は動画参照)
(6)図Gにおいて、球の塗り方は$\boxed{\ \ セソタチ\ \ }$通りある。
2023共通テスト過去問
この動画を見る
第3問
番号によって区別された複数の球が、何本かのひもでつながれている。ただし、各ひもはその両端で二つの球をつなぐものとする。次の条件を満たす球の塗り分け方(以下、球の塗り方)を考える。
【条件】
・それぞれの球を、用意した5色(赤、青、黄、緑、紫)のうちのいずれか1色で塗る。
・1本のひもでつながれた二つの球は異なる色になるようにする。
・同じ色を何回使ってもよく、また使わない色があってもよい。
例えば図A(※動画参照)では、三つの球が2本のひもでつながれている。この三つの球を塗るとき、球1の塗り方が5通りあり、球1を塗った後、球2の塗り方は4通りあり、さらに球3の塗り方は4通りある。したがって、球の塗り方の総数は80である。
(1)図B(※動画参照)において、球の塗り方は$\boxed{\ \ アイウ\ \ }$通りある。
(2)図C(※動画参照)において、球の塗り方は$\boxed{\ \ エオ\ \ }$通りある。
(3)図D(※動画参照)における球の塗り方のうち、赤をちょうど2回使う塗り方は$\boxed{\ \ カキ\ \ }$通りある。
(4)図E(※動画参照)における球の塗り方のうち、赤をちょうど3回使い、かつ青をちょうど2回使う塗り方は$\boxed{\ \ クケ\ \ }$通りある。
(5)図Dにおいて、球の塗り方の総数を求める。
そのために、次の構想を立てる。
【構想】
図Dと図Fを比較する。
図Fでは球3と球4が同色になる球の塗り方が可能であるため、図Dよりも図Fの球の塗り方の総数の方が大きい。
図Fにおける球の塗り方は、図Bにおける球の塗り方と同じであるため、全部で$\boxed{\ \ アイウ\ \ }$通りある。そのうち球3と球4が同色になる球の塗り方の総数と一致する図として、後の⓪~④のうち、正しいものは$\boxed{\boxed{\ \ コ\ \ }}$である。したがって、図Dにおける球の塗り方は$\boxed{\ \ サシス\ \ }$通りある。
$\boxed{\boxed{\ \ コ\ \ }}$の解答群
(解答群は動画参照)
(6)図Gにおいて、球の塗り方は$\boxed{\ \ セソタチ\ \ }$通りある。
2023共通テスト過去問
ナイスな整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
nを自然数とする.
$(4n-1)^{2n+1}+(4n+1)^{2n-1}$は$8n$で割り切れることを示せ.
この動画を見る
nを自然数とする.
$(4n-1)^{2n+1}+(4n+1)^{2n-1}$は$8n$で割り切れることを示せ.
【日本最速解答速報】共通テスト2023数学1A 第1問(1)【今となっては過去問解説】

整式の剰余 xの2023乗

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^{2023}を\displaystyle \sum_{n=1}^{16} x^n=1+x+x^2+・・・・+x^{16}$で割った余りを求めよ.
この動画を見る
$ x^{2023}を\displaystyle \sum_{n=1}^{16} x^n=1+x+x^2+・・・・+x^{16}$で割った余りを求めよ.
角の二等分線➕平行線=❓

自作の整数問題 効率よく絞り込め
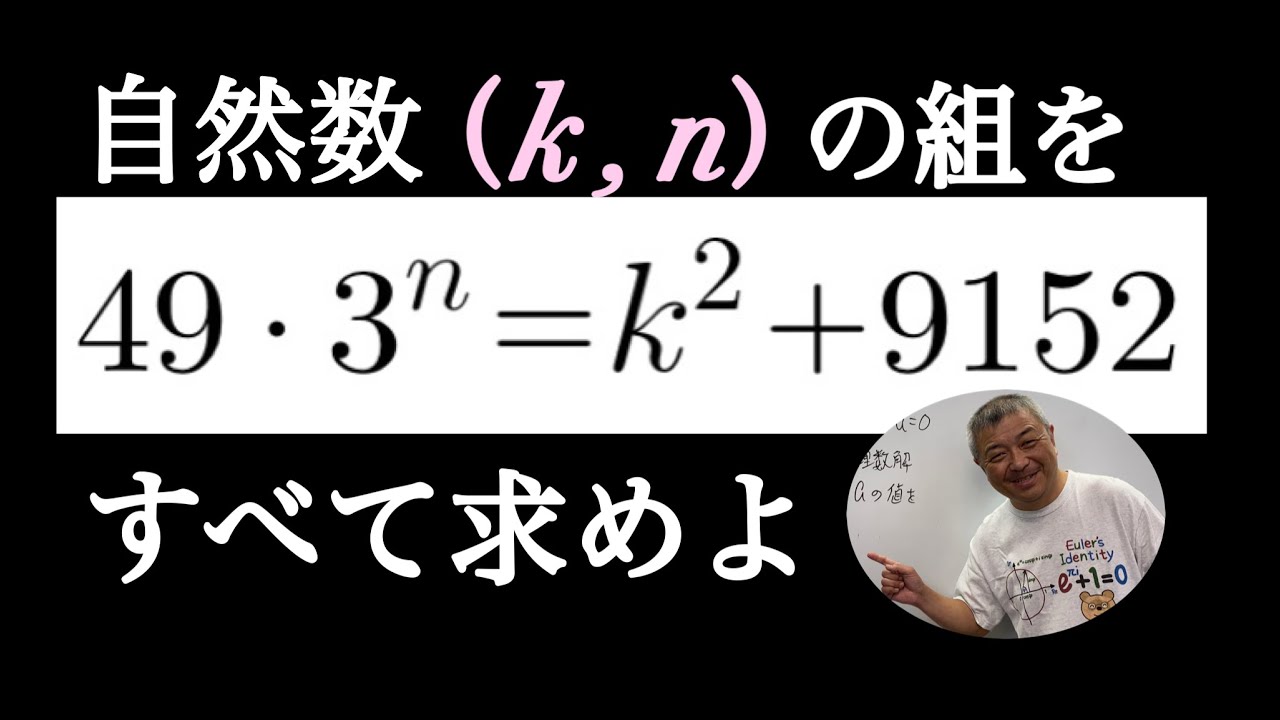
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
k,nを自然数とする.
$49・3^n=k^2+9152$
自然数(k,n)の組をすべて求めよ.
この動画を見る
k,nを自然数とする.
$49・3^n=k^2+9152$
自然数(k,n)の組をすべて求めよ.
福田の1.5倍速演習〜合格する重要問題059〜慶應義塾大学2019年度薬学部第1問(7)〜球に内接する四角錐の体積の最大値

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#円と方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (7)正四角錐ABCDEの全ての頂点は半径3の球面上にある。
この正四角錐の体積Vの最大値は$\boxed{\ \ ソ\ \ }$である。
2019慶應義塾大学薬学部過去問
この動画を見る
$\Large{\boxed{1}}$ (7)正四角錐ABCDEの全ての頂点は半径3の球面上にある。
この正四角錐の体積Vの最大値は$\boxed{\ \ ソ\ \ }$である。
2019慶應義塾大学薬学部過去問
宮崎大 整数問題基本

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
素数Pを2進法で表したらすべての位の数が1でk桁であったkは素数であることを示せ.
宮崎大過去問
この動画を見る
素数Pを2進法で表したらすべての位の数が1でk桁であったkは素数であることを示せ.
宮崎大過去問
2023高校入試解説8問目 内接円 西大和学園 内接円

単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△ABC∽△PRQ
△PRQ=?
*図は動画内参照
2023西大和学園高等学校
この動画を見る
△ABC∽△PRQ
△PRQ=?
*図は動画内参照
2023西大和学園高等学校
福田の1.5倍速演習〜合格する重要問題058〜慶應義塾大学2019年度環境情報学部第5問〜正方形の中の内接外接する円の半径

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#円と方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{5}}$ 図のように(※動画参照)、1つの正方形の中に、半径の異なる3種類の円が合計10個配置されている。
円$A_1$と$A_2$は半径が同じRで、それぞれ図のように正方形の2辺に内接している。
円$B_1,B_2,B_3,B_4,B_5,B_6$は半径が同じrで、円$B_1$と$B_2$は接し、
図のように両方とも円$A_1$に内接し円$A_2$に外接している。円$B_3$と$B_4$は接し、図のように両方とも円$A_1$と円$A_2$に内接している。円$B_5$と$B_6$は接し、
図のように両方とも円$A_1$に外接し円$A_2$に内接している。
円$C_1$と$C_2$は半径が同じ$r'$で、それぞれ図のように正方形の2辺に内接し、円$A_1$と$A_2$に外接している。なお、円$B_1,B_2,B_5,B_6$は正方形の辺に接していない。
このとき、正方形の1辺の長さをsとすると
$\left\{\begin{array}{1}
R=\displaystyle\frac{\boxed{\ \ アイ\ \ }}{\boxed{\ \ ウエ\ \ }}r \\
s=\left(\boxed{\ \ オカ\ \ }\sqrt{R}+\boxed{\ \ キク\ \ }\sqrt{r'}\right)^{\boxed{ケコ}}\\
r'=\frac{\boxed{\ \ サシ\ \ }+\displaystyle\sqrt{10}+\boxed{\ \ スセ\ \ }\sqrt{\boxed{\ \ ソタ\ \ }+\displaystyle5\sqrt{10}}}{\boxed{\ \ チツ\ \ }}r\\
\end{array}\right.$
である。
2019慶應義塾大学環境情報学部過去問
この動画を見る
$\Large{\boxed{5}}$ 図のように(※動画参照)、1つの正方形の中に、半径の異なる3種類の円が合計10個配置されている。
円$A_1$と$A_2$は半径が同じRで、それぞれ図のように正方形の2辺に内接している。
円$B_1,B_2,B_3,B_4,B_5,B_6$は半径が同じrで、円$B_1$と$B_2$は接し、
図のように両方とも円$A_1$に内接し円$A_2$に外接している。円$B_3$と$B_4$は接し、図のように両方とも円$A_1$と円$A_2$に内接している。円$B_5$と$B_6$は接し、
図のように両方とも円$A_1$に外接し円$A_2$に内接している。
円$C_1$と$C_2$は半径が同じ$r'$で、それぞれ図のように正方形の2辺に内接し、円$A_1$と$A_2$に外接している。なお、円$B_1,B_2,B_5,B_6$は正方形の辺に接していない。
このとき、正方形の1辺の長さをsとすると
$\left\{\begin{array}{1}
R=\displaystyle\frac{\boxed{\ \ アイ\ \ }}{\boxed{\ \ ウエ\ \ }}r \\
s=\left(\boxed{\ \ オカ\ \ }\sqrt{R}+\boxed{\ \ キク\ \ }\sqrt{r'}\right)^{\boxed{ケコ}}\\
r'=\frac{\boxed{\ \ サシ\ \ }+\displaystyle\sqrt{10}+\boxed{\ \ スセ\ \ }\sqrt{\boxed{\ \ ソタ\ \ }+\displaystyle5\sqrt{10}}}{\boxed{\ \ チツ\ \ }}r\\
\end{array}\right.$
である。
2019慶應義塾大学環境情報学部過去問
2023高校入試解説6問目 座標平面上の正三角形 西大和学園
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
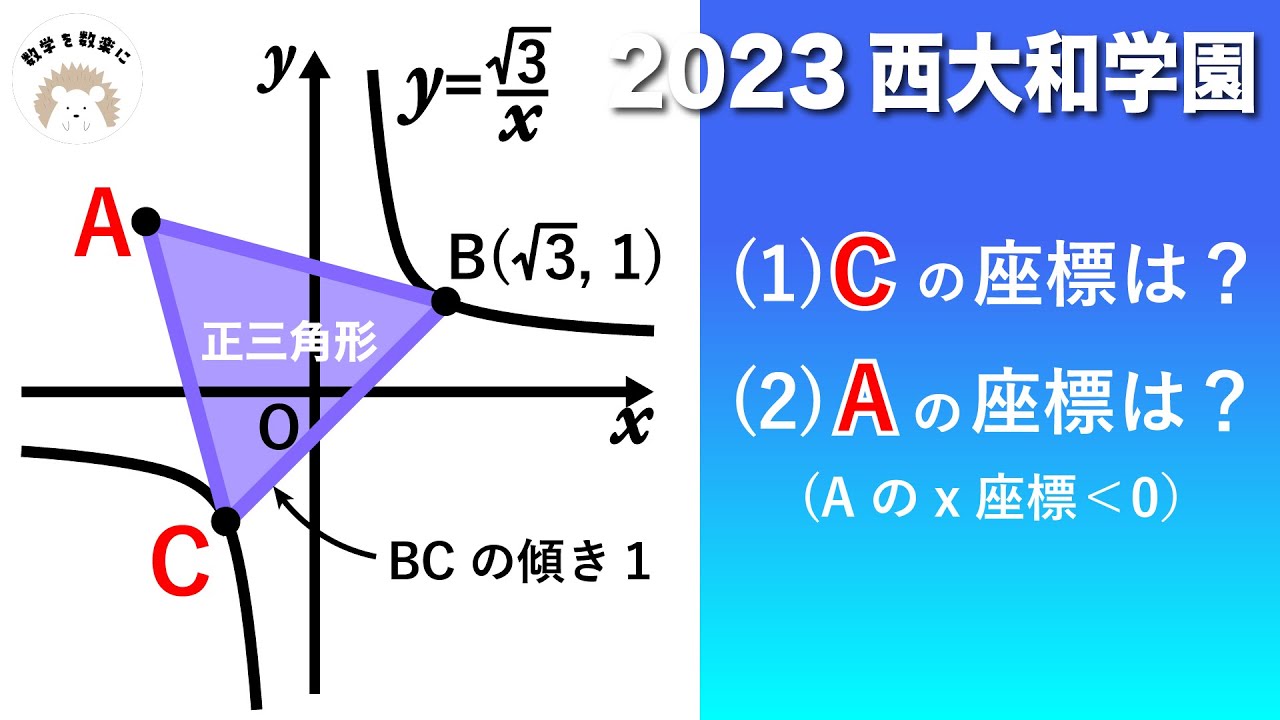
(1)Cの座標は?
(2)Aの座標は?
(Aのx座標<0)
*図は動画内参照
2023西大和学園高等学校
この動画を見る
(1)Cの座標は?
(2)Aの座標は?
(Aのx座標<0)
*図は動画内参照
2023西大和学園高等学校
福田の1.5倍速演習〜合格する重要問題057〜慶應義塾大学大学2019年度商学部第3問〜グループ分けの確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ 男子7人、女子5人の12人の中から3人を選んで第1グループを作る。次に、残った人の中から3人を選んで第2グループを作る。
(1)第1グループの男子の数が
0人である確率は$\displaystyle\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イウ\ \ }}$
1人である確率は$\displaystyle\frac{\boxed{\ \ エ\ \ }}{\boxed{\ \ オカ\ \ }}$
2人である確率は$\displaystyle\frac{\boxed{\ \ キク\ \ }}{\boxed{\ \ ケコ\ \ }}$
3人である確率は$\displaystyle\frac{\boxed{\ \ サ\ \ }}{\boxed{\ \ シス\ \ }}$
である。
(2)第1グループも第2グループも男子の数が1人である確率は$\frac{\boxed{\ \ セ\ \ }}{\boxed{\ \ ソタ\ \ }}$である。また、第2グループの男子の数が1人である確率は$\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツテ\ \ }}$である。
(3)第2グループの男子の数が1人であるとき、第1グループの男子の数も1人である確率は$\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナニ\ \ }}$である。
2019慶應義塾大学商学部過去問
この動画を見る
$\Large{\boxed{3}}$ 男子7人、女子5人の12人の中から3人を選んで第1グループを作る。次に、残った人の中から3人を選んで第2グループを作る。
(1)第1グループの男子の数が
0人である確率は$\displaystyle\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イウ\ \ }}$
1人である確率は$\displaystyle\frac{\boxed{\ \ エ\ \ }}{\boxed{\ \ オカ\ \ }}$
2人である確率は$\displaystyle\frac{\boxed{\ \ キク\ \ }}{\boxed{\ \ ケコ\ \ }}$
3人である確率は$\displaystyle\frac{\boxed{\ \ サ\ \ }}{\boxed{\ \ シス\ \ }}$
である。
(2)第1グループも第2グループも男子の数が1人である確率は$\frac{\boxed{\ \ セ\ \ }}{\boxed{\ \ ソタ\ \ }}$である。また、第2グループの男子の数が1人である確率は$\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツテ\ \ }}$である。
(3)第2グループの男子の数が1人であるとき、第1グループの男子の数も1人である確率は$\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナニ\ \ }}$である。
2019慶應義塾大学商学部過去問
