 整式の除法・分数式・二項定理
整式の除法・分数式・二項定理
 整式の除法・分数式・二項定理
整式の除法・分数式・二項定理
間違い説明できる?
単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
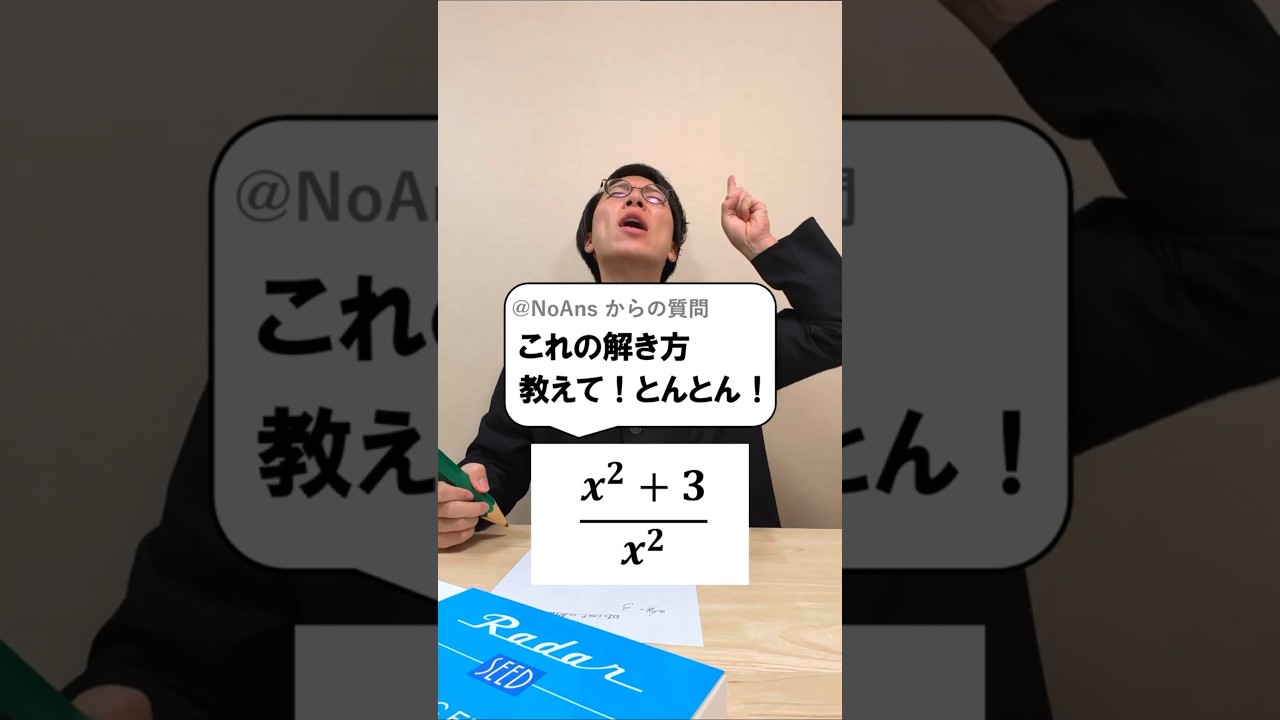
この計算の解き方を解説していきます。
$\dfrac{x^2+3}{x^2}$
この動画を見る
この計算の解き方を解説していきます。
$\dfrac{x^2+3}{x^2}$
福田のおもしろ数学564〜1分チャレンジ!数値計算

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\dfrac{2025^3+2024^3+3\cdot 2025\cdot 2024-1}{2026^2+2025^2+1}$
を計算して下さい。
この動画を見る
$\dfrac{2025^3+2024^3+3\cdot 2025\cdot 2024-1}{2026^2+2025^2+1}$
を計算して下さい。
福田のおもしろ数学553〜部分分数分解を工夫してやろう
単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
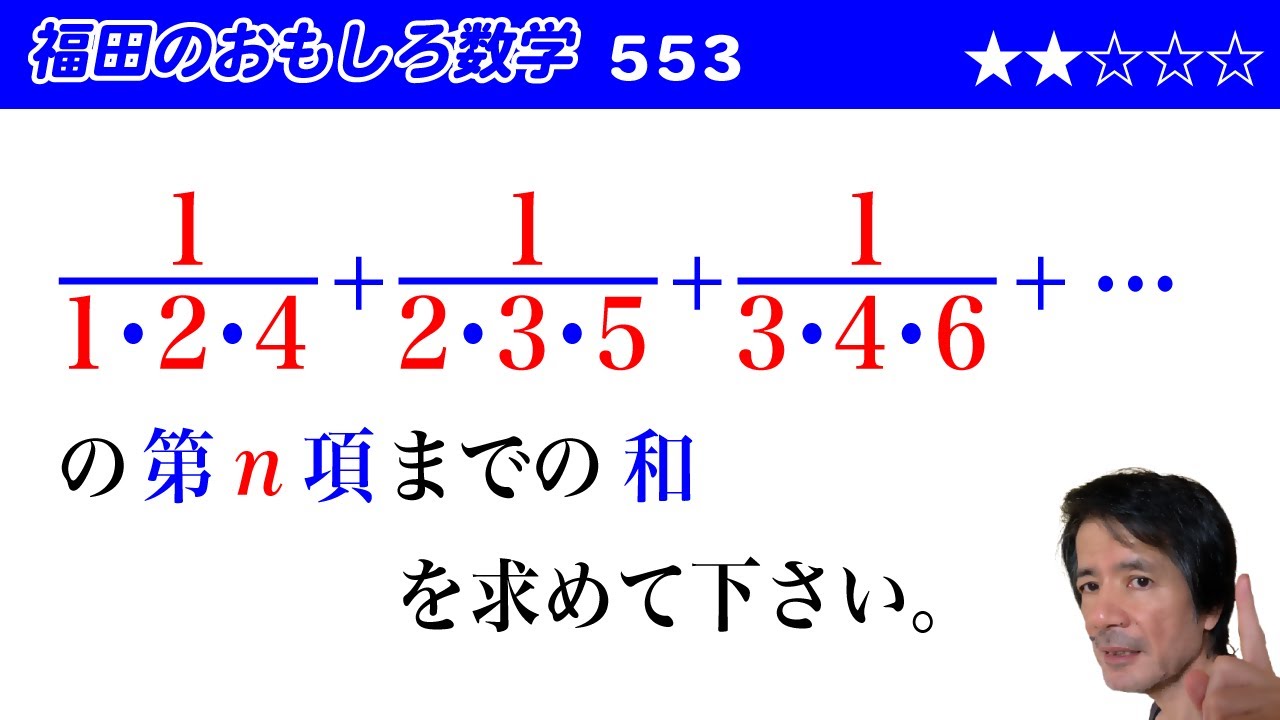
$\dfrac{1}{1\cdot 2 \cdot 4}+\dfrac{1}{2\cdot 3 \cdot 5}+\dfrac{1}{3\cdot 4 \cdot 6}+\cdots$
の第$n$項までの和を求めて下さい。
この動画を見る
$\dfrac{1}{1\cdot 2 \cdot 4}+\dfrac{1}{2\cdot 3 \cdot 5}+\dfrac{1}{3\cdot 4 \cdot 6}+\cdots$
の第$n$項までの和を求めて下さい。
福田のおもしろ数学546〜1分チャレンジ!数値計算の計算
単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
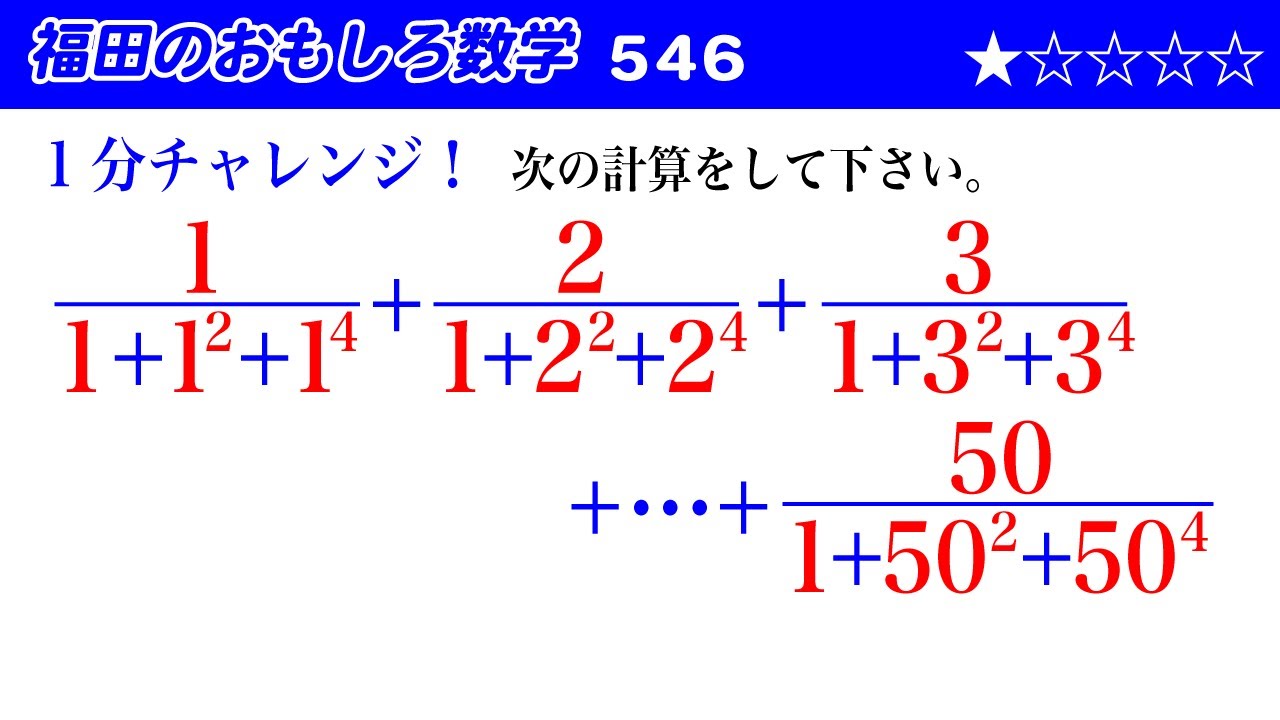
次の計算をして下さい。
$\dfrac{1}{1+1^2+1^4}+\dfrac{2}{1+2^2+2^4}+\dfrac{3}{1+3^2+3^4}+\cdots + \dfrac{50}{1+50^2+50^4}$
この動画を見る
次の計算をして下さい。
$\dfrac{1}{1+1^2+1^4}+\dfrac{2}{1+2^2+2^4}+\dfrac{3}{1+3^2+3^4}+\cdots + \dfrac{50}{1+50^2+50^4}$
福田のおもしろ数学540〜二項係数の2乗の和

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${{}_n \mathrm{ C }_0}^2+{{}_n \mathrm{ C }_1}^2+{{}_n \mathrm{ C }_2}^2+\cdots + {{}_n \mathrm{ C }_n}^2=\dfrac{(2n)!}{(n!)^2}$
を証明してください。
この動画を見る
${{}_n \mathrm{ C }_0}^2+{{}_n \mathrm{ C }_1}^2+{{}_n \mathrm{ C }_2}^2+\cdots + {{}_n \mathrm{ C }_n}^2=\dfrac{(2n)!}{(n!)^2}$
を証明してください。
福田のおもしろ数学502〜(n/10)^(n/10)の最小となるnを求める

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\left(\dfrac{n}{10}\right)^{\frac{n}{10}}$を最小にする
自然数$n$を求めて下さい。
この動画を見る
$\left(\dfrac{n}{10}\right)^{\frac{n}{10}}$を最小にする
自然数$n$を求めて下さい。
【数B】【数列】自然数の式の証明3 ※問題文は概要欄

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
理数個別チャンネル
問題文全文(内容文):
$n$は自然数とする。
$6^n+4= (5+1)^n+4$と変形することで、$6^n+4$が$5$の倍数であることを、二項定理を利用して証明せよ。
この動画を見る
$n$は自然数とする。
$6^n+4= (5+1)^n+4$と変形することで、$6^n+4$が$5$の倍数であることを、二項定理を利用して証明せよ。
福田のおもしろ数学446〜分数式の値が整数となるnをすべて求める

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\dfrac{n}{1!}+\dfrac{n^2}{2!}+\dfrac{n^3}{3!}+\cdots +\dfrac{n^{n-1}}{(n-1)!}+\dfrac{n^n}{n!}$
が整数になるような
正の整数$n$をすべて求めて下さい。
この動画を見る
$\dfrac{n}{1!}+\dfrac{n^2}{2!}+\dfrac{n^3}{3!}+\cdots +\dfrac{n^{n-1}}{(n-1)!}+\dfrac{n^n}{n!}$
が整数になるような
正の整数$n$をすべて求めて下さい。
福田のおもしろ数学439〜整数変数の分数式が整数となる条件

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$m,n$が整数であるとき
$\dfrac{m^2+n^2}{mn}$
の取りうるすべての整数値を求めよ。
この動画を見る
$m,n$が整数であるとき
$\dfrac{m^2+n^2}{mn}$
の取りうるすべての整数値を求めよ。
福田のおもしろ数学432〜ガウス記号を含んだ式が成り立たない条件

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$n+\left[\dfrac{n}{2}\right] \neq \left[\dfrac{n}{6}\right]+\left[\dfrac{2n}{3}\right]$
を満たす自然数$n$をすべて求めよ。
この動画を見る
$n+\left[\dfrac{n}{2}\right] \neq \left[\dfrac{n}{6}\right]+\left[\dfrac{2n}{3}\right]$
を満たす自然数$n$をすべて求めよ。
福田のおもしろ数学397〜与えられた連分数が整数になれないことの証明
単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
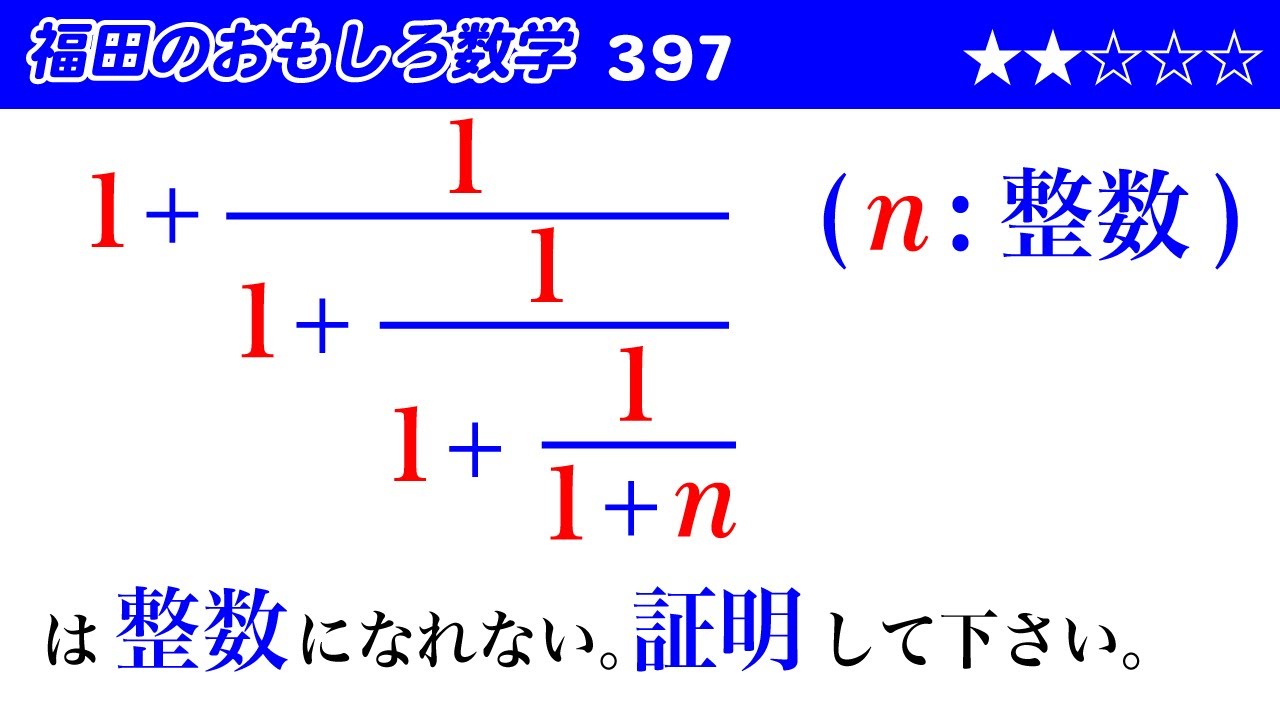
$\begin{eqnarray}
1+\frac{1}{1+\frac{1}{1+\frac{1}{1+n}}}
\end{eqnarray}$
は整数になれない。証明して下さい。
*$n$は整数である。
この動画を見る
$\begin{eqnarray}
1+\frac{1}{1+\frac{1}{1+\frac{1}{1+n}}}
\end{eqnarray}$
は整数になれない。証明して下さい。
*$n$は整数である。
【数Ⅱ】【式と証明】分数式の計算 ※問題文は概要欄

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#式と証明#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の式を計算せよ。
(1) $\dfrac{2}{1+a}+\dfrac{4}{1+a^2}+\dfrac{2}{1-a}+\dfrac{8}{1+a^4}$
(2) $\dfrac{ca}{(a-b)(b-c)}+\dfrac{ab}{(b-c)(c-a)}+\dfrac{bc}{(c-a)(a-b)}$
次の式を計算せよ。
(1) $\dfrac{x+2}{x}+\dfrac{x+3}{x+1}+\dfrac{x-5}{x-3}+\dfrac{x-6}{x-4}$
(2)$\dfrac{2}{(a-1)(a+1)}+\dfrac{2}{(a+1)(a+3)}+\dfrac{2}{(a+3)(a+5)}$
$x+\dfrac{1}{x}=4$のとき,
$x^2+\dfrac{1}{x^2}$
$x^3+\dfrac{1}{x^3}$
の値を求めよ。
この動画を見る
次の式を計算せよ。
(1) $\dfrac{2}{1+a}+\dfrac{4}{1+a^2}+\dfrac{2}{1-a}+\dfrac{8}{1+a^4}$
(2) $\dfrac{ca}{(a-b)(b-c)}+\dfrac{ab}{(b-c)(c-a)}+\dfrac{bc}{(c-a)(a-b)}$
次の式を計算せよ。
(1) $\dfrac{x+2}{x}+\dfrac{x+3}{x+1}+\dfrac{x-5}{x-3}+\dfrac{x-6}{x-4}$
(2)$\dfrac{2}{(a-1)(a+1)}+\dfrac{2}{(a+1)(a+3)}+\dfrac{2}{(a+3)(a+5)}$
$x+\dfrac{1}{x}=4$のとき,
$x^2+\dfrac{1}{x^2}$
$x^3+\dfrac{1}{x^3}$
の値を求めよ。
【数Ⅱ】【式と証明】二項定理の活用 ※問題文は概要欄

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#式と証明#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の□に入る数を,二項定理を用いて求めよ。
${}_{101} \mathrm{ C }_0+{}_{101} \mathrm{ C }_2+{}_{101} \mathrm{ C }_4+…$$…+{}_{101} \mathrm{ C }_{98}+{}_{101} \mathrm{ C }_{100}=2^□$
二項定理を用いて,次のことを証明せよ。
ただし,nは3以上の整数とする。
(1)$(1+\dfrac{1}{n})^n>2$
(2) x>0 のとき $(1+x)^n>1+nx+\dfrac{n(n-1)}{2}x^2$
この動画を見る
次の□に入る数を,二項定理を用いて求めよ。
${}_{101} \mathrm{ C }_0+{}_{101} \mathrm{ C }_2+{}_{101} \mathrm{ C }_4+…$$…+{}_{101} \mathrm{ C }_{98}+{}_{101} \mathrm{ C }_{100}=2^□$
二項定理を用いて,次のことを証明せよ。
ただし,nは3以上の整数とする。
(1)$(1+\dfrac{1}{n})^n>2$
(2) x>0 のとき $(1+x)^n>1+nx+\dfrac{n(n-1)}{2}x^2$
【数Ⅱ】【式と証明】展開式の係数 ※問題文は概要欄

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#式と証明#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の式の展開式における、[ ]内に指定された項の係数を求めよ。
(1) (2x²-1)⁶ [x⁶] (2)(2x³-3x)⁵ [x⁹]
次の式の展開式における、[ ]内に指定された項の係数を求めよ。
(1) (a+b+c)⁶ [ab²c³] (2)(x+y-3z)⁸ [x⁵yz²]
次の式の展開式における、[ ]内のものを求めよ。
(1) (x²+1/x)⁷ [x²の項の係数] (2)(2x³-1/3x²)⁵ [定数項]
次の式の展開式における、[ ]内に指定された項の係数を求めよ。
(1) (x+y+z)⁶ [x²yz³]
(2) (x+2y+3z)⁶ [x³y²z]
(3) (2x-3y+z)⁷ [x²y²z³]
(4) (x+y-3z)⁸ [x⁵z³]
この動画を見る
次の式の展開式における、[ ]内に指定された項の係数を求めよ。
(1) (2x²-1)⁶ [x⁶] (2)(2x³-3x)⁵ [x⁹]
次の式の展開式における、[ ]内に指定された項の係数を求めよ。
(1) (a+b+c)⁶ [ab²c³] (2)(x+y-3z)⁸ [x⁵yz²]
次の式の展開式における、[ ]内のものを求めよ。
(1) (x²+1/x)⁷ [x²の項の係数] (2)(2x³-1/3x²)⁵ [定数項]
次の式の展開式における、[ ]内に指定された項の係数を求めよ。
(1) (x+y+z)⁶ [x²yz³]
(2) (x+2y+3z)⁶ [x³y²z]
(3) (2x-3y+z)⁷ [x²y²z³]
(4) (x+y-3z)⁸ [x⁵z³]
【数Ⅱ】【式と証明】3次式の展開、因数分解、割り算 ※問題文は概要欄

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#式と証明#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
(a+b+c)³を展開せよ。
次の式を因数分解せよ。
(1) x³-3x²+6x-8 (2)8a³-36a²b+54ab²-27b³
次の式A,Bをxについての多項式とみて、AをBで割った商と余りを求めよ。
(1)A=2x³+7ax²+5a²x+6a³, B=x+3a
(2)A=x³-3ax²+4a³, B=x²-2ax-2a²
(3)A=x⁴+x²y²+y⁴, B=x²+xy+y²
(4)A=2x²+4xy-3y²-5x+2y-1, B=x+y+2
この動画を見る
(a+b+c)³を展開せよ。
次の式を因数分解せよ。
(1) x³-3x²+6x-8 (2)8a³-36a²b+54ab²-27b³
次の式A,Bをxについての多項式とみて、AをBで割った商と余りを求めよ。
(1)A=2x³+7ax²+5a²x+6a³, B=x+3a
(2)A=x³-3ax²+4a³, B=x²-2ax-2a²
(3)A=x⁴+x²y²+y⁴, B=x²+xy+y²
(4)A=2x²+4xy-3y²-5x+2y-1, B=x+y+2
福田のおもしろ数学368〜多項式と二項係数の関係式の証明

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$P_k(x)=1+x+x^2+\cdots +x^{k-1}$のとき、
$\displaystyle \sum^n_{k=1}{} _nC_kP_k(x)=2^{n-1}P_n(\dfrac{1+x}2)$
が成り立つことを証明せよ。
この動画を見る
$P_k(x)=1+x+x^2+\cdots +x^{k-1}$のとき、
$\displaystyle \sum^n_{k=1}{} _nC_kP_k(x)=2^{n-1}P_n(\dfrac{1+x}2)$
が成り立つことを証明せよ。
頻出!「あれ」を利用して余りを求める!

単元:
#数A#数Ⅱ#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
21^2015を400で割ったときの余りを求めよ。
この動画を見る
21^2015を400で割ったときの余りを求めよ。
不等式の証明の難問!記号が多すぎる。。。 #Shorts #ずんだもん #勉強 #数学

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#数B#お茶の水女子大学
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
mを2以上の自然数、nを自然数とするとき、次の不等式 nmCn≧m^n≧Σ[i=0,n-1]m^i が成り立つことを示せ。
この動画を見る
mを2以上の自然数、nを自然数とするとき、次の不等式 nmCn≧m^n≧Σ[i=0,n-1]m^i が成り立つことを示せ。
【数Ⅱ】【式と証明】整式の割り算2 ※問題文は概要欄

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#模試解説・過去問解説
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の第1式が第2式で割り切れるように、定数$l,m$の値を定めよ。
(1)$ x^3+lx^2+mx+2 ,x^2+2x+2
(2) $x^3+lx^2+m ,(x+2)^2$
この動画を見る
次の第1式が第2式で割り切れるように、定数$l,m$の値を定めよ。
(1)$ x^3+lx^2+mx+2 ,x^2+2x+2
(2) $x^3+lx^2+m ,(x+2)^2$
【数Ⅱ】【式と証明】整式の割り算3 ※問題文は概要欄

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$x^2+1$で割ると余りが$2x+3$ であり、
$x^2+x+1$で割ると余りが$3x+5$である3次式を求めよ。
この動画を見る
$x^2+1$で割ると余りが$2x+3$ であり、
$x^2+x+1$で割ると余りが$3x+5$である3次式を求めよ。
【数Ⅱ】【式と証明】整式の割り算1 ※問題文は概要欄

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の各場合について、定数$a,b$の値を求めよ。
(1) $2x^2+ax+10$を$x^2-3x+b$で割ると、余りが$3x-2$ である。
(2) $x^3+ax^2-5x+4$を$x^2+bx-2$で割ると、余りが$2$である。
この動画を見る
次の各場合について、定数$a,b$の値を求めよ。
(1) $2x^2+ax+10$を$x^2-3x+b$で割ると、余りが$3x-2$ である。
(2) $x^3+ax^2-5x+4$を$x^2+bx-2$で割ると、余りが$2$である。
福田のおもしろ数学328〜多項式の性質を繰り返し用いて多項式を求める

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理
指導講師:
福田次郎
問題文全文(内容文):
実数係数の多項式$P(x)$が任意の実数$\theta$に対して$P(\cos \theta +\sin \theta)=P(\cos \theta -\sin \theta)$を満たすとき、$P(x)=a_0+a_1 (1-x^2)^2+a_2 (1-x^2)^4 +\cdots+a_n (1-x^2)^{2n}$であることを証明して下さい。($a_0 ,a_1 ,\cdots ,a_n$は実数、$n$は0以上の整数)
この動画を見る
実数係数の多項式$P(x)$が任意の実数$\theta$に対して$P(\cos \theta +\sin \theta)=P(\cos \theta -\sin \theta)$を満たすとき、$P(x)=a_0+a_1 (1-x^2)^2+a_2 (1-x^2)^4 +\cdots+a_n (1-x^2)^{2n}$であることを証明して下さい。($a_0 ,a_1 ,\cdots ,a_n$は実数、$n$は0以上の整数)
福田のおもしろ数学303〜階乗のたくさんある分数の和

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \frac{1}{2! 17!} $$\displaystyle + \frac{1}{3! 16!} $$\displaystyle + \frac{1}{4! 15!}$$+ \cdots $$\displaystyle + \frac{1}{9! 10!} $$\displaystyle = \frac{N}{1! 18!}$ を満たす $N$ を求めよ。
この動画を見る
$\displaystyle \frac{1}{2! 17!} $$\displaystyle + \frac{1}{3! 16!} $$\displaystyle + \frac{1}{4! 15!}$$+ \cdots $$\displaystyle + \frac{1}{9! 10!} $$\displaystyle = \frac{N}{1! 18!}$ を満たす $N$ を求めよ。
この式はあれしかない!!どう解く?

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#積分とその応用#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
多項式(x^100+1)^100+(x^2+1)^100+1は多項式x^2+x+1で割り切れるか。
この動画を見る
多項式(x^100+1)^100+(x^2+1)^100+1は多項式x^2+x+1で割り切れるか。
福田のおもしろ数学288〜三角関数に関する不等式の証明

単元:
#数Ⅱ#式と証明#三角関数#整式の除法・分数式・二項定理#加法定理とその応用#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$sin^n2x+(sin^xx-cos^nx)^2\leqq1$を証明して下さい。
この動画を見る
$sin^n2x+(sin^xx-cos^nx)^2\leqq1$を証明して下さい。
福田のおもしろ数学277〜ガウス記号の等式の証明

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$n$は正の整数とする。
$[\sqrt{n}+\sqrt{n+1}]=[\sqrt{ 4n+2 }]$であることを証明して下さい。
$[n]$は$x$を超えない最大の整数を表します。
この動画を見る
$n$は正の整数とする。
$[\sqrt{n}+\sqrt{n+1}]=[\sqrt{ 4n+2 }]$であることを証明して下さい。
$[n]$は$x$を超えない最大の整数を表します。
よくある方程式
大学入試問題#919「昔は落ち着いた問題」
単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$x-\displaystyle \frac{1}{x}=1$のとき、
$x^5+\displaystyle \frac{1}{x^5}$の値を求めよ。
出典:一橋大(1960)
この動画を見る
$x-\displaystyle \frac{1}{x}=1$のとき、
$x^5+\displaystyle \frac{1}{x^5}$の値を求めよ。
出典:一橋大(1960)
#自治医科大学2024#式変形_21#元高校教員

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#式の計算(整式・展開・因数分解)#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)#自治医科大学
指導講師:
ますただ
問題文全文(内容文):
$x^{\frac{1}{3}}+x^{-\frac{1}{3}}$のとき
$\displaystyle \frac{x+x^{-1}}{2}$の値を求めよ。
出典:自治医科大学 式変形問題
この動画を見る
$x^{\frac{1}{3}}+x^{-\frac{1}{3}}$のとき
$\displaystyle \frac{x+x^{-1}}{2}$の値を求めよ。
出典:自治医科大学 式変形問題
分数式の計算
単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\dfrac{1}{x}+\dfrac{1}{x^2-x}=$?
この動画を見る
$\dfrac{1}{x}+\dfrac{1}{x^2-x}=$?
