解と判別式・解と係数の関係
解と判別式・解と係数の関係
福田の数学〜九州大学2022年文系第１問〜絶対値の付いた放物線と直線で囲まれた面積
単元：
#数Ⅱ#大学入試過去問(数学)#２次関数#微分法と積分法#解と判別式・解と係数の関係#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#九州大学
指導講師：
福田次郎
問題文全文(内容文)：
aを$-3 \lt a \lt 13$を満たす実数とし、次の曲線Cと直線lが接しているとする。
$C:y=|x^2+(3-a)x-3a|, l:y=-x+13$
以下の問いに答えよ。
(1)aの値を求めよ。
(2)曲線Cと直線lで囲まれた2つの図形のうち、点(a,0)が境界線上にある図形の面積を求めよ。
2022九州大学文系過去問
この動画を見る
aを$-3 \lt a \lt 13$を満たす実数とし、次の曲線Cと直線lが接しているとする。
$C:y=|x^2+(3-a)x-3a|, l:y=-x+13$
以下の問いに答えよ。
(1)aの値を求めよ。
(2)曲線Cと直線lで囲まれた2つの図形のうち、点(a,0)が境界線上にある図形の面積を求めよ。
2022九州大学文系過去問
うまい方法
単元：
#数Ⅱ#複素数と方程式#複素数#解と判別式・解と係数の関係#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ x^3+2x^2+3x+4=0$の3つの解を$ \alpha,\beta,\delta $とする.
$(\alpha^4-1)(\beta^4-1)(\delta^4-1)$の値を求めよ.
この動画を見る
$ x^3+2x^2+3x+4=0$の3つの解を$ \alpha,\beta,\delta $とする.
$(\alpha^4-1)(\beta^4-1)(\delta^4-1)$の値を求めよ.
福田の数学〜京都大学2022年理系第５問〜方程式の解と不等式の証明
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#複素数と方程式#恒等式・等式・不等式の証明#解と判別式・解と係数の関係#微分とその応用#積分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
曲線$C:y=\cos^3x$ $(0 \leqq x \leqq \frac{\pi}{2})$,x軸およびy軸で囲まれる図形の面s系をS
とする。$0 \lt t \lt \frac{\pi}{2}$とし、C上の点Q$(t,\cos^3t)$と原点O,およびP$(t,o),R(0,\cos^3t)$
を頂点にもつ長方形OPQRの面積をf(t)とする。このとき、次の問いに答えよ。
(1)Sを求めよ。
(2)$f(t)$は最大値をただ一つのtでとることを示せ。そのときのtを$\alpha$とすると、
$f(\alpha)=\frac{\cos^4\alpha}{3\sin\alpha}$ であることを示せ。
(3)$\frac{f(\alpha)}{S} \lt \frac{9}{16}$ を示せ。
2022京都大学理系過去問
この動画を見る
曲線$C:y=\cos^3x$ $(0 \leqq x \leqq \frac{\pi}{2})$,x軸およびy軸で囲まれる図形の面s系をS
とする。$0 \lt t \lt \frac{\pi}{2}$とし、C上の点Q$(t,\cos^3t)$と原点O,およびP$(t,o),R(0,\cos^3t)$
を頂点にもつ長方形OPQRの面積をf(t)とする。このとき、次の問いに答えよ。
(1)Sを求めよ。
(2)$f(t)$は最大値をただ一つのtでとることを示せ。そのときのtを$\alpha$とすると、
$f(\alpha)=\frac{\cos^4\alpha}{3\sin\alpha}$ であることを示せ。
(3)$\frac{f(\alpha)}{S} \lt \frac{9}{16}$ を示せ。
2022京都大学理系過去問
簡単な根号のついた方程式
単元：
#数Ⅰ#数Ⅱ#数と式#２次関数#複素数と方程式#式の計算（整式・展開・因数分解）#2次方程式と2次不等式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
これを解け.
$ \sqrt{3x^2-4x+11}-\sqrt{3x^2-4x-4}=3$
この動画を見る
これを解け.
$ \sqrt{3x^2-4x+11}-\sqrt{3x^2-4x-4}=3$
【数Ⅱ】虚数を解に持つ3次方程式【3次方程式の解と係数の関係】
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
めいちゃんねる
問題文全文(内容文)：
$ 3次方程式x^3-4x^2+ax+b=0の解の1つが3+iであるとき,
実際の定数a,bを求めよ.$
この動画を見る
$ 3次方程式x^3-4x^2+ax+b=0の解の1つが3+iであるとき,
実際の定数a,bを求めよ.$
【数Ⅱ】虚数を解に持つ2次方程式【最小多項式・解と係数の関係を使う】
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
めいちゃんねる
問題文全文(内容文)：
$ 2次方程式x^2+ax+b=0の解の1つが3+iであるとき,
実数の定数a,bの値を求めよ.$
この動画を見る
$ 2次方程式x^2+ax+b=0の解の1つが3+iであるとき,
実数の定数a,bの値を求めよ.$
【数Ⅱ】解と係数の関係と対称式 (2-α)(2-β)の値【もっとも簡単な解き方】
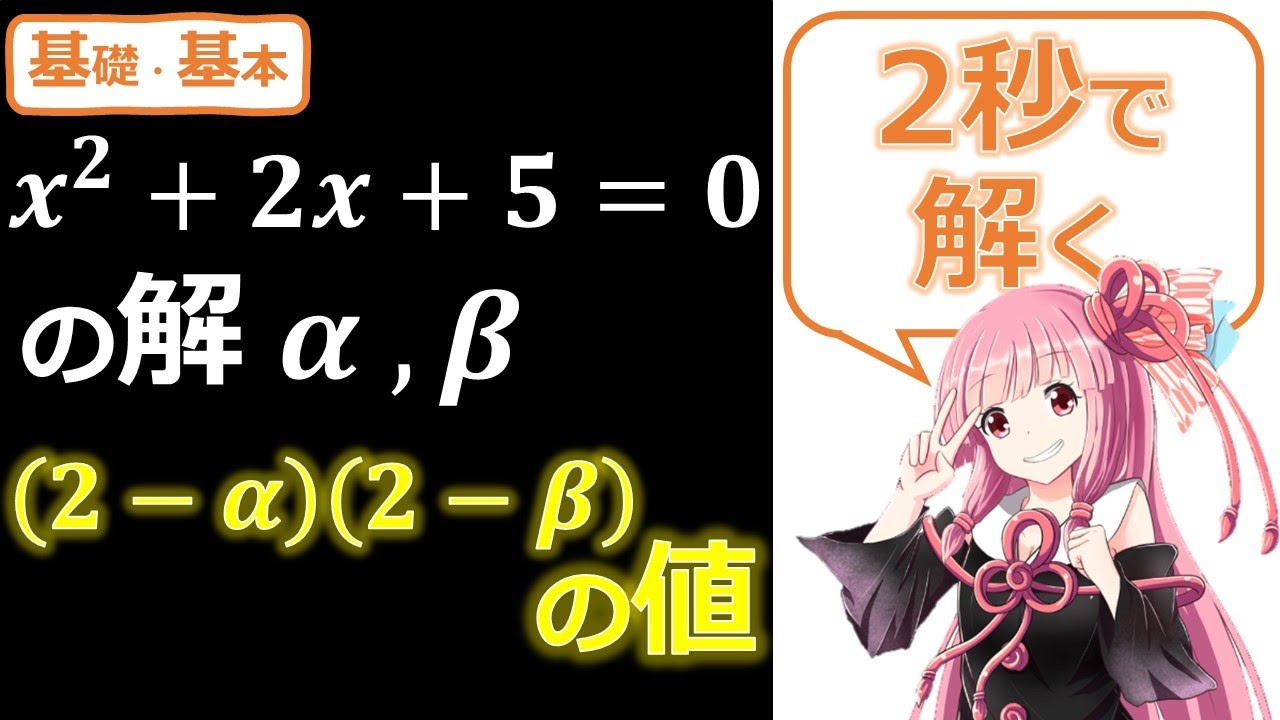
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
めいちゃんねる
問題文全文(内容文)：
$ x^2+2x+5=0の解を\alpha,\betaとする.(2-\alpha)(2-\beta)を求めよ.$
この動画を見る
$ x^2+2x+5=0の解を\alpha,\betaとする.(2-\alpha)(2-\beta)を求めよ.$
11三重県教員採用試験（数学：1番 整数問題）
単元：
#数A#数Ⅱ#複素数と方程式#整数の性質#約数・倍数・整数の割り算と余り・合同式#解と判別式・解と係数の関係#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$p$整数
$x^2-3|x+7p=0$の2つの解$\alpha,\beta$自然数とする。
$\alpha,\beta$が最大となる$p$を求めよ。
この動画を見る
$p$整数
$x^2-3|x+7p=0$の2つの解$\alpha,\beta$自然数とする。
$\alpha,\beta$が最大となる$p$を求めよ。
#49 数検1級1次 過去問 根号を外す
単元：
#数Ⅰ#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#数と式#２次関数#複素数と方程式#式の計算（整式・展開・因数分解）#2次方程式と2次不等式#2次関数とグラフ#解と判別式・解と係数の関係#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\sqrt[ 3 ]{ -5+2\sqrt{ 13 } }\ $の二重根号をはずせ
この動画を見る
$\sqrt[ 3 ]{ -5+2\sqrt{ 13 } }\ $の二重根号をはずせ
【数Ⅱ】解と係数の関係と対称式 α²+β²の値【複数の方法で理解を深める】
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
めいちゃんねる
問題文全文(内容文)：
$ x^2+2x+5=0の解を\alpha,\betaとする.\alpha^2+\beta^2を求めよ.$
この動画を見る
$ x^2+2x+5=0の解を\alpha,\betaとする.\alpha^2+\beta^2を求めよ.$
【2次方程式の知識はこれで完ペキ！】複素数と2次方程式の関係を解説！〔数学、高校数学〕
#38 数検1級1次 過去問 解と係数の関係
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#解と判別式・解と係数の関係#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$z^3+2z^2+2z+1=0$の3つの解を$\alpha,\beta,\gamma$とする
$\alpha^{2019}+\beta^{2019}+\gamma^{2019}$の値を求めよ。
この動画を見る
$z^3+2z^2+2z+1=0$の3つの解を$\alpha,\beta,\gamma$とする
$\alpha^{2019}+\beta^{2019}+\gamma^{2019}$の値を求めよ。
#29 数検1級1次 過去問 解と係数の関係
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#解と判別式・解と係数の関係#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$x^3+2x^2+4x+7=0$の3つの解を$\alpha,\beta,\gamma$とする
$\alpha^4,\beta^4,\gamma^4$の値を求めよ。
この動画を見る
$x^3+2x^2+4x+7=0$の3つの解を$\alpha,\beta,\gamma$とする
$\alpha^4,\beta^4,\gamma^4$の値を求めよ。
【数Ⅱ】複素数と方程式：x²+x+1=0の２解をα、βとする。(1)α＋β(2)α³＋β³(3)α¹⁰⁰＋β¹⁰⁰の値を求めよ。
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$x^2+x+1=0$の2解を$\alpha,\beta$とする。
(1)$\alpha+\beta$
(2)$\alpha^3+\beta^3$
(3)$\alpha^{100}+\beta^{100}$の値を求めよ。
この動画を見る
$x^2+x+1=0$の2解を$\alpha,\beta$とする。
(1)$\alpha+\beta$
(2)$\alpha^3+\beta^3$
(3)$\alpha^{100}+\beta^{100}$の値を求めよ。
福田の数学〜明治大学2021年理工学部第１問(1)〜2次方程式が整数を解にもつ条件
単元：
#数Ⅰ#数A#数Ⅱ#２次関数#複素数と方程式#2次方程式と2次不等式#整数の性質#約数・倍数・整数の割り算と余り・合同式#解と判別式・解と係数の関係#数学(高校生)#大学入試解答速報#数学#明治大学
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{1}}$(1)$a$と$b$を正の整数とし、$f(x)=ax^2-bx+4$とおく。2次方程式$f(x)=0$は
異なる2つの実数解をもつとする。
$(\textrm{a})$2次方程式$f(x)=0$の2つの解がともに整数であるとき
$\left\{
\begin{array}{1}
a=1 \\
b=\boxed{\ \ ア\ \ }
\end{array}
\right.$
または
$\left\{
\begin{array}{1}
a=\boxed{\ \ イ\ \ }\\
b=\boxed{\ \ ウ\ \ }
\end{array}
\right.\\$
である。
$(\textrm{b})b=7$とする。2次方程式$f(x)=0$の2つの解のうち一方が整数であるとき、
$a=\boxed{\ \ エ\ \ }$であり、$f(x)=0$の2つの解は
$x=\boxed{\ \ エ\ \ },\ \frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}$
である。
2021明治大学理工学部過去問
この動画を見る
${\Large\boxed{1}}$(1)$a$と$b$を正の整数とし、$f(x)=ax^2-bx+4$とおく。2次方程式$f(x)=0$は
異なる2つの実数解をもつとする。
$(\textrm{a})$2次方程式$f(x)=0$の2つの解がともに整数であるとき
$\left\{
\begin{array}{1}
a=1 \\
b=\boxed{\ \ ア\ \ }
\end{array}
\right.$
または
$\left\{
\begin{array}{1}
a=\boxed{\ \ イ\ \ }\\
b=\boxed{\ \ ウ\ \ }
\end{array}
\right.\\$
である。
$(\textrm{b})b=7$とする。2次方程式$f(x)=0$の2つの解のうち一方が整数であるとき、
$a=\boxed{\ \ エ\ \ }$であり、$f(x)=0$の2つの解は
$x=\boxed{\ \ エ\ \ },\ \frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}$
である。
2021明治大学理工学部過去問
【数Ⅱ】複素数と方程式：解と係数の関係(3次)の利用
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
3次方程式$x^3+ax^2+bx+20=0$の解の1つが$x=3-i$であるとき、実数の定数a,bの値と、他の解を求めよう。
この動画を見る
3次方程式$x^3+ax^2+bx+20=0$の解の1つが$x=3-i$であるとき、実数の定数a,bの値と、他の解を求めよう。
福田の数学〜中央大学2021年経済学部第１問(1)〜2次方程式の解
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#複素数と方程式#2次方程式と2次不等式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$(1)次の2次方程式において,1つの解が$x=\dfrac{3}{2}-i$であるとき,
実数$a,b$の値を求めよ.ただし,$i$は虚数単位とする.
$-x^2+ax+b=0$
2021中央大経済学部過去問
この動画を見る
$\boxed{1}$(1)次の2次方程式において,1つの解が$x=\dfrac{3}{2}-i$であるとき,
実数$a,b$の値を求めよ.ただし,$i$は虚数単位とする.
$-x^2+ax+b=0$
2021中央大経済学部過去問
07高知県教員採用試験（数学：2番 対数，解の個数）
単元：
#数Ⅱ#複素数と方程式#指数関数と対数関数#解と判別式・解と係数の関係#対数関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{2}$
$a$:定数である.
$\log_3 (x-1)^2+\log_3 (x+2)=a$において
異なる2つの正の解と1つの負の解をもつように
定数$a$の値の範囲を求めよ.
この動画を見る
$\boxed{2}$
$a$:定数である.
$\log_3 (x-1)^2+\log_3 (x+2)=a$において
異なる2つの正の解と1つの負の解をもつように
定数$a$の値の範囲を求めよ.
福田の数学〜慶應義塾大学2021年薬学部第１問(2)〜解の差が1の２次方程式
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#微分法と積分法#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{1}}$(2)xの関数$f(x)=x^2+ax+b$がある。方程式$f(x)=0$の2つの実数解の差が
1であり、xの値が2から5まで変わるときのf(x)の平均変化率が$\frac{13}{2}$であるとき、
aの値は$\boxed{\ \ イ\ \ }$、bの値は$\boxed{\ \ ウ\ \ }$である。
2021慶應義塾大学薬学部過去問
この動画を見る
${\Large\boxed{1}}$(2)xの関数$f(x)=x^2+ax+b$がある。方程式$f(x)=0$の2つの実数解の差が
1であり、xの値が2から5まで変わるときのf(x)の平均変化率が$\frac{13}{2}$であるとき、
aの値は$\boxed{\ \ イ\ \ }$、bの値は$\boxed{\ \ ウ\ \ }$である。
2021慶應義塾大学薬学部過去問
21三重県教員採用試験（数学：1-(3) 解と係数の関係）
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{1}-(3)$
$x^3+ax^2+bx+21=0$の1つの解が
$x=2+\sqrt3 i$のとき
$a,b$の値と実数解を求めよ.
この動画を見る
$\boxed{1}-(3)$
$x^3+ax^2+bx+21=0$の1つの解が
$x=2+\sqrt3 i$のとき
$a,b$の値と実数解を求めよ.
18兵庫県教員採用試験（数学：3 -(2) 解の個数）
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{3}-(2)$
$\vert x^2-2x-3 \vert =a(x+1)+2$
が異なる3個の実数解をもつような
$a$の値を求めよ.
この動画を見る
$\boxed{3}-(2)$
$\vert x^2-2x-3 \vert =a(x+1)+2$
が異なる3個の実数解をもつような
$a$の値を求めよ.
17和歌山県教員採用試験（数学：1-(6) 展開した係数）
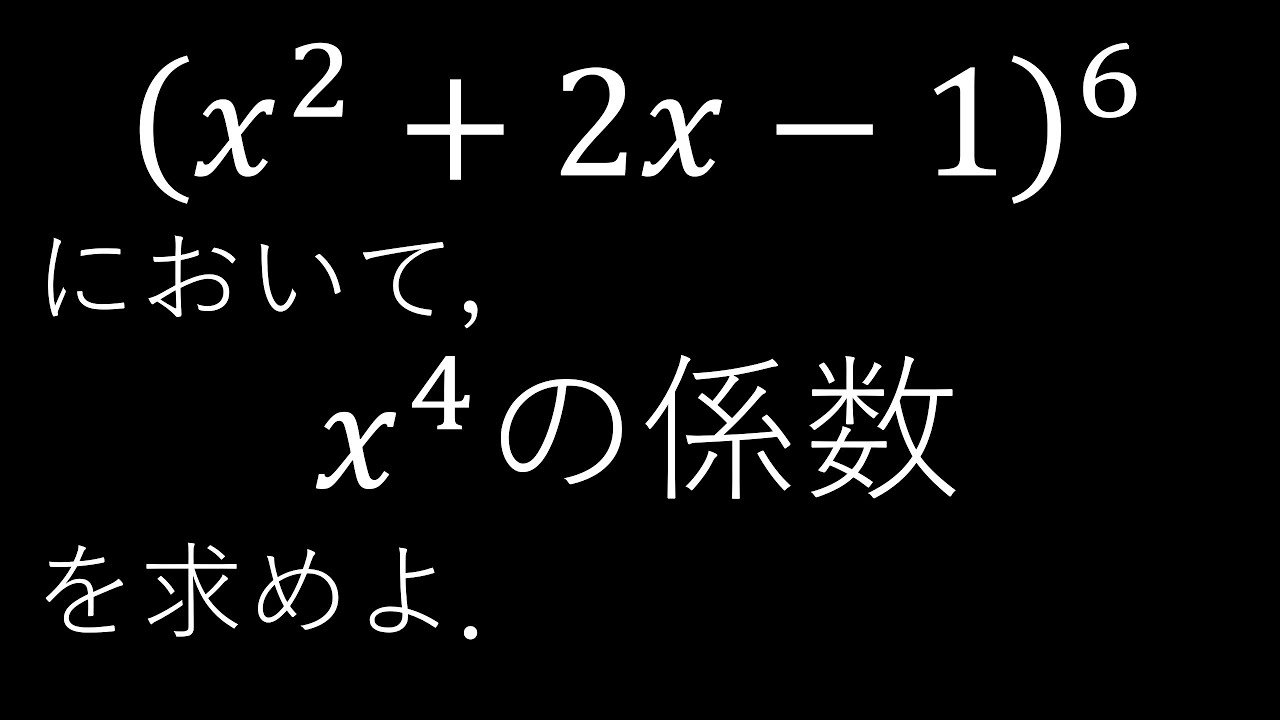
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{1}-(4)$
$(x^2+2x-1)^6$において
$x^4$の係数を求めよ.
この動画を見る
$\boxed{1}-(4)$
$(x^2+2x-1)^6$において
$x^4$の係数を求めよ.
16和歌山県教員採用試験（数学：2番 解と係数の関係）
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{2}$
$a,b$は実数とする.
$x^3+6ax+b=0$が$a-3i$を解にもつとき,
$a,b$の値とそのときの実数解を求めよ.
この動画を見る
$\boxed{2}$
$a,b$は実数とする.
$x^3+6ax+b=0$が$a-3i$を解にもつとき,
$a,b$の値とそのときの実数解を求めよ.
兵庫県教員採用試験（数学：練習問題 解の個数）
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$a\gt 0$とする.
$x^a=a^x$を満たす正の解の
個数を調べよ.
この動画を見る
$a\gt 0$とする.
$x^a=a^x$を満たす正の解の
個数を調べよ.
【判別式をイメージする！】2次関数の判別式と交点の数の解き方はこれだ！【高校数学 数学】
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
3rd School
問題文全文(内容文)：
①
$y=x^2+2x-a$が$x$軸を2つの交点を持つような$a$の条件を求めよ
②
$y=2x^2+3x+a$が$x$軸を1つの交点を持つような$a$の条件を求めよ
③
$y=ax^2-4x+2$が$x$軸と交点を1つも持たないような$a$の条件を求めよ
この動画を見る
①
$y=x^2+2x-a$が$x$軸を2つの交点を持つような$a$の条件を求めよ
②
$y=2x^2+3x+a$が$x$軸を1つの交点を持つような$a$の条件を求めよ
③
$y=ax^2-4x+2$が$x$軸と交点を1つも持たないような$a$の条件を求めよ
線形代数：#2線形写像の判定
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
次の写像$\varsigma_i(i=1,2,3,4)$は線形代数であるか調べよ.
(1)
$\varsigma_1:IR^2\to IR$を
$\varsigma_1 \begin{pmatrix}
x \\
y
\end{pmatrix}=2x+3y$と定める.
(2)
$\varsigma_2:IR^2\to IR^2$を
$\varsigma_2 \begin{pmatrix}
x \\
y
\end{pmatrix}=\begin{pmatrix}
x+1 \\
y-1
\end{pmatrix}$と定める.
(3)
$\varsigma_3:IR^2\to IR^2$を
$\varsigma_3 \begin{pmatrix}
x \\
y
\end{pmatrix}=\begin{pmatrix}
\vert x\vert \\
y
\end{pmatrix}$と定める.
(3)
$\varsigma_4:IR^2\to IR^2$を
$\varsigma_4 \begin{pmatrix}
x \\
y
\end{pmatrix}=\begin{pmatrix}
y \\
x
\end{pmatrix}$と定める.
この動画を見る
次の写像$\varsigma_i(i=1,2,3,4)$は線形代数であるか調べよ.
(1)
$\varsigma_1:IR^2\to IR$を
$\varsigma_1 \begin{pmatrix}
x \\
y
\end{pmatrix}=2x+3y$と定める.
(2)
$\varsigma_2:IR^2\to IR^2$を
$\varsigma_2 \begin{pmatrix}
x \\
y
\end{pmatrix}=\begin{pmatrix}
x+1 \\
y-1
\end{pmatrix}$と定める.
(3)
$\varsigma_3:IR^2\to IR^2$を
$\varsigma_3 \begin{pmatrix}
x \\
y
\end{pmatrix}=\begin{pmatrix}
\vert x\vert \\
y
\end{pmatrix}$と定める.
(3)
$\varsigma_4:IR^2\to IR^2$を
$\varsigma_4 \begin{pmatrix}
x \\
y
\end{pmatrix}=\begin{pmatrix}
y \\
x
\end{pmatrix}$と定める.
#11数検1級1次過去問
単元：
#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#数学検定#数学検定準1級
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{1}$
$x^4-4x^3+x^2-3=0$を解け.
この動画を見る
$\boxed{1}$
$x^4-4x^3+x^2-3=0$を解け.
福田の１日１題わかった数学〜高校２年生第３回〜高次方程式と連立方程式
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{II}$ 高次方程式
$\left\{\begin{array}{1}
a^3x+a^2y+az=1\\
b^3x+b^2y+bz=1\\
c^3x+c^2y+cz=1\\
\end{array}\right.$
を解け。
ただし、$a,b,c$は異なる数で$0$でない。
この動画を見る
数学$\textrm{II}$ 高次方程式
$\left\{\begin{array}{1}
a^3x+a^2y+az=1\\
b^3x+b^2y+bz=1\\
c^3x+c^2y+cz=1\\
\end{array}\right.$
を解け。
ただし、$a,b,c$は異なる数で$0$でない。
12京都府教員採用試験（数学：1番 解の個数）
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{1}$
$a\in IR$とする.
$\log_{2} (x+1)-\log+(2x-a+3)-1=0$が
異なる2つの解をもつ
$a$の値の範囲を求めよ.
この動画を見る
$\boxed{1}$
$a\in IR$とする.
$\log_{2} (x+1)-\log+(2x-a+3)-1=0$が
異なる2つの解をもつ
$a$の値の範囲を求めよ.
福田の１日１題わかった数学〜高校２年生第２回〜高次方程式と整数解
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{II}$ 高次方程式
3次方程式$x^3-7x+n=0$ が
3つの整数解をもつように、
$n$の値を定めよ。
この動画を見る
数学$\textrm{II}$ 高次方程式
3次方程式$x^3-7x+n=0$ が
3つの整数解をもつように、
$n$の値を定めよ。