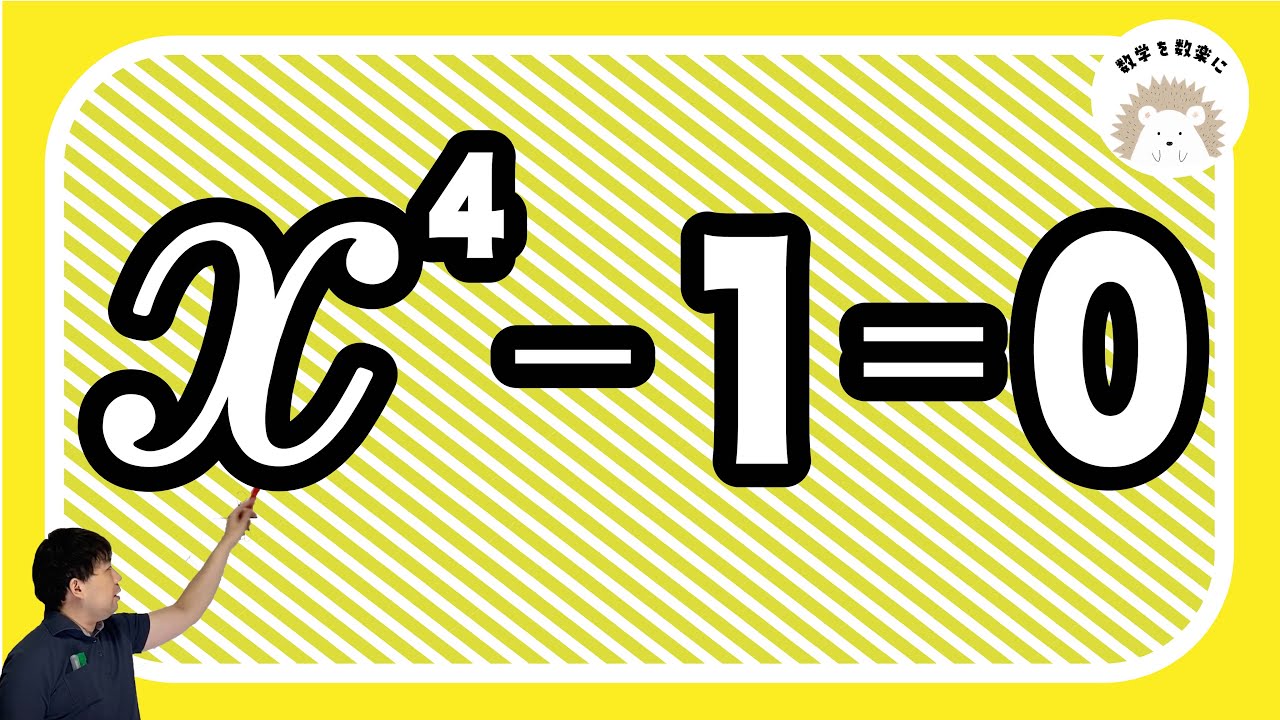剰余の定理・因数定理・組み立て除法と高次方程式
剰余の定理・因数定理・組み立て除法と高次方程式
 剰余の定理・因数定理・組み立て除法と高次方程式
剰余の定理・因数定理・組み立て除法と高次方程式
中国Jr 数学Olympic あっと驚く解法も

単元:
#数学検定・数学甲子園・数学オリンピック等#式と証明#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^5=1,x \neq 1$とするとき,
$\dfrac{x}{1+x^2}+\dfrac{x^2}{1+x^4}+\dfrac{x^3}{1+x^6}+\dfrac{x^4}{1+x^8}$の値を求めよ.
中国jr数学オリンピック過去問
この動画を見る
$ x^5=1,x \neq 1$とするとき,
$\dfrac{x}{1+x^2}+\dfrac{x^2}{1+x^4}+\dfrac{x^3}{1+x^6}+\dfrac{x^4}{1+x^8}$の値を求めよ.
中国jr数学オリンピック過去問
簡単な問題

単元:
#数A#数Ⅱ#複素数と方程式#整数の性質#約数・倍数・整数の割り算と余り・合同式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \omega=1(\omega \neq 1)$であり,
$x=a+b $
$y=a\omega+b\omega^2 $
$z=a\omega^2+b\omega $である.
$ x^3+y^3+z^3$の値をa,bで表せ.
この動画を見る
$ \omega=1(\omega \neq 1)$であり,
$x=a+b $
$y=a\omega+b\omega^2 $
$z=a\omega^2+b\omega $である.
$ x^3+y^3+z^3$の値をa,bで表せ.
2分で解ける問題

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^2+\dfrac{1}{x^2}=\sqrt2 $のとき,$ x^{2022}+\dfrac{1}{x^{2022}}$の値を求めよ.
この動画を見る
$ x^2+\dfrac{1}{x^2}=\sqrt2 $のとき,$ x^{2022}+\dfrac{1}{x^{2022}}$の値を求めよ.
方程式を解く。
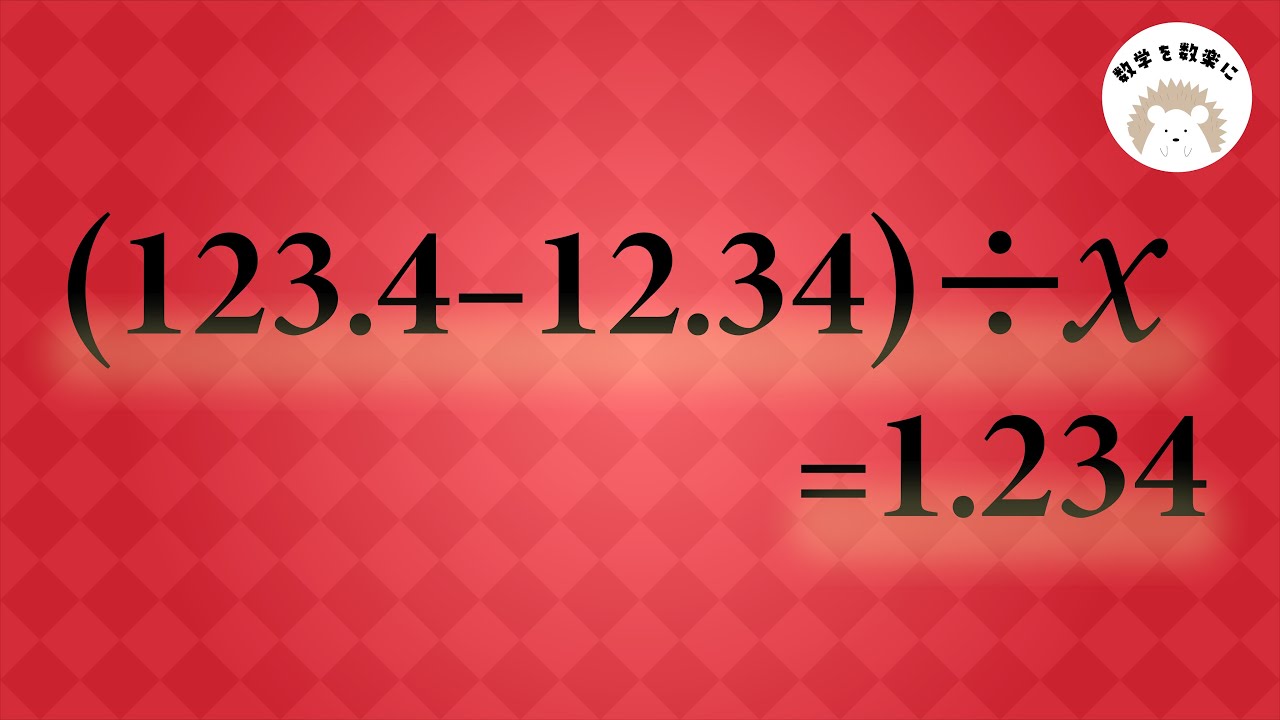
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(123.4-12.34) \div x =1.234$
この動画を見る
$(123.4-12.34) \div x =1.234$
福田の数学〜名古屋大学2022年理系第1問〜割り算の余りと異なる実数解の個数

単元:
#数A#数Ⅱ#大学入試過去問(数学)#複素数と方程式#整数の性質#約数・倍数・整数の割り算と余り・合同式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学
指導講師:
福田次郎
問題文全文(内容文):
a,bを実数とする。
(1)整式$x^3$を2次式$(x-a)^2$で割った時の余りを求めよ。
(2)実数を係数とする2次式$f(x)=x^2+\alpha x+\beta$で整式$x^3$を割った時の余りが
$3x+b$とする。bの値に応じて、このようなf(x)が何個あるかを求めよ。
2022名古屋大学理系過去問
この動画を見る
a,bを実数とする。
(1)整式$x^3$を2次式$(x-a)^2$で割った時の余りを求めよ。
(2)実数を係数とする2次式$f(x)=x^2+\alpha x+\beta$で整式$x^3$を割った時の余りが
$3x+b$とする。bの値に応じて、このようなf(x)が何個あるかを求めよ。
2022名古屋大学理系過去問
3乗根の方程式

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$ x^3+1=2\sqrt[3]{2x-1}$
この動画を見る
実数解を求めよ.
$ x^3+1=2\sqrt[3]{2x-1}$
3乗根を外すだけ

単元:
#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
3乗根を外せ.
$ \sqrt[3]{\dfrac{10-7\sqrt2}{10+7\sqrt2}}$
この動画を見る
3乗根を外せ.
$ \sqrt[3]{\dfrac{10-7\sqrt2}{10+7\sqrt2}}$
福田の入試問題解説〜北海道大学2022年文系第1問〜剰余定理と高次不等式の解

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
福田次郎
問題文全文(内容文):
kを実数の定数とし、
$f(x)=x^3-(2k-1)x^2+(k^2-k+1)x-k+1$
とする。
(1)$f(k-1)$の値を求めよ。
(2)$|k|\lt 2$のとき、不等式$f(x) \geqq 0$を解け。
2022北海道大学文系過去問
この動画を見る
kを実数の定数とし、
$f(x)=x^3-(2k-1)x^2+(k^2-k+1)x-k+1$
とする。
(1)$f(k-1)$の値を求めよ。
(2)$|k|\lt 2$のとき、不等式$f(x) \geqq 0$を解け。
2022北海道大学文系過去問
ただの対数方程式

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\log_2 x+\log_3 x=1$
この動画を見る
これを解け.
$\log_2 x+\log_3 x=1$
2022九州大

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
kは実数であり,整式f(x)を$ f(x)=x^4+6x^3-kx^2+2kx-64 $で定める.
f(x)=0が虚数解をもつとき,
(1)f(x)はx-2で割り切れることを示せ.
(2)f(x)=0は負の実数解をもつことを示せ.
(3)f(x)=0のすべての実数解が整数で,すべての虚数解の実部と虚部が
ともに整数である.kの値を求めよ.
2022九州大過去問
この動画を見る
kは実数であり,整式f(x)を$ f(x)=x^4+6x^3-kx^2+2kx-64 $で定める.
f(x)=0が虚数解をもつとき,
(1)f(x)はx-2で割り切れることを示せ.
(2)f(x)=0は負の実数解をもつことを示せ.
(3)f(x)=0のすべての実数解が整数で,すべての虚数解の実部と虚部が
ともに整数である.kの値を求めよ.
2022九州大過去問
中学生もわかる!と思う!指数の方程式
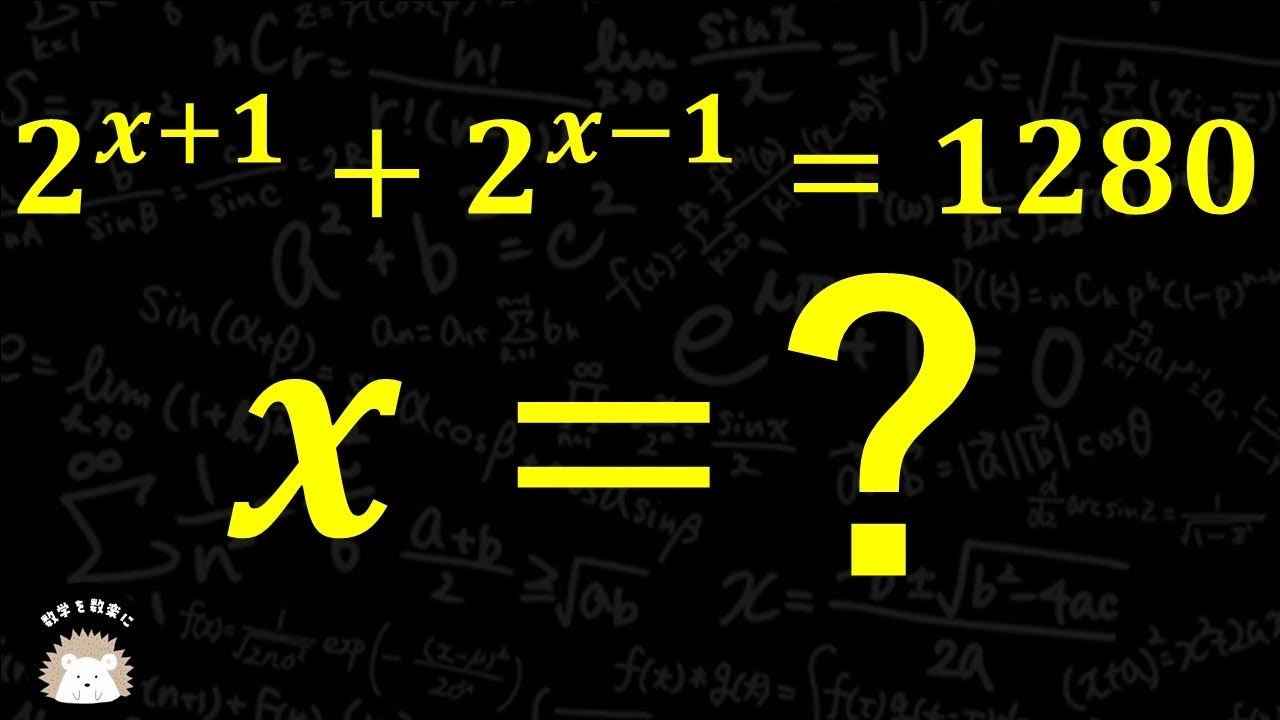
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$2^{x+1}+2^{x-1} = 1280$
x=?
この動画を見る
$2^{x+1}+2^{x-1} = 1280$
x=?
2022早稲田大(社)整式の剰余

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
整式P(x)をx-1で割ると1あまり,$ (x+1)^2 $で割ると3x+2あまる.
P(x)を次の式で割ったあまりは?
(1)$ x+1$ (2)$(x+1)(x-1)$ (3)$(x-1)(x+1)^2$
2022早稲田大過去問
この動画を見る
整式P(x)をx-1で割ると1あまり,$ (x+1)^2 $で割ると3x+2あまる.
P(x)を次の式で割ったあまりは?
(1)$ x+1$ (2)$(x+1)(x-1)$ (3)$(x-1)(x+1)^2$
2022早稲田大過去問
解けるように作られた問題

単元:
#数Ⅱ#複素数と方程式#微分法と積分法#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^3-x-1=0 $の実数解を$ \alpha $とするとき,
$ \sqrt[3]{3\alpha^2-4\alpha}+\sqrt[3]{3\alpha^2+4\alpha+2}$の値を求めよ.
この動画を見る
$ x^3-x-1=0 $の実数解を$ \alpha $とするとき,
$ \sqrt[3]{3\alpha^2-4\alpha}+\sqrt[3]{3\alpha^2+4\alpha+2}$の値を求めよ.
指数方程式
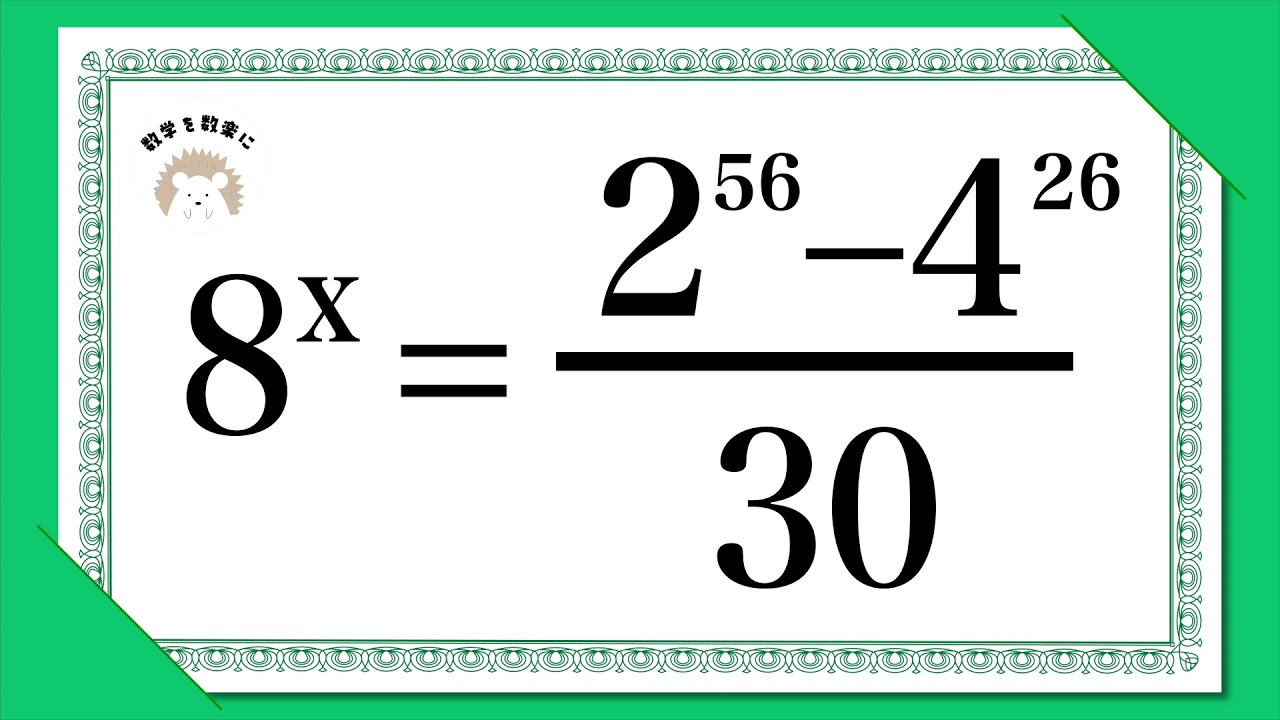
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$8^x=\frac{2^{56}-4^{26}}{30}$のときx=?
この動画を見る
$8^x=\frac{2^{56}-4^{26}}{30}$のときx=?
福田の数学〜慶應義塾大学2022年薬学部第1問(5)〜対数方程式と解の個数

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(5)$x\neq 2$である正の実数xに対して、方程式
$\log_{10}x+\log_{100}x^2-\log_{0.1}|x-2|=\log_{10}a (a \gt 0)$
がある。
$(\textrm{i})x=6$のとき、aの値は$\boxed{\ \ ク\ \ }$である。
$(\textrm{ii})$この方程式が異なる3個の実数解をもつとき、aの値の範囲は$\boxed{\ \ ケ\ \ }$である。
2022慶應義塾大学薬学部過去問
この動画を見る
(5)$x\neq 2$である正の実数xに対して、方程式
$\log_{10}x+\log_{100}x^2-\log_{0.1}|x-2|=\log_{10}a (a \gt 0)$
がある。
$(\textrm{i})x=6$のとき、aの値は$\boxed{\ \ ク\ \ }$である。
$(\textrm{ii})$この方程式が異なる3個の実数解をもつとき、aの値の範囲は$\boxed{\ \ ケ\ \ }$である。
2022慶應義塾大学薬学部過去問
大阪大の問題の背景 特に文系の人見てください

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\cos\dfrac{2}{7}\pi,\cos\dfrac{4}{7}\pi,\cos\dfrac{6}{7}\pi$を解にもつ3次方程式
$x^3+ax^2+bx+c=0$を求めよ.
ただし,$z^7=1$とする.
2022大阪大過去問
この動画を見る
$\cos\dfrac{2}{7}\pi,\cos\dfrac{4}{7}\pi,\cos\dfrac{6}{7}\pi$を解にもつ3次方程式
$x^3+ax^2+bx+c=0$を求めよ.
ただし,$z^7=1$とする.
2022大阪大過去問
福田の数学〜慶應義塾大学2022年薬学部第1問(2)〜高次方程式の解

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(2)a,bは実数とする。xの3次方程式$x^3+(a+4)x^2-3(a+4)x+b=0$
の実数解が$x=3$のみであるとき、aの値の範囲は$\boxed{\ \ エ\ \ }$である。
2022慶應義塾大学薬学部過去問
この動画を見る
(2)a,bは実数とする。xの3次方程式$x^3+(a+4)x^2-3(a+4)x+b=0$
の実数解が$x=3$のみであるとき、aの値の範囲は$\boxed{\ \ エ\ \ }$である。
2022慶應義塾大学薬学部過去問
指数の方程式 (高校範囲)
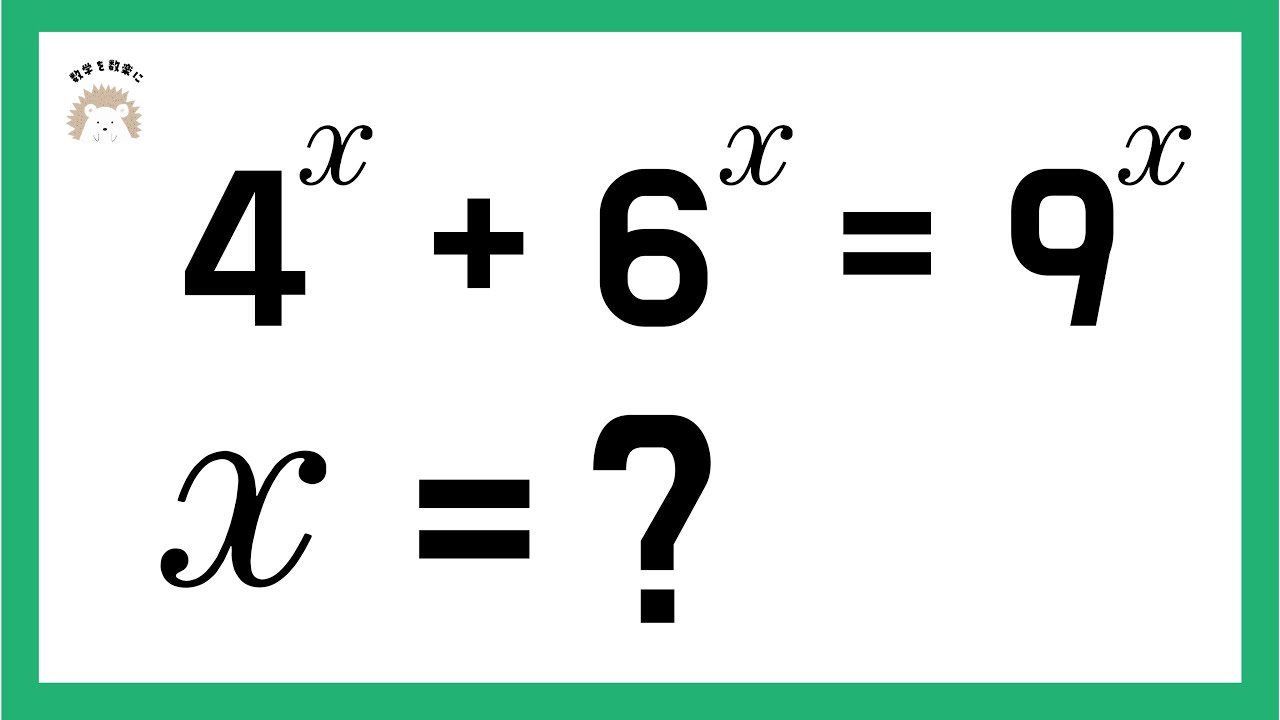
いい問題(多分)

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
a+bcd=10 \\
b+cda=10\\
c+dab=10 \\
d+abc=10 \\
\end{array}
\right.
\end{eqnarray}$
$(a,b,c,d)$の組を求めよ.
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
a+bcd=10 \\
b+cda=10\\
c+dab=10 \\
d+abc=10 \\
\end{array}
\right.
\end{eqnarray}$
$(a,b,c,d)$の組を求めよ.
三角関数。指数方程式 簡単だよ
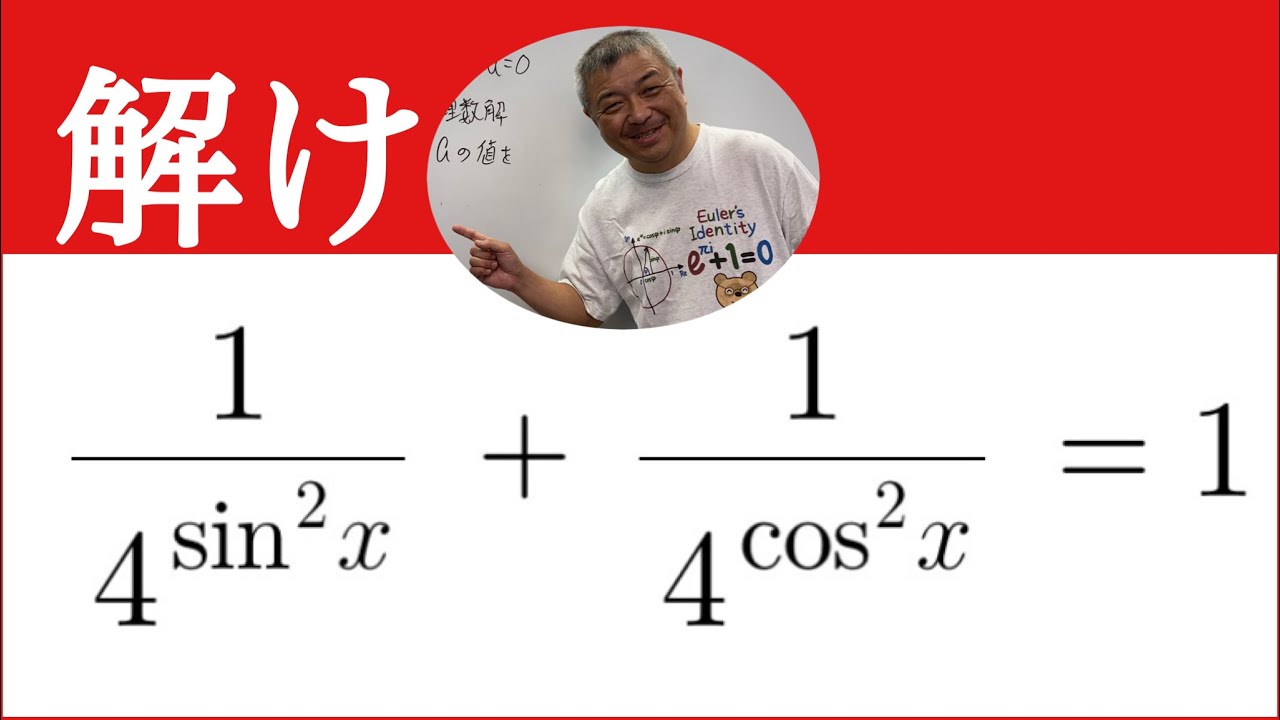
単元:
#数Ⅱ#複素数と方程式#三角関数#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\dfrac{1}{4^{\sin^2x}}+\dfrac{1}{4^{\cos^2x}}=1$
この動画を見る
これを解け.
$\dfrac{1}{4^{\sin^2x}}+\dfrac{1}{4^{\cos^2x}}=1$
ただの三次方程式

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$x(x+1)^2+(x+1)x^2=840$
この動画を見る
実数解を求めよ.
$x(x+1)^2+(x+1)x^2=840$
4次方程式 実数解4つ

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\displaystyle \frac{x-8}{x-1}+\displaystyle \frac{x-7}{x-2}+\displaystyle \frac{x-6}{x-3}+\displaystyle \frac{x-5}{x-4}=-4$
実数解4つ求めよ
この動画を見る
$\displaystyle \frac{x-8}{x-1}+\displaystyle \frac{x-7}{x-2}+\displaystyle \frac{x-6}{x-3}+\displaystyle \frac{x-5}{x-4}=-4$
実数解4つ求めよ
ただの指数・対数方程式

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$5^{\log_{ 10 }x} -50+x^{\log_{ 10 }5}=0$
実数解を求めよ。
この動画を見る
$5^{\log_{ 10 }x} -50+x^{\log_{ 10 }5}=0$
実数解を求めよ。
指数方程式 解はアレだけじゃないよ

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$5^x・16^{\frac{x-1}{x}}=100$
この動画を見る
これを解け.
$5^x・16^{\frac{x-1}{x}}=100$
4次方程式の解の立方の和

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(x+1)(x+2)(x+3)(x+4)=1$の4つの解を$\alpha,\beta,\gamma,\delta$とする.
$\alpha^3+\beta^3+\gamma^3+\delta^3$の値を求めよ.
この動画を見る
$(x+1)(x+2)(x+3)(x+4)=1$の4つの解を$\alpha,\beta,\gamma,\delta$とする.
$\alpha^3+\beta^3+\gamma^3+\delta^3$の値を求めよ.
大学入試問題#60 広島工業大学(2021) 因数定理

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$x^{2019}+x^{2020}$を$x^2+x+1$で割った余りを求めよ。
出典:2021年広島工業大学 入試問題
この動画を見る
$x^{2019}+x^{2020}$を$x^2+x+1$で割った余りを求めよ。
出典:2021年広島工業大学 入試問題
どう解くか?だ。

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
方程式を解け
$0.2(0.1x -0.8) = \frac{4x+7}{50}$
法政大学
この動画を見る
方程式を解け
$0.2(0.1x -0.8) = \frac{4x+7}{50}$
法政大学
【因数定理】因数定理の使い方と原理を解説しました!〔数学、高校数学〕

#45 数検1級1次 過去問 複雑な方程式

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$3x^2-12x+8=\displaystyle \frac{i\sqrt{ x-1 }}{\sqrt{ 3 }}$を満たす実数解$x$を求めよ
この動画を見る
$3x^2-12x+8=\displaystyle \frac{i\sqrt{ x-1 }}{\sqrt{ 3 }}$を満たす実数解$x$を求めよ
4次方程式