 図形と方程式
図形と方程式
 図形と方程式
図形と方程式
【数Ⅱ】中高一貫校問題集3(数式・関数編)376:図形と式:円と直線:定点通過の解法! x²+y²-2mx-2m-2=0がmに関係なく通る点は?

単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
教材:
#TK数学#TK数学問題集3(数式・関数編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
4S数学Ⅱ・図形と方程式・問題379
x²+y²-2mx-2m-2=0がmに関係なく通る点を求めよ。
この動画を見る
4S数学Ⅱ・図形と方程式・問題379
x²+y²-2mx-2m-2=0がmに関係なく通る点を求めよ。
【数Ⅱ】中高一貫校用問題集(数式・関数編)図形と式:円と直線:定点通過の解法! x²+y²-2mx-2m-2=0がmに関係なく通る点は?

単元:
#数Ⅱ#図形と方程式#数学(高校生)
教材:
#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$x^2+y^2-2mx-2m-2=0$がmに関係なく通る点は?
この動画を見る
$x^2+y^2-2mx-2m-2=0$がmに関係なく通る点は?
【数Ⅱ】図形と方程式:奇跡的な軌跡の解法③ PだけじゃないてQも動く!?

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
教材:
#高校ゼミスタンダード#高校ゼミスタンダード数Ⅱ#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
点Qがx²+y²=16上を動くとき、点A(8,0)と点Qを結ぶ線分AQの中点Pの軌跡を求めよ。
この動画を見る
点Qがx²+y²=16上を動くとき、点A(8,0)と点Qを結ぶ線分AQの中点Pの軌跡を求めよ。
【数Ⅱ】図形と方程式:奇跡的な軌跡の解法② 2点からの距離の比が2:1の軌跡は?アポロニウスの円

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
教材:
#高校ゼミスタンダード#高校ゼミスタンダード数Ⅱ#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
A(-2,0),B(1,0)からの距離の比が2:1である点Pの軌跡を求めよ。
この動画を見る
A(-2,0),B(1,0)からの距離の比が2:1である点Pの軌跡を求めよ。
【数Ⅱ】図形と方程式:奇跡的な軌跡の解法① 2点から等距離となる軌跡は??

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
教材:
#高校ゼミスタンダード#高校ゼミスタンダード数Ⅱ#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
A(-2,3),B(4,-1)から等距離にある点Pの軌跡を求めよ。
この動画を見る
A(-2,3),B(4,-1)から等距離にある点Pの軌跡を求めよ。
【高校数学】円と直線の交点【連立方程式の同値変形】

単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
指導講師:
受験メモ山本
問題文全文(内容文):
x²+y²=4
y=3x-2
交点を求めよ
連立をするとき余計な解が出てきたことはありませんか?
なぜそういうことがおきるかを解説します!
この動画を見る
x²+y²=4
y=3x-2
交点を求めよ
連立をするとき余計な解が出てきたことはありませんか?
なぜそういうことがおきるかを解説します!
【数学Ⅱ】図形と方程式 領域の難問を打破する!!

単元:
#数Ⅱ#図形と方程式#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【数学Ⅱ】図形と方程式 領域の難問解説動画です
-----------------
直線$2kx+y+k^=0…①$における$k$がすべての実数を満たしながら動くとき、直線①が通る領域を図示せよ。
この動画を見る
【数学Ⅱ】図形と方程式 領域の難問解説動画です
-----------------
直線$2kx+y+k^=0…①$における$k$がすべての実数を満たしながら動くとき、直線①が通る領域を図示せよ。
15奈良県教員採用試験(数学:高校3番 軌跡)

単元:
#数Ⅱ#図形と方程式#軌跡と領域#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
3⃣ P(0,a),$y=\frac{x^2}{a}$上の点をQ,
PQは最小値をとる(a≠0)
(1)Qの座標を求めよ。
(2)Qの軌跡を求めよ。
この動画を見る
3⃣ P(0,a),$y=\frac{x^2}{a}$上の点をQ,
PQは最小値をとる(a≠0)
(1)Qの座標を求めよ。
(2)Qの軌跡を求めよ。
19大阪府教員採用試験(数学:2-6番 軌跡)

単元:
#数Ⅱ#図形と方程式#軌跡と領域#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
2⃣-(6)
$y=3x+1,y=-\frac{1}{3}x+2$のなす角の二等分線の直線の方程式を求めよ。
この動画を見る
2⃣-(6)
$y=3x+1,y=-\frac{1}{3}x+2$のなす角の二等分線の直線の方程式を求めよ。
19兵庫県教員採用試験(数学:1-3番 命題)
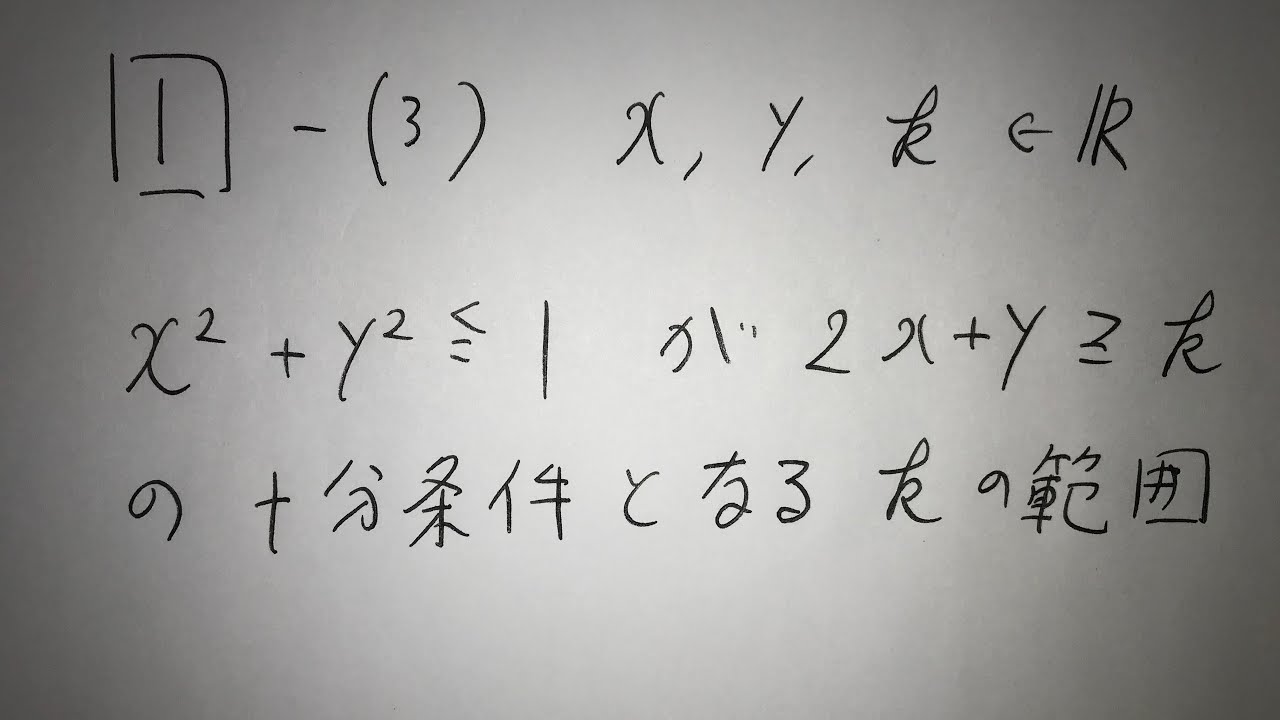
単元:
#数Ⅰ#数Ⅱ#数と式#集合と命題(集合・命題と条件・背理法)#図形と方程式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(3)
$x,y,k \in \mathbb{ R }$
$x^2+y^2 \leqq 1$が$2x+y \geqq k$の十分条件となるkの範囲
この動画を見る
1⃣-(3)
$x,y,k \in \mathbb{ R }$
$x^2+y^2 \leqq 1$が$2x+y \geqq k$の十分条件となるkの範囲
20年5月数検準1級1次試験(楕円)

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#図形と方程式#円と方程式#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{6}$
2点$A(0,-3),B(0,1)$から距離の和が6である楕円の方程式を求めよ.
20年5月数検準1級1次試験(楕円)過去問
この動画を見る
$\boxed{6}$
2点$A(0,-3),B(0,1)$から距離の和が6である楕円の方程式を求めよ.
20年5月数検準1級1次試験(楕円)過去問
20年5月数学検定準1級1次試験(円の方程式)

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#図形と方程式#円と方程式#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{2}$
円$C_1$の中心は$(-6,2)$で直線$\ell:3x-4y+1=0$に接する.
このとき円$C_1$が$x$軸から切り取る線分の長さ$\ell^1$を求めよ.
20年5月数学検定準1級1次試験(円の方程式)過去問
この動画を見る
$\boxed{2}$
円$C_1$の中心は$(-6,2)$で直線$\ell:3x-4y+1=0$に接する.
このとき円$C_1$が$x$軸から切り取る線分の長さ$\ell^1$を求めよ.
20年5月数学検定準1級1次試験(円の方程式)過去問
20年5月数学検定準1級1次試験(円の方程式)

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#図形と方程式#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
2⃣円$C_1$の中心は(-6,2)で直線$l:3x-4y+1=0$に接する。
このとき円$C_1$がx軸から切り取る線分の長さl'を求めよ。
この動画を見る
2⃣円$C_1$の中心は(-6,2)で直線$l:3x-4y+1=0$に接する。
このとき円$C_1$がx軸から切り取る線分の長さl'を求めよ。
【数学II】軌跡がイマイチ掴めない人が「見えた!」を実感するための動画【軌跡と領域】

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【数学II】軌跡と領域について解説動画です
-----------------
①2点、A(1,0) B(6,0)からの距離の比が2:3である点Pの軌跡を求めよ。
②点Qが円$x^2+y^2=4$の同上を動くとき、A(8,0)と点Qとを結ぶ線分AQの中点Pの軌跡を求めよ。
この動画を見る
【数学II】軌跡と領域について解説動画です
-----------------
①2点、A(1,0) B(6,0)からの距離の比が2:3である点Pの軌跡を求めよ。
②点Qが円$x^2+y^2=4$の同上を動くとき、A(8,0)と点Qとを結ぶ線分AQの中点Pの軌跡を求めよ。
大阪大 点と直線の距離 公式証明

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(x_0,y_0)$と$ax+by+c=0$の距離が$\dfrac{\vert ax_0+by_0+c \vert}{\sqrt{a^2+b^2}}$であることを証明せよ.
大阪大過去問
この動画を見る
$(x_0,y_0)$と$ax+by+c=0$の距離が$\dfrac{\vert ax_0+by_0+c \vert}{\sqrt{a^2+b^2}}$であることを証明せよ.
大阪大過去問
信州大 絶対値のついた2次方程式 相違4実根

単元:
#数Ⅰ#数Ⅱ#数と式#2次関数#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#2次関数とグラフ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^2+ax+b=|x|$が相異なる4個の実数解をもつような$(a,b)$の存在する領域を図示せよ
出典:2006年信州大学 過去問
この動画を見る
$x^2+ax+b=|x|$が相異なる4個の実数解をもつような$(a,b)$の存在する領域を図示せよ
出典:2006年信州大学 過去問
山口東京理科大 円の方程式 軌跡

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
点$(s,t)$が$x^2+y^2=\displaystyle \frac{1}{2}$の上を動くとき、$(s+t,st)$を座標とする点の軌跡を図示せよ
出典:山口東京理科大学 過去問
この動画を見る
点$(s,t)$が$x^2+y^2=\displaystyle \frac{1}{2}$の上を動くとき、$(s+t,st)$を座標とする点の軌跡を図示せよ
出典:山口東京理科大学 過去問
2020年東大 ヨビノりたくみさん解説

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a \gt 0,b \gt 0$
$C:y=x^3-3ax^2+b$
条件1 $C$は$x$軸に接する
条件2 $x$軸と$C$で囲まれた領域(除く境界)に格子点1つのみ
$b$を$a$で表せ
$a$の範囲を求めよ
出典:2020年東京大学 過去問
この動画を見る
$a \gt 0,b \gt 0$
$C:y=x^3-3ax^2+b$
条件1 $C$は$x$軸に接する
条件2 $x$軸と$C$で囲まれた領域(除く境界)に格子点1つのみ
$b$を$a$で表せ
$a$の範囲を求めよ
出典:2020年東京大学 過去問
最速。2020年センター試験解説。福田の入試問題解説〜2020年センター試験IIB第1問〜三角関数、指数対数関数、図形と方程式

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#図形と方程式#三角関数#指数関数と対数関数#指数関数#センター試験・共通テスト関連#センター試験#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large第1問}$
[1](1)$0 \leqq \theta \lt 2\pi$のとき
$\sin\theta \gt \sqrt3\cos\left(\theta-\displaystyle \frac{\pi}{3}\right)$ $\cdots$①
となる$\theta$の値の範囲を求めよう。
加法定理を用いると
$\sqrt3\cos\left(\theta-\frac{\pi}{3}\right)=$$\displaystyle\frac{\sqrt{\boxed{\ \ ア\ \ }}}{\boxed{\ \ イ\ \ }}\cos\theta+\displaystyle\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ イ\ \ }}\sin\theta$
である。よって、三角関数の合成を用いると、①は
$\sin\left(\theta+\displaystyle\frac{\pi}{\boxed{\ \ エ\ \ }}\right) \lt 0$
と変形できる。したがって、求める範囲は
$\displaystyle\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}\pi \lt \theta \lt \frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ ク\ \ }}\pi$
である。
(2)$0 \leqq \theta \leqq \displaystyle\frac{\pi}{2}$とし、$k$を実数とする。$\sin\theta$と$\cos\theta$は$x$の2次方程式
$25x^2-35x+k=0$の解であるとする。このとき、解と係数の関係に
より$\sin\theta+\cos\theta$と$\sin\theta\cos\theta$の値を考えれば、$k=\boxed{\ \ ケコ\ \ }$で
あることがわかる。
さらに、$\theta$が$\sin\theta \geqq \cos\theta$を満たすとすると、$\sin\theta=\displaystyle\frac{\boxed{\ \ サ\ \ }}{\boxed{\ \ シ\ \ }},$
$\cos\theta=\displaystyle\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}$である。このとき、$\theta$は$\boxed{\ \ ソ\ \ }$を満たす。
$\boxed{\ \ ソ\ \ }$に当てはまるものを、次の⓪~⑤のうちから一つ選べ。
⓪$0 \leqq \theta \lt \displaystyle\frac{\pi}{12}$
①$\displaystyle\frac{\pi}{12} \leqq \theta \lt \displaystyle\frac{\pi}{6}$
②$\displaystyle\frac{\pi}{6} \leqq \theta \lt \displaystyle\frac{\pi}{4}$
③$\displaystyle\frac{\pi}{4} \leqq \theta \lt \displaystyle\frac{\pi}{3}$
④$\displaystyle\frac{\pi}{3} \leqq \theta \lt \displaystyle\frac{5}{12}\pi$
⑤$\displaystyle\frac{5}{12}\pi \leqq \theta \leqq \displaystyle\frac{\pi}{2}$
[2](1)$t$は正の実数であり、$t^{\displaystyle\frac{1}{3}}-t^{-\displaystyle\frac{1}{3}}=-3$を満たすとする。このとき
$t^{\displaystyle\frac{2}{3}}+t^{-\displaystyle\frac{2}{3}}=\boxed{\ \ タチ\ \ }$
である。さらに
$t^{\frac{1}{2}}+t^{-\frac{1}{2}}=\sqrt{\boxed{\ \ ツテ\ \ }}, $$t-t^{-1}=\boxed{\ \ トナニ\ \ }$
である。
(2)$x,y$は正の実数とする。連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
\log_3(x\sqrt y) \leqq 5 \cdots②\\
\log_{81}\frac{y}{x^3} \leqq 1 \cdots③
\end{array}
\right.
\end{eqnarray}$
について考える。
$X=\log_3x,$ $Y=\log_3y$とおくと、②は
$\boxed{\ \ ヌ\ \ }\ X+Y \leqq \boxed{\ \ ネノ\ \ }$ $\cdots$④
と変形でき、③は
$\boxed{\ \ ハ\ \ }\ X-Y \geqq \boxed{\ \ ヒフ\ \ }$ $\cdots$⑤
と変形できる。
$X,Y$が④と⑤を満たすとき、$Y$の取り得る最大の整数の値は
$\boxed{\ \ ヘ\ \ }$である。また、$x,y$が②,③と$\log_3y=\boxed{\ \ ヘ\ \ }$を同時に
満たすとき、xの取り得る最大の整数の値は$\boxed{\ \ ホ\ \ }$である。
2020センター試験過去問
この動画を見る
${\large第1問}$
[1](1)$0 \leqq \theta \lt 2\pi$のとき
$\sin\theta \gt \sqrt3\cos\left(\theta-\displaystyle \frac{\pi}{3}\right)$ $\cdots$①
となる$\theta$の値の範囲を求めよう。
加法定理を用いると
$\sqrt3\cos\left(\theta-\frac{\pi}{3}\right)=$$\displaystyle\frac{\sqrt{\boxed{\ \ ア\ \ }}}{\boxed{\ \ イ\ \ }}\cos\theta+\displaystyle\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ イ\ \ }}\sin\theta$
である。よって、三角関数の合成を用いると、①は
$\sin\left(\theta+\displaystyle\frac{\pi}{\boxed{\ \ エ\ \ }}\right) \lt 0$
と変形できる。したがって、求める範囲は
$\displaystyle\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}\pi \lt \theta \lt \frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ ク\ \ }}\pi$
である。
(2)$0 \leqq \theta \leqq \displaystyle\frac{\pi}{2}$とし、$k$を実数とする。$\sin\theta$と$\cos\theta$は$x$の2次方程式
$25x^2-35x+k=0$の解であるとする。このとき、解と係数の関係に
より$\sin\theta+\cos\theta$と$\sin\theta\cos\theta$の値を考えれば、$k=\boxed{\ \ ケコ\ \ }$で
あることがわかる。
さらに、$\theta$が$\sin\theta \geqq \cos\theta$を満たすとすると、$\sin\theta=\displaystyle\frac{\boxed{\ \ サ\ \ }}{\boxed{\ \ シ\ \ }},$
$\cos\theta=\displaystyle\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}$である。このとき、$\theta$は$\boxed{\ \ ソ\ \ }$を満たす。
$\boxed{\ \ ソ\ \ }$に当てはまるものを、次の⓪~⑤のうちから一つ選べ。
⓪$0 \leqq \theta \lt \displaystyle\frac{\pi}{12}$
①$\displaystyle\frac{\pi}{12} \leqq \theta \lt \displaystyle\frac{\pi}{6}$
②$\displaystyle\frac{\pi}{6} \leqq \theta \lt \displaystyle\frac{\pi}{4}$
③$\displaystyle\frac{\pi}{4} \leqq \theta \lt \displaystyle\frac{\pi}{3}$
④$\displaystyle\frac{\pi}{3} \leqq \theta \lt \displaystyle\frac{5}{12}\pi$
⑤$\displaystyle\frac{5}{12}\pi \leqq \theta \leqq \displaystyle\frac{\pi}{2}$
[2](1)$t$は正の実数であり、$t^{\displaystyle\frac{1}{3}}-t^{-\displaystyle\frac{1}{3}}=-3$を満たすとする。このとき
$t^{\displaystyle\frac{2}{3}}+t^{-\displaystyle\frac{2}{3}}=\boxed{\ \ タチ\ \ }$
である。さらに
$t^{\frac{1}{2}}+t^{-\frac{1}{2}}=\sqrt{\boxed{\ \ ツテ\ \ }}, $$t-t^{-1}=\boxed{\ \ トナニ\ \ }$
である。
(2)$x,y$は正の実数とする。連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
\log_3(x\sqrt y) \leqq 5 \cdots②\\
\log_{81}\frac{y}{x^3} \leqq 1 \cdots③
\end{array}
\right.
\end{eqnarray}$
について考える。
$X=\log_3x,$ $Y=\log_3y$とおくと、②は
$\boxed{\ \ ヌ\ \ }\ X+Y \leqq \boxed{\ \ ネノ\ \ }$ $\cdots$④
と変形でき、③は
$\boxed{\ \ ハ\ \ }\ X-Y \geqq \boxed{\ \ ヒフ\ \ }$ $\cdots$⑤
と変形できる。
$X,Y$が④と⑤を満たすとき、$Y$の取り得る最大の整数の値は
$\boxed{\ \ ヘ\ \ }$である。また、$x,y$が②,③と$\log_3y=\boxed{\ \ ヘ\ \ }$を同時に
満たすとき、xの取り得る最大の整数の値は$\boxed{\ \ ホ\ \ }$である。
2020センター試験過去問
【数学】点と直線の距離 公式の覚え方・導出

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【数学】点と直線の距離 公式の覚え方・導出の解説動画です
この動画を見る
【数学】点と直線の距離 公式の覚え方・導出の解説動画です
東邦(薬)放物線内の格子点の個数

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#学校別大学入試過去問解説(数学)#数学(高校生)#東邦大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$自然数
$y=x^2-3x+3n+2$と$y=3nx$とで囲まれた図形の内部(境界線を含む)の格子点の数を求めよ
出典:1994年東邦大学 過去問
この動画を見る
$n$自然数
$y=x^2-3x+3n+2$と$y=3nx$とで囲まれた図形の内部(境界線を含む)の格子点の数を求めよ
出典:1994年東邦大学 過去問
千葉大 三次関数と円 東大数学科卒の杉山さん

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#指数関数と対数関数#円と方程式#指数関数#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
曲線$y=x^3-x$と円$(x-a^2)+(y-a)^2=2a^2$の共有点が2つ
共有点の$x$座標は?
$(a \gt 0)$
出典:千葉大学 過去問
この動画を見る
曲線$y=x^3-x$と円$(x-a^2)+(y-a)^2=2a^2$の共有点が2つ
共有点の$x$座標は?
$(a \gt 0)$
出典:千葉大学 過去問
数学諦めて7年!私文数学超苦手女子が2点を通る直線の式が暗算数秒で出せるのか?

名古屋市立(医) 関数 微分

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#軌跡と領域#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋市立大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a \gt 0$
$C_{a}:y=x(x-a)(x-2a)^2$
(1)
$(1,-1)$を通る$C_{a}$がただ1つであることを示せ
(2)
$(p,q)$を通る$C_{a}$がただ1つであるような$(p,q)$の範囲を図示せよ。
ただし$p \gt 0$
出典:1995年名古屋市立大学 医学部 過去問
この動画を見る
$a \gt 0$
$C_{a}:y=x(x-a)(x-2a)^2$
(1)
$(1,-1)$を通る$C_{a}$がただ1つであることを示せ
(2)
$(p,q)$を通る$C_{a}$がただ1つであるような$(p,q)$の範囲を図示せよ。
ただし$p \gt 0$
出典:1995年名古屋市立大学 医学部 過去問
東北大 円の方程式 領域

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
領域$D$は次の連立不等式
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2-6x+y^2+5 \leqq 0 \\
x+y \leqq 5
\end{array}
\right.
\end{eqnarray}$
$x^2+y^2-2ax-2y+a^2=0$が$D$を通るような$a$の最大値と最小値を求めよ
出典:2006年東北大学 過去問
この動画を見る
領域$D$は次の連立不等式
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2-6x+y^2+5 \leqq 0 \\
x+y \leqq 5
\end{array}
\right.
\end{eqnarray}$
$x^2+y^2-2ax-2y+a^2=0$が$D$を通るような$a$の最大値と最小値を求めよ
出典:2006年東北大学 過去問
【数Ⅱ】図形と方程式:点と直線の距離(最小値):平面上の2点をA(1,1),B(2,3)とする。点Pが放物線y=x²+4x+10上を動くとき△PABの面積の最小値を求めよ。

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
平面上の2点をA(1,1),B(2,3)とする。点Pが放物線$y=x^2+4x+10$上を動くとき△PABの面積の最小値を求めよ。
この動画を見る
平面上の2点をA(1,1),B(2,3)とする。点Pが放物線$y=x^2+4x+10$上を動くとき△PABの面積の最小値を求めよ。
信州大(医)多項式

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#円と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数$x,y$が
$2^4-2x^3y-3x^3+3x^2y-xy+y^2+x-y=0$を満たすとき、$x^2+y^2-4y+4$の最小値は?
出典:信州大学医学部 過去問
この動画を見る
実数$x,y$が
$2^4-2x^3y-3x^3+3x^2y-xy+y^2+x-y=0$を満たすとき、$x^2+y^2-4y+4$の最小値は?
出典:信州大学医学部 過去問
【マイナス】の捉え方は【世界】を変える

単元:
#数Ⅱ#物理#図形と方程式#点と直線#円と方程式#力学#数学(高校生)#理科(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
相対速度 円の方程式、直線の方程式まとめ動画です
この動画を見る
相対速度 円の方程式、直線の方程式まとめ動画です
自治医科大 円の方程式 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#円と方程式#学校別大学入試過去問解説(数学)#数学(高校生)#自治医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
円:$(x+5)^2+y^2=89$と直線$x+y=8$の交点を通り、$x=-3$に接する円の半径を求めよ
出典:2008年自治医科大学 過去問
この動画を見る
円:$(x+5)^2+y^2=89$と直線$x+y=8$の交点を通り、$x=-3$に接する円の半径を求めよ
出典:2008年自治医科大学 過去問
東工大 積分 放物線と直線 面積最小値 高校数学 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#点と直線#学校別大学入試過去問解説(数学)#不定積分・定積分#東京工業大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$y=-2x^2+x+1$上の1点における接線と$y=x^2$とによって囲まれる部分の面積の最小値を求めよ。
出典:1967年 東京工業大学 過去問
この動画を見る
$y=-2x^2+x+1$上の1点における接線と$y=x^2$とによって囲まれる部分の面積の最小値を求めよ。
出典:1967年 東京工業大学 過去問
